Classification of surfaces in a pseudo-sphere with 2-type pseudo-spherical Gauss map
Funding Information: Istanbul Teknik Üniversitesi, Grant Number: 38386.
Abstract
In this article, we study submanifolds in a pseudo-sphere with 2-type pseudo-spherical Gauss map. We give a characterization theorem for Lorentzian surfaces in the pseudo-sphere  with zero mean curvature vector in
with zero mean curvature vector in  and 2-type pseudo-spherical Gauss map. We also prove that non-totally umbilical proper pseudo-Riemannian hypersurfaces in a pseudo-sphere
and 2-type pseudo-spherical Gauss map. We also prove that non-totally umbilical proper pseudo-Riemannian hypersurfaces in a pseudo-sphere 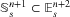 with non-zero constant mean curvature has 2-type pseudo-spherical Gauss map if and only if it has constant scalar curvature. Then, for
with non-zero constant mean curvature has 2-type pseudo-spherical Gauss map if and only if it has constant scalar curvature. Then, for  we obtain the classification of surfaces in
we obtain the classification of surfaces in  with 2-type pseudo-spherical Gauss map. Finally, we give an example of surface with null 2-type pseudo-spherical Gauss map which does not appear in Riemannian case, and we give a characterization theorem for Lorentzian surfaces in
with 2-type pseudo-spherical Gauss map. Finally, we give an example of surface with null 2-type pseudo-spherical Gauss map which does not appear in Riemannian case, and we give a characterization theorem for Lorentzian surfaces in  with null 2-type pseudo-spherical Gauss map.
with null 2-type pseudo-spherical Gauss map.



 with constant Gaussian and normal curvatures
with constant Gaussian and normal curvatures

