ORIGINAL PAPER
On Cartan's theorem for linear operators
Wei Chen,
Qi Han,
Jingjing Qu,
Wei Chen
Department of Mathematics, Shandong University, Jinan, Shandong 250100, P. R. China
Search for more papers by this authorQi Han
Department of Mathematics, Texas A&M University at San Antonio, San Antonio, Texas 78224, USA
Search for more papers by this authorCorresponding Author
Jingjing Qu
Yau Mathematical Sciences Center, Tsinghua University, Beijing 100084, P. R. China
Corresponding author: [email protected]Search for more papers by this authorWei Chen,
Qi Han,
Jingjing Qu,
Wei Chen
Department of Mathematics, Shandong University, Jinan, Shandong 250100, P. R. China
Search for more papers by this authorQi Han
Department of Mathematics, Texas A&M University at San Antonio, San Antonio, Texas 78224, USA
Search for more papers by this authorCorresponding Author
Jingjing Qu
Yau Mathematical Sciences Center, Tsinghua University, Beijing 100084, P. R. China
Corresponding author: [email protected]Search for more papers by this authorFirst published: 08 February 2017
Abstract
In this paper, we describe a second main theorem of holomorphic curves 
in 
, of hyper-order strictly less than 1, that involves a general linear operator 
. As an application, we derive a truncated second main theorem of degenerate holomorphic curves of hyper-order strictly less than 1 using Nochka weights.
References
- 1A. Biancofiore and W. Stoll, Another proof of the lemma of the logarithmic derivative in several complex variables, Ann. of Math. Stud. 100, 29–45 (1981).
- 2H. Cartan, Sur les zeros des combinaisons linéaires de p fonctions holomorphes données, Mathematica (Cluj) 7, 5–31 (1933).
- 3W. Chen, P. Hu, and Y. Zhang, On solutions to some nonlinear difference and differential equations, J. Korean Math. Soc. 53, 835–846 (2016).
- 4H. Fujimoto, Value Distribution Theory of the Gauss Map of Minimal Surfaces in
(Friedr. Vieweg & Sohn, Braunschweig, 1993).
10.1007/978-3-322-80271-2 Google Scholar - 5G. G. Gundersen and W. K. Hayman, The strength of Cartan's version of Nevanlinna theory, Bull. London Math. Soc. 36, 433–454 (2004).
- 6R. Halburd and R. Korhonen, Nevanlinna theory for the difference operator, Ann. Acad. Sci. Fenn. Math. 31, 463–478 (2006).
- 7R. Halburd and R. Korhonen, Value distribution and linear operators, Proc. Edinb. Math. Soc. 57, 493–504 (2014).
- 8R. Halburd, R. Korhonen, and K. Tohge, Holomorphic curves with shift-invariant hyperplane preimages, Trans. Amer. Math. Soc. 366, 4267–4298 (2014).
- 9Q. Han, A defect relation for meromorphic maps on generalized p-parabolic manifolds intersecting hypersurfaces in complex projective algebraic varieties, Proc. Edinb. Math. Soc. 56, 551–574 (2013).
- 10Q. Han, A hypersurface defect relation for a family of meromorphic maps on a generalized p-parabolic manifold, Colloq. Math. 139, 95–110 (2015).
- 11Q. Han and F. Lü, On the equation
, Submitted.
- 12W. K. Hayman, Meromorphic Functions (Clarendon Press, Oxford, 1964).
- 13J. Heittokangas, R. Korhonen, I. Laine, J. Rieppo, and K. Tohge, Complex difference equations of Malmquist type, Comput. Methods Funct. Theory 1, 27–39 (2001).
10.1007/BF03320974 Google Scholar
- 14A. Hinkkanen, A sharp form of Nevanlinna's second fundamental theorem, Invent. Math. 108, 549–574 (1992).
- 15R. Korhonen, A difference Picard theorem for meromorphic functions of several variables, Comput. Methods Funct. Theory 12, 343–361 (2012).
- 16R. Korhonen, N. Li, and K. Tohge, Difference analogue of Cartan's second main theorem for slowly moving periodic targets, Ann. Acad. Sci. Fenn. Math. 41, 523–549 (2016).
- 17B. Q. Li, A logarithmic derivative lemma in several complex variables and its applications, Trans. Amer. Math. Soc. 363, 6257–6267 (2011).
- 18F. Lü, Q. Han, and W. Lü, On unicity of meromorphic solutions to difference equations of Malmquist type, Bull. Aust. Math. Soc. 93, 92–98 (2016).
- 19F. Lü and Q. Han, On the Fermat-type equation
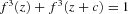, Aequationes Math. 91, 129–136 (2017).
- 20E. I. Nochka, On the theory of meromorphic curves, Soviet Math. Dokl. 27, 377–381 (1983).
- 21E. I. Nochka, A lemma on weights, Math. Notes 78, 105–113 (2005).
- 22J. Noguchi, A note on entire pseudo-holomorphic curves and the proof of Cartan–Nochka's theorem, Kodai Math. J. 28, 336–346 (2005).
10.2996/kmj/1123767014 Google Scholar
- 23J. Rieppo, Malmquist-type results for difference equations with periodic coefficients, Comput. Methods Funct. Theory 15, 449–457 (2015).
- 24J.-P. Serre, Henri Cartan 1904–2008, Bull. Lond. Math. Soc. 46, 211–216 (2014).
- 25N. Toda, A generalization of Nochka weight function, Proc. Japan Acad. Ser. A Math. Sci. 83, 170–175 (2007).
- 26N. Toda, On the truncated defect relation for holomorphic curves, Kodai Math. J. 32, 352–389 (2009).
- 27N. Toda, On the number of exceptional points of holomorphic curves and the defect relation for holomorphic curves, Kodai Math. J. 37, 120–156 (2014).
- 28P. Vojta, On Cartan's theorem and Cartan's conjecture, Amer. J. Math. 119, 1–17 (1997).
- 29P.-M. Wong, H. F. Law, and Philip P. W. Wong, A second main theorem on
for difference operator, Sci. China Ser. A 52, 2751–2758 (2009).
- 30Z. Ye, A sharp form of Nevanlinna's second main theorem of several complex variables, Math. Z. 222, 81–95 (1996).
