Original Paper
Nonlinear perturbations of a 
-Laplacian equation with critical growth in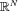 
Claudianor O. Alves,
Marcelo C. Ferreira,
Corresponding Author
Claudianor O. Alves
Universidade Federal de Campina Grande, Unidade Acadêmica de Matemática, CEP: 58429-900, Campina Grande-PB, Brazil
Corresponding author: e-mail: [email protected], Phone: +55 83 21011508, Fax: +55 83 21011030Search for more papers by this authorMarcelo C. Ferreira
Universidade Federal de Campina Grande, Unidade Acadêmica de Matemática, CEP: 58429-900, Campina Grande-PB, Brazil
e-mail: [email protected], Phone: +55 83 21011635, Fax: 55 83 21011030
Search for more papers by this authorClaudianor O. Alves,
Marcelo C. Ferreira,
Corresponding Author
Claudianor O. Alves
Universidade Federal de Campina Grande, Unidade Acadêmica de Matemática, CEP: 58429-900, Campina Grande-PB, Brazil
Corresponding author: e-mail: [email protected], Phone: +55 83 21011508, Fax: +55 83 21011030Search for more papers by this authorMarcelo C. Ferreira
Universidade Federal de Campina Grande, Unidade Acadêmica de Matemática, CEP: 58429-900, Campina Grande-PB, Brazil
e-mail: [email protected], Phone: +55 83 21011635, Fax: 55 83 21011030
Search for more papers by this authorAbstract
We prove the existence of solution for a class of 
-Laplacian equations where the nonlinearity has a critical growth. Here, we consider two cases: the first case involves the situation where the variable exponents are periodic functions. The second one involves the case where the variable exponents are nonperiodic perturbations.
References
- 1E. Acerbi and G. Mingione, Regularity results for electrorheological fluids: stationary case, C. R. Math. Acad. Sci. Paris 334, 817–822 (2002).
- 2E. Acerbi and G. Mingione, Regularity results for stationary electrorheological fluids, Arch. Ration. Mech. Anal. 164, 213–259 (2002).
- 3C. O. Alves, Existence of radial solutions for a class of
-Laplacian equations with critical growth, Differential Integral Equations 23, 113–123 (2010).
- 4C. O. Alves, Existence of solutions for a degenerate
-Laplacian Equation in 
, J. Math. Anal. Appl. 345, 731–742 (2008).
- 5C. O. Alves and G. M. Figueiredo, Existence and multiplicity of positive solutions to a p-Laplacian equation in
, Differential Integral Equations 19, 143–162 (2006).
- 6C. O. Alves and M. A. S. Souto, Existence of solutions for a class of problems in
involving 
-Laplacian, Prog. Nonlinear Differential Equations Appl. 66, 17–32 (2005).
- 7C. O. Alves, P. C. Carriãao, and O. H. Miyagaki, Nonlinear perturbations of a periodic elliptic problem with critical growth, J. Math. Anal. Appl. 260, 133–146 (2001).
- 8S. N. Antontsev and J. F. Rodrigues, On stationary thermo-rheological viscous flows, Ann. Univ. Ferrara Sez. VII Sci. Mat. 52, 19–36 (2006).
10.1007/s11565-006-0002-9 Google Scholar
- 9S. N. Antontsev and S. I. Shmarev, Elliptic equations and systems with nonstandard growth conditions: existence, uniqueness and localization properties of solutions, Nonlinear Anal. 65, 722–755 (2006).
- 10S. N. Antontsev and S. I. Shmarev, On localization of solutions of elliptic equations with nonhomogeneous anisotropic degeneracy, Siberian Math. J. 46, 765–782 (2005).
- 11A. Chambolle and P. L. Lions, Image recovery via total variation minimization and related problems, Numer. Math. 76, 167–188 (1997).
- 12Y. Chen, S. Levine, and M. Rao. Variable exponent, linear growth functionals in image restoration, SIAM J. Appl. Math. 66, 1383–1406 (2006).
- 13X. L. Fan, Global
regularity for variable exponent elliptic equations in divergence form, J. Differential Equations 235, 397–417 (2007).
- 14X. Fan,
-Laplacian equations in 
with periodic data and nonperiodic perturbations, J. Math. Anal. Appl. 341, 103–119 (2008).
- 15X. Fan and X. Y. Han, Existence and multiplicity of solutions for
-Laplacian equations in 
, Nonlinear Anal. 59, 173–188 (2004).
- 16X. Fan and D. Zhao, On the spaces
and 
, J. Math. Anal. Appl. 263, 424–446 (2001).
- 17X. L. Fan, J. S. Shen, and D. Zhao, Sobolev embedding theorems for spaces
, J. Math. Anal. Appl. 262, 749–760 (2001).
- 18X. Fan, Y. Zhao, and D. Zhao, Compact embedding theorems with symmetry of Strauss-Lions type for the space
, J. Math. Anal. Appl. 255, 333–348 (2001).
- 19Y. Fu and X. Zhang, Multiple solutions for a class of
-laplacian equations in involving the critical exponent, Proc. Roy. Soc. Edinburgh Sect. A 466, 1667–1686 (2010).
- 20Li Gongbao, Some properties of weak solutions of nonlinear scalar field equations, Ann. Acad. Sci. Fenn. Math. Ser. A I Math. 15, 27–36 (1990).
10.5186/aasfm.1990.1521 Google Scholar
- 21O. Kováčik and J. Rákosník, On spaces
and 
, Czechoslovak Math. J., 41, 592–618 (1991).
- 22A. Kristály, V. Rădulescu, and C. Varga, Variational Principles in Mathematical Physics, Geometry, and Economics: Qualitative Analysis of Nonlinear Equations and Unilateral Problems (Cambridge University Press, Cambridge, 2010).
10.1017/CBO9780511760631 Google Scholar
- 23P. L. Lions, The concentration-compacteness principle in the calculus of variations. The locally compact case, Part II, Ann. Inst. H. Poincaré Anal. Non Linéaire 1, 223–283 (1984).
- 24M. Mihăilescu and V. Rădulescu, A multiplicity result for a nonlinear degenerate problem arising in the theory of electrorheological fluids, Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 462, 2625–2641 (2006).
- 25J. Moser, A new proof de Giorgi's theorem concerning the regularity problem for elliptic differential equations, Comm. Pure Appl. Math. 13, 457–468 (1960).
- 26J. Musielak, Orlicz Spaces and Modular Spaces (Springer-Verlag, Berlin, 1983).
- 27M. Růžička, Electrorheological Fluids: Modeling and Mathematical Theory (Springer-Verlag, Berlin, 2000).
- 28M. Willem, Minimax Theorems (Birkhäuser, Boston, 1996).
