It is known that the bidual of a quasinormable Fréchet space E with local Banach spaces \documentclass{article}\usepackage{amssymb}\begin{document}\pagestyle{empty}$(E_n)_{n\in {\mathbb N}}$\end{document}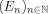 equation image is topologically isomorphic to the inverse limit of \documentclass{article}\usepackage{amssymb}\begin{document}\pagestyle{empty}$\big (E_n^{\prime \prime }\big )_{n\in {\mathbb N}}$\end{document}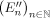. With the aid of the Arens product and by homological means, we prove that the previous result is equally valid for quasinormable Fréchet m-convex algebras. This allows showing that the bidual of a σ-C*-algebra equipped with the Arens product is a σ-C*-algebra and presenting a new direct proof of a result on acyclic spectra due to Palamodov.

References

1 C. Apostol, b*- algebras and their representation, J. Lond. Math. Soc., II. Ser. 3, 30–38 (1971).
10.1112/jlms/s2-3.1.30
Web of Science® Google Scholar
2 K. D. Bierstedt and J. Bonet, Some aspects of the modern theory of Fréchet spaces, Rev. R. Acad. Cienc. Exactas Fís. Nat., Ser. A Mat., RACSAM 97(2), 159–188 (2003).
Google Scholar
3 F. F. Bonsall and J. Duncan, Complete Normed Algebras, Ergebnisse der Mathematik und ihrer Grenzgebiete Vol. 80 (Springer–Verlag, Berlin, 1973).
Web of Science® Google Scholar
4 S. Dierolf and D. N. Zarnadze, A note on strictly regular Fréchet spaces, Arch. Math. 42, 549–556 (1984).
10.1007/BF01194053
Web of Science® Google Scholar
5 K. Floret and J. Wloka, Einführung in die Theorie der lokalkonvexen Räume, Lecture Notes in Mathematics Vol. 56 (Springer–Verlag, Berlin, 1968).
10.1007/BFb0098549
Web of Science® Google Scholar
6 M. Fragoulopoulou, Topological Algebras with Involution (North–Holland, Amsterdam, 2005).
Web of Science® Google Scholar
7 A. Grothendieck, Sur les espaces (F) et (DF), Summa Brasil. Math. 3, 57–123 (1954).
Google Scholar
8 S. L. Gulick, The bidual of a locally multiplicatively-convex algebra, Pac. J. Math. 17(1), 71–96 (1966).
10.2140/pjm.1966.17.71
Web of Science® Google Scholar
9 J. Horváth, Topological Vector Spaces and Distributions I, Addison–Wesley Publ. Co., Reading Massachusetts (1966).
Google Scholar
10 H. Jarchow, Locally Convex Spaces (B.G. Teubner, Stuttgart, 1981).
10.1007/978-3-322-90559-8
Google Scholar
11 G. Köthe, Topological Vector Spaces I (Springer–Verlag, Berlin, 1969).
10.1007/978-3-642-64988-2
Google Scholar
12 R. Meise and D. Vogt, Introduction to Functional Analysis (Oxford University Press, New York, 1997).
10.1093/oso/9780198514855.001.0001
Google Scholar
13 G. Metafune and V. B. Moscatelli, Quojections and prequojections, in: Advances in the Theory of Fréchet Spaces, edited by T. Terzioglu, NATO ASI Series C Vol. 287 (Kluwer Academic Publishers, Dordrecht, 1989), pp. 235–254.
10.1007/978-94-009-2456-7_14
Web of Science® Google Scholar
14 V. P. Palamodov, Homological methods in the theory of locally convex spaces, Usp. Mat. Nauk 26, 3–65 (1971) (in Russian); Russ. Math. Surv. 26, 1–64 (1971) (in English).
Google Scholar
15 P. Pérez Carreras and J. Bonet, Barrelled Locally Convex Spaces (North–Holland, Amsterdam, 1987).
Google Scholar
16 N. C. Phillips, Inverse limits of C*-algebras, J. Oper. Theory 19, 159–195 (1988).
Web of Science® Google Scholar
17 Z. Sebestyén, Every C*-seminorm is automatically submultiplicative, Period. Math. Hung. 10, 1–8 (1979).
10.1007/BF02018366
Google Scholar
18 J. Wengenroth, Derived Functors in Functional Analysis, Lecture Notes in Mathematics, Vol. 1810 (Springer–Verlag, Berlin, 2003).
Google Scholar

Volume285, Issue1

January 2012

Pages 127-130

On the bidual of quasinormable Fréchet algebras

Abstract

References

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

On the bidual of quasinormable Fréchet algebras

Abstract

References

References

Related

Information