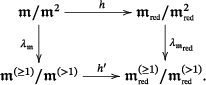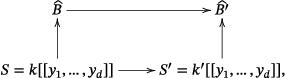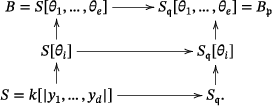1 INTRODUCTION
Let
be an algebraic variety over a field
. To give a constructive resolution of singularities of
means to describe a procedure to construct the centers of a finite sequence of blow ups at regular centers,
() so that
is regular. This is usually accomplished (when known to exist) by defining some upper-continuous functions
where
is some well-ordered set, and where the maximum value of
determines the center of the monoidal transformation
, for
. These
resolution functions also provide us with a criterion to determine that the variety
is
less singular than
.
The construction of the functions is somehow involved, and yet, it is strongly supported on the usual order function that one defines in a regular local ring. Furthermore, it vastly exploits the nice properties of the order function when defined in a smooth scheme of finite type over a perfect field. See for instance the approach to resolution followed in [17] where this fact becomes quite evident.
Some properties of the order function in regular rings that play a key role in resolution
Let
be a regular ring and let
be a prime ideal. The usual order of an element
at
is
- (A) The function is a valuation, and therefore for , .
- (B) When is essentially of finite type over a perfect field , for a fixed the function
() Actually, the inequality (1.2) holds for regular rings in general (see [16]), and it can also be read in terms of the symbolic powers of , namely, for all ,
()
- (C) When contains a field, and defines a regular subscheme in , that is, if is regular, then the ordinary and the symbolic powers of coincide,
() or in other words, for all ,
() This last property plays a special role, for instance, to control the transforms of the resolution invariants after each of the blow ups at the regular centers in sequence (1.1).
The order function is used to define the resolution functions
Let us start by considering a special case. Let
be a smooth
-algebra of finite type over a perfect field
, let
be a polynomial defining a hypersurface
of maximum multiplicity
in
, and suppose we can write,
() Already the order stratifies the singularities of
into locally closed strata. Thus, to approach a resolution of
, one may think that the problem can be reduced to lowering the maximum order of a strict transform of
below
. This is usually referred to as
resolving the pair . However, just this information might not be enough to construct the resolution function
. In particular, resolving the pair
requires the definition of new functions, usually referred as
resolution invariants. And, again, the main source to defining them relies, in one way or another, on some order function of a suitably defined local regular ring. Thus,
would look something like this:
() where the set
is ordered lexicographically. In particular this means that if
are two points with the same multiplicity and if
, then,
() The value of
is the
weighted-order at
of some ideal
that collects information coming from the coefficients of
. There are different strategies to define
: the so-called
-invariant coming from
Hironaka's polyhedron of the singularity, the order of the
coefficient ideal of the pair , or the order of an
elimination algebra of ,
, or the function
, among others (see [
4-6, 8, 11, 12, 20, 30, 33]). The rest of the functions
,
, depend in some sense on the construction of
.
The previous example covers the case of a hypersurface, since the defining equation of a hypersurface can be assumed to have the form in (1.6) after choosing a suitable local (étale) embedding in a neighborhood of a singular point. In addition, the case of an arbitrary variety can be reduced to the hypersurface case, also, after considering a suitable local (étale) embedding (see [21], or [34]). Thus, our initial example already gives us a rough picture of a procedure to construct the function .
Note that the definition of the resolution functions strongly uses local-étale embeddings of into smooth ambient spaces, where the good properties of the usual order function come in handy. As a counterpart, some (non-trivial) work has to be done in order to show that the resolution functions are independent of the embeddings. This is needed to prove, for instance, that the centers to blow up in sequence (1.1), which are determined locally, patch as to define global centers on that ultimately lead to a resolution of singularities of . And sometimes the use of the étale topology is not enough. For instance, the invariants provided by Hironaka's polyhedron are constructed at the completion of a local regular ring where the ideal of the variety is defined. In this line, we should mention the works of Cossart–Piltant in [13] and Cossart–Schober in [14], where it is shown that to construct the Hironaka's polyhedron, the completion can be avoided.
We can go one step further and explore properties of the local rings at the singular points of that allow us to collect information regarding the resolution functions: can we avoid the use of a local embedding in a regular ring and get information directly from the singular local ring of a variety?
When is a singular point, it is still possible to consider the order function at , but this does not behave very nicely. To start with, it is far from being upper semicontinuous. A function that has a much nicer behavior is the asymptotic Samuel function.
In this paper, we study some properties of the asymptotic Samuel function which could be useful to understand resolution functions from an intrinsic point of view. In this sense, we approach two different problems. On one hand, we explore the properties of the asymptotic Samuel function in comparison to the properties (A), (B), and (C) listed before. In particular, we will see that (B) and (C) hold for equimultiple primes (compare to the inequality (1.8)). On the other hand, we continue the work started in [2], where we used the asymptotic Samuel function to define an invariant, the Samuel slope of a local ring, which can be defined for any local Noetherian ring. In [2], we showed that the Samuel slope is connected to some resolution functions that appear naturally when working with algebraic varieties over perfect fields of prime characteristic. In particular, there seems to be a strong connection between the Samuel slope of a singular point and the value of the function mentioned above (see [3]). Here, we do not restrict to algebraic varieties and explore further properties of this invariant in the wider context of excellent local equicharacteristic equidimensional rings, and, among other results, we prove inequalities in the line of (1.8) when comparing the Samuel slope at equimultiple primes.
Some definitions and main results:
Definition 1.1.Let be a Noetherian ring and let be a proper ideal. The asymptotic Samuel function at , , is defined as follows:
()
This function was first introduced by Samuel in [29], when studying the behavior of powers of ideals. Afterward, Rees pursued the use of this function in [25, 26] where it is shown that the limit exists, see also [32, Lemma 6.9.2], [27, 28]. If is a local regular ring, then is the ordinary order function at the maximal ideal of (and then we write ).
The asymptotic Samuel function measures how deep a given element lies into the integral closure of an ideal, that is,
() see [
32, Corollary 6.9.1]. If
is not contained in a minimal prime of
and
is a set of Rees valuations of
, then
() (see [
32, Lemma 10.1.5, Theorem 10.2.2] and [
31, Proposition 2.2]). Therefore, if
is not nilpotent,
.
Remark 1.2.The asymptotic Samuel function is an order function. It can be checked that the following hold:
- (i) for , , with equality if ;
- (ii) for , .
In addition, it is worthwhile noticing that for
and
,
.
Definition 1.1 can be extended to the case in which arbitrary filtrations of ideals are considered. This has been studied by Cutkosky and Praharaj in [15]. On the other hand, we refer to the work of Hickel in [19] for some results on the explicit computation of the asymptotic Samuel function on complete local rings. Some of these results will play a role in our arguments, and they will be precisely stated and properly referred in Section 2.
Properties (A), (B), and (C) 1.3.In the following lines, we will revisit properties (A), (B), and (C) in the case of the asymptotic Samuel function.
- (A) In general, the asymptotic Samuel function is not a valuation and it is not hard to find examples.
Example 1.4.Let be a field. Consider the ring , with maximal ideal . We have that:
Here, it can be checked that is not a reduction of . However, there are minimal reductions of which contain the element . In fact, under some assumptions, using minimal reductions of , one can identify a regular subring of where the restriction of behaves as a valuation. The following result clarifies what is going on in the previous example, in fact, a little bit more can be stated:
Proposition 2.6.Let be an equidimensional excellent equicharacteristic local ring of dimension containing a field . Suppose has a reduction generated by elements, . Set . Then, for and ,
(B), (C) Let
be a non-necessarily regular ring. For our discussions, the case
can be left out, thus through the paper we will be assuming that
. For a prime ideal
, using the asymptotic Samuel function we can define the following filterations: for
,
In general, we do not expect that properties (B) and (C) hold:
Example 1.5.Let be a field, and let , where . Set . Notice that
In addition,
defines a regular prime in
, i.e.
is regular, however,
As indicated before, we will see that, to expect similar properties as in the regular case, we have to restrict to primes with the same multiplicity. In other words, the asymptotic Samuel function behaves as expected when restricted to a (locally closed) stratum of constant multiplicity of .
To fix notation, for a prime in and for a -primary ideal, , we will use to denote the multiplicity of the local ring at . Now, properties (B) and (C) have the following reformulation in the context of singular rings:
Theorem 3.1.Let be an equidimensional excellent ring containing a field. Let be two prime ideals such that . Then for .
In particular, this says that for
as in the theorem, and
,
Theorem 3.3.Let be an equidimensional excellent ring containing a field. Let be a prime in the top multiplicity locus of , and assume that is regular. Then, for .
Hence, in particular, for
as in the theorem, and
,
To conclude this part, if
is a regular local ring, the usual order induces the natural filtration
, where
which in turns leads to the usual graded ring
that is graded over
and finitely generated over
. For an arbitrary local ring
, we can consider the graded ring associated to the filtration induced by the asymptotic Samuel function: setting
, define
Note that by (
1.11), there is some integer
so that
is graded over
. And actually
can be taken as
if
, where
denotes
and
(see Remark
2.12). Imposing some (mild) conditions on
, we can show that
is a
-algebra of finite type:
Theorem 3.4.Let be an excellent local ring. Then, is a -algebra of finite type.
The Samuel slope of a local ring 1.6.The notion of Samuel slope of a local ring was introduced in [2]. More precisely, for a Noetherian local ring of dimension we consider the natural map:
If
is not regular, then
might be non-trivial, and its dimension as a
-vector space is an invariant of the ring. To start with, it can be proven that
is bounded above by the
excess of embedding dimension of ,
, that is,
This follows from the fact that elements
are nilpotent in
.
Local non-regular rings where the upper bound is not achieved seem to have milder singularities than the others, and in such case we say that Samuel slope of , , is 1.
When we say that is in the extremal case, and we define the Samuel slope as follows.
Set
. We say that the elements
form a
-sequence if their classes in
form a basis of
. Then,
where the supremum is taken over all the
-sequences of
.
Equivalently,
can also defined in the following way. Let
be a minimal set of generators of
. We define the
slope with respect to as
And then,
where the supremum is taken over all possible minimal ordered sets of generators
of
. To conclude, if
is regular we set
.
Example 1.7.Let be a field of characteristic 2. Set , where . Then, is in the extremal case and . Both and are -sequences. However, , while . In fact, , see Corollary 4.3.
Here, we also study the Samuel slope in the wider setting of equicharacteristic equidimensional excellent local rings. First of all, just from the definition, it is not clear that this invariant is finite in the case of non-regular rings. We show:
Theorem 4.5.Let be a non-regular reduced equicharacteristic equidimensional excellent local ring. Then, .
Next, we consider the case of non-reduced rings. Recall that the multiplicity induces the same stratification on both, and . We show that both rings share the same Samuel slope.
Theorem 4.7.Let be a non-reduced equicharacteristic equidimensional excellent local ring. Then .
From here it follows that if and only if is a regular local ring (Corollary 4.8).
Since the Samuel slope is an invariant of the local ring of a singularity, one would expect that it be preserved under étale extensions and completion. In [2], it was shown that is a local étale extension of with the same residue field, then . The argument given there also shows that , where is the -adic completion of . Here, we treat the case of arbitrary local étale extensions, which requires a different strategy.
Theorem 5.5.Let be an equicharacteristic equidimensional excellent local ring, and let be a local-étale extension. Then, .
To conclude, as we mentioned the Samuel slope of a local ring seems to be connected to the resolution invariant
in (
1.7) which has the following property: if
is an equimultiple prime then
In fact, when the characteristic is zero, then
is upper semi-continuous when restricted to points with the same multiplicity. For a Noetherian ring
, we can consider the function
In general,
is not upper semicontinuous, see Example
6.1, but it has the following nice property on the maximal spectrum,
, of
:
Theorem 6.2.Let be an equidimensional equicharacteristic excellent ring and let . Then, there is a dense open set such that
The paper is organized as follows. One of the main ingredients in our proofs is the use of the so-called finite-transversal projections together with Hickel's result on the computation of the asymptotic Samuel function. These are treated in Section 2, where we also address Proposition 2.6. The proofs of Theorems 3.1, 3.3, and 3.4 are addressed in Section 3. The rest of the paper is dedicated to the Samuel slope of a local ring. Theorems 4.5 and 4.7 are proved in Section 4, while Theorem 5.5 is proved in Section 5. Finally, a proof of Theorem 6.2 is given in Section 6.
2 FINITE-TRANSVERSAL PROJECTIONS
Finite-transversal projections were considered in [34] for the construction of local presentations of the multiplicity function of algebraic varieties defined over a perfect field. The existence of such presentations implies that resolution of singularities of algebraic varieties can be achieved via successive simplifications of the multiplicity (in characteristic zero). Finite-transversal projections were further explored in [1], where they were considered between (non-necessarily regular) algebraic varieties defined over perfect fields. Some other properties of such morphisms are discussed in [7]. In this section, we treat this notion in a more general setting, dropping the assumption that the rings involved be -algebras of the finite type.
Definition 2.1.Let be a finite extension of excellent rings with regular and equidimensional and reduced. Let be the fraction field of and let . Suppose that no non-zero element of is a zero divisor in . We say that the projection (or the extension ) is finite-transversal with respect to if:
If
is a finite-transversal extension of local rings with respect to
then we simply say that
is a
finite-transversal extension.
Using Zariski's formula for the multiplicity for finite projections, [35, Theorem 24, p. 297 and Corollary 1, p. 299], one can get the following characterization of finite-transversal projections:
Proposition 2.2. ([[34], Corollary 4.9])Let be a finite extension of excellent rings with regular, and equidimensional and reduced. Suppose that no non-zero element of is a zero divisor in . Let be a prime ideal, and let . Then, the following are equivalent:
- (1) .
- (2) The following three conditions hold:
- (i) is the only prime of dominating ,
- (ii) ,
- (iii) .
Observe that by Rees' theorem, condition (2) (iii) is equivalent to asking that be a reduction of the ideal . To be able to use Rees' theorem we will be assuming that is an excellent ring.
On finite-transversal morphisms and the asymptotic Samuel function
Finite-transversal projections will play a central role in our arguments, mainly because of the combination of the outputs of Proposition 2.3, due to Villamayor, and a theorem of Hickel for the computation of the asymptotic Samuel function, Theorem 2.4. In addition, in Section 2.5 we briefly describe how to construct finite-transversal morphisms for some faithfully flat extension of a given ring . This will be frequently used in the rest of the paper.
Proposition 2.3. ([[34], Lemma 5.2])Let be a finite extension such that the non-zero elements of are non-zero divisors in . Assume that is a regular ring and let be the quotient field of . Let and let be the monic polynomial of minimal degree such that . If denotes the -subalgebra of generated by , then:
- (1) the coefficients of are in , that is, , and
- (2) .
Theorem 2.4. ([[19], Theorem 2.1])Let be a Noetherian equicharacteristic equidimensional and excellent local ring of Krull dimension . Assume that there is a faithfully flat extension with together with a finite-transversal morphism with respect to , . Let . If
is the minimal polynomial of
over the fraction field of
,
, then
and
() where
.
Proof.Theorem 2.1 in [19] is stated in the case in which , and then a reduction to the domain case is considered. See [7, Theorem 11.6.8], where it is checked that Hickel's theorem holds in this more general setting.
Constructing finite-transversal projections 2.5.Given an excellent reduced equidimensional ring , and a point , in general, there might not be a regular ring and a finite-transversal projection with respect to , . To start with, it is a necessary condition that has a reduction generated by -elements. But even if such condition is satisfied, the existence of the required finite projection is not guaranteed (see [7, Example 11.3.11]). However, finite-transversal projections can be constructed if we are allowed to extend our ring . For instance, in [34] (see [9, Proposition 31.1]) it is proven that if is essentially of finite type over a perfect field , then a finite-transversal projection can be constructed in some étale extension of .
Existence of finite transversal projection. Suppose that
is a local equicharacteristic equidimensional excellent reduced ring. Assume also that
contains a reduction of
generated by
elements,
. Now, denote by
a coefficient field of the
-adic completion
and set
. Since
are analytically independent,
is a ring of power series in
variables. The extension
() is finite by [
10, Theorem 8, p. 68] and, moreover, finite-transversal with respect to
. See also [
19, Proof of Theorem 1.1].
The extension
is faithfully flat, this means that for any ideal
and
we have
()
Note that if the residue field of is infinite then by [32, Proposition 8.3.7], contains a reduction of generated by elements.
Extension to the case with reduction with elements. If
does not contain a reduction of
generated by
elements, then we want to produce a faithfully flat extension
such that
has such reduction. We consider two possibilities as follows:
- (a) If contains a field consider a suitable étale extension of , , so that, after localizing at a maximal ideal , the local ring
() contains a reduction generated by -elements.
- (b) Other possibility is to set the ring
() which has infinite residue field.
Note that in both cases we have that
() for any ideal
and
.
Reduction to reduced rings. In general, we will be dealing with a local ring
of Krull dimension
. And we will be interested in proving results concerning the asymptotic Samuel function,
. Now, observe, first of all, that if
and
is the image of
in
, then
() Hence, in many situations we may reduce our proofs to the case in which the ring in consideration is reduced.
Reduction to complete rings. Summing up, for a local ring
, let be
as in (
2.4) or as in (
2.5). Then, we have a chain of faithfully flat extensions,
() For any ideal
and any
, the chain of equalities
() is guaranteed (see [
32, Proposition 1.6.2]). In particular, if
, then
() Thus, given an excellent, equidimensional, equicharacteristic local ring
, in most situations we will be able to reduce our proofs to the case of a complete reduced local ring containing either an infinite residue field or a field with sufficient scalars. By assuming that
is excellent we will guarantee that
is formally equidimensional and analytically unramified. The former condition allows us to use Rees' theorem in Proposition
2.2, and the second will be implicitly used when reducing to the case of the completion of a reduced ring.
Good behavior for equimultiple prime ideals. Let be
a prime ideal in
such that
. Then, this condition is preserved if we consider some of the above extensions. Set
equal to either
, or
as in (
2.4) or as in (
2.5), or
then there exists a prime ideal
dominating
, and
() Moreover, if
defines a regular subscheme in
, then
also defines a regular subscheme in
.
When does behave as a valuation?
After the discussion in Section 2.5, we get the following result:
Proposition 2.6.Let be an equidimensional excellent equicharacteristic local ring of dimension . Suppose has a reduction generated by elements, , and let be a field. Set . Then, for and ,
Proof.Using the arguments in Section 2.5, we can assume that is reduced and complete, and consider the finite-transversal extension
where
is a coefficient field of
. Now the result follows from [
2, Proposition 2.10].
The rest of the section is devoted to the study of some more properties of finite-transversal projections.
On finite-transversal projections and the top multiplicity locus of a ring
The following three statements follow as a consequence of Proposition 2.2 when applied to a local ring . They are results concerning the primes in that have the same multiplicity as that of at , that is, the primes in the top multiplicity locus of .
Proposition 2.7.Suppose that is finite-transversal with respect to . Let be a prime ideal with . Let . Then:
- (i) The extension is finite transversal with respect to ;
- (ii) The local ring is regular if and only if is regular;
- (iii) If is regular then .
Proof.Similar results were proven in [34, Corollary 5.9, Proposition 6.3] and [1, Corollary 2.8] in the context of algebraic varieties defined over perfect fields. Here, we check that the statement holds for more general rings under the hypotheses of the proposition.
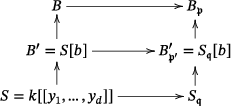
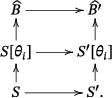
- (i) Consider the following commutative diagram with vertical finite morphisms:
Observe that the generic rank of the extension is . Hence, by definition, is finite-transversal with respect to . By Proposition 2.2 (2) (i), . In other words, is finite transversal with respect to .
- (ii) Since is finite-transversal with respect to , by Proposition 2.2 (2) (ii), . Now, consider the commutative diagram with vertical finite extensions,
Note that is a finite extension of local rings. Since conditions (2) (i)–(iii) of Proposition 2.2 hold for , the same conditions hold for . Now, apply Zariski's multiplicity formula for finite projections (Theorem 2.2) to to obtain,
- (iii) By (ii) if is regular, then is a finite extension of regular local rings with the same quotient field. Since is regular, it is normal, and hence .
Proposition 2.8. (Presentations of finite-transversal extensions)Suppose that is finite-transversal with respect to . Let be a prime ideal with , and assume in addition that is a regular local ring. Let . There are such that:
- (i) ;
- (ii) .
In addition,
- (iii) is a reduction of (in ).
Proof.We follow ideas from [34, Lemma 6.4] for part (i), [2, Lemma 8.10] for part (ii) and [1, Lemma 3.6] for part (iii), where similar results were proven in the context of algebraic varieties defined over perfect fields. To facilitate the reading of the paper we check here that the proofs can be adapted to cover a wider class of rings under the hypotheses of the proposition.
- (i) Write . By Proposition 2.7 (iii), , therefore, for each , there is some such that . Set for . Then, .
- (ii) By (i), we can write with for . Since is finite-transversal at , , therefore,
() If we are done. Otherwise, since defines a regular subscheme, there is a regular system of parameters in , , such that for some . Then
() Now,
- (iii)
By (i) we can assume that with for . By Proposition 2.7 (i) and by Proposition 2.2, we have that is a reduction of . To see that is the integral closure of in it suffices to check this condition at all the maximal ideals containing . Since is local, this amounts to checking this condition at .
Since is a regular local ring, by Proposition 2.7 (iii), is also a regular local ring. Observe that the multiplicity of is 1, and so is the multiplicity of . Hence, by Theorem 2.9, in .
Now, since the extension is finite, , and the blow up of at is finite over the blow up of at . Hence, the fibers over the closed points have the same dimensions, and therefore, . Therefore, in . Recall that , by Proposition 2.2 (iii). Finally, since is the only minimal prime of , the statement follows from Theorem 2.10.
Theorem 2.9. (Hironaka–Schickhoff, [[24], Corollary 3, p. 121])Let be a formally equidimensional local ring, and let be a prime ideal so that is regular. Then, in if and only if the local rings and have the same multiplicity.
Theorem 2.10. (Böger, [[24], Theorems 2 and 3, pp. 115–116], [[32], Corollary 11.3.2])Let be a formally equidimensional local ring. Fix an ideal so that . Consider an ideal so that . Then, is a reduction of if and only if for each minimal prime ideal of .
Proposition 2.11. (Intermediate extensions of finite-transversal extensions)Suppose that is finite-transversal with respect to . Let be a prime ideal with . Let be an intermediate extension, that is, , and consider the diagram:
Then:
- (i) The ring is local with maximal ideal ;
- (ii) The extension is finite-transversal with respect to of generic rank ;
- (iii) The extension is finite-transversal with respect to and ;
- (iv) For ,
() and
()
- (v) If is regular, then is regular, and in such case, is a reduction of in .
Proof.
- (i) This follows from the fact that is local and the extensions are finite.
- (ii) It suffices to check that the extension satisfies conditions (2)(i)–(iii) of Proposition 2.2. Condition (2)(i) has already been proven, and condition 2(ii) follows from the chain of containments,
- (iii) By Proposition 2.7(i), the extension is finite-transversal with respect to . Repeating the argument in (ii) we find that is finite-transversal with respect to . See also [34, Lemma 4.12] for (i), (ii), and (iii), in the case of domains.
- (iv) Equality (2.14) follows from (1.10), from the fact that is a reduction of , see [32, Propositions 8.1.5 and 1.6.1]. Equality (2.15) follows similarly applying the previous argument to the finite-transversal extension .
- (v) By Proposition 2.7 (ii) and (iii) is regular and, moreover . Then, the first part of the statement follows. Finally, by [32, Proposition 1.6.1] and Proposition 2.8(iii), we have .
Remark 2.12.With the same hypotheses and notation as in Proposition 2.11, observe that if for some , then, by Proposition 2.3, , where is the minimum polynomial of over , the quotient field of . The degree of is the generic rank of , that is, the dimension of the -vector space , which is bounded above by . Therefore, by Theorem 2.4, . See also [19, Theorem 1.1].
3 SOME NATURAL PROPERTIES OF THE ASYMPTOTIC SAMUEL FUNCTION
In this section, we are going to explore some natural properties of the asymptotic Samuel function, addressing the proofs of the results presented in the introduction.
Theorem 3.1.Let be an equidimensional excellent ring containing a field. Let be two prime ideals such that . Then, for .
Proof.After localizing at , we can assume that is a local ring. By the arguments in Section 2.5, see (2.11), we can start by assuming that is reduced. Consider the -adic completion of , . Let be a prime dominating . Then:
Hence, by the arguments detailed in Section
2.5, to prove the theorem we can assume that
is a reduced complete local ring and that there is a finite-transversal projection
, with
, where
is the residue field of
, and
generate a reduction of the maximal ideal
of
. Let
. By Proposition
2.7, the extension
is finite-transversal with respect to
. Now, consider the diagram:
Let
and
. By Proposition
2.11, the extension
is finite-transversal with respect to
of generic rank
and
is finite transversal with respect to
with the same generic rank,
.
Using Proposition 2.11 (iv),
hence, it suffices to prove the theorem for
. Now, by Proposition
2.3,
, where
is the minimal polynomial of
over
. The degree of this polynomial equals the multiplicity of
at
,
. By Theorem
2.4, if
then
Now, observe that
, and therefore, again by Proposition
2.3,
. Hence, again by Theorem
2.4,
To conclude by [
16, Theorem 2.11], for each
,
, thus
.
Remark 3.2.Observe that for a given the function
might not be upper semicontinuous, even after restricting ourselves to the top multiplicity locus of
. See Example
6.1, where
, whereas
, for every maximal ideal
containing
.
Theorem 3.3.Let be an equidimensional excellent ring containing a field. Let be a prime in the top multiplicity locus of and assume that is regular. Then, for .
Proof.Recall that if , , by (1.10), if and only if . On the other hand, by [32, Proposition 1.1.4(4)], for all maximal ideals . As a consequence, if and only if, for all maximal ideals . Thus, it suffices to prove that the equality in the statement holds after localizing at each maximal ideal . Hence, we can assume that is local and that . By the arguments in Section 2.5, see (2.11), and the discussion at the beginning of the proof of Theorem 3.1, we can assume that is reduced complete local ring and that there is a finite-transversal extension . Let be the minimal polynomial of over , and let . Then, following the arguments in the first part of the proof of [19, Theorem 2.1],
By Proposition
2.7, the prime
defines a regular prime in
. Hence, since
is regular and contains a field we have that the ordinary and symbolic powers of
coincide. Therefore,
As indicated in the introduction, for a local ring , the filtration leads us to the consideration of the graded ring , see [23]. Since is Noetherian, is graded over the rationals with bounded denominators, that is, there is some such that . If in addition we impose that is excellent, reduced, equidimensional and equicharacteristic, then by Remark 2.12, can be taken as , where is the multiplicity of the local ring .
Theorem 3.4.Let be an excellent local ring. Then, is a -algebra of the finite type.
Proof.First observe that by (2.7) and from the definition of , we have that , hence we may assume that is reduced. If is regular there is nothing to prove. Otherwise, let , where is the multiplicity of the local ring . Let
that is,
, where
,
if
, and
is a variable that helps us keep track of the grading. Define also,
that is,
.
Then, there is a containment of graded algebras . Observe that is finitely generated over and that is integral over , since, for a homogeneous element , we have that
Now,
is excellent, and hence so is
. Let
be the total quotient field of
. The extension
is finite and therefore the integral closure of
in
,
, is finite over
. Since
, it follows that
is finite over
, hence finitely generated over
. To conclude notice that
is a quotient of
.
4 FINITENESS OF THE SAMUEL SLOPE
We devote the last sections of this paper to study properties of the Samuel slope function defined in Section 1.6. Here, we address the proofs of Theorems 4.5 and 4.7.
In this section, and also in Section 5, we will be using two main facts: first, that the Samuel slope can be computed in the completion of the local ring (Proposition 4.1), and second, if we are given a finite-transversal extension then, there is a procedure to approximate the Samuel slope of , using translations with elements in (Proposition 4.2).
Proposition 4.1. ([[2], Proposition 3.10])Let be a Noetherian local ring.
- is an étale homomorphism such that then .
- If denotes the -adic completion of then .
Proof.The first assertion is Proposition 3.10 in [2]. And the same proof applies to the completion, since it is enough to observe that .
Proposition 4.2. ([[2], Lemma 8.9])Let be a finite-transversal extension. Write for some , . Set . Suppose that the embedding dimension of is , with , and that . Write for some , . Then, there are , such that, after reordering the elements :
- (i) , where , and
- (ii) is a minimal set of generators of with .
Furthermore,
- (iii) For a given a -sequence, , there are , , such that if then,
- (a) ,
- (b) and,
- (c) is a -sequence.
Corollary 4.3.Let be non-regular reduced equicharacteristic equidimensional excellent local ring. Let be a -sequence such that
then
.
Proof.Without loss of generality we can assume that . If , then by Proposition 4.2(iii), there exists some such that . Since , observe that for all (since then . Hence, if for some , , then , see Remark 1.2.
The following lemma, which was proven in [2, Proposition 8.6] in the context of a local ring of an algebraic variety, is valid for Noetherian local rings with the same proof, which we briefly sketch here. We will use this result in the proof of Theorem 4.5.
Lemma 4.4.Let be a Noetherian local ring of dimension which is in the extremal case. Then, contains a reduction of generated by elements.
Proof.By [22, Theorem 10.14], it suffices to find -elements such that if denote their images in , then is a graded ring of dimension 0. Suppose . By hypothesis , and if is so that , then is nilpotent. Thus, any collection of -elements in that completes a -sequence to a basis of generates a reduction of .
Theorem 4.5.Let be a non-regular reduced equicharacteristic equidimensional excellent local ring of dimension . Then, .
Proof.First of all, if is not in the extremal case then , and there is nothing to prove. Otherwise, is in the extremal case, and then it contains a reduction of generated by elements by Lemma 4.4. By Proposition 4.1, we can assume that is a local complete ring, and by Section 2.5 we can consider a finite-transversal extension .
Assume that the embedding dimension of is , where is the excess embedding dimension of . By Proposition 4.2, we can write with , , and . If then by Corollary 4.3 we are done. In fact, if there are some , , such that the result follows as well. Therefore, we can assume that for every , . Hence, the only way that the is that . Suppose that we can find a sequence of -sequences such that tends to infinity as grows. Using Proposition 4.2, we can find a sequence such that:
- (i) There exists some such that , for every and ,
- (ii) ,
- (iii) ,
- (iv) the set forms a -sequence.
Note that by the condition in (i),
and combining this with condition (iii) it follows that
() Taking a subsequence if necessary, we may assume that the sequence is strictly monotonically increasing (to those purposes note that for every , since is reduced by hypothesis). It follows then that the sequence is a Cauchy sequence, since
where the last equality is a consequence of [
2, Proposition 2.10]. Since
is complete, the sequence
converges in
to an element
. Hence, the element
is nonzero (see (
4.1)) and it is the limit of the sequence
satisfying that
, contradicting the fact that
is reduced.
Corollary 4.6.Let be non-regular reduced equicharacteristic equidimensional excellent local ring. Assume that there is a finite-transversal projection , and that for some . Then, there exist such that
Proof.This is a direct consequence of Proposition 4.2 and Theorem 4.5.
Theorem 4.7.Let be an equicharacteristic equidimensional excellent local ring. Then .
Proof.The natural surjective morphism of local rings, induces a surjective linear map of -vector spaces, , with , and a commutative diagram of -vector spaces,
Note that
is an isomorphism.
There are linear subspaces and such that
Since
, then
and there exists a linear subspace
such that
. Hence
via
.
If is a regular local ring then and by definition. In this case , and hence for any -sequence , we have that for all . The result follows since .
Assume now that is non-regular, then and by Theorem 4.5 . If then , and we have that .
If , then the result follows from (2.7) and because every -sequence can be extended to a -sequence with elements in , and, reciprocally, every -sequence contains a -sequence.
Corollary 4.8.Let be an equicharacteristic equidimensional excellent local ring. Then, if and only if is regular.
5 THE SAMUEL SLOPE AFTER SOME FAITHFULLY FLAT EXTENSIONS
In this section, we will show that the Samuel slope of a local ring remains the same after the faithfully flat extensions considered in Section 2.5.
Proposition 5.1.Let be a Noetherian local ring. Set and let be the maximal ideal of . Then, .
Proof.If is regular, there is nothing to prove. Otherwise, observe that the excess of embedding dimension of , , is the same as that of . If is not in the extremal case, then is not in the extremal case either, and then . Therefore, it remains to prove the statement if is in the extremal case, and hence so is . The inequality is straightforward. Let us prove that .
Every element can be expressed, up to a unit, as a polynomial
for some
and where
. Note that
This follows from the fact that
and
, see [
32, Lemma 8.4.2(9)].
Assume that is a -sequence. Up to some units in , every can be expressed as a polynomial
where
. We may assume that
for all
.
We have that
() If the classes of
in
are linearly independent then
is a
-sequence and we conclude that
.
If the classes of are linearly dependent, there are , not all zero in , such that
Since
for
, there are at least two indices
such that
. Let
be such that
Then, either
or
. Assume that
and define
We have that
is a
-sequence and
so that inequality (
5.1) also holds and the degree of the polynomial for
is smaller. After finitely many steps we arrive to the case where
form a
-sequence.
Definition 5.2. ([[6], Definition 4.4])Let be a regular ring and let be a prime such that the quotient is a regular ring. Let be a monic polynomial of degree in :
Set
for
, and set
For every
, if
then set
, and if
, set
.
We define the weighted initial form of at as the polynomial:
() where
. Note that
is a weighted polynomial of degree
, where the degree of
is
and the degree of elements in
is one.
Remark 5.3.Let be a finite-transversal projection. Let , and set . If is the minimal polynomial of over , we can associate with the weighted initial form of at , . Note that is a monic polynomial on of degree different from since is reduced. In particular, there is some with .
In fact, there exists some such that if and only if is an th power. See [6, Remark 4.6] for a discussion on the context of algebraic varieties.
Remark 5.4.Let be a finite-transversal projection of equicharacteristic local rings. Assume that for some . By Corollary 4.6, there exists some such that . Remark 5.3 gives us an iterative procedure to find :
If is not an th power then .
If is an th power then choose such that . Note that in this case must be an integer. Set . We know that , and then we can repeat the procedure with . Observe that is the minimal polynomial of .
Now, since (Theorem 4.5), it is clear that, after finitely many steps, the weighted initial form is not an power.
Theorem 5.5.Let be an equicharacteristic equidimensional excellent local ring, and let be a local-étale extension. Then, .
Proof.If is regular or if there is nothing to prove. Otherwise let and let . If then the result is [2, Proposition 3.10]. After ruling over the previous cases, by Theorem 4.7, we can assume that both and are reduced, in the extremal case, and that is a separable finite extension. Set . Since is in the extremal case, by Lemma 4.4, has a reduction generated by elements, . Observe that also expands to a reduction of in , and similarly, expands to reductions of in and in , respectively.
Since is étale, by [18, Proposition 17.6.3], is formally étale over for the -adic topologies, furthermore, is faithfully flat over and finite. To ease notation, let us denote again by some coefficient field of . By the natural map , the image of maps into some coefficient field of which for simplicity we denote by . Then, we have the following commutative diagram:
where the lower horizontal map is local étale, the vertical maps are finite-transversal, and we write
for the images of these elements in both
and
.
Write for some (see 2.5). Then, it can be checked that (here we use the fact that is finite over ).
Denote by (resp. ) the maximal ideal of (resp. of ). For , let be the weighted initial form of , the minimal polynomial of over . Note that is also the minimal polynomial of over . To justify this consider the following diagram:
By Proposition
2.3,
, and
.
The image of in is . Now we conclude, since is an -power in if and only if is an -power in . Here, we are using the fact that and the extension is étale (see [18, Proposition 16.2.2], in fact flatness is enough to guarantee the isomorphism). Now, the result follows from Remark 5.3 and Corollary 4.6, because:
6 COMPARING SLOPES AT PRIME IDEALS
As indicated in Section
1, for a Noetherian ring
, the function
is not upper semicontinuous in general, even after restricting to the top multiplicity locus of
. This can be checked in the following example:
Example 6.1.Let be a prime number, and let where . Observe that determines a non-closed point in of maximum multiplicity . It can be checked that . However for every maximal ideal we have that .
Observe that in the example for all maximal ideals . In fact this will happen quite generally, as the following result states.
Theorem 6.2.Let be an equidimensional excellent ring containing a field and let . Then, there is a dense open set such that
Before addressing the proof of the theorem we need an auxiliary result.
Proposition 6.3.Let be a finite-transversal projection of equicharacteristic local rings. Suppose that for some . Let be a prime in such that is regular, and . Then, there is some such that:
Proof.Set , and let be the minimal polynomial of over ,
By Proposition
2.3(1),
is also the minimal polynomial of
over
. By Proposition
2.3(2),
, therefore the generic rank of the finite-transversal extension
is
. Since
, and
is finite-transversal (Proposition
2.7(i)) the generic rank is also
and also
.
By Corollary 4.6, there is some with . Remark 5.4 indicates that can be obtained looking at the weighted initial form .
Since is a regular prime in , is a regular prime in (see Proposition 2.7(ii)). Consider the natural map
() Note that
is the image of
by the map in (
6.1). Then, both rings in (
6.1) are regular, in particular they are Unique Factorization Domain (UFDs) and the second is a localization of the first. Now, it follows that
is an
th power if and only if
is an
th power. Hence, there is some
in
such that
Proof of Theorem 6.2.Since is excellent, by [11, Theorem 2.33], there exists a dense open set in such that for every . After shrinking if needed, we can also assume that is regular at all maximal ideals in . Hence, we can assume to be in the case where is the localization at some maximal ideal .
By Proposition 5.1, we may assume that the residue field of is infinite, and by Theorem 4.7 we may assume that is reduced. By Proposition 4.1 and the arguments in Section 2.5 we may assume that is complete: here we use the fact that and , hence it suffices to prove that .
Again, by the arguments if Section 2.5 we have a finite-transversal extension . Set . By Proposition 2.7 we have that is finite-transversal and .
By Proposition 2.8, is a reduction of and there are such that ,
Now, consider the commutative diagram:
Set
and
, for
.
By Proposition 6.3, there are some such that for ,
Therefore, after translation by elements of
, we can assume that
. On the other hand, note that
Now the result follows since for
we have:
and
 from where the claim in (ii) follows.
from where the claim in (ii) follows.