Noninvasive monitoring of cerebral perfusion pressure in patients with acute liver failure using transcranial doppler ultrasonography†
See Editorial on Page 915
Abstract
Elevated intracranial pressure (ICP) leads to loss of cerebral perfusion, cerebral herniation, and irreversible brain damage in patients with acute liver failure (ALF). Conventional techniques for monitoring ICP can be complicated by hemorrhage and infection. Transcranial doppler ultrasonography (TCD) is a noninvasive device which can continuously measure cerebral blood flow velocity, producing a velocity-time waveform that indirectly monitors changes in cerebral hemodynamics, including ICP. The primary goal of this study was to determine whether TCD waveform features could be used to differentiate ALF patients with respect to ICP or, equally important, cerebral perfusion pressure (CPP) levels. A retrospective study of 16 ALF subjects with simultaneous TCD, ICP, and CPP measurements yielded a total of 209 coupled ICP-CPP-TCD observations. The TCD waveforms were digitally scanned and seven points corresponding to a simplified linear waveform were identified. TCD waveform features including velocity, pulsatility index, resistive index, fraction of the cycle in systole, slopes, and angles associated with changes in the slope in each region, were calculated from the simplified waveform data. Paired ICP-TCD observations were divided into three groups (ICP < 20 mmHg, n = 102; 20 ≤ ICP < 30 mmHg, n = 74; and ICP ≥ 30 mmHg, n = 33). Paired CPP-TCD observations were also divided into three groups (CPP ≥ 80 mmHg, n = 42; 80 > CPP ≥ 60 mmHg, n = 111; and CPP < 60 mmHg, n = 56). Stepwise linear discriminant analysis was used to identify TCD waveform features that discriminate between ICP groups and CPP groups. Four primary features were found to discriminate between ICP groups: the blood velocity at the start of the Windkessel effect, the slope of the Windkessel upstroke, the angle between the end systolic downstroke and start diastolic upstroke, and the fraction of time spent in systole. Likewise, 4 features were found to discriminate between the CPP groups: the slope of the Windkessel upstroke, the slope of the Windkessel downstroke, the slope of the diastolic downstroke, and the angle between the end systolic downstroke and start diastolic upstroke. The TCD waveform captures the cerebral hemodynamic state and can be used to predict dynamic changes in ICP or CPP in patients with ALF. The mean TCD waveforms for corresponding, correctly classified ICP and CPP groups are remarkably similar. However, this approach to predicting intracranial hypertension and CPP needs to be further refined and developed before clinical application is feasible. Liver Transpl 14:1048–1057, 2008. © 2008 AASLD.
Acute liver failure (ALF), the sudden onset of liver failure with no prior history of liver disease, is a life-threatening condition. Short-term survival without transplant ranges from 17% for cryptogenic liver failure to nearly 70% in acetaminophen-related liver failure.1 Cerebral ischemia and herniation caused by cerebral edema and intracranial hypertension are common causes of death (38%-81% of cases) in ALF patients.2-4 Even patients without signs of cerebral swelling in computerized tomography brain scans are at risk for developing clinically significant intracranial hypertension and cerebral ischemia despite aggressive medical care.5 Autoregulation of cerebral perfusion, which is usually maintained by cerebral vasoconstriction or dilation in response to the rate of cerebral metabolism, is impaired in patients with advanced encephalopathy in ALF.6
Maintenance of cerebral perfusion is a major goal in the clinical management of ALF patients. The driving force for cerebral blood flow is cerebral perfusion pressure (CPP), which is related to the mean arterial pressure (MAP) and intracranial pressure (ICP) by
 (1)
(1)Generally, CPP greater than 60 mmHg is considered sufficient to maintain intact neurological function. CPP falling below 40 mmHg for more than 2 hours is considered a contraindication for liver transplantation in some centers.7
ICP is a major determinant of CPP. ICP measurement by insertion of a monitoring probe into dural space is the currently accepted method of detecting the presence of intracranial hypertension in ALF patients.8 Because ALF patients uniformly develop coagulopathy and sepsis, intracranial placement of an ICP sensor is often complicated by hemorrhage, infection, and death.9 Consequently, reliable, noninvasive, continuous monitoring of cerebral perfusion and ICP should be able to help in assessing cerebral hemodynamics and viability with minimal complications.
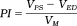 (2)
(2)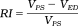 (3)
(3)Despite the importance of ICP monitoring in ALF, surprisingly little work has been done with TCD as a tool for estimating ICP.21-26 Sidi and Mahla21 found a weak correlation between CPP and PI in a case study of 1 ALF patient.21 Larsen and coworkers have shown that changes in CBFV can be used to detect changes in cerebral autoregulation24, 26 and can be predictive of brain herniation.22
Because CPP is the difference between the pressures driving and opposing cerebral perfusion, MAP and ICP, respectively, we hypothesize that TCD waveform analysis can be used to detect transitions in CPP or ICP that signal the need for immediate medical attention in patients with ALF. Such a diagnostic capability could delay the placement of a traditional ICP monitor until it is actually required and possibly avoid placement of an ICP probe entirely if either CPP remains above or ICP remains below a threshold that mandates medical intervention. Previous clinical experience in head trauma suggests that ICP rising above about 30 mmHg is a critical transition.27 We suggest a corresponding critical transition of CPP below about 60 mmHg. The aim of this study is to determine the feasibility of using components from the TCD waveform to discriminate the critical CPP or ICP transition in ALF patients.
Abbreviations
αED, end diastole angle; αPS, peak systole angle; αPW, peak Windkessel angle; αPS, peak systole angle; αSD, start diastole angle; αSW, start Windkessel angle; ALF, acute liver failure; CBFV, cerebral blood flow velocity; CPP, cerebral perfusion pressure; HR, heart rate; ICP, intracranial pressure; MAP, mean arterial pressure; PaCO2, CO2 partial pressure; PI, pulsatility index; RI, resistive index; SDD, diastolic downstroke slope; SDU, diastolic upstroke slope; SSD, systolic downstroke slope; SSU, systolic upstroke slope; SWD, Windkessel downstroke slope; SWU, Windkessel upstroke slope; SEM, standard error of the mean; τS, fraction of time spent in systole; T, core body temperature; TCD, transcranial Doppler ultrasonography; tED, end diastole time; tPD, peak diastole time; tPS, peak systole time; tPW, peak Windkessel time; tSD, systolic downstroke time; tSS, start systole time; tSW, start Windkessel time; VED, end diastolic velocity; VM, mean velocity over 1 cycle; VPD, peak diastole velocity; VPS, peak systolic velocity; VPW, peak Windkessel velocity; VSD, start diastole velocity; VSW, start Windkessel velocity.
PATIENTS AND METHODS
Subject Population
In accordance with a protocol approved by the University of Pittsburgh Institutional Review Board, 16 subjects who (1) were admitted to the Liver Transplant Intensive Care Unit at the University of Pittsburgh Medical Center (Pittsburgh, PA) with a diagnosis of ALF over a contiguous 2-year period (to ensure comparable standards of care), (2) had an epidural fiber optic continuous ICP monitor (Ladd Research Laboratories, Burlington, VT) placed as part of routine medical care, and (3) had readable noninvasive TCD cerebral blood flow scans were retrospectively identified for inclusion in this study.
The mean age of the subject population was 38 years (range: 16-67); 14 females, 2 males. The admission diagnosis varied and included acetaminophen overdose (5), viral hepatitis (3), macrodantin (1), postpartum hepatitis (1), halothane (1), and undetermined (5). All subjects were in grade 3 or 4 hepatic coma (grade 3, coma but responsive to painful stimuli; grade 4, coma unresponsive to painful stimuli) and were intubated and mechanically ventilated.
Clinical management was directed toward maintenance of MAP through administration of volume (crystalloid, colloid, and packed red blood cells) and vasopressors (dopamine, epinephrine, and norepinephrine) as needed. ICP sensor placement was by insertion into the epidural space after gentle stripping of the dura off the inner table of the skull via a burr hole. If necessary, fresh frozen plasma and/or platelets were administered to optimize coagulation as determined by thromboelastography (reaction time < 8 minutes and maximum amplitude > 40 mm)13 prior to ICP sensor placement.
Periodic TCD measurements of CBFV in the middle cerebral artery were obtained once every 24 hours or whenever a significant change in the patient's clinical status or monitored ICP occurred. The TCD measurements were made with a 2-MHz Doppler ultrasound probe (Transpect, Medasonic, Mountain View, CA), which was mechanically fixed in place by probe holders. The depth of insonation of the middle cerebral artery was 45-50 mm. After observation of the TCD signal for 2 minutes for stability, a velocity tracing containing several consecutive cycles was printed at a speed of 25 mm/s. A zero velocity baseline was included with each tracing.
The 16 patients yielded a total of 209 coupled CPP-ICP-TCD observations with associated physiologic status measurements, which included electrocardiogram, systemic blood pressure from an indwelling intra-arterial catheter, arterial blood gas tensions [O2 partial pressure, CO2 partial pressure (PaCO2), pH, and base excess], core body temperature, and coagulation profile (prothrombin time and/or thromboelastography).
Relationship Between the Cardiac Cycle Pressure Pulse Waveform and TCD Waveform
Figure 1 schematically depicts the relationship between the cardiac cycle aortic pressure pulse waveform (solid line) and the TCD waveform (dotted line). The pressure pulse and TCD waveforms each consist of 2 phases: systolic and diastolic. The start of the systolic phase correlates with the opening of the aortic valve. The systolic pressure pulse first rises with myocardial contraction and volume ejection and then tapers as the volume ejection tapers. The systolic part of the TCD waveform exhibits 2 peaks. The first peak is predominantly related to myocardial contractility. The second peak (Windkessel effect) is related to the distensibility (compliance) of the arterial wall and subsequent volume displacement effect. The dicrotic notch, which marks the start of the diastolic phase, corresponds to closure of the aortic valve and is associated with resistance in the distal vessels.
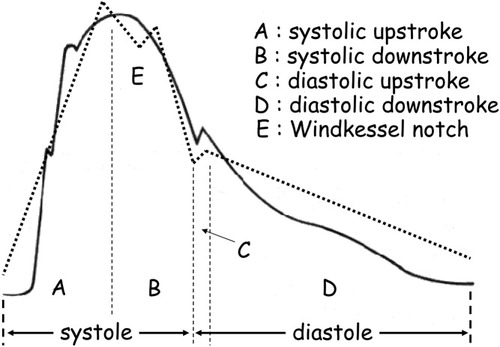
Relation between the cardiac output pressure pulse (solid line; adapted from Bruner33) and linearized TCD waveform (dashed line) at an equivalent time scale. Both the pressure pulse and the TCD waveform have distinct (A) systolic upstroke, (B) systolic downstroke, (C) diastolic upstroke, and (D) diastolic downstroke. (E) In addition, the TCD waveform has a Windkessel notch during the systolic downstroke.
A simplified, linear TCD waveform that captures the changes seen with rising ICP in ALF28 is depicted in Fig. 2. The linearized waveform is represented by 7 [time (s), velocity (cm s−1)] pairs: (1) start systole (start of a new cycle), (tSS, VED); (2) peak systole, (tPS, VPS); (3) start Windkessel effect, (tSW, VSW); (4) peak Windkessel effect, (tPW, VPW); (5) start diastole, (tSD, VSD); (6) peak diastole, (tPD, VPD); and (7) end diastole, (tED, VED). Characteristic features of the waveform, such as the slope in each linearized segment, angle between linear segments, mean velocity over a cycle, PI, RI, and fraction of the cycle spent in systole (related to narrowing of the systolic peak) can be calculated from the (velocity, time) data. The algebraic equations used to calculate the characteristic features are provided in the appendix.
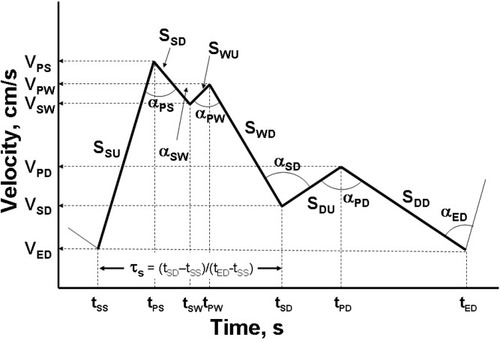
Schematic of a linearized 7-point TCD waveform showing Windkessel effect during systolic downstroke. The seven (velocity, time) points are used with the equations provided in the appendix to calculate TCD waveform features including: slope systolic upstroke (SSU); slope systolic downstroke (SSD); slope Windkessel upstroke (SWU); slope Windkessel downstroke (SWD); slope diastolic upstroke (SDU); slope diastolic downstroke (SDD); the angles between adjacent slopes (α); and the fractional time spent in systole (τS).
TCD waveforms were digitally scanned. The pixel coordinates corresponding to the waveform origin, velocity scale, time scale, and 7 (velocity, time) points of the linearized waveform were visually determined and recorded. The pixel values were then converted into appropriate (velocity, time) pairs for use in the analysis.
Statistical Analysis
The 209 observations were classified into 3 ICP groups based on the following ranges: ICP < 20 mmHg (group 1, n = 102), 20 mmHg ≤ ICP < 30 mmHg (group 2, n = 74), and ICP ≥ 30 mmHg (group 3, n = 33). The ICP groupings were chosen to represent the breakpoints at which clinical attention to and possible intervention for rising ICP is warranted27: no intervention (ICP < 20 mmHg),; close monitoring (20 mmHg ≤ ICP < 30 mmHg), and probable need for ICP monitor placement (ICP ≥ 30 mmHg). The 209 observations were also independently classified into 3 CPP groups based on the following ranges: CPP ≥ 80 mmHg (group A, n = 42), 80 mmHg > CPP ≥ 60 mmHg (group B, n = 111), and CPP < 60 mmHg (group C, n = 56). The CPP groupings were also chosen to represent breakpoints at which clinical attention to and possible intervention for falling CPP might be warranted.
Stepwise linear discriminant analysis (SPSS, Inc., Chicago, IL) was used to identify which, if any, TCD waveform features identified previously and listed in the appendix discriminate between the 3 ICP groups and, independently, the 3 CPP groups. Linear discriminant analysis is a useful tool for determining whether any known variables distinguish between 2 or more groups. Computationally, linear discriminant analysis is similar to analysis of variance or multivariate analysis of variance. The stepwise approach builds the linear discriminant model variable by variable: at each step, all variables not currently in the model are evaluated to determine which contributes most to discrimination between the groups. That variable is then added to the model. The process continues until the remaining (excluded) variables do not significantly contribute to discrimination between the groups. The F probability for a waveform feature to enter and be removed from the discriminant analysis was set at 0.05 and 0.10, respectively.
RESULTS
Means and standard errors of the mean by ICP or CPP and group are presented in Table 1 for the selected physiologic variables of ICP, CPP, MAP, core body temperature (°C), heart rate (min−1), and arterial PaCO2 (mmHg). ICP increases and CPP decreases as ALF progresses from group 1 to group 3 for either ICP or CPP groupings. Likewise, MAP declines from group 1 to group 3 despite the clinical objective of MAP maintenance. The core body temperature remained near normal for all groupings. The heart rate tended to rise as ALF progressed. Finally, PaCO2 declined somewhat as ALF progressed. This occurred because of an attempt made to reduce ICP by hyperventilation.
| ICP Groups | Group 1 | Group 2 | Group 3 | |||
|---|---|---|---|---|---|---|
| Mean | SEM | Mean | SEM | Mean | SEM | |
| ICP | 14.4 | 0.5 | 24.2 | 0.4 | 37.1 | 1.3 |
| CPP | 75.7 | 1.7 | 67.3 | 2.4 | 48.7 | 3.4 |
| MAP | 90.2 | 1.4 | 91.5 | 2.2 | 85.8 | 2.8 |
| T | 37.5 | 36.5 | ||||
| HR | 103.2 | 3.2 | 99.1 | 1.9 | 112.4 | 3.7 |
| PaCO2 | 30.6 | 0.7 | 28.7 | 1.2 | 28.6 | 0.9 |
| Discriminating waveform features | ||||||
| VSW | 55 | 2 | 96 | 5 | 79 | 3 |
| τS | 0.42 | 0.01 | 0.46 | 0.01 | 0.46 | 0.01 |
| SWU | 3 | 27 | −103 | 38 | −618 | 46 |
| αSD | 66 | 2 | 52 | 2 | 35 | 2 |
| CCP Groups | Group A | Group B | Group C | |||
| Mean | SEM | Mean | SEM | Mean | SEM | |
| ICP | 15.9 | 1.2 | 18.7 | 0.9 | 28.9 | 1.8 |
| CPP | 90.6 | 1.3 | 69.8 | 0.9 | 45.9 | 1.9 |
| MAP | 106.5 | 1.2 | 88.5 | 1.0 | 74.8 | 1.8 |
| T | 37.5 | 35.3 | ||||
| HR | 91.3 | 3.8 | 100.4 | 1.7 | 110.7 | 2.6 |
| PaCO2 | 31.9 | 0.8 | 29.5 | 1.0 | 26.3 | 0.9 |
| Discriminating waveform features | ||||||
| SSD | −293 | 17 | −421 | 20 | −727 | 54 |
| SWU | 34 | 23 | −10 | 25 | −582 | 39 |
| SDD | −53 | 2 | −76 | 5 | −84 | 8 |
| αSD | 51 | 1 | 68 | 2 | 39 | 2 |
- Abbreviations: αSD, start diastole angle; CPP, cerebral perfusion pressure (mmHg); HR, heart rate (min−1); ICP, intracranial pressure (mmHg); MAP, mean arterial pressure (mmHg); PaCO2, arterial CO2 pressure (mmHg); SDD, diastolic downstroke slope; SEM, standard error of the mean; SSD, systolic downstroke slope; SWU, Windkessel upstroke slope; τS, fraction of time spent in systole; T, core body temperature (°C); VSW, start Windkessel velocity.
Linear discriminant analysis of the ICP groups isolated 4 waveform features (the blood velocity at the start of the Windkessel effect, the slope of the Windkessel upstroke, the angle between the end systolic downstroke and start diastolic upstroke, and the fraction of time spent in systole) that could be used to successfully classify 61% of group 1 (ICP < 20 mmHg), 53% of group 2 (20 mmHg ≤ ICP < 30 mmHg), and 67% of group 3 (ICP ≥ 30 mmHg) into the proper groups (see Table 2). Means and standard errors of the mean of the 4 discriminant waveform features for subjects correctly classified (true classification) in each group are provided in Table 1.
| Predicted ICP Group | |||
| Actual ICP group | 1 | 2 | 3 |
| 1 | 61 (62) | 28 (29) | 11 (11) |
| 2 | 27 (20) | 53 (39) | 20 (15) |
| 3 | 18 (6) | 15 (5) | 67 (22) |
| Predicted CPP Group | |||
| Actual CPP group | A | B | C |
| A | 76 (32) | 19 (8) | 5 (2) |
| B | 38 (42) | 43 (48) | 19 (21) |
| C | 21 (12) | 16 (9) | 63 (35) |
- NOTE: n in parentheses.
Figure 3 depicts TCD waveforms constructed from the average values of the variables for correctly classified subjects in each ICP group. As ICP rises from group 1 to group 2, the blood flow velocity increases because of external compression on the artery reducing the vessel diameter. Consequently, the blood velocity at the start of the Windkessel effect becomes greater because of the overall velocity shift upward. The slope associated with Windkessel upstroke decreases because of reduced compliance of the arteries. The angle between the systolic and diastolic phases becomes more acute as ALF progresses from group 1 to group 3. Finally, despite contraction of the waveform cycle with respect to time with progressing disease state, the fraction of time spent in systole increases.
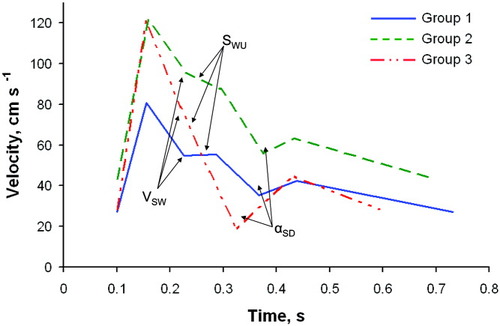
Average linearized TCD waveforms calculated from Group 1 (ICP < 20 mmHg; mean ICP = 14 mmHg; range ICP = 5-19 mmHg), Group 2 (20 mmHg ≤ ICP < 30 mmHg; mean ICP = 24 mmHg; range ICP = 20-29 mmHg), and Group 3 (ICP ≥ 30 mmHg; mean ICP = 37 mmHg; ICP range = 30-48 mmHg) data correctly classified by linear discriminant analysis. Highlighted significant classification features found by the discriminant analysis are: blood velocity at start of the Windkessel effect (VSW); slope of the Windkessel upstroke (SWU); angle between systolic downstroke and diastolic upstroke (αSD). Although not specifically identified in order to maintain clarity, note that the time associated with αSD, which is tS, decreased (shifts left) with increasing ICP.
Linear discriminant analysis of the CPP groups isolated 4 waveform features (the slope of the Windkessel upstroke, the slope of the Windkessel downstroke, the slope of the diastolic downstroke, and the angle between the end systolic downstroke and start diastolic upstroke) that could be used to successfully classify 76% of group A (CPP > 80 mmHg), 43% of group B (80 mmHg > CPP ≥ 60 mmHg), and 63% of group C (CPP < 60 mmHg) into the proper groups (see Table 2). Means and standard errors of the mean of the 4 discriminant waveform features for subjects correctly classified in each group are provided in Table 1.
Figure 4 depicts TCD waveforms constructed from the average values of the variables for correctly classified subjects in each CPP group. The Windkessel effect is dampened and is lost as CPP decreases from group A to group C. This is reflected in the increasingly negative slopes associated with the Windkessel upstroke and the Windkessel downstroke. Unlike the ICP groupings, the angle between the systolic and diastolic phases is more obtuse for group B than group A and more acute for group C than both group A and group B. The fourth discriminating waveform feature in the CPP analysis, increasingly negative diastolic downstroke slope, is also evident in Fig. 4.
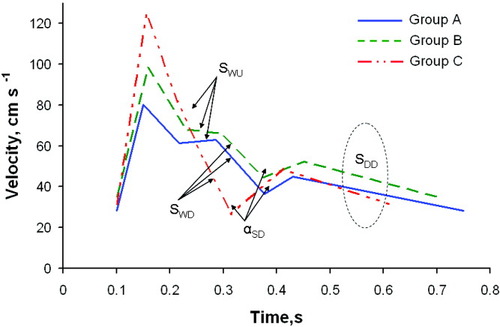
Average linearized TCD waveforms calculated from Group A (CPP ≥ 80 mmHg; mean CPP = 91 mmHg; range CPP = 81-110 mmHg), Group B (80 mmHg > CPP ≥ 60 mmHg; mean CPP = 70 mmHg; range CPP = 61-79 mmHg), and Group C (CPP < 60 mmHg; mean CPP = 46 mmHg; range CPP = 16-59 mmHg) data correctly classified by linear discriminant analysis. Highlighted significant classification features found by the discriminant analysis are: slope of the Windkessel upstroke (SWU); slope of the Windkessel downstroke (SWD); slope of the diastolic downstroke (SDD); and the angle between the end systolic downstroke and the start diastolic upstroke (αSD).
A time series of TCD scans (middle cerebral artery blood flow velocity versus time) from a patient with progressing ALF is shown in Fig. 5A-E. The dark line above the TCD scan in each frame represents a linearization of the waveform from the scan that was used in the data analysis. The linearized waveforms in Fig. 5A,B have a second peak in the systolic phase that reflects the Windkessel effect. As ICP increases and CPP decreases (Fig. 5C-E), the Windkessel effect disappears, and the systolic peak sharpens and narrows.
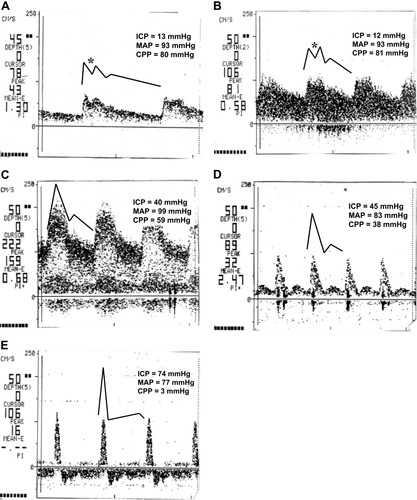
Transcranial Doppler waveform recordings from a single patient with progressing acute liver failure. In addition to sharpening of the systolic peak in the waveform, the waveform changes from one that includes a Windkessel effect (asterisks in panels A and B) to one that does not as liver failure progresses. Abbreviations: CPP, cerebral perfusion pressure; ICP, intracranial pressure; MAP, mean arterial pressure.
DISCUSSION
The time series of TCD scans presented in Fig. 5 is a vignette representing a natural history of the progressing disease states in ALF with respect to cerebral perfusion. Figure 5A reflects a nearly normal velocity waveform with a distinguishable Windkessel notch and relatively small acceleration at the start of diastole. Even though MAP, ICP, and CPP are almost the same in Fig. 5B and in Fig. 5A, there is a marked difference in the shape of the TCD waveform because of the 50% increase in cerebral blood flow [from 20 (Fig. 5A) to 31 mL/100 g/minute (Fig. 5B)] and cerebral vasodilation as evidenced by the increased CBFV. As the cerebral hemodynamics continue to deteriorate (Fig. 5C, ICP = 40 mmHg), the TCD waveform shows loss of the Windkessel effect because of dysfunctional elasticity of the intracranial vessels (vasoparalysis)24 and increased extramural pressure from cerebral swelling. Both of these effects limit expansion of the intracranial arteries during the opening of the aortic valve in the cardiac cycle. However, MAP is still sufficient to drive significant blood flow through the narrowed vessels as evidenced by the high CBFV. Figure 5D depicts the combination of rising ICP and falling MAP, which results in a sharply defined systolic flow peak at lower peak velocity as the net driving force, CPP, drops. In the final stage of disease progression, with a net driving force near zero, Fig. 5E shows a very sharp systolic peak with probable retrograde flow during diastole as the extramural pressure squeezes the arterial vessel closed between cardiac cycle pressure pulses.
The TCD sequence in Fig. 5 indicates that TCD can provide information about the dynamic state of the intracranial circulation and perfusion. However, the determination of quantitative relationships between the various parameters that characterize the state of intracranial hemodynamics with the physiologic status of a patient is difficult because of the complexity and variation of the many physiological factors acting at the same time in the regulation of the cerebral circulation. For example, unlike peripheral circulation, the magnitude of the cranial blood pressure pulse is dependent on the restricted volume of the intracranial contents as well as the elasticity and volume of the blood vessels, and this makes interpretation of the TCD waveform more complex. Fluctuations in PaCO2, MAP, and temperature, which are common in ALF patients, further complicate interpretation. For example, declining PaCO2 with progressing disease state (Table 1) is associated with reduced blood vessel elasticity and thus reduced elastic rebound (Windkessel effect) from the pressure pulse. Such complex interactions limit the ability to develop rigorous and quantitative descriptions for the prediction of intracranial conditions based on simple measurements.
PI has been the most commonly used parameter for estimating changes in ICP because of its simplicity of calculation. Indeed, PI has certain advantages; for example, it is not affected by minor changes in the angle of insonation, and it reflects a combination of several physiological factors, including the resistance in the distal vessels, elasticity of the vessel wall, and size of the vessels. However, the shortcomings of PI are that it is influenced by multiple factors such as the heart rate, systemic blood pressure, and arterial oxygen and carbon dioxide tension. Consequently, PI alone is insufficient to characterize the overall intracranial hemodynamic condition.14, 29-32
In particular, PI cannot capture information about the Windkessel effect. The Windkessel effect arises from the elastic compliance of arterial vessels. A pressure wave (forward systole) traveling along an artery causes (elastic) expansion of the artery against the surrounding tissue. The amount of expansion is proportional to the pressure difference between the interior (arterial) and exterior (cranial) sides of the vessel. As the pressure pulse recedes (reverse systole), the artery returns to its original diameter, returning energy to the flow, which is evidenced as an acceleration in flow velocity. Increased extramural pressure (for example, cerebral swelling) or arterial vasoparalysis due to declining CO2 concentration reduces the ability of the cranial arteries to expand and contract with the change in pressure generated by the opening and closing of the cardiac aortic valve. As a result, rising ICP reduces the arterial expansion from the pressure pulse and thus reduces the secondary acceleration associated with the Windkessel effect. Sufficiently high ICP prevents arterial expansion with the systolic pressure wave and leads to loss of the Windkessel effect.
Rather than use a single lumped parameter index such as PI (which simply looks at the extrema in flow velocities), this study indicates that other easily identifiable and calculable features of the TCD waveform that noticeably change as both ICP and CPP change can be advantageously used to infer the state of cerebral perfusion with little addition of complexity. The visual, linearized TCD waveform, as presented in Fig. 2, is characterized by 7 (time, velocity) pairs from which additional parameters such as the mean cycle velocity, PI, RI, accelerations, and angles can be calculated (see the appendix). The present work is a retrospective analysis used to determine whether these features contain useable information about ICP and CPP suitable for clinical decision purposes.
As illustrated in Figs. 3 and 4, the average TCD waveforms that characterize the state of cerebral perfusion based on the linear discrimination analysis are remarkably similar, regardless of whether ICP or CPP is used as the grouping variable. The ICP group 1 (Fig. 3) and CPP group A (Fig. 4) waveforms reflect the expectations of normal cerebral perfusion with a pronounced Windkessel effect. As ICP begins to rise or CPP begins to fall, the ICP group 2 (Fig. 3) and CPP group B (Fig. 4) waveforms both reflect an increase in the systolic velocity and loss in arterial compliance, as reflected by the Windkessel notch angle becoming more obtuse and by lessening of the Windkessel upstroke slope. Finally, the waveforms associated with the elevated ICP group 3 (Fig. 3) and low CPP group C (Fig. 4) evidence complete loss of the Windkessel effect. The similarity in waveform shapes between ICP and CPP for the various groups is even more striking when one considers that ICP and CPP are intimately related by Equation 1 and that clinical management strategy is to maintain constant MAP through the use of volume and vasopressors.
The value of any classification system has to be evaluated in terms of its clinical usefulness. The fact that the linear discriminant analysis produced remarkably similar average waveforms regardless of classification by ICP or CPP indicates that it may be a clinically useful tool for helping to guide the decision of whether further invasive monitoring, such as placement of an ICP probe, is warranted.
Even though the present TCD waveform analysis could correctly classify subjects into the proper ICP/CPP group 43%-76% of the time (see Table 2), the results are encouraging given that this is a retrospective study used to determine whether further effort in developing ICP/CPP group predictive capability from TCD waveform analysis is worth pursuing. Known factors that limited the ability of the linear discriminant analysis to correctly classify the linearized TCD waveforms used in this work into appropriate groups include the following: (1) the TCD scans that were used were of variable quality (for example, light to dark contrast and skewed time and velocity axes); (2) the (velocity, time) points that characterized an individual, linearized TCD waveform were visually identified, were somewhat subjective, and could vary between different observers; (3) stratification into groups arbitrarily converted continuous variables, ICP and CPP, into classification variables; and (4) the choice of the ICP or CPP cutoff between the groups, based on current clinical practice with respect to medical intervention, was somewhat arbitrary.
The first 2 factors can be overcome by real-time fast Fourier spectral transformation of the TCD waveform. The resulting spectral information will contain all of the original waveform information and is not subject to the problems cited. Given that the objective of this work is a clinical decision-making tool about the need for intervention rather than accurate prediction of actual ICP, the second 2 factors represent constraints on classification performance that should be investigated more rigorously in a prospective study.
In conclusion, measurement of CBFV by TCD is useful as a screening tool in the qualitative assessment of vasospasm, stenosis, cerebral blood flow, ICP, and cerebral embolic episodes. Information obtained by TCD waveform analysis can not only assist in screening but can also provide quantitative assessment of cerebral hemodynamics. The preliminary results on the correlation of TCD waveform features with the state of cerebral perfusion are promising. Improved predictive capability for ICP and CPP from TCD is expected from the correlation of the real-time fast Fourier transform spectrum of the waveform with ICP and CPP.
APPENDIX
| Feature | Symbol | Equation |
|---|---|---|
| Mean cycle velocity (cm s−1) | VM | VM = 0.5∑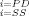 (Vi+1 + Vi)(ti+1 − ti)/(tED − tSS) (Vi+1 + Vi)(ti+1 − ti)/(tED − tSS) |
| Pulsatility index | PI | PI = (VPS − VED)/VM |
| Resistive index | RI | RI = (VPS − VED)/VED |
| Fractional time in systole | τS | τS = (tSD − tSS)/(tED − tSS) |
| Slopes (ΔV/Δt; cm s−2) | ||
| Systolic upstroke (SU) | SSU | SSU = (VPS − VED)/(tPS − tSS) |
| Systolic downstroke (SD) | SSD | SSD = (VSW − VPS)/(tSW − tPS) |
| Windkessel upstroke (WU) | SWU | SWU = (VPW − VSW)/(tPW − tSW) |
| Windkessel downstroke (WD) | SWD | SWD = (VSD − VPW)/(tSD − tPW) |
| Diastolic upstroke (DU) | SDU | SDU = (VPD − VSD)/(tPD − tSD) |
| Diastolic downstroke (DD) | SDD | SDD = (VED − VPD)/(tED − tPD) |
| Angles (°) | ||
| Peak systole (PS) | αPS | αPS = 180(1 + (tan−1(SSD/100) − tan−1(SSU/100))/π) |
| Start Windkessel | αSW | αSW = 180(1 + (tan−1(SSD/100) − tan−1(SWU/100))/π) |
| Peak Windkessel (PW) | αPW | αPW = 180(1 + (tan−1(SWD/100) − tan−1(SWU/100))/π) |
| Start diastole (SD) | αSD | αSD = 180(1 + (tan−1(SWD/100) − tan−1(SDU/100))/π) |
| Peak diastole (PD) | αPD | αPD = 180(1 + (tan−1(SDD/100) − tan−1(SDU/100))/π) |
| End diastole (ED) | αED | αED = 180(1 + (tan−1(SDD/100) − tan−1(SSU/100))/π) |
- Abbreviations: tED, end diastole time; tPD, peak diastole time; tPS, peak systole time; tPW, peak Windkessel time; tSD, systolic downstroke time; tSS, start systole time; tSW, start Windkessel time; VED, end diastolic velocity;VPD, peak diastole velocity; VPS, peak systolic velocity; VPW, peak Windkessel velocity; VSD, start diastole velocity; VSW, start Windkessel velocity; ΔV, change in velocity; Δt, change in time.




