Characteristics of Bubble Oscillations During Laser-Activated Irrigation of Root Canals and Method of Improvement
Conflict of Interest Disclosures: All authors have completed and submitted the ICMJE Form for Disclosure of Potential Conflicts of Interest and have disclosed the following: Two of the authors (Matjaž Lukač and Nejc Lukač) are affiliated also with Fotona, d.o.o.
Contract grant sponsor: Ministry of Education, Science and Sport, Slovenia; Contract grant numbers: L3-7658, P2-0392; Contract grant sponsor: Fotona d.o.o.
Abstract
Background and Objectives
Laser-activated irrigation of dental root canals is being increasingly used as its efficacy has been shown to be superior compared with conventional techniques. The method is based on laser-initiated localized fluid evaporation and subsequent rapid bubble expansions and collapses, inducing microfluid flow throughout the entire volume of the cavity. The irrigation efficacy can be further improved if optimally delayed “SWEEPS” double laser pulses are delivered into the canal. This study aims to show that the irrigation efficacy, as measured by the induced pressure within the canal, is related to the double pulse delay, with the maximal pressure generated at an optimal delay. The second aim is to find a method of determining the optimal delay for different cavity dimensions and/or laser parameters.
Study Design/Materials and Methods
Experiments were made in transparent models of root canals where Er:YAG laser (λ = 2.94 μm, pulse duration tp = 25 or 50 microseconds, and pulse energies up to EL = 40 mJ) was used with a combination of cylindrical and conical fiber-tip geometries (diameters 400 and 600 µm). High-speed photography (60,000 fps) and average pressure measurements inside the canal were used for process characterization.
Results
The results show that a pressure amplification of more than 1.5 times occurs if the laser pulse delay approximately coincides with the bubble oscillation time. Correlations between normalized oscillation time and canal diameter for a wide range of laser pulse energies (R2 = 0.96) and between the average pressure within the canal and the bubble oscillation periods (R2 = 0.90) were found. A relationship between the bubble oscillation time and the diameter of the treated cavity was found depending on the bubble oscillation time in an infinite fluid reservoir.
Conclusions
The bubble oscillation time within a constrained volume can be determined based on the known oscillation time in infinite space, which offers a fast and simple solution for optimization of the laser parameters. These findings enable determination of optimal conditions for shock wave generation, and improvement of root canal irrigation at the same dose of laser energy input, leading to improved treatment efficacy and safety. Lasers Surg. Med. © 2020 The Authors. Lasers in Surgery and Medicine published by Wiley Periodicals, Inc.
INTRODUCTION
Laser-activated irrigation (LAI) of root canals is a procedure, where elimination of pathogenic substances from the root canal system is driven by laser-induced cavitation [1]. Due to the complex, three-dimensional anatomy of root canals, a significant portion of canal wall surfaces (20–60%) remain un-instrumented with standard mechanical techniques [2]. Furthermore, mechanical instrumentation creates a smear layer along with an accumulation of surface debris [3]. To remove the smear layer and debris produced during instrumentation, as well as eradicate potential pathogens, irrigation is required [4].
Numerous techniques have been introduced to improve the efficacy of standard syringe root canal irrigation [5-9]. One such technique is a LAI, which generates a micro-cavitation within the irrigant inside the root canal system [10-13].
Due to the high absorption of Erbium lasers with a wavelength around 3 μm in the irrigant, the LAI concept initiates the rapid formation of a vapor bubble at the fiber tip (FT) while it is immersed in the irrigant [14-16]. This triggers a turbulent fluid movement within the entire canal, leading to improved chemomechanical debridement [13, 17-20]. An example of LAI is the photon-induced photoacoustic streaming method, performed with a single Er:YAG laser super short pulse with a duration of 50 microseconds [16, 18, 19].
The principle behind the cavitation phenomena is the difference in compressibility between a gas and a liquid. The volume of liquid hardly changes in response to a variation in pressure, whereas the volume of the gaseous interior of a bubble can change dramatically. Any contraction or expansion of the bubble is inevitably accompanied by a displacement of an equal volume of the much denser surrounding liquid. As a result, a strong bubble response in combination with the compressible interior can provide not only localized fluid motion, but also a tremendous focusing of liquid kinetic energy. Of particular interest for cleaning are the shock waves that may form during the bubble's collapse. These shock waves spread through the volume at supersonic speeds and interact disruptively with the surrounding environment (e.g., cavity walls). These waves are not only very effective in removing any contamination from the cavity surfaces, but can also kill bacteria, leading to a partial or complete disinfection of the treated cavity. Significant inactivation of the Escherichia coli bacteria has been reported in Šarc et al. [21] where cavitation has been induced hydrodynamically.
In an infinite liquid, a shock wave is emitted during the accelerated contraction of the bubble cavity. However, in a confined environment such as an endodontic access opening, a free expansion of the bubble is not possible, and the expansion and contraction of the bubble is slowed down by the added resistance to flow due to the impermeability and the no-slip condition on the cavity's surface. This process slows down the dynamics of the bubble's expansion and implosion compared with a free liquid situation, and the period of the bubble's oscillations can be significantly extended up to ten times [22].
For this reason, a SWEEPS (Shock Wave Enhanced Emission Photoacoustic Streaming) technique has been developed, as a solution for improving the efficacy of LAI in narrow endodontic cavities [13, 20, 22-24]. The SWEEPS shock wave enhancing technique consists of delivering a properly timed second laser pulse during the collapse phase of the primary bubble generated by a first laser pulse. The growth of the second cavitation bubble accelerates the collapse of the first cavitation bubble, leading to a violent collapse, during which shock waves are emitted. The shock waves are generated not only by the accelerated collapse of the primary cavitation bubble but also by the simultaneous collapse of the accompanying smaller secondary bubbles deeper within the endodontic space, potentially increasing the cleaning and disinfecting efficacy of laser-induced irrigation to a significant degree.
As the optimal delay between the two SWEEPS laser pulses depends on the cavitation bubble's oscillation period, this presents a challenge. Namely, for the same laser parameters the bubble oscillation period and consequently the optimal SWEEPS delay varies with the size and shape of each individual endodontic access opening. For this reason, it is important to understand how bubble dynamics changes in constrained endodontic spaces.
In this research, we first studied how the cavitation bubble size and oscillation period depend on the diameter of a cylindrical model of the endodontic cavity. We then measured the dependence of the internal pressures generated in a root canal model on the bubble oscillation period. Finally, we studied the dependence of the generated pressures on the SWEEPS pulse pair temporal separation.
MATERIALS AND METHODS
Experimental System
The experimental system for studying characteristics of cavitation bubbles as generated by single or dual laser pulses in constrained cavity is shown in Figure 1. The simulated transparent root canal models of different shapes and sizes were submerged 4 mm deep under the water level of a large reservoir (150 × 100 × 100 mm). The cavitation inside the canal was induced using an Er:YAG laser (LightWalker; Fotona d.o.o., Slovenia, λ = 2.94 μm) equipped with a dental handpiece (H14, Fotona d.o.o.) optically coupled with an interchangeable FT.
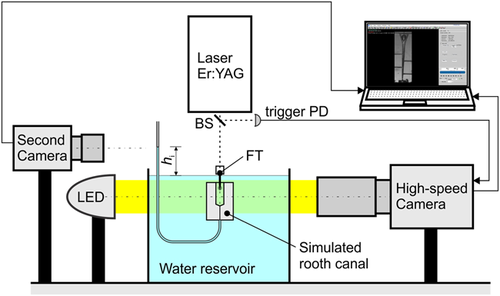
A high-speed camera (Fastcam SA-Z; Photron, Japan) with 1:1 magnification lens (Sigma APO Macro, Sigma corporation, Japan, f = 180 mm, F2.8) was used to observe cavitation dynamics within a simulated root canal. Its frame rate at full resolution (1,024 × 1,024 pixels) is 20,000 fps. We typically used a frame rate 60,000 fps at reduced resolution of 300 × 1,024 pixels, and shutter time 200 nanoseconds. In order to see a sharp boundary between the bubble and surrounding liquid, we used back illumination with one 50,000 lumen LED reflector (XHP 50000; X-LED technology, Netherlands). The camera was triggered by laser pulses using a trigger photodiode, which detects laser light partially reflected by a beam splitter.
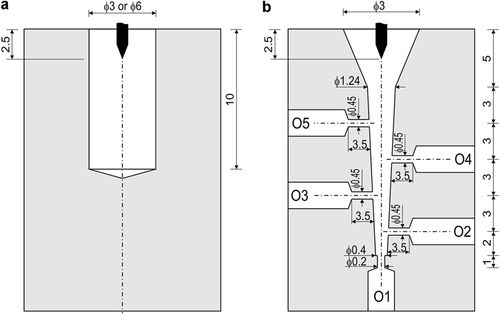
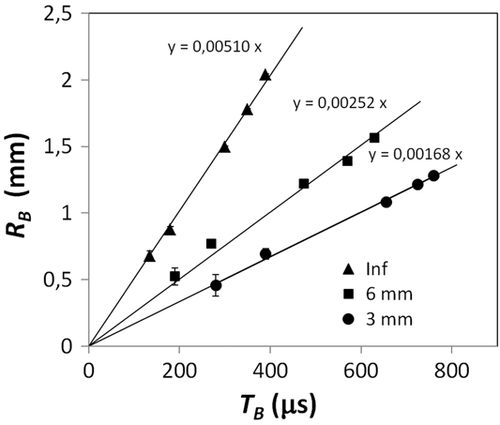
The simulated root canals were made from transparent polymethyl methacrylate blocks (15 × 15 × 30 mm) in three shapes (see Fig. 2): cylindrical with diameter 3 and 6 mm and conical with side openings. The cylindrical canals were used for measuring the bubble's maximal radius (RB) characterizing the bubble's maximal volume (Vmax), and its oscillation period (TB), while the conical canal was used for measuring laser-induced pressures at different regions inside the canal.
Measurement of the bubble size and oscillation period was based on analyzing the image sequences acquired by the high-speed camera. A typical example is shown in Figure 3, where the yellow ellipse (at 170 microseconds) marks the image with the maximal bubble size and the yellow rectangle (at 380 microseconds) marks the moment of the first collapse.

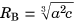 (1)
(1)The oscillation period TB is determined simply by finding the image and the corresponding time where the first collapse occurs.
The pressure measurement was based on observation of water column heights inside of each tube connected to the five openings (O1…O5) located at different depths of the conically shaped root canal (see Fig. 2b). The tubes with an internal diameter of 1.6 mm were ended with a vertical section extending 10 cm above the water level. A second camera (Chameleon3, 1.3 MP; PointGrey, Richmond, Canada) was used for measuring the water level heights simultaneously for all five water columns, with a resolution of 0.25 mm and frequency of 10 measurements per second. A custom computer program was developed for video data processing in order to detect the water level in each tube and store the measured values, hi, into a data file.
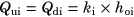 (2)
(2)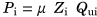 (3)
(3)Here, μ is the fluid's viscosity (µwater = 8.90 × 10−4 Pa·s at 25°C), Qui is the measured downward average fluid flow at the equilibrium stage, and Zi = 8li/(πri4) is the constriction's flow resistance where ri is the radius and li is the length of the constriction. It is to be noted that at the equilibrium, that is, when during laser irradiation the height of the columns stops rising (see Fig. 4), the pressure difference (Pi) resulting from the water column's weight, that is, pushing the liquid back into the root canal, and the root canal's internal pressure (Pint−i) resulting from the laser-generated bubble dynamics, that is, pushing the liquid out of the root canal, become equal and therefore Pint−i = Pi.
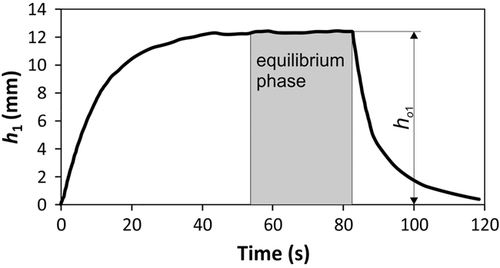
This technique is advantageous in comparison with other pressure measurement techniques such as with piezo transducers or fiber-optic pressure sensors, as it allows simultaneous pressure measurements at different closely spaced locations (see Fig. 2b). With our technique, the number of simultaneous measurement locations is limited only by the camera's measuring range.
The average pressure within the entire canal (Pavg) was calculated as Pave = (P1 + P2 + P3 + P4 + P5)/5.
Experiments
Analysis of the bubble size and oscillation period in relation to the diameter of the simulated canal cavity was done in cylindrical models with diameters of 3 and 6 mm. In addition, we also measured bubble dynamics in a water reservoir without a canal to simulate infinite space. Single Er:YAG laser pulses of duration tp = 50 microsecond and pulse energies EL = 5, 7.5, 19, 26, and 34 mJ were used. A flat-ended 14 mm long cylindrical FT of 400 µm diameter (Fotona Flat Sweeps400, Sigma corporation) was used.
Pressure measurements were made in a conical root canal using single laser pulses of durations tp = 25 and 50 microseconds, and pulse energies EL = 10, 20, 30, and 40 mJ. Each combination of pulse duration and energy was used on four FT (all were 14 mm long): a flat-ended cylindrical FT of 400 µm diameter (Fotona Flat Sweeps400), a flat-ended cylindrical FT of 600 µm diameter (Fotona Flat Sweeps600), a conically-ended (with subtended angle of 34°) cylindrical FT of 400 µm diameter (Fotona Radial Sweeps400) and a conically-ended (with subtended angle of 34°) cylindrical FT of 600 µm diameter (Fotona Radial Sweeps600). Bubble oscillation times TB were measured with a high-speed camera during the pressure measurements.
Finally, the dependence of the temporal separation of the SWEEPS dual pulses (Tp) on the generated pressures was measured using two FT geometries (Radial Sweeps400 and Radial Sweeps600). The sum of the energies of the first and second laser pulse in the SWEEPS pulse pair was 20 ± 4 mJ and the energy of the first pulse was EL = 12 ± 2 mJ. The duration of each laser pulse was tp = 25 microseconds. The temporal separation time Tp was varied in intervals from 220 to 570 microseconds with increments of 20 or 40 microseconds. Coarser increments were used at the beginning and at the end of the interval, where we didn't expect significant pressure amplification.
In all cases, the laser FT endings were positioned 2.5 mm deep into the access cavity, according to the photon-induced photoacoustic streaming protocol [18]. An XYZ micrometer positioning stage and a camera with the optical resolution of 0.1 mm were used in order to assure repeatable FT positioning. In all experiments, at least seven measurements were repeated for each combination of parameters. Average values and standard deviations were then calculated and presented in the results.
RESULTS
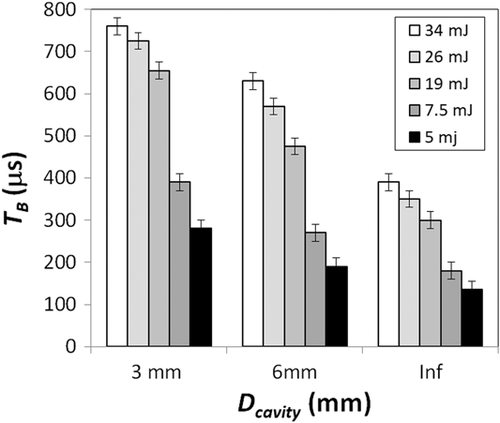
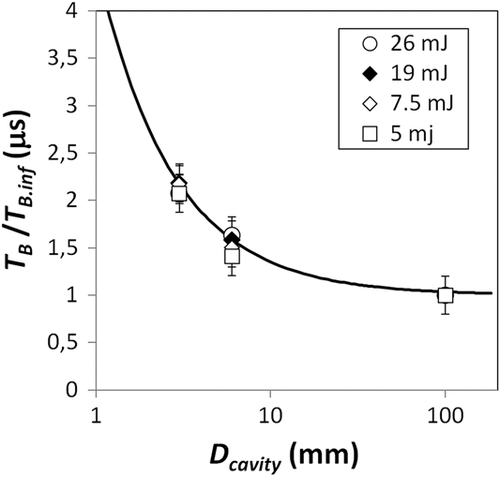
Figure 5 shows the measured dependence of the bubble oscillation period TB on the diameter Dcavity of the cylindrical cavity model for Er:YAG laser pulse energies EL in the range from 5 to 34 mJ.
The maximal bubble radiuses RB, corresponding to the bubble oscillation periods shown in Figure 5 above are depicted in Figure 6.
The temporal rate of the bubble's growth and collapse as represented by RB/TB is shown in Figure 7. As can be seen, the rate of the bubble's collapse is by a factor of about three or two times slower in cylindrical cavities of diameter 3 and 6 mm, correspondingly, in comparison with the rate of the bubble's collapse in an unconstrained infinitely large fluid reservoir.
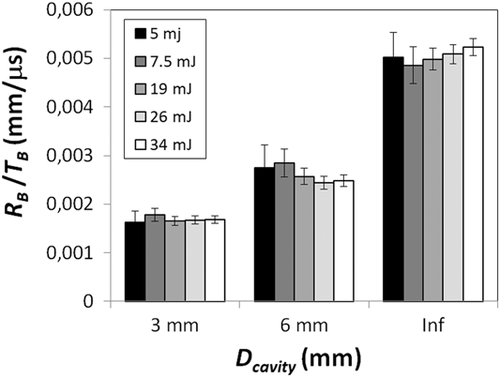
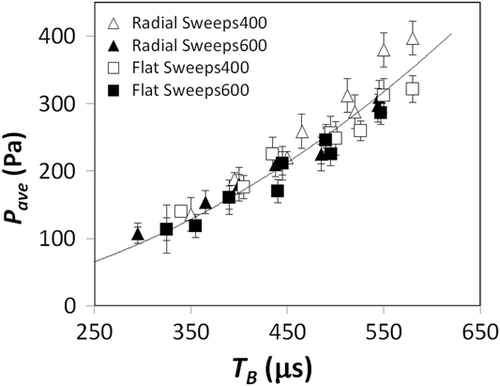
Figure 8 shows the relationship between the measured average pressures in the root canal model and the corresponding cavitation bubble oscillation periods, TB, as generated by single Er:YAG laser pulses. The eight data points for each of the FT geometries used represent the results as obtained for pulse durations tp = 25 and 50 microseconds and laser pulse energies EL = 10, 20, 30, and 40 mJ.
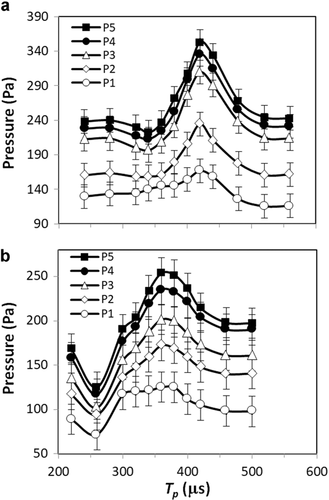
Finally, Figure 9 shows the dependence of the pressures along the depth of the root canal, as a function of the temporal separation (Tp) of the SWEEPS dual pulses for two FT geometries, Radial Sweeps400 (Fig. 9a) and Radial Sweeps600 (Fig. 9b). For each FT geometry, the maximum pressure is located approximately at the pulse separation being equal to the oscillation period of the primary bubble as generated by the first pulse of the SWEEPS pulse pair. The oscillation periods were TB = 405 ± 15 microseconds for the 400 µm FT and TB = 365 ± 15 microseconds for the 600 µm FT.
DISCUSSION
A challenge involved in using the innovative SWEEPS technique is that the separation between the two laser pulses (Tp) should not deviate substantially from the optimal separation (Tp.opt). This was shown in Lukač and Jezeršek [22], where the optimal separation time (Tp.opt) for the enhanced shock wave generation was found to be the pulse repetition time where the subsequent bubble starts to develop near the end of the first bubble's period (TB). Our pressure measurements are in agreement with these findings since the pulse separation time where the largest pressure increase was observed to approximately coincide with TB (Fig. 8), that is, when the start of the rapid growth of the second bubble at t ≈ TB coincides with the collapse of the first bubble toward the end of its oscillation period TB. It is to be noted that during its development, the first bubble moves downwards and collapses at about half of its maximal diameter away from the FT (see Fig. 3), thus providing sufficient space for the growth of the second bubble.
When the same device is intended to be used for cleaning differently sized cavities, and/or with different device parameters (laser pulse energy or FT geometry, for example), obtaining a “SWEEPS” type enhancement poses a challenge, since as shown in Figure 5 the bubble oscillation time (TB) and consequently the optimal pulse repetition time (Tp.opt) depend critically on these conditions, being longer for smaller cavities and/or for higher laser pulse energies.
The main reason for this dependence is related to the confined cylindrical cavity where free expansion of the bubble in a lateral direction is not possible, and hence the fluid is pushed forward and backward in the canal. The pressure inside the bubble remains high for a longer time, as it has to fight against the resistance of the water, which has to be displaced in the small canal. This process slows down the dynamics of expansion and implosion, and introduces additional losses compared with a free space situation. In the cavity, the lateral and forward bubble expansion is limited by the cavity wall, while the backward expansion is blocked by the fiber, making the lumen of the cavity even smaller. This results in a two- or three-times slower bubble growth and collapse rate (RB/TB) compared with an infinite reservoir (see Fig. 7). Consequently, no shock waves were observed in our experiments for Dcavity = 3 and 6 mm, which is in agreement with [22]. More important, in the free reservoir, shock wave emission was present during the bubble's collapse [27].
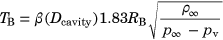 (4)
(4)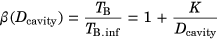 (5)
(5)
It is to be noted that the above relationship appears to be applicable not only to bubbles generated by Er:YAG laser pulses, but to bubble generation by any energy device means.
In endodontic root canal treatments, the endodontist makes an access cavity in the crown of the tooth in order to enable cleaning and shaping of the interior of each of its root canals. It is to be noted that in endodontics the cavitation bubble dynamics is determined mainly by the dimensions of the access cavity in the vicinity of the FT, and not by the size, curvature, and complexity of the root canal beneath the cavity. Clinically, the size and shape of the lateral surface of the access cavity depends on the tooth type, the patient, and also on the endodontist's skill and preference. For upper central and lateral incisors, the shape of the lateral surface is typically circular. For the first, second, and third molars the shape of the lateral surface is approximately quadrangular with rounded corners. And for other teeth, the shape of the lateral surface is approximately elliptical. The size and shape of the lateral surface is typically described by the mesiodistal (minor) Dmin, and buccolingual (major) Dmax cavity diameter, the diameters being in the range of about 0.5–7 mm. Our preliminary measurements on extracted teeth indicate that Equation (4) can be used also in clinical endodontics, provided that the diameter Dcavity in Equation (5) is taken as the average diameter of the access cavity (Dave = (Dmin + Dmax)/2), but further research needs to be carried out to confirm this conclusion.
Our results also show that there is an approximately square relationship between the bubble oscillation period and the generated average pressure within a cavity (Fig. 8), where Pave = 0.001 TB2 with R2 = 0.90. This offers the possibility of optimizing device parameters, such as laser wavelength, laser pulse energy, pulse duration, or FT geometry, by simply comparing measured bubble oscillation periods within the same cavity for all considered device parameters. The parameter combination, which results in the longest bubble oscillation period will be most effective also for pressure generation.
In a clinical setting, the access chamber is during the treatment kept filled-up using a syringe. In our experiment, the model root canal was for simplicity and constancy of experimental conditions, immersed in a water bath in order to avoid the need for replenishment of the irrigant due to the irrigant being pushed out of the model by the generated bubbles. This does not affect the conclusions of our experiment since in a separate research [22] it was shown that the bubble oscillation time is almost invariant to the FT depth within the irrigant reservoir.
In addition to irrigation efficacy, the patient's safety and the reduction of post-operative pain must also be considered. One of the questions involving SWEEPS is whether cavitation effects can extend also to the area outside of the apical constriction or outside of a perforated tooth. In our study, cavitation was observed only inside of the root canal, with no cavitation detected in the transparent tubes outside of any of the root canal model openings. We attribute this observation to the fact that cavitation occurs only if the liquid volume is subjected to sufficiently low pressure, and that due to the high flow resistance of the root canal narrow openings the pressure difference between the root canal and the surrounding falls below the cavitation pressure threshold. Therefore, we consider the risk of outside cavitation to be relatively small, especially for apical sizes ISO 10 to 40.
Another crucial safety consideration associated with any irrigation is the extrusion of the irrigant through the apical constriction, which can cause serious complications. The highest risk represents the chemical action of the extruded irrigant with the tissue and nerves, while the risk of bacteria getting expelled into the surrounding tissue is minimized because of the bactericidal effect of the irrigant. Apical extrusion studies [10, 19, 29, 30], have shown that the extrusion during LAI, including when using the SWEEPS technique [31], is smaller in comparison with conventional irrigation techniques such as needle and ultrasonic irrigation. However, further research is recommended to evaluate extrusion during SWEEPS irrigation under the enhanced pressure conditions.
Finally, it is worth noting that recently published studies with novel laser systems [32-34] suggest that laser ablation may be used also as an alternative to standard mechanical instrumentation in order to reduce generated debris and smear layer.
CONCLUSIONS
Laser-induced cavitation dynamics in constrained canals was examined with two measuring techniques. A high-speed camera was used to observe the life cycle of a cavitation bubble, where its maximal diameter and oscillation time were measured. A second measuring system was used for internal pressure measurement, where the principle of water level difference was used to measure time-average pressures at five regions within the model of the root canal.
Our study shows that internal pressure can be increased by a factor of 1.5 by using double Er:YAG laser pulses if they are optimally separated. The results show that for the pressure increase the separation time must approximately coincide with the single bubble oscillation time. Similar condition was found also for the generation of shock waves in spatially confined cavities [22].
Therefore, if the SWEEPS method is to be used in a wide spectrum of canal sizes, the relation between the bubble oscillation time and canal size must be known. We found good correlation (R2 = 0.96) between normalized oscillation time and canal diameter for a wide range of laser pulse energies. This means that we can determine the bubble oscillation time within a constrained volume if the oscillation time in infinite space is known. The practicability of this finding is in the fact that the oscillation time is much easier to measure in vitro in a large fluid reservoir using an optical method in comparison with in vivo techniques.
Our results also show good correlation (R2 = 0.90) between average pressure within the canal and the bubble oscillation periods. This offers a new method of laser parameter optimization by simply measuring the bubble oscillation periods within the same cavity. The parameter combination, which results in the longest bubble oscillation period will be most effective also for pressure generation.
These findings enable determination of optimal conditions for shock wave generation, and improvement of root canal irrigation at the same dose of laser energy input. Although only root canal treatments were considered in this study, our findings may be of benefit also for other medical procedures based on cavitation phenomena, such as fragmentation of urinary stones in laser lithotripsy [35], or removal of arterial blood clots in laser thrombolysis [36].
ACKNOWLEDGMENTS
This research was supported by the Ministry of Education, Science and Sport, Slovenia, under grants L3-7658, P2-0392, and Fotona d.o.o.