Deconvolution Techniques in Optical Coherence Tomography: Advancements, Challenges, and Future Prospects
Abstract
Optical coherence tomography (OCT) has become a breakthrough in medical imaging, providing high-resolution, non-invasive visualization of tissue microstructures. However, resolution degradation caused by the system's imperfect point spread function (PSF) necessitates advanced deconvolution algorithms. Despite progress, a comprehensive review of these techniques in the OCT field is lacking. This review examines the current state of deconvolution strategies to overcome the PSF-induced blurring and discusses their applications, challenges, potential solutions, and future directions. By surveying previous works, this work identifies technical milestones and categorizes them accordingly. Deconvolution in OCT continues to evolve, contributing to both fundamental research and biological imaging. Despite significant improvements in image resolution and signal-to-noise ratio (SNR), challenges remain in real-time clinical imaging, including optimization robustness and balancing accuracy with computational complexity. Future developments need to address these challenges, emphasizing the importance of comprehensive methodologies that integrate deconvolution with other image enhancement solutions like noise removal. Interdisciplinary collaboration and validation are crucial. The future of OCT deconvolution is rich with opportunities, from combining real-time artificial intelligence (AI)-aided OCT and multi-modal imaging to exploring complex algorithms with growing computational capabilities. As clinical adoption nears, rigorous testing and ethical diligence remain essential to fully realize the potential of OCT deconvolution techniques.
1 Introduction
1.1 The Advent of Optical Coherence Tomography (OCT), Image Degradation and Solutions
OCT has revolutionized medical imaging with its high-resolution, non-invasive imaging capabilities. Utilizing low-coherence interferometry, OCT captures tissue morphology at considerable penetration depths.[1] By virtue of its distinct advantages, OCT has become an indispensable tool across various medical fields, from ophthalmology to oncology.[2] For instance, OCT is the gold standard for retinal imaging, enabling early detection of macular holes and monitoring of diabetic retinopathy.[3] It has also gained significance in cardiology for plaque characterization in coronary arteries.[4] and in oncology for margin assessment during tumor resection.[5] Despite its high resolution, there are practical limitations.[6, 7] in achieving ideal resolution due to various unaddressed impairments by standard detection schemes. Figure 1 illustrates the OCT image formation process that leads to degradation (Top) and the types of enhancement processes (Bottom). Degraded OCT images often blur the distinction between pathology and normality, hindering diagnostic accuracy.
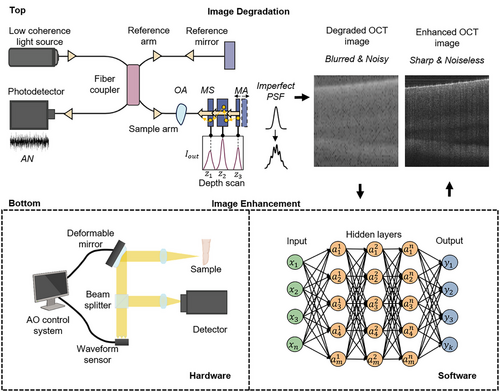
- (a) Noise: Noise in OCT imaging, both additive and multiplicative, originates from electronic noise of the apparatus, biological noise within tissues and speckle due to the coherence nature of OCT imaging, impeding the discernment of minute details crucial for precise diagnosis.[8, 9]
- (b) Light scattering: Tissue heterogeneity causes light path deviation, diminishing contrast, and creates a veil-like haze that obscures sharp tissue distinction, reducing the signal-to-noise ratio.[10]
- (c) Optical aberrations: Imperfections in OCT's optical elements and tissue refractive peculiarities cause aberrations, leading to image warping and ghosting effects that distort tissue structure interpretation.[11-14]
- (d) Blurring: Sample features that should be sharply defined appear indistinct due to defocus,[15] convolution with imperfect system point spread functions (PSFs), and patient or scanner motion,[16] veiling the subtle, yet critical, tissue alterations indicative of pathological conditions.
- (a) Light source enhancements: Shifting toward broadband and tunable lasers in swept-source OCT (SS-OCT).[17]
- (b) Additional optical components: Improved polarization control[18] through optical filters[19, 20] and microlenses.[21-23]
- (c) Adaptive optics (AO): AO[24] corrects wavefront distortions using devices like Shack-Hartmann wavefront sensors[25] and deformable mirrors (Figure 1, Hardware).
- (a) Light scattering mitigation: Computational adaptive optics (CAO)[26] and multiple scattering correction.[27]
- (b) Noise reduction: AI,[28-30] signal averaging[31] and Fourier-Domain techniques.[32]
- (c) Digital deblurring: Digital refocusing[33-35] to enhance clarity outside the focal plane and motion correction algorithms[36, 37] to remove motion blur.
- (d) System-agnostic remedies: AI-facilitated image processing[38] offers significant advancements.
CAO methods like single or multiple aperture synthesis[39-41] and interferometric synthetic aperture microscopy (ISAM)[42, 43] achieve high lateral resolution and extended depth of field. However, ISAM's limitations in imaging speed and highly scattering samples hinder real-time in vivo applications.[15] Optical coherence refraction tomography (OCRT) reconstructs clear images with isotropic resolution, where the image resolution is equivalently fine at all dimensions,[44, 45] but these solutions depend on specific illumination and detection. SHARP,[35] developed for phase-unstable SS-OCT systems, compensates for aberrations in multiple directions. When paired with phase correction,[32] noise suppression,[46] and digital refocusing[26] significant image performance improvements are achieved. Deconvolution techniques are noteworthy for reconstructing sharp images by rectifying the convolved PSFs, compensating for intrinsic system blurring. AI-assisted image processing (Figure 1, Software) stands out for its flexibility and promise. Deep learning models like artificial neural networks (ANN) have been adopted to eliminate noise,[8, 29, 30] enhance images,[38, 47, 48] remove scattering,[49] and blur.[50] Computational enhancement triumphs highlight its independence from specific hardware configurations, demonstrating field applicability while acknowledging processing demands and real-time operational challenges for widespread clinical adoption.
2 The Necessity of Deconvolution in OCT
Maintaining high OCT image resolution is critical for visualizing fine tissue structures, enabling accurate quantification of subtle tissue changes for early disease diagnosis and timely treatments.[4, 51] OCT systems' performance is characterized by axial and transverse resolutions reflected by the respective PSFs. In practice, the PSFs deteriorate, posing unique convolutional blurring challenges and an imbalance between theoretical perfection and actualized imperfection. Deconvolution provides a solution by directly reversing the blurring effect of the PSFs.[52] Accurate PSF modelling in the deconvolution process significantly enhances image resolution and contrast.[53] Deconvolution is particularly vital in specialties like ophthalmology, where minute retinal layer details can indicate early disease stages.[54] Additionally, deconvolution can compensate for patient or environmental motion, further enhancing OCT imaging reliability.[55, 56] Hence, deconvolution holds critical implications for patient outcomes and diagnostics. Exploring advanced deconvolution algorithms, combined with cutting-edge image enhancement and AI, is imperative to propel OCT into unprecedented diagnostic acuity.
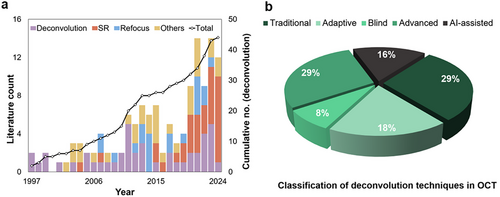
2.1 Objective and Outline of the Review
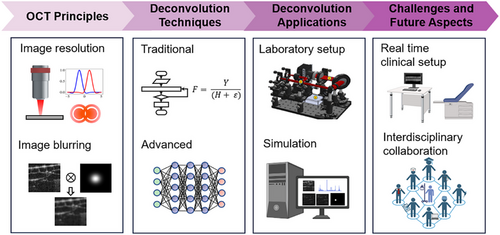
This review aspires to guide researchers and clinicians in OCT's progressive journey, offering an exhaustive analysis of deconvolution's present state and prospects, inspiring future research to enhance diagnostic clarity indispensable for patient care. Beginning with OCT's technological underpinnings and imaging challenges, the review explores various deconvolution strategies, appraising their merits, evaluative benchmarks, and clinical applicability. Significant image improvements are discussed, acknowledging existing barriers and future research required to expand OCT imaging proficiency by merging multiple image enhancement techniques. The review anticipates increased AI integration to refine deconvolution processes innovatively and comprehensively. A comprehensive literature review supports our insights, with sources like Google Scholar, PubMed, and OCT News informing our database from June 2022 till March 2025. Keywords like “Deconvolution OCT,” “De-blurring OCT,” “OCT super resolution,” and “OCT resolution enhancement” guided our review, identifying and analyzing research works implementing deconvolution techniques to mitigate PSF blurring in OCT. The identified deconvolution techniques are classified into traditional, adaptive, blind, advanced, and AI-assisted methods (Figure 2b). Increasing trends of computational OCT image resolution enhancement are summarized in Figure 2a, showcasing the evolution from basic deconvolution (Figure 2a, Deconvolution), dispersion and aberration compensation (Figure 2a, Others), to more advanced methods like refocus (Figure 2a, Refocus) and super resolution (Figure 2a, SR). Despite the rise of advanced technologies like AI-assisted SR that often require extensive datasets and may lack generalizability, deconvolution remains crucial for addressing PSF-induced blurring in OCT due to its clear understanding of the underlying degradation process. Unlike deconvolution, SR and AI-based methods frequently lack physical modeling of image degradation that essential for establishing confidence in medical image reconstruction. By emphasizing the strengths and weaknesses of deconvolution techniques, we aim to inspire future research integrating deconvolution interpretability with AI and computational methods for more robust and clinically reliable OCT image enhancement.
- 1) Technological Foundations and Imaging Challenges: Establishes the context by spotlighting challenges necessitating deconvolution within OCT.
- 2) Deconvolution Techniques: Explores an array of deconvolution strategies, from traditional methods to recent innovations.
- 3) Clinical Relevance and Case Studies: Highlights tangible clinical values through comparative analysis and case studies.
- 4) Current Limitations, Prospects for Advancement, and Future Directions: Reflecting on prevailing limitations and exciting prospects, particularly AI integration.
3 Fundamentals of OCT and Deconvolution in OCT
3.1 OCT Principles
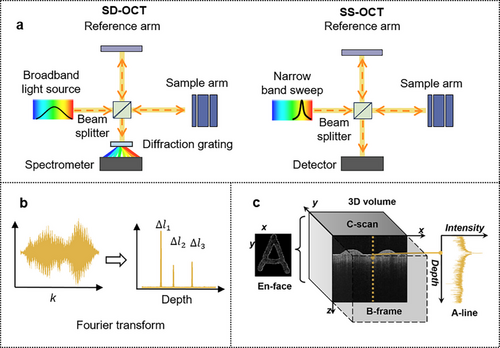
OCT utilizes low-coherence interferometry to generate high-resolution, cross-sectional images of biological samples. The technology pioneered through time-domain OCT (TD-OCT) and advanced by Fourier-domain variations (FD-OCT) including Spectral-Domain OCT (SD-OCT) and Swept-Source OCT (SS-OCT) 1, offering improved imaging speed and sensitivity[57, 58] (Figure 4a). Image construction is achieved by mechanically scanning the reference arm in TD-OCT and via spectral analysis in FD-OCT. General detection schemes in OCT use a focused Gaussian beam with common mode or confocal detection. Moreover, alternative illumination patterns like Bessel beams with double-pass illumination and detection,[21, 59] decoupled Gaussian mode detection,[60, 61] or the utilization of annular pupils,[39, 40, 62] are also prevalent, broadening the scope and adaptability of OCT in diverse applications.
4 Defining OCT Resolution and Associated Degradation
Resolution in OCT is decoupled into axial (depth) and lateral (transverse) components and can be characterized by the full-width-at-half-maximum (FWHM) of the respective PSFs. Coherence plays a critical role in defining these PSFs. Specifically, low temporal coherence[63] essentially improves the axial resolution and increases discrimination of depth-resolved features because interference only occurs within the short coherence length. Similarly, spatially incoherent illumination reduces the sensitivity of the PSF to optical aberrations,[64] improving the robustness of lateral resolution.
The axial resolution is determined theoretically by the coherence length of the light source, where is the central wavelength and the spectral bandwidth. Optimization of axial resolution can therefore be achieved through the employment of a broadband light source, that is, a shorter temporal coherence, particularly within the short-wavelength spectrum. Shorter wavelengths (800–950 nm) offer shallower penetration, while longer wavelengths (1050–1310 nm) achieve deeper penetration and visualization due to reduced scattering in biological tissues.[65-68]
However, complications arise within FD-OCT due to dispersion.[15, 69] As for SD-OCT, the material dispersion, particularly the high order ones, at 800 nm and 1060 nm domains are more severe compared to the counterpart operating at 1330 nm.[70] Additionally, SD-OCT suffers from the sensitivity roll-off.[71, 72] Both dispersion mismatch and sensitivity roll-off lead to signal strength degradation and axial resolution variation with depth (Figure 5a). In contrast, SS-OCT minimizes roll-off via swept lasers;[73, 74] but residual material dispersion still degrades the PSF and causes PSF variation with depth. Longitudinal chromatic aberration (LCA), caused by wavelength-dependent focal shifts, aggravates depth-dependent axial PSF degradation in broadband systems.[14, 75] Such effects are magnified when penetration depth differences between spectral components exceed the axial resolution, necessitating adaptive correction strategies to maintain resolution across imaging depths. Conversely, The lateral resolution for a focused Gaussian beam is inversely related to the effective numerical aperture (NA) of the objective, which controls the minimum focal spot size of the beam on the sample.[76, 77] While the spot sizes in x and y dimensions determine the respective resolutions, the focus spot is commonly regarded as a uniform circular shape, indicating that the x and y resolutions are equivalent. Hence, the terms “lateral” and “transverse” can refer to both the x and y resolutions interchangeably. The depth of field (DOF) or the confocal parameter b is related to by: , where b is twice the Rayleigh length, . Although a larger NA improves the lateral resolution,[2, 78] it yields a proportional reduction in DOF, revealing the trade-off between transverse clarity and the DOF. A narrow lateral PSF reflects high lateral resolution near the beam waist but broadens with the spread out of the beam (Figure 5b). Moreover, the signal strength decreases at out-of-focus regions. With the correspondingly reduced SNR and image quality, signal enhancement techniques need to be followed. Similar to LCA, transverse chromatic aberration (TCA) degrades the lateral resolution.[79, 80] However, if the focal shift is within the Rayleigh range, the resolution loss in the lateral direction would not be apparent.[14] These PSF degradations and variations are particularly critical in clinical settings, where fine structural changes and subtle pathologies require high and constant resolution to avoid misinterpretation.
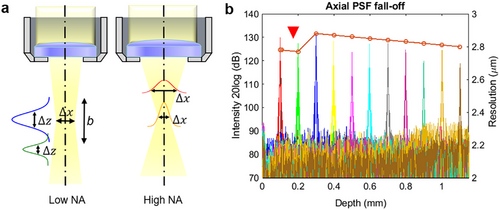
The degraded resolutions are reflected in the corresponding PSFs, leading to undesired convolution outcomes (Equation 2) that result in blurred images. Among the many techniques developed to combat image blurring, deconvolution stands as a cornerstone due to its straightforwardness. Its wide application across different imaging methods substantiates its fundamental role in image enhancement. However, despite its potential, deconvolution's application in OCT has its unique set of challenges. For instance, it is highly sensitive to noise, and without careful handling, the deconvolution process can amplify the noise, leading to a degradation of the image quality rather than an improvement. The coming subsections elaborate more on the general concept of deconvolution and narrow down to an overview of its application in OCT.
5 The Concept of Deconvolution
Deconvolution is the mathematical inverse of convolution, vital in rectifying PSF blurring. It defines a systematic approach to restore the original object function (sharp image) from the recorded image , a convolution of with the PSF in the presence of noise , expressed as . Deconvolution in the spatial domain is essentially designing and applying a reverse filter to convolve with and estimate is involved. Meanwhile, deconvolution can be simpler in the frequency domain. Just like how convolution in the spatial domain is equivalent to multiplication in the frequency domain are the Fourier Transforms (FT) of the sharp image, recorded image, PSF and additive noise, respectively. Here, the inverse of , like a Wiener filter,[81] is applied. An inverse FT of O would theoretically return the deblurred image. Deconvolution reveals supreme versatility and significance, particularly for upgrading OCT image quality. This advanced signal-processing technique can leverage the FT to transition a blurred image from its original spatial domain into a computationally malleable frequency domain. With the progression of OCT technologies and the increasing demand for more precise image resolution enhancements, OCT deconvolution follows a change from simple, general techniques to advanced and tailored algorithms.
6 Deconvolution in OCT – Techniques and Trends
OCT deconvolution is based on two foundations: the processing methodology, and the utilization of the PSFs. From the PSF point of view, deconvolution can be branched into non-blind or blind methods. Non-blind deconvolution requires prior knowledge of obtained either through mathematical modelling[82] or direct measurements[83, 84] of the OCT system PSF. However, the precision of using a single PSF is hampered by the spatial variation of PSFs (Figure 5a), hence necessitating advancement to adaptive deconvolution using spatially variant PSFs[55, 85] and combined PSF.[86] More challenges arise when values approach zero, producing unstable or insignificant division results of and worsening the SNR.[86] Meanwhile, the concern about the computational cost of accurately obtaining multiple PSFs has led to the implementation of blind deconvolution. Blind deconvolution signifies a breaking point in OCT image processing by eliminating the need for directly measured PSFs, instead extrapolating them from the image data itself. From the processing flow perspective, OCT has utilized diverse deconvolution approaches from single-step or non-iterative modalities to iterative methods. These refinements elevate both axial and lateral resolutions for OCT systems,[87, 88] seeking to expand the diagnostic precision and potential in OCT. The evolution of OCT deconvolution reflects a paradigm shift from iterative procedures to adaptive, automated methods. Figure 6 illustrates the classification of these principles. Furthermore, with the emergence of deep learning, more promising avenues for computational efficiency and performance enhancement are available.
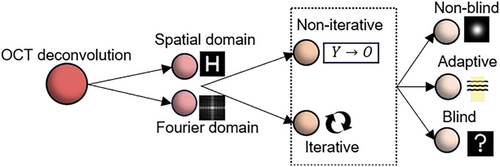
While traditional and adaptive blind methods have proven effective for deconvolution in OCT, new state-of-the-art (SOTA) deconvolution techniques, designed for other imaging modalities, have potential for even greater image quality improvements.[52] Custom neural networks specifically designed for blind deconvolution, such as the Deep Unfolded Richardson-Lucy framework (Deep-URL)[89] and Deep-Wiener,[90] have shown potential in quickly rectifying natural images. Hybrid models combine traditional deconvolution algorithms with deep learning techniques by leveraging the strengths of both approaches to achieve better deblurring performance and increase the interpretability. The RLN[91] and LUCYD[92] are hybrid deconvolution networks combining RL deconvolution with convolutional neural networks (CNNs) for a residual learning framework, demonstrating high-resolution image reconstruction proficiency on microscopic images. Large-scale dataset training empowers such networks to recognize and apply optimally tailored PSFs to distinct cases. As the field continues to evolve, these SOTA techniques are anticipated to pave the way for future advancements in OCT deconvolution. Nevertheless, further adaptations are required to accommodate real-time data variations, diverse tissue types, and motion artifacts specific to OCT images. Upcoming sections delve into further dissection, offering a critical examination of various deconvolution strategies applied in OCT. This exploration contrasts the virtues and shortcomings of established versus emergent methodologies, casting light on their functional implications and domain applications. Concluding with an assessment of present-day techniques, the discussion prompts forward-looking projections that tease out promising prospects and potential refinements in deconvolution technologies for OCT.
7 Analysis of Deconvolution Technologies in OCT
7.1 Fundamental Technologies
7.1.1 Non-Iterative Deconvolution Techniques
The earliest forms of deconvolution applied in OCT commenced with the development of non-iterative, or single-step processes. These methodologies are distinguished by their capacity to enhance resolution significantly, though there is a chance of SNR degradation. Non-iterative deconvolution employs Fourier-space inverse filters derived from the PSF, tailored to minimize the overall mean square error (MSE) between the reconstructed and true images. Described mathematically as where serves as a stabilization factor to counteract the nullification risks when approaches zero, the method facilitates an axial resolution enhancement by up to 2.5-folds.[83] While low-pass spectral filters have been deployed to mitigate SNR reduction, the resultant SNR still experiences a slight diminishment in comparison to the original, blurred images. To secure higher SNR while improving resolution, Resolution-Enhanced OCT (RE-OCT) 31 uses computational spatial-frequency bandwidth expansion followed by deconvolution with a magnitude mask in the Frequency domain to increase the transverse resolution from 2.1 to 1.4 µm. At the same time, coherent averaging in the spatial domain is used for efficient noise suppression.[31] Phase-only deconvolution is a viable strategy, owing to the complex nature of OCT data, by exclusively targeting phase distortions that occur within the spatial frequency domain due to de-focusing phenomena (blurring). Experimental validations confirmed a transverse resolution improvement by twofolds at out-of-focus regions and SNR enhancement of ≈1dB.[55] The random nature of the noise phase implies that noise energy remains largely unchanged post-deconvolution, this indicates a stark contrast to the noise amplification observed in intensity-based deconvolution. However, care must be taken regarding phase error attributable to sample motion—a common challenge in imaging live subjects.
Non-iterative deconvolution is important for its rapid processing capabilities, simplicity, and robustness. The singular processing step is significant in reducing both time and computational resources. Moreover, non-iterative deconvolution is unrestrained from the pitfalls of non-convergence or entrapment in local minima, issues commonly associated with iterative deconvolution strategies. Prominent among non-iterative deconvolution methodologies that have found widespread application in OCT is the Wiener deconvolution method, which is discussed in the next subsection.
Wiener Deconvolution
Despite its merits as a non-iterative method, the constraints associated with Wiener deconvolution must be acknowledged. The practical application of Wiener deconvolution relies heavily on accurate knowledge of signal and noise power spectral density. These parameters are often challenging to obtain in real-world settings.[86] The nature of single-step reverse filtering reduces flexibility, further challenged by the additional computational complexity introduced by Fourier domain and spectral operations. Therefore, Wiener deconvolution hinges on stringent calibration procedures whilst maintaining minimal processing overhead. Nevertheless, Wiener deconvolution remains a prominent solution suitable to real-time application, though it may occasionally sacrifice the preservation of fine details that iterative methods can offer.
7.1.2 Iterative Deconvolution
Iterative deconvolution algorithms represent repeated applications of probabilistic estimations, guaranteeing highly adaptive and refined image restorations, though at the cost of extended processing durations. One major advantage of iterative deconvolution is its inherent affirmation of non-negativity, which is a critical constraint in OCT imaging because recorded intensity values intrinsically bear positive magnitudes.
Iterative methods begin with an initial guess of the clear image which approximates to the recorded image y. Subsequent iterations invoke the chosen deconvolution technique, such as Richardson-Lucy (RL) or Constrained Iterative Restoration (CIR) 53, to obtain an iteratively refined image , where i represents the iteration index. This repetitive refinement is pursued until a satisfactory image quality is realized. An examination of various iterative deconvolution algorithms on OCT data has underscored the respective strengths and limitations.[95] The evaluation concludes as the Van Cittert's algorithm introduces artifacts in the reconstructed image, constrained and relaxation-based methods exhibit improved computational swiftness, though at the expense of partial data fidelity. The Gold's ratio method offers speedy outcomes, yet its effectiveness is dependent upon a high SNR. Hence, the relaxed and Gold's ratio deconvolution may be employed in imaging scenarios where high SNR is guaranteed. The Jansson's algorithm, given its foundational assumption of depth-invariant intensity, is unsuitable with OCT's depth-profiled nature. Amidst these diverse methods, RL emerges as the paradigm of stability across varying SNR levels, underscoring its broad utility in OCT.[95] The RL, along with the CLEAN algorithm, are archetypes of iterative deconvolution, have been deployed in OCT and demonstrated image quality enhancements along both axial and transverse dimensions. The subsequent discussion will analyze these pivotal techniques, dissecting their contributions and key developments within the field of OCT deconvolution.
Adaptation of the CLEAN Algorithm
Originally designed for radio astronomy,[96] the CLEAN algorithm has been sophisticatedly repurposed for OCT applications to mitigate the effects of blurring by the PSF. As the earliest deconvolution method documented in OCT, it has impressively demonstrated enhancements in image clarity along axial and transverse axes.[97] This algorithm proceeds through well-defined stages (Figure 7), beginning with estimation, followed by the iterative subtraction of a scaled fraction (by a gain factor) of the PSF from the highest intensity pixel locations in the “dirty” image, then updating the “cleaned” model image with residuals until a predetermined stopping criterion is met, like when the magnitude of the residuals in the dirty image falls below the root mean-square shot-noise level.[97] The final image, , is the result of convolving the “cleaned” model image with the clean and adding the residuals (noise).
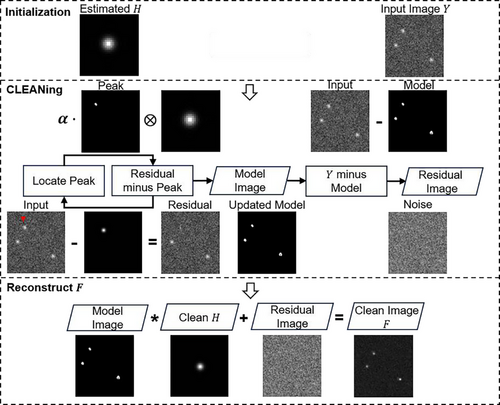
The basic CLEAN algorithm excels in scenarios characterized by sparse scattering elements, akin to the isolation of celestial bodies in astronomy. Conversely, OCT imaging contexts often involve densely populated scatterer arrays within biological samples, presenting a significantly different challenge. In response, amplitude-based adaptations of the CLEAN deconvolution have been crafted to better accord with OCT imaging characteristics.[97, 98] By utilizing the Fourier transform of the reciprocal of a Wiener filter as the deconvolution kernel, the modified approach effectively doubles both axial and transverse resolutions.[81] The technique has proven its feasibility on both tissue phantoms and in vivo dermal tissues. Its strengths include straightforward implementation and a commendable resistance to noise, especially when compared against inverse filtering techniques. Moreover, CLEAN's proficiency in identifying point sources and refining the PSF shares conceptual similarities with modern adaptive deconvolution techniques. CLEAN was also shown to remove sidelobe artifacts[99] in tooth OCT data, enhancing image contrast at the same time.[100] Sidelobes are coherent artifacts in B-scans resulting from imperfect PSFs, causing false positives to appear and effecting accurate interpretations. The traditional method for sidelobe suppression is spectral reshaping, but comes with a degradation in axial resolution.[2] Although its historical contributions are undisputed, prospects for enhancement remain, specifically concerning the exploitation of phase information in CLEAN. Moreover, the efficacy of CLEAN depends critically on precise PSF estimations and cautious determinations of gain factors and halting criteria.
Richardson-Lucy Deconvolution
Like CLEAN, RL is also iterative in nature, yet it exhibits distinctive features that make it particularly effective for OCT applications. Unlike CLEAN, which assumes an image composition of discrete point sources, RL does not assume specific image characteristics. This flexibility makes it particularly favourable for imaging the complexities of biological tissues. The RL method utilizes a statistical approach of maximum likelihood estimation (MLE) to iteratively refine an approximation of the sharp image, improving both image sharpness and contrast.

Gaussian deconvolution using the RL algorithm[104] was an early attempt into OCT deconvolution. It has been shown to yield the lowest MSE compared to other techniques such as truncated singular value decomposition (TSVD) and Tikhonov regulation. When compared with Wiener deconvolution across the metrics of image sharpness (K) and contrast (C), RL demonstrated superior performance.[86] K is calculated as the ratio between a peak pixel value and those neighboring it, while C is the ratio of the mean of pixel values of the object and background regions. Validation experiments on glass slides and orange samples proved that RL obtains superior values of K and C, showing its exceptional ability to restore fine details.[86] The RL algorithm has been combined with advanced techniques like step frequency encoding[105] by adding OCT data at different carrier frequencies. It was shown to improve the axial resolution of a TD-OCT system by twofolds but introduces unwanted side-lobes to the data. While beneficial for improving resolution, the RL approach is prone to noise sensitivity, posing a risk of artifact amplification if not properly regulated. A joint method of RL and phase modulation, RPM-deconvolution,[106] uses random phase masks in the Fourier domain to eliminate additive ringing artifacts in deconvolved OCT images. Phase stability is essential to guarantee optimal noise suppression, which is challenging in live imaging. Similarly, to address the issue of artifact convergence, RL was combined with sparse continuous deconvolution.[107] Sparsity, to preserve high-resolution details in the image, and continuity, ensuring smooth processing of biological structures, are used as regularization terms to help enhance resolution and reduce noise. Experimental results show nearly twofold and more than twofolds[107] improvement in axial and lateral resolutions compared to traditional RL deconvolution. However, its slow processing speed can limit real-time applications, while optimal parameter selection is crucial; incorrect settings can lead to erroneous reconstructions.
Operational challenges arise as PSFs vary in both spatial directions, rendering singular PSF reconstructions inaccurate. Various adaptations of RL deconvolution address this by employing oversampling techniques for PSFs at various transverse locations[108] or averaging PSFs across multiple depth planes.[109, 110] An automatic PSF estimation protocol[111] applies RL deconvolution using a set of pre-defined Gaussian PSFs, evaluating the best transverse PSF via information entropy. Simulation on electronic phantoms and experiments on onion and in vivo tissues demonstrated extension of the effective imaging range to 2.8 mm.[111] A Gaussian low-pass filter can reduce noise but sacrifices the transverse resolution. An estimation model using an averaged PSF obtained across a C-scan image demonstrates SNR and CNR improvements by 10 dB and a factor of 4, respectively.[110] Spatially deconvolved OCT,[112] using RL within subdivided OCT B-scans, attains significant resolution enhancements: from 10.9 to 6.4 µm and from 8.2 to 5.1 µm in the axial and transverse dimensions, respectively. However, these PSF estimation methods are constrained by the Gaussian beam properties and their generalizability in different imaging conditions.
While the advancement of RL deconvolution with multiple PSFs brings about significant computational demands, the application of blind RL deconvolution omits the requirement for predefined PSFs, paving the way for broader usability.
Blind Richardson-Lucy Deconvolution
Blind RL holds the highest noise tolerance among other blind deconvolution methods like Wiener filtering, although necessitating a trade-off with increased computation time.[113] To summarize, blind RL opens broader application possibilities, by removing the need for predefined PSFs. While its AI adaptations triumph in other imaging fields,[89] blind RL networks have yet to be verified explicitly on OCT.
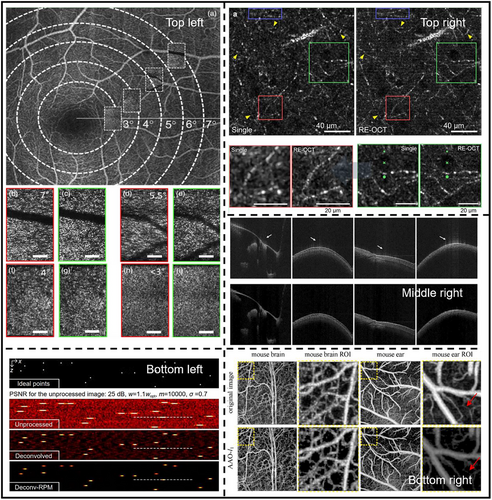
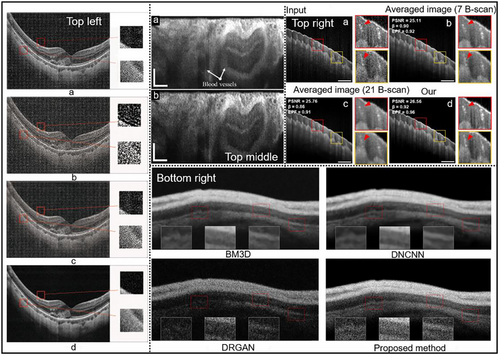
Figure 9 provides visual insights of various deconvolution methods for OCT image enhancement.
7.2 Advanced Deconvolution Technologies: Guiding the Future of OCT Imaging
Iterative, non-iterative and adaptive deconvolution methods paved the way for fundamental image enhancement technologies in OCT. These foundational methods are essential in motivating advancements into cutting-edge methodologies and inspiring future research. The advent of more powerful computational tools and the rise of AI signifies a new era in image deconvolution. Driven by the limitations and experiences from traditional methods, the discussion will expand on these modern techniques that offer new possibilities in image processing that collectively push the boundaries of resolution, speed, and functional imaging.
7.2.1 Blind and Accelerated Deconvolution Techniques
Blind deconvolution methods eliminate the laborious tasks of computing PSFs. The Phase Gradient Autofocus algorithm[117] achieves re-focusing by compensating the calculated defocus phase in complex OCT en-face images. Although preliminary outcomes are promising—achieving a transverse resolution of 5 µm at distance of 10 Rayleigh lengths from the focal plane115—the algorithm's highest performance is noted on simulated images. This emphasizes the need for additional empirical validation using real-world OCT datasets. Blind deconvolution with dictionary learning[115] tackles the noise and sidelobe problems in OCT, facilitating the determination of a spatially varying PSF without additional measurements. In this method,[115] deconvolution is achieved by only acquiring the complex OCT data, and hence the complex PSF, once. Initial experiments on the human finger demonstrate notable SNR and contrast improvements of 2.2 and 5.8 dB, respectively (Figure 9, Middle right) 113. Overall, blind deconvolution marks a progressive technique for OCT image enhancement by infusion with advanced methodologies like complex OCT data and artifact suppression. Though especially convenient for practical imaging cases where the PSF is unavailable, the promising aspects of blind deconvolution are challenged by potential limitations. The absence of comprehensive PSF knowledge may impact method accuracy. Moreover, the iterative nature of many blind deconvolution approaches demands more robust computational resources.
Efforts were made to enhance the performance and lighten the prolonged processing time[154] of iterative deconvolution. RL followed by least square regularization demonstrated notable enhancement in SNR and peak-signal-to-noise ratio (PSNR) 116, as high as 7% improvement from the RL-only method. This signifies the preservation of higher signal power and finer image border details. Spatially adaptive optimization (SAO), like Blind RL deconvolution using the accelerated alternating optimization (AAO) algorithm[116] elevates computational rapidity. Through a combination of different kinds of regularization terms, the computation time was reduced by approximately two-thirds without compromising SNR significantly. Results were demonstrated on in vivo OCT and OCT angiography (OCT-A) images (Figure 9, Bottom left). Multi-frame super-resolution OCT[119] with RL deconvolution aims to reduce effects of sub-pixel level lateral variations at multiple depths. This method leverages the acquisition of multiple image frames, reduces artifacts, and enhances transverse resolution by three times. In vitro and in vivo studies on human skin and retina were demonstrated.[119]
In summary, blind and accelerated deconvolution methods mark significant advancements in overcoming the computation and time constraints associated with traditional iterative methods. By reducing the dependency on prior PSF knowledge and enhancing accelerating processing speeds, these innovations promise broader application scopes and enhanced patient care delivery. Nonetheless, challenges in accuracy, adaptability, and real-time integration persist, where AI integration may offer groundbreaking solutions.
7.2.2 AI-Enhanced Deconvolution in OCT
While generalized AI strategies have been propelling the enhancement and analytical abilities of OCT imaging,[47, 120, 121] the advent of AI-enhanced deconvolution techniques further advances these capabilities. AI-based methods often utilize the expertise of robust deep learning algorithms such as generative adversarial networks (GANs) and CNNs, leveraging large datasets to generalize across diverse imaging conditions. These techniques present an ability to learn and predict complex patterns within OCT data, offering a substantial leap in image processing capabilities. Specifically, certain AI-based super-resolution frameworks can be viewed as a form of blind deconvolution when they implicitly learn the degradation model, that is, blur, from the data. Nevertheless, this review focuses on methods that explicitly focus on PSF-induced blurring. Similarly, AI-assisted digital refocusing techniques that estimate the defocus PSF and restore focus fall under the category of deconvolution.
GANs consist of a generator network that produces deblurred images and a discriminator network that distinguishes between real and generated images.[122] The one-step enhancer (OSE) 50 extracts and removes noise and blur in a single step using an unsupervised GAN approach, by separating the content, blur, and noise from the raw OCT images. This allows the model to generate clearer images without needing to know the exact nature of the blur. Experiment validation on enhanced image quality is reported, improving PSNR and structural similarity index measure (SSIM) by 10.59 and 0.24, respectively (Figure 10, Bottom right). More specific to retinal OCT imaging, a CNN based network was proposed[56] that can resolve both out-of-focus (axial direction) and motion (transverse direction) blurs individually. This method uses the blurred image as input to the CNN to predict the blurring PSFs, then reverses the blurring using deconvolution, hence a combination of data-driven and model-driven techniques. Superior performance in terms of SNR and PSNR is reported (Figure 10, Top left).[56] Similarly, Deep OCT Deconvolution Network[123] was proposed as a CNN-based deconvolution approach for OCT image restoration in an endoscopic OCT system (Figure 10, Top middle). This 1-D deep deconvolution network[123] was able to enhance the lateral resolution by 1.5 times while maintaining image quality and network simplicity. A deep learning-based method that exploits interference fringes[48] to enhance image quality while preventing blurring caused by traditional speckle reduction techniques was proposed (Figure 10, Top right). This method shares the same goal of improving image clarity and preventing blur with deconvolution. The framework consists of two distinct models: NetA focuses on enhancing the axial resolution of A-scans by using spectrograms derived from the short-time Fourier transform of raw interference fringes, and NetB aims to improve lateral resolution and reduce speckle noise in B-scan images. Both axial and lateral resolutions were improved by 1.2 times.[48] While effective, these supervised approaches require paired datasets and lack adaptability to unseen imaging conditions. A recent breakthrough introduces a self-supervised PSF-informed deep learning framework that addresses two critical limitations of traditional AI methods: reliance on paired clear/blurred datasets, and computational inefficiency for real-time applications.[124] By combining despeckling pre-processing, blind 2D PSF estimation, sparse deconvolution and a lightweight network, this method achieves real-time denoising and deblurring using only noisy B-scans as input, eliminating the need for experimental ground truth. Axial and transverse resolutions can be improved by 50% while CNR can be enhanced by almost seven times in human eye OCT images.[124] However, this work only considers a spatially-invariant PSF which limits its applicability to depth-varying PSFs, and relies heavily on data-driven noise modeling, which may fail in complex noise conditions. Intelligent deconvolution models, that unify deep learning with conventional physics-informed deconvolution, hold considerable promise, providing pathways to bypass the traditional reliance on extensive pre-processing and iterative calculations. These advancements suggest a not-too-distant future where the ultimate goal of real-time, high-resolution and accurate diagnostic and intraoperative OCT image deconvolution can be achieved. Yet, challenges emerge predominantly in the form of computational requisites, spatially varying PSFs and the complexities inherent in biological systems. A data-rich environment, reflective of diverse OCT imaging scenarios, synergized with physics-based regularization is vital for broad-scale AI deployment in the field.
8 Comparative Analysis of OCT Deconvolution Technologies
- 1) PSF Prediction – Adaptive versus Blind Deconvolution: The precision in PSF prediction is vital in non-blind deconvolution algorithms. Methods employing multiple PSFs, though providing truer predictions of the spatially variant blurring in the image, are restrained by heavier computational loads due to their complex multi-step processes. Blind deconvolution approaches, conversely, base their performance on the validity of their underlying assumptions, including the stringent prediction of both the clear image and PSF.
- 2) Robustness – Iterative versus Non-Iterative Deconvolution: Iterative methods achieve superior reconstruction results while necessitating vigilant monitoring of algorithmic performance to avoid premature convergence and overfitting. Premature convergence happens when the iteration is stopped before the algorithm has reached the best solution. Overfitting occurs when there are too many iterations, where further iterations fail to improve outcomes but pointlessly consume computational resources. Both lead to defective reconstructed images that can mislead interpretation. Efforts were made to improve the robustness of iterative deconvolution using regularization techniques. In contrast, non-iterative techniques rely on the accuracy of a singular reverse computation, favoring a swift yet less refined approach, especially limited in situations with high noise level or low SNR.
- 3) Noise Suppression – Non-Iterative versus Iterative Deconvolution: Although non-iterative deconvolutions present considerable resolution improvements, they can diminish SNR, posing limitations for high-noise contexts. Strategies like spectral filtering attempt to alleviate these deficiencies, yet they scarcely match the inherent SNR of blurred originals. In the case of Wiener deconvolution, knowing the noise power spectra allows its suppression, which can be a significant hurdle in practical implementations due to the challenges in precise calibration and estimation. On the iterative spectrum, techniques like the RL stand resilient across varying SNRs but struggle with the computational latency that constrain throughput and real-time applicability. The intense computational requirements associated with iterative algorithms significantly limits them to applications where computational efficiency can be secondary to image quality. Progressions in AI and signal averaging have improved their noise resistance.
- 4) Algorithm Performance – AI-Assisted Deconvolution versus Traditional Methods: AI-assisted deconvolution methods can often outperform traditional methods in terms of speed and results quality, especially in noisy or complex scenarios. However, they require a large amount of training data and can be complex to set up and use.
- 5) Performance Evaluation Metrics: The comprehensive assessment is guided by key metrics such as resolution improvements and CNR and SNR amplifications. Such performance indicators are captured in Table 1, aggregating a comprehensive understanding of these technologies. For the AI-assisted deconvolution, a more detailed table on the network performances is necessary. Table 2 provides another perspective in selecting deep learning networks for OCT image de-blurring, from processing cost and efficacy points of view. Processing time is especially important for real-time applications.
- 6) OCT Applications-Clinical versus Research Needs: Non-iterative methods may be more appropriate for real-time imaging needs, whereas iterative methods might be better suited for diagnostic contexts where the highest quality imaging is required, notwithstanding the longer processing times. While tested on biological samples in lab environments, the demonstration of similar performance of OCT deconvolution in clinical disease scenarios are yet to be achieved.
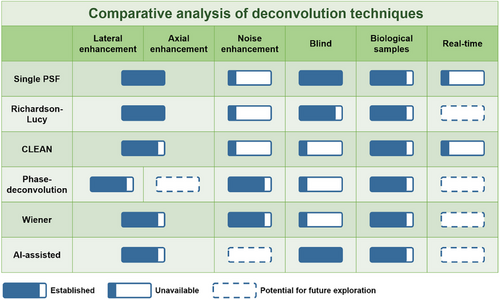
- 7) Technological Development Trajectories: The evolution trends for OCT deconvolution techniques establishes on enhanced computational proficiency for iterative variants, advanced noise management for non-iterative methods, and a seamless integration that favors clinical implementation. These developments depict a realm where OCT deblurring transitions from a post-processed enhancement to a fundamental real-time diagnostic instrument. Figure 11 illustrates this outlook by portraying the present state and prospective advancements in OCT deconvolution, thereby offering a view of the innovation trajectory within the field.
| Deconvolution methods | Examples | Evaluation methods | Results and Applications |
|---|---|---|---|
| Non-iterative | 1D and 2D Wiener's (W) and RL[86] |
K C |
RLK = 8.32, WK = 2.48 RLC = 36.28, WC = 26.25 |
| W[93] | Lateral resolution | From 18 to 11 µm | |
| Wiener and Autoregressive Spectral Extrapolation (ASE) 93 | Axial resolution |
SS-OCT: 21 to 5 µm TD-OCT: 12 to 6 µm |
|
| Phase deconvolution[55] | SNR |
One dB SNR improvement. Lateral resolution improved by twofold. |
|
| W with fall-off compensation[71] |
Local contrast CNR Averaged SNR |
Local contrast = 5.56 CNR improved by 3.40 dB Avg SNR improved by 4.60 dB |
|
| Iterative | TSVD, Tikhonov and RL[104] | MSE | RL with least MSE of 4.766e−4. |
| CLEAN[97] | Axial resolution | Enhanced by two times | |
| RL[108] | Lateral resolution | From 18 to 4.5 µm. | |
| RL[87] |
Axial resolution SNR (onion) CNR (onion) |
From 4.2 to 1.4 µm. SNR = 80.21 dB CNR = 7.14 dB |
|
| Adaptive | RL[112] |
Lateral resolution Axial resolution |
Lateral resolution improved by 3.10 µm Axial resolution improved by 4.50 µm |
| Spatially adaptive blind deconvolution[116] |
PSNR SSIM CPU Times (s) |
PSNR = 79.57 SSIM = 0.99 CPU Times (s) = 94.22 |
|
| Regularized RL[118] |
PSNR (onion) SNR (onion) |
PSNR = 76.5 dB SNR = 14.5 dB |
|
| Blind and advanced | Blind RL with Gaussian family PSFs[111] |
Axial resolution Lateral resolution |
Axial resolution: 12 µm Lateral resolution: 16 µm |
| Phase Gradient Autofocus algorithm[117] | Lateral resolution | Diffraction limited: 5µm. | |
| Blind deconvolution with dictionary learning[115] |
SNR C |
Improved by 2.2 dB Improved by 5.8 dB |
|
| Multi-frame superresolution[119] | Lateral resolution | From 25.0 to 7.81 µm | |
| AI-assisted | 1D deconvolution network[123] |
SNR Lateral resolution |
SNR improved by 1.76 dB Lateral resolution improvement by 1.2 times |
| DL exploiting interference fringe[48] | Axial and Lateral resolution | Both enhanced by ≈1.2 times | |
| Lightweight self-supervised PSF-informed DNN[124] |
Axial and Lateral resolution CNR enhancement: |
Both enhanced by approximately two times CNR (Swine artery): 5.64 to 6.19 CNR (Human retina): 6.00 to 28.42 CNR (Human eye): 2.53 to 17.71 CNR (Rabbit retina):12.03 to 72.45. |
| Method | PSNR | SSIM | Time per frame (Size) |
|---|---|---|---|
| Lian, J. et al.[56] | 27.27 | - | 2.270s (1024 × 420) |
| Lee M., et al.[123] | 23.80 | 0.39 | 0.083s (1024 × 256) |
| Li, S., et al.[50] | 26.71 | 0.81 | 0.120s (10 000 × 1024) |
| Lee, W., et al.[48] | 24.96 | 0.78 | 1.5s (2048 × 1024) |
| Zhang, W., et al.[124] | - | - | 0.000024s (1024 × 1024) |
| Li, Y., et al.[91] (non-OCT) | 24.40 | 0.89 | 4–6 folds improvement |
| Cobola, T., et al.[92] (non-OCT) | 28.57 | 0.95 | - |
In summary, the comparative evaluation effectively assesses the pros and cons of deconvolution methods, providing the reader with a comprehensive understanding. It is essential to consider the particular OCT imaging requirements against the trade-offs of these technologies, ensuring the selected deconvolution strategy aligns with operational goals and resource availability.
9 Discussion and Conclusion
9.1 Highlights of Advancements
We have highlighted how deconvolution addresses OCT system limitations, significantly improving image quality. Inherent blurring in axial, transvers or both directions were tackled via deconvolution with corresponding PSFs under careful considerations. Iterative deconvolution algorithms like RL have demonstrated superior image refinement compared to non-iterative methods. The accuracy of non-blind deconvolution remains closely tied to precise PSF prediction.[55] Adaptive PSF combination methods[112] show promise in enhancing clinical specificity for different tissue characteristics. Research trends point to merging AI with deconvolution methods to develop adaptable algorithms for a wide range of disease imaging. Early successes in retinal imaging[56] suggest broader future applicability, moving toward precise and patient-specific diagnostics. The progression from deconvolution as a promising post-processing tool to widespread instantaneous, intra-operative clinical applications depends on rigorous validation and cross-disciplinary collaboration.
10 Challenges and Proposed Solutions
This review uncovers the delicate balance between computational efficiency and image fidelity in deconvolution. Real-time implementation of deconvolution in OCT faces both computational and practical challenges. Iterative methods risk inefficiencies like premature convergence, while non-iterative methods depend on precise PSF predictions. Deep learning offers a solution to enhance both efficiency and quality but requires sophisticated user training, regulatory issues and generalizability to different OCT imaging conditions. Clinical adoption of OCT deconvolution strategies requires validation against tissue variability and the need for rapid, accurate imaging. While AI-assisted deconvolution is a powerful approach for addressing PSF-induced blur, it is important to recognize that other AI-based image enhancement methods, such as super-resolution or denoising networks, may achieve resolution improvement through different mechanisms. These methods can complement deconvolution by addressing additional sources of degradation, such as speckle or multiple scattering, with the expense of requiring large datasets and significant computational resources.
Noise amplification, particularly problematic in low-signal regions, is an inevitable consequence of deconvolution, necessitating the incorporation of noise suppression strategies. Advanced noise suppression techniques, such as wavelet thresholding[125] or anisotropic filtering,[44] could be incorporated to refine SNRs. Similarly, the growing use of DNNs for denoising, like a GAN-based matching of low-resolution and high-resolution images,[28] were proposed to simultaneously denoise and enhance OCT images. Traditional deconvolution approaches assume additive noise models; while speckle85—a granular interference pattern inherent to coherent imaging—introduces multiplicative noise that varies with image intensity.[126, 152] Unlike additive noise, which can be directly subtracted, this sample-dependent noise further complicates the noise removal process, making it challenging to denoise without distorting the image signal.[127] De-speckling can be done through multi-frame averaging[128] or more recent approaches[155] using tensor singular value decomposition,[129] discrete wavelet transform,[130] multiscale denoising GANs (MDGAN),[131] and physics-informed noise modeling[127] that separately handles additive and multiplicative noise. Ultimately, a universal deconvolution approach capable of addressing the diverse noise conditions in OCT remains a challenging but essential goal.
A major challenge in deconvolution is the potential loss of fine image details, particularly in sparse samples where the signal-to-noise ratio is inherently low. Over-regularization in deconvolution algorithms can suppress crucial image features, leading to diminished diagnostic utility. Studies have shown that adaptive deconvolution methods incorporating structure-preserving priors or sparsity constraints can mitigate this issue by balancing resolution enhancement with detail retention.[132] Furthermore, hybrid techniques, such as wavelet-based denoising combined with deconvolution,[125] have demonstrated improved fine-structure preservation while reducing artifacts. Deep-learning-based approaches, including blind deconvolution networks trained on diverse dataset,[133, 134] have also shown promise in maintaining structural integrity while enhancing image resolution. Integrating these strategies can provide robust solutions to prevent excessive detail loss in deconvolved OCT images.
Deep learning, promising rapid and accurate deconvolution, could actualize real-time diagnostics in OCT. Yet, challenges persist, such as creating extensive validation datasets, ensuring algorithmic generalizability, and addressing ethical issues related to automated diagnostics. Furthermore, while advanced deconvolution techniques have substantial potential across medical disciplines, their clinical integration faces hurdles, including the costs of advanced OCT systems, the need for expertise in interpretation, and the necessity for robust studies to confirm their efficacy in various conditions. Future developments may see advanced OCT technologies with real-time deconvolution capabilities becoming more portable and integrated into telemedicine, greatly expanding the accessibility of high-quality diagnostic imaging.
10.1 Application Scenarios of Advanced Deconvolution Techniques in OCT Imaging
Despite the success in controlled laboratory environments, the clinical validation of these algorithms under diverse pathological conditions and their integration into healthcare systems, such as taking regulatory, cost, and accessibility aspects into account, remain unexplored.[4, 7] Nevertheless, the success in OCT deconvolution for clinical imaging is foreseeable, with real-time imaging increasingly attainable with current computational improvements. Ophthalmology has been at the forefront of adopting OCT imaging. Advanced deconvolution techniques promise to refine retinal diagnostics by improving image resolution[56] and potentially aiding early disease detection and leading to interventions that can prevent vision loss.[6] Correlation-based techniques[135-137] have facilitated non-invasive blood flow visualization in OCT angiography (OCT-A), but noise and PSF-induced blur limit their ability to resolve fine vascular networks in complex pathologies like choroidal neovascularization (CNV).[138, 139] Deconvolution, such as Wiener filtering combined with coherence techniques,[140] has demonstrated promising OCT image quality enhancement, but are not yet tailored for PSF-induced blurring. Hybrid AI-driven approaches could further enhance CNV imaging by integrating adaptive deconvolution with correlation methods, improving diagnostic accuracy in clinical imaging. Furthermore, high-speed imaging and motion correction strategies are critical, particularly for addressing eye movement challenges in ophthalmology. More potential applications of OCT deconvolution include, but not limited to, elevating non-invasive margin mapping in skin cancer,[141] vascular plaque analysis in cardiology,[142] and observing the retinal nerve fiber layer[6] for monitoring the progression of neurological conditions like glaucoma.[143]
10.2 A Future with Emerging OCT Technologies
10.2.1 Harnessing Interpretable AI for Real-Time OCT Imaging
AI is set to revolutionizing OCT image deconvolution, aiming to deliver real-time, accurate diagnostics with high-precision algorithms. Unsupervised learning techniques, specifically variational autoencoders[144, 145] show potential for autonomous deblurring of OCT image without the need for labeled training samples. While AI can generate enhanced images, interpretability and explainability are crucial in medical imaging to ensure responsible decision-making. Physics-informed AI methods combine the strengths of data-driven learning with physical models of OCT image formation. By incorporating constraints derived from the physics of light-tissue interaction, these methods can jointly address blur, speckle, and other sources of degradation, leading to more accurate and robust image reconstruction. Tailored networks like Deep-URL,[89] RLN[91] and DWDN[90] need customization for OCT's diverse imaging scenarios.
10.2.2 Advancing OCT Deconvolution with Visible-Light OCT and Enhanced Angiography
Visible light OCT (Vis-OCT) offers superior resolution and high-contrast capabilities, resolving finer vascular details via OCT-A.[146] Nonetheless, the penetration of light decreases as the wavelength decreases due to the aggravated scattering. Deconvolution methods tailored for Vis-OCT could preserve more detail within limited depth ranges. Research in this area is crucial to harness Vis-OCT's potential for broader medical applications, extending OCT deconvolution beyond the current focus on systems in the 800 or 1300 nm wavelength range.
10.2.3 Synergizing with Cutting-Edge OCT Techniques
Integrating routine deconvolution with advanced OCT technologies suggests a promising future for imaging. High-speed, miniaturized, high-resolution endoscopic OCT[147, 148] could benefit from deconvolution for enhanced real-time intraoperative imaging. AI-enhanced image segmentation[120, 149] could translate deconvolved OCT images into more precise clinical insights. The success of these integrated techniques depends on comprehensive data and computational resources[153], emphasizing the need for collaborative efforts from both hardware and software perspectives.
10.3 Additional Insights for Impactful Perspectives
10.3.1 A Unified Strategy for Precise OCT Reconstruction
Hence, reconstructing the clean OCT image requires an all-rounded solution that achieves both deconvolution, to remove the blur effect, and denoising, to remove the noise effects. Simultaneous deblurring and denoising of OCT images was demonstrated using a GAN approach,[28] methods like this however lacks interpretability and generalizability. The distinct requirements for effective OCT image enhancement lie in the importance of utilizing the PSFs and noise characteristics. In real world, where these properties are not easy obtained, precise modelling should be made under certain assumptions. These factors are crucial for preserving the structural integrity and diagnostic value of the OCT images, ensuring that enhancements are both precise and clinically useful. Finally, a generalist approach for OCT reconstruction must address the coherence- and dispersion-induced PSF variations along the depth, highlighting the need for adaptive deconvolution strategies tailored to the OCT system. By integrating physics-informed AI, it is possible to achieve more robust and accurate OCT image enhancement across diverse imaging conditions.
10.3.2 Interdisciplinary Collaboration and Longitudinal Studies with Patient-Centric Applications
Bringing together experts from optics, computer science, biomedical engineering, and clinical medicine can foster innovative solutions for complex challenges. Deconvolution on multimodal data such as combining OCT with photoacoustic imaging,[150] magnetic resonance imaging (MRI)[151] and ultrasound could unlock new dimensions of diagnostic capability. Collaborative efforts and publicly available datasets, algorithms, and research findings can drive innovation and ensure the reproducibility of deconvolution techniques.
Tracking patient outcomes and diagnostic accuracy over time can help refine deconvolution algorithms to better meet clinical needs, ensuring their reliability in diverse clinical settings. Comprehensive educational and training programs are also necessary for the adoption of advanced deconvolution techniques. Personalized deconvolution algorithms tailored to individual patient characteristics can advance precision medicine in OCT imaging. Integrating patient data while ensuring privacy and ethical use of AI is crucial. Last, adherence to clinical guidelines is essential for safe implementation.
10.4 Conclusion
This review has methodically examined the SOTA OCT image deconvolution techniques, envisioned their applications to diverse fields, and identified their transformative impact on both research and clinical practice. We present a comprehensive comparative analysis of OCT deconvolution techniques, from single-step, Gaussian PSF-based to adaptive, and AI-assisted algorithms. Our findings depict significant advances in image resolution and SNR across various application categories. This review examines existing methods and recognizes the potential of more complex algorithms, aiming to fill critical gaps in current technologies and offer a balanced perspective on the trajectory of OCT image enhancement. Our research underscores the pivotal role of this fusion in shaping the future laser and photonics, specifically within the context of OCT image enhancement. However, translating these enhancements into real-time clinical imaging presents ongoing challenges, particularly regarding optimization robustness and the balance between accuracy and computational complexity. By embracing interdisciplinary collaboration, patient-centric approaches, ethical frameworks, and innovative research, we can continue to enhance the quality and impact of OCT imaging, ultimately improving patient care and advancing the field of medical imaging.
Acknowledgements
This work is supported by the Science, Technology, and Innovation Commission (STIC) of Shenzhen Municipality (SGDX20220530111005039), the Research Grants Council (RGC) of Hong Kong SAR (ECS24211020, GRF14203821, GRF14216222, GRF14201824), the Innovation and Technology Fund (ITF) of Hong Kong SAR (ITS/252/23). The authors are grateful to Dr. Jiarui Wang and Dr. Mehmood Nawaz for their advice during manuscript writing. The authors thank BioRender.com for the platform to create the figures for this paper. The authors also acknowledge the use of GPT-4o for language editing and improving readability during manuscript preparation.
Conflict of Interest
The authors declare no conflict of interest.
Author Contribution Statement
S.A.A and W.Y. conceived and designed the review theme; S.A.A. and D.M. gathered and analyzed the literature; S.A., Y.W., and D.M. drafted the manuscript; S.A. and D.M. created the figures. S.A.A. and S.M.T.A. created the tables and charts; S.S. and C.X. critically revised the manuscript for important intellectual content; W.Y. oversaw the project and acquired funding. All authors discussed the results and implications and commented on the manuscript at all stages.
Biographies

Aimen is an MPhil. student in biomedical engineering at CUHK, specializing in physics-aware AI for OCT image enhancement. Her research focuses on integrating machine learning with OCT physics to improve diagnostic clarity. She co-authored this comprehensive review on OCT deconvolution and developed AI frameworks for resolution recovery. Her work bridges computational optics and clinical translation, aiming to advance AI-driven solutions for biomedical imaging challenges.

Di Mei is a postdoctoral fellow in biomedical engineering at CUHK. His research spans computational optical imaging, robotic OCT, multi-ocular vision, and AI for science. He develops adaptive algorithms for OCT resolution enhancement and multi-modal imaging integration.

Yuanyuan Wei is currently a postdoctoral scholar in the Neurology Department at the University of California, Los Angeles (UCLA). Before that, she was a Research Associate in the Department of Biomedical Engineering (BME) at The Chinese University of Hong Kong (CUHK). She received her B.E. degree in Precision Instrument from Tsinghua University in 2018. She earned her Ph.D. in BME from CUHK in 2023. Her research encompasses computational bioassay, droplet-based microfluidics, neurodegenerative disease diagnosis, and integrative systems for biochemical assays. To date, she has published 19 peer-reviewed research papers, including 10 first-author journal (6) / conference (4) papers.

Chao Xu is a postdoctoral fellow at the Chinese University of Hong Kong, specializing in high-resolution optical coherence tomography (OCT) and optical endomicroscopy. He earned his Ph.D. in biomedical engineering from CUHK in 2024 and has published 17 papers in leading journals, such as Nature Communications and Science Advances. His research focuses on minimally invasive OCT imaging systems for clinical applications, particularly in endoscopy and intravascular imaging. Dr. Xu has received several honors, including the Hong Kong Medical and Healthcare Device Industries Association Student Research Award and the National Scholarship.

Tariq holds a B.Eng. in computer science from the University of Hong Kong and specializes in data analysis, coding, and AI applications in medical imaging. As a research assistant at ABI Lab, he developed deep learning pipelines for OCT image segmentation.

Sadia is a research assistant professor in Biomedical Engineering at CUHK, with expertise in biosignal processing and AI-driven neuroimaging. As a Fulbright and Schlumberger Fellow, she pioneers portable neurotechnologies for stroke rehabilitation and brain-computer interfaces. Her interdisciplinary work integrates OCT with computational models for real-time interpretable diagnostics. She has led international collaborations in neuroengineering and co-founded a startup focused on AI-driven healthcare solutions. Her research is interdisciplinary encompassing various domains such as engineering, neuroscience, psychology, multimedia, and computer science.

Yuan, an assistant professor in Biomedical Engineering at the Chinese University of Hong Kong (CUHK), leads the Advanced Biomedical Imaging Laboratory (ABI Lab). His research focuses on high-resolution biomedical imaging and AI-assisted image processing for translational applications. He pioneered innovative biophotonics tools, including portable ultrahigh-resolution endoscopic OCT systems, deep-brain microneedles, and 3D airway imaging technologies. With 100+ publications in journals like Nature Communications and Science Advances (H-index 30, 4000+ citations), he advances optical imaging for clinical use. Dr. Yuan serves as Vice-President of the Hong Kong Optical Engineering Society and sits on editorial boards for bioengineering and medical journals.




