Advances in Quantum Imaging with Machine Intelligence
Abstract
Quantum imaging exemplifies the fascinating and counter-intuitive nature of the quantum world, where non-local correlations are exploited for imaging of objects by remote and non-interacting photons. The field has exploded of late, driven by advances in our fundamental understanding of these processes, but also by advances in technology, for instance, efficient single photon detectors and cameras. Accelerating the progress is the nascent intersection of quantum imaging with artificial intelligence and machine learning, promising enhanced speed and quality of quantum images. This review provides a comprehensive overview of the rapidly evolving field of quantum imaging with a specific focus on the intersection of quantum ghost imaging with artificial intelligence and machine learning techniques. The seminal advances made to date and the open challenges are highlighted, and the likely trajectory for the future is outlined.
1 Introduction
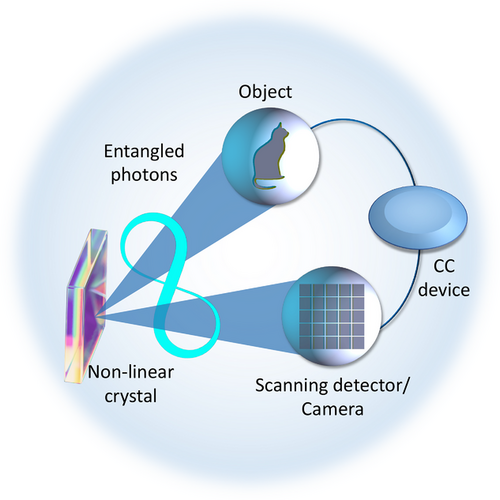
The notion of entanglement between particles could be said to have its origins in the famous 1935 paper outlining what is now referred to as the EPR paradox.[1] Notions of object detection using this resource found their way into textbooks as thought experiments, e.g., the Bohm bomb, but had little connection to practical implementation. It wasn't until more than half a century later that the term “quantum ghost imaging” arose in the context of studying EPR correlations, ushering in a quantum version of imaging.[2] To appreciate the advance it is instructive to compare it to conventional imaging. In conventional imaging, light travels from the object to the image plane (detector), while position correlations between the object and image plane ensure a “sharp” image. The necessary correlations are established by virtue of the imaging system, e.g., pinholes, lenses and judicious distances between the planes. In contrast, the seminal quantum ghost imaging experiment utilized position correlations shared between two entangled photons, one of which is sent to the object and collected in a large “bucket” detector, thus removing any object information, while the other, which has never interacted with the object, is sent to a spatially resolving detector, a “camera”, which in the original experiment was a scanning single mode fibre. Crucially, neither photon has any information of the object, but the when the photons are measured in coincidence, the spatial correlations allow for image reconstruction. This process is illustrated in Figure 1.
Since this seminal work, many demonstrations of ghost imaging have been realized, including the use of thermal light,[3-5] momentum correlated ghost imaging,[6] spiral ghost imaging with orbital angular momentum,[7, 8] time domain ghost imaging,[9, 10] computational and compressive ghost imaging,[11, 12] and dual wavelength ghost imaging.[13, 14] The field has since exploded to cover other forms of quantum imaging too, collectively harnessing quantum properties of light to reconstruct images with a precision, sensitivity and photon flux that is beyond what is possible by classical methods,[15-17] including imaging with undetected photons,[18, 19] interaction-free imaging[20] and quantum-inspired detection and imaging of remote objects.[21-23] Where quantum imaging has lagged behind its classical counterpart is the time to reconstruct images of sufficient quality to be recognized by a human eye. It is here that the intersection of computer intelligence and quantum imaging has come to the fore.
The field of computer vision emerged earlier than quantum imaging, in the 1960s, with the goal of enabling computers to interpret visual information as would a human.[24] Early research in computer vision focused on optical character recognition and processing satellite images, for instance, seminal works such as The Summer Vision Project in 1966[25] enabled computers to interpret visual information. In the 1970s and 1980s, algorithms to extract features from images, e.g., corners and edges, for object recognition emerged. These early efforts focused on basic image processing tasks such as edge detection,[26] pattern recognition,[27] and template matching.[28-30] Feature extraction-based approaches gained prominence in the late 1990s and early 2000s,[31] but involved manually designing algorithms to detect specific features in images. Scale-invariant feature transform (SIFT) and histogram of oriented gradients (HOG) were popular methods for object detection and recognition.[32, 33] Despite their effectiveness, these approaches struggled with variations in lighting, scale, and viewpoint, limiting their accuracy in complex representations and applications.[34] In the later 2000s there was a shift towards machine learning techniques in computer vision, pertinent to applications within quantum imaging and imaging as a whole. Many research groups invested time in classifiers, such as Support Vector Machines (SVMs), to improve object recognition within images.[35] The ImageNet Large Scale Visual Recognition Challenge (ILSVRC) significantly accelerated progress by providing larger datasets for training and evaluation which led to more robust solutions predicted by machine learning algorithms.[36] Deep learning gained notable traction with the development of Convolutional Neural Networks (CNNs); originally introduced in the 1980s but popularized in the 2010s and revolutionized computer vision through establishing automatic feature extraction.[37] CNNs were inspired by the visual processing mechanisms in the human brain and led to a new era within computer vision and image processing.[38-40]
The convergence of quantum imaging and artificial intelligence (AI) has paved the way for significant advancements in quantum imaging resolution, sensitivity, and object identification, with the basics covered in recent tutorials.[41-43] In this review, we will delve into the recent advancements and applications with a focus on quantum ghost imaging and AI. We highlight the seminal advances, modern and popular AI algorithms, as well as their implementation and utilization in quantum imaging. We highlight the advantages that the convergence of these seemingly disparate technologies have brought to the field, and provide insights into the open challenges and future prospects within this emerging field.
1.1 An Aside: Back to Basics
2 Advances in Ghost Imaging
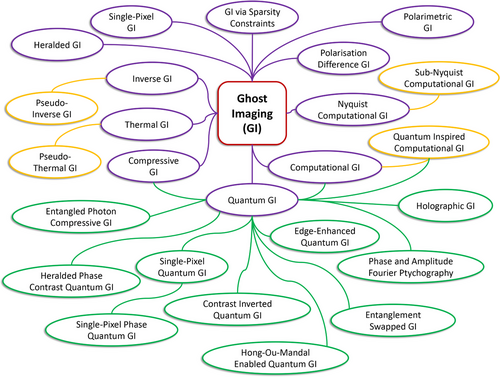
Ghost imaging comes in many variant forms, spanning classical to quantum, as illustrated in Figure 2. What they have in common is an image acquisition technique which utilizes the correlations between two spatially separated fields of light (or photons) to reconstruct an image of an object, where one of the fields (or photon) does not physically interact with the object.[44, 45] By virtue of its setup, each individual field cannot offer any information on the object, however the correlations between them allows for the reconstruction of an image.[46, 47] Originally, quantum ghost imaging was demonstrated as a phenomenon of quantum entanglement[2] as a result of a spontaneous parametric downconversion (SPDC) process.[48] Subsequently, it was demonstrated that ghost imaging can be conducted through the use of classical correlations.[3, 5, 49] In this section, we introduce the advances in the quantum version of ghost imaging, omitting the integration of AI and machine learning as well as the development of other forms of quantum imaging for the sections that follow.
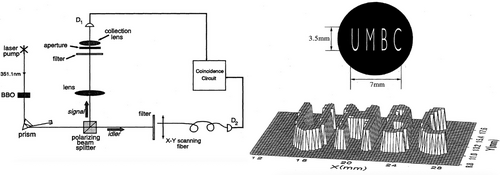
Quantum ghost imaging saw its inception in 1995 when Pittman et al., demonstrated optical imaging by means of two-photon quantum entanglement.[2] Figure 3 depicts the original experimental setup employed (left), as well as the coincidence counts as a function of the coordinates in the transverse plane of the fiber tip (right). The coincidence counts in the transverse plane were summed together to reconstruct an image of the aperture placed in the signal arm of the experimental setup. As this was a proof-of-principle demonstration of two-photon geometric optics, the lengthy image acquisition times were not considered. In this experiment, the signal and idler photons that emerge from the SPDC process, occurring within a non-linear crystal (NLC), are spatially separated so that coincidence detections may be performed. Importantly, the photon counting detectors are distant, which warrants the use of the phrase “spooky action at a distance”.[1] In the experiment initiated by Pittman et al., an aperture with the letters UMBC (as shown in Figure 3) was placed in front of one of the detectors and illuminated by the signal photons passing through a convex lens.[2] The other detector was placed at a distance prescribed by the two-photon Gaussian thin lens equation, which was subsequently scanned in the transverse plane of the idler photons. A sharp magnified image of the aperture was obtained and observed in the coincidence counting rate while the single photon counting rates remained constant, this is shown in Figure 3 (bottom right). Significantly, this experiment realized a quantum two-photon geometric effect for the first time. At this point in time while the classical theory of imaging was well established, this experiment successfully performed optical imaging by means of a quantum entangled source for the very first time.[2]
Ghost imaging has seen significant growth and development in the past two decades ranging from the development and advancement of computational and compressive ghost imaging[3, 5, 12, 49-51] to single-pixel imaging techniques[52-54] in both the quantum and classical domains. Compressive sensing is an area of great interest within the imaging space as it requires significantly less sampling data than necessary under the Nyquist–Shannon criterion.[55-57] Shapiro[11] and Duarte et al.,[58] were the first to introduce binary pattern masks as the scanning method to image amplitude objects in a ghost imaging configuration. Subsequently, the imaging of phase-only objects in a ghost imaging configuration is non-trivial and has progressed much slower than the growth and development of quantum imaging of amplitude-only objects.
2.1 Beyond Position Correlations
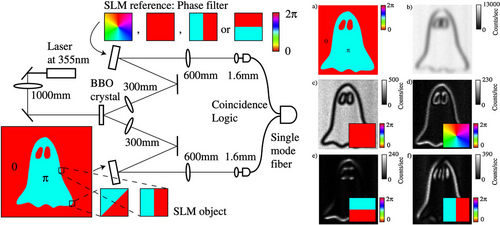
Since the seminal work by Pittman et al., many manifestations of ghost imaging have been realized, here we delve into a few approaches that stand out in path towards imaging with a single photon of light. Notably, there were many groundbreaking advances such as momentum correlated ghost imaging first realized by Howell and co-workers[6] where the EPR paradox was demonstrated using both position- and momentum-entangled photon pairs. It was found that both position and momentum correlations generated by spontaneous parametric downconversion were strong enough to allow for either the position or momentum of a photon to be inferred from that of its twin correlated photon.[6] A position-momentum realization of the EPR paradox using direct detection in both the near and far fields of the entangled photon source was reported by Howell and colleagues, paving the way for both near and far field quantum imaging. In 2014, Aspden and colleagues presented an experimental demonstration of the Klyshko advanced-wave picture in both the near and far fields, coincidence imaging was also demonstrated with both position- and momentum-correlated photons (both the near and far fields) in comparison to the Klyshko advanced-wave picture where the equivalence between the spatial distributions in both sets of data was demonstrated.[59] The Klyshko advanced-wave picture can be understood as an effect that corresponds to classical diffraction, where one coherent mode is needed for illumination of the object in order to generate a diffraction pattern.[17] In 2009 Jack et al., proposed a holographic approach to quantum ghost imaging where phase filters were used in lieu of binary patterned masks.[7] The experimental setup is shown in Figure 4 (left), and is similar to that shown in Figure 3, however light modulating devices known as spatial light modulators (SLMs) have been incorporated into the experimental setup for ease of access to phase filters and speed of either a dynamic phase filter, stepping through the object or imaging various phase objects. In ref. [7] edge enhancement techniques were applied to quantum ghost imaging to demonstrate that a phase filter can lead to enhanced coincidence images. The high contrast images which were obtained and are shown in Figure 4 (right) are interpreted as a violation of the Bell inequality and demonstrates the quantum nature of ghost imaging.[7] Jack et al., successfully demonstrated both theoretically and experimentally that holographic ghost imaging setups have the ability to violate the Bell inequality which provided evidence for the presence of quantum correlations in this particular ghost imaging process.[7] Although this technique was demonstrated with phase filters, the object was stepped through to determine the coincidence counts, which is indicative of a raster type scan as demonstrated in refs. [2, 48, 60].
2.2 Single Pixel and Compressive Approaches
Raster scanning was already well known at the time as a cheap and simple scanning method by a single-pixel detector to acquire the image in quantum ghost imaging.[2, 47, 48] However, to acquire high resolution images with a high signal-to-noise ratio long integration times are necessary.[61, 62] In 2011, in the pursuit of resource-efficient quantum ghost imaging Zerom et al., accordingly introduced compressive sensing to quantum imaging, utilizing entangled photons for the purpose of imaging.[61] At the time of introduction to quantum imaging, compressive sensing was already successfully applied to seminal work in quantum state tomography[63] and quantum process tomography[64] in an effort to reduce the sampling data. Among the first to employ deterministic modulation, or what is better known as a basis scan (in lieu of the single-pixel scanning detector), to ghost imaging were Shapiro et al.,[11] and Duarte et al.,[58] where 2D random binary patterns were utilized. An example of the 2D random binary patterned masks is shown in the upper panel of Figure 5, while computational ghost imaging employs these patterns to project binary intensity patterns of modulated light onto the object for imaging purposes, quantum ghost imaging using compressive sensing employs these patterned masks as a basis scan. The photons are projected onto patterned masks that are then weighted by a factor determined by the measured coincidences between the signal and idler photons. Summation over these weighted projective masks then allows for reconstruction of an image of the object.
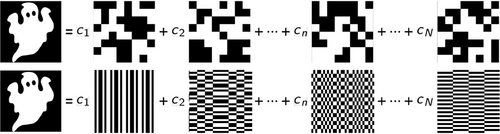
Random patterns, as shown in the upper panel of Figure 5, since they are not correlated to each other form an over-complete set with randomly distributed binary pixels that are either turned on or off.[11] The random masks form a pseudo-complete set and therefore it is commonly known that approximately twice the amount of random masks are required for a fully general image solution. In the random basis, for a fully general image solution, masks are required. Figure 5 (upper panel) shows examples of the random patterned mask types. A drawback is that a large number of these patterned masks are required ( or more, where is the number of pixels in the image and subsequently the number of pixels in each projective mask) to reconstruct an image that is noisy and therefore of poor quality.[54] Importantly random patterns do not constitute a complete spatial basis as the patterns are non-orthogonal, therefore many more measurements are required for a general image solution.
Compressive sensing is a signal processing technique that allows the reconstruction of sparse or compressible signals from a small number of measurements. The seminal work by Candés and co-workers introduced the theoretical framework of compressive sensing,[65] in this work the conditions under which perfect signal recovery is possible from sub-Nyquist sampling rates were established.[65] Compressive sensing provides an alternative method to Nyquist-Shannon sampling theory,[66] by leveraging prior knowledge that signals are often sparse or can be represented using a sparse basis.[67] The theory of compressive sensing has gained significant attention and has been widely applied in various fields, including image processing, signal processing, data acquisition, and application spanning to rapid magnetic resonance imaging.[68]
A schematic diagram of the experimental setup implemented for compressive quantum ghost imaging, by Zerom et al., is shown in Figure 6 (left). A SLM and a bucket detector replace the single-pixel scanning detector required for a raster scan. This substitution was a pivotal point for quantum ghost imaging as this was when quantum ghost imaging moved from the inefficient and lengthy raster scanning technique requiring long integration times to a condensed integration time two-dimensional scanning method. The inset of Figure 6 (left) shows the corresponding Klyshko advanced wave picture.[69] For a good practical understanding of Klyshko's advanced wave picture, Aspden and co-workers demonstrated an experimental realization of Klyshko's advanced wave picture in 2014.[59]
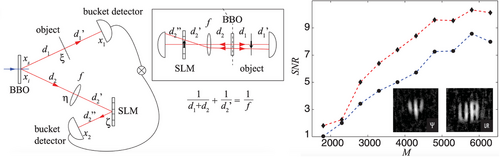
In ref. [61] the phase-only SLM (as utilized in Figure 4, ref. [7]) was adapted to function as an amplitude-only SLM. The raster scanning technique, as demonstrated in ref. [2], requires approximately 2.6 10 photons to reconstruct a 128 128 pixel image. Through the use of the compressive sensing technique demonstrated in ref. [61], this number was reduced an estimated to 1.4 10 photons for an image of the same resolution. Employing the use of random masks leads to oversampling the object to fully reconstruct a general image solution. Orthogonal bases are therefore the bases of choice which avoids oversampling leading to better time-efficiency in quantum ghost imaging.
The Walsh–Hadamard basis is one such orthogonal basis where each element is generated from the Hadamard matrix of specific order when the number of pixels making up the image is . The Hadamard transform is commonly used for recording spatial frequencies,[70, 71] or for multiplexing the direction of the illumination of an object.[72, 73] The Walsh–Hadamard patterns are orthogonal and derived from the Hadamard matrix. Walsh–Hadamard projective masks are generated by extracting the Walsh functions from the Hadamard matrix of order . By performing the outer product between columns of a Hadamard matrix of order , the result is a complete set of Walsh-Hadamard projective masks of pixel resolution. Walsh–Hadamard projective masks are orthogonal to each other.[58] Choosing the order of the Hadamard matrix will therefore result in the corresponding mask resolution. The added advantage to employing the Walsh–Hadamard basis as the patterned projective masks to spatially resolve the signal photon is that it is an orthogonal basis and will result in a general image solution. An orthogonal basis set of patterned projective masks systematically samples the object and an image is acquired in measurements, for a pixel general image solution.
The mask resolution, independent of the type of mask chosen to spatially resolve the signal photons, will determine the resolution at which the object will be imaged. A higher resolution results in a larger number of basis elements and therefore an increased number of masks is needed to reconstruct the image. Increasing the resolution has direct consequences on the reconstruction time, the number of Walsh–Hadamard masks required to form a complete set scales as . Specifically for a complete or general image solution, in the Walsh–Hadamard basis, masks are required. Examples of Walsh–Hadamard masks are shown in the lower panel of Figure 5.
The use of Walsh–Hadamard and random masks in quantum ghost imaging marked another pivotal point in ghost imaging history. This brought forth the introduction of all-digital quantum ghost imaging utilizing light modulating devices such as SLMs for both the object and the basis scan. Figure 7 left shows a schematic of an all-digital quantum ghost imaging setup. Important to note are the differences between this setup and that shown in Figure 3. While the main components and layout of a quantum ghost imaging setup have remained constant through time, experimental setups have evolved to employ SLMs and bucket detectors as a spatial resolution detector. The spatial resolution detector can mimic that of a single-pixel scanning detector, but more efficiently two-dimensional patterned masks are used to detect the position of the signal photons. As shown in Figure 7 (left), Walsh-Hadamard masks outperform random masks both in terms of resolving capability (reconstructed images are clearer) and efficiency (less Walsh-Hadamard masks are required for image reconstruction).
In recent years, there have been advancements in experimental setups for quantum ghost imaging, particularly with the incorporation of spatial light modulators (SLMs) and other light modulating devices. These advancements have enabled spatial resolution of the idler photon, thus enhancing the imaging capabilities of the system. Despite these technological developments, the fundamental components and layout of the experimental setup for quantum ghost imaging have remained largely unchanged. These experimental advancements propel us forward to specialized optical advancements in quantum ghost imaging.
2.3 Camera-Based Advances
Traditionally, quantum ghost imaging systems have previously consisted of a spatially resolving detector that is a scanning single-pixel detector or comprises patterned masks. In parallel, the field of single-pixel imaging has seen immense growth within the last two decades.[74-76] Basing the system on a single scanning detector imposes a fundamental limit on the detection efficiency of the system to where is the number of pixels in the image. To overcome this limitation a detector array was used to increase the detection efficiency, this enabled the acquisition of images while illuminating the sample with -times fewer photons.[77] This work has shown that not only can the photon count per pixel be reduced, but the quantum correlations allow the background noise to suppressed for high signal-to-noise images with just a few signal photons, a feat shown not to be possible with a classical analogue (reducing the noise by further gating or pulsing concomitantly reduces the signal). This marked a another pivotal point in the history of quantum ghost imaging, where employing detector arrays with single-photon sensitivity transformed quantum imaging marking a significant step towards biological imaging or where reducing photon flux prevents sample damage.[78-80]
The camera-enabled, time-gated system implemented by Morris et al., used the detection of one of the photons (known as the heralding photon) to trigger the detection of the twin position-correlated photon by an intensified CCD camera (ICCD).[77] The heralding nature of this imaging system allowed for the ability to count the number of single photons present in each image that was recorded. Images were acquired through three different system configurations as illustrated in Figure 8. In the quantum ghost imaging configuration (GI) the object is placed in the heralding arm or the arm without a camera or spatial resolution detector. An image is formed despite none of the imaging photons having interacted with the object. In the heralded imaging (HI) configuration the object is placed in the arm of the spatial resolution detector, the spatial resolution detector (or camera) is triggered for each detected single photon but the image is formed by only correlated photons that pass through the object. Comparatively, direct imaging (DI) is when the camera is triggered by an internal trigger mechanism and the image is formed by the subset of photons that pass through the object and arrive at the camera during the camera trigger window. These imaging systems are illustrated from the top to the bottom of Figure 8, respectively. The images acquired from all three imaging configurations are shown in Figure 9, respectively. Importantly, Morris et al., developed a low-light imaging technique employing a camera-enabled, time-gated imaging system. The natural sparsity in the spatial frequency domain of typical images was exploited and it was shown that it is possible to retrieve a target image with approximately 7000 detected photons, leading to an average photon-per-pixel ratio of 0.45.[77]
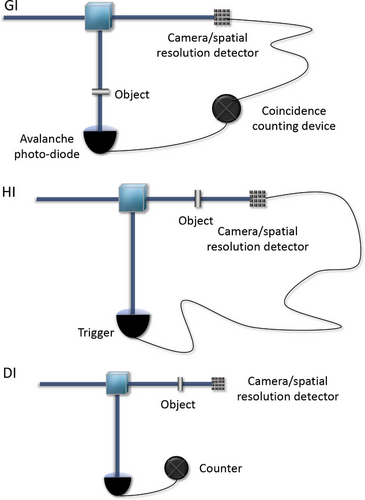
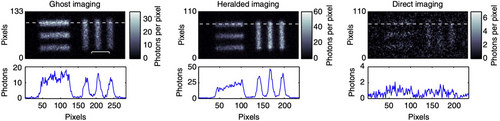
Morris and colleagues developed a low-light level imaging technique employing a single-photon sensitive time-gated camera system.[77] The nature sparsity in the spatial frequency domain of images was exploited along with the Poissonian nature of the acquired data to apply image enhancement techniques that subjectively improved the image quality.[77] Figure 9 shows the images that were acquired using each of the systems shown in Figure 8. For both the ghost- and heralded-imaging configurations a clear image of the test target was obtained with a contrast of 0.7.[77] By comparison, when using the direct imaging configuration, only a very faint image of the object was obtained with a contrast of 0.2. Notably, although the total number of image photons were similar for both the ghost and heralded imaging configurations, the image of ghost imaging configuration was obtained with fewer triggers than the heralded configuration. This type of difference arises, although the photon pair generation in each imaging type was the same, when the partially transmitting object was placed in the heralding arm the trigger rate was reduced in proportion to the transmission of the object.[77] For higher flux rates, the ghost imaging configuration proved to be beneficial as it made a lower demand on the ICCD camera.
The authors worked to reduced the number of photons required to form an image.[77] Typically 10 000 photons per pixel are required for a conventional imaging system, however, when an image is sparse in a chosen basis, it is possible to implement compressive techniques to store or even reconstruct the image from far fewer measurements.[57, 81, 82] This use of compressive techniques in a quantum imaging system have allowed for an image to be reconstructed using single-pixel detectors and far fewer samples than required by the Nyquist limit, albeit while still requiring many photons per pixel.[7, 61] Even with the longer acquisition times reported by Morris et. al. the images have very small numbers of detected photons per pixel (20). Although the signal-to-background ratio of these images was high, the signal-to-noise ratio was not.[77] However, the noise contributions in the reconstructed images were well-defined both in terms of the Poissonian characteristics of photon counting and a known rate of noise events.[77]
Single-photon sensitive time-tagging cameras marked another milestone for quantum imaging enhancements. These cameras are capable of resolving the number of individual photons in each pixel of the detector array. The single-photon camera can be used to detect single photons and resolve the number of photons in each pixel of the detector array which is advantageous in the recording of quantum imaging data.[83] A single-photon sensitive camera can distinguish between a two-photon event and a one-photon event, which enabled an increased amount of information to be extracted from experimental data and improve the efficiency of quantum imaging systems.[84] Additionally single-photon sensitive cameras have the potential to improve the efficiency of quantum imaging systems and expand the applications of quantum imaging.[83-85] Extracting as much information as possible about an object when probing with a limited number of photons is an important goal. As is a sub-theme of this review imaging with a few photons is a challenging task as the detector noise and stray light are predominant, which precludes the use of conventional imaging methods. Quantum correlations between photon pairs have been exploited in a heralded imaging scheme to eliminate this problem.[77] However these implementations have so-far been limited to intensity imaging and the crucial phase information is lost in these methods. A novel quantum-correlation enabled Fourier ptychography technique(for a full review on ptychography see ref. [86]) was implemented by Aidukas et. al.[87] The authors captured high-resolution amplitude and phase images with only a few photons. Notably, this demonstration of phase and amplitude imaging presented a low efficiency in terms of photons detected compared to the number of photons that illuminated the object (about 1%).[87] This was enabled by the heralding of single photons combined with Fourier ptychographic reconstruction employing an ICCD single-photon sensitive camera.[87]
2.4 Holographic Quantum Imaging
An essential tool of modern optics, in the reconstruction of phase objects, is holography.[88] Holography comprises the origin of many applications such as microscopic imaging,[89] optical security[90] and data storage.[91] Holography is traditionally based on the classical interference of light waves, however the quantum properties of light have inspired a range of imaging modalities employing entanglement,[15] and including interaction-free imaging,[20] induced-coherence imaging,[18] sensitivity-enhanced imaging,[78, 92] and super-resolution imaging protocols.[93, 94] Specializing in the non-classical realm, non-classical sources are able to produce holograms[95, 96] which has been observed with both single photons[97] and photon pairs.[98]
In 2021, Defienne and colleagues introduced and demonstrated a holographic imaging concept that relies on quantum entanglement to carry and relay the image information.[99] A key component in holography is the coherence required to extract phase information via interference with a reference beam. However, a holographic imaging approach was introduced by Defienne and colleagues that operates on first-order incoherent and unpolarized beams, so that no phase information can be extracted from a classical interference measurement.[99] Instead, the holographic information was encoded in the second-order coherence of entangled states of light. Using spatial-polarization hyper-entangled photon pairs phase images were remotely reconstructed. Specifically phase images were encoded in polarization hyper-entangled photons and were retrieved through spatial intensity correlation measurements, specifically through photon coincidence counting. The quantum holographic scheme, implemented by Defienne et al.,[99] has several distinguishing features: the holography is based on remote interference between two distant photons, this removes the traditional path overlap requirement between the illumination and reference photons, a subspace for encoding the phase information was employed that is robust against dephasing decoherence such as the presence of dynamic random phase disorder on the imaging paths, reliance on the quantum approach provided an immunity to classical noise, the spatial entanglement enhanced the spatial resolution by almost 2 in comparison to classical holography.
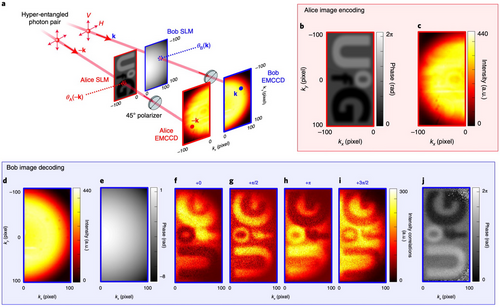
Despite the advances towards current state of the art, it can be seen that optical phase imaging has progressed much more slowly even though the applications of quantum phase imaging span various fields such as biological,[77, 100] materials,[101, 102] and communicating with quantum images.[103] While classical holography techniques have been very successful in diverse areas such as microscopy, manufacturing technology, and basic science. There still remains constraints on detection for wavelengths outside the visible range which in turn restricts the applications for imaging and sensing. To overcome these detection limitations, Töpfer et. al. implemented phase-shifting holography with non-classical states of light, where quantum interference was exploited between two-photon probability amplitudes in a non-linear interferometer.[104] It was demonstrated that this technique allows for retrieving the spatial shape (amplitude and phase) of the photons transmitted or reflected from the object thereby obtaining an image of the object.[104] In 2023, Sephton and colleagues developed a method employing traditional imaging masks already employed in ghost imaging setups to retrieve complex phase and amplitude information.[105] The authors introduced a novel approach that leveraged correlations in single-pixel environments for these measurements. Traditional masks, like the Hadamard masks, were shown to provide phase information naturally. By modifying the mask construction, a new method was developed that reconstructs full complex amplitude images with just one additional measurement per mask.[105]
The approach introduced by Sephton et. al. replaces the need for physical interferometry through the use of scanning masks encoded on spatial light modulators, making it simpler and more accessible to retrive phase and complex amplitude images.[105] Figure 11 illustratively compares the numerical simulations (Sim) with the experimentally (Exp) reconstructed phase only objects, insets show both the experimentally reconstructed cosine and sine projections.[105] Apart from noise distortion, good visual agreement between the numerical simulation and the reconstructed experimental images was shown in the upper panel of Figure 11. Noise was suppressed in the region where there is no signal which is illustrated by the dashed white circle.[105] The bottom panel of Figure 11 shows the reconstruction of a complex amplitude object as well as a 3D reconstruction of the phase and amplitude image.

The authors showed that this technique demonstrates the ability to visualize detailed phase objects without physical adjustments, enhancing the capabilities of quantum imaging setups.[105] This method is advantageous to reconstruct high resolution images at low flux rates and may therefore be suitable for imaging biological samples using entangled photons, to avoid photo-damage. The study concludes that this digital approach enables both amplitude and phase retrieval without complex techniques, holding promise for quantum and biomedical imaging applications.[105]
2.5 Quantum Imaging and HOM Interference
In parallel, the key signature of the Hong–Ou–Mandel (HOM) effect is the bunching of indistinguishable photons at the outputs of a beamsplitter.[106] Since the first demonstration,[106] the HOM effect has found several applications spanning many different fields of quantum optics such as quantum state engineering,[107, 108] quantum information processing,[109, 110] and quantum metrology.[111, 112] In the context of quantum imaging, the HOM effect has been employed to engineer quantum states through post-selection and multi-photon imaging.[113, 114] As is well-known, a limitation of quantum imaging is the requirement that the image is reconstructed one spatial mode at a time. To overcome this limitation modern scientific cameras, such as single-photon cameras, have seen significant growth.[15, 17, 115] In the pioneering work done by Ndagano et al., a full-field scan-free quantum imaging technique enabled by HOM interference was demonstrated.[116] This imaging protocol leverages the fact that group-velocity delays along the rising (or falling) edge of the HOM interference signal have a 1:1 mapping to the coincidence rate.
The idea of the HOM imaging technique is illustrated on the left of Figure 12. The paths of two distinguishable photons are overlapped onto a 50/50 beamsplitter. The signal photon travels through a sample with varying thickness and the idler photon does not interact with the sample. The signal photon incurs different group-velocity delays, leading to different arrival times with respect to the idler photon on a matching trajectory.[116, 117] Coincidence detections on the outputs of the beamplitter will show that the two-photon interference signals are shifted with respect to each other.[116] Through the recorded coincidence rates a contrast image of the sample was obtained. The layout of the HOM imaging system is shown in Figure 12. The two outputs from the beamsplitter are shown in the left panel of Figure 12(b), where pixel positions A (B) and A' (B') map to photon paths in the two outputs of the beamsplitter. In the event of bunching, pairs of photons would be detected at either A (B) or A' (B'). Meanwhile, in the event of anti-bunching, one photon in a pair would be detected at A (B) and the other at A' (B'). By applying a rotation on one of the output arms, it was noted that the spatially correlated pair detection indicates bunching, whereas spatially anti-correlated pair detection indicates anti-bunching.[117]
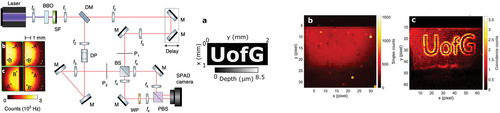
The surface of a micro-structured transparent sample was imaged, where letters “UofG” were etched to a depth of 8.45 on a glass substrate. Imaging was achieved by resolving HOM interference in space and time by the use of a single-photon avalanche diode (SPAD) camera. A sketch of the sample, the corresponding direct intensity image, and the reconstructed image are shown to the right of Figure 12. The direct intensity image confirmed that losses through the sample are negligible and no first order diffraction of the image was observed.[116, 117] The HOM image was instead reconstructed from an average over a set of 250 million intensity images from the second order correlations. To achieve this, the interferometer delay stage was adjusted such that photons going through the non-etched part of the glass showed partial destructive HOM interference; this delay corresponds to a location along the falling edge of HOM dip.[116] Therefore, photons that went through the sample travelled through less glass, leading to a different spatial delay that mapped to a higher number of coincidences at the spatial locations of the etched letters.
HOM interference was used in full-field imaging to directly retrieve spatially resolve depth profiles of transparent samples. Importantly, access to both bunching and anti-bunching images can be used to also assess losses and, in turn, reduce the noise variance in the images.[117] In terms of number of photons, on average coincidence values were of the order of for each pixel, which at 60 000 frames per second implies roughly only one frame in every 60 frames detected an actual photon pair. If the photon detection probability of the camera ( fill factor and quantum efficiency) were considered, this corresponded to an actual average photon-pair flux in the interferometer of photon pairs per second at each pixel or photon pairs per frame.[117] Despite the low levels of photons, the authors were able to retrieve clear images with a micrometer precision level in the depth measurements. Next-generation SPAD cameras can operate at rates[118, 119] and have been used to increase the video frame rate. An increase in count rates would also allow to apply high-precision HOM sensing approaches with 10–100 sensitivity and competing with classical interferometric approaches.[117]
2.6 Toward Quantum Microscopy
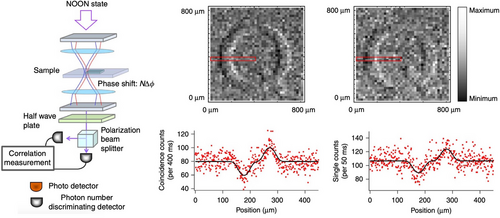
In 2013 Ono and co-workers demonstrated an entanglement-enhanced microscope employing the highly coveted states represented by polarization states.[93] Multi-photon quantum interference was utilized consisting of a quantum superposition of states with photons in the polarization mode and photons in the polarization mode. Characteristically, the polarization modes are orthogonal to each other. The experimental setup that was employed is shown in the left panel of Figure 13. A confocal-type differential interference contrast microscope was equipped with an entangled-photon source used to probe the sample. Images of the sample are shown in the right panel of Figure 13, the sample was a glass plate where a Q shape was carved on the surface with an ultra-thin step of 17 nm. The image of the glass plate is obtained with better visibility than a classical light source, the results of which are presented in the right panel of Figure 13. An improved signal-to-noise ratio of 1.35 0.12 is achieved and consistent with the predicted value. While this is not strictly quantum ghost imaging, this is a significant step towards entanglement-enhanced microscopy to image biological samples. The NOON state is relevant in quantum optics and imaging due to the potential of it's applications in high-precision measurements and imaging techniques.[120] The NOON offers advantages in quantum interferometry, where the phase sensitivity scales with , providing enhanced precision compared to classical strategies that scale with N. This property is valuable in various applications, such as gravitational wave detection, quantum metrology, and quantum lithography.[125] Taylor and Bowen provide a comprehensive review on quantum metrology and its application to biological tissue.[131]
2.7 Teleportation and Entanglement Swapped Imaging
Although applications in quantum ghost imaging are not currently common practise, the technique of entanglement swapping is pertinent to long distance image transfers across a quantum network. Figure 14 illustrates the differences between quantum ghost imaging and entanglement swapped quantum ghost imaging. In entanglement swapped quantum ghost imaging two pairs of entangled photons are generated separately and subsequently brought into a joint entangled state through a Bell state measurement,[132, 133] typically with a beamsplitter. Entanglement swapping generates correlations between systems that have not interacted[134] and can be observed in many degrees of freedom, examples include polarization[135] and orbital angular momentum.[136]
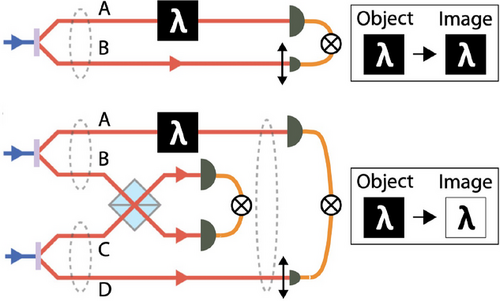
The first entanglement swapped ghost imaging used a four-photon set-up, as shown in the lower panel of Figure 14, to establish an object in arm A and an image in arm D, even though initially these were independent photons with no correlations. A major discovery was that by projecting onto the antisymmetric state at the beamsplitter, the resulting image was contrast-inverted with respect to the object.[113] This study constitutes the first experimental implementation of ghost imaging using non-interacting photons that were initially independent, and the first observed ghost imaging using entanglement swapping. What the study also showed is that to teleport an image would require many extra entangled pairs of photons, similar to the number of pixels to be teleported. Using the four-photon entanglement swapped set-up, only a two pixel image could be teleported with high fidelity. Recently a new approach to transporting images with high contrast has been demonstrated,[137, 138] enabled by nonlinear optics in the detection. This is an exciting avenue to explore in regards to teleporting images across a network.
Quantum imaging with undetected photons was introduced and demonstrated based on induced coherence without induced emission by Lemos et. al. in 2014.[18] The experiment used two separate downconversion non-linear crystals where each crystal was illuminated by the same pump beam generating a pair of entangled photons. When the signal photon from the first photon pair passes through the object and is overlapped with the idler photon from the second photon pair, the source of the photon is then undefined. Interference of the signal amplitudes coming from the two crystals then reveals the image of the object. The photons that pass through the imaged object were never detected, while images are exclusively obtained with the signal photons, which do not interact with the object.[18] This experiment was fundamentally different from previous quantum imaging techniques, such as interaction-free imaging[20] and ghost imaging, because now the photons used to illuminate the object were not detected at all and no coincidence detection was necessary. This enables the probe wavelength to be chosen in a range for which suitable detectors are not available. To illustrate this technique, images of objects that are either opaque or invisible to the detected photons were reconstructed. This experiment was a prototype in quantum information where knowledge can be extracted by, and about, a photon that was never detected.[18]
In 2019 a quantum diffraction imaging technique was proposed whereby one photon of the entangled photon pair was diffracted off a sample and detected in coincidence with its twin. The image was obtained by scanning the photon that did not interact with the sample.[96] This study in particular showed that when a dynamic quantum system interacts with an external field, the phase information of an object is imprinted in the state of a field in a detectable manner. In the quantum case the source intensity is weak in comparison to that of classical diffraction further showing that it was possible to image with weak fields while providing a high signal-to-noise ratio.[96] Importantly, this characteristic avoids damage to delicate and photon sensitive samples, further paving the way towards a quantum microscope. The photon that did not interact with the sample revealed the image and additionally uncovered phase information, similar to that shown by Dorfman and colleagues also in 2019 for linear diffraction where heterodyne-like detection of quantum light was achieved due to vacuum fluctuations of the detector.[139]
Microscopy with mid–infrared illumination holds tremendous promise for a wide range of biomedical and industrial applications.[140] The primary limitation, however, remains detection, with current mid-infrared detection technology often marrying inferior technical capabilities with prohibitive costs. In 2020 it was experimentally demonstrated that non-linear interferometry with entangled light provided a powerful tool for mid-infrared microscopy while requiring only near-infrared detection with a silicon based camera,[140] while Kviatkovsky et. al. did not harness quantum entanglement, entangled light was used in this. Wide-field imaging was demonstrated by Kviatkovsky et. al. over a broad wavelength range covering 3.4 to 4.3 while demonstrating a spatial resolution of 35 for images that contained 650 resolved elements. Moreover, it was demonstrated the the technique was suitable for acquiring microscopic images of biological tissue samples in the mid-infrared.[140] These results are a significant advancement towards quantum microscopy of biological matter.
2.8 Summary
Although there have been many advances to date which have pushed the boundaries of quantum ghost imaging, this discipline is still in it's infancy. Over the past 7 years, quantum imaging, quantum ghost imaging and ghost imaging have seen an emergence of AI technologies pivoting this discipline into a “super-tech” space. The ultimate goal being to apply ghost imaging in real-time for biological and security purposes.
3 Computational Advances in Imaging
Computational techniques were introduced to overcome efficiency limitations in ghost imaging.[141] Although these techniques have been extensively used in classical ghost imaging, their application to quantum ghost imaging is relatively new. In this section, we offer an introduction to machine learning and deep learning, while highlighting their distinctions. We also introduce deep learning algorithms and delve into their unique characteristics, while showcasing how they apply to ghost imaging as a whole. Here, we provide an encompassing view of the computational methods that have expanded the horizons of ghost imaging in terms of efficiency, enhancement, and photon utilization.
3.1 Computer Vision AI Architectures
Machine learning is a type of artificial intelligence (AI) that allows a computer system to learn and improve from experience without explicit programming.[142] Machine learning involves the use of algorithms and statistical models to enable computers to learn from data and to make predictions based on that data.[143] Subsequently, deep learning is a subset of machine learning that employs artificial neural networks to model and solve complex problems.[144] Deep learning involves the use of multiple layers of interconnected nodes, similar to neurons of the human brain, to learn and extract features from data.[145] The predictions or decisions output by the deep learning algorithm are accompanied by confidence scores which determine how trustworthy the prediction is.[38, 39, 144, 146]
There are, however, several key differences between machine learning and deep learning that are described in-depth in refs. [142-145]. Here we provide a brief yet comprehensive description on the key differences. Machine learning algorithms require structured data while deep learning networks can work with both structured and unstructured data. Deep learning networks process data through several network layers, this allows the networks to learn a hierarchical representations of the data.[38, 144] Feature extraction is often carried out manually in machine learning. Domain experts will select features in the data that are deemed relevant. In deep-learning however feature extraction is an aspect carried out by the neural network which learns to extract useful features from the data it is fed.[146] In machine learning the algorithms typically require fewer computational resources and time.[147, 148] Deep learning algorithms are computationally intense due to the large amounts of data required as well as the complexity of the network architectures.[144] Machine learning models are often more interpretive, as the features and decision-making processes are easily examined and understood. Deep learning models are often more challenging to interpret and are referred to as “black boxes”.[149] Machine learning sees applications in various disciplines while deep learning has shown significant success in computer vision where large amounts of unstructured data are involved.[150]
3.2 Convolutional Neural Networks and their Building Blocks
A significant leap in image processing was brought about by the introduction of deep convolutional neural networks (CNNs). CNNs are rooted in the 1990s,[37] but gained traction in the 2010s due to their remarkable ability to automatically learn and extract features from raw data, particularly in computer vision. Unlike traditional manually extracted features used in earlier computer vision methods, CNNs learn hierarchical features directly from the data, this makes CNNs highly effective for various tasks such as image classification, object detection, and denoising.[39]
CNNs consist of convolutional layers that apply filters to input images, these filters are used to automatically detect various features within the image. These layers are followed by pooling and fully connected layers that serve various purposes. As aforementioned, convolutional layers apply filters to input images. Each filter is a small matrix of weights that is convolved with the input image, hence a “convolutional” layer. This is a key feature of convolutional layers, called parameter sharing, where the same weights are used to process different parts of the input image. The result is a feature map that highlights the presence of automatically detected features in the input image.[151] Convolutional layers have the capacity to learn multiple features in parallel for a given input image, with each layer typically learning from 32 to 512 filters. The filters in the earlier layers of the neural network tend to focus on low level features (such as edges), while the deeper hidden layers have the capacity and ability to detect the more complex features within an image, such as object recognition of complex shapes and objects.[38, 144, 151]
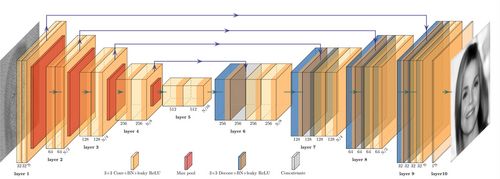
The VGG-16 architecture is a well-known CNN architecture trained on the ImageNet dataset.[40] The model architecture is shown in Figure 15 which begins with five convolutional blocks that comprise the feature extraction segment. A convolutional block is a sequence of layers containing both convolutional layers and maximum pooling layers. As the input images pass through the CNN, the shape of the image data is transformed. The spatial dimensions are intentionally reduced while the depth of the data is increased, as illustrated in Figure 15. The depth of data is referred to as the number of channels.[151] In the VGG-16 architecture the feature extractor is followed by a classifier which transforms the extracted features into class predictions in the final layer.[40] The final output layer consists of 1000 neurons, each representative of the 1000 classes present in the ImageNet dataset. The value of each neuron represents the probability that the input image corresponds to that class, the neuron with the highest predicted probability is therefore the predicted class.[40] The neurons in a convolutional layer are encoded to look for and extract features.
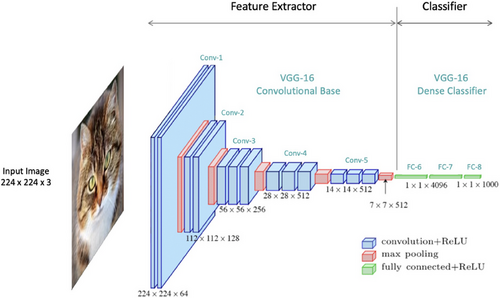
At the most basic level, the input to a convolutional layer is a two-dimensional array which can be the input image to the network or the output from a previous layer in the network. After implementing a convolutional layer, it is common practice to implement pooling layers which are used to reduce the spatial dimensions of the resulting feature maps.[144] Pooling layers assist to extract the most important information from the feature maps and reduce the computational complexity of the network. Common pooling operations include maximum (max) pooling and average pooling.[38, 144] Pooling layers summarize the feature map and reduce the number of parameters in the network as the input size to subsequent layers is then reduced, this in turn reduces the computations required for training. Pooling layers make CNNs more robust and invariant to translations as these layers capture the most salient features regardless of their exact location in the input. This allows the network to extract features from an object of interest regardless of its position.[144]
Finally, fully connected layers or dense layers are essential layers in the decision making process based on the extracted features by the convolutional and pooling layers.[144] Fully connected layers are responsible for connecting every neuron in one layer to every neuron in the next layer, this allows for the learning of complex relationships and features.[145] Fully connected layers are employed as the final layers of most CNN architectures for classification or regression tasks. Fully connected neural networks (FCNN) are networks constructed by fully connected layers. These three types of layers make up the basis units or blocks of a CNN. Stacking CNN blocks together generates different types of specialized neural network architectures such as autoencoders, generative adversarial networks, and U/Y network architectures. These types of networks are discussed below.
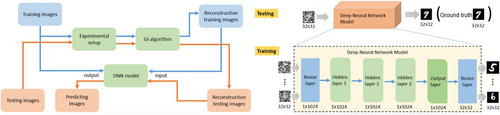
In 2017, a significant advancement was made in ghost imaging through the introduction of deep learning.[153] Lyu and colleagues pioneered an approach utilizing deep convolutional neural networks to improve the quality of image reconstruction.[153] This concept had its origins in the work conducted by Horisaki et al., who first applied machine learning techniques to enhance optical imaging.[154] The period between 2015 and 2018 witnessed rapid progress in applying deep learning to address various problems in optical imaging. The use of deep learning ranged from use in fluorescence lifetime imaging,[155] phase imaging,[156, 157] to imaging through scattering media.[158, 159] Figure 16 displays a flowchart (left) and a framework (right) of the neural network architecture employed by Lyu et al.,[153] The deep FCNN was trained to denoised undersampled data, shown on the right of Figure 16, thereby reducing image reconstruction time in classical ghost imaging to 20%.
Similar approaches were carried out, where deep learning methods were employed in the domain of classical ghost imaging.[160-165] The deep learning applications involved the utilization of CNN blocks, either stacked sequentially or adjusted in various ways depending on the nature of the required outcome. Figures 17-19 show vastly different neural network architectures that vary in depth of layers as well as complexity of layers, however all these architectures share a common trait in that their development began from that of CNNs.
3.3 Generative Networks
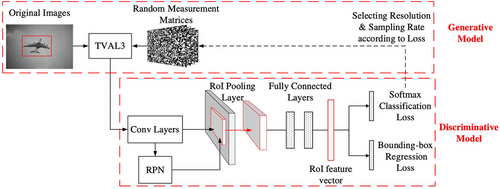
Figure 17 illustrates the architecture of a generative adversarial network (GAN) used in compressive sensing ghost imaging for object detection.[166] GANs are often challenging to implement and to train, and consist of two internal networks—a generator and a discriminator that are trained competitively.[169] The generator network creates data from random noise. It generates samples that resemble real data. The discriminator network subsequently tries to distinguish between real data and the synthetic data that is produced by the generator.[169] In this manner the generator and discriminator are trained against each other. The generator learns to improve its data by receiving feedback from the discriminator whose ability is to distinguish real data from generated data. Simultaneously, the discriminator learns to become better at this discrimination.[169] Training a GAN is a challenging task caused by issues such as mode collapse, training instability, and hyperparameter tuning. Unlike supervised learning, where the model is trained on labelled data with explicit input-output pairs, GANs do not require labelled data during training. Instead, they learn from the underlying patterns and distributions within the training data to generate new data samples. This makes GANs a prime example of an unsupervised neural network architecture.[169] In 2019, Zhai et al. focused on enhancing the accuracy and sharpness of the ghost imaging process by employing an object modeling tool that enabled high-quality image reconstruction with few measurements through the use of GANs.[166] By incorporating GANs into the compressive sensing ghost imaging framework the reconstruction of the ghost images was enhanced to improve the detection accuracy of the object contained within the image. The approach conducted by Zhai and co-workers allowed for high accuracy object detection within a low-resolution image reconstructed by undersampling.[166] Notably, GANs have been employed in other imaging techniques related to, but outside the boundaries of ghost imaging, such as single-pixel imaging.[170, 171]
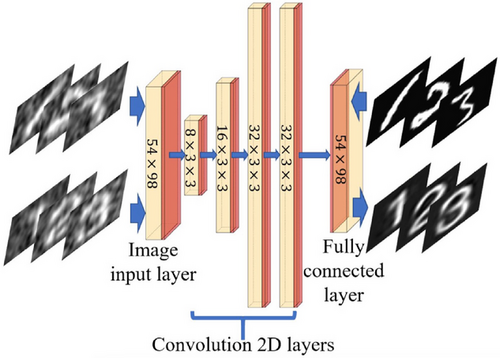
A framework for computational ghost imaging based on deep learning was presented in 2020 by Song and colleagues.[167] The deep CNN employed in this work consisted of five convolutional blocks including the image input layer, as shown in Figure 18. The final layer of the deep CNN was a fully connected layer to predict the output image. While the architecture adopted in Figure 18 was less complex than that of a GAN (Figure 17) and an autoencoder (Figure 19) significant training and hyperparameter tuning was carried out to ensure that the predicted result was the desired outcome. This demonstrates the versatility and capability of convolutional layers and blocks when implemented at various layers and depths. The deep CNN was trained on simulated data and learnt a sensing model wherein image reconstruction quality was enhanced. The conventional computational ghost imaging results and deep learning-based ghost imaging results were compared under various sampling ratios subjected to different noise conditions.[167] The CNN framework achieved high-quality images while reducing the sampling ratios to less than 5%. Similarly to the aforementioned work, the reconstructed images were undersampled and the quality of which was enhanced through the use of a deep CNN.[167]
3.4 Autoencoder and U-Net Architectures
In line with the expected challenges in the building and training of GANs, the autoencoder is also a type of unsupervised neural network that learns efficient codings of unlabelled data.[172] The autoencoder consists of two functions, the encoding function and the decoding function. The encoding function transforms the input data while the decoding function recreates the output data. Autoencoders are built with the practicality of image denoising, reconstruction and data compression and decompression.[173] These neural networks are also used in principle component analysis as a dimensionality reduction technique and can also be used to generate higher resolution images.[172] Autoencoders are a type of neural network which compress the input into a latent-space representation (also known as a bottleneck). The output is then reconstructed from the latent-space representation, thereby making autoencoders an unsupervised, or more specifically a self-supervised deep learning algorithm.[174] An autoencoder can also be thought of as a feature extraction algorithm in which the output is produced by the features learnt during training.[38] A limitation that exists with autoencoder networks is their decreased capacity to generalize their output. These particular networks generally enhance images according to what they have already learnt.
While Wang et al., implemented a physics enhanced deep learning approach, the principle method employed was that which constitutes a U-Net architecture.[168] The structure of the implemented U-Net is shown in Figure 19. The encoder takes in a low-quality image reconstructed through single pixel scanning and compresses it to a latent space representation. The decoder then extracts the high-quality image from the latent space representation as shown in Figure 19. The U-Net architecture is similar to that of an autoencoder architecture which includes both an encoder and decoder, the fundamental difference is that in autoencoders, the encoding part compresses the input linearly, this creates a bottleneck where all the extracted features are not transmitted. While U-Nets involve the deconvolution on the upsampling side and therefore overcomes the bottleneck problem of lost features due to connections from the encoder side of the architecture.
The justification for the use of deep learning in ghost imaging is to solve problems such as resolving undersampled images, classification, denoising, upsampling and enhancement. The base of many specialized deep learning architectures is formed by CNN blocks and layers. While this subsection discussed the architectures of neural networks, the structure, the layers, the versatility of CNNs and the use of CNNs within ghost imaging, the next section showcases the use of intelligence attributed to deep learning to enhance quantum ghost imaging.
3.5 Intelligent Enhancements to Quantum Imaging
Although deep learning techniques (and in particular CNNs and sub-variations thereof) are applied across various ghost imaging regimes, their utilization in quantum ghost imaging has only recently gained significant traction. Initially employed in computational ghost imaging, deep learning has been harnessed to enhance the quality of ghost imaging results, as illustrated in the upper panel of Figure 20. While classical ghost imaging involves much higher photon levels compared to quantum ghost imaging, image enhancement was achieved by deliberately undersampling the object.[153] In a study conducted by Rizvi and colleagues in 2020, they introduced a rapid image reconstruction framework named “DeepGhost”, which leverages a deep convolutional autoencoder neural network. This network was trained by transferring prior knowledge from the training dataset to a network driven by physical data. The study successfully reconstructed high accuracy images, as shown in the lower panel of the Figure 20. Rizvi and team assessed three distinct deep learning approaches for ghost imaging. They compared the seminal work in this sub-domain conducted by Lyu et al. in 2017 (GIDL)[153] with the methodologies presented by He et al. in 2018 (DLGI)[175] and their own work in 2020 (DeepGhost).[176] DeepGhost was proposed to strike a balance between depth of convolutional layers and speed of computation by a novel CNN architecture.[176] The network was fed undersampled images and was trained to reconstruct clear target images, reducing image reconstruction time to 10-20%.

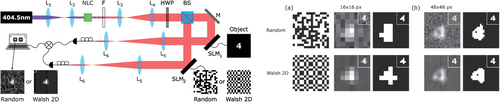
The deep learning architectures that were introduced in the previous subsection, were extended to quantum ghost imaging with the aim of bringing about a new era of intelligent quantum imaging. The aims are to leverage the capabilities of intelligent systems, such as deep learning frameworks, to enhance quantum images; reduce photon numbers required for imaging; and acquire images through computer identification (opposed to human identification). The first study to introduce deep learning to quantum imaging was conducted in 2020.[62] The authors implemented a fifty node neural network as an identification algorithm to recognize the image reconstructed after each mask (i.e., scan). The experimental setup as well as the results are shown in Figure 7. In this multi-parameter study the authors found an interesting trend whereby low-resolution reconstructions coupled with low integration times yield the best results from the neural recognition algorithm. This reveals that for recognition purposes it was convenient to use masks with low resolution and short integration times.[62]
In 2021, Moodley et. al. built on the work by Rodriguez et. al.[62] by implementing a two step deep learning approach to further reduce image acquisition time by object identification during early image reconstruction.[177] The two-step approach consisted of an image denoising and enhancing autoencoder neural network, followed by a neural classifier. The implemented autoencoder network was similar to that shown in Figure 19, however it was trained to denoise and enhance images reconstructed after each mask.[177] In the first step, a deep convolutional autoencoder was used to enhance the reconstructed image after each measurement. This step improved the quality of the image by leveraging an autoencoder. In the second step, a classifier was used to recognize the image after each measurement. This step was necessary to establish an optimal early stopping point based on object recognition, even for sparsely filled images.[177] This two step deep learning approach allowed for a five-fold decrease in image acquisition time in quantum ghost imaging.
Accordingly, a method for super-resolving quantum images was developed in 2022.[178] Super-resolving quantum ghost images is based on neural networks and involves experimentally reconstructing a low-resolution image, denoising it, and then super-resolving it to a high-resolution image, the results of which are shown in Figure 21. The authors implemented both a generative adversarial network and a super-resolving autoencoder in conjunction with an experimental quantum ghost imaging setup to implement the intelligent approach.[178] The efficacy of the approach was demonstrated across a range of objects and mask types. The proposed method involved several steps. First, a low-resolution image was reconstructed using a quantum ghost imaging setup. Then, a neural network, specifically a generative adversarial network (GAN), was employed to denoise the low-resolution image. Finally, a super-resolving autoencoder was used to enhance the resolution of the denoised image, resulting in a high-resolution image.[178] The performance of this technique was compared to traditional quantum ghost imaging techniques and it was found that the super-resolved approach achieved significantly improved resolution and allowed for faster image reconstruction speeds.

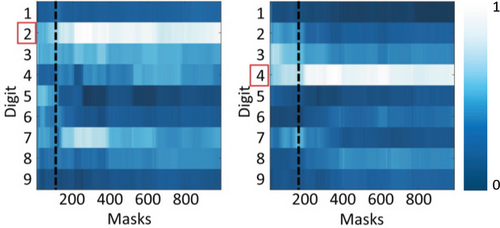
In 2023, Moodley et. al. applied machine learning techniques to quantum ghost imaging introducing a method for object recognition within the early reconstruction process of quantum ghost imaging.[179] In contrast to deep learning, as discussed in the previous subsection, machine learning requires fewer computational resources. In this work the authors implemented four different machine learning classifiers which were subjected to identifying the image reconstructed after each mask. This method requires only 1/10th of the measurements needed for a general image solution.[179] The goal being that a computer may be able to recognize an image through the early image reconstruction process quicker than a human could. This was successfully achieved, as shown in Figure 22, by a uniquely generated dataset. While the studies reported till now have used publicly available datasets, the work conducted by Moodley and colleagues was a special advancement in quantum imaging due to the unique dataset that was curated for the purposes of early image identification.[179] As can be seen in Figure 22, the images are not easily identified by a human being and in some cases not identified at all, rather the algorithm is capable of identifying the image with a confidence score of 75% or higher.

The aforementioned confidence scores are shown in Figure 23. The confidence scores predicted by the logistic regression classifier are shown in Figure 23 where the black dashed lines indicate the point in time (number of masks required) where the early stopping criteria was achieved. This established that the algorithm accurately recognized the reconstructed images 10 faster than a human would. The work carried out by Moodley et. al. successfully reduced image acquisition time in a quantum imaging optical setup to 10%.[179]
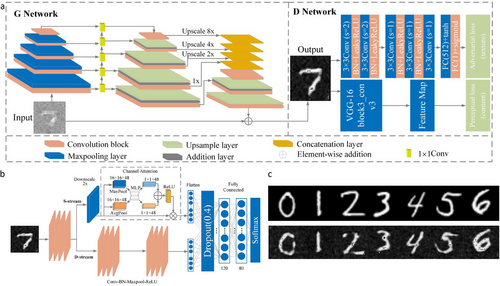
Currently there has been significant uptake on the use of intelligence for imaging although the intersection of these fields (artificial intelligence and quantum imaging) is still relatively new. Also in 2023, Wang and colleagues implemented an intelligent system based on deep learning for target recognition in quantum imaging.[180] The use of GANs is gaining traction in ghost imaging with specific applications to quantum imaging.[178, 180] Wang et. al. employed a GAN for denoising, the architecture of which is shown in Figure 24a, in this instance the GAN contains a generator and discriminator which are trained competitively against each other until the results are favourable. Figure 24b shows the structure and pipeline implemented for image recognition in entangled optical quantum imaging systems. Entangled optical quantum imaging is a technique that employs entangled photons to improve the resolution of an imaging system.[181] Figure 24a,b together form what is termed the RestoreCGAN. This specialized GAN restores and constructs missing edge contour structures of the target object in an entangled optical quantum imaging approach.[180] Finally, in Figure 24c the training dataset (top) as well as the RestoreCGAN results (bottom) are shown. A full comparison of all the tested deep learning algorithms and the resulting images can be found in ref. [180]. The experimental results have shown that RestoreCGAN outperforms the state-of-the-art methods in terms of both peak signal-to-noise ratio (PSNR) and structural similarity (SSIM). Additionally, the recognition accuracy of the RestoreCGAN reached 97.42%.[180]
While entangled optical quantum imaging has been enhanced by artificial intelligence through deep learning restoration and recognition,[180] it has also benefited from intelligence applied to quantum entanglement from incomplete measurements[182] and seen an advancement based on adaptive block compressed sampling.[181] This leads to the use of intelligence as deep learning algorithms in fields such quantum state tomography[182, 183] this, however, is beyond the scope of this review article. Although, still in it's infancy, the nexus of quantum ghost imaging and artificial intelligence has seen significant growth in the past 4 years, extending far beyond it's original application to classical ghost imaging and accelerating growth within quantum imaging.
At this juncture, it is instructive to provide a concise overview of the discussed network architectures, employed datasets, and outcomes arising from the integration of AI into classical and quantum ghost imaging. Table 1 presents a selected subset of illustrative examples showcasing noteworthy advancements facilitated by AI. Although numerous investigations have employed the conventional CNN architecture with variations in blocks and layers, the application of a FCNN deep learning technique in classical ghost imaging was pioneered in 2017, achieving substantial reductions in sampling ratios to 0.1 and 0.4 with high-fidelity images, as reported in ref. [153]. The pioneering deep learning work, conducted in 2017, employed a fully-connected neural network (FCNN) architecture,[153] not to be mistaken for a fully convolutional neural network architecture.
| Architecture | Dataset | Outcome | Quantum source | Ref. |
|---|---|---|---|---|
| FCNN | MNIST digits | Sampling ratio (SR) reduced - 0.1, 0.4 | No | [153] |
| U-Net | Caltech-256 | Completely denoised images | No | [160] |
| FCNN, CNN | MNIST digits | SR reduced - 6% | No | [161] |
| DRU-Net | MSRA10K | Image quality enhanced 3 | No | [163] |
| FCNN | MNIST digits | Classification at SR of 12.76% | No | [165] |
| GAN | MSCOCO 2017 | Object detection | No | [166] |
| DCAN | STL-10 dataset | SR reduced to 10% | No | [176] |
| Autoencoder | MNIST digits | SR reduced to 20% | Yes | [177] |
| GAN, Autoencoder | MNIST digits | Image quality enhanced 8 | Yes | [178] |
| Logistic Regression | MNIST digits | SR reduced to 10% | Yes | [179] |
| RestoreCGAN, TSFFCNet | MNIST digits | Completely denoised images | Yes | [180] |
Similar studies achieved a sampling ratio reduction to 10% in both classical and quantum ghost imaging, respectively.[176, 179] While one study adopted a straightforward logistic regression classification approach to reduce the sampling ratio in quantum ghost imaging,[179] another opted for the implementation of a sophisticated and inherently challenging Generative Adversarial Network (GAN) architecture during the nascent phase of GAN development in classical ghost imaging.[176] The successful results obtained by these methods using both advanced and simple machine learning techniques highlight their effectiveness when properly trained and rigorously evaluated. This emphasizes the necessity of carefully evaluating the constraints and limitations associated with predictions from various AI architecture types, illustrating the comparable capabilities between both intricate and straightforward architectures.
Conversely, previous studies demonstrated improvements in image quality by factors of 3- and 8.[52, 178] One study employed an innovative DRU-Net architecture in classical ghost imaging,[52] while another integrated both a Generative Adversarial Network (GAN) and Autoencoder to devise a super-resolving network architecture, subsequently applied to quantum ghost imaging. Remarkably, a predominant trend in the previously discussed studies reveals an inclination towards the utilization of either the Sigmoid or Rectified Linear Unit (ReLU) activation functions. The widespread adoption of Sigmoid and ReLU activation functions suggests a consensus, potentially rooted in their well-established performance characteristics, computational efficiency, and interpretability. Addressing the choice of the loss function, it can be seen that the use of MSE and cross entropy as common loss functions underscores the considerations surrounding the nature of the task at hand, emphasizing the importance of aligning the choice of loss function with the specific objectives and characteristics of the given problem such as classification, sampling ratio reduction and/or image quality enhancement.
Table 1 highlights distinct implementations in both classical and quantum ghost imaging, again elucidating how different network architectures can achieve analogous objectives, yet yield different image quality enhancement outcomes. Overall, this highlights the promise of both simple and complex AI methods for advancing classical and quantum ghost imaging capabilities through customized AI architectures. Careful bench-marking and analysis is critical to elucidate the trade-offs and constraints inherent to different AI design choices when applied to image enhancement and optimization.
3.6 Physics Driven AI in Ghost Imaging
In recent years physics enhanced AI has been applied to ghost imaging for optimization and enhancement purposes. In 2017, Lyu et. al. proposed a physics informed deep learning method where deep learning was used to reduce the sampling ratio. In this study, the input to the neural network was an approximant that was recovered using a conventional correlation algorithm.[153] As the modulation efficiency of the aforementioned approach was low, a further study conducted by Higham et. al. proposed a deep convolutional autoencoder in which the trained binary weights of the encoder were used to scan the target object,[184] this was a purely data-driven method. Additionally several studies have shown that it is possible to reconstruct an image from the detected signal without any physical priors,[161, 185] it is however pertinent to note that incorporating the physics of the imaging system into the neural network has paramount consequences for various aspects of the imaging system. One of the aforementioned aspects consists of applying physics informed methods to the data acquisition process as demonstrated by Goy et. al. and Wang et. al. in 2019, respectively.[161, 186] Neural networks face limitations in their generalization and interpretability, however the generalization aspect has been addressed by Goy et. al. and Wang et. al. by incorporating physics priors into AI based approaches,[187, 188] while the interpretability aspect was addressed by Iten et. al. in 2020.[189] In 2022 Wang et. al. reported a physics enhanced deep learning technique for single pixel imaging that leverage aspects relying on the forward propagation model of the imaging system.[168] A general framework leveraging both data and physics driven priors, called VGenNet, was proposed to enhance single pixel imaging and to solve existing inverse imaging problems.[170] In another study, single 1D data collected by a photodiode was required to feed a URNet architecture, the network was automatically optimized to retrieve the 2D image without training tens of thousands of labeled data points.[190]
4 Applications of Quantum Imaging and AI
While it is still too early to provide a comprehensive review on the convergence of advances within quantum imaging and computational technologies, there have been significant strides in this direction. Notably, the intersection between quantum imaging and AI has paved the way toward imaging with a single photon. In this section we showcase special applications that contributed to either the optical advances within quantum imaging, AI advances within quantum imaging, or both.
In a quantum ghost imaging based photon-sparse microscopy, infrared photons at a wavelength of 1550 nm were used to illuminate the object.[191] The infrared photons were detected by an InGaAs/InP single-photon avalanche diode. The entangled twin photon has a significantly different wavelength at 460 nm and is position-correlated with the infrared photon. The image data was recorded from the coincidently detected, position-correlated, visible and infrared photons using a highly efficient, low-noise, photon-counting camera. This wavelength transforming quantum ghost-imaging technique has potential for the imaging of light-sensitive specimens or where covert operation is desired.[191]
A schematic of the implemented imaging system is shown to the left of Figure 25. Photon pairs were generated through a highly nondegenerate SPDC process which gave signal and idler wavelengths of 460 and 1550 nm, respectively. The signal and idler photons were separated at a dichroic mirror and directed along different optical paths. The idler path contained an object that was placed in an image plane of the SPDC crystal. The idler photons that were transmitted through the object were then detected by a single-element, freespace coupled InGaAs/InP single-photon avalanche diode (SPAD), the heralding detector. In the signal path, the plane of the crystal was reimaged to a time-gated, intensified camera with a CCD detector array (ICCD).[191] The detection of an infrared probe photon by the heralding detector was used to trigger the gate of the intensifier in the ICCD such that the signal photon that was imaged was the position-correlated visible twin of the idler photon. Each triggering of the camera should, in principle, yield a measured photon. However, in practice, this efficiency was set by the optical throughput of the signal path and the quantum efficiency of the ICCD camera to .[191] Although this gave 50–100 photons per frame, the large number of camera pixels means there was on average much less than one photon per pixel in each frame. To each frame, the photon-counting methodology to convert these frames into photons-per-pixel was applied. The photons were summed over many frames to give an accumulated image.[191]
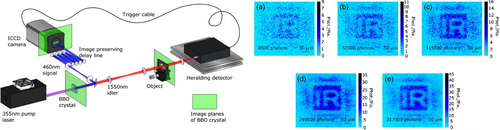
The object was formed from a polished silicon wafer onto which was patterned a microscopic gold test target. The height of the letters (“IR”) to be imaged were 120 . At a wavelength of 1550 nm, the silicon was transparent whereas the gold layer was not. Figure 25 (right) shows images obtained corresponding to the accumulation of photons as more of the ICCD camera frames were summed together to recover the accumulated images.[191] The work conducted by Aspden and colleagues marked a pivotal point for non-degenerative quantum ghost imaging, but also showcased how iterative and inefficient the technique is due to the low light levels and the significant increase in the number of frames required to achieve high-quality images.[191] This paved the way for photon-sparse microscopy with non-degenerate entangled photons.
Preserving the spatial profile of each detected photon in a quantum ghost imaging optical setup is of the utmost importance. The spatial modes of photons constitute valuable resources for quantum optics and in particular for quantum ghost imaging. In 2021, Bhusal and co-workers exploited the self-learning and self-evolving features of deep neural networks to correct the complex spatial profile of distorted Laguerre–Gaussian modes at the single-photon level.[192] Problematically, photon vulnerabilities to phase distortions, induced by random media, impose significant limitations on the realistic implementation of numerous quantum-photonic technologies which is magnified at the single-photon level.[192] The results reported by Bhusal and colleagues have important implications for real-time turbulence correction of structured photons and single-photon images. Figure 26 shows experimental results obtained by Bhusal et. al. The first column in each of the panels shows the spatial profile of the undistorted modes. The spatial profiles of the modes were distorted due to atmospheric turbulence. The aberrated modes are shown in the second column of Figure 26. In the experiment, hundreds of realizations of the aberrated beams were collected to train the CNN. The strength of turbulence predicted by the CNN was utilized to perform the phase mask optimization by means of a feedback gradient descent optimization (GDO) loop. The CNN with the GDO generated the correction phase masks which were encoded on a spatial light modulator to alleviate the turbulence effects.[192] This process enables obtaining optimized phase masks which were used to correct turbulence-induced distortions. The corrected intensity profiles are depicted in the last column of each panel of Figure 26. Shown in Figure 26a is the spatial profile of a structured beam corrected by the protocol, Figure 26b,c shows the experimental results for complex modes with radial structure. The robustness of this technique to correct the spatial profile of heralded single photons was also demonstrated and shown in Figure 26d–f. Figure 26d–f displays the turbulence correction of single photons prepared in superpositions with different azimuthal and radial quantum numbers.[192] The high fidelities achieved in the reconstruction of the spatial profile of single photons make this technique a robust tool for free-space quantum technologies, such as quantum ghost imaging.[192]
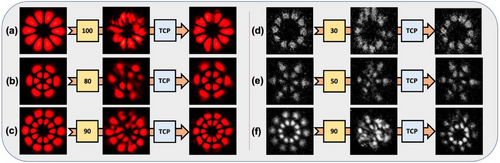
While excellence has been defined in both optical advances and AI in quantum imaging, as discussed above, a prime example of the nexus between the two domains was demonstrated by Li et. al. in 2022.[193] Li et. al. reduced the requirements for high-quality imaging by introducing a deep learning architecture for imaging with NOON states. Specifically it was shown that the fluctuation of images obtained by the NOON states when N = 2 can be reduced to that of the currently infeasible imaging by NOON states when N = 8.[193] The results obtained by two different types of deep neural networks were investigated and the imaging quality was characterized by the root mean square error. It was found that small-N NOON state imaging data is sufficient to train deep learning models to recover the full image. This process supports direct application to quantum imaging.[193]
To date, for NOON state imaging when N = 8 has not been experimentally implemented.[193] To bridge the gap between large-N NOON state imaging and small-N NOON state imaging Li et. al. introduced a deep learning approach to model the mapping of the imaging data of the two schemes.[193] The reason for choosing the scheme for when N = 2 is that it was a relatively simple scheme for NOON state imaging and was the best starting point for real applications. Two deep learning methods were introduced, a deep neural network method (DNN) and a CDAE autoencoder network.
The DNN method was a supervised deep learning framework that was designed to generate a computational model employing a large number of samples. The computational model was a multilayer network composed of linearly and fully connected layers and nonlinear activation functions associated with each neuron of the layers. The layers of the network can be generally divided into input layer, hidden layer and output layer. The structure of the DNN is shown to the right of Figure 27. The predicted results of noisy image examples are shown to the left of Figure 27 in the second to last row. Compared with the images in the second row of Figure 27 where N = 2, it can be seen that the DNN effectively reduced the noise level of the images. The noise level of all digital images by the NOON state when N = 2 can be even lower than that by the NOON state when N = 8, when the DNN was employed.[193]
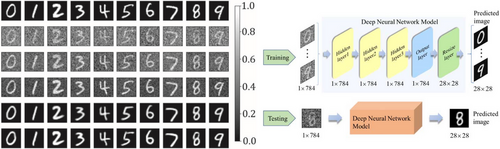
A CDAE is a denoising autoencoder whose architecture is similar to that shown in Figure 19. Compared to a standard denoising autoencoder, CDAE can take advantage of the convolution operation and has proven to be more suitable for the imaging process.[194] The predicted results by the CDAE of noisy images are shown in to the right of Figure 27 in the last row. Compared with the images in the second row of Figure 27 where N = 2, the reduction in noise level can be seen clearly. The CDAE model also suppresses the noise level of the images by NOON states when N = 2 to that by NOON states when N = 8. The effect of suppression is even greater than that obtained by the DNN.[193] The results by Li et. al. indicate that it is possible to obtain images as good as illuminated by large-N NOON states using only the simplest NOON state by incorporating intelligent deep learning methods.
5 Open Challenges and Future Opportunities
In 2020 Johnson et al., postulated that for a fully generalized image solution one requires orthogonal masks to fully reconstruct an -pixel image.[195] Under the assumption that the mask comprises independent and randomly set pixels and overlaps with the object of the time, the average signal would be with a standard deviation of per mask. As the number of photons required per mask is then the number of photons to measure a fully general image solution is .[195] It is now common knowledge that for most quantum imaging applications, a general image solution is not necessary.[179, 193, 195] The necessity lies in whether or not the image can be accurately identified or described with a high enough confidence prediction, or denoised to a point where it is identifiable by a human.[180, 193] This has led to the reduction in the number of measurements required not only for a general image solution but also for identifying the image earlier in the reconstruction process. As aforementioned, a general image solution is no longer required therefore allowing for image acquisition at fewer photon numbers.
Significant effort has gone into optimizing the optical components and including intelligent approaches within quantum imaging. While the exact capabilities and limitations of the quantum imaging paradigm shift toward imaging with a single photon may vary and is dependent of the use of specific intelligence techniques, technological advances and experimental conditions, the findings presented in this review indicate that significant progress has been made at the nexus of these fields. Quantum imaging with a single photon has the potential to revolutionize various applications, including microscopy, long-distance imaging, security and optical communications. Figure 28 provides an overview on the inception, the growth, the introduction of single-photon sensitive cameras, and the introduction of intelligent approaches employed to optimize and enhance the capabilities of quantum ghost imaging. These approaches highlight the efforts towards imaging with a single photon of light.
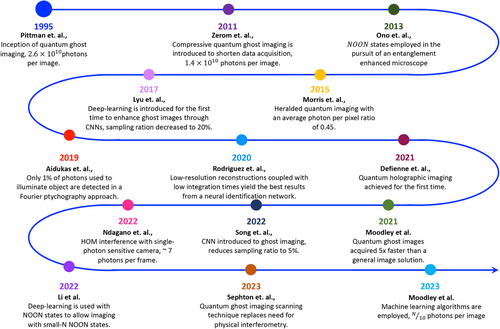
While there have been significant ground-breaking advances to-date it is apparent that both optical advances and intelligent approaches are required to realize quantum imaging with a single photon. Quantum imaging showcases capabilities that result in applications to biological imaging where the impact would transform medical imaging, diagnosis and pharmaceuticals. However, to fully unlock the potential of quantum imaging with a single photon, it is essential to delve even further into the convergence of these two critical components: specialized optical advancements and intelligent approaches. These two disciplines are not only complementary but also mutually reinforcing, paving the way for a new era of imaging technology that holds immense promise, particularly in the discipline of biological imaging.
As is well known, quantum optical systems are highly susceptible to noise therefore maintaining the quantum state, particularly at large scale or in application, remains an on-going challenge and a large area of focus within the quantum community.[120] Quantum imaging challenges continue to extend into scalability, when precise control of the system is required as well as detection efficiency for single photons. A technical challenge is achieving a high enough detection efficiency while minimizing the impact of noise which directly impacts the noise within the quantum images.[83-85] Quantum imaging currently requires detectors with ultra-high sensitivity and minimal noise to extract the signals of single photons.[99, 117] These scientific advancements are crucial to enhancing the overall signal-to-noise ratio and the quality of the images obtained. Within the practical and commercial perspective, it is essential to identify feasible applications where quantum imaging provides clear advantages over classical methods, this is essential for the growth, development, and integration of the field into feasible applications.
In parallel, the discipline of AI faces many challenges. Deep learning models require large amounts of data to achieve high performance. Ensuring that the data is accurate, representative, and unbiased is also a large area of focus and an on-going challenge. Deep learning models are prone to overfitting whereby the training data is memorized rather than generalized to identified patterns, regularization techniques and more robust datasets are a possible avenue to mitigating this issue. Shang and co-workers have contributed significantly to address unreliable image reconstruction results, their method based on a Bayesian Neural Network estimates this uncertainty in image reconstruction in single-pixel imaging.[196] Active areas of research within AI include, but not limited to, explainability as DNNs are often referred to as “black boxes”; computational resources as DNNs require substantial computational power for training; ethical bias as DNNs inherit biases that are present in the training data. It is therefore pertinent to build and train models that are explainable, computationally sustainable and fair. By incorporating physics priors into physics-informed and/or physics-driven AI it may be possible to shed light on many topics of historic debate, not limited to quantum imaging but rather for imaging and quantum optics in their entirety.
Optical and AI advances have been demonstrated to a point of good understanding, as illustrated by examples highlighted in this review. It can be seen that quantum imaging offers promising capabilities that surpass classical limits. Translating these advances into practical imaging applications, however, faces substantial technological obstacles. Efficient quantum light source availability, processing protocols, and complete end-to-end commercial quantum imaging systems must mature to rival the already established classical standards.
Realizing the potential of quantum imaging requires patience and persistent research and engineering efforts. Applications benefiting from quantum advantages will likely remain restricted in the coming years. Classical techniques retain advantages in critical areas like availability, efficiency, scalability, and ease of use. They will continue serving most imaging needs until quantum imaging systems can compete across all such aspects. Sustained efforts to nurture quantum imaging protocols and sufficient technological advancements, including but not limited to AI, could enable transformational capabilities. But scientific prudence suggests measured expectations regarding the timeline and scope. Incremental advances on specific promising fronts are a realistic path forward for now. While quantum techniques may someday catalyse imaging revolutions, measured expectations are currently advised. Order-of-magnitude improvements remain elusive in most domains thus far, with incremental progress more likely in the near term. Cost, complexity, and efficiency challenges persist.
6 Discussion and Concluding Remarks
Quantum ghost imaging holds promise for applications in highly photon-sensitive imaging and imaging through noisy or scattering environments. The fundamental signal-to-noise ratio advantages of quantum ghost imaging could enable reduced photon doses compared to classical microscopy in photon-sensitive applications such as biological imaging. Additionally, the ability to spatially correlate photons that do not preserve coherence propagating from the object to the detector can improve imaging through scattering media like fog. However, technical limitations pose barriers to practical quantum imaging applications. Efficient single photon bucket detectors are limited to visible and near-infrared wavelengths, while efficient megapixel spatial detector arrays lag in photon timing abilities. Although promising, SPAD arrays currently lack both the necessary efficiency and resolution required for current practical applications. Further detector improvements will help unlock the potential of quantum imaging. By combining quantum imaging and artificial intelligence, the benefits of quantum entanglement can potentially be harnessed for faster, cheaper, and more efficient systems. But concrete applications require advancing detector technology and processing techniques. While promising for specific niches like photon-sensitive and scattering media imaging, quantum techniques still face challenges in competing with established classical methods across applications. Incremental advances relying on quantum entanglement correlations show paths forward in overcoming current practical limitations.
To summarize, this review has provided a glimpse into the fields of quantum, classical, computational, machine learning and artificial intelligence-based ghost imaging, shedding light on the possible promising trajectory of intelligent quantum imaging. Although concise, we have explored the landscape while acknowledging the gaps that exist in our current understanding of this emerging field. Our investigation of the nexus of quantum imaging and artificial intelligence is still in its early stages, with the precise metrics governing their synergy still emerging as a developing area of research. Despite these advancements, open challenges persist in both quantum optics and AI. Quantum systems face ongoing hurdles related to noise, scalability, and detection efficiency for single photons. Overcoming these challenges is crucial for realizing the full potential of quantum imaging, particularly in biological applications where transformative impacts are anticipated.
Looking ahead, it becomes evident that the integration of artificial intelligence and quantum technology will herald a new era in imaging capabilities. The amalgamation of optical advancements, specialized optical elements, ultra-high sensitivity single-photon detectors, and sophisticated AI algorithms is poised to catapult ghost imaging, quantum ghost imaging and quantum imaging into new and uncharted territories of resolution, sensitivity, and real-time decision-making. The trajectory paved by current advancements not only holds promise for enhanced capabilities but also leads towards the recognition and reconstruction of complex objects at the single-photon level. The field of AI confronts issues such as data accuracy, model overfitting, explainability, computational resources, and ethical bias. Incorporating physics priors into AI models may provide insights into various aspects of imaging and quantum optics, contributing to a more robust and reliable integration of these technologies. This will indeed pave the way towards a practical and feasible quantum imaging solution.
While acknowledging the limitations inherent in the scope of this review, the broader narrative points towards a promising landscape for intelligent quantum imaging. The canvas is far from complete, and the evolving nature of these interdisciplinary fields ensures that future explorations will unravel even more profound connections between quantum principles, artificial intelligence, and the frontiers of imaging technologies. In this emerging field, the contours of an impactful future for intelligent quantum imaging emerge, this will be fueled by the relentless pursuit of innovation and the convergence of diverse scientific disciplines.
Conflict of Interest
The authors declare no conflict of interest.
Biography

Andrew Forbes is a distinguished professor at the University of the Witwatersrand where he leads a laboratory that focuses on Structured Light and its applications. He is active in promoting photonics in Africa, a founding member of the Photonics Initiative of South Africa and Director of South Africa's Quantum Roadmap. He is a Fellow of SPIE, Optica, the South African Institute of Physics (SAIP), and an elected member of the Academy of Science of South Africa. He has won several awards, including the national NSTF Photonics award (2015), the Alexander von Humboldt Georg Forster Prize and Fellowship (2020), the SAIP Gold Medal (2020), the Sang Soo Lee award from the Korean Optical Society and OPTICA (2022) and the Physics prize by TWAS (2024).




