2.1 Sagnac Interferometer Loop Measurements

The experimental setup for the characterization of forward SBS processes in a Sagnac interferometer loop is presented in Figure 1a.^{[16, 36, 38]} Light from a first laser diode at 1550 nm wavelength was modulated into short and isolated pump pulses of 1 ns duration and 5 μs period using an electro-optic amplitude modulator. The broadband pulses excited a packet of multiple acoustic modes. The pump pulses were amplified by an erbium-doped fiber amplifier (EDFA) to 100 mW average power and launched into a section of fiber under test that was embedded in a Sagnac interferometer loop.^{[16, 36, 38]} Pump pulses were coupled into the fiber in the clockwise direction only and were blocked from reaching the loop output by a tunable optical bandpass filter. In some experiments a polarization controller was used to adjust the pump pulses polarization for maximum stimulation of torsional-radial guided acoustic modes (see Section 3). In other measurements, a polarization scrambler was used instead in order to eliminate the contribution of the same modes from the ensemble average of repeating acquisitions.^{[16, 36, 38]} The temporal shape of the pump pulses $P(t)$ was recorded, and its Fourier transform $\stackrel{\sim }{P}(\mathrm{\Omega })$ was calculated offline and used in data analysis (see below). The standard SMF under test was 30 m long, and it was stripped of its protective polymer coating to obtain stronger acoustic stimulation.

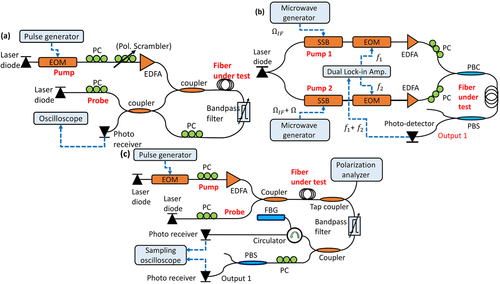
A continuous probe wave from a second laser diode source at 1532 nm wavelength was coupled into the loop in both directions. The tunable optical bandpass filter inside the loop was aligned to transmit the probe wavelength. Forward SBS induced phase modulation $\mathrm{\Delta }\phi (t)$ to the clockwise-propagating probe wave. For the fiber length and the pump power levels used, $\mathrm{\Delta }\phi (t)\ll 2\pi$. Due to the wavenumber matching characteristics of the process, the counter-clockwise propagating probe wave was largely unaffected.^[38] The nonreciprocal phase modulation due to acoustic waves was converted to intensity modulation of the probe wave at the Sagnac loop output. The output probe wave was detected by a photoreceiver of responsivity $R$ = 27 [V × W⁻¹] and 15 ps rise time. Polarization controllers were used to adjust the bias value of the non-reciprocal phase difference between the two directions of propagation of the probe wave.^{[16, 36]} Given proper bias adjustments, the detected voltage $V(t)$ is simply related to the forward SBS phase modulation: $V(t)\approx R{P}_{\mathrm{s}}[1+\mathrm{\Delta }\phi (t)]$.^{[16, 29]} Here $P_{\mathrm{s}}$ = 2 mW is the probe power at the loop output with the pump pulses turned off. The detector output voltage was sampled using a real-time digitizing oscilloscope, averaged over 4096 repeating acquisitions and processed further offline.

2.2 Measurements of Optical Power Coupling between Pump Waves

The coupling of power between two orthogonal pump tones due to forward SBS was measured using the setup illustrated in Figure 1b. Light from a laser diode of 1550 nm wavelength was split into two paths. The optical wave in one branch was upshifted by a fixed intermediate frequency offset ${\mathrm{\Omega }}_{\mathrm{IF}}$ of 2π × 10 GHz using a single-sideband electro-optic modulator. A sine wave of radio frequency $f_1=$ 2π × 40 kHz from one output port of a dual lock-in amplifier was superimposed on the modulating waveform using an electro-optic amplitude modulator. Light in the first branch was then amplified by an EDFA to 500 mW power. The laser output in the second branch was upshifted by a variable frequency ${\mathrm{\Omega }}_{IF}+\mathrm{\Omega }$ using another single-sideband electro-optic modulator, amplitude modulated by a sine wave of frequency $f_2$ = 2π × 50 kHz from a second output port of the same lock-in amplifier in another electro-optic amplitude modulator, and amplified in a second EDFA to 500 mW power.

The two pump waves were connected to the two input ports of a polarization beam combiner. The device transmits $\widehat{x}$ ($\widehat{y}$) polarized light only from input port 1(2) to the common output. Manual polarization controllers were used to align both pump waves for maximum transmission to the polarization beam combiner output. The combined tones were therefore of linear and orthogonal polarizations. The pump waves were then launched into a bare, 6 m long section of SMF under test. The fiber length was shorter than typical beat lengths of residual birefringence in SMF, hence polarization rotations remained small. A polarization beam splitter at the output end of the fiber routed a single pump wave component to a photoreceiver and rejected the other. The properties of the receiver were the same as above. The detected voltage was analyzed by the lock-in amplifier input. Coupling of optical power between the two tones due to forward SBS at frequency $\mathrm{\Omega }$ was identified through oscillations of the detected voltage at the sum radio frequency $f_1+f_2$.^[40] The coupling scales with the imaginary part of the inter-modal forward SBS coefficient: $2\mathrm{Im}[\gamma (\mathrm{\Omega })]$ (see Section 3).

2.3 Measurements of Phase Modulation and Cross-Polarization Scattering of Probe Waves

The setup for measuring the scattering of probe waves by torsional-radial guided acoustic modes is shown in Figure 1c. Light from a first laser diode at 1544 nm wavelength was modulated into short and isolated pump pulses of 1 ns duration and 5 μs period using an electro-optic amplitude modulator. The pump pulses were amplified by an EDFA to 500 mW average power and launched into a 30 m long section of bare fiber under test. The state of polarization of the pump pulses at the fiber under test input was adjusted by a manual polarization controller. A tunable optical bandpass filter blocked the pump pulses at the output of the fiber under test.

A continuous probe wave from a second laser diode source at 1550 nm wavelength was coupled into the fiber under test alongside the pump pulses. The input probe power was 50 mW. The input state of polarization of the probe wave was adjusted by a second polarization controller. The tunable optical bandpass filter at the fiber under test output was aligned to transmit the probe wavelength. Phase modulation and cross-polarization coupling of the probe wave were monitored in parallel by two detection channels. In one analysis branch, the probe wave passed through a fiber Bragg grating with maximum reflectivity of 90% at 1550 nm wavelength and a spectral full width at half maximum of 0.04 nm. The exact wavelength of the probe wave was adjusted to a maximum slope of the grating spectrum using temperature and current tuning of the laser diode source. Reflection from the grating converted phase modulation of the probe wave to an intensity signal.

Light at the grating output was detected by a photoreceiver ($R$ = 27 [V × W⁻¹] and 15 ps rise time), and the detected voltage was sampled by a real-time digitizing oscilloscope at 4 Giga-samples per second. The power spectral density of the sampled trace was calculated in real time by the digital oscilloscope and monitored near a frequency of 2π × 139.6 MHz. This frequency corresponds to a resonance of guided acoustic mode $\mathrm{T}{\mathrm{R}}_{2,7}$. The contribution of radial modes to the forward SBS process at that frequency is negligible. The magnitude of the power spectral density peak was used as feedback for polarization adjustments.

The output probe wave in the second analysis branch passed through a polarization beam splitter. Another polarization controller at the common input port of the beam splitter adjusted the state of polarization of the probe wave. The state was chosen so that when the pump pulses were turned off, the probe wave was equally split between the two output ports of the beam splitter. A second photoreceiver (with the same responsivity and rise time) detected the probe wave at output port 1 of the beam splitter. Detected signals represented cross-polarization coupling of the probe wave along the fiber under test. The detector voltage was sampled by a second channel of the digitizing oscilloscope, and the power spectral density of collected traces was calculated digitally. The power spectral density was monitored near the same central radio frequency as above. In addition to the two probe detection channels, a tap coupler at the output of the fiber under test routed 1% of the power of both pump and probe to a polarization analyzer instrument. The analyzer recorded the states of polarization on the Poincare sphere.

3.1 Stimulation of Torsional-Radial Modes by Linearly Polarized, Coaligned Pump Waves

Consider two continuous optical pump tones that are linearly copolarized and copropagate along an SMF in the positive $\widehat{z}$ direction. We denote the direction of electric fields of the two pump waves as the transverse $\widehat{x}$ axis, and the orthogonal transverse direction as $\widehat{y}$. The optical frequencies of the two tones are ${\omega }_{\mathrm{p}}\pm \frac{1}{2}\mathrm{\Omega }$, where ${\omega }_{\mathrm{p}}$ is a central frequency and $\mathrm{\Omega }$ represents a radio-frequency detuning variable. The optical power of the two tones combined includes constant terms and a beating pattern. The beating term is propagating with frequency $\mathrm{\Omega }$, axial wavenumber $K=n\mathrm{\Omega }/c$ and magnitude of $\stackrel{\sim }{P}(\mathrm{\Omega })=2n{\epsilon }_{0}c{A}_1{A}_2^{\ast }$ [W]. Here $n$ is the effective index of the optical mode, ${\epsilon }_0$ is the vacuum permittivity, $c$ represents the speed of light in vacuum, and $A_{1,2}$ are the complex magnitudes [V] of the field components of higher and lower frequencies, respectively. The transverse profile of the single optical mode is noted by $E_T(r)$ [m⁻¹], where $r$ is the radial transverse coordinate. It is normalized so that $2\pi \int |E_T(r){|}^{2}r\mathrm{d}r=1$. We also assume that the pump tones are undepleted, and neglect for the time being the possible exchange of power between the two along $\widehat{z}$.

In the above equations $\varphi$ is the transverse azimuthal coordinate with respect to the $\widehat{x}$ axis, $\widehat{r}$ and $\widehat{\varphi }$ denote unit vectors in the radial and azimuthal directions, respectively, $z$ is the axial coordinate, and $t$ stands for time. The coefficients $a_{1,2}$ are drawn from elements of the photoelastic tensor $p$ of the material:^[1-6] $a_1=-n^4(p_{11}-p_{12})$ and $a_2=-n^4{p}_{12}$. In pure silica, $a_1=$ 0.66 and $a_2=$ −1.19. Note that $\stackrel{\sim }{P}(\mathrm{\Omega })$ in Equation (2) is not restricted to the power of beating between two continuous waves only. It may also represent the Fourier transform of the instantaneous optical power of modulated coherent or incoherent light sources.^{[16, 18, 33]} The force per unit volume $\genfrac{}{}{0pt}{}{\rightharpoonup }{F}$ propagates with the same phase velocity $c/n$ of guided light.

The transverse dependence $\genfrac{}{}{0pt}{}{\rightharpoonup }{f}(r,\varphi )$ of the force per unit volume in Equation (3) consists of two terms. The first term ${\genfrac{}{}{0pt}{}{\rightharpoonup }{f}}_0(r)$ depends on the radial coordinate $r$ only, and points in the radial direction $\widehat{r}$ only. This term drives the oscillations of purely radial guided acoustic modes $R_{0,m}$.^[1-6] The second term ${\genfrac{}{}{0pt}{}{\rightharpoonup }{f}}_2(r,\varphi )$ depends on both $r$ and $\varphi$, includes components in both the radial and azimuthal directions, and is characterized by twofold azimuthal symmetry. It can therefore stimulate the oscillations of torsional-radial guided acoustic modes of the same symmetry, namely $\mathrm{T}{\mathrm{R}}_{2,m}$ modes. If the pump tones are polarized along the $\widehat{y}$ axis instead, the argument $2\varphi$ in Equation (3) is replaced with $2(\varphi -\frac{\pi }{2})$ and ${\genfrac{}{}{0pt}{}{\rightharpoonup }{f}}_2(r,\varphi )$ changes sign.

For calculations of $u_{2,m}^{(r)}(r)$ and $u_{2,m}^{(\varphi )}(r)$, see Supporting Information S1.^{[33, 39, 40]}

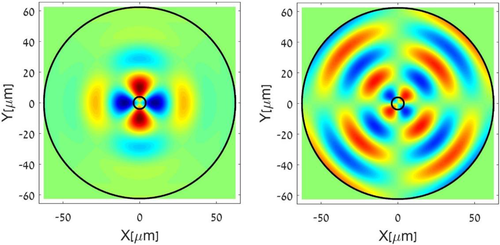
The modal oscillations may make take place through two degenerate, spatially orthogonal profiles: one characterized by azimuthal dependence according to the upper terms in the curled brackets of Equation (5), and another by the lower terms. The second profile is rotated by $\pi /4$ radians with respect to the first. In the former case, radial displacement is maximal for $\varphi =0$ or $\varphi =\pi /2$. In the latter solution, radial displacement is maximal at $\varphi =\pm \pi /4$. We refer to the transverse directions of maximum radial displacement as the principal axes of the guided acoustic $\mathrm{T}{\mathrm{R}}_{2,m}$ mode. The principal axes are therefore $\widehat{x}$ and $\widehat{y}$ for the first possible solution, and ${\widehat{e}}_{\pm 45}=(1/\sqrt{2})(\widehat{x}\pm \widehat{y})$ for the second. Figure 2 shows the normalized calculated transverse profile of mode $T{R}_{2,7}$ (cutoff frequency near 2π × 139.6 MHz), with principal axes along the $\widehat{x}$ and $\widehat{y}$ directions. Note that the principal axes are the same for $\widehat{x}$ or $\widehat{y}$ polarized pump waves. Supporting Video S1 shows calculations of the normalized instantaneous density variations: $\nabla ·{\genfrac{}{}{0pt}{}{\rightharpoonup }{U}}_{2,7}/\rho$, in the fiber cross-section. Here $\rho$ denotes the density of silica.

The stimulation efficiency scales with the spatial overlap integral between the transverse profiles of the driving force and the modal displacement:^[1-6]$Q_{ES}^{(2,m)}\equiv \int \int {\genfrac{}{}{0pt}{}{\rightharpoonup }{u}}_{2,m}^{†}(r,\varphi )·{\genfrac{}{}{0pt}{}{\rightharpoonup }{f}}_2(r,\varphi )r\mathrm{d}r\mathrm{d}\varphi$. ${\mathrm{\Gamma }}_{2,m}$ denotes the modal linewidth, which also signifies the decay rate of acoustic intensity. For bare fibers in air, there is little loss of acoustic energy to the surroundings and the linewidths ${\mathrm{\Gamma }}_{2,m}$ are determined entirely by internal acoustic dissipation in the silica cladding. The modal line widths are evaluated experimentally. For brevity, we represent hereunder the radio-frequency response of the modal stimulation by $H_{2,m}(\mathrm{\Omega })\equiv 1/({\mathrm{\Omega }}_{2,m}^2-{\mathrm{\Omega }}^2-j{\mathrm{\Gamma }}_{2,m}\mathrm{\Omega })$. The stimulation of acoustic mode $T{R}_{2,m}$ is maximal at its cutoff frequency $\mathrm{\Omega }={\mathrm{\Omega }}_{2,m}$.

The azimuthal dependence of the driving force ${\genfrac{}{}{0pt}{}{\rightharpoonup }{f}}_2(r,\varphi )$ (see Equation 3) matches that of ${\genfrac{}{}{0pt}{}{\rightharpoonup }{u}}_{2,m}(r,\varphi )$ with principal axes $\widehat{x}$ and $\widehat{y}$ (Equation 3). The pump tones may therefore stimulate the oscillations of the $T{R}_{2,m}$ mode with one of its principal axes aligned with their common linear polarization. On the other hand, the profile ${\genfrac{}{}{0pt}{}{\rightharpoonup }{u}}_{2,m}(r,\varphi )$ with principal axes along ${\widehat{e}}_{\pm 45}$ leads to $Q_{ES}^{(2,m)}=0$. This profile of the guided acoustic mode cannot be driven by coaligned, linearly polarized pump waves.

3.2 Stimulation of Torsional-Radial Modes by Linearly Polarized, Orthogonal Pump Waves

Here we denote $\stackrel{\sim }{P}(\mathrm{\Omega })=2n{\epsilon }_{0}c{A}_1{A}_2^{\ast }$ as before, even though the term does not signify intensity beating between orthogonally polarized pump tones in the context of this discussion. The electrostrictive force induced by orthogonal pump waves has been considered in specialty nanostructured fibers and polarization-maintaining fibers,^{[6, 24]} but not in SMF. Comparison of Equations (8) and (3) reveals that the driving force induced by the two orthogonal pump tones matches ${\genfrac{}{}{0pt}{}{\rightharpoonup }{f}}_2(r,\varphi )$, with $\pi /4$ radians rotation. We therefore expect that the two pump waves may stimulate $T{R}_{2,m}$ modes, with the same magnitudes expressed in Equation (6) above. This time, however, the transverse profile of the driving force matches ${\genfrac{}{}{0pt}{}{\rightharpoonup }{u}}_{2,m}(r,\varphi )$ with principal axes along the ${\widehat{e}}_{\pm 45}$ directions, rather than $\widehat{x}$ and $\widehat{y}$. Note also that the driving force induced by the orthogonal, linearly polarized pump waves does not include a radially symmetric term in the form of ${\genfrac{}{}{0pt}{}{\rightharpoonup }{f}}_0(r)$. Pump waves of linear and orthogonal polarizations therefore do not stimulate the radial acoustic modes $R_{0,m}$.

3.3 Scattering of Optical Probe Waves by Torsional-Radial Modes

The definition allows for possible small-scale differences between the photoelastic parameters of core and cladding.

where $A_{sig}$ is the input magnitude of the probe wave. For those input states, cross-polarization coupling takes place instead of phase modulation. Probe waves of arbitrary input polarization would undergo a combination of phase modulation and cross-polarization coupling. If the principal axes of the $\mathrm{T}{\mathrm{R}}_{2,m}$ mode are randomly scrambled along a series of repeating measurements, the ensemble average of photoelastic scattering for any input probe polarization would cancel out to zero. In contrast to the torsional-radial modes, the tensors of dielectric perturbations $\overline{\mathrm{\Delta }{\epsilon }_{0,m}}(z,t)$ due to the radial acoustic modes $R_{0,m}$ are proportional to the identity matrix $I$.^{[1, 2]} Radial modes therefore induce the same phase modulation on probe waves of all input polarizations.

The imaginary part of ${\gamma }_{2,m}(\mathrm{\Omega })$ is positive. The forward SBS process therefore leads to the attenuation of the higher-frequency pump wave, and the amplification of the lower frequency one.^[18] Forward SBS processes involving $\mathrm{T}{\mathrm{R}}_{2,m}$ modes were characterized experimentally through measurements of their effects on pump and probe waves, as detailed next.

3.4 Experimental Results: Stimulation of Torsional-Radial Modes

In a first set of measurements, a 30 m long standard SMF under test was placed within a Sagnac interferometer loop,^{[16, 36, 38]} (see the Experimental Section). The fiber was stripped of its protective polymer coating to obtain stronger forward SBS interactions. Polarized pump pulses of 1 ns duration, 5 μs period and 100 mW average power were launched into the fiber, in the clockwise direction of propagation only. An optical bandpass filter kept the pump pulses from reaching the loop output. Continuous probe light of a different wavelength was launched into the loop in both directions. The probe wave in the clockwise direction copropagated with the pump pulses and acquired phase modulation due to acoustic waves, whereas the probe in the counter-clockwise direction was largely unaffected due to lack of phase matching.^[38] The two replicas of the probe field were mixed together at the loop output. The beating converted the nonreciprocal phase modulation imposed by the acoustic waves into an intensity signal. The output probe wave was detected by a broadband photoreceiver. For small signals, the modulation of the detector voltage was proportional to the phase modulation of the clockwise-propagating probe. The voltage was sampled by a digitizing oscilloscope for further offline processing.

Figure 3a shows measurements and calculations of the normalized phase modulation spectrum of the probe wave, as functions of radio frequency $\mathrm{\Omega }$. The spectrum consists of sparse and narrow resonances, corresponding to $R_{0,m}$ and $T{R}_{2,m}$ modes. The modal linewidths used in calculations were fitted as a quadratic function of frequency, based on the measured spectrum.^[39] Agreement between model and experiment is very good. The magnitudes of peaks corresponding to $R_{0,m}$ modes were unaffected by the specific polarization of the input pump pulses, whereas those associated with $\mathrm{T}{\mathrm{R}}_{2,m}$ modes exhibited polarization dependence, as expected. The polarization of the pump pulses was adjusted to maximize the phase modulation due to $\mathrm{T}{\mathrm{R}}_{2,m}$ modes. The largest nonlinear coefficient ${\gamma }_{2,m}^{(0)}$ for torsional-radial modes was calculated as 3 W⁻¹ m⁻¹, as opposed to 20 W⁻¹ m⁻¹ for the strongest radial modes. Results are shown on logarithmic scale to emphasize the weaker contributions of $\mathrm{T}{\mathrm{R}}_{2,m}$ modes. Figure 3b presents another experiment in which the polarization of pump pulses was randomly scrambled among repeating acquisitions. The contributions of $\mathrm{T}{\mathrm{R}}_{2,m}$ modes to the phase modulation spectrum cancel out in this case, while those of $R_{0,m}$ modes remain, in agreement with analysis and previous observations.^{[16, 36, 38]}

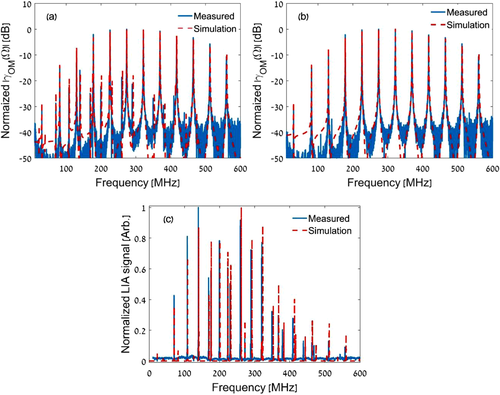
In the next set of experiments, two continuous pump tones were used instead of short and isolated pulses. The states of polarization of the two tones at the input end of a 6 m long bare fiber under test were adjusted to be linear and orthogonal (see the Experimental Section). The optical frequencies of the two pump waves were tuned separately using single-sideband electro-optic modulators to obtain a precise and variable difference $\mathrm{\Omega }$. In addition, the intensities of the two waves were modulated by respective signals of low radio frequencies $f_{1,2}$, drawn from two output ports of a lock-in amplifier. The instantaneous magnitude of acoustic waves stimulated by the two pump tones was therefore modulated at low frequencies $f_1\pm f_2$. The stimulation is accompanied by the coupling of optical power between the pump tones, as discussed above. The intensities of the two pump waves at the output of the fiber under test were therefore modulated at frequencies $f_1\pm f_2$ as well.^[40] A polarization beam splitter at the output end of the fiber was used to select a single pump tone, which was then detected by a photoreceiver. The lock-in amplifier monitored the magnitude of the detected voltage component at the sum frequency $f_1+f_2$.

Figure 3c shows the normalized magnitude of the lock-in amplifier output signal as a function of $\mathrm{\Omega }$, alongside corresponding calculations. Spectral peaks matching the cut-off frequencies of $\mathrm{T}{\mathrm{R}}_{2,m}$ modes are observed in the measurements, whereas those associated with the radial $R_{0,m}$ modes are eliminated (see also panel (a)), in agreement with analysis. The results constitute a first demonstration of stimulated Brillouin coupling between orthogonally polarized waves in SMF.

3.5 Experimental Results: Scattering by Torsional-Radial Modes

A final set of experiments examined the polarization dependence of probe waves scattering by a torsional-radial mode. The setup is described in detail in the Experimental Section. Short pump pulses were launched into a 30 m long section of bare SMF under test, in a similar manner to the Sagnac loop measurements presented earlier. The polarization of the pump pulses was adjusted by a manual polarization controller. A continuous probe wave of different wavelength copropagated alongside the pump pulses. The input state of polarization of the probe was independently controlled as well. A tunable optical bandpass filter blocked the pump pulses at the output end of the fiber. The probe wave at the output was split in two analysis branches. One replica was reflected by a narrow fiber Bragg grating filter. The exact wavelength of the probe was aligned with a maximum slope of the grating spectrum. Reflection from the grating converted phase modulation of the probe wave by guided acoustic waves to an intensity reading. The reflected waveform was detected by a broadband photoreceiver and sampled by one channel of a digitizing oscilloscope.

The output probe in the second detection branch passed through a polarization beam splitter. Another polarization controller aligned the probe for equal projections on its two output ports. A second photoreceiver at output port 1 of the beam splitter was used to identify cross-polarization coupling of the probe wave due to guided acoustic waves. The detector output was sampled by a second channel of the oscilloscope. The radio frequency power spectral densities of the two sampled signals were digitally calculated. The power spectral densities near frequency ${\mathrm{\Omega }}_{2,7}$ = 2π × 139.6 MHz were monitored. This frequency corresponds to a resonance of mode $\mathrm{T}{\mathrm{R}}_{2,7}$, with little forward SBS contribution from any of the radial modes (see also Figure 3). In addition, the states of polarizations of the pump and probe waves at the output of the fiber under test were recorded by a polarization analyzer.

In a first acquisition, the states of polarization of the input pump and probe were adjusted until maximum phase modulation at ${\mathrm{\Omega }}_{2,7}$ was identified at the Bragg grating output. According to the analysis of Sections 3.2 and 3.4, maximum should be reached when two conditions are met: i) the pump pulses are linearly polarized for the strongest stimulation of the acoustic mode; and ii) the probe polarization is aligned either with that of the pump pulses, or with the orthogonal linear state. Figure 4a,b (red traces) show the normalized power spectral densities of the fiber Bragg grating and polarization beam splitter measurement channels, respectively. Maximum phase modulation of the probe wave is accompanied with weak cross-polarization coupling. Figure 4c shows the states of polarization of the pump and probe waves. Maximum phase modulation is obtained at two pump polarizations: one aligned with the probe wave and the other orthogonal, as anticipated.

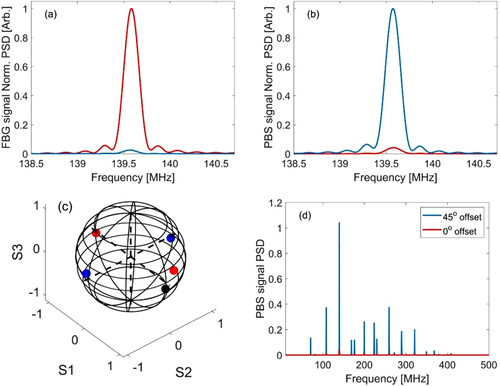
In a second measurement, the pump pulses polarization was adjusted for maximum cross-polarization coupling of the probe wave (see Figure 4b, blue trace). Figure 4c shows the two pump polarizations. The states of polarization form $\pi /2$ angles with that of the probe on the Poincare sphere, in agreement with expectations. In these settings, phase modulation of the output probe is significantly reduced (Figure 4a, blue trace). Figure 4d shows the power spectral density of probe cross-polarization coupling over a broader range of frequencies. The polarization of pump pulses was aligned for maximum coupling, similar to the blue trace of panel (b). The spectrum consists entirely of $\mathrm{T}{\mathrm{R}}_{2,m}$ modes, with no contributions of purely radial modes $R_{0,m}$. The trace is not the same of that of Figure 3c earlier: Here the measured power spectral density is proportional to $|{\gamma }_{2,m}(\mathrm{\Omega }){|}^2$, as opposed to $2\mathrm{Im}\{{\gamma }_{2,m}(\mathrm{\Omega })\}$ in Figure 3c (see Section 3.2). In addition, Figure 4d also depends on the power spectral density of the specific pulse modulation used. Nevertheless, the sets of resonance frequencies in both panels are equal and represent $\mathrm{T}{\mathrm{R}}_{2,m}$ modes only.

3.6 Stimulation of Torsional-Radial Modes by Circularly Polarized Pump Tones

Those two terms cancel each other as well. The same outcome is reached for two pumps aligned with the opposite circular polarization ${\widehat{e}}_{\mathrm{LC}}=(1/\sqrt{2})(\widehat{x}-j\widehat{y})$. Therefore, two pump tones of a common circular polarization do not provide a driving force for the stimulation of $\mathrm{T}{\mathrm{R}}_{2,m}$ modes.

The modal magnitude $B_{2,m}(\mathrm{\Omega })$ above remains that of Equation (6). The material displacement of Equation (24) is therefore rotating in the ${\widehat{e}}_{\mathrm{RC}}$ direction with twofold azimuthal periodicity, representing an acoustic vortex beam.^[25-30] Supporting Video S2 shows calculations of the normalized instantaneous density variations in a $\mathrm{T}{\mathrm{R}}_{2,7}$ mode vortex beam: $\nabla ·{\genfrac{}{}{0pt}{}{\rightharpoonup }{U}}_{2,7}/\rho$. If the polarizations of the higher and lower frequency pump waves are switched, the azimuthal dependence in Equation (24) would take up the form of $\exp (-j2\varphi )$ instead.

The stimulation of an acoustic vortex beam may be interpreted as follows:^[25-30] The forward SBS process eliminates a photon of frequency ${\omega }_p+\frac{1}{2}\mathrm{\Omega }$ and unit angular momentum in one direction, associated with its polarization degree of freedom. The same process generates a photon of frequency ${\omega }_p-\frac{1}{2}\mathrm{\Omega }$ with a unit angular momentum in the opposite direction. The overall angular momentum is conserved by the orbital angular momentum of the stimulated acoustic wave, which represents two units in the same direction of the eliminated, higher-frequency photon.^[25-30] The Brillouin stimulation therefore transfers angular momentum between the polarization degree of freedom of the light field and the acoustic wave.