Mathematical modeling of 13C label incorporation of the TCA cycle: The concept of composite precursor function
Abstract
A novel approach for the mathematical modeling of 13C label incorporation into amino acids via the TCA cycle that eliminates the explicit calculation of the labeling of the TCA cycle intermediates is described, resulting in one differential equation per measurable time course of labeled amino acid. The equations demonstrate that both glutamate C4 and C3 labeling depend in a predictible manner on both transmitochondrial exchange rate, VX, and TCA cycle rate, VTCA. For example, glutamate C4 labeling alone does not provide any information on either VX or VTCA but rather a composite “flux”. Interestingly, glutamate C3 simultaneously receives label not only from pyruvate C3 but also from glutamate C4, described by composite precursor functions that depend in a probabilistic way on the ratio of VX to VTCA: An initial rate of labeling of glutamate C3 (or C2) being close to zero is indicative of a high VX/VTCA. The derived analytical solution of these equations shows that, when the labeling of the precursor pool pyruvate reaches steady state quickly compared with the turnover rate of the measured amino acids, instantaneous labeling can be assumed for pyruvate. The derived analytical solution has acceptable errors compared with experimental uncertainty, thus obviating precise knowledge on the labeling kinetics of the precursor. In conclusion, a substantial reformulation of the modeling of label flow via the TCA cycle turnover into the amino acids is presented in the current study. This approach allows one to determine metabolic rates by fitting explicit mathematical functions to measured time courses. © 2007 Wiley-Liss, Inc.
To gain insight into important cerebral metabolic reactions, many modern methods have been established, such as radiotracer methods, e.g., PET (Raichle et al., 1975; Reivich et al., 1979), SPECT, and autoradiography (Sokoloff et al., 1977), or methods based on stable isotopes, such as MR [17O (Ligeti et al., 1995), 13C (Beckmann et al., 1991)]. Typically, in all these approaches, the rate of label incorporation into a product, P, from a single precursor, S, is modeled by using a set of one or more ordinary differential equations (ODEs). The complexity of the used network of ODEs depends on the specific reactions and isotope fluxes being studied (van den Berg and Garfinkel, 1971; Cremer and Heath, 1974). Systems of up to 200 coupled ODEs have been proposed for 13C NMR studies (Chance et al., 1983) which allow the resolved detection of multiple metabolites and resonance positions. Efficient and powerful software with a graphic user interface (e.g., SAAM; The SAAM Institute, Seattle, WA) has become available, with contemporary computing power allowing us to extract metabolic fluxes even from complex multi-TCA cycle models. This classical approach has already uncovered very important features of label scrambling of glucose metabolism via the TCA cycle (Mason et al., 1992; Gruetter et al., 2001).
However, not only a thorough understanding of the involved biochemical processes but also knowledge of the mathematics and good computer skills are required to adapt the model for a specific problem and to implement it in the chosen software. Thus, interpretation of the underlying mathematical equations and the results revealed by numerical solution are usually not intuitively interpretable, as reviewed by Henry et al. (2006), and thus are the subject of debate (Gruetter et al., 2001; Choi et al., 2002; Mangia et al., 2003; Hyder et al., 2006).
As a result of the current experimental sensitivity limitations, time courses of metabolite pools with low concentrations such as TCA cycle intermediates are difficult, if not impossible, to determine. As a consequence, the number of differential equations to be solved can be higher than the number of measured time courses, which is not a practical problem but obscures practical insight into existing relationships. For example, it has been well established that calculating the labeling of glutamate C4 requires the solution of the labeling of oxoglutarate C4 (Mason et al., 1992). It is, however, not discussed in the literature that glutamate C4 labeling can be described by a single differential equation, with a simple mathematical solution, as will be demonstrated. The present study had three aims: First, to establish a mathematical formalism that requires solving only one differential equation for each measurable time course of 13C label incorporation into glutamate and aspartate via the TCA cycle intermediates; second, to combine all terms incorporating the labeling from precursor pools into only one expression representing a composite “driving function,” for which the concept composite precursor functions (CPF) is introduced; and, third, to establish analytical solutions for the amino acid labeling, allowing determination of quantitative criteria under which the precise measurement of the rate of precursor labeling is obviated.
MATERIALS AND METHODS
Theory
The model is based on a previous model (Gruetter et al., 2001) that includes the following steady-state assumptions: metabolite concentrations and fluxes were considered to be constant, and the concentration of TCA cycle intermediates is small compared with the concentrations of amino acids. The current paper concerns the 13C label incorporation into the amino acids via the TCA cycle intermediates, without considering anaplerotic pathways or neuroglial compartmentation; i.e., only a single TCA cycle will be considered (Fig. 1).
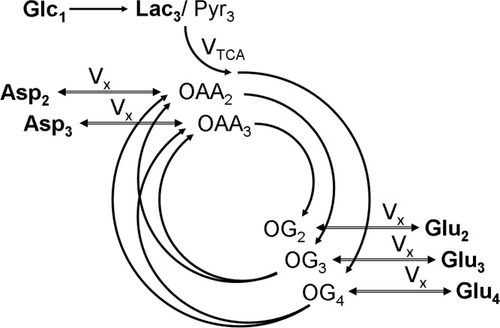
The chemical pathways involved in the label incorporation into amino acids via the TCA cycle included in the mathematical model. Metabolites that can be measured by 13C MRS are printed in boldface. The splitting of the arrows after label passed the pool of 2-oxoglutarate (OG) represents the symmetry at the succinate level. Glc, Lac, Pyr, OG, Glu, OAA, and Asp stand for glucose, lactate, pyruvate, 2-oxoglutarate, glutamate, oxaloacetate, and aspartate, respectively. The index at each metabolite name represents the position of the carbon that gets labeled in that pool. The TCA cycle flux is represented by VTCA, whereas the transmitochondrial flux is VX. The indices denote the carbon position that becomes labeled according to the pathways of the scheme after an injection of 1-13C glucose.
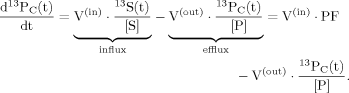 (1)
(1)
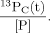
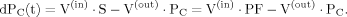 (2)
(2)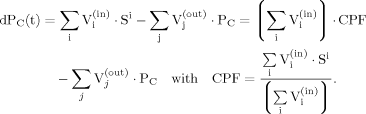 (3)
(3)In this paper, three cases were examined: case 1 deals with the label incorporation into Glu4, case 2 with incorporation into Glu4 and Glu2 or Glu3, and case 3 with incorporation into Glu4, Glu2, or Glu3 and Asp2 or Asp3.
Case 1
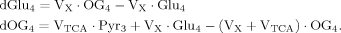 (4)
(4)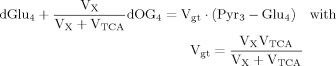 (5)
(5)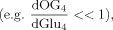
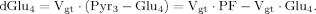 (6)
(6)Case 2
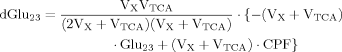 (7)
(7)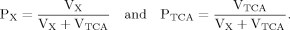
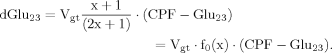 (8)
(8)Case 3
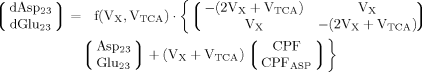 (9)
(9)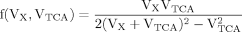
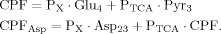 (10)
(10)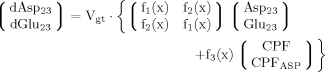 (11)
(11)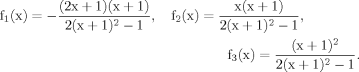
Analytical Solutions
In the following section, we show that for case 1 and case 2 the ODEs for Glu4 (eq. 6) and Glu23 (eq. 8) can be solved analytically. However, it is of advantage to assume an analytical expression for the labeling of the precursor pyruvate at position C3, Pyr3(t).
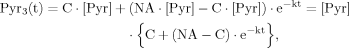 (12)
(12)The solution of ODEs as used in this model can be found using the variation of constants method as shown in part B of the Appendix. Additionally, the same method will be used to derive the analytical expressions for the case in which labeling of the precursor pyruvate reaches steady state infinitely fast, i.e., that Pyr3 is constant for all times, which mathematically equals performing the transition k→∞.
Case 1
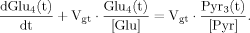 (13)
(13)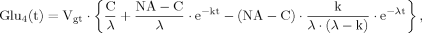 (14)
(14)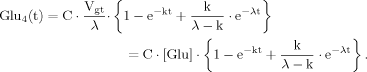 (15)
(15)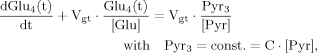 (16)
(16)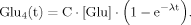 (17)
(17)Case 2
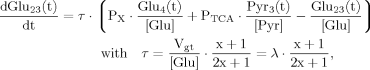 (18)
(18)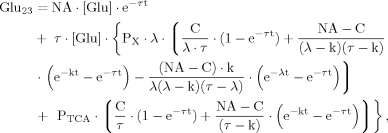 (19)
(19)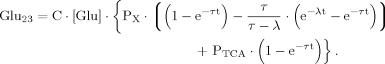 (20)
(20)Numerical Evaluation
Elimination of TCA Cycle Intermediates
To investigate the impact of the simplification of the set of ODE, numerical solutions of the original complete set of ODE were derived and compared with the results from simulating the simplified new model. This comparison was carried out for case 2 and case 3 and different values of VX = 1, 2, 8 · VTCA, where VTCA = 0.25 μmol/(g · min). The comparison for case 2 was expanded by adding the time courses of Glu4 and Glu23 as calculated from the analytical expressions. The pool concentrations for pyruvate, glutamate, aspartate, oxoglutrate, and oxaloacetate were assumed to be 0.1, 10, 3, 0.1, and 0.1 μmol/g, respectively.
Assumption of a Constant Precursor Labeling
Moreover, to analyze the assumption of an immediate steady state of the precursor labeling of pyruvate (k→∞), the residual between the correct analytical solutions for Glu4 (eq. 14) and for Glu23 (eq. 19) with different labeling velocities of pyruvate, i.e., different values of k (k = 0.1, 0.25, 0.5, 1, 2, 5, 10, 25, 50, 100 min–1), and the analytical expressions simplified with k-> ∞ were calculated. As defined in eq. 12, the range of k values represents possible labeling velocities, so that 95% steady-state FE of Pyr3 is reached after 30, 12, 6, 3, 1.5, 0.6, 0.3, 0.2, 0.1, <0.1 min, respectively. This analysis was performed with all integer values ranging from 1 to 100 for a ratio of VX/VTCA using VTCA = 0.25 μmol/(g · min).
RESULTS
Theory
By using the mathematical formulation of labeling kinetics (eq. 1), it was found that eliminating all terms related to the labeling of TCA cycle intermediates resulted in one equation per observable metabolite. Assuming that labeling of the precursor pyruvate is known, as a result the solution of the simplified ODE is unambiguous.
Case 1
The labeling time course of Glu4 was described by a single ODE, which was used in all three cases and permits the derivation of a single flux Vgt. Insofar as this ODE depends only on Vgt and thus on both VX and VTCA, it is explicitly obvious that no information can be obtained on VTCA per se from the enrichment curve of Glu4 without a priori knowledge of VX.
Case 2
In addition to eq. 6 for Glu4, the inclusion of the isotopic enrichment of Glu23 requires one additional ODE. By using the concept of precursor functions, both equations can be brought into a similar analytical form separating the terms related to influxes from terms concerning the effluxes. The terms PX and PTCA in the CPF (eq. 8) can be interpreted as probabilities that label comes from the last previously labeled amino acid (here Glu4) or is passed from the preceding chemical pathway (i.e., from Pyr3) directly to Glu23. From this relation, it became apparent that the route of label entering Glu23 was determined by the ratio of VX/VTCA, because this ratio in turn determines the probabilities PX and PTCA.
Case 3
Including Glu4, Glu23, and Asp23, a matrix equation containing two terms was found to describe labeling of Glu23 and Asp23 (eq. 11). The symmetric matrix contains the fluxes, which are the same for Asp23 and Glu23, whereas the additional term with the CPFs contains in addition to the common CPF an extra term for Glu23, according to an input into Glu23 coming from Asp23. Asp23 and Glu23 are coupled in this case, so they can be treated as one system. Thus the matrix represents the effluxes and the exchange of label between Glu23 and Asp23 across the TCA cycle, and the CPFs have to be interpreted as the input to this system of coupled pools.
It can be seen that the CPFs attain an analogous analytical form as for case 2 (for Glu23); as follows: The pool being labeled after Glu4 is Asp23, implying a CPF for Asp23 similar to that of Glu23 in case 2, as was shown eq. 7. Conversely, the CPF for Glu23 must incorporate contributions from Asp23 as precursor. Thus, the precursor fluxes for Glu23 changed to CPFAsp as a combination of all precursor fluxes, where the factors PX and PTCA again were interpreted as probabilities as in case 2 above. Therefore, the probability that label enters into the pool of Glu23 from the precursor Asp23 is PX, the probability that it comes from Glu4 is determined by the product PX · PTCA and the probability for Glu23 to receive label from the pool Pyr3 is (PTCA)2.
The evaluation of eq. 8 and 11 for x >> 1 reveals that the numerical values of fi(x) do not vary strongly (see Materials and Methods), whereas the CPF change their complete shape, because Glu4 labels with a time constant λ–1 = (Vgt/[Glu])–1 when pyruvate is labeled fastest. With increasing VX/VTCA, the probability that label is coming directly from a preceding labeled amino acid is increasingly dominating (PX approaching 1) such that Pyr3 loses its functionality as an isotopic label precursor.
Numerical Evaluation
Elimination of TCA Cycle Intermediates
The solutions of the exact and the simplified ODEs (Fig. 2) show the typical evolution of 13C labeling time courses as presented previously (Gruetter et al., 2001). In both cases 2 and 3, when increasing the ratio VX/VTCA Glu4 approaches steady state faster, and subsequent labeling of Glu23 starts more slowly but later also increases more strongly, thus describing an increasingly sigmoid curve. In case 3, increasing VX/VTCA also emphasize the increasing sigmoid shape of the FE of Asp23. In comparison with case 2, the sigmoid shape for the time course of Glu23 becomes slightly more intense in case 3 because of the further delay caused by preceding labeling of Asp23.
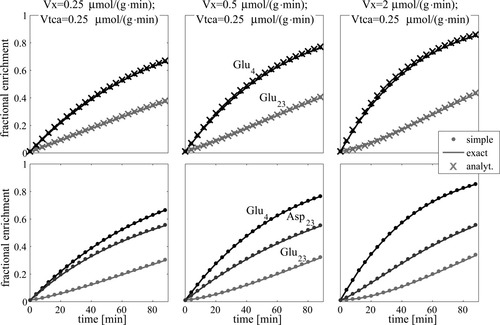
The fractional enrichment of Glu4, Glu23, and Asp23 calculated with the set of ODEs describing the labeling pathway either including the TCA cycle intermediates (exact = sold lines) or without them (simple = dots) and calculated from the analytical solutions of the simplified ODE (analyt. = crosses). This calculation was performed for different ratios of VX/VTCA = 1, 2, 8 (columns from left to right). The FEs in the upper row of graphs are derived from the model neglecting the labeling of oxaloacetate and aspartate but include the analytical solutions (case 2), whereas the lower row shows FEs resulting from the model including labeling of aspartate (case 3). With increasing VX, the sigmoid character of the time courses becomes more intense.
For all three cases and any choice of parameters, the time courses verified that the simplification in the derivation of the present model yields a negligible deviation from the enrichment curves calculated using the full set of ODEs (Fig. 2). The deviation was maximally below ∼0.6%, which is far below the experimental error. Evaluating the dependence of the error on the two cases, the error of Glu23 increases when Asp23 was included, whereas the error of Glu4 remained constant. The error was lower with faster Pyr3 labeling, i.e., larger k (data not shown). For Figure 2, k = 4 min–1 was used to yield an estimation of the upper bound of the error.
The upper row of graphs in Figure 2 also contains a plot of the analytical solutions for Glu4 (eq. 14) and Glu23 (eq. 19; crosses). As expected, the solutions are identical to those of the simplified ODEs.
Assumption of a Constant Precursor Labeling
When assuming that pyruvate labeling is rapid, i.e., k/λ >> 1 and k/τ >> 1, and comparing this with the solution assuming a constant instantaneous Pyr3 labeling C at t > 0, a small dependence on the ratio VX/VTCA was observed (Fig. 3), which overall was negligible. As expected, as k was increased, the deviations decreased exponentially. The time course of Glu23 showed less deviation for low values of k in comparison with Glu4 (Fig. 3). Adapting the infusion protocol of the labeled glucose, such that 95% of the steady-state concentration is reached after 30 min, results in a deviation below 16% and 8% for the FE of Glu4 and Glu23, respectively (Fig. 4). If such a label concentration can be reached after only 12 min, this already reduces the deviation to 8% and 3%, respectively. These errors can be assumed to be negligible in relation to experimental error.
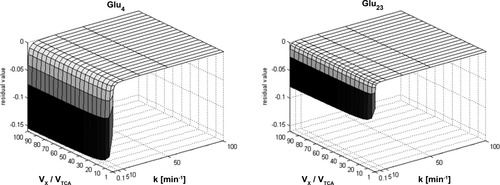
The two graphs show the maximal residual value of the FE of Glu4 (left) and Glu3 (right) if calculated with the assumption that the precursor pyruvate labels infinitely fast instead of using the exact equation depending on the ratio VX/VTCA and the velocity of pyruvate labeling, represented by k. Even for very low k, the residual will not exceed 16% for Glu4 and 8% for Glu3. There is no remarkable dependence on the ratio VX/VTCA.
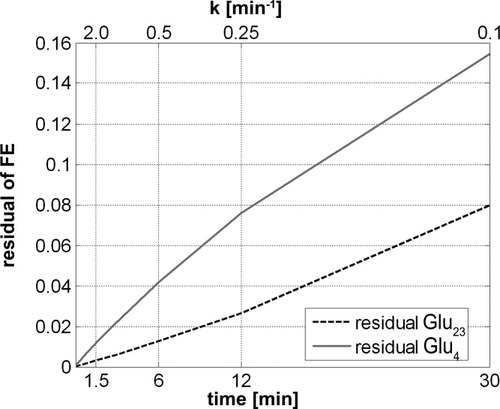
Similar to Figure 3, the graph shows the residual of the exact FE of Glu4 and Glu3 and these FEs calculated assuming that the pyruvate labeling is infinitely fast. The residual is plotted vs. the velocity constant of pyruvate labeling k, assigned to the abscissa at the top. The time displayed on the bottom abscissa corresponds to the time at which pyruvate reached 95% of the steady-state labeling. When using the simplification of an infinitely fast precursor labeling, this graph shows which deviation has to be taken into account for a given infusion protocol, represented by value k or the time until 95% labeling is achieved. Conversely, this graph can be used to adapt the infusion protocol to minimize the deviation.
DISCUSSION
The current paper describes a novel mathematical framework for simplifying the mathematical modeling of tracer incorporation, illustrated with the example of TCA cycle rate determination by 13C NMR. We show that, if changes in the labeling of TCA cycle intermediates can be neglected compared with that in amino acids, the number of differential equations required to describe the label incorporation can be halved. Interestingly, the flux rate into Glu4 calculated thus is identical to the Vgt derived by Mason et al. (1992), who used probability arguments. Here we demonstrate that this derivation is valid only if the rate of labeling of OG4 is negligible compared with that of Glu4, which is a condition that has not been established to date.
Specifically, the presented model yielded a simplified set of a reduced number of ODEs describing the label incorporation into the amino acids resulting from metabolic reactions ascribed to the TCA cycle. The labeling of glutamate at positions C2, C3, C4, and of aspartate at positions C2, C3 can be described with only five ODEs, namely, eq. 6 and 9.
Label flows into Asp23 from either Pyr3 or Glu4 and similarly for Glu23, and this flow can be described by composite precursor functions. We are not aware of any description of the labeling of Asp23 and Glu23 in such a manner. When interpreting the driving input functions of the ODEs (composite precursor function) as terms representing the probability that label comes from the directly previously labeled amino acid or from preceding labeled pools, for example, for a very high VX/VTCA, the label is mostly received from the latest labeled amino acid pool instead of any other pool labeled earlier in the metabolic pathway.
From eq. 6, it is clear that, with a step function in Pyr3, Glu4 will follow an exponential time course (1 – e–kt) with k = Vgt/Glu, which is confirmed by the analytical expression for Glu4 (eq. 17). As has been shown previously (Choi and Gruetter, 2004), with such a significant delay, when Glu4 is the precursor, (VX/VTCA >> 1) will lead to a sigmoidal shape of the label curve for Glu23. For example, from eq. 20, VX/VTCA >> 1 implies PX ∼ 1 and PTCA ∼ 0 and hence Glu23/[Glu] = C(1 – 2e–τt + e–λt) = C(1 – e–τt)2. Clearly, the first derivative of this function with time is initially zero; hence, with VX/VTCA >> 1, it is shown analytically that Glu23 labeling at t = 0 should be very slow. The approximations for this derivation require fast precursor labeling for Glu23 (k/λ >> 1) and a high enrichment (NA/C << 1), so they can be easily verified from experimental data fulfilling these conditions. As expected from eq. 8 or analytically from eq. 20, it was found that the sigmoid nature of the labeling curves increases with VX. If VX is higher, more label enters into the amino acids and thus arrives later in the next pool of amino acids on the pathway. This delay causes a less steep slope at the beginning of the labeling time course of later-labeled amino acids and thus a more curved sigmoid, implying that the CPF is dominated by the direct precursor, e.g., Glu4 for Asp23, Asp23 for Glu23, or Glu4 for Glu23, if Asp23 is not included. Hence, with the formulation of the CPFs, the sensitivity of the labeling time courses to VX/VTCA can be evaluated. The increasing sigmoidal shape further implies that the ratio of VX/VTCA is best determined at the initial points of the labeling time courses and not in the data acquired at steady state.
This interpretation of the ODEs as presented above confirms former findings based on an analysis of experimental data with the help of mathematical modeling (Mason et al., 1992). Thus this interpretation of the mathematical expressions reflects only the intuitive character of the concept of CPFs. Furthermore, eq. 6 explicitly states that it is not possible to determine either the TCA cycle flux VTCA or the mitochondrial flux VX from measuring the labeling time course of glutamate in position C4. Instead, from the definition of Vgt (eq. 6), it is apparent that Vgt is always smaller than VTCA. Thus, assuming that Vgt = VTCA (VX >> VTCA) leads to an underestimation of VTCA and consequently of the total glucose consumption (CMRglc) rate of the brain. In this context, it is of interest to note that some previously published values of VTCA, ranging from ∼0.47 to ∼0.53 μmol/g, obtained with the assumption that VX >> VTCA (Hyder et al., 1996, 1997; Sibson et al., 1998; Patel et al., 2004), are lower than results found with 13C NMR (Henry et al., 2002) as well as with other tracer methods, such as 17O NMR (Zhu et al., 2002) or autoradiography (Nakao et al., 2001), which ranged from ∼0.71 to ∼0.83 μmol/g under similar anesthesia conditions (α-chloralose).
Analytical solutions of the ODEs could also be derived. However, not using any further simplification, unlike the resulting expressions for Glu4 (eq. 14), which is fairly simple, the function Glu23 (eq. 19) already has a fairly complex structure, which is difficult to interpret. Solving the coupled ODEs of Glu23 and Asp23 yields terms that are beyond the scope of this manuscript and will be presented elsewhere.
However, the fact that now one analytical solution is available for either fitting the time course of Glu4 to determine Vgt or Glu3 to determine the ratio VX/VTCA reveals a unique tool for analyzing the data of a 1-13C-glucose MRS experiment. Consequently, measuring both labeling curves allows for derivation of both fluxes, VX and VTCA.
Moreover, the model presented shows that a precise knowledge of the precursor labeling of pyruvate is no longer required, as long as the infusion protocol guarantees a sufficiently fast labeling compared with the amino acid label turnover rates. Even a less perfectly adapted infusion protocol that reaches a steady state of pyruvate labeling after about 30 min results in negligibly low deviations from the correct expression of the time courses of Glu4 and Glu23 when related to experimental accuracy. Henry et al. (2002) established an infusion protocol of labeled glucose that fulfills this criterion. With this additional simplification, Pyr3 = const, the analytical expressions of Glu4 and Glu23 fall into a straightforward form such that the fitting process can be done with even common software, such as Excel or Origin. With this step, a significant practical problem of in vivo 13C MRS studies is solved.
CONCLUSIONS
We conclude that the explicit solution of the labeling of the TCA cycle intermediates can be eliminated from the mathematical model, resulting in a reduced number of necessary ODEs to one equation per measurable metabolite pool. Formulation of the composite precursor functions showed that measuring time points at the beginning of the labeling yields valuable information for the determination of VX. The model thus offers a formal method to investigate the principles of label kinetics in such 13C turnover experiments leading to analytical expressions. We further conclude that, provided that the precursor, e.g., Pyr, approaches steady-state quickly compared with the rate of labeling of the amino acid investigated, the analytical solution assuming instantaneous labeling can be used.
APPENDIX
Derivation of the Simplified ODE
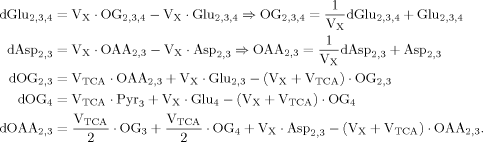 (A1)
(A1)Due to the symmetry of succinate, labeling of glutamate and aspartate at carbon position 2 and 3 can be described by the same equation in our model (Yu et al., 1997), which will be denoted below by the index “23.”
Case 2
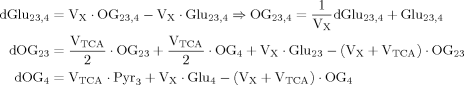 (A2)
(A2)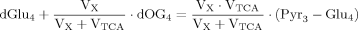 (5)
(5)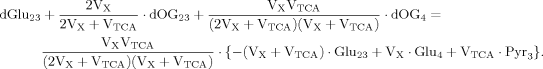 (A3)
(A3)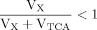
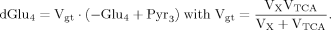 (6)
(6)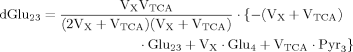
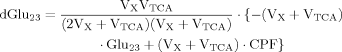 (7)
(7)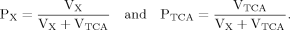
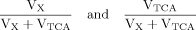
Case 3
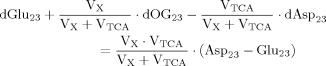 (A4)
(A4)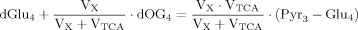 (A5)
(A5)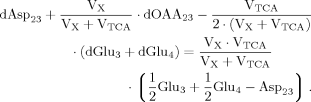 (A6)
(A6)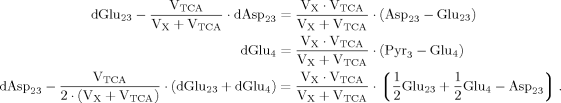 (A7)
(A7)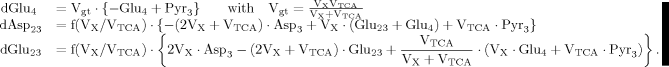 (A8)
(A8)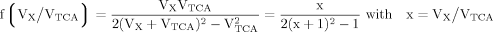
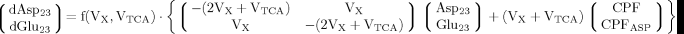 (9)
(9)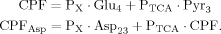 (10)
(10)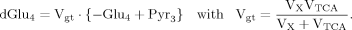 (6)
(6)Analytical Solutions of the Simplified ODE
In the following, according to case 1 and case 2, the ODEs for Glu4 and Glu23 will be solved analytically.
Case 1
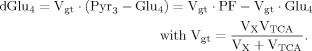 (6)
(6)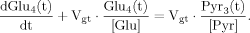 (13)
(13)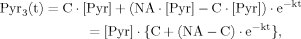 (12)
(12)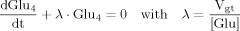 (B1)
(B1)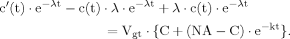 (B2)
(B2)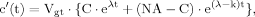 (B3)
(B3)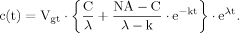 (B4)
(B4)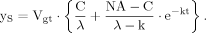 (B5)
(B5)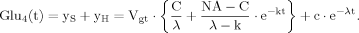 (B6)
(B6)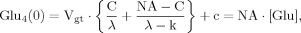 (B7)
(B7)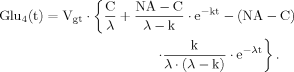 (14)
(14) (16)
(16)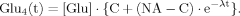 (B8)
(B8)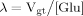
 (17)
(17)Case 2
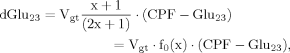 (8)
(8)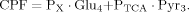
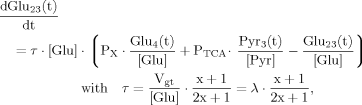 (18)
(18)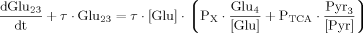
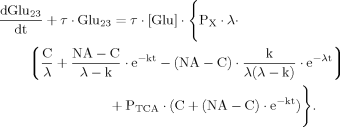 (B9)
(B9)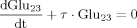
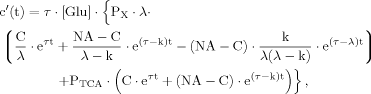 (B10)
(B10)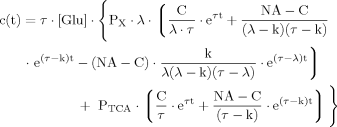 (B11)
(B11)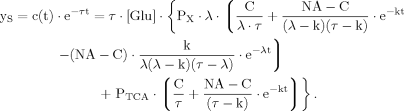 (B12)
(B12)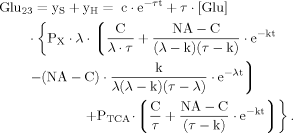 (B13)
(B13)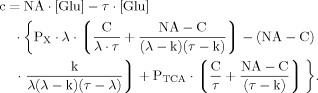 (B14)
(B14)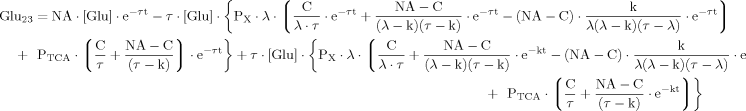 (B15)
(B15)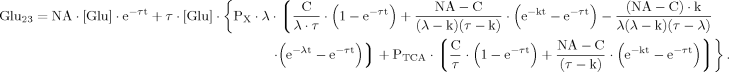 (19)
(19)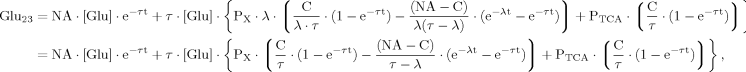 (B16)
(B16)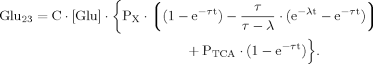 (20)
(20)



