Filling the complexity gaps for colouring planar and bounded degree graphs
Konrad K. Dabrowski
Department of Computer Science, Durham University, Lower Mountjoy, Durham, United Kingdom
Search for more papers by this authorFrançois Dross
Inria, CNRS, Université Côte d'Azur, I3S, Sophia Antipolis, France
Search for more papers by this authorMatthew Johnson
Department of Computer Science, Durham University, Lower Mountjoy, Durham, United Kingdom
Search for more papers by this authorCorresponding Author
Daniël Paulusma
Department of Computer Science, Durham University, Lower Mountjoy, Durham, United Kingdom
Correspondence Daniël Paulusma, Department of Computer Science, Durham University, Lower Mountjoy, South Road, Durham DH1 3LE, United Kingdom. Email: [email protected]
Search for more papers by this authorKonrad K. Dabrowski
Department of Computer Science, Durham University, Lower Mountjoy, Durham, United Kingdom
Search for more papers by this authorFrançois Dross
Inria, CNRS, Université Côte d'Azur, I3S, Sophia Antipolis, France
Search for more papers by this authorMatthew Johnson
Department of Computer Science, Durham University, Lower Mountjoy, Durham, United Kingdom
Search for more papers by this authorCorresponding Author
Daniël Paulusma
Department of Computer Science, Durham University, Lower Mountjoy, Durham, United Kingdom
Correspondence Daniël Paulusma, Department of Computer Science, Durham University, Lower Mountjoy, South Road, Durham DH1 3LE, United Kingdom. Email: [email protected]
Search for more papers by this authorAbstract
A colouring of a graph 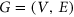 is a function
is a function 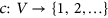 such that
such that 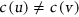 for every
for every  . A
. A 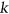 -regular list assignment of
-regular list assignment of 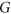 is a function
is a function 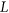 with domain
with domain 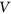 such that for every
such that for every 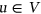 ,
, 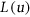 is a subset of
is a subset of 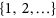 of size
of size 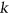 . A colouring
. A colouring 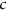 of
of 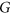 respects a
respects a 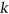 -regular list assignment
-regular list assignment 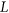 of
of 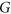 if
if  for every
for every 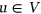 . A graph
. A graph 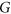 is
is 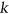 -choosable if for every
-choosable if for every 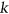 -regular list assignment
-regular list assignment 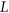 of
of 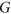 , there exists a colouring of
, there exists a colouring of 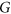 that respects
that respects 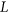 . We may also ask if for a given
. We may also ask if for a given 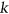 -regular list assignment
-regular list assignment 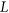 of a given graph
of a given graph 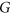 , there exists a colouring of
, there exists a colouring of 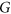 that respects
that respects 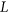 . This yields the
. This yields the 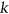 -Regular List Colouring problem. For
-Regular List Colouring problem. For 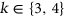 , we determine a family of classes
, we determine a family of classes 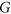 of planar graphs, such that either
of planar graphs, such that either 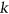 -Regular List Colouring is
-Regular List Colouring is 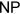 -complete for instances
-complete for instances 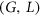 with
with 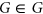 , or every
, or every 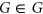 is
is 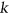 -choosable. By using known examples of non-
-choosable. By using known examples of non-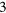 -choosable and non-
-choosable and non-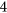 -choosable graphs, this enables us to classify the complexity of
-choosable graphs, this enables us to classify the complexity of 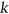 -Regular List Colouring restricted to planar graphs, planar bipartite graphs, planar triangle-free graphs, and planar graphs with no
-Regular List Colouring restricted to planar graphs, planar bipartite graphs, planar triangle-free graphs, and planar graphs with no 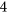 -cycles and no
-cycles and no 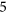 -cycles. We also classify the complexity of
-cycles. We also classify the complexity of 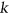 -Regular List Colouring and a number of related colouring problems for graphs with bounded maximum degree.
-Regular List Colouring and a number of related colouring problems for graphs with bounded maximum degree.
REFERENCES
- 1N. Alon and M. Tarsi, Colorings and orientations of graphs, Combinatorica 12 (1992), 125–134.
- 2K. Appel and W. Haken, Every planar map is four colorable, Contemporary Mathematics, vol. 89, AMS Bookstore, Providence, RI, 1989.
10.1090/conm/098 Google Scholar
- 3M. Bonamy et al., Recognizing graphs close to bipartite graphs, In K. G. Larsen, H. L. Bodlaender and J.-F. Raskin (Eds.), Proceedings of MFCS 2017, LIPIcs. 83, no. 70:1-70:14, Germany: Schloss Dagstuhl - Leibniz-Zentrum fuer Informatik, Full version: arXiv:1707.09817.
- 4R. L. Brooks, On colouring the nodes of a network, Math. Proc. Cambridge Philos. Soc. 37 (1941), 194–197.
- 5M. Chen, M. Montassier, and A. Raspaud, Some structural properties of planar graphs and their applications to 3-choosability, Discrete Math. 312 (2012), no. 2, 362–373.
- 6M. Chlebík and J. Chlebíková, Hard coloring problems in low degree planar bipartite graphs, Discrete Appl. Math. 154 (2006), 1960–1965.
- 7M. Chudnovsky, Coloring graphs with forbidden induced subgraphs, In S. Y. Jang, Y. R. Kim, D.-W. Lee and I. Yie (Eds.), Proceedings of ICM 2014, Kyung Moon Sa: Seoul, Korea, IV, 291-302.
- 8K. K. Dabrowski et al., Filling the complexity gaps for colouring planar and bounded degree graphs, In Z. Lipták and W. Smyth (Eds.), Proceedings of IWOCA 2015, LNCS 9538, Kyung Moon Sa: Seoul, Korea, 100-111.
- 9F. Dross, M. Montassier, and A. Pinlou, Partitioning a triangle-free planar graph into a forest and a forest of bounded degree, European J. Combin. 66 (2017), 81–94.
- 10Z. Dvořák and K. Kawarabayashi, List-coloring embedded graphs, In S. Khanna (Ed.), Proceedings of SODA 2013, SIAM, 1004–1012.
- 11Z. Dvořák, B. Lidický, and R. Škrekovski, Planar graphs without 3-, 7-, and 8-cycles are 3-choosable, Discrete Math. 309 (2009), 5899–5904.
- 12Z. Dvořák and R. Thomas, List-coloring apex-minor-free graphs, Manuscript, arXiv:1401.1399.
- 13T. Emden-Weinert, S. Hougardy, and B. Kreuter, Uniquely colourable graphs and the hardness of colouring graphs of large girth, Combin. Probab. Comput. 7 (1998), 375–386.
- 14P. Erdős, A. L. Rubin, and H. Taylor, Choosability in graphs, In P. Z. Chinn and D. McCarthy (Eds.), Proceedings of the West Coast Conference on Combinatorics, Graph Theory and Computing (Humboldt State University, Arcata, CA, 1979), Congress. Numer. XXVI, Winnipeg, Manitoba, Util. Math., 1980, 125–157.
- 15L. Esperet et al., A complexity dichotomy for the coloring of sparse graphs, J. Graph Theory 73 (2013), 85–102.
- 16M. R. Garey, D. S. Johnson, and L. J. Stockmeyer, Some simplified NP-complete graph problems, In R. L. Constable, R. W. Ritchie, J. W. Carlyle and M. A. Harrison (Eds.), Proceedings of STOC 1974, ACM, 47–63.
- 17P. A. Golovach et al., Choosability on
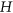 -free graphs, Inform. Process. Lett. 113 (2013), 107–110.
-free graphs, Inform. Process. Lett. 113 (2013), 107–110.
- 18P. A. Golovach et al., A survey on the computational complexity of colouring graphs with forbidden subgraphs, J. Graph Theory 84 (2017), 331–363.
- 19P. A. Golovach, D. Paulusma, and J. Song, Closing complexity gaps for coloring problems on
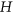 -free graphs, Inform. Comput. 237 (2014), 204–214.
-free graphs, Inform. Comput. 237 (2014), 204–214.
- 20S. Gutner, The complexity of planar graph choosability, Discrete Math. 159 (1996), 119–130.
- 21J. Kratochvíl, Precoloring extension with fixed color bound, Acta Math. Univ. Comenian. 62 (1993), 139–153.
- 22J. Kratochvíl and Z. Tuza, Algorithmic complexity of list colourings, Discrete Appl. Math. 50 (1994), 297–302.
- 23P. C. B. Lam, B. Xu, and J. Liu, The 4-choosability of plane graphs without 4-cycles, J. Combin. Theory Ser. B 76 (1999), 117–126.
- 24M. Molloy and B. Reed, Colouring graphs when the number of colours is almost the maximum degree, J. Combin. Theory Ser. B 109 (2014), 134–195.
- 25M. Montassier, A note on the not 3-choosability of some families of planar graphs, Inform. Process. Lett. 99 (2006), 68–71.
- 26M. Montassier, A. Raspaud, and W. Wang, Bordeaux 3-color conjecture and 3-choosability, Discrete Math. 306 (2006), 573–579.
- 27C. Thomassen, Every planar graph is
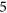 -choosable, J. Combin. Theory Ser. B 62 (1994), 180–181.
-choosable, J. Combin. Theory Ser. B 62 (1994), 180–181.
- 28C. Thomassen, 3-List-coloring planar graphs of girth 5, J. Combin. Theory Ser. B 64 (1995), 101–107.
- 29C. Thomassen, Color-critical graphs on a fixed surface, J. Combin. Theory Ser. B 70 (1997), 67–100.
- 30V. G. Vizing, Coloring the vertices of a graph in prescribed colors, Diskret. Anal., no. 29, Metody Diskret. Anal. v. Teorii Kodov i Shem 101 (1976), 3–10.
- 31V. G. Vizing, Vertex colorings with given colors, Diskret. Anal. 29 (1976), 3–10.
- 32M. Voigt, List colourings of planar graphs, Discrete Math. 120 (1993), 215–219.
- 33M. Voigt, A not 3-choosable planar graph without 3-cycles, Discrete Math. 146 (1995), 325–328.
- 34M. Voigt, A non-3-choosable planar graph without cycles of length 4 and 5, Discrete Math. 307 (2007), 1013–1015.
- 35M. Voigt and B. Wirth, On 3-colorable non-4-choosable planar graphs, J. Graph Theory 24 (1997), 233–235.
- 36Y. Wang, H. Lu, and M. Chen, Planar graphs without cycles of length 4, 5, 8, or 9 are 3-choosable, Discrete Math. 310 (2010), 147–158.
- 37Y. Wang, H. Lu, and M. Chen, Planar graphs without cycles of length 4, 7, 8, or 9 are 3-choosable, Discrete Appl. Math. 159 (2011), 232–239.
- 38D.-Q. Wang, Y.-P. Wen, and K.-L. Wang, A smaller planar graph without 4-, 5-cycles and intersecting triangles that is not 3-choosable, Inform. Process. Lett. 108 (2008), 87–89.




