The size-Ramsey number of powers of paths
Dennis Clemens
Institut für Mathematik, Technische Universität Hamburg, Hamburg, Germany
Search for more papers by this authorMatthew Jenssen
Department of Mathematics, London School of Economics, London, UK
Search for more papers by this authorYoshiharu Kohayakawa
Instituto de Matemática e Estatística, Universidade de São Paulo, São Paulo, Brazil
Search for more papers by this authorNatasha Morrison
Department of Pure Mathematics and Mathematical Statistics, University of Cambridge, Cambridge, UK
Search for more papers by this authorCorresponding Author
Guilherme Oliveira Mota
Centro de Matemática, Computação e Cognição, Universidade Federal do ABC, Santo André, Brazil
Correspondence Guilherme Oliveira Mota, Centro de Matemática, Computação e Cognição, Universidade Federal do ABC, Avenida dos Estados 5001, Santa Terezinha, Santo André 09210-580, SP, Brazil. Email: [email protected]
Search for more papers by this authorDamian Reding
Institut für Mathematik, Technische Universität Hamburg, Hamburg, Germany
Search for more papers by this authorBarnaby Roberts
Department of Mathematics, London School of Economics, London, UK
Search for more papers by this authorDennis Clemens
Institut für Mathematik, Technische Universität Hamburg, Hamburg, Germany
Search for more papers by this authorMatthew Jenssen
Department of Mathematics, London School of Economics, London, UK
Search for more papers by this authorYoshiharu Kohayakawa
Instituto de Matemática e Estatística, Universidade de São Paulo, São Paulo, Brazil
Search for more papers by this authorNatasha Morrison
Department of Pure Mathematics and Mathematical Statistics, University of Cambridge, Cambridge, UK
Search for more papers by this authorCorresponding Author
Guilherme Oliveira Mota
Centro de Matemática, Computação e Cognição, Universidade Federal do ABC, Santo André, Brazil
Correspondence Guilherme Oliveira Mota, Centro de Matemática, Computação e Cognição, Universidade Federal do ABC, Avenida dos Estados 5001, Santa Terezinha, Santo André 09210-580, SP, Brazil. Email: [email protected]
Search for more papers by this authorDamian Reding
Institut für Mathematik, Technische Universität Hamburg, Hamburg, Germany
Search for more papers by this authorBarnaby Roberts
Department of Mathematics, London School of Economics, London, UK
Search for more papers by this authorAbstract
Given graphs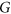 
and 
and 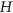a positive integer 
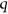, say that 
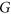is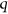 
-Ramsey for 
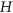, denoted 
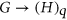, if every 
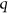-coloring of the edges of 
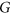contains a monochromatic copy of 
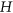. The size-Ramsey number 
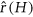of a graph 
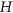is defined to be 
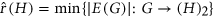. Answering a question of Conlon, we prove that, for every fixed 
, we have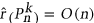 
, where 
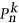is the 
th power of the 
-vertex path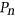 
(ie, the graph with vertex set 
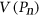and all edges 
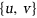such that the distance between 
and 
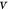in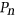 
is at most 
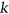). Our proof is probabilistic, but can also be made constructive.
REFERENCES
- 1P. Allen, G. Brightwell, and J. Skokan, Ramsey goodness and otherwise, Combinatorica 33 (2013), no. 2, 125–160.
- 2N. Alon and F. R. K. Chung, Explicit construction of linear sized tolerant networks, Discrete Math. 72 (1988), no. 1-3, 15–19.
- 3J. Beck, On size Ramsey number of paths, trees, and circuits. I, J. Graph Theory 7 (1983), no. 1, 115–129.
- 4J. Beck, On size Ramsey number of paths, trees and circuits. II, Mathematics of Ramsey theory, Algorithms and Combinatorics, vol. 5, Springer, Berlin, Heidelberg, 1990, pp. 34–45.
10.1007/978-3-642-72905-8_4 Google Scholar
- 5I. Ben-Eliezer, M. Krivelevich, and B. Sudakov, The size Ramsey number of a directed path, J. Combin. Theory Ser. B 102 (2012), no. 3, 743–755.
- 6D. Conlon, Question suggested for the ATI-HIMR focused research workshop: large-scale structures in random graphs, Alan Turing Institute, 2016.
- 7D. Conlon, J. Fox, and B. Sudakov, Recent developments in graph Ramsey theory, Surv. Combin. 424 (2015), 49–118.
- 8D. Dellamonica Jr., The size-Ramsey number of trees, Random Struct. Algorithms 40 (2012), no. 1, 49–73.
- 9A. Dudek et al., On the size-Ramsey number of hypergraphs, J. Graph Theory 86 (2017), no. 1, 104–121.
- 10A. Dudek and P. Prałat, An alternative proof of the linearity of the size-Ramsey number of paths, Combin. Probab. Comput. 24 (2015), no. 3, 551–555.
- 11P. Erdős, On the combinatorial problems which I would most like to see solved, Combinatorica 1 (1981), no. 1, 25–42.
- 12P. Erdős et al., The size Ramsey number, Period. Math. Hungar. 9 (1978), no. 1-2, 145–161.
10.1007/BF02018930 Google Scholar
- 13P. Erdős and L. Lovász, Problems and results on 3-chromatic hypergraphs and some related questions, Infinite and finite sets (Colloq., Keszthely, 1973; dedicated to P. Erdős on his 60th birthday), Vol. II, Colloq. Math. Soc. János Bolyai 10 (1975), 609–627.
- 14J. Friedman and N. Pippenger, Expanding graphs contain all small trees, Combinatorica 7 (1987), no. 1, 71–76.
- 15P. E. Haxell and Y. Kohayakawa, The size-Ramsey number of trees, Israel J. Math. 89 (1995), no. 1-3, 261–274.
- 16P. E. Haxell, Y. Kohayakawa, and T. Łuczak, The induced size-Ramsey number of cycles, Combin. Probab. Comput. 4 (1995), no. 3, 217–239.
10.1017/S0963548300001619 Google Scholar
- 17X. Ke, The size Ramsey number of trees with bounded degree, Random Struct. Algorithms 4 (1993), no. 1, 85–97.
- 18Y. Kohayakawa, T. Retter, and V. Rödl, The size-Ramsey number of short subdivisions of bounded degree graphs, Random Struct. Algorithms (2018), 1–36. https://doi.org/10.1002/rsa.20783
- 19Y. Kohayakawa et al., Sparse partition universal graphs for graphs of bounded degree, Adv. Math. 226 (2011), no. 6, 5041–5065.
- 20T. Kővári, V. T. Sós, and P. Turán, On a problem of K. Zarankiewicz, Colloq. Math. 3 (1954), 50–57.
- 21S. Letzter, Path Ramsey 278 number for random graphs, Combin. Probab. Comput. 25 (2016), no. 4, 612–622.
- 22A. Pokrovskiy, Partitioning edge-coloured complete graphs into monochromatic cycles and paths, J. Combin. Theory Ser. B 106 (2014), 70–97.
- 23A. Pokrovskiy, Calculating Ramsey numbers by partitioning colored graphs, J. Graph Theory 84 (2017), no. 4, 477–500.
- 24F. P. Ramsey, On a problem of formal logic, Proc. London Math. Soc. S2-30 (1930), no. 1, 264.
10.1112/plms/s2-30.1.264 Google Scholar
- 25D. Reimer, The Ramsey size number of dipaths, Discrete Math. 257 (2002), no. 1, 173–175.
