AutoMeKin2021: An open-source program for automated reaction discovery
Funding information: Ministerio de Ciencia e Innovación, Grant/Award Number: PID2019-107307RB-I00; National Science Foundation, Grant/Award Number: 1763652
Abstract
AutoMeKin2021 is an updated version of tsscds2018, a program for the automated discovery of reaction mechanisms (J. Comput. Chem. 2018, 39, 1922). This release features a number of new capabilities: rare-event molecular dynamics simulations to enhance reaction discovery, extension of the original search algorithm to study van der Waals complexes, use of chemical knowledge, a new search algorithm based on bond-order time series analysis, statistics of the chemical reaction networks, a web application to submit jobs, and other features. The source code, manual, installation instructions and the website link are available at: https://rxnkin.usc.es/index.php/AutoMeKin
1 INTRODUCTION
Over the last several years, computational chemistry has witnessed a surge in the development of methods for reaction mechanism discovery.1-65 Many of these methods predict complex reaction networks in an automated manner, where the search of reactions is usually more thorough than the traditional “by hand” approach.
Our group is actively involved in this endeavor, and a few years ago we presented a new automated method called Transition State Search using Chemical Dynamics Simulations (TSSCDS).44, 45 Our algorithm relied on a molecular dynamics (MD)-based exploration of configurational space, followed by a post-processing analysis to locate promising transition state (TS) candidates from the MD snapshots.43-45 While other methods also use the ability of MD simulations to discover reaction mechanisms, the distinctive feature of our approach is the focus on finding saddle-point structures. Up until now, locating TSs from MD simulations has been difficult, but the procedure described here has proven to be very effective and useful in predicting unexpected mechanisms. Our approach has been applied in combustion chemistry,66, 67 cycloaddition reactions,68 photodissociations,69-71 organometallic catalysis,43 radiation damage of biological systems,72 simulation of mass spectrometry experiments,73, 74 and other applications.75-77
The first version of the computer program implementing our approach was released 3 years ago under the name tsscds2018.46 This approach, along with the algorithms described in this paper, has now been combined and implemented in the software package named AutoMeKin,78 which stands for Automated Mechanisms and Kinetics.
AutoMeKin2021 includes the following new features: (a) the rare-event acceleration method boxed molecular dynamics in energy space (BXDE)76, 79; (b) a generalization of a graph theory-based algorithm to locate TS structures for the study of non-covalent interactions80; (c) a chemical knowledge-based method for reaction discovery; (d) a new TS search algorithm based on a bond-order time series analysis81; (e) a statistical analysis of the chemical reaction networks using the Python library NetworkX82; (f) a web application for online job submission; as well as other features.
After a brief introduction of the original method, a description will be given of the new methods incorporated into AutoMeKin2021, as well as some test cases and sample input files. Its new capabilities, as well as some proposed future improvements, will be summarized in the conclusions.
2 METHODS
- Short-time reactive MD simulations
- Post-processing analysis of the MD simulations
- Kinetics simulations
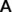 , whose elements,
, whose elements, 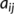 , are given by45:
, are given by45:
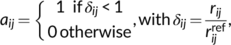 (1)
(1)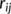 and
and 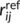 are the interatomic and reference distances, respectively, of each pair,
are the interatomic and reference distances, respectively, of each pair, 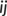 , of atoms. Reference distances are determined from the sum of the covalent radii of atoms
, of atoms. Reference distances are determined from the sum of the covalent radii of atoms  and
and 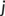 .
.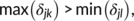 (2)
(2)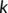 runs over the set of atoms that are covalently bonded to
runs over the set of atoms that are covalently bonded to 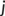 (neighbors), and index
(neighbors), and index 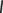 runs over the remaining (non-neighbor) atoms. In other words, the criterion of Equation (2) is met when the nearest atom to
runs over the remaining (non-neighbor) atoms. In other words, the criterion of Equation (2) is met when the nearest atom to 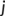 is a non-neighbor. Since more than two bonds can be part of the reaction coordinate in a given TS, reactive events occurring within an adaptive time window of ~10–20 fs are merged.45 The resulting structures are first subjected to a partial relaxation, with the atoms involved in the reactive event kept frozen, and then optimized to a TS (saddle point of index one). This search algorithm is named bbfs, which stands for bond breaking/formation search.
is a non-neighbor. Since more than two bonds can be part of the reaction coordinate in a given TS, reactive events occurring within an adaptive time window of ~10–20 fs are merged.45 The resulting structures are first subjected to a partial relaxation, with the atoms involved in the reactive event kept frozen, and then optimized to a TS (saddle point of index one). This search algorithm is named bbfs, which stands for bond breaking/formation search.For the sake of efficiency, the trajectories are integrated with either MOPAC201683 or Entos Qcore84 at a semiempirical quantum-mechanical (SQM) level, while the stationary points are re-optimized with Gaussian0985 or Entos Qcore84 using a higher level of electronic structure theory. More details about the method can be found in the original papers.44, 45
Table 1 shows a summary of the most important tools that have been implemented in the last version of AutoMeKin. They will be described in the next sections.
| Methoda | Features | Dependencies | Ref |
|---|---|---|---|
| BXDE | Accelerated MD simulation | ASE | 76, 79 |
| vdW | Sampling vdW structures | ASE | 80 |
| ChemKnow | Graph transformations and NEB | ASE NetworkX |
This work |
| bots | Reactive event search algorithm | - | 81 |
| Reaction network properties | Graph-Theory-based statistics | NetworkX | 76 |
| Web application | Online submission of jobs | - | This work |
- Abbreviations: ASE, Atomistic Simulation Environment; BXDE, boxed molecular dynamics in energy space; vdW, van der Waals.
- a Name of the tool/method.
2.1 Rare-event acceleration method BXDE
Standard MD simulations are typically biased toward the entropically favored reaction pathways. AutoMeKin's standard MD module employs initial conditions with substantial amounts of vibrational energy to accelerate the incidence of reactive events.
An alternative way of accelerating reactive events, called BXDE79 has recently been proposed. BXDE belongs to the family of BXD methods,86-89 which introduce reflective barriers in the phase space of an MD trajectory along a particular (collective) variable. The boundaries are employed to push the dynamics along the collective variable into regions of phase space which would rarely be sampled in an unbiased trajectory.
In BXDE, the bias is introduced into the potential energy, rather than in any particular collective variable of the system. The different chemical reaction channels are sampled by gradually scanning through potential energy “boxes” or energetic “windows.” The BXDE simulation module in AutoMeKin utilizes the Atomistic Simulation Environment (ASE) package, and MOPAC2016 or Entos Qcore is interfaced via the ASE calculator class.90
Figure 1 shows the section of an input file where a BXDE calculation is requested. Each line in the input file consists of a keyword value pair. BXDE is one of the different sampling methods employed in AutoMeKin for finding stationary states in a potential energy surface, with other sampling alternatives such as: MD, MD-micro, external, Chemical Knowledge (ChemKnow), association, and van der Waals (vdW). Although some of the options are described in this work, the reader is referred to the documentation for more details.78
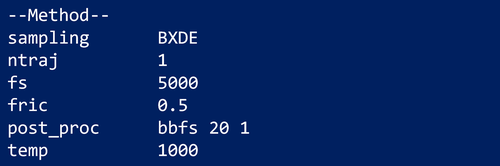
The number of trajectories and simulation time are specified through the keywords fs and ntraj, respectively. BXDE employs a Langevin thermostat whose friction coefficient in ps−1 (keyword fric) and temperature in K (keyword temp) must be entered as well.
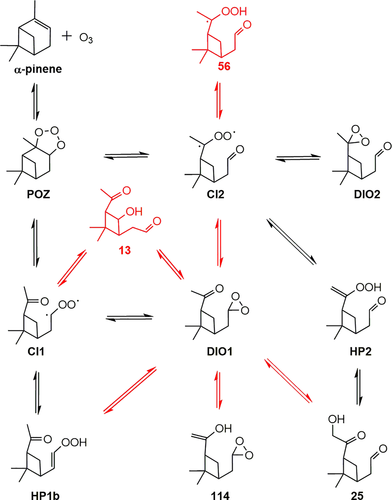
An example of the use of BXDE combined with AutoMeKin's TS search algorithms is the recent study of the ozonolysis of α-pinene.76 This reaction is known to follow the “Criegee mechanism” of alkene ozonolysis (see Figure 2), and was previously studied using ab initio methods.91 Despite the low level of electronic structure (PM7) employed to run BXDE and to optimize the stationary points,76 not only was the new approach capable of predicting the major pathways (shown in black in Figure 2), but a significant number of new intermediates and pathways were also predicted. The figure also shows (in red) some of the most important pathways that were overlooked in the previous ab initio study and found in the BXDE sampling.76 A full account of the new mechanisms predicted by BXDE is detailed elsewhere.76
2.2 Non-covalent interactions (van der Waals)
The original search algorithm relies on the adjacency matrix of Equation (1), where the reference distance is determined from the covalent radii of the atoms. Consequently, a complex where two molecules are held together by intermolecular interactions would not be regarded as a single entity, but as two separated fragments.
 should be recast in a block structure that accounts for a system made up of molecules B and C80:
should be recast in a block structure that accounts for a system made up of molecules B and C80:
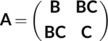 (3)
(3)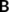 and
and  refer to the (covalent) connectivity within B and C, respectively, whereas the off-diagonal
refer to the (covalent) connectivity within B and C, respectively, whereas the off-diagonal 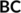 block corresponds to the non-covalent, that is, vdW, interacting system B–C. The matrix elements for
block corresponds to the non-covalent, that is, vdW, interacting system B–C. The matrix elements for  and
and  are evaluated according to Equation (1), with the reference distances determined from the covalent radii. In contrast, the matrix elements of the
are evaluated according to Equation (1), with the reference distances determined from the covalent radii. In contrast, the matrix elements of the 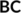 block are calculated using Equation (1) but with the reference distances determined from van der Waals radii.92
block are calculated using Equation (1) but with the reference distances determined from van der Waals radii.92In this new ansatz, non-covalent interactions in B–C are treated on the same footing as covalent ones within any of the fragments, thus permitting the detection of TSs connecting vdW structures. The method can be easily extended to more than two interacting molecules, and has been recently applied to study the Ar–benzene, N2–benzene, (H2O)n–benzene (n = 1–3), and (NO2–benzene)+ systems.80
To prevent the inherent bias of standard high-energy MD simulations toward dissociation of the complex, the BXDE sampling option is automatically used when a vdW calculation is called for. Figure 3 shows an example input file for a vdW calculation on the pyrene + NO2 system.93, 94
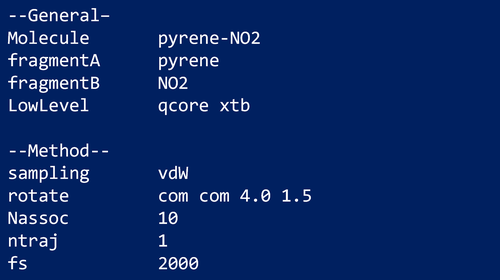
In this example, a total simulation time of 2 ps is employed. The electronic structure level of theory employed in this example is GFN1-xTB95 (xtb) using the Entos Qcore program,96 which is requested using the keyword LowLevel followed by the computer program (qcore) and the method (xtb).
The keyword Nassoc is used to select the number of initial structures generated. The randomly generated structures are subjected to optimization using xtb. The global minimum from the set of optimized structures is then used as the starting point for the MD simulations.
This calculation results in a total of 112 minima and 115 TSs for the NO2 + pyrene system. Ignoring the unconnected minima, the reaction network and its corresponding minimum energy structures are displayed in Figure 4.
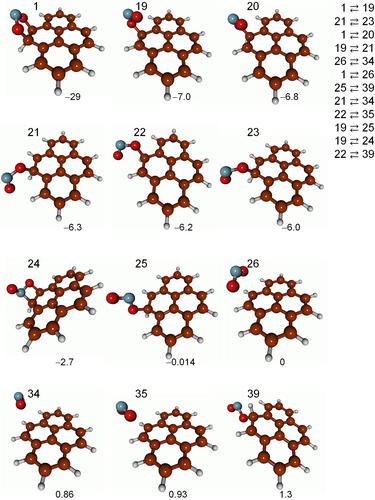
In sum, the more general definition of the adjacency matrix of Equation (3) permits exploring both covalently and non-covalently bound structures, as seen in Figure 4. In particular, nine of the 12 structures of Figure 4 present covalent bonds between NO2 and pyrene, while three correspond to vdW structures. The geometries of all the structures, including those not connected to the network of Figure 4 (the vast majority), are collected in the Supporting Information.
2.3 Chemical Knowledge
MD-based methods have shown great success exploring reaction mechanisms in small-medium sized systems. However, for larger ones, a thorough search of the full chemical reaction space with such approaches soon becomes intractable. One way to circumvent this is to focus only on those reactions which are relevant at the conditions of interest. With MD-based methods, this could be achieved simply by imposing upper limits to the energies of the TSs (an option available in AutoMeKin). We propose in this section an alternative method for this. The new approach, called ChemKnow, allows to impose a greater number of constraints in the search rendering the whole process more efficient than MD-based methods.
The potential gain in efficiency of ChemKnow comes from: (i) exploring only those reactions in which there is an interest, (ii) imposing limits for the minimum and maximum number of neighbors (valencies) of an atom, and (iii) restricting the maximum number of bonds that can break and form in each step.
The method also benefits from working in graph space, where reactions are simply graph transformations. This has been shown to be a practical way to explore reactive events by Habershon and co-workers.26, 27, 97-100
- The reactive sites (active atoms) of the system are selected, along with the maximum number of bonds that can break (nb) and form (nf) per elementary step, the allowed minimum (min_val) and maximum valencies (max_val) of each atom, and the maximum energy (emax) of the system.
- Beginning with a given minimum energy geometry turned into its graph analogue, ChemKnow generates all possible graph transformations that comply with the constraints of the previous step. Three additional restrictions are imposed on top of those specified by the user: (1) reactions where the closest distance between the (linear) paths followed by the atoms in their rearrangement is lower than a threshold value are ignored, (2) bond formations between atoms that are at a distance greater than a certain value startd are not allowed; and, (3) only those bonds whose bond order is lower than 1.5 can be broken.
- The newly generated graphs are converted back into 3D structures using constrained Langevin dynamics, with external forces applied to the active atoms. The adjacency matrix is monitored along the trajectory, and the constraints are lifted once the product graph is obtained. At this point, the final geometry is optimized, and its connectivity is checked once more to make sure that the desired product is obtained. As a second check, its energy must be lower than emax to retain the newly generated geometry.
- A path connecting the initial and final geometries is constructed using the nudged elastic band (NEB) method, and the highest point along the path is subjected to TS optimization.
- Successive iterations of AutoMeKin start from a new (connected) graph, and steps 1–4 are repeated until no new graphs are found.
 (4)
(4) and
and 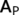 are the reactant and product adjacency matrices, respectively, with the atomic numbers filling the diagonals. This descriptor has the property of being invariant with respect to permutations of like atoms, thus avoiding sampling equivalent paths more than once.
are the reactant and product adjacency matrices, respectively, with the atomic numbers filling the diagonals. This descriptor has the property of being invariant with respect to permutations of like atoms, thus avoiding sampling equivalent paths more than once.Additionally, steps 3 and 4 of the above pipeline are carried out using ASE's ExternalForces and AutoNEB classes, respectively,90 with all the graph analysis and transformations performed using NetworkX.82
- All atoms are active.
- nf ≤ 2 and nb ≤ 2, where transformations with both nf = 2 and nb = 2 are discarded.
- min_val = [1,1,1] and max_val = [1,4,2] for the list of atoms = [H,C,O], respectively.
- startd = 2.75 Å
- emax = 150 kcal/mol.
When the initial structure is cis-FA, a total of 77 distinct (nf,nb) combinations are found, which breaks down into 3 (0,1); 3 (0,2); 5 (1,0); 15 (1,1); 15 (1,2); 9 (2,0); and 27 (2,1) combinations. This number excludes the cleavage of bonds with bond orders greater than 1.5. Additionally, when the other constraints were imposed, the number of combinations (paths) that start in cis-FA became 8.
Overall, this approach only needs four iterations of the workflow to reach convergence (no further minima found) for FA, which affords a total of 8 TSs and 4 minima at the PM7 SQM level after exploring a total of 24 paths. The CO2:CO branching ratio obtained at 150 kcal/mol of excitation energy is 3:97. In comparison, an MD sampling with 200 trajectories leads to 11 TSs and 7 minima and a CO2:CO ratio of 2:98.
A test was also done on vinyl cyanide (VC),71 to compare the performance of ChemKnow versus an MD-based sampling. Chemknow's constraints are similar to those employed for FA, including now (2,2) combinations of (nf,nb) for the graph transformations, and min_val and max_val for N are 1 and 4, respectively. In this example, ChemKnow needs to sample 850 paths to obtain 59 TSs and 31 minima versus 2000 trajectories employed by the MD module, which affords 64 TSs and 27 minima.
On the other hand, if the set of active atoms and range of valences are reduced, ChemKnow probably outperforms MD-based methods in terms of efficiency. However, the decision to employ this method should also rely on its efficacy in finding the relevant structures for the system under study.
It was noted in passing that, while the MD-based methods have been heavily tested, ChemKnow needs further assessment and perhaps an optimization of steps 3 and 4, which are the major components of the TS search algorithm.
2.4 New TS search algorithm (bots)
Our previous version of AutoMeKin included only one algorithm for the detection of reactive events. The algorithm (named bbfs, see above) is based on monitoring geometries along the MD trajectories and therefore does not encode information on the subtle changes that bond orders experience in some chemical reactions. It is therefore desirable to implement new search algorithms based on bond orders rather than interatomic distances to identify possible flaws in bbfs.
- A low-pass filter is applied to remove the fast fluctuations from the time series using a cutoff frequency
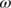 .
. - The first time derivative of the smoothed time series is obtained using the central difference formula.
- A threshold
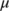 is applied to the first-order derivatives to select the peaks (those above
is applied to the first-order derivatives to select the peaks (those above 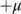 and below
and below  ).
). - As in bbfs, peaks within an adaptive time window45 are merged and regarded as multi-bond reactive events.
Figure 5 shows part of an input file to run a BXDE sampling, followed by bots analysis of the trajectories. The keyword post_proc is employed to select bbfs (the default) or bots. In the latter case, two parameters are required:  in cm−1, and
in cm−1, and  , given as a multiple of
, given as a multiple of  .By way of example, the simple test case FA is employed to run 100 BXDE trajectories, which were then analyzed using bots with the parameters in Figure 5. The resulting structures and kinetics are very similar to the ones obtained using the standard bbfs method.
.By way of example, the simple test case FA is employed to run 100 BXDE trajectories, which were then analyzed using bots with the parameters in Figure 5. The resulting structures and kinetics are very similar to the ones obtained using the standard bbfs method.

Figure 6 shows the variation of three bond orders and their time derivatives for a reactive BXDE simulation leading to H2O + CO. In the figure, the three bonds correspond to those that change from reactant to products.
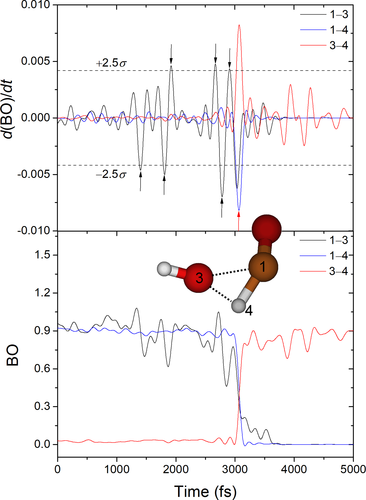
The use of bots requires fine-tuning two parameters ( and
and  ) for the system under study. These values should be selected to find as many peaks (reactive events) as possible, while minimizing the number of false positives. Figure 6 shows that the only reactive event is successfully detected at ~3.1 ps, that is, the breaking of the 1–3 and 1–4 bonds and formation of the 3–4 bond. However, this comes at the cost of finding six false positives, at 1.4, 1.8, 1.9, 2.7, 2.8, and 2.9 ps. Although false positives also occur in bbfs, the major disadvantage of bots is its dependence on two parameters that strongly affect its performance.
) for the system under study. These values should be selected to find as many peaks (reactive events) as possible, while minimizing the number of false positives. Figure 6 shows that the only reactive event is successfully detected at ~3.1 ps, that is, the breaking of the 1–3 and 1–4 bonds and formation of the 3–4 bond. However, this comes at the cost of finding six false positives, at 1.4, 1.8, 1.9, 2.7, 2.8, and 2.9 ps. Although false positives also occur in bbfs, the major disadvantage of bots is its dependence on two parameters that strongly affect its performance.
2.5 Properties of the reaction network
Complex reaction mechanisms can be represented as networks of reactions and studied by Graph Theory. A node of the network corresponds to either an intermediate or to a reaction product. Edges represent pathways connecting two nodes. Studying the structure of such reaction networks can be very useful to identify the number of steps between reactants and products or to spot the presence of important (highly connected) intermediates (or hubs) in the network.
In this section, statistical properties of the networks are presented seeking to answer two questions: (1) Do these networks exhibit “small-world” behavior? (2) are they scale-free? Small-world networks are defined as networks that present a short path length, even between distant nodes. In scale-free networks there exists a hierarchy of nodes, that is, a small number of them (called hubs) are highly connected and a large number of them present only a few connections.
In AutoMeKin2021, properties of the reaction networks are analyzed using the NetworkX Python library.101 Two types of networks are constructed in the example shown here. In the “all-states” network, every single intermediate constitutes a node, while in the “coarse-grained” one a family of conformers is lumped together to form each node. Additionally, in both networks, edges have weights representing the number of pathways connecting a pair of nodes. Finally, self-loops are avoided by removing paths connecting permutation-inversion isomers of the same node.
Common properties of a network can be studied in this new version of the program: the average shortest path length, the average clustering coefficient, the transitivity, and the assortativity. Some example systems that have been described using similar approaches are the network of organic chemistry,102 the network involved in the ozonolysis of α-pinene,76 and a network of small clusters.103 Below, we give a brief description of the properties provided in AutoMeKin's output.
The shortest path is the one connecting a pair of nodes through the least number of edges.104 The clustering coefficient indicates the degree to which the neighbors of a node are also neighbors of each other, and an average clustering coefficient can be calculated for the network.105 In turn, the transitivity is proportional to the ratio of the number of triangles over the number of triads in the network. For any three nodes in the network, a triangle is formed when the three possible pairs of nodes are connected, while in a triad only two pairs are connected.
The assortativity is a measure of the tendency of nodes to have connections with nodes of a similar degree and can be measured through a coefficient106 that varies from −1 to 1. Values close to 1 indicate that nodes have a preference to connect with nodes of a similar degree, which is called assortative mixing, while values close to −1 indicate the opposite and is called disassortative mixing.
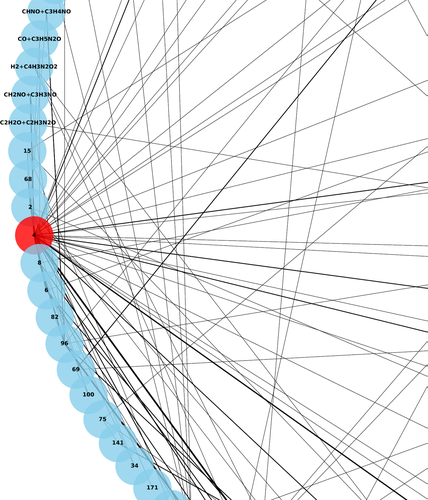
Figure 7 shows part of the coarse-grained network constructed from the results obtained with AutoMeKin for the decomposition of protonated uracil, which was chosen as an example. Table 2 shows the properties of the “all-states” and “coarse-grained” networks obtained from the same results.
| All-statesb | Coarse-grainedc | |
|---|---|---|
| Nodes | 208 | 116 |
| Edges | 244 | 136 |
| Density of edges (%)d | 1.1 | 2.0 |
| Average shortest path length | 5.49 (0.5) | 3.89 (0.4) |
| Average clustering coefficient | 0.026 (3.5) | 0.070 (5.0) |
| Transitivity | 0.019 (1.7) | 0.033 (1.7) |
| Assortativity | −0.024 | −0.18 |
- a Numbers in parenthesis give the ratio of the value of the property over the corresponding value of a random (Erdös–Rényi) network with the same number of nodes and edges.
- b Every structure is a node in the network.
- c Families of conformers form a node of the network.
- d Percentage of edges with respect to the maximum number of edges between the nodes of the network.
In general, the networks of chemical reactions are sparsely connected76 with a low density of edges (1%–2% in this example). An important feature of any network is whether they present small-world behavior, that is, when pairs of nodes are connected through a small number of edges. This property can be assessed by comparing the transitivity values and the average shortest path length with those of random networks. In this case, average shortest path lengths (5.49 and 3.89) are considerably shorter than those for the corresponding random networks, and the transitivities are 1.7 times greater. These results point out a clear “small-world” behavior. Similar results of other chemical reaction networks can be found in the literature.76, 102, 103
Clustering coefficients provide the proportion of interlinking between neighbors of a given node. The so-called scale-free networks are characterized by an enhanced clustering compared with a random network, just like the networks in this study (see Table 2).
Finally, the negative values of the assortativity indicate disassortativity mixing. That is, nodes of different degree tend to be connected. Disassortative mixing has also been observed in the ozonolysis of α-pinene,76 in the network of organic chemistry,102 and in biological and technological networks.107
The detailed reaction networks corresponding to the fragmentation of protonated uracil can be found in the Supporting Information.
2.6 Web application
The web application is available at https://rxnkin.usc.es/amk/ and works on most widely used web browsers. It is for demonstration and test purposes only. Therefore, reaction mechanisms and kinetics results are predicted at the PM7 SQM level of theory and the maximum number of atoms is limited to 15.
Figure 8 shows three screenshots of the most relevant sections of the web application. Briefly, users first need to register using a valid email account. Once this is done they can request a “New Job,” whose details need to be specified (Figure 8B): geometry of the system, charge, and the temperature or energy of the kinetics simulations.
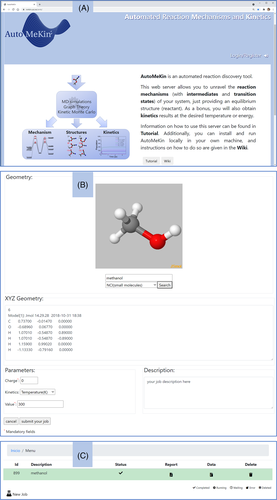
To input the geometries, a JSmol viewer integrated in our web interface was employed.108 Once all parameters are specified, users can submit their jobs by clicking the “submit your job” button. The number of jobs is not limited, but users should try to limit the number of jobs they submit at once so that other users can also use the server at the same time.
The status of the jobs is shown on a different page (Figure 8C). Depending on the size of the system and workload, the execution time can vary substantially, and users can log out. Upon job completion, they will receive a notification in their email account.
Finished jobs appear with a “Completed” status in Figure 8C and users will be able to download a brief summary of the results in PDF format (“Report”), as well as a tarball file with detailed data (“Data”).
The web interface was built following HTML5 recommendations.109 The Bootstrap framework110 is included to develop a responsive design. The Apache HTTP server, the MariaDB server, and PHP are used to build the backend. A batch system written in Perl and C deals with the execution of each job, balancing the system workload, updating the status of the jobs, moving the results to the Apache download area and notifying the users upon job completion.
2.7 Other improvements
This new version also includes the possibility of employing Entos Qcore84 for the electronic structure calculations. An example input file (FA_qcore.dat) employing this option for both low-level and high-level calculations can be found in the examples folder. The corresponding test can be run using:
-
run_test.sh --tests = FA_qcore
Briefly, these calculations can be requested through the keywords LowLevel and HighLevel. An example of a low-level calculation using Entos Qcore is also given above for the pyrene + NO2 system. For the high-level calculations, the syntax is:
-
HighLevel qcore qcore_template
-
dft(
-
xc=PBE
-
ao='6-31G*'
-
)
Since IRC calculations are not available in Entos Qcore, a damped velocity Verlet algorithm111 is utilized to follow the reaction pathways.
A useful feature to study the decomposition of ions is the assignment of charges (and multiplicities) of the resulting fragments. This option is only available for high-level calculations using Gaussian.85 Charges and multiplicities are assigned using the keyword pop = (mk,nbo). This keyword is added to a single point calculation for the geometry of the last point of an IRC leading to fragmentation.
As an example, Figure 9 shows part of the high-level pathways obtained for the decomposition of protonated uracil at the B3LYP/6-31+G(d,p) level of theory. The figure displays only a reduced part of the pathways (those involving different fragments) with the positive charges assigned to the corresponding fragments.
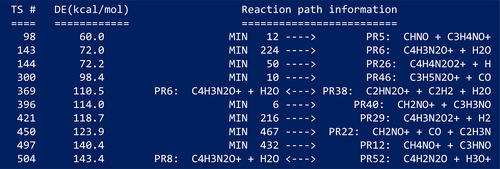
Since the reaction detection algorithms focus on bond formation/breakage, there is an additional tool to scan dihedral angles and find TSs for interconverting conformers. Torsions around bonds with bond orders greater than 2.0 and/or those belonging to rings are excluded.
Finally, an auto-installer script is now available, which eases the burden of installing third-party packages. The script installs singularity112 and downloads the latest container image from sylabs (https://sylabs.io/). An instance of the container is started using a sandbox image deployed under $(TMPDIR-/tmp) folder. The container comes with all AutoMeKin's tools installed in $AMK.
3 CONCLUSIONS
Presented here is the open-source software package AutoMeKin, for automated reaction discovery. AutoMeKin is an updated version of tsscds2018 featuring several new tools: rare-event MD simulations, a search algorithm to study van der Waals complexes, a chemical-knowledge based search procedure, a reactive-event detection method based on bond orders, statistics of the chemical reaction networks, and a web application to submit online jobs.
- An interface with M3C113 to study fragmentation of vibrationally excited molecules including barrierless mechanisms.
- A deep-learning correction to SQM barrier heights to boost the performance and efficiency of the calculations.114
- An interface with Pilgrim,115 a code to calculate thermal rate constants of chemical reactions including variational and tunneling effects.
ACKNOWLEDGMENTS
This work was partially supported by the Ministerio de Ciencia e Innovacion (Grant # PID2019-107307RB-I00). G. L. B. gratefully acknowledges support from the National Science Foundation under grant No. 1763652.




