Factor timing in the Chinese stock market
Abstract
I conduct an exploratory study about the feasibility of factor timing in the Chinese stock market, covering 24 representative and well-identified risk factors in 10 categories from the literature. The long–short portfolio of short-term reversal exhibits strong out-of-sample predictability, which is robust across various models and all types of predictors. This predictability is significant both statistically and economically, with a simple investment strategy obtaining its return three times higher than the buy-and-hold return in the sample period and a significant annualized 20.4% CH-3 alpha. Portfolio historical volatility and market volatility measurement predictors play crucial roles in the reversal factor premium's robust predictability. However, such results are not evident in predicting all other factors' long–short portfolios as well as all factors' long-wing and short-wing portfolios, and this failure cannot be attributed to their exposure to unpredictable market returns.
1 INTRODUCTION
Asset return predictability is the holy grail in empirical asset pricing research. Theoretically, researchers have shown that stock return time-series predictability should exist (e.g., Cochrane, 2008, 2011). Empirically, more researchers are exploring strong predictors for predicting stock returns. As a cornerstone for understanding stock returns, factor models decompose stock returns into exposures to systematic risks and stocks' idiosyncratic risks. Systematic risks are common risk sources inherent to the entire market, so they fluctuate with the macroeconomy and investor behavior dynamics. Idiosyncratic risks, on the other hand, have more sophisticated formation channels and are, therefore, harder to understand or predict. By decomposing stock prediction into predictions towards two types of risks, researchers may find better predictors for predicting systematic risks and idiosyncratic risks, respectively, and hence deepen their understanding about stock return predictability. Meanwhile, modern portfolio theory tries to minimize or even eliminate idiosyncratic risks within the investment portfolio, but it cannot avoid exposing the portfolio to some systematic risks. A better understanding of systematic risks, therefore, helps investors to understand their investment risks better.
This starts researchers' exploration towards factor timing in the past 10 years. However, the evidence on the effectiveness of timing is still diverse. The majority of relevant research stays positive for the feasibility of factor timing, including Greenwood and Hanson (2012), Hodges et al. (2017), Hasler et al. (2019), Haddad et al. (2020), Lioui and Tarelli (2020), and Neuhierl et al. (2023). But there are also negative voices towards factor timing, including Asness et al. (2017) and Dichtl et al. (2019). Besides, there has been no consensus yet on which predictors to use either. Moreover, most research focuses only on the US stock market. As is introduced by Liu et al. (2019), many of the previous findings about anomalies and factor models fail to be replicated in the Chinese stock market, which has a much shorter history, more policies and trading constraints, and higher percentage of retail investor trading volume. Given that China has the world's second-largest stock market, and that the Chinese stock market can offer global investors the opportunity for diversification as well as high average returns (Carpenter et al., 2021), it is necessary to re-evaluate previous research's findings in the Chinese stock market.
In this paper, I conduct an exploratory study about the feasibility of factor timing in the Chinese stock market. My investigation has several key features. First, this study focuses on factors that have been documented as significant in the Chinese stock market by the literature (as summarized by Liu et al., 2019). Second, I employ out-of-sample expanding-window tests, since such tests provide the most rigorous and relevant evidence on return predictability (e.g., Martin & Nagel, 2022; Welch & Goyal, 2008). Third, I aggregate predictors applied in previous research and examine the predictive ability of two types of predictors, including portfolio-specific predictors (portfolio aggregated characteristics and historical portfolio performance measurements) and macroeconomic variable predictors. Fourth, I aggregate predictive models from the previous literature and apply various predictive models, as well as variable screening and dimension reduction techniques to guard against overfitting the data in a high-dimensional setting. Fifth, this study also tries to apply unsupervised learning methods to construct specific economic cycles for each factor portfolio and to analyze whether such data-driven economic cycles can depict factor portfolio performance dynamics over time. The concept of the “economic cycle” has been prevalent over decades, with gross domestic product (GDP) and inflation being the most widely accepted criteria. However, China's economic growth performance has remained robust since 2000, which means it is hard to construct such an artificial cycle. This study, therefore, tries to model economy cycles in a data-driven and nonparametric method, with a high dimension of macroeconomic variables as potential criteria.
Empirically, I find that conducting factor timing in the Chinese stock market is indeed challenging in general. Most factors' long–short portfolios and quantile portfolios cannot exhibit predictability that could outperform the historical mean. However, there is one exception: reversal factor long–short portfolio exhibits very strong and statistically significant out-of-sample predictability, which is robust across various regression models and all types of predictors. Moreover, such strong predictability can be transformed into an economically significant investment strategy, which can generate a significant annualized 20.4% alpha based on the CH-3 model developed by Liu et al. (2019). After the expanding-window variable screening towards the two types of predictors, portfolio volatility and market volatility measurement predictors turn out to be the most crucial across models and have their coefficients consistently positive across windows. Given that it is a common practice for the state-backed funds (“National Teams”) to stabilize the market during market fluctuations, this finding may enlighten future research to dig further towards the mechanism of this strong predictability from the perspective of different market participants and their behavior.
There has been research arguing whether market excess return can be predicted, with the positive voice from Dong et al. (2022) and the negative voice from Cakici et al. (2024). My replication yields the conclusion that market excess return cannot be significantly or robustly predicted. Noticing that most factors' quantile portfolios have their market betas very close to 1, one conjecture is that the high exposure to the unpredictable market excess return results in those failures to predict these factor portfolios. Empirically, I find that the size factor long-wing portfolio and long–short portfolio become very strongly predictable. However, most of the other factors' quantile portfolios still cannot be well predicted after the market exposure neutralization. The effect of factor portfolios' market exposure on factor timing therefore requires further discussions and explorations.
This study directly relates to the literature on factor timing. There has been research exploring effective factor timing predictors via portfolio historical performance (e.g., Blitz et al., 2020; Ehsani & Linnainmaa, 2022) and portfolio aggregate characteristics (e.g., Kagkadis et al., 2024). This study includes both types in the high-dimensional predictors and tests their performance in the Chinese stock market. Other research discusses factor portfolio performance dynamics across economic cycles (e.g., Baltussen et al., 2023) or through economic uncertainty or commodity price fluctuations (e.g., Huang & Kilic, 2019; Li et al., 2023). This study incorporates a considerable amount of macroeconomic variables, and exhibits their predictability under various prediction methods.
This paper also contributes to the estimation of the stochastic discount factor (SDF), which plays a crucial role in asset pricing. Cochrane (2009) explains the equivalence among factor models, SDF estimation, and mean–variance frontiers. Haddad et al. (2020) simplify SDF estimation from stock-based estimation into factor-based estimation. By better-estimating factor expected returns, the optimal portfolio construction and SDF estimation can benefit from the predictability. The strong predictability towards the reversal factor, as well as the insignificant predictability towards the rest of the factors, provides empirical evidence foundation for future research to further explore effective estimation methods towards SDF in China.
Lastly, our article suggests methodology improvements in machine learning applications in empirical asset pricing studies. First, facing high-dimensional predictors, variable shrinkage and principal component (PC) methods are commonly seen (e.g., Dong et al., 2022; Gu et al., 2020) to control the dimensionality problem. Such measurements can effectively guard against overfitting, while at the same time it may lead to lower explanation power. Besides, given that there exists a replication crisis in finance and predictors reported effectiveness might be due to data snooping or see-forward problems (Cakici et al., 2024), merely applying all predictors from the literature into the rolling-window dimension reduction and predictions will possibly lead to incorporating unpredictive information into predictors and thus results in poor predictions. This study, therefore, suggests a rolling-window variable screening method, which not only abandons uncontributing predictors and reduces dimensionality at the first step but also allows researchers to easier explore possible explanations from predictors with much lower dimensions. Second, for researchers who try to depict factor performance dynamics across economic cycles, one central discussion is how such cycles should be constructed. Baltussen et al. (2023) choose to apply the traditional business cycle with a very long history, while Blitz (2022) suggests constructing such cycles directly from factor returns themselves. With more macroeconomic variables being announced to contain predictability towards factor performance (e.g., Hodges et al., 2017; Li et al., 2023), this study suggests a potential unsupervised learning method to construct data-driven cycles based on the high-dimensional macroeconomic variable predictors.
The remainder of this paper is organized as follows. Section 2 introduces data sources and detailed factor and predictor construction methods. Section 3 describes the construction and evaluation methods of out-of-sample predictions. Section 4 reports comprehensive prediction performance results. Section 5 further discusses the real influence of market exposure on factor timing effectiveness, as well as the source of the reversal factor's strong predictability. Section 6 exhibits strategy implementation and performance based on factor timing results. Section 7 concludes.
2 DATA
This section exhibits the details and summary statistics of target factor portfolios in this study. Also, two types of predictors are introduced.
2.1 Factor portfolios
From the typical single-factor capital asset pricing model (Sharpe, 1964) to the famous three-factor model (Fama & French, 1993), now towards a huge and under doubt factor zoo (Harvey et al., 2016), lots of research has been conducted in the US stock market to figure out anomalies, put the best into factor models and compare their explanatory power with other factor models. However, not all anomalies, factors, or factor models can maintain their performances when being directly replicated in the Chinese stock market (Chen et al., 2010; Cheung et al., 2015; Fan & Shan, 2004; Hu et al., 2019; Liu et al., 2019; Yang & Chen, 2003). To deepen our understanding of systematic risks in the Chinese stock market via factor timing, factors under testing in this study need to be documented as significantly by the literature. In the study conducted by Liu et al. (2019), a total of nine categories of factors reported as significant in China are compiled and provided. This study extends the construction methods of Profitability factors (follow Li et al., 2023), Volatility factors (inspired by Blitz et al., 2020), and Investment factors (inspired by Fama & French, 2015) to ensure the robustness of testing results for these factor categories. Also, the long-term Momentum factor (follow Jegadeesh & Titman, 1993) is introduced, which compliments the testing results for the short-term reversal factor. Our starting point is, therefore, these 24 factors within 10 categories.
The stock trading data comes from Datastream database on Wharton Research Data Services (WRDS). The firm financial data comes from Worldscope database on WRDS. Our sample period is January 2000–December 2021. The market index data (CSI300) used in this study was launched on April 8, 2005, and is obtained from Datastream database on WRDS. The series for the risk-free rate from January 2000 to December 2006 is the 1-year deposit rate1; after the 1-year treasury rate data become available since January 2007, the series switch to the 1-year treasury rate as the risk-free rate.2
The factor portfolios in this study are constructed monthly and are reconstituted at the end of each month. This study generally follows Liu et al. (2019) in the data preprocessing procedure. Specifically, from all A-share stocks from the main boards and growth enterprise market of the Shanghai and Shenzhen exchange, I exclude newly listed stocks within the past 6 months, stocks with insufficient trading days in the past year or the past month, and stocks with the bottom 30% of market capitalization by the end of the previous month. To sort stocks into portfolios, I replicate most portfolios defined in the original paper that introduced the anomaly. The exception is the Investment factor category, which I find the original Conservative-minus-Aggressive long–short portfolio introduced by Fama and French (2015) brings a significant negative return in the sample period. This study, therefore, reverses the direction for the Investment factor category. Stocks are divided into 10 groups based on the target factor, and the return for each group is calculated by the market capitalization weighted aggregate return. Moreover, since the size factor has been reported as significant in many studies (including Cheung et al., 2015; Hu et al., 2019; Liu et al., 2019), for all factors other than the size factor, a three-group market capitalization conditional double sort is applied. This measurement aims to neutralize the size factor from all other factors so that the prediction results can better explain which component of those factor portfolios can be really predicted.
Table 1 provides all factor portfolios' annualized mean excess returns in the sample period. Among 24 factors, only six factors have their long–short portfolio returns statistically different from 0 at the 0.1 significant level. After reversing the direction of factors in the Investment category, both factors exhibit a positive mean annualized return. Table 2 provides the full-sample market beta of all factor portfolios. Similar to the finding in the US stock market by Blitz (2023), most factors' long–short portfolios exhibit negative full-sample market betas, among which Accruals, Profitability, Turnover, and Volatility factor categories are the most significant. On the other hand, all factors' long-wing and short-wing portfolios have very significant positive market betas close to one, with short-wing portfolios' beta slightly higher than long-wing portfolios' beta.
| p1 | p2 | p3 | p4 | p5 | p6 | p7 | p8 | p9 | p10 | LongShort | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| accruals_accruals | 4.8 | 5.47 | 5.54 | 6.5 | 7.27 | 6.81 | 7.68 | 7.85 | 6.21 | 4.65 | −0.14 |
| (0.72) | (0.83) | (0.85) | (0.98) | (1.07) | (1.03) | (1.18) | (1.22) | (1.01) | (0.8) | (−0.05) | |
| accruals_noas | 6.79 | 5.23 | 6.97 | 2.67 | 9.39 | 8.12 | 10.89 | 8.2 | 9.1 | 6.67 | −0.12 |
| (1.03) | (0.79) | (1.06) | (0.41) | (1.4) | (1.25) | (1.64) | (1.28) | (1.48) | (1.2) | (−0.03) | |
| illiquidity_illiquidity | 2.06 | 4.0 | 8.26 | 9.34 | 9.15 | 8.9 | 9.83 | 10.42* | 11.36* | 8.01 | 5.95 |
| (0.38) | (0.7) | (1.27) | (1.48) | (1.46) | (1.4) | (1.57) | (1.72) | (1.93) | (1.32) | (1.29) | |
| investment_annualassetgrowth | 3.85 | 5.47 | 3.62 | 6.52 | 1.57 | 4.73 | 6.25 | 7.93 | 7.97 | 7.12 | 3.27 |
| (0.57) | (0.87) | (0.63) | (1.16) | (0.29) | (0.79) | (1.01) | (1.21) | (1.18) | (1.07) | (0.99) | |
| investment_quarterlyassetgrowth | 4.12 | 2.56 | 4.08 | 4.08 | 2.58 | 6.84 | 10.67* | 9.8 | 10.11 | 13.41** | 9.29*** |
| (0.59) | (0.39) | (0.68) | (0.67) | (0.45) | (1.11) | (1.7) | (1.52) | (1.58) | (1.98) | (3.09) | |
| momentum_lagelemreturn | 2.82 | 5.46 | 6.78 | 4.16 | 5.71 | 8.07 | 4.14 | 6.24 | 7.1 | 9.29 | 6.47 |
| (0.43) | (0.9) | (1.09) | (0.7) | (0.99) | (1.39) | (0.72) | (1.04) | (1.16) | (1.42) | (1.34) | |
| profitability_PMU | −2.69 | 0.56 | 2.25 | 4.75 | 3.09 | 5.99 | 4.48 | 10.28 | 15.79** | 20.25*** | 22.94*** |
| (−0.38) | (0.08) | (0.33) | (0.7) | (0.47) | (0.92) | (0.72) | (1.6) | (2.46) | (3.3) | (4.89) | |
| profitability_PMUTTM | 1.02 | 4.72 | 6.28 | 5.71 | 7.45 | 7.37 | 7.05 | 6.34 | 14.65** | 15.44** | 14.42*** |
| (0.14) | (0.67) | (0.9) | (0.84) | (1.14) | (1.04) | (1.08) | (1.01) | (2.21) | (2.58) | (3.02) | |
| profitability_roe | 5.29 | 8.3 | 8.62 | 7.93 | 10.34 | 8.03 | 6.5 | 6.8 | 5.93 | 7.88 | 2.59 |
| (0.72) | (1.17) | (1.23) | (1.17) | (1.51) | (1.2) | (1.04) | (1.1) | (0.97) | (1.17) | (0.63) | |
| reversal_onemonthreturn | −0.31 | 4.28 | 5.62 | 10.59* | 7.34 | 7.38 | 7.44 | 7.85 | 8.08 | 9.11 | 9.42* |
| (−0.05) | (0.74) | (0.98) | (1.78) | (1.28) | (1.24) | (1.29) | (1.3) | (1.31) | (1.36) | (1.96) | |
| size_mktcap | 4.85 | 7.89 | 7.03 | 8.77 | 7.5 | 8.63 | 9.93 | 10.51 | 11.71* | 13.47* | 8.62 |
| (0.9) | (1.28) | (1.11) | (1.33) | (1.11) | (1.27) | (1.42) | (1.47) | (1.66) | (1.82) | (1.52) | |
| turnover_onemabturnover | −5.84 | 5.08 | 5.3 | 7.97 | 10.64* | 8.12 | 10.54* | 8.94 | 8.68 | 6.45 | 12.28*** |
| (−0.85) | (0.78) | (0.87) | (1.34) | (1.87) | (1.37) | (1.81) | (1.61) | (1.48) | (1.12) | (2.94) | |
| turnover_twelvemturnover | 0.13 | 4.57 | 6.3 | 9.01 | 7.05 | 9.18 | 9.99 | 9.99* | 6.82 | 5.47 | 5.33 |
| (0.02) | (0.66) | (0.94) | (1.4) | (1.14) | (1.53) | (1.64) | (1.7) | (1.2) | (1.08) | (0.99) | |
| value_bmratio | 3.62 | 6.13 | 5.75 | 5.45 | 4.01 | 6.69 | 7.02 | 7.33 | 4.01 | 8.0 | 4.38 |
| (0.55) | (0.91) | (0.85) | (0.82) | (0.61) | (1.0) | (1.02) | (1.17) | (0.67) | (1.36) | (0.79) | |
| value_cpratio | 4.88 | 5.03 | 5.08 | 2.23 | 6.69 | 8.78 | 7.99 | 11.6* | 7.78 | 10.28* | 5.4** |
| (0.78) | (0.76) | (0.77) | (0.34) | (1.04) | (1.33) | (1.27) | (1.75) | (1.27) | (1.68) | (2.0) | |
| value_epratio | 4.57 | 8.97 | 9.44 | 4.87 | 6.05 | 4.48 | 3.94 | 5.5 | 5.77 | 7.33 | 2.75 |
| (0.69) | (1.34) | (1.48) | (0.79) | (0.99) | (0.76) | (0.67) | (0.95) | (1.02) | (1.28) | (0.59) | |
| volatility_MAX | 0.49 | 6.6 | 5.13 | 5.57 | 7.56 | 8.61 | 11.46* | 7.2 | 7.96 | 3.53 | 3.04 |
| (0.07) | (1.0) | (0.8) | (0.89) | (1.23) | (1.47) | (1.92) | (1.2) | (1.42) | (0.71) | (0.68) | |
| volatility_onemonthv | −1.03 | 4.7 | 8.2 | 8.92 | 6.75 | 6.59 | 10.35* | 7.95 | 8.36 | 5.38 | 6.41 |
| (−0.14) | (0.68) | (1.22) | (1.34) | (1.06) | (1.1) | (1.69) | (1.38) | (1.54) | (1.13) | (1.23) | |
| volatility_oneyearmv | 2.28 | 6.22 | 6.41 | 7.28 | 8.77 | 7.74 | 7.49 | 8.26 | 7.54 | 5.76 | 3.49 |
| (0.33) | (0.9) | (1.01) | (1.14) | (1.41) | (1.3) | (1.23) | (1.4) | (1.34) | (1.16) | (0.75) | |
| volatility_sixmonthv | −1.22 | 2.8 | 2.75 | 7.55 | 6.68 | 7.43 | 9.68 | 9.26 | 7.94 | 4.52 | 5.74 |
| (−0.16) | (0.4) | (0.41) | (1.13) | (1.06) | (1.19) | (1.6) | (1.59) | (1.44) | (0.96) | (0.98) | |
| volatility_threemonthv | −1.55 | 4.35 | 5.73 | 5.07 | 8.6 | 8.3 | 7.29 | 7.43 | 9.45* | 5.67 | 7.22 |
| (−0.21) | (0.6) | (0.86) | (0.77) | (1.33) | (1.34) | (1.22) | (1.29) | (1.67) | (1.18) | (1.29) | |
| volatility_threeyearmv | 2.0 | 4.43 | 8.35 | 5.69 | 9.01 | 6.78 | 9.86 | 8.4 | 9.15 | 4.92 | 2.92 |
| (0.27) | (0.61) | (1.16) | (0.83) | (1.3) | (1.03) | (1.48) | (1.33) | (1.49) | (0.92) | (0.56) | |
| volatility_twelvemonthv | 0.23 | 4.31 | 3.7 | 6.12 | 7.42 | 10.29 | 8.07 | 9.46 | 9.74* | 5.07 | 4.84 |
| (0.03) | (0.61) | (0.53) | (0.94) | (1.14) | (1.63) | (1.38) | (1.63) | (1.66) | (1.09) | (0.82) | |
| volatility_twoyearmv | 1.96 | 3.74 | 5.99 | 7.03 | 8.53 | 7.68 | 6.81 | 6.68 | 5.85 | 4.24 | 2.28 |
| (0.27) | (0.53) | (0.9) | (1.08) | (1.27) | (1.2) | (1.09) | (1.16) | (1.05) | (0.82) | (0.45) |
- Note: This table reports mean annualized returns (in percentage) and t statistics (in brackets) on each factor portfolio net of the risk-free rate. The order of quantiles has been adjusted by factors' long–short portfolio construction methods, such that p10 denotes the long wing, p1 denotes the short wing, and portfolios from p2 to p9 follow the direction from the short wing to the long wing. The column LongShort lists mean returns by longing p10 and shorting p1. All factor portfolio returns are monthly data from January 2000 to December 2021.
- * Significant at the 0.10 level
- ** significant at the 0.05 level
- *** significant at the 0.01 level.
| p1 | p2 | p3 | p4 | p5 | p6 | p7 | p8 | p9 | p10 | LongShort | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| accruals_accruals | 1.06*** | 0.99*** | 0.93*** | 0.94*** | 0.94*** | 0.92*** | 0.95*** | 0.98*** | 0.95*** | 0.9*** | −0.16*** |
| (48.5) | (27.03) | (22.48) | (21.38) | (20.28) | (21.17) | (25.4) | (31.9) | (34.07) | (38.27) | (−5.31) | |
| accruals_noas | 0.95*** | 0.96*** | 0.96*** | 0.96*** | 0.99*** | 0.97*** | 0.98*** | 0.95*** | 0.93*** | 0.8*** | −0.15*** |
| (27.76) | (27.13) | (28.31) | (30.66) | (31.22) | (32.35) | (30.6) | (33.56) | (39.75) | (31.55) | (−3.19) | |
| illiquidity_illiquidity | 0.89*** | 0.96*** | 1.06*** | 1.01*** | 0.99*** | 0.98*** | 0.95*** | 0.91*** | 0.86*** | 0.85*** | −0.05 |
| (41.36) | (51.09) | (36.29) | (33.95) | (30.09) | (28.06) | (25.9) | (24.39) | (22.69) | (19.75) | (−0.81) | |
| investment_annualassetgrowth | 1.03*** | 0.97*** | 0.9*** | 0.85*** | 0.83*** | 0.96*** | 0.98*** | 1.04*** | 1.04*** | 1.0*** | −0.03 |
| (32.05) | (35.42) | (39.02) | (32.54) | (33.9) | (52.97) | (42.97) | (37.25) | (31.53) | (27.41) | (−0.7) | |
| investment_quarterlyassetgrowth | 1.02*** | 0.99*** | 0.91*** | 0.92*** | 0.84*** | 0.92*** | 0.95*** | 0.96*** | 0.94*** | 1.02*** | −0.01 |
| (28.15) | (35.18) | (34.31) | (34.24) | (31.5) | (34.07) | (33.79) | (30.4) | (28.9) | (30.07) | (−0.18) | |
| momentum_lagelemreturn | 0.98*** | 0.94*** | 1.0*** | 0.96*** | 0.94*** | 0.94*** | 0.93*** | 0.96*** | 0.95*** | 0.96*** | −0.02 |
| (25.01) | (30.78) | (35.84) | (37.8) | (39.82) | (41.64) | (35.12) | (34.24) | (25.75) | (20.67) | (−0.31) | |
| profitability_PMU | 1.04*** | 1.06*** | 1.04*** | 1.0*** | 0.99*** | 0.96*** | 0.91*** | 0.96*** | 0.93*** | 0.83*** | −0.21*** |
| (28.36) | (31.49) | (33.52) | (30.36) | (32.66) | (28.64) | (27.35) | (30.42) | (26.31) | (20.81) | (−4.13) | |
| profitability_PMUTTM | 1.05*** | 1.04*** | 1.06*** | 1.01*** | 0.95*** | 1.04*** | 0.93*** | 0.9*** | 0.97*** | 0.79*** | −0.25*** |
| (27.08) | (30.79) | (37.44) | (31.86) | (28.84) | (29.59) | (26.53) | (27.42) | (27.57) | (20.64) | (−4.93) | |
| profitability_roe | 0.97*** | 0.95*** | 0.95*** | 0.93*** | 0.95*** | 0.94*** | 0.92*** | 0.9*** | 0.89*** | 0.98*** | 0.01 |
| (24.34) | (24.58) | (25.85) | (27.48) | (28.17) | (31.52) | (42.56) | (38.21) | (40.16) | (38.51) | (0.21) | |
| reversal_onemonthreturn | 1.05*** | 0.94*** | 0.91*** | 0.96*** | 0.93*** | 0.97*** | 0.91*** | 0.93*** | 0.93*** | 0.97*** | −0.08 |
| (27.47) | (32.21) | (33.81) | (37.93) | (41.14) | (39.48) | (33.21) | (29.41) | (26.96) | (21.46) | (−1.44) | |
| size_mktcap | 0.91*** | 1.0*** | 0.97*** | 0.97*** | 0.96*** | 0.94*** | 0.95*** | 0.95*** | 0.93*** | 0.96*** | 0.06 |
| (57.05) | (33.84) | (24.95) | (21.59) | (20.36) | (18.6) | (17.68) | (16.7) | (16.25) | (16.0) | (0.8) | |
| turnover_onemabturnover | 1.07*** | 1.07*** | 1.0*** | 0.98*** | 0.92*** | 0.95*** | 0.92*** | 0.86*** | 0.9*** | 0.85*** | −0.22*** |
| (28.09) | (36.33) | (37.13) | (41.21) | (37.28) | (35.34) | (34.26) | (30.45) | (27.45) | (23.58) | (−4.32) | |
| turnover_twelvemturnover | 1.07*** | 1.07*** | 1.08*** | 1.03*** | 1.01*** | 1.0*** | 1.02*** | 0.99*** | 0.94*** | 0.78*** | −0.28*** |
| (20.7) | (26.17) | (30.86) | (33.51) | (36.36) | (47.45) | (48.51) | (51.47) | (51.17) | (32.67) | (−4.37) | |
| value_bmratio | 0.88*** | 0.93*** | 0.96*** | 0.98*** | 0.96*** | 1.03*** | 1.04*** | 0.94*** | 0.88*** | 0.85*** | −0.02 |
| (18.92) | (20.64) | (24.3) | (27.67) | (27.42) | (36.45) | (32.44) | (34.11) | (30.14) | (28.3) | (−0.38) | |
| value_cpratio | 0.94*** | 0.98*** | 0.98*** | 0.96*** | 0.93*** | 0.98*** | 0.92*** | 0.99*** | 0.9*** | 0.9*** | −0.04 |
| (37.29) | (31.21) | (33.22) | (30.05) | (28.04) | (30.95) | (29.89) | (33.88) | (33.6) | (34.47) | (−1.14) | |
| value_epratio | 0.99*** | 0.97*** | 0.96*** | 0.94*** | 0.98*** | 0.95*** | 0.95*** | 0.96*** | 0.92*** | 0.89*** | −0.1* |
| (23.82) | (20.83) | (23.8) | (25.64) | (30.43) | (33.57) | (39.68) | (42.67) | (38.38) | (31.53) | (−1.68) | |
| volatility_MAX | 1.07*** | 1.02*** | 1.04*** | 1.01*** | 1.02*** | 0.92*** | 0.97*** | 0.95*** | 0.89*** | 0.77*** | −0.3*** |
| (27.41) | (28.15) | (35.79) | (34.8) | (41.75) | (30.8) | (39.43) | (35.28) | (32.76) | (27.34) | (−5.73) | |
| volatility_onemonthv | 1.04*** | 1.1*** | 1.07*** | 1.07*** | 1.04*** | 0.98*** | 1.0*** | 0.94*** | 0.86*** | 0.73*** | −0.31*** |
| (21.77) | (31.09) | (31.95) | (34.28) | (38.61) | (39.24) | (40.16) | (40.51) | (31.16) | (27.6) | (−5.01) | |
| volatility_oneyearmv | 1.07*** | 1.07*** | 1.03*** | 1.02*** | 1.0*** | 0.98*** | 1.0*** | 0.98*** | 0.91*** | 0.78*** | −0.28*** |
| (24.87) | (27.17) | (35.99) | (33.08) | (33.16) | (42.06) | (44.99) | (43.82) | (38.96) | (31.93) | (−5.1) | |
| volatility_sixmonthv | 1.05*** | 1.05*** | 1.07*** | 1.07*** | 1.04*** | 1.03*** | 1.01*** | 0.97*** | 0.91*** | 0.72*** | −0.33*** |
| (18.65) | (25.0) | (29.73) | (31.99) | (41.49) | (43.79) | (45.64) | (46.17) | (40.34) | (27.45) | (−4.7) | |
| volatility_threemonthv | 1.06*** | 1.12*** | 1.06*** | 1.06*** | 1.07*** | 1.0*** | 0.99*** | 0.93*** | 0.92*** | 0.74*** | −0.32*** |
| (20.53) | (27.26) | (30.47) | (33.79) | (41.41) | (36.21) | (43.67) | (36.2) | (37.28) | (26.51) | (−4.83) | |
| volatility_threeyearmv | 1.05*** | 1.07*** | 1.06*** | 1.02*** | 1.06*** | 1.01*** | 1.03*** | 0.96*** | 0.94*** | 0.78*** | −0.26*** |
| (23.65) | (29.16) | (28.26) | (30.48) | (36.12) | (38.37) | (40.35) | (36.84) | (41.74) | (30.24) | (−4.38) | |
| volatility_twelvemonthv | 1.06*** | 1.07*** | 1.1*** | 1.04*** | 1.05*** | 1.06*** | 0.96*** | 0.95*** | 0.97*** | 0.73*** | −0.32*** |
| (18.69) | (24.55) | (28.76) | (32.45) | (33.92) | (41.79) | (40.42) | (41.56) | (42.35) | (30.45) | (−4.62) | |
| volatility_twoyearmv | 1.05*** | 1.09*** | 1.04*** | 1.03*** | 1.08*** | 1.03*** | 1.02*** | 0.92*** | 0.88*** | 0.79*** | −0.26*** |
| (22.69) | (28.45) | (30.28) | (33.65) | (36.28) | (39.95) | (40.89) | (38.77) | (41.54) | (31.6) | (−4.29) |
- Note: This table reports full-sample market betas and t statistics (in brackets) on each factor portfolio. The order of quantiles has been adjusted by factors' long–short portfolio construction methods, such that p10 denotes the long wing, p1 denotes the short wing, and portfolios from p2 to p9 follow the direction from the short wing to the long wing. The column LongShort lists market betas of portfolios constructed by longing p10 and shorting p1. All factor portfolio betas are constructed based on monthly return data from May 2005 to December 2021.
- * Significant at the 0.10 level
- ** significant at the 0.05 level
- *** significant at the 0.01 level.
2.2 Predictors
This study uses a board set of predictors that are proposed in the literature. These predictors are classified into two types: portfolio-specific predictors and macroeconomic variable predictors.
Portfolio-specific predictors are constructed using target portfolios' specific characteristics or historical performance measurements, and hence may vary among factor portfolios at the same time period. Prior studies in the US stock market raise momentum (e.g., Arnott et al., 2023; Ehsani & Linnainmaa, 2022; Gupta & Kelly, 2018), volatility (e.g., Blitz et al., 2020) and portfolio aggregate characteristics (e.g., Haddad et al., 2020; Kagkadis et al., 2024) as solid and informative indicators that explain the dynamics of factor portfolios or their PCs. In this study, various types of portfolio momentum and volatility measurements are constructed. The portfolio aggregate characteristics are constructed based on the 24-factor characteristics, aggregated by the weighting of stocks in each portfolio. I also add two predictors that measure the historical portfolio turnover rate when reconstituted monthly. In total 38 portfolio-specific predictors in three categories are finally applied in the predictions.
Macroeconomic variable predictors, on the other hand, consist of numerous quantifiable macroeconomic variables that may influence on the systematic risk of the Chinese stock market. Prior studies usually discuss factor portfolio performance or predictability based on business and economic cycles (e.g., Baltussen et al., 2023; Neuhierl et al., 2023; Sheth & Lim, 2017). Li et al. (2023) exhibit the strong predictability of economic policy uncertainty (EPU) towards the size factor. There are also researchers discussing the relationship between commodity prices and the equity market (e.g., Huang & Kilic, 2019; Jones & Kaul, 1996). This study considers in total 178 macroeconomic variables in eight categories, including but not limited to GDP and inflation level, global market performance, CNY exchange rate and global treasure yield curve measurements, EPU and geopolitical risk (GPR) indexes, global commodity prices, and the historical overall factor returns (inspired by Blitz, 2022). EPU index3 is first introduced by Baker et al. (2016) and GPR index4 is first introduced by Caldara and Iacoviello (2022). All other macroeconomic variables, if not accessible from the previously mentioned databases or websites, are obtained from Tonghuashun iFind finance database. Moreover, since the announcement date of some macroeconomic variables may be later than the time periods these macroeconomic variables describe, such as the GDP data and CPI data, I construct these macroeconomic variable predictors in two types: “Realtime,” which is recorded once macroeconomic variables are updated (whether the data is public or not yet public), and “Announcement,” which is recorded only when the updated macroeconomic variables are publicly announced.
3 METHODOLOGY
This section introduces the construction of out-of-sample expanding-window predictions, as well as the evaluation method of the prediction performance.
3.1 Regression methods
There have been many studies working on return prediction across various types of assets, based on various types of predictors, and applying various types of models. Gu et al. (2020) apply different machine learning models, from simple to complex, and find that complex and nonlinear tree models and neural network models can bring significant predictive gains. On the other hand, with relatively small samples, most recent studies towards factor portfolio and market portfolio predictions tend to choose simpler and more linear models. Haddad et al. (2020) apply the simple restricted VAR(1) model using a single predictor and announce predictability towards the PCs of many factor long–short portfolios. In the studies towards market portfolio prediction that remain controversial, both Dong et al. (2022) and Cakici et al. (2024) apply seven linear models, most of which are designed to shrink or remove duplicated variables so that the dimension of variables can be controlled.
Since the development of factor models, factors in these models are always viewed as proxies of systematic risks in the economy, and people decompose one stock's return into the exposure to every systematic risk and the stock's idiosyncratic risk. Market return naturally reflects systematic risk towards the whole economy, while other factor portfolios also reflect, although narrower, systematic risk towards their specific part of the economy. Idiosyncratic risks tend to be complex across assets such that complex and nonlinear models may better predict their performance. For systematic risks, on the other hand, this study chooses to start from simple models. Specifically, I use seven prediction models employed by Dong et al. (2022) and Cakici et al. (2024). Following Haddad et al. (2020), I include an unrestricted VAR(1) model, and to better replicate the method in their study, the input of this model is the first PC of all predictors. To provide a comparison for the unrestricted VAR(1) model, I also include a simple ordinary least squares (OLS) model, with the model input as the first PC of all predictors.
3.2 Clustering analysis
Applying the macroeconomic variable predictors, this study also conducts an innovative trial in improving factor portfolio return prediction beyond the prevailing benchmark of the historical mean based on unsupervised learning methods. As is introduced in Section 2, a very traditional method taken by researchers and industry professionals is first to classify the economy into different stages, and then analyze if factor portfolios have their specific and significant performance differences across these stages. Typical economic stage classification methods include the “Recession/Recovery/Overheating/Stagflation” cycle and the “Inflation/Deflation/Stagflation” cycle, both based on GDP and inflation. However, such methods cannot work well in the Chinese stock market. The main reason is that since the establishment of the Chinese stock market, China's GDP growth and inflation level remain stable and high in this study's data sample period. In other words, China's economy in the classical economic stage classification methods remains at the “Inflation,” “Recovery,” or “Overheating” stages, and therefore cannot form a cycle. Suppose we choose to ignore these two widely acknowledged macroeconomic variables. In that case, there exist too many highly correlated macroeconomic variables that can be said to be able to “classify the cycle of market stages,” each of which requires its own “classification rule” to construct this artificial market cycle.
This study, therefore, develops a new method to classify the cycle of market stages using clustering algorithms. Since time periods in the same economic stage share highly similar economic situations by definition, a quantitative explanation is that, for any time period in an economic stage, the distance between its macroeconomic variable vector and that of any other time period in the same economic stage should be significantly smaller than that of any time period in other economic stages. This concept matches the idea of clustering algorithms very well. This study, therefore, uses five clustering algorithms to classify economic stages: K-Means Clustering, Balanced Iterative Reducing and Clustering using Hierarchies (Birch), Gaussian Mixture Model, Spectral Clustering, and Agglomerative Hierarchical Clustering. Following the clustering results, the prediction for a factor portfolio's return is the historical mean return of this factor portfolio within the same cluster. All five algorithms allow us to decide the amount of clusters manually. Such property is essential because the data set has a relatively limited number of samples, and we would prefer sufficient samples in each cluster to make robust predictions for each cluster. In empirical tests, I set the target cluster amount to be 2, 3, and 4.
Moreover, it should be noticed that the ultimate goal of classifying economic stages is to test whether there is a significant factor portfolio return difference across different economic stages. I, therefore, construct another prediction based on the clustering results of all these five clustering algorithms. Specifically, in each window, I rank and equally divide the time periods in the train data set into clusters by the real factor portfolio returns, the amount of which is set to be the target cluster amount for the five clustering algorithms. These artificial clusters serve as the “true label” of the train data set. I then evaluate each clustering algorithm's performance on the train data set using the Adjusted Rand Index (ARI), which was developed by Hubert and Arabie (1985) and measures the similarity between two data clustering results, with the higher score meaning the more accurate clustering performance. I finally choose the clustering algorithm with the highest ARI score and record its prediction for the test data set.
3.3 Details of expanding-window predictions
Since the history of the Chinese stock market is not very long and the data was not generally available until around 2000, the entire data set has a relatively limited number of data points. Therefore, this study applies an expanding-window method to construct predictions in empirical tests, with the train data set in the first window as the first 60% of the total data set. The return predictions are always out-of-sample because only data available through month is used to predict factor portfolios' returns in month .
Another thing to notice is that the dimensions of both portfolio-specific predictors and macroeconomic variable predictors are relatively high compared with the data length. This will not only result in overfitting problems in some regression models, but also in too much redundant information for all predictive methods. For clustering analysis, including variables unrelated to the target factor portfolio may still allow algorithms to construct clusters. However, these clusters will be unrelated to the factor portfolio return and hence cannot work well for return prediction. For regression methods, including redundant variables will dilute the predictive components in other variables after principal component analysis (PCA) or other dimension reduction methods. Therefore, in each window, the first step before any model training is to screen out redundant predictors. This is done by first calculating each predictor's Pearson correlation with the target factor portfolio return in the train data sets, followed by removing all predictors with the p value of the Pearson correlation bigger than 0.05.
3.4 Prediction evaluation
4 EMPIRICAL RESULTS
4.1 Portfolio-specific predictor regression results
Table 3 reports for monthly factor long–short portfolio excess return predictions, based on regression methods introduced in Section 3 and portfolio-specific predictors introduced in Section 2. The conventional OLS method generally produces a negative , which is large in magnitude. Even though variable screening is implemented before fitting the OLS model, the OLS model may still encounter overfitting and multicollinearity problems. At the same time, the OLS model and VAR(1) model after the PCA1 preprocess still cannot perform well, indicating the dimension of the predictive component in predictors is neither too small. The other regression methods, in contrast, produce more positive and significant . It comes to our attention that the reversal factor exhibits positive and solid predictability among regression models, with ElasticNet, PC, and partial least squares (PLS) models performing the best. Size factor, profitability-roe factor, and illiquidity factor exhibit predictability in some models, but obtain negative in other competing models. For other factors, almost no predictability can be found.
| PCA1 OLS | PCA1 VAR(1) | OLS | ElasticNet | PC | PLS | C-Simple | C-ENet | Predictor Average | |
|---|---|---|---|---|---|---|---|---|---|
| accruals_accruals | −2.6 | −3.56 | −20.06 | −3.33 | −5.9 | −4.57 | −0.89 | −5.37 | −4.85 |
| (0.03) | (0.03) | (−0.72) | (0.37) | (0.12) | (0.06) | (0.05) | (−1.07) | (0.14) | |
| accruals_noas | −1.77 | −4.35 | −1.77 | −0.67 | −2.18 | −1.52 | 1.12 | 1.69 | −1.45 |
| (1.08) | (0.58) | (1.45) | (1.01) | (1.35) | (1.17) | (1.2) | (1.46) | (1.41) | |
| illiquidity_illiquidity | 0.97 | −0.6 | 4.47** | 2.46* | −0.28 | 2.02 | 1.2 | 2.64* | −2.16 |
| (0.84) | (0.08) | (2.47) | (1.89) | (0.67) | (1.34) | (1.04) | (1.9) | (0.86) | |
| investment_annualassetgrowth | −3.04 | −4.38 | 0.55 | −1.07 | 2.72 | 1.68 | 2.05 | −0.53 | 4.99** |
| (−1.02) | (−1.31) | (1.12) | (0.18) | (1.48) | (1.25) | (1.32) | (0.3) | (2.0) | |
| investment_quarterlyassetgrowth | −1.4 | −1.87 | −18.28 | −12.01 | −10.88 | −12.38 | −1.82 | −2.04 | −3.32 |
| (0.9) | (0.87) | (−0.5) | (−0.75) | (−0.22) | (−0.83) | (−0.44) | (−0.49) | (−0.22) | |
| momentum_lagelemreturn | −2.49 | −2.93 | −7.9 | −3.56 | −1.47 | −1.21 | 0.38 | −0.51 | −1.06 |
| (−0.14) | (−0.22) | (−0.85) | (−0.24) | (0.73) | (0.74) | (0.71) | (0.2) | (0.25) | |
| profitability_PMU | 2.87 | −0.03 | −4.85 | −1.96 | −3.35 | −7.61 | −1.81 | −2.72 | −8.63 |
| (1.47) | (1.02) | (0.71) | (0.27) | (0.57) | (−0.21) | (−0.55) | (−0.35) | (−0.8) | |
| profitability_PMUTTM | −7.56 | −8.48 | −10.84 | −1.19 | −8.22 | −9.34 | −3.38 | −6.6 | −2.13 |
| (−1.38) | (−1.68) | (−2.27) | (−1.8) | (−2.3) | (−2.52) | (−2.51) | (−3.02) | (−0.32) | |
| profitability_roe | −0.38 | −4.51 | 3.48*** | 3.7*** | −1.23 | 2.22** | −0.96 | −0.04 | −2.05 |
| (0.38) | (−0.83) | (2.6) | (2.58) | (0.82) | (2.41) | (−0.27) | (0.27) | (−0.5) | |
| reversal_onemonthreturn | −1.3 | −4.26 | 2.68*** | 4.05*** | 3.56** | 2.81** | 1.86 | 2.46** | 0.38 |
| (0.18) | (−0.46) | (2.64) | (2.87) | (2.53) | (2.33) | (1.6) | (2.08) | (0.75) | |
| size_mktcap | 0.75 | 0.53 | −6.42 | 4.16* | 5.09** | 2.59* | 2.52 | 2.73 | −0.65 |
| (0.66) | (0.78) | (1.2) | (1.88) | (2.09) | (1.68) | (1.51) | (1.54) | (0.88) | |
| turnover_onemabturnover | −4.97 | −8.35 | −11.47 | −0.03 | −10.96 | −11.6 | −3.22 | −4.05 | −6.91 |
| (−0.48) | (−0.72) | (−0.72) | (0.1) | (−0.77) | (−0.69) | (−0.94) | (−0.86) | (−1.0) | |
| turnover_twelvemturnover | −3.16 | −3.5 | −1.56 | −2.23 | −2.21 | −2.07 | 1.17 | 1.59 | 4.55* |
| (0.72) | (0.66) | (1.32) | (1.16) | (0.79) | (1.23) | (1.05) | (1.18) | (1.88) | |
| value_bmratio | 1.78 | −0.53 | −7.6 | −4.84 | −5.31 | −7.13 | −1.8 | −2.22 | −3.5 |
| (0.8) | (0.46) | (0.2) | (0.23) | (0.24) | (0.14) | (−0.4) | (−0.57) | (−1.42) | |
| value_cpratio | 1.68 | 1.51 | −12.95 | −4.22 | −8.82 | −6.23 | 1.19 | 0.19 | 0.66 |
| (1.12) | (1.2) | (0.55) | (0.18) | (0.79) | (0.87) | (0.88) | (0.82) | (1.18) | |
| value_epratio | 0.5 | −1.17 | −3.58 | 0.13 | −4.41 | −2.67 | 0.01 | −2.71 | 1.01 |
| (0.78) | (0.14) | (0.77) | (1.16) | (0.52) | (0.93) | (0.32) | (−1.17) | (0.75) | |
| volatility_MAX | 0.08 | −0.99 | −10.02 | −6.83 | −6.64 | −9.21 | −2.28 | −1.23 | −5.84 |
| (0.71) | (0.18) | (−0.96) | (−0.62) | (−0.84) | (−0.76) | (−1.39) | (−0.69) | (−1.38) | |
| volatility_onemonthv | −4.28 | −2.94 | −5.62 | −3.82 | −7.02 | −5.35 | −1.04 | −1.3 | −1.41 |
| (−1.54) | (−0.54) | (0.41) | (0.52) | (−0.33) | (0.23) | (−0.37) | (−0.54) | (0.41) | |
| volatility_oneyearmv | 0.06 | −0.95 | −4.82 | −3.91 | −5.09 | −6.21 | −0.06 | 0.0 | −4.02 |
| (0.74) | (0.34) | (0.49) | (0.41) | (−0.21) | (0.17) | (0.36) | (0.4) | (−0.8) | |
| volatility_sixmonthv | −2.08 | −2.4 | 2.52 | 2.82 | 3.2 | 4.69* | 2.35 | 3.16 | −1.02 |
| (0.89) | (0.74) | (1.64) | (1.56) | (1.58) | (1.75) | (1.41) | (1.57) | (−0.04) | |
| volatility_threemonthv | −4.4 | −6.37 | −5.49 | −3.82 | −7.86 | −9.02 | −1.6 | −1.34 | −3.66 |
| (−1.57) | (−1.41) | (−0.05) | (0.1) | (−0.25) | (−0.86) | (−0.91) | (−0.7) | (−0.03) | |
| volatility_threeyearmv | −0.07 | −1.39 | −0.07 | −0.55 | −3.08 | 0.32 | 0.73 | 1.29 | −2.26 |
| (0.55) | (−0.06) | (1.41) | (1.2) | (0.47) | (1.49) | (0.9) | (1.32) | (−0.37) | |
| volatility_twelvemonthv | −3.4 | −5.2 | −4.83 | −2.18 | −3.89 | −3.84 | 0.05 | −0.07 | −2.11 |
| (−0.11) | (−0.25) | (0.69) | (0.72) | (0.82) | (0.8) | (0.49) | (0.47) | (−0.5) | |
| volatility_twoyearmv | −3.62 | −5.78 | −6.2 | −6.46 | −5.11 | −8.71 | −0.14 | 1.55 | −2.81 |
| (−0.98) | (−1.59) | (0.8) | (0.14) | (0.62) | (0.26) | (0.32) | (1.2) | (−0.92) |
- Note: This table reports the Campbell and Thompson (2008) out-of-sample () statistics in percent for every factor's long–short portfolio monthly excess return expanding-window predictions based on portfolio-specific predictors. The full sample starts from January 2000 to December 2021, with the first 60% of data sets as the first window's train set. The out-of-sample period starts from September 2013 to December 2021. Prediction methods are introduced in more detail in Section 3. On the basis of the Clark and West (2007) test, *, **, and *** indicate significance at the 10%, 5%, and 1% levels, respectively, for the positive statistics.
- Abbreviations: OLS, ordinary least squares; PC, principal component; PCA, principal component analysis; PLS, partial least squares.
The positive and significant predictability towards the reversal factor leads to my further attention to the details of these predictions. To expand the summarized results in Table 3, Figure 1 depicts details of monthly reversal factor long–short portfolio excess return predictions. The conventional OLS model, which keeps the most amount of predictors, produce highly volatile predictions. The other methods with only one aggregated predictor, which include PCA1 OLS, PCA1 VAR(1), C-Simple, C-ENet, and Predictor Average, produce more smooth predictions. ElasticNet, PC, and PLS models, which balance between the amount of predictors and predictive components within predictors, yield more stable and accurate predictions.
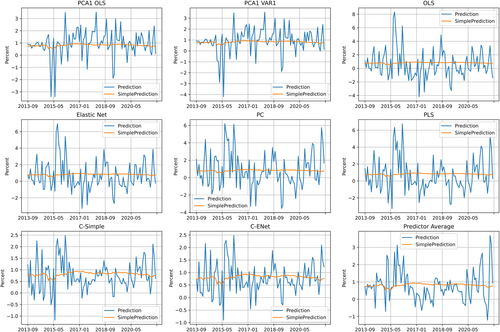
Furthermore, Figure 2 depicts the real return of the reversal factor long–short portfolio in the out-of-sample period, with the market portfolio and momentum factor long–short portfolio as a comparison. In the sample period from September 2013 to December 2021, the reversal factor long–short portfolio encountered external impact before and during the 2015 Chinese stock market crash. More specifically, when the bubble was forming in late 2014, the reversal long–short portfolio, constructed by longing stocks that underperformed and shorting stocks that outperformed in the past month, naturally encountered a severe crash, leading to an almost 40% loss within 1 month. On the other hand, when the bubble burst in 2015 June and July, the reversal long–short portfolio received significant and unusual gains. If such extreme and unusual cases are ignored in the analysis, based on the Campbell and Thompson (2008) statistic, these very few data points may still bring a very massive influence on the value and significance of statistics.
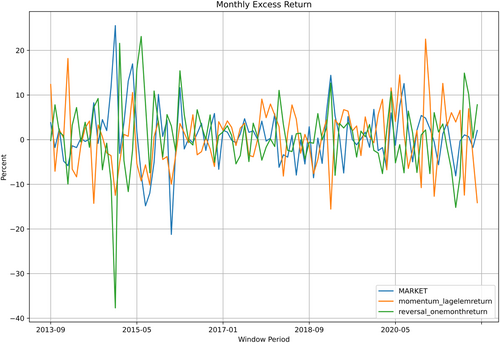
Therefore, to make the findings in this study more robust and general, I recalculate statistics, removing data points with the highest 1% and lowest 1% of real factor portfolio return. In this study's out-of-sample period, this measurement means just to remove two data points from the calculation. Table 4 reports after this adjustment. It can be noticed that the size factor and illiquidity factor no longer have any significant . Their significant in some models in Table 3 may be just from some “lucky coincidences” that allow these models to have nice predictions on the most extreme windows. On the other hand, the reversal factor long–short portfolio exhibits even stronger and significant predictability among almost all regression models, with ElasticNet, PC, and PLS models still performing the best. Almost no predictability can be found for other factors.
| PCA1 OLS | PCA1 VAR(1) | OLS | ElasticNet | PC | PLS | C-Simple | C-ENet | Predictor Average | |
|---|---|---|---|---|---|---|---|---|---|
| accruals_accruals | −4.13 | −4.89 | −21.08 | −1.73 | −9.02 | −6.35 | −1.43 | −4.85 | −6.37 |
| (−0.2) | (−0.07) | (−0.52) | (0.83) | (−0.15) | (−0.09) | (−0.08) | (−0.82) | (0.06) | |
| accruals_noas | −2.31 | −3.91 | −5.14 | −1.75 | −4.33 | −4.36 | 0.9 | 0.81 | −4.19 |
| (1.15) | (0.93) | (1.13) | (0.82) | (1.15) | (0.85) | (0.89) | (1.03) | (1.08) | |
| illiquidity_illiquidity | −0.21 | −3.53 | −1.49 | −0.13 | −2.51 | 2.87 | 1.3 | 0.76 | −3.87 |
| (0.36) | (−0.79) | (1.86) | (1.26) | (0.4) | (1.4) | (0.92) | (0.82) | (1.03) | |
| investment_annualassetgrowth | −3.4 | −4.92 | −0.97 | −2.56 | 1.78 | 0.39 | 1.67 | −1.15 | 4.02* |
| (−1.04) | (−1.32) | (0.85) | (−0.24) | (1.28) | (1.04) | (1.1) | (0.01) | (1.77) | |
| investment_quarterlyassetgrowth | −7.52 | −8.19 | −20.39 | −14.54 | −14.83 | −12.61 | −2.6 | −2.83 | −4.76 |
| (0.11) | (0.03) | (−0.42) | (−0.79) | (−0.36) | (−0.6) | (−0.57) | (−0.61) | (−0.39) | |
| momentum_lagelemreturn | −1.25 | −1.76 | −5.83 | −1.88 | 0.34 | 1.61 | 1.95 | 1.04 | 0.76 |
| (0.38) | (0.26) | (−0.23) | (0.47) | (1.32) | (1.63) | (1.62) | (1.1) | (1.0) | |
| profitability_PMU | 1.86 | −0.83 | −9.47 | −3.84 | −7.27 | −12.48 | −3.31 | −3.96 | −11.62 |
| (1.16) | (0.88) | (0.2) | (−0.09) | (0.06) | (−1.04) | (−1.33) | (−0.63) | (−1.11) | |
| profitability_PMUTTM | −8.81 | −9.32 | −13.53 | −1.46 | −10.51 | −12.03 | −4.4 | −8.14 | −3.52 |
| (−1.32) | (−1.49) | (−2.31) | (−1.8) | (−2.62) | (−2.8) | (−2.79) | (−3.02) | (−0.62) | |
| profitability_roe | −0.8 | −3.05 | 2.31** | 2.8** | −1.78 | 0.81** | −1.3 | −0.14 | −1.9 |
| (0.31) | (−0.3) | (2.52) | (2.52) | (0.76) | (2.32) | (−0.36) | (0.21) | (−0.3) | |
| reversal_onemonthreturn | 4.42* | 1.16 | 9.36*** | 10.55*** | 11.03*** | 9.96*** | 5.45*** | 6.21*** | 0.28 |
| (1.76) | (0.94) | (3.58) | (4.04) | (4.11) | (3.89) | (3.68) | (3.81) | (0.66) | |
| size_mktcap | −0.36 | −2.38 | −13.89 | −0.84 | 1.03 | −6.59 | 1.78 | 1.25 | −2.7 |
| (0.08) | (−0.09) | (0.94) | (1.13) | (1.42) | (0.96) | (0.95) | (0.84) | (0.72) | |
| turnover_onemabturnover | −10.3 | −17.91 | −21.17 | −0.07 | −20.97 | −22.01 | −6.12 | −7.61 | −13.0 |
| (−0.95) | (−1.13) | (−1.2) | (0.05) | (−1.29) | (−1.19) | (−1.49) | (−0.86) | (−1.01) | |
| turnover_twelvemturnover | −4.32 | −4.96 | −7.5 | −4.38 | −3.15 | −6.92 | 1.22 | 1.24 | 2.3* |
| (0.66) | (0.57) | (0.98) | (1.01) | (0.75) | (0.94) | (0.96) | (0.93) | (1.7) | |
| value_bmratio | −3.4 | −6.74 | −17.45 | −13.5 | −13.35 | −16.03 | −3.5 | −4.06 | −4.25 |
| (0.05) | (−0.38) | (−0.52) | (−0.56) | (−0.46) | (−0.53) | (−0.74) | (−0.88) | (−1.54) | |
| value_cpratio | −1.67 | −1.92 | −19.69 | −5.9 | −15.11 | −12.62 | −0.84 | −1.84 | −4.05 |
| (0.55) | (0.64) | (0.13) | (0.0) | (0.39) | (0.4) | (0.44) | (0.52) | (0.3) | |
| value_epratio | 1.26 | −0.27 | −3.75 | −0.32 | −4.92 | −3.1 | 0.29 | −2.8 | 1.1 |
| (1.0) | (0.55) | (0.88) | (1.05) | (0.62) | (0.96) | (0.46) | (−0.93) | (0.69) | |
| volatility_MAX | −0.49 | −1.84 | −12.87 | −9.21 | −7.21 | −12.22 | −2.65 | −1.42 | −7.96 |
| (0.41) | (−0.12) | (−1.31) | (−1.0) | (−0.71) | (−1.14) | (−1.42) | (−0.7) | (−1.93) | |
| volatility_onemonthv | −4.04 | −4.11 | −9.68 | −7.51 | −10.72 | −9.39 | −2.18 | −2.5 | −3.31 |
| (−1.32) | (−0.74) | (−0.13) | (−0.09) | (−0.78) | (−0.35) | (−0.93) | (−1.08) | (−0.0) | |
| volatility_oneyearmv | −0.7 | −1.61 | −8.48 | −6.95 | −6.73 | −10.19 | −0.74 | −0.66 | −4.95 |
| (0.37) | (0.1) | (−0.05) | (−0.11) | (−0.4) | (−0.45) | (−0.04) | (−0.01) | (−0.92) | |
| volatility_sixmonthv | −2.65 | −2.85 | −6.64 | −5.05 | −5.13 | −4.26 | 0.57 | 1.12 | −1.66 |
| (0.88) | (0.82) | (1.13) | (1.02) | (1.12) | (1.35) | (0.81) | (1.04) | (−0.2) | |
| volatility_threemonthv | −5.35 | −8.67 | −8.16 | −5.78 | −9.96 | −12.27 | −2.29 | −2.08 | −6.55 |
| (−1.62) | (−1.61) | (−0.35) | (−0.13) | (−0.35) | (−1.16) | (−1.23) | (−1.08) | (−0.53) | |
| volatility_threeyearmv | −0.34 | −1.79 | −3.12 | −3.36 | −6.44 | −2.68 | 0.26 | 1.02 | −2.51 |
| (0.45) | (−0.08) | (1.05) | (0.83) | (0.01) | (1.14) | (0.55) | (1.02) | (−0.26) | |
| volatility_twelvemonthv | −3.8 | −5.19 | −12.61 | −8.02 | −12.49 | −12.51 | −1.56 | −1.42 | −2.71 |
| (−0.02) | (0.0) | (−0.25) | (−0.21) | (−0.18) | (−0.18) | (−0.43) | (−0.32) | (−0.58) | |
| volatility_twoyearmv | −3.92 | −5.7 | −9.2 | −10.37 | −9.07 | −13.03 | −0.79 | 1.0 | −4.08 |
| (−0.85) | (−1.41) | (0.62) | (−0.23) | (0.24) | (−0.05) | (0.06) | (0.86) | (−1.29) |
- Note: This table reports the Campbell and Thompson (2008) out-of-sample () statistics in percent for every factor's long–short portfolio monthly excess return expanding-window predictions based on portfolio-specific predictors, with the removal of the most extreme market fluctuation data points. The full sample starts from January 2000 to December 2021, with the first 60% of data sets as the first window's train set. The out-of-sample period starts from September 2013 to December 2021. Prediction methods are introduced in more detail in Section 3. On the basis of the Clark and West (2007) test, *, **, and *** indicate significance at the 10%, 5%, and 1% levels, respectively, for the positive statistics.
- Abbreviations: OLS, ordinary least squares; PC, principal component; PCA, principal component analysis; PLS, partial least squares.
At the same time, to provide a comparison for the results of macroeconomic variable predictions, I also recalculate statistics, based on the shortened out-of-sample period that starts from October 2015 to December 2021. Results are reported in Table 5. The reversal factor long–short portfolio maintains solid and significant predictability among models. The illiquidity factor also exhibits significant predictability in this table, but since it fails to exhibit robust predictability in Tables 3 and 4, such predictability cannot be affirmed. A summary of these results is, the reversal factor long–short portfolio exhibits solid predictability based on the portfolio-specific predictors. At the same time, all other factor portfolios, including the reversal factor's every quantile portfolio, cannot exhibit any robust predictability.
| PCA1 OLS | PCA1 VAR(1) | OLS | ElasticNet | PC | PLS | C-Simple | C-ENet | Predictor Average | |
|---|---|---|---|---|---|---|---|---|---|
| accruals_accruals | −4.08 | −2.67 | −13.64 | −1.07 | −5.77 | −3.65 | −0.3 | −3.75 | −3.0 |
| (−0.34) | (0.13) | (0.06) | (0.8) | (0.22) | (0.28) | (0.27) | (−0.59) | (0.52) | |
| accruals_noas | −3.26 | −4.43 | −8.08 | −2.83 | −6.62 | −6.0 | 0.85 | 1.56 | −7.56 |
| (1.12) | (1.0) | (1.01) | (0.74) | (0.97) | (0.78) | (0.8) | (1.15) | (0.8) | |
| illiquidity_illiquidity | −1.13 | −1.66 | 4.41** | 6.37** | 7.11** | 13.19*** | 5.82** | 6.13** | 5.78** |
| (0.02) | (−0.14) | (2.25) | (2.32) | (2.27) | (2.79) | (2.44) | (2.57) | (2.32) | |
| investment_annualassetgrowth | −0.81 | −1.46 | −3.57 | −1.43 | 2.05 | −2.07 | 1.88 | −0.21 | 5.36* |
| (0.09) | (−0.02) | (0.35) | (0.16) | (1.2) | (0.65) | (1.08) | (0.35) | (1.81) | |
| investment_quarterlyassetgrowth | −8.14 | −7.71 | −19.01 | −15.18 | −16.27 | −14.13 | −2.38 | −2.88 | −7.75 |
| (−0.01) | (0.06) | (−0.46) | (−0.97) | (−0.84) | (−1.09) | (−0.64) | (−0.78) | (−1.69) | |
| momentum_lagelemreturn | −1.0 | −1.43 | −10.36 | −3.79 | −2.99 | −2.74 | −0.09 | −0.7 | −3.16 |
| (0.26) | (0.1) | (−0.96) | (−0.1) | (0.45) | (0.46) | (0.43) | (0.18) | (−0.49) | |
| profitability_PMU | 0.07 | −1.55 | −4.19 | −1.17 | −3.4 | −2.83 | 0.21 | −2.03 | −4.92 |
| (0.54) | (0.28) | (0.72) | (0.13) | (0.34) | (0.57) | (0.52) | (−0.04) | (−0.42) | |
| profitability_PMUTTM | −11.04 | −11.89 | −10.21 | −0.12 | −6.65 | −5.14 | −1.54 | −5.25 | 3.36** |
| (−2.32) | (−2.55) | (−1.85) | (−1.06) | (−1.52) | (−1.45) | (−1.42) | (−2.38) | (2.41) | |
| profitability_roe | −2.02 | −5.55 | 1.52** | 2.27** | −1.27 | 0.47* | −1.59 | −0.66 | −2.67 |
| (−0.11) | (−1.1) | (2.08) | (2.11) | (0.91) | (1.91) | (−0.68) | (−0.21) | (−0.61) | |
| reversal_onemonthreturn | −0.12 | −0.68 | 8.66*** | 12.26*** | 12.77*** | 10.58*** | 5.23*** | 5.35*** | 8.08** |
| (0.74) | (0.62) | (3.1) | (3.66) | (3.5) | (3.53) | (3.35) | (3.3) | (2.55) | |
| size_mktcap | −1.16 | 1.66 | −14.34 | −1.14 | 7.97* | −2.95 | 5.28* | 2.2 | 7.21* |
| (−0.38) | (1.25) | (0.81) | (0.99) | (1.93) | (0.87) | (1.84) | (1.19) | (1.91) | |
| turnover_onemabturnover | −6.59 | −6.58 | −14.87 | 0.03 | −14.64 | −16.41 | −5.9 | −5.95 | −12.46 |
| (−0.34) | (−0.35) | (−1.1) | (0.35) | (−1.03) | (−1.26) | (−1.5) | (−0.83) | (−1.07) | |
| turnover_twelvemturnover | −4.81 | −4.93 | −6.87 | −6.3 | 0.74 | −5.83 | 1.08 | 1.04 | 1.89 |
| (0.64) | (0.63) | (0.65) | (0.57) | (1.23) | (0.69) | (0.9) | (0.89) | (1.36) | |
| value_bmratio | 4.32 | 3.91 | −2.05 | −0.6 | 2.52 | −2.48 | 1.71 | 1.09 | −3.62 |
| (1.07) | (1.01) | (0.96) | (0.81) | (1.39) | (0.83) | (1.15) | (0.85) | (−1.52) | |
| value_cpratio | 1.99 | 1.46 | −8.79 | 1.18 | −1.69 | −0.76 | 3.01 | 2.57 | 1.38 |
| (1.12) | (1.14) | (0.74) | (0.96) | (1.22) | (1.22) | (1.22) | (1.1) | (1.46) | |
| value_epratio | −0.71 | −1.27 | −2.13 | 0.72 | −1.45 | −1.21 | 1.31 | −0.34 | 0.34 |
| (0.43) | (0.23) | (1.1) | (1.09) | (1.06) | (1.23) | (1.13) | (0.06) | (0.58) | |
| volatility_MAX | 1.85 | 0.71 | −6.69 | −5.66 | −3.8 | −6.66 | −1.67 | −1.48 | −4.62 |
| (1.64) | (0.82) | (−0.32) | (−0.28) | (−0.33) | (−0.28) | (−1.03) | (−0.88) | (−0.86) | |
| volatility_onemonthv | −3.67 | −4.25 | −4.5 | −3.57 | −6.44 | −4.53 | −0.95 | −1.21 | −1.85 |
| (−1.24) | (−1.08) | (0.21) | (0.18) | (−0.25) | (−0.04) | (−0.25) | (−0.39) | (0.39) | |
| volatility_oneyearmv | −0.44 | −2.33 | −9.68 | −8.15 | −7.01 | −10.97 | −1.06 | −1.03 | −4.05 |
| (0.2) | (−0.58) | (−0.76) | (−0.72) | (−1.13) | (−1.14) | (−0.42) | (−0.41) | (−0.51) | |
| volatility_sixmonthv | −1.47 | −1.68 | −6.35 | −5.08 | −7.24 | −5.42 | −0.54 | −0.04 | −2.65 |
| (−0.38) | (−0.42) | (0.35) | (0.26) | (−0.16) | (0.23) | (0.01) | (0.24) | (−0.83) | |
| volatility_threemonthv | −3.09 | −5.07 | −7.53 | −5.95 | −8.01 | −8.75 | −1.49 | −1.29 | −4.93 |
| (−0.71) | (−0.83) | (−0.49) | (−0.41) | (−0.53) | (−0.82) | (−0.72) | (−0.57) | (−0.09) | |
| volatility_threeyearmv | −3.49 | −4.41 | −5.87 | −5.51 | −3.13 | −5.25 | 0.16 | 0.73 | −1.59 |
| (−0.81) | (−1.11) | (0.51) | (0.44) | (0.59) | (0.6) | (0.46) | (0.76) | (0.1) | |
| volatility_twelvemonthv | −3.47 | −4.74 | −12.47 | −6.37 | −8.64 | −11.51 | −0.86 | −0.92 | −2.39 |
| (−0.99) | (−1.22) | (−0.56) | (−0.24) | (−0.02) | (−0.4) | (−0.15) | (−0.23) | (−0.6) | |
| volatility_twoyearmv | −1.65 | −2.9 | −4.59 | −5.69 | −6.04 | −6.04 | 0.49 | 1.94 | −0.61 |
| (−0.09) | (−0.56) | (0.99) | (0.4) | (0.67) | (0.73) | (0.54) | (1.08) | (0.02) |
- Note: This table reports the Campbell and Thompson (2008) out-of-sample () statistics in percent for every factor's long–short portfolio monthly excess return expanding-window predictions based on portfolio-specific predictors. The full sample starts from January 2000 to December 2021, with the first 60% of data sets as the first window's train set. The out-of-sample period starts from September 2013 to December 2021. In this table, the sample period for statistic calculation is shortened to be from October 2015 to December 2021. Prediction methods are introduced in more detail in Section 3. On the basis of the Clark and West (2007) test, *, **, and *** indicate significance at the 10%, 5%, and 1% levels, respectively, for the positive statistics.
- Abbreviations: OLS, ordinary least squares; PC, principal component; PCA, principal component analysis; PLS, partial least squares.
4.2 Macroeconomic predictor clustering results
To implement clustering analysis towards the screened-out macroeconomic variables for each factor portfolio, the first step is to figure out whether these macroeconomic variables can be classified into clusters; in other words, whether these selected variables have cluster tendencies. This study applies Hopkins statistic to measure cluster tendency. Hopkins statistic is first developed by Hopkins and Skellam (1954) and proven effective in testing the random position hypothesis by Banerjee and Dave (2004). A Hopkins statistic close to 0 denotes a strong cluster tendency, while a Hopkins statistic close to 0.5 denotes a random distribution. Table 6 reports the Hopkins statistics for each factor's long-wing, short-wing, and long–short portfolios in the first window. It can be noticed that, for every factor, the long-wing and short-wing portfolios have much lower Hopkins statistic values than the long–short portfolio, and the short-wing portfolio generally tends to have lower Hopkins statistic than the long-wing portfolio. Furthermore, almost no factor's long–short portfolio can exhibit a clustering tendency at the 90% confidence level. The results for both “Realtime” and “Announcement” macroeconomic variables remain similar.
| LongWing | ShortWing | LongShort | LongWing | ShortWing | LongShort | ||
|---|---|---|---|---|---|---|---|
| Realtime | Announcement | ||||||
| accruals_accruals | 0.289 | 0.194 | 0.295 | accruals_accruals | 0.275 | 0.234 | 0.249 |
| accruals_noas | 0.288 | 0.180 | 0.295 | accruals_noas | 0.292 | 0.244 | 0.303 |
| illiquidity_illiquidity | 0.253 | 0.264 | 0.354 | illiquidity_illiquidity | 0.254 | 0.279 | 0.374 |
| investment_annualassetgrowth | 0.208 | 0.180 | 0.228 | investment_annualassetgrowth | 0.230 | 0.234 | 0.254 |
| investment_quarterlyassetgrowth | 0.252 | 0.222 | 0.359 | investment_quarterlyassetgrowth | 0.283 | 0.226 | 0.350 |
| momentum_lagelemreturn | 0.185 | 0.222 | 0.253 | momentum_lagelemreturn | 0.251 | 0.192 | 0.251 |
| profitability_PMU | 0.237 | 0.215 | 0.291 | profitability_PMU | 0.264 | 0.229 | 0.291 |
| profitability_PMUTTM | 0.245 | 0.205 | 0.255 | profitability_PMUTTM | 0.270 | 0.227 | 0.261 |
| profitability_roe | 0.183 | 0.220 | 0.338 | profitability_roe | 0.207 | 0.234 | 0.353 |
| reversal_onemonthreturn | 0.221 | 0.235 | 0.379 | reversal_onemonthreturn | 0.252 | 0.229 | 0.355 |
| size_mktcap | 0.210 | 0.247 | 0.343 | size_mktcap | 0.186 | 0.279 | 0.304 |
| turnover_onemabturnover | 0.250 | 0.193 | 0.334 | turnover_onemabturnover | 0.256 | 0.231 | 0.361 |
| turnover_twelvemturnover | 0.272 | 0.192 | 0.343 | turnover_twelvemturnover | 0.295 | 0.229 | 0.348 |
| value_bmratio | 0.217 | 0.228 | 0.365 | value_bmratio | 0.243 | 0.259 | 0.378 |
| value_cpratio | 0.255 | 0.268 | 0.288 | value_cpratio | 0.259 | 0.265 | 0.299 |
| value_epratio | 0.205 | 0.223 | 0.431 | value_epratio | 0.255 | 0.243 | 0.423 |
| volatility_MAX | 0.292 | 0.221 | 0.378 | volatility_MAX | 0.310 | 0.246 | 0.329 |
| volatility_onemonthv | 0.275 | 0.175 | 0.351 | volatility_onemonthv | 0.285 | 0.233 | 0.365 |
| volatility_oneyearmv | 0.292 | 0.171 | 0.309 | volatility_oneyearmv | 0.288 | 0.252 | 0.327 |
| volatility_sixmonthv | 0.284 | 0.165 | 0.337 | volatility_sixmonthv | 0.311 | 0.170 | 0.317 |
| volatility_threemonthv | 0.296 | 0.171 | 0.318 | volatility_threemonthv | 0.298 | 0.210 | 0.338 |
| volatility_threeyearmv | 0.262 | 0.192 | 0.372 | volatility_threeyearmv | 0.266 | 0.244 | 0.401 |
| volatility_twelvemonthv | 0.264 | 0.210 | 0.322 | volatility_twelvemonthv | 0.274 | 0.250 | 0.364 |
| volatility_twoyearmv | 0.267 | 0.173 | 0.401 | volatility_twoyearmv | 0.279 | 0.248 | 0.414 |
- Note: This table reports the Hopkins and Skellam (1954) Hopkins statistics for each factor's long-wing portfolio, short-wing portfolio and long–short portfolio macroeconomic variable predictors. The results of both the real-time macroeconomic variables and the updated-when-announced macroeconomic variables are included in this table. The full sample starts from May 2006 to December 2021, with the first 60% of data sets as the first window's train set. The sample period for this table starts from May 2006 to September 2015. A value lower than 0.25 indicates a clustering tendency at the 90% confidence level.
Table 7 reports for reversal factor monthly long–short portfolio excess return predictions, based on the clustering algorithms and corresponding prediction methods introduced in Section 3 and macroeconomic variable predictors introduced in Section 2. It can be noticed that the “Realtime” predictors generally generate higher and more significant than the “Announcement” predictors. This is not surprising since the former contains information that has happened but is not yet available to the market, such that the prediction results are based on the most up-to-date information. However, these clustering prediction methods fail to provide stable and robust predictions even for this most predictable factor portfolio. Such a result also matches the insignificant clustering tendency for the reversal factor's long–short portfolio, as is shown in Table 6. In summary, no factor portfolio can exhibit robust predictability using clustering analysis methods.
| K-Means | Birch | Gaussian Mixture | Spectral Clustering | Agglomerative Clustering | Many Method Combination | |
|---|---|---|---|---|---|---|
| Realtime 2 Cluster | 6.11** | 6.07** | 4.21* | 0.06 | 4.87* | 7.45** |
| (2.18) | (2.26) | (1.76) | (0.28) | (1.75) | (2.35) | |
| Realtime 3 Cluster | 8.1** | 4.41* | 0.43 | −0.48 | 7.6** | 11.31*** |
| (2.5) | (1.81) | (1.04) | (−0.88) | (2.23) | (2.93) | |
| Realtime 4 Cluster | 4.17* | 3.08* | 2.96 | −3.1 | 7.67** | 6.52** |
| (1.78) | (1.72) | (1.35) | (−1.02) | (2.35) | (2.25) | |
| Announcement 2 Cluster | 3.19 | 2.23 | −3.5 | 0.27 | 4.52* | 2.82 |
| (1.45) | (1.45) | (−0.24) | (0.69) | (1.82) | (1.48) | |
| Announcement 3 Cluster | 6.32** | 2.89 | 1.03 | −0.32 | 5.96* | 4.03 |
| (2.0) | (1.51) | (1.21) | (−0.48) | (1.93) | (1.57) | |
| Announcement 4 Cluster | 4.68* | 0.18 | −1.18 | −0.55 | 6.85** | −0.81 |
| (1.72) | (1.02) | (0.81) | (−0.57) | (2.15) | (1.0) |
- Note: This table reports the Campbell and Thompson (2008) out-of-sample () statistics in percent for reversal factor long–short portfolio monthly excess return expanding-window predictions based on macroeconomic variable predictors and clustering algorithms. The full sample starts from May 2006 to December 2021, with the first 60% of data sets as the first window's train set. The out-of-sample period starts from October 2015 to December 2021. Clustering algorithms are introduced in more detail in Section 3. On the basis of the Clark and West (2007) test, *, **, and *** indicate significance at the 10%, 5%, and 1% levels, respectively, for the positive statistics.
4.3 Macroeconomic predictor regression results
Table 8 reports for monthly factor long–short portfolio excess return predictions, based on regression methods introduced in Section 3 and macroeconomic variable predictors introduced in Section 2. The “Announcement” macroeconomic variable predictors are applied in the regressions to avoid the future information problem. Reversal, size, and illiquidity factors exhibit strong predictability among regression models. Comparing the reversal factor prediction performance result with Table 7, macroeconomic variables still contain predictive components towards reversal factor premium, while at the same time, parametric models appear to work better in predicting returns than those nonparametric clustering-and-taking-average prediction methods. Another possible explanation is that there exists a solid but complex system of mechanisms between selected predictors and the reversal factor premium, but those predictors themselves do not exhibit simultaneity such that they have no significant clustering tendency. Moreover, comparing this table with Table 5, it can be noticed that the size factor's predictability is not robust across predictors; the illiquidity factor, as is explained before, cannot be robustly predicted across sample periods. The reversal factor premium stands out and exhibits the most robust predictability across models, predictors, and sample periods. Nonetheless, all factors' quantile portfolios still cannot exhibit predictability.
| PCA1 OLS | PCA1 VAR(1) | OLS | ElasticNet | PC | PLS | C-Simple | C-ENet | Predictor Average | |
|---|---|---|---|---|---|---|---|---|---|
| accruals_accruals | −2.95 | −1.65 | −10.19 | 2.42** | −0.24 | −0.95 | 0.33 | 1.11 | −5.52 |
| (0.92) | (1.04) | (2.14) | (2.08) | (1.44) | (2.07) | (0.79) | (1.07) | (−0.41) | |
| accruals_noas | 6.25 | 5.13 | −3.63 | −3.27 | 0.64 | 4.64 | 3.78 | 2.24 | 6.28** |
| (1.55) | (1.39) | (1.23) | (0.37) | (1.34) | (1.5) | (1.42) | (1.05) | (2.24) | |
| illiquidity_illiquidity | 11.25** | 11.62** | 1.4*** | 0.92** | −3.6 | 7.17** | 5.51* | 4.28** | 3.66 |
| (2.36) | (2.43) | (2.61) | (2.44) | (1.71) | (2.36) | (1.93) | (2.22) | (1.63) | |
| investment_annualassetgrowth | −10.07 | −11.04 | −8.61 | −7.68 | −6.02 | −9.88 | −3.22 | −3.02 | −2.93 |
| (−1.17) | (−1.22) | (−0.13) | (−0.43) | (−0.21) | (−0.98) | (−0.85) | (−0.67) | (−0.28) | |
| investment_quarterlyassetgrowth | −9.74 | −9.44 | −12.72 | −6.55 | −8.82 | −11.84 | −3.2 | −4.5 | −9.02 |
| (−0.39) | (−0.18) | (−0.8) | (−1.65) | (−0.51) | (−0.68) | (−1.35) | (−0.63) | (−0.4) | |
| momentum_lagelemreturn | −3.6 | −4.11 | −17.42 | −6.6 | −3.97 | −3.76 | −1.24 | −0.42 | −3.0 |
| (0.27) | (0.19) | (−0.19) | (−0.11) | (0.3) | (0.31) | (0.33) | (0.66) | (0.56) | |
| profitability_PMU | −9.13 | −10.14 | −13.74 | −3.36 | −14.34 | −11.14 | −3.11 | −1.8 | −3.05 |
| (−0.41) | (−0.61) | (−0.52) | (0.69) | (−1.18) | (−0.3) | (−0.49) | (−0.09) | (0.46) | |
| profitability_PMUTTM | −4.44 | −4.09 | −10.86 | −3.93 | −10.0 | −5.19 | −3.24 | −2.45 | −3.29 |
| (−0.21) | (−0.24) | (0.09) | (0.05) | (−0.59) | (0.37) | (−1.31) | (−0.98) | (−0.84) | |
| profitability_roe | −9.22 | −7.49 | −23.27 | −15.14 | −14.28 | −18.6 | −5.3 | −5.93 | −9.61 |
| (−1.53) | (−0.85) | (−1.65) | (−1.47) | (−0.79) | (−1.42) | (−1.83) | (−1.85) | (−1.12) | |
| reversal_onemonthreturn | 6.22** | 5.64** | 13.19*** | 9.38*** | 8.62*** | 8.79*** | 5.48*** | 5.38** | 10.86*** |
| (2.57) | (2.46) | (3.44) | (3.48) | (2.77) | (2.89) | (2.87) | (2.45) | (2.96) | |
| size_mktcap | 12.37** | 13.95** | −5.37 | 2.4* | 11.85** | 12.68** | 8.19* | 6.18* | 7.95* |
| (2.02) | (2.17) | (2.04) | (1.94) | (2.24) | (2.16) | (1.75) | (1.72) | (1.74) | |
| turnover_onemabturnover | −13.48 | −13.17 | −27.47 | −12.83 | −19.49 | −18.98 | −3.53 | −1.94 | −12.28 |
| (−1.25) | (−1.18) | (−0.26) | (0.3) | (−0.17) | (−0.27) | (−0.59) | (−0.06) | (−0.28) | |
| turnover_twelvemturnover | 0.82 | 1.12 | −5.49 | −2.48 | −0.61 | −1.74 | 2.52 | 2.35 | 0.82 |
| (1.12) | (1.28) | (1.34) | (1.06) | (1.26) | (1.57) | (1.3) | (1.25) | (1.12) | |
| value_bmratio | −5.54 | −6.6 | −12.53 | −1.15 | −8.35 | −11.26 | −0.06 | −1.0 | −3.95 |
| (−0.52) | (−0.81) | (0.26) | (0.37) | (0.2) | (−0.09) | (0.39) | (0.19) | (−0.95) | |
| value_cpratio | −15.48 | −14.8 | −45.2 | −17.1 | −40.07 | −36.11 | −8.3 | −11.37 | −3.83 |
| (−0.25) | (−0.25) | (−1.6) | (−1.42) | (−1.39) | (−1.16) | (−1.4) | (−1.62) | (−0.36) | |
| value_epratio | −7.09 | −6.91 | −21.53 | −5.88 | −15.09 | −23.52 | −2.37 | −4.67 | −2.36 |
| (−0.42) | (−0.47) | (−0.4) | (0.44) | (−0.31) | (−0.7) | (−0.31) | (−0.85) | (0.07) | |
| volatility_MAX | 0.37 | −0.96 | −6.52 | −5.04 | 1.09* | −0.17 | 2.35 | 1.74 | −1.62 |
| (0.77) | (0.56) | (1.5) | (1.25) | (1.68) | (1.49) | (1.35) | (1.14) | (0.25) | |
| volatility_onemonthv | −0.24 | −2.78 | −3.27 | −2.96 | −2.53 | −1.59 | 1.64 | 0.71 | −3.32 |
| (0.56) | (0.12) | (1.47) | (1.23) | (1.04) | (1.26) | (1.24) | (0.79) | (−1.18) | |
| volatility_oneyearmv | 0.17 | −2.63 | −16.73 | −2.6 | 0.49 | −6.23 | 1.7 | 1.17 | −1.61 |
| (0.76) | (0.35) | (0.78) | (1.02) | (0.82) | (0.63) | (1.11) | (0.97) | (−0.65) | |
| volatility_sixmonthv | 2.74 | 1.96 | −3.27 | 2.38* | 0.13* | 3.58* | 3.18 | 3.35* | −1.66 |
| (1.34) | (1.2) | (1.72) | (1.8) | (1.69) | (1.93) | (1.6) | (1.66) | (−0.32) | |
| volatility_threemonthv | −1.24 | −2.35 | −5.65 | −2.78 | −4.81 | −0.58 | 0.96 | 1.15 | −1.9 |
| (0.31) | (0.18) | (1.38) | (1.3) | (0.77) | (1.09) | (0.95) | (1.19) | (−0.37) | |
| volatility_threeyearmv | −0.78 | −1.53 | −12.15 | −10.34 | −4.01 | −5.25 | 1.73 | 0.2 | −3.14 |
| (0.58) | (0.47) | (0.95) | (0.68) | (1.46) | (1.07) | (1.13) | (0.59) | (−0.03) | |
| volatility_twelvemonthv | 2.22 | 0.15 | −1.18 | 2.66 | 1.11 | −0.01 | 2.91 | 2.43 | −1.17 |
| (1.34) | (1.01) | (1.71) | (1.5) | (1.31) | (1.38) | (1.36) | (1.3) | (0.01) | |
| volatility_twoyearmv | 1.42 | 0.12 | −5.37 | −0.71 | −0.21 | −3.1 | 3.18 | 3.48* | 1.71 |
| (0.95) | (0.71) | (1.79) | (1.77) | (1.63) | (1.52) | (1.62) | (1.75) | (0.96) |
- Note: This table reports the Campbell and Thompson (2008) out-of-sample () statistics in percent for every factor's long–short portfolio monthly excess return expanding-window predictions based on macroeconomic variable predictors and prediction methods. The full sample starts from May 2006 to December 2021, with the first 60% of data sets as the first window's train set. The out-of-sample period starts from October 2015 to December 2021. Prediction methods are introduced in more detail in Section 3. On the basis of the Clark and West (2007) test, *, **, and *** indicate significance at the 10%, 5%, and 1% levels, respectively, for the positive statistics.
- Abbreviations: OLS, ordinary least squares; PC, principal component; PCA, principal component analysis; PLS, partial least squares.
5 FURTHER ANALYSIS
5.1 Market neutralization analysis
The empirical results in Section 4 show that all factors' all quantile portfolios cannot be well predicted. From Table 2, all these portfolios have their market betas very significant and close to 1. Can market return be predicted? Dong et al. (2022) use factor long–short portfolio returns to predict the market excess return and find significant predictability in the US stock market. However, a broader replication work among 42 markets, including the Chinese stock market, done by Cakici et al. (2024) doubts this conclusion. Suppose the market excess return cannot be predicted. In that case, a better way to predict quantile portfolio returns is to accept the market return component is unpredictable, neutralize the market return from quantile portfolio returns, and then try to predict the residuals of these quantile portfolio returns.
This section, therefore, starts by predicting the Chinese stock market's monthly excess return. Table 9 reports for monthly market excess return predictions based on regression methods introduced in Section 3. Besides the factor long–short portfolio returns as predictors, this study also conduct trials with the “Announcement” macroeconomic variables as predictors. Similar to the findings of Cakici et al. (2024), none of the long-wing, short-wing, or long–short factor portfolio returns or factor category portfolio returns can effectively predict the market excess return. Predictions based on macroeconomic variable predictors exhibit significant predictability in ElasticNet and PLS models while bringing a very negative in the PC model. The market excess return predictability in the Chinese stock market still cannot be assured.
| PCA1 OLS | PCA1 VAR(1) | OLS | ElasticNet | PC | PLS | C-Simple | C-ENet | Predictor Average | |
|---|---|---|---|---|---|---|---|---|---|
| Factor LongWing | −1.66 | −3.44 | −41.79 | −11.04 | −2.52 | −1.99 | −1.43 | −1.5 | −1.68 |
| (−0.19) | (0.12) | (−0.41) | (−0.77) | (−0.53) | (−0.17) | (−0.27) | (−0.12) | (−0.2) | |
| Factor ShortWing | −1.03 | −8.77 | −23.88 | −0.53 | 0.89 | −0.98 | −0.9 | −0.41 | −1.03 |
| (−0.12) | (−0.15) | (−0.05) | (−1.79) | (0.89) | (−0.03) | (−0.15) | (0.09) | (−0.11) | |
| Factor Longshort | −2.03 | −3.97 | −20.72 | −1.38 | 0.24 | −11.97 | −0.54 | −0.99 | −2.11 |
| (−1.23) | (−0.38) | (−0.37) | (0.32) | (0.97) | (0.56) | (−0.64) | (0.6) | (−1.38) | |
| Category LongWing | −1.71 | −3.57 | −14.19 | −11.0 | −2.04 | −1.78 | −1.45 | −1.84 | −1.73 |
| (−0.24) | (0.18) | (0.3) | (−0.99) | (0.32) | (−0.17) | (−0.28) | (−0.37) | (−0.25) | |
| Category ShortWing | −1.18 | −8.71 | −8.33 | −1.25 | 1.63 | −1.08 | −0.96 | −1.05 | −1.17 |
| (−0.14) | (0.01) | (−0.5) | (−2.43) | (0.9) | (−0.03) | (−0.12) | (−0.1) | (−0.14) | |
| Category Longshort | −1.59 | −2.22 | −5.97 | −1.07 | 0.98 | −1.45 | 0.34 | −0.74 | −1.51 |
| (−2.12) | (−0.05) | (0.5) | (−0.03) | (1.11) | (1.04) | (0.49) | (0.51) | (−1.77) | |
| Macro Realtime | 1.83 | −0.72 | −23.37 | 2.51** | 4.23** | 3.37** | 5.56** | 5.46** | −2.45 |
| (1.45) | (0.85) | (2.64) | (2.15) | (1.98) | (2.2) | (2.18) | (2.55) | (−2.46) | |
| Macro Announcement | 2.11 | −0.56 | −15.04 | 4.84*** | −5.21 | 11.01** | 5.6** | 6.49** | 0.01 |
| (1.5) | (0.94) | (3.02) | (2.58) | (1.43) | (2.55) | (2.21) | (2.37) | (0.41) |
- Note: This table reports the Campbell and Thompson (2008) out-of-sample () statistics in percent for monthly market excess return expanding-window predictions. The full sample starts from May 2006 to December 2021, with the first 60% of data sets as the first window's train set. The out-of-sample period starts from October 2015 to December 2021. Predictors include all factors' long–short portfolio performance, all factor categories' aggregated long–short portfolio performance, and macroeconomic variables. Prediction methods are introduced in more detail in Section 3. On the basis of the Clark and West (2007) test, *, **, and *** indicate significance at the 10%, 5%, and 1% levels, respectively, for the positive statistics.
- Abbreviations: OLS, ordinary least squares; PC, principal component; PCA, principal component analysis; PLS, partial least squares.
Table 10 reports for monthly size and reversal excess return predictions based on regression methods introduced in Section 3>. The reversal factor premium still maintains robust predictability after market neutralization. However, neither long-wing nor short-wing portfolios can benefit from market neutralization and exhibit predictability. On the other hand, the size factor long-wing portfolio exhibits very strong and robust predictability. Furthermore, comparing this table with Tables 5 and 8, we can find a considerable improvement in predictability for the size factor premium. Nonetheless, market neutralization cannot benefit any other factor's quantile portfolio predictability.
| PCA1 OLS | PCA1 VAR(1) | OLS | ElasticNet | PC | PLS | C-Simple | C-ENet | Predictor Average | |
|---|---|---|---|---|---|---|---|---|---|
| Size predictor | |||||||||
| LongWing | 2.86* | 4.39* | 10.18*** | 6.23*** | 4.81 | 4.88* | 3.54** | 2.46* | 0.68 |
| (1.72) | (1.87) | (2.85) | (2.87) | (1.48) | (1.92) | (1.97) | (1.77) | (0.89) | |
| ShortWing | 0.49 | 1.9 | −1.98 | −5.28 | 8.49*** | 7.0*** | 7.12*** | 8.82*** | 9.52*** |
| (1.27) | (1.64) | (2.35) | (0.8) | (3.1) | (2.83) | (2.73) | (2.87) | (3.12) | |
| LongShort | −36.55 | −28.5 | −11.09 | −8.02 | −14.65 | −19.37 | −3.92 | −2.21 | −25.21 |
| (−2.6) | (−1.93) | (1.51) | (0.92) | (0.37) | (−0.06) | (−0.73) | (0.06) | (−1.39) | |
| Size macro | |||||||||
| LongWing | 12.89*** | 14.95** | 1.39*** | 8.63*** | 11.68*** | 13.82*** | 10.78*** | 13.8** | 8.07* |
| (2.58) | (2.57) | (2.86) | (2.9) | (2.65) | (2.78) | (2.79) | (2.5) | (1.89) | |
| ShortWing | 12.11*** | 10.99*** | −42.5 | −1.65 | −15.15 | 1.59*** | 9.9*** | 7.36** | 7.28*** |
| (3.1) | (2.99) | (1.42) | (0.64) | (1.91) | (2.62) | (2.73) | (2.06) | (2.91) | |
| LongShort | 14.83*** | 16.69*** | −0.58 | 6.9** | 13.22*** | 15.41*** | 11.54*** | 12.66*** | 8.89* |
| (2.64) | (2.68) | (2.84) | (2.53) | (2.76) | (2.77) | (2.77) | (2.89) | (1.8) | |
| Reversal predictor | |||||||||
| LongWing | −5.28 | −6.5 | 0.73 | 3.19 | 3.42 | 4.41* | 3.46* | 1.42 | −3.91 |
| (−0.53) | (−0.62) | (1.26) | (1.59) | (1.54) | (1.69) | (1.79) | (0.99) | (−2.08) | |
| ShortWing | −2.7 | −2.45 | −2.96 | −0.25 | −2.62 | −3.95 | −1.49 | 0.68 | −3.54 |
| (−0.3) | (−0.19) | (0.15) | (−1.33) | (0.0) | (−0.27) | (−0.26) | (0.85) | (−0.2) | |
| LongShort | −1.6 | −2.81 | 5.2** | 9.31*** | 8.24*** | 7.45*** | 5.51*** | 5.32*** | 8.95*** |
| (0.29) | (0.08) | (2.38) | (3.23) | (2.87) | (2.92) | (2.92) | (3.07) | (2.91) | |
| Reversal macro | |||||||||
| LongWing | 0.38 | −0.11 | −23.87 | −12.15 | −5.24 | −13.15 | 0.28 | −1.4 | −2.3 |
| (1.04) | (1.06) | (−0.07) | (0.23) | (0.35) | (0.24) | (0.56) | (0.13) | (0.98) | |
| ShortWing | −2.26 | −3.35 | −5.75 | −3.3 | −3.64 | −3.46 | −1.38 | 2.01 | −3.12 |
| (−0.22) | (−0.48) | (−0.6) | (−0.99) | (−0.24) | (−0.36) | (−0.37) | (0.94) | (−0.34) | |
| LongShort | 6.32*** | 5.64*** | 5.01** | 4.67*** | 6.47*** | 6.82*** | 4.79*** | 3.98** | 8.87*** |
| (2.77) | (2.68) | (2.49) | (2.8) | (2.83) | (2.9) | (2.79) | (2.3) | (3.08) |
- Note: This table reports the Campbell and Thompson (2008) out-of-sample () statistics in percent for size factor and reversal factor's long–short portfolio monthly excess return expanding-window predictions. Factor portfolio monthly excess returns are market neutralized: , where is obtained by regressing the factor portfolio's daily return series in the past 252 days in the market return series and a constant term: . The full sample starts from May 2006 to December 2021, with the first 60% of data sets as the first window's train set. The out-of-sample period starts from October 2015 to December 2021. Both portfolio-specific predictors and macroeconomic variables are, respectively, applied in the prediction. Prediction methods are introduced in more detail in Section 3. On the basis of the Clark and West (2007) test, *, **, and *** indicate significance at the 10%, 5%, and 1% levels, respectively, for the positive statistics.
- Abbreviations: OLS, ordinary least squares; PC, principal component; PCA, principal component analysis; PLS, partial least squares.
5.2 Predictor importance analysis
How is the reversal factor premium so well predicted? The variable screening result (methodology introduced in Section 3 Part C) can provide us with insights into this question. It can be observed from Figure 3 that, for both portfolio-specific predictors and macroeconomic variable predictors, predictor categories that summarize historical factor portfolio performance and market performance commonly appear across the entire out-of-sample periods. More specifically, historical factor portfolio return and volatility measurements, historical market volatility measurements, and all factor portfolio aggregated return and volatility measurements play the most crucial role.
Besides the predictor category analysis, this study also implements a gradient-based method to analyze each predictor's strength and direction towards the final prediction. A similar method has been implemented in many studies about return predictability, including Gu et al. (2020) and Kaniel et al. (2023). However, most of these literature apply very complex neutral network models and set many constrains and assumptions when testing predictor importance (e.g., test the output of y with different values of the target variable and set other variables to be at its mean). This study, on the other hand, can directly provide predictor importance measurements without any constraint, as most models are linear and their coefficients naturally serve as the gradient-based variable importance measurements. Since this study is implemented on an expanding-sample basis, predictor importance test should be aggregated across all windows, which ensures the result to be robust across the entire sample period.
To analyze each predictor's strength towards the final prediction, this study selects ElasticNet, PC, and PLS models and summarizes their variable shrinkage and selection results. For the ElasticNet model, in each window, coefficients of the model after training are collected. Since predictors in any training data set have all been standardized, the absolute value of the coefficient for each predictor can reflect the contribution of the predictor towards the final prediction and can be directly compared with other predictors within the window. For the PC model, the contribution of each predictor can be obtained by the inverse projection of the absolute value of coefficients onto the target predictor with the PC transformation matrix. For the PLS model, this study applies the Variable Importance in Projection (VIP) score raised by Wold et al. (1993). The VIP method gives predictors that can best explain the variance of the prediction target higher scores and becomes prevalent in variable importance analysis for the PLS model. To aggregate the result from all three models, in each window and for each model, scores for all predictors are rescaled to have their sum to be 1. This study gives all three models the same weight and all windows the same weight, and scores for all predictors can be obtained by the double weighted sum aggregation.
Results of the predictor importance test are provided in Figure 4. Consistent with previous findings, not only can most of the volatility measurements pass the variable screening test, but they also play the most important roles in reversal factor premium prediction. It should be noticed that the portfolio book-to-market ratio also appears to be a strong predictor towards the portfolio return. From a behavioral perspective, a portfolio with a lower book-to-market ratio will contain more growth stocks and less value stocks, and hence tends to react more irrationally towards historical economic shocks. Therefore, such portfolio should behave stronger reversal effect than other portfolios with higher book-to-market ratios. With the result in Figure 4, it is natural to conjecture that the book-to-market ratio should negatively predict the portfolio return.
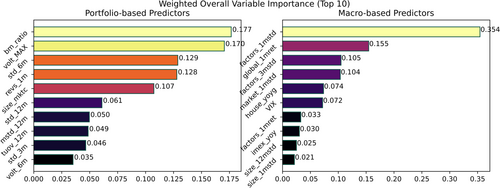
Following the conjecture, this study provides a further analysis towards predictors' prediction directions towards the portfolio return. The methodology is similar to the previous predictor importance test, except that it is now the original values, instead of the rescaled absolute values, of coefficients that are aggregated across all windows. Figure 5 shows the results for the ElasticNet and PC models and for both types of predictors. Consistent with the previous conjecture, the book-to-market ratio indeed negatively predicts the reversal factor premium in the ElasticNet model. An interesting finding is that most volatility measurements in both types of predictors consistently and positively predict the portfolio return in both models. A possible explanation for this strong and positive predictability is that when the Chinese stock market is more volatile, it is a common practice for the government to instruct state-backed funds (“National Teams”) to inject capital and stabilize the market. It is reasonable to expect such operations will bring a more positive shock to those “past loser” stocks than those “past winner” stocks and hence will directly contribute to a positive reversal factor premium. With the significant empirical phenomenon shown in this study, this conjecture about the mechanism beneath this strong predictability will be an exciting topic for future research to explore.
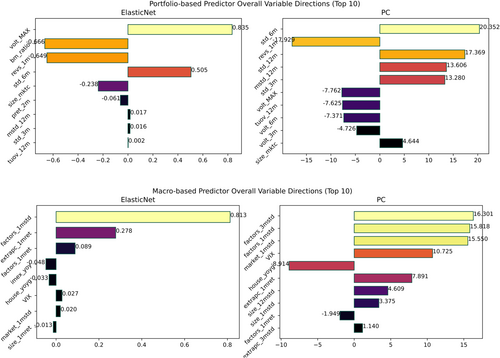
6 STRATEGY PERFORMANCE
Inspired by the previous results, this section discusses whether the strong predictability of the reversal factor premium has been arbitraged away by the market participants. As is observed in Table 1, the simple buy-and-hold strategy in the entire sample brings an annualized return of 9.42%, which deviates from 0 at the 0.1 significance level. A straightforward strategy towards this portfolio is to long the portfolio when a regression model prediction yields a positive value and to short the portfolio when a regression model prediction yields a negative value. To better match the previous empirical results in Tables 3, 4, 5, and 8, this study also constructs this simple strategy based on: (1) full-sample portfolio-specific predictor predictions, (2) portfolio-specific predictor predictions with the removal of the most extreme portfolio returns, (3) portfolio-specific predictor predictions with the time period on or after October 2015, and (4) macroeconomic variable prediction predictions. The sample period for the first two strategies is from September 2013 to December 2021, while the sample period for the last two strategies is from October 2015 to December 2021.
Table 11 reports the mean monthly return and Sharpe ratio for these strategies. It can be noticed that ElasticNet, PC, PLS, and even OLS models work out pretty well, with significant mean returns and much higher Sharpe ratios than the simple buy-and-hold strategy. To better illustrate the economic gain from this strong predictability, Figure 6 visualizes the cumulative return of the strategy based on the simple OLS model with portfolio-specific predictors. The sample period in this figure starts from September 2013 to December 2021. Since the 2015 Chinese stock market crash is included in this figure, this simple strategy encounters a massive drawdown during the bubble period in late 2014. However, this strategy still recovers after the financial crisis. With its accurate prediction, especially during COVID-19, this strategy obtains a much higher cumulative return than the simple buy-and-hold strategy till the end. Moreover, since the reversal factor long–short portfolio is reconstituted monthly, this strategy naturally has a very low turnover ratio. Therefore, it bears very low transaction or execution costs that will not affect this strategy's robust profitability.
| Buy and hold | PCA1 OLS | PCA1 VAR(1) | OLS | ElasticNet | PC | PLS | C-Simple | C-ENet | Predictor Average | |
|---|---|---|---|---|---|---|---|---|---|---|
| Predictor-FullSample | ||||||||||
| Mean return | 0.851 | 0.823 | 0.268 | 1.811** | 1.392* | 1.468* | 0.93 | 1.101 | 0.984 | 0.836 |
| (1.109) | (1.072) | (0.348) | (2.413) | (1.832) | (1.936) | (1.213) | (1.441) | (1.285) | (1.088) | |
| Sharpe ratio | 0.384 | 0.371 | 0.12 | 0.836 | 0.635 | 0.671 | 0.42 | 0.499 | 0.445 | 0.377 |
| Predictor-ExtremeRemove | ||||||||||
| Mean return | 1.017 | 1.46** | 0.894 | 2.469*** | 2.041*** | 2.119*** | 1.57** | 1.744*** | 1.625** | 1.002 |
| (1.598) | (2.327) | (1.401) | (4.155) | (3.342) | (3.485) | (2.512) | (2.813) | (2.607) | (1.573) | |
| Sharpe ratio | 0.559 | 0.814 | 0.49 | 1.454 | 1.169 | 1.22 | 0.879 | 0.984 | 0.912 | 0.55 |
| Predictor-After201509 | ||||||||||
| Mean return | 0.765 | 0.972 | 0.745 | 1.909*** | 1.762*** | 1.887*** | 1.378** | 1.205* | 0.986 | 1.362** |
| (1.195) | (1.527) | (1.163) | (3.144) | (2.874) | (3.103) | (2.2) | (1.91) | (1.55) | (2.174) | |
| Sharpe ratio | 0.478 | 0.611 | 0.465 | 1.258 | 1.15 | 1.241 | 0.88 | 0.764 | 0.62 | 0.869 |
| Macro-FullSample | ||||||||||
| Mean return | 0.765 | 0.882 | 0.995 | 1.521** | 1.559** | 1.472** | 1.544** | 1.043 | 0.67 | 1.336** |
| (1.195) | (1.381) | (1.564) | (2.446) | (2.513) | (2.36) | (2.486) | (1.643) | (1.044) | (2.128) | |
| Sharpe ratio | 0.478 | 0.552 | 0.626 | 0.978 | 1.005 | 0.944 | 0.994 | 0.657 | 0.418 | 0.851 |
- Note: This table reports mean monthly returns (in percentage), t statistics (in brackets), and annualized Sharpe ratio for each strategy based on reversal factor long–short portfolio predictions. The strategy is simply longing the long–short portfolio when the prediction result for one window is positive, and shorting the long–short portfolio when the prediction result for the window is negative. Both portfolio-specific predictors and macroeconomic variables are, respectively, applied in the prediction. The sample period for the first two subtables starts from September 2013 to December 2021. The sample period for the last two subtables starts from October 2015 to December 2021. Prediction methods are introduced in more detail in Section 3.
- Abbreviations: OLS, ordinary least squares; PC, principal component; PCA, principal component analysis; PLS, partial least squares.
- * Significant at the 0.10 level
- ** significant at the 0.05 level
- *** significant at the 0.01 level.
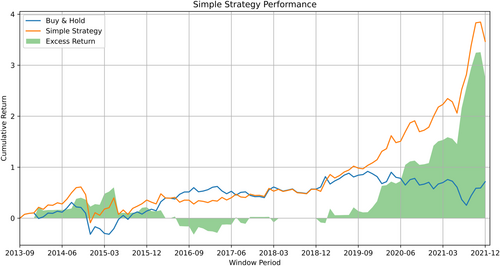
Table 12 further decomposes these strategy returns by the Liu et al. (2019) CH-3 model. The simple buy-and-hold strategy cannot obtain a significant alpha in the sample period. In contrast, strategies based on OLS, ElasticNet, PC, or PLS model predictions generally obtain significant alphas. For example, the strategy performance shown in Figure 6 generates a significant annualized 20.4% CH-3 alpha, compared with the insignificant 9.6% CH-3 alpha from the simple buy-and-hold strategy. Moreover, the strategy performance's exposure to CH-3 factors does not exhibit significance or robustness, indicating that the CH-3 model cannot explain this strategy's performance.
| Buy and hold | PCA1 OLS | PCA1 VAR(1) | OLS | ElasticNet | PC | PLS | C-Simple | C-ENet | Predictor Average | |
|---|---|---|---|---|---|---|---|---|---|---|
| Predictor-FullSample | ||||||||||
| Alpha | 0.008 | 0.007 | 0.001 | 0.017*** | 0.013* | 0.013** | 0.008 | 0.009 | 0.008 | 0.008 |
| (1.164) | (1.002) | (0.156) | (2.731) | (1.895) | (2.056) | (1.279) | (1.322) | (1.181) | (1.091) | |
| Beta-MKT | −0.26 | −0.112 | −0.065 | −0.137 | −0.095 | −0.11 | −0.116 | −0.066 | −0.079 | −0.21 |
| (−2.206) | (−1.002) | (−0.553) | (−1.351) | (−0.858) | (−1.025) | (−1.065) | (−0.594) | (−0.709) | (−1.737) | |
| Beta-SMB | 0.368*** | 0.336*** | 0.325** | 0.302*** | 0.244** | 0.283** | 0.204* | 0.422*** | 0.38*** | 0.337*** |
| (2.964) | (2.851) | (2.612) | (2.814) | (2.087) | (2.503) | (1.784) | (3.627) | (3.239) | (2.647) | |
| Beta-VMG | 0.088 | −0.214 | −0.127 | −0.361 | −0.325 | −0.329 | −0.425 | −0.116 | −0.163 | 0.099 |
| (0.6) | (−1.539) | (−0.871) | (−2.862) | (−2.367) | (−2.476) | (−3.162) | (−0.846) | (−1.185) | (0.661) | |
| R2 | 0.174 | 0.252 | 0.178 | 0.355 | 0.251 | 0.296 | 0.295 | 0.267 | 0.257 | 0.132 |
| Adjusted R2 | 0.148 | 0.229 | 0.152 | 0.335 | 0.228 | 0.274 | 0.273 | 0.244 | 0.234 | 0.104 |
| Predictor-ExtremeRemove | ||||||||||
| Alpha | 0.009 | 0.012* | 0.006 | 0.021*** | 0.018*** | 0.018*** | 0.013** | 0.014** | 0.013** | 0.009 |
| (1.344) | (1.877) | (0.999) | (3.798) | (2.936) | (3.065) | (2.125) | (2.318) | (2.124) | (1.342) | |
| Beta-MKT | −0.012 | 0.066 | 0.151 | 0.017 | 0.102 | 0.066 | 0.059 | 0.12 | 0.106 | 0.069 |
| (−0.098) | (0.585) | (1.288) | (0.165) | (0.927) | (0.61) | (0.537) | (1.099) | (0.955) | (0.584) | |
| Beta-SMB | 0.221* | 0.26** | 0.229** | 0.237** | 0.157 | 0.207** | 0.127 | 0.342*** | 0.3*** | 0.174 |
| (1.941) | (2.384) | (2.033) | (2.392) | (1.472) | (1.989) | (1.191) | (3.241) | (2.799) | (1.516) | |
| Beta-VMG | 0.129 | 0.008 | 0.121 | −0.159 | −0.095 | −0.114 | −0.219 | 0.116 | 0.065 | 0.159 |
| (0.941) | (0.064) | (0.894) | (−1.337) | (−0.745) | (−0.909) | (−1.704) | (0.915) | (0.505) | (1.157) | |
| R2 | 0.039 | 0.091 | 0.06 | 0.164 | 0.084 | 0.117 | 0.119 | 0.127 | 0.108 | 0.026 |
| Adjusted R2 | 0.009 | 0.062 | 0.03 | 0.138 | 0.055 | 0.089 | 0.09 | 0.099 | 0.08 | −0.005 |
| Predictor-After201509 | ||||||||||
| Alpha | 0.007 | 0.009 | 0.007 | 0.018*** | 0.016*** | 0.018*** | 0.012** | 0.011* | 0.009 | 0.013** |
| (1.063) | (1.39) | (1.031) | (3.087) | (2.7) | (2.988) | (2.051) | (1.788) | (1.4) | (2.081) | |
| Beta-MKT | 0.205 | 0.177 | 0.168 | 0.172 | 0.282** | 0.223* | 0.214* | 0.228* | 0.219* | 0.121 |
| (1.598) | (1.398) | (1.324) | (1.471) | (2.361) | (1.89) | (1.769) | (1.839) | (1.729) | (0.969) | |
| Beta-SMB | 0.126 | 0.137 | 0.153 | 0.123 | 0.009 | 0.097 | −0.01 | 0.21* | 0.146 | 0.169 |
| (1.074) | (1.176) | (1.315) | (1.154) | (0.082) | (0.894) | (−0.094) | (1.845) | (1.256) | (1.481) | |
| Beta-VMG | 0.14 | −0.007 | −0.037 | −0.15 | −0.069 | −0.103 | −0.193 | 0.134 | 0.072 | −0.026 |
| (1.068) | (−0.055) | (−0.284) | (−1.26) | (−0.566) | (−0.852) | (−1.553) | (1.051) | (0.553) | (−0.203) | |
| R2 | 0.047 | 0.06 | 0.072 | 0.125 | 0.102 | 0.111 | 0.114 | 0.084 | 0.062 | 0.063 |
| Adjusted R2 | 0.007 | 0.02 | 0.033 | 0.089 | 0.064 | 0.073 | 0.077 | 0.045 | 0.022 | 0.024 |
| Macro-FullSample | ||||||||||
| Alpha | 0.007 | 0.008 | 0.009 | 0.015** | 0.015** | 0.015** | 0.016** | 0.009 | 0.007 | 0.013** |
| (1.063) | (1.368) | (1.514) | (2.407) | (2.367) | (2.316) | (2.567) | (1.496) | (1.028) | (2.137) | |
| Beta-MKT | 0.205 | 0.185 | 0.192 | 0.15 | 0.234* | 0.096 | 0.034 | 0.254** | 0.117 | 0.047 |
| (1.598) | (1.509) | (1.544) | (1.22) | (1.89) | (0.762) | (0.275) | (2.009) | (0.916) | (0.372) | |
| Beta-SMB | 0.126 | −0.054 | −0.028 | −0.091 | 0.064 | −0.018 | 0.068 | 0.085 | 0.063 | 0.009 |
| (1.074) | (−0.482) | (−0.248) | (−0.808) | (0.566) | (−0.154) | (0.601) | (0.732) | (0.537) | (0.082) | |
| Beta-VMG | 0.14 | 0.32** | 0.278** | 0.197 | 0.161 | 0.183 | 0.29** | 0.187 | 0.284** | 0.211 |
| (1.068) | (2.544) | (2.182) | (1.568) | (1.27) | (1.42) | (2.311) | (1.447) | (2.174) | (1.633) | |
| R2 | 0.047 | 0.124 | 0.092 | 0.074 | 0.054 | 0.039 | 0.077 | 0.063 | 0.066 | 0.044 |
| Adjusted R2 | 0.007 | 0.087 | 0.054 | 0.035 | 0.014 | −0.002 | 0.038 | 0.024 | 0.026 | 0.004 |
- Note: This table reports the Liu et al. (2019) CH-3 model decomposition results for each strategy's performance shown in Table 11. The smallest 30% of stocks is eliminated when constructing SMB and VMG, and VMG is constructed using stocks' earning-to-price ratio. The regression coefficients, t statistics (in brackets), R2 and adjusted R2 are reported in this table. The sample period for the first two subtables starts from September 2013 to December 2021. The sample period for the last two subtables starts from October 2015 to December 2021. Prediction methods are introduced in more detail in Section 3.
- Abbreviations: MKT, market; OLS, ordinary least squares; PC, principal component; PCA, principal component analysis; PLS, partial least squares; SMB, small-minus-big; VMG, value-minus-growth.
- * Significant at the 0.10 level
- ** significant at the 0.05 level
- *** significant at the 0.01 level.
7 CONCLUSION
Is factor timing feasible in the Chinese stock market? This paper conducts an exploratory study on this question and provides comprehensive empirical results. Specifically, the reversal factor long–short portfolio exhibits significant time-series predictability over time, which is robust across different types of predictors and various models, provided that the models can guard against underfitting or overfitting the data. On the other hand, all other factors' long–short portfolios and all factors' quantile portfolios cannot exhibit robust predictability. Additionally, market excess return cannot be robustly predicted using factor portfolio returns or macroeconomic variables. After market neutralization, size factor long-wing and long–short portfolios become time-series predictable, but all other quantile portfolios remain hard to predict. In light of the positive finding towards the significant predictability of reversal factor premium, together with the economic logic under the predictor important analysis, it would be interesting in future research to explore the mechanism between market participant behavior and factor premium in the Chinese stock market, as well as the implication of reversal factor premium predictability towards the market dynamic.
CONFLICT OF INTEREST STATEMENT
The author declares no conflict of interest.
ETHICS STATEMENT
None declared.
REFERENCES
- 1 Public available via HERE (http://www.pbc.gov.cn/zhengcehuobisi/125207/125213/125440/125838/125888/2814475/index.html).
- 2 Public available via HERE (https://yield.chinabond.com.cn/cbweb-czb-web/czb/moreInfo?locale=cn_ZH).
- 3 Public available via HERE (https://www.policyuncertainty.com/index.html).
- 4 Public available via HERE (https://www.matteoiacoviello.com/gpr.htm).




