Macroeconomic consequences of alternative reforms to the health insurance system in the United States
Abstract
This paper presents a dynamic general equilibrium model designed to examine the macroeconomic effects and welfare implications of alternative reforms to the US health insurance system. Specifically, it scrutinizes the extent to which health care reform can mitigate inefficiencies stemming from market imperfections in the health insurance industry. The model considers a stochastic overlapping generations framework, incorporating heterogeneous agents who are subject to uncertain health shocks. These individuals make optimal decisions regarding labor supply, health insurance, and medical services. Given that the optimal levels of medical consumption and hours worked are endogenous, this setting encapsulates general equilibrium effects. The model is calibrated to US data, and numerical simulations suggest that suitable adjustments to the present health insurance system can broaden coverage and enhance welfare. This improvement is achieved by reducing adverse selection, improving overall health status, and lessening tax distortions on labor supply.
1 INTRODUCTION
The American health care system, while boasting numerous merits, is also marked by substantial, well-documented inefficiencies. These primarily stem from high costs associated with medical care delivery and market imperfections within the health insurance sector. OECD data reveals that in 2020, a significant 17.8% of the US economy was dedicated to health care, compared with a 9.6% average in OECD countries and 11.8% in Switzerland, the second highest. Despite this substantial expenditure, the US life expectancy lags behind other high-income countries, and its infant mortality rate considerably exceeds those of other developed nations.
Market failures in health insurance provision encourage socially inefficient coverage levels. In 2019, Kaiser (2022) reported that 10.9% of the nonelderly in the United States were uninsured. This lack of insurance leads to serious consequences, such as limited access to necessary care, declining health, and potential financial hardships. Uninsured adults are far more likely to delay or forego health care altogether and struggle to afford prescription medications or recommended treatments. Chen et al. (2022) found that uninsured individuals experience faster health deterioration and face higher premature mortality rates than insured individuals. Additionally, uninsured individuals impose financial externalities on third parties through uncompensated care, estimated to cost $57.4 billion in 2008 (Hadley et al., 2008).
In response to these circumstances, there has been an influx of proposals aimed at transforming the US health care system and extending coverage to the uninsured. In 2012, the United States enacted the Affordable Care Act (ACA) with the primary goal of enhancing access to health care by broadening health insurance coverage for millions of uninsured Americans. The ACA aimed to accomplish this through a variety of key measures. These included establishing health insurance marketplaces, expanding Medicaid, implementing an individual mandate that required most individuals to secure health insurance, and prohibiting insurance companies from denying coverage due to pre-existing conditions. Numerous empirical studies have explored the impacts of such reforms on individual behaviors, such as the crowding-out effect of public insurance (Cutler & Gruber, 1996; Gruber & Simon, 2008; Lo Sasso & Buchmueller, 2004), medical usage (Cheng & Chiang, 1997), and health status (Currie & Gruber, 1996; Decker & Remler, 2005; Hanratty, 1996; Lurie et al., 1984). However, there is a scarcity of economic models addressing the macroeconomic and welfare implications of US health care system reform. Some recent studies, like Gruber and Simon (2008) and Meara et al. (2008), have used microsimulation models to evaluate reform proposals. While these models offer detailed institutional insight and utilize ample microdata, they do not provide insights into the general equilibrium effects of such reforms and their welfare implications.
The health care system encompasses both medical care delivery and health insurance provision. Fundamentally, most existing reform proposals aim to slow health cost growth and expand insurance coverage. Given the size and complexity of the health care delivery system, cost growth cannot be easily or swiftly contained. Understanding the factors driving this cost growth, which is less studied compared to adverse selection and other health insurance market imperfections, is crucial. This paper, therefore, focuses on reform aspects aiming to reduce these market imperfections in health insurance provision.
A reform of the health insurance system could potentially influence macroeconomic variables by altering the labor market through tax rate adjustments, decreasing the number of uninsured individuals, and elevating the overall health expenditure. Such a reform is likely to modify household demand for health insurance. Consequently, some individuals may transition from their existing private insurance coverage to a newly subsidized form of private coverage, or to public coverage. This shift will change the demographics of those insured, thus affecting insurance premiums. Different insurance choices can also lead to changes in health status and labor productivity, which in turn, can influence wages and working hours. A change in labor income tax may be required to fund the reform, which will further impact individual labor supply decisions. Reform is also likely to alter saving behaviors, subsequently affecting the aggregate capital stock and factor prices. This is because health insurance can diminish precautionary saving motives. Conversely, improved health, leading to increased life expectancy, can motivate higher savings. These intricate tradeoffs can only be fully understood within a general equilibrium framework.
The objective of this study is to examine the macroeconomic impacts and welfare implications of potential reforms to the US health insurance system. To capture critical welfare tradeoffs, I extend the existing literature by incorporating endogenous health expenditure and labor-leisure choice. The following reform proposals are considered: (i) expansion of Medicare to the entire population; (ii) expansion of Medicaid; (iii) implementation of an individual mandate; (iv) removal of the subsidy for purchasing employer-sponsored insurance. These reforms are fundamental components of major reform proposals. I calibrate my model to US data and conduct several policy experiments to elucidate the costs and benefits of altering the health insurance system. My numerical experiments suggest that the effects of general equilibrium are substantial, and the impact of various reforms on social welfare can be quite sizable.
My research is closely related to a number of studies. My model builds upon the seminal works of Bewely (1986), Imrohoroglu (1989), Huggett (1993), and Aiyagari (1994). These works provide a valuable framework for studying an economy with heterogeneous agents and incomplete markets. Numerous papers integrate exogenous health expenditure shocks into the Bewley-type models. For instance, De Nardi et al. (2010), Kopecky and Koreshkova (2014), and Palumbo (1999) have incorporated heterogeneous medical expenses to comprehend the pattern of savings among the elderly population. Jung and Tran (2008) undertook an analysis of the impact of Health Savings Accounts on health expenditure and individual insurance decisions. Similarly, Jeske and Kitao (2009) scrutinized the welfare costs associated with tax policy changes relating to health insurance. Zhao (2015, 2017) explored the demand for private and public insurance within the context of health shocks, using a dynamic life-cycle model. Furthermore, Feng and Zhao (2018), Feng and Villamil (2022), along with Chivers et al. (2017), analyzed the effects of escalating health care costs on labor market decisions. Recently, Fang and Kruger (2022) reviewed prototype models used in macro and labor literature, extended to incorporate health and health insurance, to study the short- and long-term consequences of the ACA. However, unlike these papers, I consider households' optimal consumption of medical services, following the health capital literature in line with Grossman (1972). Recent instances of this approach can be found in the works of Hall and Jones (2007), Suen (2006), He et al. (2021), as well as Zhao (2014), all of whom provide explanations for the rapid growth in health expenditure in the United States.
This study contributes to the existing literature in two significant ways. Primarily, it aims to create a macroeconomic framework to assess the effects of various health care reform alternatives. While the prevailing literature typically concentrates on a single health-related policy, this paper deliberately incorporates public health insurance into the model. This allows for the evaluation of a wide range of health care reforms. Second, the model takes into account the general equilibrium effects related to both the demand and supply of labor, as well as the consumption of medical services. As will be demonstrated later, the inclusion of labor-leisure choice offers fresh perspectives for understanding the welfare implications of health care reforms. Numerical simulations indicate that the impact of reforms on labor supply is far from negligible, illustrating the value of this broader, more integrated approach.
The paper is organized as follows. Section 2 introduces the overlapping generation model model, and Section 3 is devoted to the calibration of the utility and production functions with emphasis on some parameters related to health. Section 4 details some reform proposals and presents all numerical results. The last section concludes.
2 THE BENCHMARK MODEL
2.1 Demographics
The benchmark model considers an open economy with overlapping generations of agents who live a maximum of three periods as young, middle-aged, and old. Let 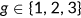 denote the age. In the first period, the measure of newly born agents is normalized to 1. Individuals alive in period
denote the age. In the first period, the measure of newly born agents is normalized to 1. Individuals alive in period  survive to the next period with a certain probability. For old people this probability is always 0. For young and middle-aged people, the survival probability is given by
survive to the next period with a certain probability. For old people this probability is always 0. For young and middle-aged people, the survival probability is given by 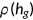 , which depends on the health status
, which depends on the health status 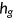 at the end of age
at the end of age 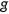 as described below. The population of young individuals grows at a constant rate
as described below. The population of young individuals grows at a constant rate  , implying that the population of young in period
, implying that the population of young in period 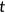 is
is 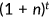 . I denote the relative size of age
. I denote the relative size of age 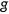 to the population as
to the population as 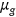 , which is determined in the equilibrium.
, which is determined in the equilibrium.
2.2 Agent types
All individuals enter the economy with the same level of health 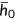 , an idiosyncratic endowment
, an idiosyncratic endowment 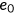 , and an idiosyncratic health risk types
, and an idiosyncratic health risk types 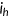 . Health risk type determines the probability of drawing a certain health shock
. Health risk type determines the probability of drawing a certain health shock 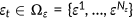 . The probability distribution of the shock is assumed to be age-type-dependent. Specifically, the probability of drawing
. The probability distribution of the shock is assumed to be age-type-dependent. Specifically, the probability of drawing  by type
by type 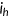 agent at age
agent at age 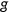 is denoted by
is denoted by 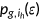 , with
, with 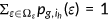 for all
for all 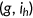 .1 A typical history of shocks up to time
.1 A typical history of shocks up to time  is denoted by
is denoted by 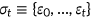 , with
, with 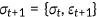 . Agents are endowed with a fixed amount of time per period that can be allocated to leisure or labor. Agents participate in the labor market during the first two periods and receive a wage income
. Agents are endowed with a fixed amount of time per period that can be allocated to leisure or labor. Agents participate in the labor market during the first two periods and receive a wage income 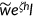 . Here
. Here  measures the effect of health on labor productivity.2 Health is an important form of human capital. It can enhance workers' productivity by increasing their physical capacities, such as strength and endurance, as well as their mental capacities. I postulate a positive relationship between health and labor productivity.
measures the effect of health on labor productivity.2 Health is an important form of human capital. It can enhance workers' productivity by increasing their physical capacities, such as strength and endurance, as well as their mental capacities. I postulate a positive relationship between health and labor productivity.
During their work stage agents supply labor and receive wage income from the firm. They can also save 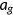 units of the consumption good by investing in physical capital with gross rate of return
units of the consumption good by investing in physical capital with gross rate of return 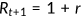 , where
, where 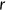 is the world real interest rate. Retired agents have income through previous saving, and consume all of their income at their last period of life.
is the world real interest rate. Retired agents have income through previous saving, and consume all of their income at their last period of life.
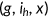 , where
, where 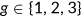 is age;
is age; 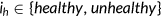 presents health risk type; and
presents health risk type; and  denotes their disposable resources at the beginning of each period defined as follows:
denotes their disposable resources at the beginning of each period defined as follows:
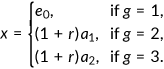 ()
()2.3 Preferences
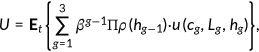 ()
()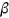 denotes the discount factor,
denotes the discount factor, 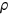 the survival probability,
the survival probability, 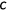 consumption,
consumption, 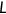 leisure, and
leisure, and 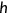 health status.
health status. 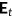 denotes the conditional expectation with the information available when the agent is born.
denotes the conditional expectation with the information available when the agent is born.2.4 The evolution of health
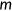 to offset the negative effect of health shock
to offset the negative effect of health shock 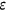 on health and builds up health capital
on health and builds up health capital 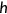 . The accumulation process of health is given by:
. The accumulation process of health is given by:
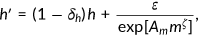 ()
()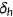 represents the natural deprecation rate of health and
represents the natural deprecation rate of health and 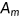 measures the medical technology.3 I assume that technological progress in the production of medical service
measures the medical technology.3 I assume that technological progress in the production of medical service 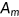 is exogenously given. The price of medical care
is exogenously given. The price of medical care 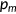 is exogenously given so that each unit of consumption good can be transformed into
is exogenously given so that each unit of consumption good can be transformed into 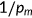 units of medical care.
units of medical care.In previous literature that explores the macroeconomic effects of health-related policies (e.g., Jeske & Kitao, 2009), the health expenditure is treated as an exogenous random shock. Individuals must pay the full amount for necessary health care after the health expenditure shock is revealed, independent of their income level and current health stock. In the current study, medical expenditures are endogenously chosen by agents to build up their health stocks. Since health expenditure is an endogenous choice, richer agents will spend more on health care to build up better health stock than the poor who has the same health status and faces the same health shocks. This can be explained by the fact that rich individuals have higher levels of consumption and lower marginal utility from consumption goods, therefore they will substitute some health for consumption goods.4
Conditional on being alive at the current age with end of period health stock 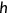 , agent will survive to the next period with probability
, agent will survive to the next period with probability 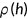 . Death is certain when health falls below zero (
. Death is certain when health falls below zero (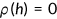 if
if 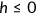 ). I assume that
). I assume that  . Deceased agents leave their savings
. Deceased agents leave their savings 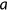 as an accidental bequest that is collected by the government as revenues.
as an accidental bequest that is collected by the government as revenues.
2.5 Medical expenses and health insurance
Nonelderly can choose one out of three possible insurance states labeled as 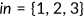 . To purchase private health insurance is
. To purchase private health insurance is 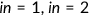 denotes that the agent has Medicaid, and
denotes that the agent has Medicaid, and 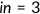 indicates that the agent is uninsured. The out of pocket health expenditure will be
indicates that the agent is uninsured. The out of pocket health expenditure will be 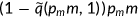 if the agent chooses to buy insurance and
if the agent chooses to buy insurance and  when he/she is covered by the government program. It will cost the entire expenditure
when he/she is covered by the government program. It will cost the entire expenditure 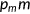 if the agent does not have insurance (
if the agent does not have insurance (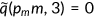 ). Here
). Here 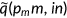 is function that represents the coinsurance rate and varies with the health insurance state
is function that represents the coinsurance rate and varies with the health insurance state 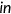 as we discuss in the following section. Agents take coinsurance rate as given and it is calibrated from the data. Retired agents are insured under Medicare.
as we discuss in the following section. Agents take coinsurance rate as given and it is calibrated from the data. Retired agents are insured under Medicare.
2.5.1 Private health insurance
To simplify the analysis, I only consider the Employer-Sponsored Health Insurance (EHI).5 Even when an employer offers health insurance, not all workers get coverage. Some choose not to enroll, perhaps because they are young or very healthy and feel that health insurance is not a pressing need, and others' incomes are so low that they cannot afford insurance. These tradeoffs will be presented in the benchmark simulation.
Once an agent decides to purchase EHI, a fixed premium, denoted as 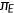 , is due to the insurance company. A fraction,
, is due to the insurance company. A fraction, 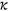 , ranging between 0 and 1 of this premium is paid at the firm level as part of the compensation. Importantly, the premium is not contingent upon any previous health history or individual conditions. This reflects the general practice in group health insurance, where pricing does not discriminate based on such personal attributes. It also signifies the presence of moral hazard and adverse selection problems within the private health insurance market. The health insurance company can only track the medical services consumed by a household, but it cannot discern the specific health type of the insured individuals or the health shock they received. To maintain the zero profit condition, the health insurance company set the premium
, ranging between 0 and 1 of this premium is paid at the firm level as part of the compensation. Importantly, the premium is not contingent upon any previous health history or individual conditions. This reflects the general practice in group health insurance, where pricing does not discriminate based on such personal attributes. It also signifies the presence of moral hazard and adverse selection problems within the private health insurance market. The health insurance company can only track the medical services consumed by a household, but it cannot discern the specific health type of the insured individuals or the health shock they received. To maintain the zero profit condition, the health insurance company set the premium 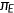 such that it is enough to cover the insurance company's share
such that it is enough to cover the insurance company's share 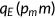 of the total medical expenditure incurred by the costumers.
of the total medical expenditure incurred by the costumers.
2.5.2 Public health insurance
The government provides two type of health insurances, Medicaid and Medicare, to the population.
Medicaid
Medicaid is a joint federal-state program that provides health insurance coverage to four main categories of nonelderly low-income individuals (typically below 134% of the federal poverty level, which is $13,100 for individual in 2007): children, their parents, pregnant women, and individuals with disabilities. Individuals who do not fall into one of these groups may be ineligible for Medicaid regardless of their income. Although Medicaid covers 45% of those below the poverty level, the categorical requirement leaves 35% of low-income individuals without insurance coverage. I assume that young and middle-aged individuals are eligible to receive Medicaid if their current income is lower than the poverty line  . There is also an exogenous probability
. There is also an exogenous probability 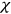 of getting a Medicaid offer. This captures the categorical requirement of Medicaid. The program will cover the fraction
of getting a Medicaid offer. This captures the categorical requirement of Medicaid. The program will cover the fraction 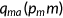 of the total medical expenditure. Medicaid is a part of government spending.
of the total medical expenditure. Medicaid is a part of government spending.
Medicare
All retirees are enrolled in the Medicare program. Each retiree pays a fixed premium 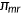 for Medicare and the program will cover the fraction
for Medicare and the program will cover the fraction 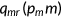 of the total medical expenditures. Medicare is funded by government revenues.
of the total medical expenditures. Medicare is funded by government revenues.
2.6 Aggregate production function
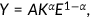 ()
()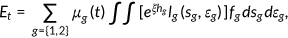 ()
()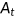 is a total factor productivity,
is a total factor productivity, 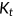 denotes the total capital stock, and
denotes the total capital stock, and 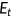 is an aggregate efficiency labor input, which depends on individual worker's health status. The distribution of households
is an aggregate efficiency labor input, which depends on individual worker's health status. The distribution of households 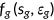 is defined over their state
is defined over their state 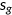 as discussed in the next section, and idiosyncratic health shock
as discussed in the next section, and idiosyncratic health shock 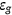 . The firm takes factor prices as given and demand capital stock and labor to maximize the profit. It also subtracts the cost of providing health insurance
. The firm takes factor prices as given and demand capital stock and labor to maximize the profit. It also subtracts the cost of providing health insurance 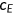 . The adjusted wage is given by
. The adjusted wage is given by 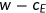 , where
, where 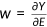 and
and 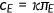 .
.2.7 The representative agent's problem
A representative agent of generation 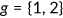 enters the economy with characteristics
enters the economy with characteristics 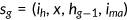 , where
, where 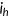 is the risk type of the agent,
is the risk type of the agent, 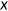 is the net wealth,
is the net wealth, 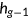 is the health status at the beginning of the period, and
is the health status at the beginning of the period, and 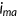 is the indicator function that signals the availability of the Medicaid benefit in the current period. Since all old agents are automatically enrolled in the Medicare program and leave the labor market, their characteristics simply are
is the indicator function that signals the availability of the Medicaid benefit in the current period. Since all old agents are automatically enrolled in the Medicare program and leave the labor market, their characteristics simply are 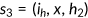 .
.
 at the beginning of the period. They take prices and taxes as given and make the insurance decision
at the beginning of the period. They take prices and taxes as given and make the insurance decision 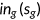 and choose a set of state-contingent decision rules, which can be denoted by
and choose a set of state-contingent decision rules, which can be denoted by 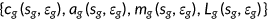 , to solve the following problem.
, to solve the following problem.
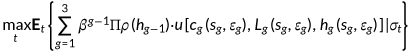 ()
()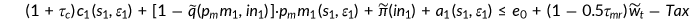 ()
()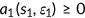 ()
()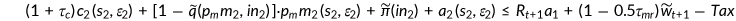 ()
()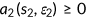 ()
() ()
()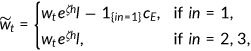 ()
()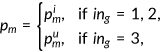 ()
()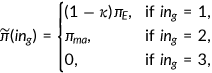 ()
()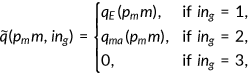 ()
()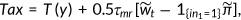 ()
()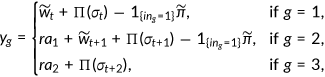 ()
()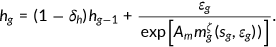 ()
()The timeline for the generation who was born in period  is shown in Figure 1. Each agent born at
is shown in Figure 1. Each agent born at  is endowed with
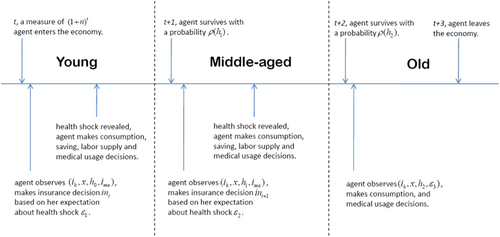
is endowed with 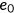 . Consumptions, out-of-pocket medical expenditures, payments of insurance premium and savings are financed by gross return from assets, labor incomes if applicable, net of incomes, and payroll taxes.
. Consumptions, out-of-pocket medical expenditures, payments of insurance premium and savings are financed by gross return from assets, labor incomes if applicable, net of incomes, and payroll taxes.
Equation (12) presents the individual's after-Medicare-tax adjusted wage income. The firm needs to share the Medicare tax 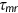 with the agent. Hence, in equilibrium a fraction
with the agent. Hence, in equilibrium a fraction 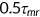 of tax is subtracted from the wage. The price of medical service
of tax is subtracted from the wage. The price of medical service 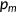 , marginal cost of the insurance premium
, marginal cost of the insurance premium 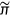 and coinsurance rate
and coinsurance rate  depend on the insurance states
depend on the insurance states 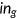 as given in Equations (13), (14), and (15). The individual is responsible to Medicare tax and a progressive income tax
as given in Equations (13), (14), and (15). The individual is responsible to Medicare tax and a progressive income tax 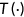 which is imposed on the labor income paid to a worker plus accrued interest on savings and profit from the firm as in (16). Equation (17) represents the income tax base, which depends on the agent's age. Health plays three important roles in the economy: good health promotes labor productivity at a factor of
which is imposed on the labor income paid to a worker plus accrued interest on savings and profit from the firm as in (16). Equation (17) represents the income tax base, which depends on the agent's age. Health plays three important roles in the economy: good health promotes labor productivity at a factor of 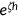 , agents derive utility from health and survive to the next period with probability
, agents derive utility from health and survive to the next period with probability 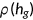 . Equation (18) explains the evolution of health.
. Equation (18) explains the evolution of health.
2.8 The government
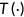 , consumption taxation at rate
, consumption taxation at rate 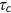 , Medicare taxation at rate
, Medicare taxation at rate 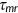 , Medicare premium
, Medicare premium 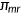 , Medicaid premium
, Medicaid premium 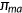 , and accidental bequests
, and accidental bequests 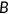 collected from deceased agents.
collected from deceased agents.
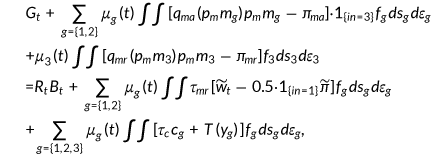 ()
()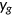 is the taxable income for age
is the taxable income for age 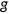 agent.
agent.2.9 Health insurance company
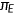 is charged such that expected expenditures on the insured are precisely covered.
is charged such that expected expenditures on the insured are precisely covered.
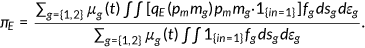 ()
()Notice the coverage ratio function 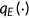 is taken as exogenously given.
is taken as exogenously given.
2.10 Stationary competitive equilibrium
Let 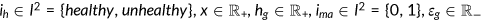 . The state space for age
. The state space for age 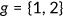 year old agents is
year old agents is 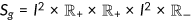 , and the state space for the old is
, and the state space for the old is 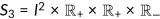 .
.
Definition 2.1.A stationary competitive equilibrium is (i) fiscal variables 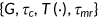 ; (ii) price for medical services
; (ii) price for medical services 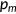 ; (iii) health insurance choices
; (iii) health insurance choices 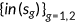 , a set of state-contingent decision rules
, a set of state-contingent decision rules 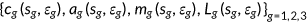 for the agents; (iv) a state-contingent sequence of labor demand
for the agents; (iv) a state-contingent sequence of labor demand 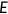 ; (v) insurance premium
; (v) insurance premium 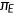 ; (vi) distributions of agents
; (vi) distributions of agents 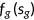 over the state space
over the state space 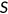 such that
such that
- 1.
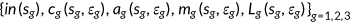 solve the consumers problem (6) taking prices and fiscal variables as given;
solve the consumers problem (6) taking prices and fiscal variables as given; - 2.
given the distribution
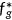 of households, the insurance companies choose
of households, the insurance companies choose 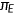 such that the budget constraint of insurance companies (20) holds;
such that the budget constraint of insurance companies (20) holds; - 3.
the government sets
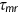 , and
, and  such that Equation (19) holds;
such that Equation (19) holds; - 4.
given price
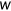 , the labor market clears
, the labor market clears
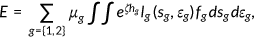 ()
() - 5.
given world interest rate, the capital market clears
where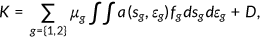 ()
() is the net inflow of capital.
is the net inflow of capital.
- 6.
the accidental bequests matches the remaining assets.
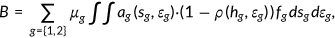 ()
() - 7.
the aggregate resource constraint holds
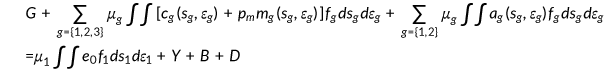 ()
() - 8.
there is a consistency between beliefs and the actual prices.
- 9.
the relative size of age
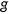 to the population
to the population 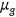 is recursively determined by
is recursively determined by
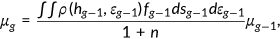 ()
() - 10.
the law of motion for the distribution of agents over the state space
 satisfies
satisfies
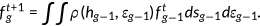 ()
()
3 CALIBRATION
In this section, I outline the calibration of the model. Table A1 summarizes the values and describes the parameters.
 ), the health production function (
), the health production function (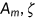 ), the survival probability function (
), the survival probability function (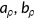 ), the magnitude of the negative health shock (
), the magnitude of the negative health shock (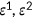 ), the probability distribution of the shock
), the probability distribution of the shock 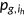 and the price of medical service
and the price of medical service 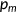 . Hence, I use a minimization procedure to determine these parameter values. More specifically, I pick parameter values to match key moments in the stationary distribution of the benchmark model with the real-world statistics listed in Table A5. Formally, let
. Hence, I use a minimization procedure to determine these parameter values. More specifically, I pick parameter values to match key moments in the stationary distribution of the benchmark model with the real-world statistics listed in Table A5. Formally, let 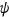 denote the vector of parameters, and
denote the vector of parameters, and 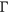 be the vector of selected real-world moments. Given
be the vector of selected real-world moments. Given 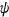 , a prediction
, a prediction 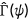 on
on 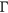 can be computed in the stationary distribution of the benchmark. The minimization procedure can be defined as the following problem:
can be computed in the stationary distribution of the benchmark. The minimization procedure can be defined as the following problem:
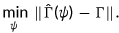 ()
()3.1 Data sources
The data used for estimating the process of health insurance decisions and health production come from the Household Component of the Medical Expenditure Panel Survey (MEPS), which is based on a series of national surveys conducted by the US Agency for Health Care Research and Quality (AHRQ). The MEPS consists of eight 2-year panels from 1996/1997 up to 2003/2004 and includes data on demographics, income, and most importantly health status and health insurance.
3.2 Demographics
 ) and survive up to the maximum age of 85 (
) and survive up to the maximum age of 85 (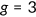 ). In line with Suen (2006), I assume that the survival probability function
). In line with Suen (2006), I assume that the survival probability function 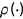 takes the form of the cumulative Weibull distribution function:
takes the form of the cumulative Weibull distribution function:
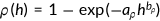 ()
()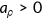 and
and 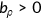 . The endogenous survival probability rules out the case that agents survive to the next period with negative health stock.
. The endogenous survival probability rules out the case that agents survive to the next period with negative health stock.I consider a yearly population growth of 1.25%. Together with the survival probability 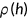 , the ratio of retired people to active population (the dependency ratio) is equal to 30% (24.3% according to the 2000 Population Census for the United States).6 The initial level of health when agent enter the economy,
, the ratio of retired people to active population (the dependency ratio) is equal to 30% (24.3% according to the 2000 Population Census for the United States).6 The initial level of health when agent enter the economy, 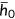 , is assumed to be constant and is normalized to be 100.
, is assumed to be constant and is normalized to be 100.
3.3 Preferences and technology
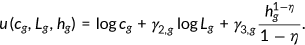 ()
()The parameter 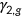 is age-dependent and I choose parameter values such that the average fraction of the time endowment allocated to market work is 0.33, which implies
is age-dependent and I choose parameter values such that the average fraction of the time endowment allocated to market work is 0.33, which implies 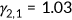 , and
, and 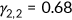 . Notice old agents retire from the labor market and they spend all time on leisure. For simplicity, I set
. Notice old agents retire from the labor market and they spend all time on leisure. For simplicity, I set 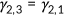 .
. 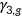 , which is age-dependent as is
, which is age-dependent as is 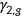 , measures the importance of health, and
, measures the importance of health, and 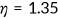 denotes the coefficient of relative risk aversion of health.
denotes the coefficient of relative risk aversion of health.
The annual subjective discount factor is taken to be 0.97, so 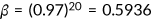 . The average annual interest rate in the United States is 4%, so
. The average annual interest rate in the United States is 4%, so 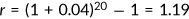 .
.
3.4 Production of health and health shocks
The health measure 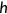 used in this paper is the Physical Component Summary scores formed from the answers to the Short-Form 12 questions. For people aged between 25 and 85, the lowest health level is 4.56 and the highest level is 72.17 in the MEPS data.7 This paper assumes that human beings can live up to 85 years without any accident or illness. I choose
used in this paper is the Physical Component Summary scores formed from the answers to the Short-Form 12 questions. For people aged between 25 and 85, the lowest health level is 4.56 and the highest level is 72.17 in the MEPS data.7 This paper assumes that human beings can live up to 85 years without any accident or illness. I choose 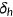 such that
such that 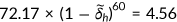 , where
, where 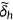 refers to annual health depreciation rate. I also assume that the depreciation rate increases with age. Therefore I choose depreciation rate of
refers to annual health depreciation rate. I also assume that the depreciation rate increases with age. Therefore I choose depreciation rate of 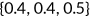 .
.
The transition of agent's health is described by Equation (3). Agents can offset the negative effect of a health shock by purchasing medical care. The productivity of medical care is captured by 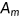 , and the price of medical care is
, and the price of medical care is 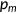 . Both are exogenously given.
. Both are exogenously given.
Brown (2006) found that uninsured people in California pay 65% more for common prescription drugs than the federal government does for the same medications. Anderson (2007) found that the uninsured patients pay up to 2.5 times for hospital service than health insurers. I assume that uninsured consumers pay a 60% higher price for medical services than the insured, so that 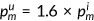 . This is similar to Jung and Tran (2008). I assume that the relative price of medical service
. This is similar to Jung and Tran (2008). I assume that the relative price of medical service 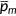 is the weighted average price paid by the insured and the uninsured, that is,
is the weighted average price paid by the insured and the uninsured, that is, 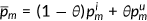 , where
, where 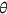 is the fraction of uninsured in the population. According to Kaiser Family Foundataion (2007), the value of
is the fraction of uninsured in the population. According to Kaiser Family Foundataion (2007), the value of 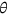 was 17% in 2006. Therefore, I pick
was 17% in 2006. Therefore, I pick 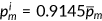 , and
, and 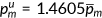 .
.
I differentiate agents into two groups, which are high-risk and low-risk, by using the estimation procedure of Bundorf et al. (2005). The health shocks take two possible values 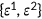 . For the same age cohort high-risk people are different from low-risk people in terms of the probabilities
. For the same age cohort high-risk people are different from low-risk people in terms of the probabilities 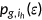 of getting the same shock
of getting the same shock 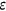 . The health shocks
. The health shocks 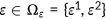 and the probability distribution of the shock
and the probability distribution of the shock 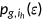 are chosen so that the health insurance take-up rate (percentage of workers buying private insurance per age-type group) and the share of health expenditure in GDP are approximated.
are chosen so that the health insurance take-up rate (percentage of workers buying private insurance per age-type group) and the share of health expenditure in GDP are approximated.
3.5 Health insurance
3.5.1 Private health insurance
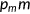 and takes the following form similar to Jeske and Kitao (2009).
and takes the following form similar to Jeske and Kitao (2009).
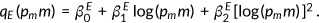 ()
()First, I estimate the set of parameters 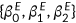 using the MEPS data. I sort the health expenditure into quantiles and use five uniform-sized bins for health expenditure data. Then I plug in the health expenditure data to attain the average coverage ratio for each bin.
using the MEPS data. I sort the health expenditure into quantiles and use five uniform-sized bins for health expenditure data. Then I plug in the health expenditure data to attain the average coverage ratio for each bin.
The coverage ratios of Medicaid and Medicare are estimated by the same procedure. I report the parameter values and coverage ratios for each expenditure grid in Tables A3 and A4. In Table A4, the standard errors in brackets and all coefficient estimates are significant at the 1% level. The insurance premium 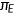 is determined in the equilibrium to ensure zero profits for the insurance company.
is determined in the equilibrium to ensure zero profits for the insurance company.
3.5.2 Medicaid
I use Medicaid as a proxy of public health insurance for the nonelderly population, which includes S-CHIP. I use the MEPS data to calculate the acceptance rate of Medicaid 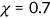 . The beneficiaries of Medicaid typically do not pay anything for enrolling in the program. I pick
. The beneficiaries of Medicaid typically do not pay anything for enrolling in the program. I pick 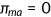 in the simulation.
in the simulation.
Medicaid is funded by general government revenue. The income level characteristic of Medicaid is typically 100% to 133% of the federal poverty line (FPL; Kenney et al., 2003). I set 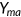 = $13,000 or about 34% of annual per capita GDP in the benchmark.
= $13,000 or about 34% of annual per capita GDP in the benchmark.
3.5.3 Medicare
I assume that every old agent is enrolled in Medicare. Medicare taxes are levied on all labor income and split between employer and employee contributions. The Medicare premium was $799.20 annually in 2004 or about 2.11% of annual GDP. The Medicare tax rate 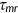 is determined within the model so that the government budget is balanced.
is determined within the model so that the government budget is balanced.
3.6 Firms
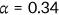 from NIPA. Without loss of generality, total factor productivity is normalized to
from NIPA. Without loss of generality, total factor productivity is normalized to  such that the average labor income equals 10 in the benchmark. In line with Bloom and Canning (2005), I assume that individual worker's health status affects the efficiency of labor input by a factor of
such that the average labor income equals 10 in the benchmark. In line with Bloom and Canning (2005), I assume that individual worker's health status affects the efficiency of labor input by a factor of  . Therefore, labor income is given by
. Therefore, labor income is given by 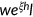 , where
, where 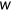 is the average wage rate. I estimate the parameter
is the average wage rate. I estimate the parameter  that fits the following equation using the MEPS data.
that fits the following equation using the MEPS data.
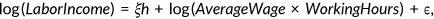 ()
()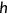 is the Physical Component Summary scores that measure the individual's health status ranging from 0 to 100. I normalize the average labor income observed in the data to be 10.0 and I calculate
is the Physical Component Summary scores that measure the individual's health status ranging from 0 to 100. I normalize the average labor income observed in the data to be 10.0 and I calculate 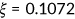 in the benchmark.
in the benchmark.3.7 Government
The value for 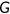 is exogenously given and is fixed across all policy experiments. I calibrate it to 18.0% to match the share of government consumption, social security, and gross investment excluding transfers, at federal, state, and local levels. The consumption tax rate is 5.67%, as in Mendoza et al. (1994).
is exogenously given and is fixed across all policy experiments. I calibrate it to 18.0% to match the share of government consumption, social security, and gross investment excluding transfers, at federal, state, and local levels. The consumption tax rate is 5.67%, as in Mendoza et al. (1994).
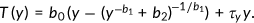 ()
()Parameter 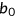 is the limit of marginal taxes in the progressive part as income goes to infinity,
is the limit of marginal taxes in the progressive part as income goes to infinity, 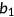 denotes the curvature of marginal taxes and
denotes the curvature of marginal taxes and 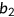 is a scaling parameter. I use the parameters estimated by Gouveia and Strauss (1994), which are
is a scaling parameter. I use the parameters estimated by Gouveia and Strauss (1994), which are 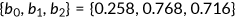 . When they calibrate the tax function, the income has been normalized to the range of
. When they calibrate the tax function, the income has been normalized to the range of 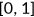 . In my model, I divide taxable income of every agent by the maximum income observed in the simulated economy to get the normalized income. Then I use this normalized income directly in Equation (32) to get the tax rate. The parameter
. In my model, I divide taxable income of every agent by the maximum income observed in the simulated economy to get the normalized income. Then I use this normalized income directly in Equation (32) to get the tax rate. The parameter  in the proportional term of the income tax equals 4.46% in the benchmark.
in the proportional term of the income tax equals 4.46% in the benchmark.
4 NUMERICAL RESULTS
In this section, I will first discuss the features of my benchmark model. Then I conduct counterfactual experiments in which alternative policies are carried out.
4.1 Benchmark model
Table A5 reports the main features of the benchmark simulation. Under the baseline parameterizations the model is able to match the health insurance demand and aggregate health expenditure in the United States. The fraction of insured agents among all young and middle-aged agents is 82.9%, which is almost the same as 83.0% in the data. Among nonelderly, 10.3% are covered by the Medicaid program (12.9% in the data). The model slightly understates total health expenditure as a ratio of GDP, which is about 16.3% according to the Department of Health and Human Services. The model reports 16.1%.
My model does not match the wealth distribution accurately even though I introduce idiosyncratic health shock. This can be explained by the fact that agents do not have bequest motive and the profits generated from production have been uniformly distributed back as a lump sum payment in the model economy. Nevertheless, the accuracy of approximation of the entire wealth distribution won't impose strong effect on the prediction of health insurance demand, which will be determined by the fraction of the population whose wealth is below certain threshold. As described in the previous paragraph, the health insurance take-up profile and aggregate health expenditure match with the data fairly well. Therefore, I leave the current setting as it is.
Next, I examine the model's predictions on the life-cycle patterns of medical spending and consumption. Panel 1 of Figure 2 displays medical spending over various age groups with the same statistics from the MEPS. Both in the data and model, the average health expenditure is roughly constant between ages 25 and 64 and climbs afterward. The benchmark model is able to replicate the increasing pattern. However, the size of the health expenditure of nonelderly agents as a ratio of GDP is bigger than the one observed in the data. The main reason is that the agent enters the economy with same amount of health stock in the model. The labor productivity effect of health may overstate the investment in medical service among young agents. This can be resolved by introducing heterogeneity in initial health but with some extra computational cost. In the model, a representative agent age between 25 and 44 spends $4676 or about 11.9% of per capita GDP (7.5% in the data). Agents between ages 45 and 64 years old on average spend $4667, or about 11.8% of per capita GDP (11.0% in the data). Agents over 65 spend $12,848, or about 32.7% of per capita GDP (32.6% in the data).
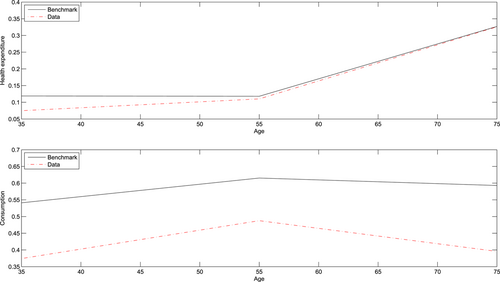
Panel 2 of Figure 2 shows the consumption over various age groups. Fernandez-Villaverde and Krueger (2002) estimated the life-cycle consumption profiles using data from the Consumer Expenditure Survey. They found that nondurable consumption peaked at age 52 and was about 29% higher than at age 25. The current model is able to generate a similar hump-shaped pattern. However, there is a gap between the benchmark prediction and data. This can be attributed to the fact that there is no capital in the model for the sake of simplification. The direct consequence of this strategy is that the demand for saving is inelastic and therefore part of the government income taxation is distortion free as discussed in the section explaining the firm's problem.
4.2 Policy experiments
I now conduct experiments to determine the effect of reforming the health insurance system. All potential reforms start from the same initial steady state of the benchmark economy. In period 1, an unanticipated change of the policy is announced and implemented and the economy starts to make a transition to the new steady state. I first compare moments of associated invariant distributions and then discuss the welfare analysis associated with each of the reforms considered.
I am interested in changes in health expenditure as a ratio of GDP, changes in taxes that balances the government budget, aggregate labor supply, aggregate health status, savings rate, the output as well as welfare implications. I treat changes in government revenue as follows: expenditures  , consumption tax rate
, consumption tax rate  , and the income tax remaining unchanged from the benchmark. The government adjusts the medicare tax
, and the income tax remaining unchanged from the benchmark. The government adjusts the medicare tax 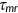 to balance the budget.
to balance the budget.
In each experiment, I compute a steady state outcome under the stationary equilibrium. In line with the methodology as explained by Conesa and Krueger (1999), this paper measures the welfare effect of a reform by computing the consumption equivalent variation 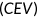 . I quantify the welfare change of a given policy reform for an individual type
. I quantify the welfare change of a given policy reform for an individual type 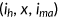 by asking how much (in percent) this individual's consumption has to be increased in all future periods and contingencies (keeping health expenditure, leisure and health insurance status constant) in the old steady state so that his expected life-time utility equals that under a specific policy reform. I denote it with
by asking how much (in percent) this individual's consumption has to be increased in all future periods and contingencies (keeping health expenditure, leisure and health insurance status constant) in the old steady state so that his expected life-time utility equals that under a specific policy reform. I denote it with 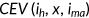 . For example, a
. For example, a 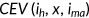 of −1.0% indicates that if the given policy reform is put into place, an individual type
of −1.0% indicates that if the given policy reform is put into place, an individual type 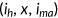 will experience a welfare loss which is equivalent to sacrificing 1.0% of her consumption in the initial steady state with leisure, health insurance and health expenditure constant at the initial choices.
will experience a welfare loss which is equivalent to sacrificing 1.0% of her consumption in the initial steady state with leisure, health insurance and health expenditure constant at the initial choices.
To isolate the distortion effect of the labor taxation, I also conduct companion experiments in which the government funds the reform through a lump-sum transfer.
4.2.1 Policy experiment A: Expansion of Medicare/EHI
In this experiment, the private health insurance and Medicaid program are abolished. The government extends Medicare to the entire population. Since the paper is about the aspects of the reform which aim at reallocating existing resources more efficiently by reducing the market imperfection in the provision of health insurance, I keep the average price level for medical service 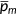 and medical technology
and medical technology 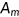 the same as the benchmark. It is also important to understand how individuals will respond to the changes in cost-sharing. Therefore, I consider two cases in which the government extends Medicare with different coinsurance rate to the nonelderly population. It is worth noting that Medicaid has the lowest cost-sharing in terms of coinsurance rate and Medicare has the highest according to MEPS data.
the same as the benchmark. It is also important to understand how individuals will respond to the changes in cost-sharing. Therefore, I consider two cases in which the government extends Medicare with different coinsurance rate to the nonelderly population. It is worth noting that Medicaid has the lowest cost-sharing in terms of coinsurance rate and Medicare has the highest according to MEPS data.
In experiment A-1, the government extends the Medicare coverage to the entire population which implies that the reform provides an incentive for the nonelderly to be more cautious about their medical spending due to higher cost-sharing. While in experiment A-2, the nonelderly will be covered by a uniform health insurance program with premium 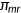 and coinsurance rate
and coinsurance rate 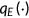 . Specifically, they pay for a premium that equals 2.1% of the per capita GDP which is cheaper than the counterpart in the benchmark.8 A fraction
. Specifically, they pay for a premium that equals 2.1% of the per capita GDP which is cheaper than the counterpart in the benchmark.8 A fraction 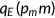 of their health expenditure will be paid by the government. This reform leaves the majority of the nonelderly, namely those who have insurance coverage through their employers in the benchmark, unchanged in terms of cost-sharing. However, those low-income agents who rely on Medicaid will be responsible for a bigger share of their health expenditure.
of their health expenditure will be paid by the government. This reform leaves the majority of the nonelderly, namely those who have insurance coverage through their employers in the benchmark, unchanged in terms of cost-sharing. However, those low-income agents who rely on Medicaid will be responsible for a bigger share of their health expenditure.
The experiment results are summarized in columns A-1 and A-2 of Table 1. The top section displays some statistics of aggregate variables: fraction of insured nonelderly, Medicare tax rate, average effective income tax rate, average hours worked, and health expenditure as a ratio of GDP. The mortality rate for each age group is also presented as a proxy of health status. The lower section displays the welfare effects of each reform. % w/consumption equivalent variation (CEV)  0 indicates the fraction of agents in the benchmark that would experience a welfare gain (positive CEV) if an alternative reform is taken place.
0 indicates the fraction of agents in the benchmark that would experience a welfare gain (positive CEV) if an alternative reform is taken place.
| Bench. | A-1 | A-2 | |
|---|---|---|---|
| Insured nonelderly (in %) | 82.9 | 100.0 | 100.0 |
| Medicare tax (in %) | 2.2 | 6.0 | 14.7 |
| Ave. income tax (in %) | 20.4 | 20.6 | 20.1 |
| Ave. working hours | 32.4 | 30.2 | 27.3 |
| Health exp. (in % of GDP) | 16.1 | 14.8 | 16.4 |
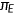 (in % of per capita GDP) (in % of per capita GDP) |
8.7 | 2.1 | 2.1 |
| Output | 100.0 | 97.8 | 94.5 |
| Aggregate saving rate (in %) | 26.9 | 27.5 | 27.9 |
| Average consumption | 100.0 | 99.2 | 94.0 |
| Mortality rate (age 25–44) | 0.0322 | 0.0324 | 0.0322 |
| Mortality rate (age 45–64) | 0.1343 | 0.1343 | 0.1323 |
| Lifetime CEV after transition | |||
| All (in %) | – | 0.1 | −2.6 |
Income 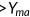 (in %) (in %) |
– | 1.9 | −0.03 |
Income 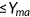 (in %) (in %) |
– | −5.7 | −10.9 |
% w/CEV 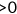 |
– | 77.6 | 37.3 |
- Note: A-1, Medicare expansion to the entire population. A-2, EHI expansion to all working age population.
Universal coverage is achieved by expanding Medicare to the entire population or extending Employer Health Insurance (EHI) to all individuals of working age, as evidenced by the increased proportion of insured nonelderly individuals. However, the aggregate health expenditure does not necessarily grow as the number of uninsured drops. In experiment A-1, the share of total spending in health care as a ratio of GDP shrinks to 14.8%, while the share expands by 0.3% in A-2. This can be attributed to the difference in changing cost-sharing which affects the agent's incentive. Higher cost sharing will contain spendings in health care by providing an incentive for the consumer to use the resource more cautiously as in experiment A-1. Consequently, the aggregate level of health status will deteriorate and the mortality rate will rise. While lower cost-sharing in experiment A-2 will encourage the nonelderly to spend more on medical service which results in improved health. A natural question is whether this deterioration/improvement in health can be justified by the cost saving/growth. The answer seems positive if we ignore the effect of tax distortion and reduced adverse selection which are the subject of welfare analysis. In experiment A-1, the government will save approximately $150 billion at a cost of higher mortality rate which will be around $136 billion if we assume that the value of statistical life is $6.8 million (c.f. Bellavance et al., 2009). Similarly, the value of life saved will amount to $406 billion after experiment A-2 is implemented, while the extra health cost is merely $34.6 billion.
The expansion of public health insurance requires the government to raise tax revenue to cover 17.1% of the nonelderly who would be uninsured in the benchmark. The government also needs to pay for part of the expenditure of the previously insured who pay about 20.0% of the premium before the reform. Meanwhile, the reform also saves some tax revenues through changes in the arrangement in the health care sector. In the benchmark, the government provides Medicaid to low incomes, which costs 1.2% of total GDP. It also subsidizes the purchase of group insurance, and the total subsidy amounts to 0.8% of total GDP. Once the reform is implemented, the government can save these spendings, since both Medicaid and private insurance are abolished. Considering both of them, the government raises the Medicare tax rate to 6.0% in experiment A-1 and 14.7% in A-2 which will discourage labor supply and the average hours worked decrease by 6.8% and 15.7% accordingly. Total output shrinks by 2.2% in A-1 and 5.5% in A-2 as labor supply drops.
Although agents are subject to a higher labor tax after the reform is implemented, the agents will benefit from the policy A-1 with guaranteed access to insurance coverage. The health insurance market is free of adverse selection problems after the reform is implemented. As shown in % w/CEV 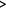 0, 77.6% of agents would experience a welfare gain from this reform and the average welfare effect is in the order of 0.1% in terms of consumption in all states. However, low-income agents, especially those covered by Medicaid before the reform, will suffer from this policy because the new insurance program from such a reform is less generous than Medicaid. On average, low-income individuals would experience a welfare loss equivalent to 5.7% of consumption, compared with a welfare gain equivalent to 1.9% of consumption for agents who have incomes above the poverty line. In contrast to A-1, A-2 makes most of the individuals worse off because the after-reform labor tax is so high that the benefit cannot compensate for the cost.
0, 77.6% of agents would experience a welfare gain from this reform and the average welfare effect is in the order of 0.1% in terms of consumption in all states. However, low-income agents, especially those covered by Medicaid before the reform, will suffer from this policy because the new insurance program from such a reform is less generous than Medicaid. On average, low-income individuals would experience a welfare loss equivalent to 5.7% of consumption, compared with a welfare gain equivalent to 1.9% of consumption for agents who have incomes above the poverty line. In contrast to A-1, A-2 makes most of the individuals worse off because the after-reform labor tax is so high that the benefit cannot compensate for the cost.
4.2.2 Policy experiment B: Expansion of public health insurance
Reform B entails the expansion of public health insurance, encompassing programs such as Medicaid and S-CHIP, as per Gruber (2006) study. Strategies following this model typically enhance existing public programs by increasing income thresholds, thus extending coverage to a larger number of individuals in need. They eliminate all eligibility criteria except income. The outcomes of this experimental approach are summarized in columns B-1 and B-2 of Table 2. In experiment B-1, the government increases the Medicaid offer rate to 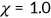 , compared to a probability of 0.7 in the benchmark, that is, the new Medicaid program covers all the low income but not just eligible low-income parents and children as required in the current system. While in experiment B-2, the government keeps the categorical requirement of Medicaid unchanged and increases the maximum income requirement to 200% of the poverty line.
, compared to a probability of 0.7 in the benchmark, that is, the new Medicaid program covers all the low income but not just eligible low-income parents and children as required in the current system. While in experiment B-2, the government keeps the categorical requirement of Medicaid unchanged and increases the maximum income requirement to 200% of the poverty line.
| Bench. | B-1 | B-2 | |
|---|---|---|---|
| Insured nonelderly (in %) | 82.9 | 85.0 | 93.4 |
| Medicare tax (in %) | 2.2 | 5.1 | 5.7 |
| Ave. income tax (in %) | 20.4 | 20.3 | 20.3 |
| Ave. Working hours | 32.4 | 31.4 | 31.1 |
| Health exp. (in % of GDP) | 16.1 | 16.6 | 16.6 |
 (in % of per capita GDP) (in % of per capita GDP) |
8.7 | 8.5 | 8.5 |
| Output | 100.0 | 99.5 | 99.0 |
| Aggregate saving rate (in %) | 26.9 | 27.1 | 27.2 |
| Average consumption | 100.0 | 99.1 | 98.6 |
| Mortality rate (age 25–44) | 0.0322 | 0.0321 | 0.0321 |
| Mortality rate (age 45–64) | 0.1343 | 0.1335 | 0.1328 |
| Lifetime CEV after transition | |||
| All (in %) | – | 0.2 | −1.1 |
Income  (in %) (in %) |
– | −1.1 | −0.6 |
Income  (in %) (in %) |
– | 0.8 | −1.3 |
% w/CEV 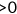 |
– | 7.5 | 4.3 |
- Note: B-1, Public health insurance expansion 1. B-2, Public health insurance expansion 2.
The spending in Medicaid as a ratio of GDP increases from 1.2% to 2.5% when the government extends Medicaid to include more low-income agents. These newly insured consume more medical services because Medicaid provides them with better insurance coverage. Aggregate health expenditure increases by 0.5% and the Medicare tax rate has been more than doubled to match this spending. Average hours worked decreases by 4.0% even though the labor productivity has been improved due to improved health. Medicaid expansion alone cannot achieve “universal insurance coverage” and this reform will still leave 15.0% of the nonelderly without insurance coverage. Those are agents in better health condition who think insurance is not critical important to them.
When the government increases the maximum income requirement in experiment B-2, some previously insured agents will choose to apply for Medicaid because Medicaid is the best insurance money can buy, even though they will face the risk of being uninsured because of categorical requirements of Medicaid. Overall, the insured as a fraction of nonelderly increases to 93.4%. Similar to the preceding experiment, the aggregate health expenditure increases. While average health outcome is better than after experiment B-1 is taken place due to the higher insurance coverage. Consequently, the aggregate hours worked decreases by 3.1% as Medicare tax jumps to 5.7%.
Compared to the benchmark, policy B-1 is intended to be beneficial for agents with income below the poverty line. These agents are qualified for Medicaid with a certain probability determined by categorical requirements of this program in the benchmark. Now they benefit from this reform with a guaranteed public insurance coverage and pay a cost in terms of a higher labor tax. Given the small size of the program, the benefit is enough to compensate for the loss due to the tax increment. They experience a welfare gain in the order of 0.8% in terms of consumption in all states. For high-income agents, their health benefits are intact after the reform since they are not qualify for Medicaid, but they subject to a higher income tax to support the expanded Medicaid program. Their welfare loss is equivalent to 1.1% in terms of consumption in all states.
To increase the maximum income requirement makes more agents worse off. Agents whose income is below the existing maximum income requirement have the same public insurance coverage as in the benchmark. However, they are required to pay for a higher tax rate to fund the expanded Medicaid. Therefore, they experience a welfare loss in the order of 1.3% in consumption equivalence. High-income agents benefit from the reform with a chance of being covered by Medicaid depending on their income level. While the cost of higher income tax cannot be offset by this benefit. Consequently, they experience a welfare loss of the order of 0.6% in terms of consumption, which is in a smaller magnitude compared with low-income agents who do not benefit from this reform.
4.2.3 Policy experiment C: Individual mandate
In this experiment, those agents who are uninsured in the benchmark are required to purchase private insurance. Their entry into the insurance market makes the risk pool more inclusive and the price of the group insurance falls to $3340 from the benchmark price of $3418. The aggregate health expenditure as a ratio of GDP rises to 16.7% as the insurance coverage increases, see column C of Table 3. The aggregate health status has been improved and the average hours worked decrease by 2.2% as the reform requires a higher Medicare tax 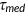 since the tax deductibility has been extended to the previously uninsured. In terms of welfare, an individual mandate makes everybody worse off. Such a reform imposes a higher tax rate since more individuals will deduct premiums from income taxes. This welfare loss cannot be compensated by the cheaper insurance resulting from a more inclusive risk pool. On average, agents experience welfare loss in the order of 0.6% of consumption in all states. Among low-income agents, only a small fraction holds private insurance since most of them are covered by Medicaid. Consequently, they benefit less from the cheaper insurance and they experience a welfare loss at the magnitude of 3.8% in consumption equivalence, compared with a loss in the order of 1.1% for high-income agents.
since the tax deductibility has been extended to the previously uninsured. In terms of welfare, an individual mandate makes everybody worse off. Such a reform imposes a higher tax rate since more individuals will deduct premiums from income taxes. This welfare loss cannot be compensated by the cheaper insurance resulting from a more inclusive risk pool. On average, agents experience welfare loss in the order of 0.6% of consumption in all states. Among low-income agents, only a small fraction holds private insurance since most of them are covered by Medicaid. Consequently, they benefit less from the cheaper insurance and they experience a welfare loss at the magnitude of 3.8% in consumption equivalence, compared with a loss in the order of 1.1% for high-income agents.
| Bench. | C | D | |
|---|---|---|---|
| Insured nonelderly (in %) | 82.9 | 100 | 79.2 |
| Medicare tax (in %) | 2.2 | 4.8 | 1.8 |
| Ave. income tax (in %) | 20.4 | 20.2 | 20.5 |
| Ave. Working hours | 32.4 | 31.7 | 32.5 |
| Health exp. (in % of GDP) | 16.1 | 16.8 | 15.9 |
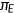 (in % of per capita GDP) (in % of per capita GDP) |
8.7 | 8.3 | 9.0 |
| Output | 100.0 | 99.3 | 100.1 |
| Aggregate saving rate (in %) | 26.9 | 27.0 | 26.8 |
| Average consumption | 100.0 | 98.2 | 100.5 |
| Mortality rate (age 25–44) | 0.0322 | 0.0321 | 0.0322 |
| Mortality rate (age 45–64) | 0.1343 | 0.1317 | 0.1349 |
| Lifetime CEV after transition | |||
| All (in %) | – | −1.7 | −2.1 |
Income 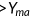 (in %) (in %) |
– | −1.1 | −2.8 |
Income 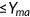 (in %) (in %) |
– | −3.8 | −0.1 |
% w/CEV 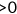 |
– | 0.0 | 16.4 |
- Note: C, Individual mandate on private insurance purchase. D, Abolish private insurance deductibility from income tax base.
4.2.4 Policy experiment D: Abolishing tax-deductibility of EHI premiums
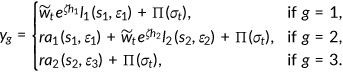 ()
()Experiment results are summarized in column D of Table 3. Removing the subsidy in D leads to a drop in insurance take-up as found by Jeske and Kitao (2009). Since I don't differentiate between group insurance and insurance purchased in the private market, the magnitude of drop is much smaller. The fraction of nonelderly who purchase private insurance falls from 72.6% to 68.9%. There are only about 4% of the nonelderly opt out of the private insurance market and choose to be self-insured. Those are healthy agents who face a lower probability of suffering a bad health shock. The exit of these agents out of the insurance market deteriorates the risk pool and the price of the private insurance jumps by 3.5% to $3536. The aggregate health expenditure as a ratio of GDP falls by 1.2% because taking away the tax deductibility discourages investment in health.
The Medicare tax 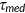 on labor income that balances the government budget falls from 2.2% to 1.8%, since the income tax base is expanded by eliminating the deductibility of the EHI premium. Consequently, the average hours worked increase by 0.5%. Although the tax rate
on labor income that balances the government budget falls from 2.2% to 1.8%, since the income tax base is expanded by eliminating the deductibility of the EHI premium. Consequently, the average hours worked increase by 0.5%. Although the tax rate 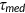 is lower than in the benchmark, it is not enough to compensate for the welfare loss due to the lower insurance coverage, increased exposure to health shocks, and deteriorated health. Most agents will face a welfare loss except those low-income individuals who relies on Medicaid will benefit from the policy with their insurance coverage intact.
is lower than in the benchmark, it is not enough to compensate for the welfare loss due to the lower insurance coverage, increased exposure to health shocks, and deteriorated health. Most agents will face a welfare loss except those low-income individuals who relies on Medicaid will benefit from the policy with their insurance coverage intact.
Compared with the findings in Jeske and Kitao (2009), the welfare implications are qualitatively identical. While my numerical simulations complement theirs by suggesting that output will expand as labor supply increases and medical spending drops as agents are more aware of the cost of insurance. Furthermore, the agents will spend more on consumption goods instead of less as found in their paper.
4.3 To fund reforms by a lump-sum transfer
The analysis so far indicates that the change in taxes may play a dominant role in how health care reforms affect the welfare. To isolate the effect of tax distortion, I also conducted companion exercises in which the government funds the reform through a lump sum transfer. In the companion experiments, the tax rates are kept intact as in the benchmark. The government returns a lump sum transfer to each individual. The transfer is determined so that the government's budget is balanced.
Numerical results in Table 4 indicate that the labor supply effect of health care reforms is rather small. The greatest change in hours worked is observed in experiment A-1 in which the hours worked decreases by 2.2%, compared to an average 5.3% change when the reforms are funded through the Medicare tax. Nevertheless, reforms to the health insurance system have quite sizable effects on the welfare. Medicare expansion increases welfare by improving health status and reducing adverse selection in the health insurance market. While expansion of Medicaid and individual mandate decreases welfare by distorting health insurance purchase and health expenditure decision, even thought average health status has been improved after reforms are carried out.
| Bench. | A-1 | A-2 | B-1 | B-2 | C | D | |
|---|---|---|---|---|---|---|---|
| Insured nonelderly (in %) | 82.9 | 100.0 | 100.0 | 87.3 | 93.6 | 100 | 80.5 |
| Medicare tax (in %) | 2.2 | 2.2 | 2.2 | 2.2 | 2.2 | 2.2 | 2.2 |
| Ave. income tax (in %) | 20.4 | 20.8 | 20.9 | 20.4 | 20.5 | 20.3 | 20.4 |
| Ave. Working hours | 32.4 | 31.7 | 32.6 | 32.5 | 32.4 | 32.7 | 32.3 |
| Health exp. (in % of GDP) | 16.1 | 14.7 | 16.1 | 16.5 | 16.7 | 16.7 | 16.0 |
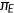 (in % of per capita GDP) (in % of per capita GDP) |
8.7 | 2.1 | 2.1 | 8.7 | 8.5 | 8.3 | 9.0 |
| Output | 100.0 | 99.5 | 100.7 | 100.3 | 100.4 | 100.4 | 99.9 |
| Aggregate saving rate (in %) | 26.9 | 27.4 | 27.6 | 26.9 | 27.1 | 26.9 | 26.8 |
| Average consumption | 100.0 | 100.9 | 99.3 | 99.8 | 100.6 | 99.2 | 100.3 |
| Mortality rate (age 25–44) | 0.0322 | 0.0324 | 0.0322 | 0.0320 | 0.0320 | 0.0321 | 0.0322 |
| Mortality rate (age 45–64) | 0.1343 | 0.1341 | 0.1318 | 0.1337 | 0.1328 | 0.1316 | 0.1347 |
| Lifetime CEV after transition | |||||||
| All (in %) | – | 0.9 | −1.1 | 0.9 | 0.5 | −1.7 | −2.2 |
Income 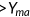 (in %) (in %) |
– | 2.5 | 0.6 | 0.2 | 0.6 | −1.2 | −2.8 |
Income 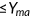 (in %) (in %) |
– | −3.9 | −6.7 | 1.8 | 0.4 | −3.3 | −0.3 |
% w/CEV 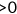 |
– | 80.6 | 71.6 | 19.4 | 10.3 | 0.0 | 16.4 |
- Note: A-1, Medicare expansion to the entire population. A-2, EHI expansion to all working age population. B-1, Public health insurance expansion 1. B-2, Public health insurance expansion 2. C, Individual mandate. on private insurance purchase. D, Abolish private insurance deductibility from income tax base.
Overall, reforms that can decrease the number of uninsured (as in A-2, B-1, B-2, and C) while do not alter agents incentives in medical spending will improve the aggregate health status. As the newly insured can invest more in health, the aggregate health spending rises as well. Improved health encourages labor supply as labor productivity is positively correlated with health. As shown in experiment C, average hours worked increases by 0.9%. Among the reforms considered, only experiment D fails to decrease the number of the uninsured. Aggregate health expenditure decreases as fewer people have insurance coverage in experiment D. The average health stock falls as well.
The comparison between policy A-1 and A-2 highlights the importance of cost-sharing in containing the health care growth. Both policies expand the insurance coverage to the entire population. While policy A-1 can actually save more than $150 billion per year if we assume that the delivery of health care maintains at the current state. This cost-saving mainly comes from providing incentive for consumers so that they are more aware of their spending.
5 CONCLUDING REMARKS
In this paper, I construct a microfounded dynamic general equilibrium model to scrutinize the effects of varying health care reforms on critical economic indicators such as aggregate labor supply, health expenditures, savings, welfare, and the proportion of the uninsured population. This stands in contrast to certain studies in the literature where I incorporate not just a labor-leisure choice, but also a health expenditure decision into the model. These decisions can potentially alter the demand for medical services, which subsequently impacts an individual's health status and labor productivity. Additionally, financing reform may impose distortions on the labor supply by necessitating increased tax revenues. The extent of this distortion hinges on both the specifics of the reform and the chosen method of funding.
When contemplating diverse strategies for reforming the US health insurance system, it is essential to weigh several critical trade-offs: reducing the number of uninsured individuals, potential labor market distortions, and the financial burden of raising public funds to support government programs. These intricate trade-offs can only be adequately captured within a general equilibrium framework, much like the one employed in this study. The findings of my analysis suggest that the expansion of Medicare and the implementation of an individual mandate emerge as promising strategies for achieving universal health care. Conversely, the elimination of the tax subsidy for purchasing private insurance could precipitate a significant decrease in insurance coverage.
The outcomes of my research suggest that, based on the specifics of the reforms and their funding mechanisms, the impact on aggregate labor supply due to various reforms fluctuates between a decrease of 8.4% and an increase of 0.9%. Certain reforms, like the broad expansion of Medicare and Medicaid, lead to more affordable insurance, thereby creating a healthier risk pool, reduced premiums, and improved health. This series of changes subsequently enhances labor productivity and the number of work hours. On the contrary, certain reforms that necessitate higher taxes, such as the Medicare expansion and the individual mandate, end up decreasing work hours.
Furthermore, I discovered that expanding insurance coverage does not invariably result in improved social welfare. In this context, social welfare is evaluated through the lens of CEV, and the impact of diverse reforms ranges between a decrease of 2.6% and an increase of 0.9%. While extending health insurance coverage doesn't necessarily equate to increased medical costs, it's worth mentioning that the government can balance welfare maintenance and cost containment during insurance coverage expansion by modifying cost-sharing, as demonstrated in Experiment A-1.
Given that the central focus of this paper is on the impact of reforms within the health insurance system, the decision was made to maintain the status quo in the health production sector during the transition. However, it is important to note that potential alterations in the demand for medical services postreform may indeed influence the supply side. A compelling expansion to the current paper would involve exploring the determinants of productivity in the medical sector and the pricing of medical services, as well as their potential shifts in response to these health insurance reforms. Moreover, comprehending the Pareto optimum within this framework is of paramount importance, particularly when considering how the policy experiments under review compare to the Pareto optimal solution.9 These intriguing aspects, however, are earmarked for future research.
ACKNOWLEDGMENTS
I am very grateful to Adrian Peralta-Alva and Manuel Santos for their advice and encouragement. My sincere thanks also extend to Luca Bossi, Pedro Gomis-Porqueras, Juergen Jung, David Kelly, Luis Locay, Jianjun Miao, Oscar Mitnik, Kai Zhao, the referee and Associate Editor of this journal, and seminar participants at the 14th International Conference on Computing in Economics and Finance, 2009 Midwest Macro Meeting, 2010 Royal Economic Society Conference, CUNY Queens College, FAU, FIU, Tilburg University, University of Miami, University of Zurich for helpful comments and insightful discussions. All remaining errors are mine.
CONFLICT OF INTEREST STATEMENT
The author declares no conflict of interest.
ETHICS STATEMENT
Not applicable.
APPENDIX A:
A.1 Computation algorithm to stationary equilibrium
Given the parameter values as shown in the text, I compute the stationary equilibrium as follows:
- Step 1.
Discretize the state space
 .
. - Step 2.
Start with an arbitrary pair of the steady state values of aggregate labor supply
 , tax rate
, tax rate  , bequest
, bequest 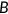 , and private health insurance premium
, and private health insurance premium 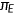 . Define
. Define 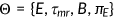 . Compute the value of wage
. Compute the value of wage  .
. - Step 3.
Agents solve their optimization problem.
- Step 4.
Simulate the economy:
- 4.1.
Set
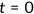 , there are
, there are 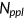 agents live in the economy, who are randomly assigned the values of
agents live in the economy, who are randomly assigned the values of 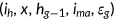 if young or middle-aged, and
if young or middle-aged, and 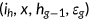 if retired.
if retired. - 4.2.
Given shocks agents choose whether to insure, how much to save, and how much to spend;
- 4.3.
New period starts,
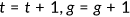 , the government collects the assets left behind by the accidentally deceased.
, the government collects the assets left behind by the accidentally deceased. - 4.4.
A sequence of time series is generated by repeating steps 4.2 and 4.3;
- 4.5.
Store the distribution of
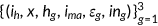 with
with 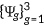 ;
; - 4.6.
Stop the process if the economy enters the stationary distribution.
- 4.1.
- Step 5.
Compute the insurance premium
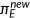 , aggregate labor supply
, aggregate labor supply 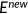 , bequest
, bequest 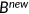 , and tax rate
, and tax rate 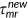 based on the distribution
based on the distribution 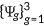 according to Equations (20), (5), (23), and (19). Denote
according to Equations (20), (5), (23), and (19). Denote 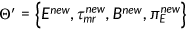 .
. - Step 6.
Find the fixed point of
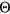 by iteration. If
by iteration. If  , set
, set  and return to step 3. Otherwise set
and return to step 3. Otherwise set  and define
and define
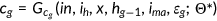 ()
()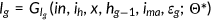 ()
()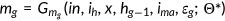 ()
()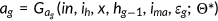 ()
()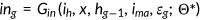 ()
()
A.2 Calibration
See Table A1.
| Parameter | Description | Values |
|---|---|---|
 |
Population growth rate | 1.25% |
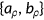 |
Parameters in survival probability | 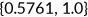 |
 |
Discount factor | 0.97 |
 |
Preference on leisure | 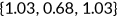 |
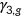 |
Preference on health | 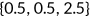 |
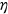 |
Relative risk aversion over health | 1.35 |
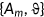 |
Health production | 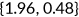 |
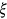 |
Parameter in health on labor | 0.1072 |
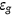 |
Health shock | See Table A2 |
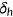 |
Health depreciation | See text |
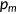 |
Price for medical service | See text |
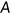 |
Total factor productivity | 8.0 |
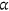 |
Capital share | 0.34 |
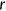 |
Interest rate | 4% |
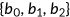 |
Income tax parameters (progressive part) | 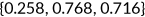 |
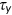 |
Income tax parameter (proportional part) | 4.46% |
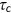 |
Consumption tax | 5.67% |
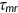 |
Medicare tax | 2.2% |
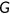 |
Government expenditure | 18.0% of GDP |
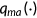 |
Medicaid coverage rate | See text |
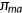 |
Medicaid premium | See text |
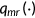 |
Medicare coverage rate | See text |
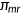 |
Medicare premium | See text |
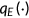 |
Private insurance coverage rate | See text |
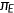 |
Private insurance premium | See text |
See Table A2.
| Age | Shock 1 | Shock 2 |
|---|---|---|
| 25–44 | −0.5 | −10.0 |
| 45–64 | −2.5 | −10.0 |
| 65–85 | −10.0 | −20.0 |
See Table A3.
| Bin | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
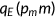 |
0.55487 | 0.61017 | 0.65671 | 0.70503 | 0.78060 |
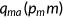 |
0.76524 | 0.81319 | 0.85763 | 0.88673 | 0.94784 |
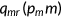 |
0.49942 | 0.57952 | 0.63345 | 0.69578 | 0.77799 |
See Table A4.
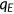 |
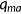 |
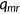 |
|
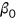 |
0.63632 (0.00144) | 0.83671 (0.00353) | 0.51344 (0.00416) |
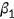 |
0.05444 (0.00079) | 0.02315 (0.00165) | 0.03223 (0.00266) |
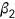 |
0.00546 (0.00371) | 0.00349 (0.00067) | 0.01477 (0.00094) |
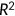 |
0.0863 | 0.0475 | 0.1634 |
A.3 Numerical results
See Table A5.
| Parameters | Data | Benchmark |
|---|---|---|
| All insured (in % of nonelderly) | 83.0 | 82.9 |
| w/Private insurance (in % of nonelderly) | 71.1 | 72.6 |
| w/Medicaid (in % of nonelderly) | 12.9 | 10.3 |
| Health expenditures (in % of GDP) | 16.3 | 16.1 |
| Labor supply (in % of total time) | 33.3 | 32.4 |
| Ratio of retired to active population (in %) | 24.3 | 24.9 |
| Marginal income tax at 10% quantile | 15.0 | 20.0 |
| Marginal income tax at 50% quantile | 26.0 | 25.4 |
| Marginal income tax at 99% quantile | 35.0 | 27.0 |
| Medicare tax (in %) | 2.9 | 2.2 |
| Ave. insurance premium (in % of per capita GDP) | 10.9 | 8.9 |
| Size of Medicaid & Medicare (in % of GDP) | 4.6 | 5.2 |
| Consumption and health expenditure profiles | See Figure 2 | |
| Gross saving rate (in %) | 21.0 | 24.5 |
| Mortality rate (age 25–44) | 0.0292 | 0.0322 |
| Mortality rate (age 45–64) | 0.1271 | 0.1343 |
REFERENCES
- 1 The distributions of health and health shock are known to the market and the government. However, the realization of health shock
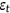 is not observable, which leads to asymmetric information in the insurance market.
is not observable, which leads to asymmetric information in the insurance market. - 2 See Bloom and Canning (2005). They model the human capital of the worker by
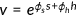 , where
, where 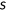 represents years of schooling and
represents years of schooling and 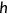 represents health. Here I normalize the effect of schooling.
represents health. Here I normalize the effect of schooling. - 3 In Suen (2006), Jung and Tran (2008) the health accumulation technology is characterized by
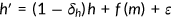 , which implies that the agent can be perpetual young and healthy as long as she/he invests enough into health. Here I modify their assumption and bound the current health by the remained health after natural aging.
, which implies that the agent can be perpetual young and healthy as long as she/he invests enough into health. Here I modify their assumption and bound the current health by the remained health after natural aging. - 4 Wobus and Olin (2005) found that the average health expenditure decreases with income level. This can be reconciled by the following fact. The low income has lower health insurance coverage rate. For people age under 65, the un-insurance rate among person in families with income less than 200% of poverty line is 24.5%, while the number is only 8.7% among person in middle and high income families. The price of medical services is much higher for uninsured due to the cost shifting (see Anderson, 2007), which implies the medical services utilized by low income families can be less than those used by the rich counterpart.
- 5 In the data, more than 90% nonelderly who have private insurance purchase through their employers.
- 6 Data source: http://www.census.gov/population/estimates/nation/intfile2-1.txt.
- 7 As for how to calculate these summary scores, please refer to Ware et al., How to Score the SF-12(r) Physical and Mental Health Summary Scales, QualityMetric, Inc., Lincoln, RI.
- 8 In the benchmark, 72.6% of nonelderly who purchase private insurance pay an actuarially fair premium
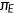 , which is about 8.9% of the per capita GDP.
, which is about 8.9% of the per capita GDP. - 9 I want to thank the referee for this insightful comment.




