International Journal of Intelligent Systems

Volume 37, Issue 10 pp. 7058-7078

RESEARCH ARTICLE

Open Access

Toward machine intelligence that learns to fingerprint polymorphic worms in IoT

Fangwei Wang,

Fangwei Wang

Key Laboratory of Network and Information Security of Hebei Province, Hebei Normal University, Shijiazhuang, China

College of Computer and Cyber Security, Hebei Normal University, Shijiazhuang, China

Search for more papers by this author

Shaojie Yang,

Shaojie Yang

College of Computer and Cyber Security, Hebei Normal University, Shijiazhuang, China

Search for more papers by this author

Changguang Wang,

Changguang Wang

Key Laboratory of Network and Information Security of Hebei Province, Hebei Normal University, Shijiazhuang, China

College of Computer and Cyber Security, Hebei Normal University, Shijiazhuang, China

Search for more papers by this author

Qingru Li,

Qingru Li

Key Laboratory of Network and Information Security of Hebei Province, Hebei Normal University, Shijiazhuang, China

College of Computer and Cyber Security, Hebei Normal University, Shijiazhuang, China

Search for more papers by this author

Kehinde O. Babaagba,

Kehinde O. Babaagba

School of Computing, Edinburgh Napier University, Edinburgh, UK

Search for more papers by this author

Zhiyuan Tan,

Corresponding Author

Zhiyuan Tan

[email protected]

School of Computing, Edinburgh Napier University, Edinburgh, UK

Correspondence Zhiyuan Tan, School of Computing, Edinburgh Napier University, 10 Colinton Road, Edinburgh EH10 5DT, UK.

Email: [email protected]

Search for more papers by this author

Fangwei Wang,

Fangwei Wang

Key Laboratory of Network and Information Security of Hebei Province, Hebei Normal University, Shijiazhuang, China

College of Computer and Cyber Security, Hebei Normal University, Shijiazhuang, China

Search for more papers by this author

Shaojie Yang,

Shaojie Yang

College of Computer and Cyber Security, Hebei Normal University, Shijiazhuang, China

Search for more papers by this author

Changguang Wang,

Changguang Wang

Key Laboratory of Network and Information Security of Hebei Province, Hebei Normal University, Shijiazhuang, China

College of Computer and Cyber Security, Hebei Normal University, Shijiazhuang, China

Search for more papers by this author

Qingru Li,

Qingru Li

Key Laboratory of Network and Information Security of Hebei Province, Hebei Normal University, Shijiazhuang, China

College of Computer and Cyber Security, Hebei Normal University, Shijiazhuang, China

Search for more papers by this author

Kehinde O. Babaagba,

Kehinde O. Babaagba

School of Computing, Edinburgh Napier University, Edinburgh, UK

Search for more papers by this author

Zhiyuan Tan,

Corresponding Author

Zhiyuan Tan

[email protected]

School of Computing, Edinburgh Napier University, Edinburgh, UK

Correspondence Zhiyuan Tan, School of Computing, Edinburgh Napier University, 10 Colinton Road, Edinburgh EH10 5DT, UK.

Email: [email protected]

Search for more papers by this author

First published: 27 March 2022

https://doi.org/10.1002/int.22871

Share a link

Email
Wechat
Bluesky

Abstract

Internet of Things (IoT) is fast growing. Non-personal computer devices under the umbrella of IoT have been increasingly applied in various fields and will soon account for a significant share of total Internet traffic. However, the security and privacy of IoT and its devices have been challenged by malware, particularly polymorphic worms that rapidly self-propagate once being launched and vary their appearance over each infection to escape from the detection of signature-based intrusion detection systems. It is well recognized that polymorphic worms are one of the most intrusive threats to IoT security. To build an effective, strong defense for IoT networks against polymorphic worms, this study proposes a machine intelligent system, termed Gram-Restricted Boltzmann Machine (Gram-RBM), which automatically generates generic fingerprints/signatures for the polymorphic worm. Two augmented N-gram-based methods are designed and applied in the derivation of polymorphic worm sequences, also known as fingerprints/signatures. These derived sequences are then optimized using the Gaussian–Bernoulli RBM dimension-reduction algorithm. The results, gained from the experiments involved three different types of polymorphic worms, show that the system generates accurate fingerprints/signatures even under “noisy” conditions and outperforms related methods in terms of accuracy and efficiency.

1 INTRODUCTION

The recent advancement of Internet of Things (IoT) technologies has turned our world more closely connected, and has begun to transform manufacturing, healthcare, transportation, and many other businesses. This revolutionary transformation will soon change the way we live, work, study, and entertain. However, data collected and stored on IoT devices tend to be sensitive personal information, which has always been in favor of cybercriminals. Attacks against IoT devices have seen a drastic increase since 2016. The outbreak of the VPNFilter malware^1-4 in 2018 resulted in serious damage to IoT infrastructure, and breach of sensitive data. The Mirai worm, for another example, has posed an active threat to the Internet infrastructure and IoT applications via its signatured massive Distributed Denial-of-Service (DDoS) attacks. Protecting IoT and its devices from being compromised by malware, therefore, is not only critical to assure the quality of services but also challenging due to the distributed, pervasive nature of IoT.

The 2019 Internet security threat report shows that the targets of ransomware attacks have shifted from consumers to enterprises, and the infection rate of enterprises in 2019 increased by 12% compared with the figure of 2018, which led to immeasurable economic loss. Meanwhile, worms have been used to attack IoT devices, with 75% of the intrusions targeting routing devices and 25% on connected cameras. Polymorphic worms are the height of sophistication in computer malware. They have been extensively studied and found posing the most damaging threats to IoT and its applications.⁵ Polymorphic worms can easily evade detection through changing their appearance, such as altering their byte sequence or varying their payload via compression, encryption, among other methods required no human intervention.⁶ Replicating themselves to appear differently in each infection makes polymorphic worms survive longer in a network. As polymorphic worms posing greater threats to the Internet infrastructures, the need for Internet service providers to secure their assets and protect their customers is growing. Fast detection and prevention against polymorphic worms have become more imperative.^{5, 7, 8}

Researchers have been working hard to develop defensive methods against them, for example, signature-based detection, statistical-based detection, behavior-based detection, and for forth. Generating reliable signatures to detect polymorphic worms is one of such means.^{9, 10} Signature-based detection methods are easy to implement and incorporate into firewalls, Network Intrusion Detection Systems (NIDSs) or antivirus software. At the initial stage of polymorphic worm discovery research, signatures were mostly generated by domain experts or at least with human intervention. The manual signature generation methods are slow and hence fail to keep up with the rate of propagation of polymorphic worms. Therefore, we need to automate the generation of signatures for newly found polymorphic worms to reduce the aforementioned time lag. Traditional automated signature generation approaches rely mainly on algorithm-generated tokens or regular expressions,^{1, 9, 11} capturing the critical sequence segments of known polymorphic worms. Although signature-based detection methods are suited for real-time detection, most of the traditional ones fail to recognize unseen variants of polymorphic worms as they reshape themselves over each propagation. The sequence segments found in new variants tend to be different from those previously obtained from older versions. As such, the detection systems based on these traditional automated signature generation methods suffer from a high false-negative rate,¹² and they are prone to new polymorphic worms.

Due to the above issues, more research in the polymorphic worm detection is yet to be carried out to find a suitable method to automate the generation of robust signatures. Some research has attempted to approach the problem by adopting machine learning frameworks to solve the corresponding mass malicious events. However, the re-active mechanism will never bring us a victory in the war with polymorphic worms. To win this battle, we need to proactively gain a good understanding of how the worms mutate themselves. A recent research proposed to use a Recurrent Neural Network (RNN) to predict and generate new variants of known polymorphic worms.¹³ This new invention was shown to be effective in contributing synthetic signatures of new predicted variants and providing a means of assessing the detection ability of NIDSs. However, this and other major related work still follow traditional weight-based and regular-matched automatic generation methods that do not take semantics-derived characteristics of worm payloads into account. So, they cannot predict the deformation of polymorphic worms.

To leverage the semantics-derived characteristics, a natural-language processing (NLP) algorithm, N-gram, is adopted in this paper. The N-gram algorithm has a strong binding force that retains correlation between words. As the data format of most polymorphic worm traffic (including Hypertext Transfer Protocol [HTTP] request methods, proxy information, data content, etc) is relatively fixed during their propagation and the worms are comprised of different sequence segments, each of which is with a different meaning, the N-gram can help extract semantics-derived characteristics between segments to derive more accurate polymorphic worm signatures. However, the N-gram algorithm might ignore some reasonable words, resulting in a zero probability phenomenon. The N-gram smoothing techniques can not only eliminate the zero probability problem but also make the probability of prediction words more uniform. So, we improve it through some smoothing methods until it is suitable to generate signatures of polymorphic worms with high efficiency. Besides, we investigate the dimension-reduction algorithm—Gaussian–Bernoulli Restricted Boltzmann Machine (Gaussian–Bernoulli RBM) and combine it with N-gram to improve the accuracy of signature generation. Finally, the system does not only classify many kinds of polymorphic worms but also generates new polymorphic worm sequences, which are used to verify the effectiveness of the proposed system. Experiment results show that Gram-RBM achieves better performance even under noisy condition.

The rest of this paper is organized as follows. Section 2 gives the background to this study and presents a review of related work. Section 3 presents the automated signature generation scheme for polymorphic worms with subsections that discuss our smoothing N-gram algorithm as well as explain and implement the Gaussian Bernoulli RBM algorithm. Section 4 presents our experimental results supporting our theoretical analysis. It describes how the signatures are generated, and the processes involved in classifying some types of polymorphic worms. Finally, Section 5 concludes this paper.

2 RELATED WORK

Polymorphic worms can identify potentially vulnerable hosts, launch directed attacks against such targets, and destroy the Internet infrastructure and target services. In the IoT environment, polymorphic worms are even more dangerous and destructive. As signature-based detection is easy to implement, signature generation for polymorphic worms has been extensively studied over the past decade.^14-16 The accuracy of worm detection mainly depends on the quality and quantity of worm signatures. Most related research works relied mainly on manual or semiautomated methods.¹⁷ However, due to their polymorphism and harms to network participants and infrastructure, polymorphic worms need to be studied promptly once being discovered to mitigate their propagation and minimize losses. Automated signature generation methods or systems have been increasingly studied in recent years. In this section, some important related automated signature generation methods for polymorphic worms based on invariant bytes or other signatures are emphasized. The approaches of signature generation for polymorphic worms can be classified into four categories, which are as follows: content-based, multiple-sequence-alignment-based, simplified-regular-expression-based, and natural-language-processing-based signature generation.

2.1 Content-based signature generation

Content-based detection relies on tokens as worm signatures to detect worm traffic. The term “token” refers an independent substring that appears in at least $K$ out of $n$ samples in a pool of suspects. When the byte pattern of a given network traffic flow matches the token(s), the traffic is identified as worm traffic. Since polymorphic engines protect the payload of worms, the semantics of worm traffic does not change in nature over each infection, which makes content-based signature generation possible. Newsome et al. proposed the polygraph to automatically detect polymorphic worms for the first time.¹⁴ For a given suspicious traffic pool, the polygraph generated three types of tokens: conjunction signature, token-subsequence signature, and Bayes signature. Combined with the above three types of tokens, the polygraph generated complicated signatures using hierarchical clustering methods. However, the polygraph probably generates wrong signatures under noisy condition.¹⁸ On the basis of polygraph, Li et al. presented the HAMSA to improve the accuracy of the generated signatures of polymorphic worms even under noisy conditions.¹⁵ Moreover, compared with the polygraph, the HAMSA is fast and resilient to attack. The HAMSA takes the frequency of token occurrences as a part of the signature, and uses the score function to determine the set of tokens as the final signature to detect polymorphic worms, which could cause unmatched signatures, and lead to a higher false-positive rate. Moreover, the HAMSA is also sensitive to suspicious pool size. Thus, to detect unknown worms, it is best to enlarge the suspicious pool size. Bar et al. used the Markov chain model to capture diverse vulnerability-based polymorphic worms.¹⁹ They found that it was difficult to obtain such tokens. The reason is that the signature could not work properly if there was not a return address. These content-based signatures might not be generic enough and could be evaded by other exploits.

2.2 Multiple-sequence-alignment-based signature generation

Inspired by bioinformatics, the Multiple-Sequence Alignment (MSA) technique converts every worm sample to a DNA-like sequence, and adopts Needleman–Wunsch and Smith–Waterman algorithms to compute the similarity between two proteins or multiple proteins. Using MSA, Ki et al. identified malicious functions in different types of malware and turned them into an Application Programming Interface (API) call sequence.²⁰ This method adopts dynamic information of API call sequence patterns instead of malware's static information, such as file size, process, and it can even be used to detect new unknown malware. Kim et al. used MSA to generate malware behavioral “feature-chain” patterns.²¹ To deal with some obfuscation techniques, such as encoding, antivirtualization, and encapsulation, used by polymorphic worms, Kim et al. implemented a detection system using API and MSA,²² which achieved higher performance in terms of precision, accuracy, and false positive. The main drawback of these methods is that they need a huge amount of memory and have a high computational complexity.

2.3 Simplified-regular-expression-based signature generation

Building simplified-regular expressions to match patterns of malicious content is a common approach of detecting polymorphic worms. Accurate regular expressions can efficiently match the critical content in a polymorphic worm traffic sequence, thus distinguishing polymorphic worms from normal traffic. Aljawarneh et al. proposed a polymorphic worm detection method based on regular expressions and pointed out the feasibility of using a simplified-regular expression matching method in the signature generation of polymorphic worms.¹¹ Their method takes the distance constraint of polymorphic worm traffic sequences into consideration and generates separate signatures for different polymorphic worms, which leads to low efficiency and a high false-negative rate in detecting polymorphic worms. Eskandari et al. remedied the aforementioned issues and proposed an extended regular expression signature extraction method, referred to as ERES.²³ However, the signature generation system of polymorphic worm based on regular expression matching is complicated in designing, and the traditional matching algorithm needs to adjust when it is used in variants of polymorphic worms.

2.4 Natural-language-processing-based signature generation

N-gram is an important concept in NLP. The N-gram algorithm can be used to evaluate the difference between two strings. In recent years, researchers have used the N-gram algorithm in worm detection and worm signature generation. Lim proposed an approach to represent malicious behaviors of software with API functions,²⁴ which combined the N-gram algorithm with API sequences to detect unknown malware. However, the model was relatively simple so that it did not involve in generating the signature of unknown malware. Due to quite predictable behaviors in IoT devices, An et al. presented a naive anomaly classifier for home router based on the N-gram algorithm.²⁵ This classifier detected abnormal behaviors by investigating the Probability Mass Function (PMF) difference of bi-grams between clean traces and those of infected traces, and the system can detect Mirai three variants. Experiment results show that the naive anomaly classifier based on N-grams outperforms the Principal Components Analysis (PCA)-based anomaly detector. Zhao et al. proposed a feature selection method of hybrid N-gram with joint cross entropy.²⁶ On the basis of the dynamic behavior tracking and feature analysis of native API in virtual environment, the method is of adaptive variable length N-gram. In the paper, N-gram method is used to distinguish malicious behaviors.

We can find, most literatures use N-gram algorithm to distinguish the abnormal from the normal traffic; few papers use N-gram algorithm to generate a worm signature. Moreover, smoothing N-gram algorithm is rarely involved in worm detection and generating the signature of the polymorphic worm. Meanwhile, the smoothing N-gram algorithm has achieved better effect in NLP.^{27, 28} Inspired by the payload of a polymorphic worm being a string sequence and the better performance of the smoothing N-gram algorithm in NLP, in this paper, we propose a novel system of signature generation for polymorphic worms, named Gram-RBM, in which the N-gram model is improved according to data characteristics of polymorphic worm traffic and combined with the Gaussian–Bernoulli RBM algorithm.

3 AN AUTOMATED SIGNATURE GENERATION SYSTEM FOR POLYMORPHIC WORM

To reduce the losses caused by polymorphic worms in IoT, overcome the drawbacks of current methods and generate more accurate signatures of such worms, we propose an automated signature generation system based on NLP. First, we use two smoothing N-gram algorithms to generate invariant sequences. Second, we transform invariant sequences into a matrix. Finally, we use Gaussian–Bernoulli RBM to reduce the dimension for generating accurate lower-dimensional polymorphic worm signatures. Our proposed automated signature generation system for a polymorphic worm is shown in Figure 1, which consists of seven components: N-gram algorithms, selection of N-gram algorithm, invariant extraction, transforming the invariants into a matrix, dimension reduction, signature generation, and classification, which are briefly explained below and detailed in Sections 3.1–3.6.

Smoothing N-gram algorithms: This comprises the Laplace N-gram algorithm and the Good-Turing N-gram algorithm. These two algorithms are based on traditional N-gram, and they have different performances for different types of polymorphic worms.
Selection of an optimal N-gram algorithm: We use the degree of perplexity to evaluate two N-gram smoothing algorithms, which are more suitable for invariant extraction of a specific type of polymorphic worm.
Invariant extraction: After a suitable smoothing N-gram algorithm is selected, it is used to generate multiple invariant sequences.
Transforming the invariants into a matrix: In this step, invariant sequences are transformed into a matrix using Term Frequency-Inverse Document Frequency (TF-IDF), because RBM can only deal with numeric matrix in the standard format.
Dimension reduction: Although the Bernoulli-RBM algorithm is well suited for training small-sample data sets, it retains noise in the processing of signature extraction. Gaussian–Bernoulli RBM can solve this problem; therefore the signature accuracy is improved.
Signature generation: In this part, Gaussian–Bernoulli RBM is used to generate signatures.
Classification: The generated signatures are then used to classify new instances of polymorphic worms.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The flowchart of an automated signature generation system for polymorphic worm

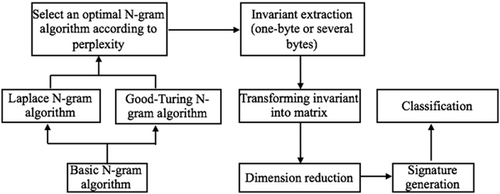
3.1 Smoothing N-gram algorithms

The advantage of the N-gram algorithm lies in its strong constraint, which can contain enormous word information. In the transmission process of a polymorphic worm, each small signature sequence has its meaning, which enables the N-gram algorithm to generate worm signatures through strongly constrained static analysis.

However, the N-gram algorithm has its disadvantages: complicated calculation, sparsity, and high dimensionality. In the following sections, we will use smoothing N-gram algorithms to avoid these problems. The presentation of the principle of the basic N-gram model will help understand the smoothing N-gram methods. So we will introduce the principle of basic N-gram in the following section.

3.1.1 The principle of the basic N-gram model

The N-gram algorithm is based on the Markov assumption²⁹ and uses the Maximum Likelihood Estimation (MLE) as a conditional probability. The N-gram algorithm builds the context characteristics of sentences by the comparison of sentence similarity, the query of ambiguity, the analysis of sentence rationality, and finally produces signatures. The basic N-gram model is easy to implement and improve. So, it has gained popularity and is one of the most commonly used language models in NLP. As a special “language” traffic signatures can be extracted by the N-gram algorithm.

To better describe the principle of the N-gram algorithm, we follow the functions and notations of Reference [23] throughout this paper. Let us take the Apache-knacker worm as an example. The probability $P(x)$ of each word $x$ in a sentence serves as a reference for the imitation statement. Taking the Apache-knacker worm¹⁴ as an example, which has the following three related HTTP requests.

S1:
$GET\ldots HTTP\unicode{x02215}1.1\backslash r\backslash n\ldots \backslash r\backslash nHost\ldots$
S2:
$GET\ldots HTTP\unicode{x02215}1.1\backslash r\backslash n\ldots \backslash r\backslash nHost\ldots$
S3:
$POST\ldots HTTP\unicode{x02215}1.1\backslash r\backslash n\ldots \backslash r\backslash nHost\ldots$

Given S1 treated as a statement of length

n

, its probability is computed using (1) and denoted as

P(\,S1\,)=P({x}_{1},{x}_{2},\ldots ,{x}_{n})

, where

{x}_{i}

(

1\le i\le n

) refers to the

i

th word in S1. This results in a conclusion that the word

{x}_{1}

= “POST” in S3 is a typo, as the probabilities of HTTP requests S1, S2, and S3 show the following relationship:

P\text{(}\,S1)\approx P(S2)\gt P(S3\,)

. Consequently, “GET” will be selected as the word appearing at

{x}_{1}

P(\,S\,)=p({x}_{1},{x}_{2},\ldots ,{x}_{n}).

(1)

According to the formula of conditional probability, the joint probability of a long sequence S is the product of the probabilities of individual word

{x}_{i}

in S =

\{{x}_{1},{x}_{2},\ldots ,{x}_{n}\}

P({x}_{1},{x}_{2},\ldots ,{x}_{n})=P({x}_{1})P({x}_{2}| {x}_{1})P({x}_{3}| {x}_{1},{x}_{2})P({x}_{n}| {x}_{1},{x}_{2},\ldots ,{x}_{n-1}).

(2)

However, (2) is difficult to compute in practice, we use the Kolmogorov and Markov hypothesis to reduce the computational complexity and deduce the general form. Supposing that each word

{x}_{i}

(

1\le i\le n

) is related to the first

m-1

(

m\in {n}^{+}

) finite words, we obtain the following equation:

P({x}_{n}| {x}_{1},{x}_{2},\ldots ,{x}_{n-1})=P({x}_{n}| {x}_{n-m+1},\ldots ,{x}_{i},\ldots ,{x}_{n-1}).

(3)

Now, let $N$ be the number of elements in the gram algorithm. When $N=1$ , the algorithm is called as Uni-gram, also known as the context-free model. When $N=2$ , it is called Bi-gram, and When $N=3$ , it is called ternary grammar (Tri-gram). The length of $N$ determines the computational complexity. Considering the required resource for calculation, $N$ usually takes a smaller value in practice. The common N-gram algorithm is as follows:

Uni-gram: $P({x}_{1},{x}_{2},\ldots ,{x}_{n})={\prod }_{i=1}^{n}P({x}_{i})$ .

Bi-gram: $P({x}_{1},{x}_{2},\ldots ,{x}_{n})={\prod }_{i=1}^{n}P({x}_{i}| {x}_{i-1})$ .

Tri-gram: $P({x}_{1},{x}_{2},\ldots ,{x}_{n})={\prod }_{i=1}^{n}P({x}_{i}| {x}_{i-2},{x}_{i-1})$ .

N-gram is very complicated to calculate, so MLE is used to reduce computational complexity.

3.1.2 Maximum likelihood estimation

MLE²² is a statistical method used to find the parameters of the probability density function of a sample set. In general, the N-gram model is constructed by calculating the MLE. Meanwhile, MLE solves the problem of complicated calculation and sparsity. The most critical problems to be solved after constructing the basic N-gram algorithm are to estimate the conditional probability of the next word appearing and calculate the occurrence probability $P({x}_{i})$ of the word ${x}_{i}$ ( $1\le i\le N$ ). Assuming that $C({x}_{i})$ is the number of occurrences of the word ${x}_{i}$ occurrence in the polymorphic worm data set used to train the model, the following equation is derived according to different values of $N$ :

Uni-gram:

P({x}_{i})=\frac{C({x}_{i})}{\,\text{Total words in data sets}\,}.

(4)

Bi-gram:

P({x}_{i}| {x}_{i-1})=\frac{C({x}_{i-1},{x}_{i})}{C({x}_{i-1})}.

(5)

Tri-gram:

P({x}_{i}| {x}_{i-2},{x}_{i-1})=\frac{C({x}_{i-2},{x}_{i-1},{x}_{i})}{C({x}_{i-2},{x}_{i-1})}.

(6)

N-gram:

P({x}_{i}| {x}_{i-n-1},\ldots ,{x}_{i-1})=\frac{C({x}_{i-n-1},\ldots ,{x}_{i})}{C({x}_{i-n-1},\ldots ,{x}_{i-1})}.

(7)

In the processing of calculation, in many cases, the probability estimated from the training set is likely to be zero, which leads to useless output. To avoid zero probability problems, most N-gram models use some smoothing algorithms. More importantly, the smoothing technologies can improve the accuracy of MLE and can find more reliable estimations that help extract the signature of a polymorphic worm. The algorithm implementation is shown in Algorithm 1.

Algorithm 1. Pseudocode for N-gram algorithm.

Input:

N

, polymorphic worm data sets

Output: Signatures of polymorphic worm

1: Confirming the number

N\ge 1

;

2: Preprocessing the data sets, deleting special characters, such as

\backslash

and space;

3: Testing data for formatting problem;

4: Forming the new data set NEW_Data according to the optimal N-gram algorithm and training it;

5: Getting the total word count of NEW_data and creating a dictionary of word combinations by the optimal N-gram algorithm;

6: If the training sets are changed, appending words to the dictionary;

7: Building N-gram model according to Equation (7);

8: Generating signature using the MLE.

3.1.3 Laplace-smoothing N-gram algorithm

This smoothing technique is used to solve the sparsity problem in a data set. According to the N-gram model with MLE, a Laplace-smoothing parameter

V

is added to adjust the smoothness in the probability calculation. On the one hand, the problem of zero probability is solved by parameter

V

. On the other hand, Laplace smoothing introduces a substantial allocation of the probability space for words or word pairs in the corpus missing from the observed next sentences. To improve computational efficiency, we use a distinct parameter

V

for every type of polymorphic worms to adjust the smoothing problem in the probability calculation. The Laplace-smoothing N-gram conditional probability is now defined as

P({x}_{i}| {x}_{i-n-1},\ldots ,{x}_{i-1})=\frac{C({x}_{i-n-1},\ldots ,{x}_{i})+V}{C({x}_{i})+V}.

(8)

To further improve the Laplace-smoothing performance, Equation (8) is improved as follows according to Reference [15]:

{C}^{* }({x}_{i-n-1},\ldots ,{x}_{i})=\frac{\lfloor C({x}_{i-n-1},\ldots ,{x}_{i})+V\rfloor }{C({x}_{i})+V}.

(9)

Therefore, the Laplace-smoothing algorithm can be expressed as

P({x}_{i}| {x}_{i-n-1},\ldots ,{x}_{i})=\frac{{C}^{* }({x}_{i-n-1},\ldots ,{x}_{i})+V}{C({x}_{i})+V}.

(10)

In our experiment, the range of $V$ is $[0.0001,1]$ . The performance of the Laplace-smoothing N-gram algorithm with respect to different smoothing parameters is observed.

3.1.4 Good-Turing smoothing N-gram algorithm

The Good-Turing smoothing is a statistical technique for estimating the probability of encountering an N-gram from an unseen piece of text, given a set of past observations of N-grams from different pieces of text. The principle of Good-Turing is to smooth the frequency by using the category information and finally solve the sparsity problem. The smoothing improvement is useful in small-sample data sets. In the real world, because polymorphic worm data is scarce compared with normal traffic, it is essential to use a small amount of data to generate the invariants of polymorphic worms.

According to the literature,³⁰ the Good-Turing N-gram smoothing model with MLE can be expressed as

P({x}_{i})=\frac{1}{{N}_{r}}\frac{(C({x}_{i})+1){N}_{C({x}_{i})+1}}{{N}_{C({x}_{i})}},

(11)

where

{N}_{r}={{\rm{\Sigma }}}_{C({x}_{i})}C({x}_{i}){N}_{C({x}_{i})},C({x}_{i})

is the number of occurrences of the word

{x}_{i}

occurrence,

{N}_{C({x}_{i})}

denotes the number of N-grams that occurred

C({x}_{i})

times.

Now we have two smoothing algorithms, which are Laplace-smoothing and Good-Turing Smoothing N-gram algorithm, respectively. To achieve a better smoothing effectiveness, we use different smoothing techniques for different training data sets.

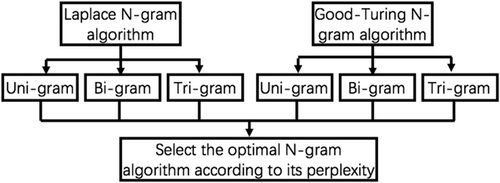
3.2 Selection of N-gram algorithms

Perplexity measures how well a probability distribution/model that predicts a sample. It can be used to evaluate probability models. A lower perplexity indicates the probability distribution is better at predicting the samples.³¹ Perplexity can also be interpreted as the weighted average branching factor of a language. The branching factor of a language is the number of possible next words that can follow any word.

The perplexity, also known as PP, of a language model on a test set is a function of the probability that the language model assigns to the test set. For a test set

W={w}_{1}{w}_{2}\ldots {w}_{N}

, the perplexity is the probability of the test set, normalized by the number of words:

PP(W)=P{({w}_{1}{w}_{2}\ldots {w}_{N})}^{-\frac{1}{N}}=\sqrt[N]{\frac{1}{P({w}_{1}{w}_{2}\ldots {w}_{N})}}.

(12)

We can use the chain rule to expand the probability of

W

PP(W)=\sqrt[N]{\prod _{i=1}^{N}\frac{1}{P({w}_{i}| {w}_{1}{w}_{2}\ldots {w}_{i-1})}}.

(13)

Minimizing perplexity is equivalent to maximizing the test set probability according to the language model.

The different N-gram algorithms will achieve different perplexities on a polymorphic worm data set. The degree of perplexity is a key criterion for selecting the algorithm. As such, we select a proper N-gram algorithm for every data set involved in this study work according to its perplexity, as illustrated in Figure 2, in which two smoothing methods are for consideration, each is evaluated against Uni-gram, Bi-gram, Tri-gram, respectively. Each of these smoothed N-gram algorithms, where N = [1, 2, 3], is used to evaluate against different polymorphic worm data sets and obtain a perplexity value. The algorithm achieving the lowest perplexity is selected in accordance with the principle that the lower perplexity of a probability model, the less optional invariants and more accurate fingerprints it provides. In Section 4, we will demonstrate how an N-gram algorithm is selected according to its perplexity.

3.3 Invariant extraction

After the optimal N-gram algorithm is selected for a type of polymorphic worm, it is then used to generate invariant sequences of the polymorphic worm.

The sequence of invariants generated will increase gradually over time. With the increase of generated sequences, the frequency of certain words increases. The words that occur frequently can distinguish different types of polymorphic worms. These words can be roughly identified as signatures. However, to further confirm whether these words are signatures of a given polymorphic worm, there is a need for conversion from multiple sequences to a matrix for further dimension reduction in the training process.

3.4 Transforming the invariants into a matrix

In Section 3.3, some invariant sequences which we have achieved may be very long and have many signatures. To find the signatures of polymorphic worms, we transform these sequences into a matrix, then use a dimension-reduction algorithm to exactly confirm the signatures of polymorphic worms.

The TF-IDF Vectorizer functions in the framework of scikit-learn are used in signature transformation; finally, invariants are transformed into a matrix.

3.5 Dimension reduction

Neither the smoothing Laplace N-gram algorithm nor the smoothing Good-Turing N-gram algorithm solves the dimension explosion issue. To solve this problem, first we observed Bernoulli RBM algorithm, then its improvement—Gaussian–Bernoulli RBM is utilized to address the dimension curse. Before the Gaussian–Bernoulli RBM algorithm is used, we need to generate multiple invariant sequences by selecting proper smoothing N-gram algorithm, and then transform them into a matrix.

A Bernoulli RBM can be used for dimension reduction, classification, and signature extraction. It is suited for training small-sample data sets, however, it retains noise in signature extraction. With the increasing number of polymorphic worm data sets, it is difficult for the Bernoulli RBM algorithm to make a more detail division of the eigenvalues, which tend to be the same because the worm sequences are more irregular than natural language. To better classify the characteristics of polymorphic worms and improve the accuracy of signature generation, this paper adopts the precision matrix to parameterize the Gaussian distribution.³²

The Gaussian–Bernoulli RBM algorithm, which is an improvement of Bernoulli RBM, reduces effectively the dimension curse that may be caused by noise interference of the smoothing N-gram algorithm in the detection system, which results in a large number of useless signatures in the detection system and affects classification accuracy. Its advantages are as follows. First, compared with PCA and other algorithms, the Gaussian Bernoulli RBM algorithm can retain the invariant of polymorphic worms for training, so it can improve the accuracy of signature generation. Second, the Gaussian Bernoulli RBM is easy to implement and can quickly generate polymorphic worm signatures.

The processes of using the Gaussian–Bernoulli RBM algorithm to generate signatures are as follows. First, the visible unit is used as a conditional distribution by Gaussian distribution, which reduces noise interference. Second, the accuracy of signature extraction is improved through the use of an accuracy matrix. Finally, we evaluate the experimental results to ascertain improvement feasibility.

3.6 Signature generation

The invariant sequence with polymorphic worm signatures is converted into a vector matrix and then put into the Gaussian–Bernoulli RBM. First, the hidden layer converts the vector matrix to a weight matrix. Then, to obtain the invariants, the visible layer divides the weight matrix according to the threshold which is gotten from the training processing. The subtrings whose weights are higher than the threshold are considered as invariants. Finally, the invariants are sorted in a descending order of frequency and the signatures of the polymorphic worm are determined by the reduced dimensions generated from RBM. Compared with the Bernoulli RBM algorithm, the signatures generated by Gaussian–Bernoulli RBM are more accurate. We classify the new-coming polymorphic worms under noisy conditions according to the signatures generated by different species of polymorphic worms. We then compare the performance of several algorithms and evaluate the effectiveness of the Gaussian–Bernoulli RBM algorithm in generating signatures for polymorphic worms.

4 EXPERIMENT RESULTS AND ANALYSIS

4.1 Data sets

We evaluate the feasibility of our proposed N-gram algorithm in this section. The experiments are carried out on a Windows 7 machine with a maximum memory space of 2 GB. The original data sets used in the experiment are all from real polymorphic worm traffic, and the whole data set includes 13,292 records, which consists of three families of polymorphic worms: Apache-knacker, ATPhttpd, and BIND-TSIG. Noisy data is collected from legitimate traffic of the real environment.

4.2 Signature generation under noise-free condition

4.2.1 Invariants extraction by N-gram algorithm

To test the effectiveness of the N-gram algorithm in processing large-scale polymorphic worm data, this paper first considers the signature extraction problem in noise-free conditions. Three types of polymorphic worms are selected and 2000 pieces of data are randomly selected for each type of worm. Thereafter, the data is divided into a training set and a test set according to the ratio of 8:2. The training process is done using unsupervised learning. The running time of each N-gram smoothing improvement algorithm is shown in Table 1. LS and GTS represent Laplace_Smoothing, Good-Turing_Smoothing, respectively.

Table 1. Running time of each algorithm

Worm type	Method	Parameter ( $V$ )	Uni-gram (S)	Bi-gram (S)	Tri-gram (S)
Apache-knacker	LS	0.0001–0.1	2.53	3.46	7.72
	GTS	NA	2.84	3.72	$\gt 60$
ATPhttpd	LS	0.0001–0.1	3.34	4.10	9.94
	GTS	NA	4.36	3.61	$\gt 60$
BIND-TSIG	LS	0.0001–0.1	2.78	3.82	9.27
	GTS	NA	3.44	4.27	$\gt 60$

Abbreviations: LS, Laplace_Smoothing; GTS, Good-Turing_Smoothing.

As can be seen from Table 1, different smoothing algorithms with different parameters need different running times. Without considering the accuracy, the Uni-gram Laplace-smoothing is the most time-efficient regardless of the model and polymorphic worm family. We also notice that the Tri-gram Laplace-smoothing takes a significantly longer time compared with the other two algorithms. The reason is that Tri-gram needs to retrieve three words at a time as a combination, and the semantics of polymorphic worm sequences are very complex. So multiple combinations are generated, thus the complexity of prediction is increased. Since it takes a too long time, Tri-gram is not suitable for fast, automatic polymorphic worm signature extraction. Thus, this paper does not consider the comparison of Tri-gram Good-Turing smoothing algorithm with others.

We also find from Table 1, the Bi-gram takes a longer time than the Uni-gram, however, less than the Tri-gram, that is, showing a relatively eclectic performance. Therefore, based on the running time of the algorithms, it is impossible to determine which algorithm is better suited to deal with multifamilies polymorphic worm signatures extraction. To further assess the performance of each method, the perplexity is used to evaluate each algorithm. Figure 3 demonstrates that the relation between the Laplace-smoothing parameters and the different perplexity values generated by the algorithm under different Laplace-smoothing parameters. The lower the perplexity is, the less the predicted word number is, and the more accurate the signatures of the polymorphic worm is. On the contrary, if the algorithm has larger perplexity, it means that the algorithm can choose a large number of words, and thus the algorithm cannot accurately predict the sequence format of this kind of worm, so the signature extraction of polymorphic worm is not accurate. Therefore, N-gram algorithms can implement preliminary invariants extraction.

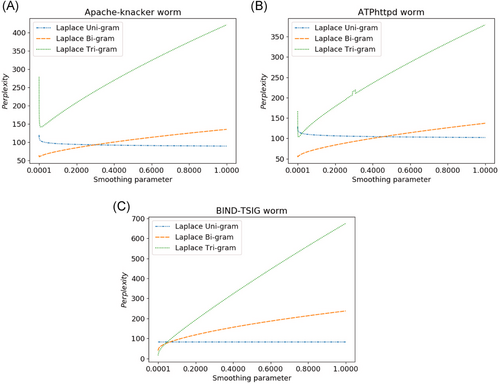
To further assess the performance of each method, we calculate the perplexity value of unsmoothing and each algorithm, shown in Table 2. Table 2 gives the optimal perplexity values corresponding to Laplace-smoothing and Good-Turing smoothing algorithm. As seen from Table 2, Laplace-smoothing and Good-Turing smoothing algorithms are better than the unsmoothing algorithm. Relatively, the Bi-gram algorithm has an average performance in terms of its operation time and perplexity values. In general, each algorithm has its advantages and disadvantages. In this section, the invariant extraction of the three types of polymorphic worms is mainly based on the optimal perplexity. Therefore, more accurate polymorphic worm invariants are generated. Under noise-free conditions, two optimal algorithms are selected for the invariant extraction experiment, and the results are shown in Table 3.

Table 2. Perplexity comparison of unsmoothing, LS, and GTS

Type	N-gram algorithm	Unsmoothing perplexity	V	Perplexity	GTS perplexity
			LS
Apache-knacker	Uni-gram	88.9275	1.0000	88.9284	72.4946
	Bi-gram	134.8406	0.0015	59.6890	34.3630
	Tri-gram	421.5418	0.0102	141.2369	NA
ATPhttpd	Uni-gram	101.9952	1.0000	102.0265	89.0469
	Bi-gram	137.1170	0.0011	54.8025	34.2018
	Tri-gram	379.1658	0.0047	103.1268	NA
BIND-TSIG	Uni-gram	82.4154	0.5025	82.3783	91.0920
	Bi-gram	237.3715	0.0001	39.0999	42.4032
	Tri-gram	675.1257	0.0001	15.6948	NA

Abbreviations: LS, Laplace_Smoothing; GTS, Good-Turing_Smoothing.

Table 3. Invariants under noise-free condition

Best algorithm	Apache-knacker	ATPhttpd	BIND-TSIG
Good-Turing smoothing (Bi-gram)	“GET,” “HTTP/1.1\r\n,” “\r\nHost,” “nHost:,” “xff\xbf,” “x*f $\unicode{x0007E}$ ,” “x^$ $\unicode{x0007E}$ ”	“GET/,” “HTTP/1.1\r\n,” “xff\xbf,” “x*f $\unicode{x0007E}$ ,” “Accept:”	“\x00\x00 $\unicode{x0007E}$ ,” “\x00\xF,” “xFF\xBF,” “xdf $\unicode{x0007E}$ ,” “xFF\x**,” “xee:”
Laplace-smoothing (Tri-gram)	“GET,” “HTTP/1.1\r\n,” “\r\nHost,” “nHost:,” “xff\xbf,” “\r\n,” “nGET”	“GET/,” “HTTP/1.1\r\n,” “xff\xbf,” “nGET\1.1\r\n”	“\x00\x00 $\unicode{x0007E}$ ,” “ $\unicode{x0007E}$ \x00\xFA,” “\xFF\xBF,” “.\xx00**”

The invariant extraction process of the smoothing N-gram algorithm is as follows. Take the Apache-knacker worm, for example, when the signature set is {“GET,” “HTTP/1.1\r\n,” “\r\nHost”}, the traffic data is normal. Since the training set consists of noise-free worm data sets, the smoothing N-gram algorithm carries out probability distribution based on the characteristics of polymorphic worm, so the suspicious Apache-knacker sequence segments are inferred as the characteristics of this kind of worm. Take Good-Turing smoothing and Laplace-smoothing as examples, the set of Apache-knacker worm characteristics inferred from Good-Turing smoothing is {“GET,” “HTTP/1.1\r\n,” “\r\nHost,” “xff\xbf”}. Since the signature “xff\xbf” is abnormal traffic data, and this signature “xff\xbf” appears frequently in the data set, it can be considered as worm signature. Because the polymorphic worms change their appearance, the other invariant set may be {“GET,” “HTTP/1.1\r\n,” “\r\nHost,” “xff\xbf,” “x^$ $\unicode{x0007E}$ ”}, and “x^$ $\unicode{x0007E}$ ” represents the morphological deformation of polymorphic worm caused by the nonoperation instruction or encryption. In terms of Laplace-smoothing invariant extraction, although the set {“GET,” “HTTP/1.1\r\n,” “\r\nHost,” “xff\xbf”} containing worm signatures are generated, the polymorphism of Apache-knacker results in false inference of worm signatures, such as “nGET.”

Although the smoothing N-gram algorithm can sometimes make wrong inferences on invariants, such as “nGET” in the training stage, its invariant inference method is still very effective to find potential signatures of polymorphic worms. Thus, the algorithm does not only extract the invariants of known polymorphic worms but also continuously infer the possible deformation invariants of worms. However, this step might extract a huge number of invariants of polymorphic worms, which causes the problem of dimension curse and increases the difficult of defending against polymorphic worms.

4.2.2 Signature generation by Gaussian–Bernoulli RBM

The Gaussian–Bernoulli RBM is used to prevent effectively the dimension curse caused by the smoothing N-gram algorithms. It determines whether the generated invariants by smoothing N-gram algorithm are polymorphic worm signatures through dimension reduction, so the accuracy of worm signatures is improved. To better present the validity of the Gaussian–Bernoulli RBM algorithm, the results of signature generation are compared with those of the Bernoulli RBM algorithm. The experiment is based on the invariant sequence of Apache-knacker worm inferred by the Good-Turing smoothing Bi-gram algorithm. To better show the experimental results in the form of thermal map, 100 invariant sequences are selected and divided into a training set and a test set by a ratio of 5:5. And two dimension-reduction algorithms are adopted for signature extraction. The extraction results of Apache polymorphic worm are shown in Figures 4 and 5.

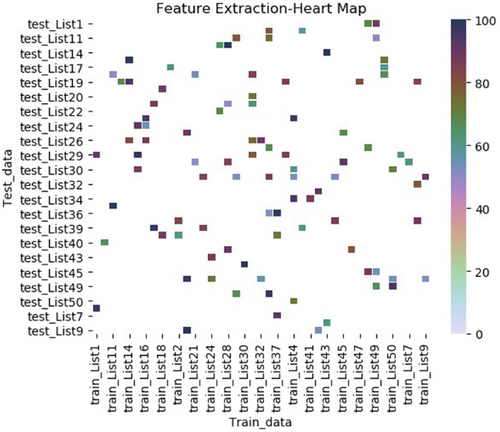
The performance of the two RBM algorithms is shown in the form of thermal diagram. The importance of signatures generated can be observed by the combination of signature weights. In the thermal map, the darker the points are, the more important the invariants are. In this paper, we show the thermal diagram of the Apache-knacker worm. As can be seen from the figures, there are more points in Figure 4 than those in Figure 5, which indicates that the signatures generated by the Gaussian Bernoulli RBM are more accurate than those generated by the Bernoulli RBM. In Figure 4, the colors of the points are relatively dark and there is not an obvious difference, which means that Bernoulli regards many invariants as important signatures, which leads to the decline of classification accuracy. In Figure 5, the color of the points can be clearly distinguished, which means that Gaussian–Bernoulli RBM can distinguish important signatures and implement accurate classification. In Figure 5, the darker points correspond to the verifiable signatures of Apache-knacker worm, and the lighter points might be the signatures produced by some polymorphic worm deformation, which can be considered as alternative signatures. Alternative signatures can provide support for a more accurate classification of worms. The signatures produced by the Gaussian–Bernoulli RBM algorithm are shown in Table 4.

Table 4. Signatures from Gaussian–Bernoulli RBM

Type	Verifiable signature	Alternative signature
Apache-knacker	“GET,” “HTTP/1.1\r\n,” “\r\nHost,” “nHost:,” “xff\xbf”	“xf $\unicode{x0007E}$ ,” “x^$ $\unicode{x0007E}$ ,” “xff\xbf=,” ” “x?/,” “xe/xff”
ATPhttpd	“GET/,” “HTTP/1.1\r\n,” “xff\xbf”	“xf $\unicode{x0007E}$ ,” “Accept:,” “xf/xbf,” “xcc/? $\unicode{x0007E}$ ,” “x9d= $\unicode{x0007E}$ ,” “x86&”
BIND-TSIG	“\x00\x00\xFA,” “\x00,” “\XFF\XBF”	“.\xx00,” “x04/xb7,” “\xx\ $\unicode{x0007E}$ ”

Abbreviation: RBM, Restricted Boltzmann Machine.

As seen from Table 4, the verifiable signatures after dimension reduction are more accurate, and alternative signatures can distinguish and detect polymorphic worm deformation more effectively. In Section 4.3, we further study the worm signature generation problem with noisy condition.

4.3 Signature generation under noisy condition

This section mainly discusses the signature generation of three types of polymorphic worms by Gram-RBM algorithm in a noisy environment and applies the worm signatures to the classification of polymorphic worms. To evaluate the classification performance of the Gram-RBM system, Apache-knacker, ATPhttpd, or BIND-TSIG worms are randomly selected as test data sets. Thereafter, 1000, 5000, and 9000 normal sequences as noisy traffic are mixed with the worm data, and the total number of test data is 10,000 pieces of sequence, with other parameters remaining the same as the previous experiment setting in Section 4.2. The final classification results are shown in Table 5.

Table 5. Classification accuracy under different numbers of noise

Number of noise	Apache-knacker (%)	ATPhttpd (%)	BIND-TSIG (%)	Normal (%)
1000	100	100	100	99.7
5000	100	99.89	100	99.62
9000	99.63	99.71	100	99.51

In Table 5, the “Normal” indicates that the model considers such sequences as the normal sequences. It can be seen from Table 5 that the system model can effectively classify unknown worm accurately after it is trained on multiple worm data sets through unsupervised learning under noise-free conditions. With the increase of noise, it can be observed that the detection model can still discover malicious worms from the noise data set and accurately classify them, however, the accuracy is slightly reduced. The reason may be that as the number of normal traffic increases, the model may underfit the classification of worms due to the small number of worm training samples. In the face of appearance changes of polymorphic worms, the smoothing N-gram algorithm can partially infer their appearance, so it can extract deep-hidden worm sequences, preventing the invasion of polymorphic worms. To verify the effectiveness of our proposed system model, we compare it with the works of References [16, 23, 33], and the findings are summarized in Table 6.

Table 6. Accuracy comparison with current algorithms

Algorithms	FP	FN	FP	FN	FP	FN
	Apache-knacker		ATPhttpd		BIND-TSIG
Polygraph¹⁴	NA	NA	0.009	0	0.0011	0
HAMSA¹⁵	0	0	0	0	NA	NA
CCSF¹⁶	0	0	0	0	NA	NA
Token subsequence¹⁸	0.029	0	0.263	0.05	0.578	0.08
ERES²³	0	0.33	NA	NA	0	0
PRSA³³	0.005	0	0.126	0.03	0.168	0.01
Our Gram-RBM	0.001	0	0.001	0	0	0

Abbreviations: CCSF, color coding signature finding; ERES, extended regular expression signature; FN, false negative; FP, false positive; PRSA, Production Rule Sequence Alignment; RBM, Restricted Boltzmann Machine.

In Table 6, FP represents the proportion of normal sequences that are misclassified as malicious, called the false positive. FN represents the proportion of polymorphic worm sequences that are misclassified as normal traffic, called the false negative. As seen from Table 6, our proposed system achieves better performance than other works. Due to the similarity of Apache-knacker and ATPhttpd worm sequences, the model generates a false-positive classification with the increase of noise. However, FP is relatively low, so we think that our model can still accurately extract the signatures of the two types of polymorphic worms under noisy conditions. Therefore, compared with other algorithms, our automatic signature extraction model of polymorphic worms has better robustness.

5 CONCLUSIONS AND FUTURE DIRECTIONS

To solve the problem of automatic signature generation of polymorphic worms and detect worm-type malware in IoT, this paper presents two smoothing N-gram algorithms which can effectively extract signatures of various types of polymorphic worms, and improves the accuracy of polymorphic worm signature extraction through Gaussian–Bernoulli RBM algorithm. The proposed system is particularly useful in accurately extracting polymorphic worm signatures under noisy settings. The Gram-RBM system can also generate worm sequences according to the different worm signatures to predict possible variants of polymorphic worms. This method can not only dig out the potential variants of polymorphic worms, but also provide the support for the scalability of the model, which will help mitigate and prevent the emerging IoT cyberthreats.

ACKNOWLEDGMENTS

The authors would like to thank the anonymous reviewers for the useful suggestions given to improve the quality of the manuscript significantly. This study was supported by NSFC under Grant No. 61572170, Natural Science Foundation of Hebei Province under Grant Nos. F2019205163 and F2021205004, Science and Technology Foundation Project of Hebei Normal University under Grant No. L2021K06, Science Foundation of Hebei Province Under Grant No. C2020342, Science Foundation of Department of Human Resources and Social Security of Hebei Province under Grant Nos. 201901028 and ZD2021062, and Foundation of Hebei Normal University under Grant No. L072018Z10.

REFERENCES

1Sicato S, Costa J, Sharma P, Loia V, Park J. VPNFilter malware analysis on cyber threat in smart home network. Appl Sci. 2019; 9(13): 1-20.
Google Scholar
2Xu Y, Ren J, Wang G, Yang J, Zhang Y. A blockchain-based nonrepudiation network computing service scheme for industrial IoT. IEEE Trans Ind Inf. 2019; 15(6): 3632-3641.
10.1109/TII.2019.2897133
Web of Science® Google Scholar
3Zhou R, Zhang X, Wang X, Yang G, Wang H, Wu Y. Privacy-preserving data search with fine-grained dynamic search right management in fog-assisted Internet of things. Inf Sci. 2019; 491(4): 251-264.
10.1016/j.ins.2019.04.003
Web of Science® Google Scholar
4Yao Z, Ge J, Wu Y, Jian L. A privacy preserved and credible network protocol. J Parallel Distrib Comput. 2019; 132(2): 150-159.
10.1016/j.jpdc.2019.06.002
Web of Science® Google Scholar
5Sulieman SMA, Fadlalla YA. Detecting zero-day polymorphic worm: a review. In: 2018 21st Saudi Computer Society National Computer Conference (NCC). Four SeaRiyadh, Saudi Arabia. IEEE; 2018: 1-7.
10.1109/NCG.2018.8593085
Google Scholar
6Staniford S, Paxson V, Weaver N. How to own the internet in your spare time. In: Stephen T, ed. Proceedings of the 11th USENIX Security Symposium. San Francisco, California, USA. IEEE; 2002: 14-15.
Google Scholar
7Xu Y, Zeng G, Zhang C, Ren J, Zhang Y. An efficient privacy-enhanced attribute-based access control mechanism. Concurrency Comput Pract Exper. 2020; 32(5): 1-10.
10.1002/cpe.5556
CAS Web of Science® Google Scholar
8Ma Y, Wu Y, Li J, Ge J. APCN: a scalable architecture for balancing accountability and privacy in large-scale content-based networks. Inf Sci. 2020; 527(7): 511-532.
10.1016/j.ins.2019.01.054
Web of Science® Google Scholar
9Yao Y, Sheng C, Fu Q, Liu H, Wang D. A propagation model with defensive measures for PLC-PC worms in industrial network. Appl Math Modelling. 2019; 69(2): 696-713.
10.1016/j.apm.2019.01.014
Web of Science® Google Scholar
10Almarshad M, Mohammed M, Pathan A. Detecting zero-day polymorphic worms with Jaccard similarity algorithm. J Commun Networks Inf Secur. 2016; 8(3): 203-213.
Google Scholar
11Aljawarneh S, Moftah R, Maatuk A. Investigations of automatic methods for detecting the polymorphic worms signatures. Future Gener Comput Syst. 2016; 60(7): 67-77.
10.1016/j.future.2016.01.020
Web of Science® Google Scholar
12Silalahi D, Asnar Y, Perdana R. Rule generator for IPS by using honeypot to fight polymorphic worm. In: Candra MZC, ed. 2017 International Conference on Data and Software Engineering (ICoDSE). Palembang, Indonesia. IEEE; 2017: 1-5.
10.1109/ICODSE.2017.8285886
Google Scholar
13Sohi S, Ganji F, Seifert J. Recurrent neural networks for enhancement of signature-based network intrusion detection systems. arXiv preprint arXiv:1807.03212. 2020.
Google Scholar
14Newsome J, Karp B, Song D. Polygraph: automatically generating signatures for polymorphic worms. In: Tate S, ed. 2005 IEEE Symposium on Security and Privacy (S&P'05). Oakland, CA, USA. IEEE; 2005: 226-241.
10.1109/SP.2005.15
Google Scholar
15Li Z, Sanghi M, Chen Y, Kao M, Chavez B. Hamsa: fast signature generation for zero-day polymorphic worms with provable attack resilience. In: Orman H, ed. 2006 IEEE Symposium on Security and Privacy (S&P'06). Oakland, CA, USA. IEEE; 2006: 31-47.
Google Scholar
16Wang J, Wang J, Chen J. Automated signature generation approach for polymorphic worm based on color coding. J Software. 2009; 21(10): 2599-2609.
Google Scholar
17Sommer R, Paxson V. Outside the closed world: on using machine learning for network intrusion detection. In: McNeill J, ed. 2010 IEEE Symposium on Security and Privacy (S&P'0). Oakland, CA, USA. IEEE; 2010: 305-316.
10.1109/SP.2010.25
Google Scholar
18Kaur R, Singh M. A survey on zero-day polymorphic worm detection techniques. IEEE Commun Surv Tutorials. 2014; 16(3): 1520-1549.
10.1109/SURV.2014.022714.00160
Web of Science® Google Scholar
19Bar A, Shapira B, Rokach L, Unger M. Identifying attack propagation patterns in honeypots using Markov chains modeling and complex networks analysis. In: 2016 IEEE International Conference on Software Science, Technology and Engineering (SWSTE). Beer-Sheva, Israel. IEEE; 2016: 28-36.
10.1109/SWSTE.2016.13
Google Scholar
20Ki Y, Kim E, Kim H. A novel approach to detect malware based on API call sequence analysis. Int J Distrib Sens Networks. 2015; 11(6): 1-9.
Google Scholar
21Kim HJ, Kim JH, Kim JT, Kim IK, Chung TM. Feature-chain based malware detection using multiple sequence alignment of API call. IEICE Trans Inf Syst. 2016; 99(4): 1071-1080.
10.1587/transinf.2015CYP0007
Web of Science® Google Scholar
22Kim H, Kim J, Kim Y, Kim I, Kim KJ, Hyuncheol K. Improvement of malware detection and classification using API call sequence alignment and visualization. Cluster Comput. 2019; 22(16): 921-929.
10.1007/s10586-017-1110-2
Web of Science® Google Scholar
23Eskandari R, Shajari M, Ghahfarokhi M. ERES: an extended regular expression signature for polymorphic worm detection. J Comput Virol Hacking. 2019; 15(3): 177-194.
10.1007/s11416-019-00330-1
Web of Science® Google Scholar
24Lim H. Detecting malicious behaviors of software through analysis of api sequence k-grams. Comput Sci Inf Technol. 2016; 4(3): 85-91.
Google Scholar
25An N, Duff A, Naik G, Faloutsos M, Weber S, Mancoridis S. Behavioral anomaly detection of malware on home routers. In: Carli LD, Torres R, Modelo-Howard G, Tongaonkar A, Jha S, eds. 2017 12th International Conference on Malicious and Unwanted Software (MALWARE). Fajardo, PR, USA. IEEE; 2017: 47-54.
10.1109/MALWARE.2017.8323956
Google Scholar
26Zhao Y, Bo B, Feng Y, Xu C, Yu B. A feature extraction method of hybrid gram for malicious behavior based on machine learning. Secur Commun Networks. 2019; 2019(2): 1-8.
CAS Google Scholar
27Björklund J, Cleophas L, Karlsson M. An evaluation of structured language modeling for automatic speech recognition. J Univers Comput Sci. 2017; 23(11): 1019-1034.
Web of Science® Google Scholar
28Falahatgar M, Ohannessian M, Orlitsky A, Pichapati V. Towards competitive N-gram smoothing. In: Chiappa S, Calandra R, eds. Proceedings of the Twenty Third International Conference on Artificial Intelligence and Statistics. Palermo, Italy. IEEE; 2020: 4206-4215.
Google Scholar
29Popel MD. Perplexity of n-gram and dependency language models. In: Sojka P, Horák A, Kopeček I, Pala K, eds. International Conference on Rext, Speech and Dialogue. Brno, Czech Republic. IEEE; 2010: 173-180.
10.1007/978-3-642-15760-8_23
Google Scholar
30Pagliardini M, Gupta P, Jaggi M. Unsupervised learning of sentence embeddings using compositional n-gram features. In: Liu Y, Paek T, Patwardhan M, eds. Proceedings of the 2018 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies. New Orleans, Louisiana, USA. IEEE; 2018: 528-540.
10.18653/v1/N18-1049
Google Scholar
31Kirchhoff K, Vergyri D, Bilmes J, Duh SA. Morphology-based language modeling for conversational Arabic speech recognition. Comput Speech Lang. 2006; 20(4): 589-608.
10.1016/j.csl.2005.10.001
Web of Science® Google Scholar
32Fahlman SE, Hinton GE, Sejnowski TJ. Massively parallel architectures for AI: NETL, Thistle, and Boltzmann machines. In: Proceedings of the National Conference on Artificial Intelligence. Washington D.C., USA, IEEE; 1983: 45-64.
Google Scholar
33Xue M, Yu W. An attack signatures generation sequence alignment algorithm based on production rules. In: Cardoso A, Teixeira C, Henriques J, Gil P, eds. 2018 13th APCA International Conference on Automatic Control and Soft Computing. Ponta Delgada, Portugal. IEEE; 2018: 118-127.
10.1109/ICCSN.2018.8488280
Google Scholar

All articles

Toward machine intelligence that learns to fingerprint polymorphic worms in IoT

Abstract

1 INTRODUCTION

2 RELATED WORK

2.1 Content-based signature generation

2.2 Multiple-sequence-alignment-based signature generation

2.3 Simplified-regular-expression-based signature generation

2.4 Natural-language-processing-based signature generation

3 AN AUTOMATED SIGNATURE GENERATION SYSTEM FOR POLYMORPHIC WORM

3.1 Smoothing N-gram algorithms

3.1.1 The principle of the basic N-gram model

3.1.2 Maximum likelihood estimation

3.1.3 Laplace-smoothing N-gram algorithm

3.1.4 Good-Turing smoothing N-gram algorithm

3.2 Selection of N-gram algorithms

3.3 Invariant extraction

3.4 Transforming the invariants into a matrix

3.5 Dimension reduction

3.6 Signature generation

4 EXPERIMENT RESULTS AND ANALYSIS

4.1 Data sets

4.2 Signature generation under noise-free condition

4.2.1 Invariants extraction by N-gram algorithm

4.2.2 Signature generation by Gaussian–Bernoulli RBM

4.3 Signature generation under noisy condition

5 CONCLUSIONS AND FUTURE DIRECTIONS

ACKNOWLEDGMENTS

REFERENCES

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Toward machine intelligence that learns to fingerprint polymorphic worms in IoT

Abstract

1 INTRODUCTION

2 RELATED WORK

2.1 Content-based signature generation

2.2 Multiple-sequence-alignment-based signature generation

2.3 Simplified-regular-expression-based signature generation

2.4 Natural-language-processing-based signature generation

3 AN AUTOMATED SIGNATURE GENERATION SYSTEM FOR POLYMORPHIC WORM

3.1 Smoothing N-gram algorithms

3.1.1 The principle of the basic N-gram model

3.1.2 Maximum likelihood estimation

3.1.3 Laplace-smoothing N-gram algorithm

3.1.4 Good-Turing smoothing N-gram algorithm

3.2 Selection of N-gram algorithms

3.3 Invariant extraction

3.4 Transforming the invariants into a matrix

3.5 Dimension reduction

3.6 Signature generation

4 EXPERIMENT RESULTS AND ANALYSIS

4.1 Data sets

4.2 Signature generation under noise-free condition

4.2.1 Invariants extraction by N-gram algorithm

4.2.2 Signature generation by Gaussian–Bernoulli RBM

4.3 Signature generation under noisy condition

5 CONCLUSIONS AND FUTURE DIRECTIONS

ACKNOWLEDGMENTS

REFERENCES

Figures

References

Related

Information