Economic benefits of technical analysis in portfolio management: Evidence from global stock markets
Abstract
Producing good economic value in trading strategies for investors based on technical analysis is an issue of major interest in the academe and in practice. This study considers 9,555 trading rules and examines the usability of technical analysis. The double-or-out (DO) and the optimal-portfolio (OP) strategies are used to investigate how investors construct their ass et allocation. The sample for empirical study is comprised of 20 major stock indexes from global markets as risky assets from 1998 to 2013. The DO strategy on average produces higher terminal wealth rather than does the buy-and-hold (BH) strategy, but the average utility (AU) of the former is worse than the latter. Nevertheless, using the OP strategy not only increases the terminal wealth of investors but also generates higher utility. Given a starting investment of one dollar and considering the best 100 trading rules, the DO and OP strategies result in average terminal wealth of 17.6 dollars and 5.9 dollars, respectively. In addition, in terms of AU, both of them are better than the BH strategy. These pieces of evidence demonstrate that investors who use an appropriate strategy of technical analysis in ass et allocation can produce good economic value, a finding that supports the continued use of technical analysis in practice.
1 INTRODUCTION
Fama (1970) provides the efficient market hypothesis (EMH), which proposes that asset prices always fully reflect available information. Based on the EMH, any trading strategy produced from certain financial or economic model cannot make additional economic profits, including fundamental and technical analyses. However, several empirical studies have challenged the EMH. For example, a number of studies have been made of equity predictability, such as the work of Rozeff (1984), Campbell and Shiller (1988), Campbell and Shiller (1988), Fama and French (1988), and Lo and MacKinlay (1988). Their empirical results reveal that equity return is predictable when certain fundamental factors are included in the analysis. Besides considering fundamental factors, many investors often predict stock prices based on technical analysis, which is a method that applies past prices and other past statistics in forecasting future price trends.
Technical analysis has been examined extensively in academic studies. Brock, Lakonishok, and LeBaron (1992) verified the outperformance of simple technical trading rules, a moving average oscillator, and a trading range break-out, comparing the market to Dow Jones Industrial Average (DJIA) from 1897 to 1986. Lo, Mamaysky, and Wang (2000) found that technical analysis has a practical value to the investment process using the nonparametric kernel regression.1 Recently, relevant studies have discussed the effectiveness of technical analysis, such as in the studies of Wang, Chiao, and Chang (2012); Yu, Nartea, Gan, and Yao (2013); Hou and Li (2014); Taylor (2014); and Ni, Liao, and Huang (2015). However, some literature has also been suspicious of the usefulness of technical analysis because of mixed empirical results. For example, Sullivan, Timmermann, and White (1999) applied the bootstrap reality check methodology proposed by White (2000) to verify the technical trading rules proposed in Brock et al. (1992); they suggested that the outperformance result from the data-snooping bias was due to the misuse of statistics. Furthermore, Park and Irwin (2007) showed that among 95 empirical tests, 56, 20, and 19 studies generated positive, negative, and mixed results, respectively, regarding technical trading strategies.
The focus of the present study is on the use of technical analysis in predicting future trends in the stock market and on its application in portfolio management for two reasons. First, certain trading strategies based on technical indicators reflect the behavior of investors. Specifically, contrarian strategies work well when the financial mark et always overreact to some information. The momentum strategies are efficient when investors always herd in the market. Therefore, a useful technical indicator can identify the behavior of investors and can be applied in a trading strategy to make more profit or reduce risks.
Second, the use of technical analysis is heavily debated in the academe; however, several commentaries on the major brokerage firms or professional advisory services still use the analysis. Billingsley and Chance (1996) found that approximately 60% of commodity-trading advisors relied heavily for their investment decisions on the technical trading system. Gehrig and Menkhoff (2006) showed that technical analysis had become increasingly important for foreign exchange traders and international fund managers. Menkhoff (2010) investigated the use of technical analysis by 692 fund managers in five countries. Approximately 87% of these fund managers emphasized the importance of technical analysis, and 18% of them thought that technical analysis revealed information more useful than that provided by other approaches. However, technical analysis is considered the most important approach for fund managers when their investing horizon is less than one month. Therefore, although the problem is fairly basic, several practitioners have expressed concern with this approach.
This study aims to verify whether the use of technical analysis can produce further economic benefit for investors. Individual investors or brokerage firms need to decide upon specific trading strategies to improve the performance of their portfolios. However, the studies that have covered the economic value of technical analysis in portfolio management are limited. Therefore, this study focuses on the technical analysis and its use in determining whether to buy or sell risky assets in their portfolio. The evidence in Brock et al. (1992) implies that technical analysis has predictive power when it uses the moving average (MA) method. Lento, Gradojevic, and Wright (2007) indicated that Bollinger band (BB) is a popular approach. We consider the use of these two types of technical indicators—MA and BB—for specific trading strategies and for learning about the behavior of investors. Different from other studies, we use the double-or-out (DO) or the optimal-portfolio (OP) strategy after determining buy-and-sell points to decide upon the ass et allocation of investors. Our portfolios include one market index among 20 major countries as a risky asset and one risk-free asset. Investors can construct good ass et allocation with their utility functions using the DO or OP strategies. Finally, 9,555 trading rules are constructed to investigate the effectiveness of the above setting. We measure the economic value of the trading strategy based on the degree of the average utility (AU) of investors. The result will also reveal whether technical analysis offers different utility to investors in various markets.
The remainder of this paper is organized as follows. Section 2 states the setting of our trading strategy, including the trading rules, the allocating of the portfolio, and an evaluation of the economic benefit. Section 3 reports our empirical results and the main findings. Section 4 presents the conclusions.
2 TRADING STRATEGY
Technical analysis is designed to predict the stock trends using historical trading information. Various technical rules for trading are prevalent in the finance industry, and their investment performance has been examined and discussed extensively in the literature, such as Sullivan et al. (1999); Marshall, Cahan, and Cahan (2008); Marshall, Cahan, and Cahan (2008); Hsu, Hsu, and Kuan (2010); Park and Irwin (2010); and Shynkevich (2012). Three important subjects should be noticed when using certain trading rule. Trading rules can provide buy-and-sell signals; thus, investors can determine when to buy or sell a risky asset. In this study, approximately 9,555 trading rules are discussed. Subsequently, the portfolio positions of investors are regulated, and two ass et allocation rules are adopted in this paper. Following Brock et al. (1992) and Sullivan et al. (1999), we first consider the DO strategy, in which the positions are considered as follows. We borrow at a risk-free interest rate on a buy signal in order to hold a double long position in the risky asset. We sell all long positions and invest in risk-free assets when a sell signal appears. However, placing all wealth in the risky asset is an impossible choice for investors in reality. Therefore, we further consider the OP strategy, in which the positions are determined by the expected utility of investors. We give a specific description of the procedure of the OP strategy in Section 2.2. Finally, the economic benefit of using the trading strategy is evaluated in terms of the AU of investors.
2.1 Trading rules
Covering all technical indicators in a study would be impossible. Therefore, we select two families of trading rules, the MA and BB rules, which are widely used by practitioners. The description of trading rule families and the related parameter settings are presented below. The MA rule generates buy-and-sell signals based on the relation between the long-term MA of a recent L-period price (LMA) and the short-term MA of a recent S-period price (SMA). LMA (SMA) is calculated by adding the closing prices of the most recent L (S)-trading days, excluding the current price, and then by dividing the sum by L (S). MA rule aims to identify an upward (downward) trend merges when SMA moves above (below) the LMA. We further set a Λ-period filter to confirm the trend. Thus, a buy (sell) signal is generated when SMA moves above (below) LMA, and all SMAs are larger (smaller) than LMAs in the following Λ days. Brock et al. (1992) and Sullivan et al. (1999) showed that MA rules are profitable over a long period even after data-snooping adjustment.
The other family of trading rule is the BB rule, which measures the highness and lowness of the price relative to previous levels. Various studies (e.g., Lento et al., 2007; Balsara, Chen, & Zheng, 2007) have shown mixed results on the effectiveness of BB rules. BBs comprises an N-period MA, an upper band at K times, an N-period standard deviation (SD) above the MA, and a lower band at K times an N-period SD below the MA. When the asset price is between the upper and lower bands, we usually consider this price at a general level. However, when the price exceeds the upper or lower band, it means that the price has changed abnormally. At such a time, investors can do something to respond to this signal. If people believe the financial market to be overreacting, they can buy stock when the price reaches the lower BB and sell the stock when the price achieves the upper band. On the contrary, if people agree on the existence of herd behavior that represents the tendency for investors to mimic the actions of the public, no matter these actions are rational or irrational. In this way, a buy (sell) signal is triggered when the price touches the upper (lower) BB. According to the preliminary results of our empirical tests, we find the performance of the latter is obviously better than that of the former. Therefore, we use the herding principle to determine the buying or selling actions in the following study.
We evaluate the economic benefit of MA and BB rules based on the measure of excess utility over the BH benchmark. When the trading rules are implemented, we consider two further points to make these rules more realistic and flexible. First, investors are allowed to create a stop-loss-level (ψ) to avoid serious loss in a single trading. That is, an investor will immediately sell his position in risky assets when the current stock price is below his buying price 1-ψ. Second, we assume that the level of transaction costs is 0.3% when the position of a risky asset is being bought or sold. A few technical trading rules are well known in possibly producing high transaction costs caused by a high turnover rate. We set H-length holding periods for investors, which means that the position is held during this period, ignoring any sell signal to reduce the turnover rate.
2.1.1 Summary of trading rules
-
MA rules: MA(L,S,Λ,H,φ)
- - L: the number of days in a long-term MA; L=10, 15, 20, 25, 30, 40, 50, 60, 80, 100, 120, 240.
- - S: the number of days in a short-term MA, in which its value is strictly less than L; S=5, 10, 15, ,20, 25, 30, 40, 50, 60, 80, 100, 120.
- - Λ: the number of days to define the time delay filter; Λ=1, 2, 3, 4, 5.
- - H: the number of days a position is held, ignoring any signal during that period; H=1, 2, 3, 4, 5, 10, 20.
- - φ: a stop-loss level, φ=0.1, 0.2, 1, where φ = 1 means that investors do not consider to stop loss.
Number of trading rules in MA class= (1 + 2 + ⋯ + 12) × 5 × 7 × 3 = 8190
-
BB rules: BB(K,N,H,φ)
- - K: a fixed band multiplicative value; K=1, 1.5, 2, 2.5, 3.
- - N: the number of days to estimate SD and MA; N=5, 10, 15, ,20, 25, 30, 40, 50, 60, 80, 100, 120, 240.
- - H: the number of days a position is held, ignoring any signal during that period; H=1, 2, 3, 4, 5, 10, 20.
- - φ: a stop loss level; φ=0.1, 0.2, 1, where φ = 1 means that investors do not consider to stop loss.
Number of trading rules in BB class= 5 × 13 × 7 × 3 = 1365
2.2 OP strategy
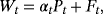 (1)
(1) , that is,
, that is,
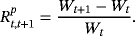
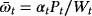 , when the investor allocates
, when the investor allocates
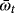 in the risky asset and 1-
in the risky asset and 1-
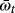 in the risk-free asset, the return of this portfolio is
in the risk-free asset, the return of this portfolio is
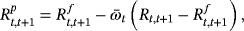 (2)
(2)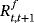 are the returns of risky and risk-free assets between t and t + 1, respectively.
are the returns of risky and risk-free assets between t and t + 1, respectively.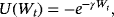 (3)
(3)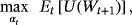 (4)
(4)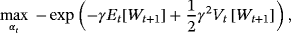 (5)
(5)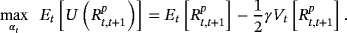 (6)
(6)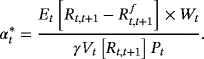 (7)
(7)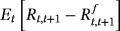 is decided by the expectation of the investor. The other parameter
is decided by the expectation of the investor. The other parameter
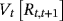 in Equation 7 can be estimated by the empirical data, which can be achieved by applying the exponentially weighted moving average (EWMA) model to update variance estimates. The model is expressed as follows:
in Equation 7 can be estimated by the empirical data, which can be achieved by applying the exponentially weighted moving average (EWMA) model to update variance estimates. The model is expressed as follows:
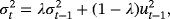 (8)
(8)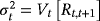 and ut − 1 is the most recent daily return. Variance estimate responds relatively slowly to the new information provided by the most recent daily return when the value of λ is high. Conversely, variance estimate has highly volatile on successive days when the value of λ is low. The RiskMetrics database created by J.P. Morgan use the EWMA model with λ = 0.94 to update daily volatility estimates; we also select this setting in our empirical studies.
and ut − 1 is the most recent daily return. Variance estimate responds relatively slowly to the new information provided by the most recent daily return when the value of λ is high. Conversely, variance estimate has highly volatile on successive days when the value of λ is low. The RiskMetrics database created by J.P. Morgan use the EWMA model with λ = 0.94 to update daily volatility estimates; we also select this setting in our empirical studies.2.3 Evaluating economic benefit
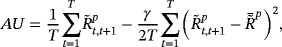 (9)
(9)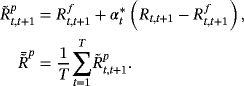
3 EMPIRICAL STUDY
3.1 Data
This study employs daily stock market indexes from 20 markets listed in the website of Yahoo Finance (http://finance.yahoo.com) to observe the performance of these trading strategies. These stock market indexes include most developed and emerging markets. The sample period ranges from January 2, 1998 to June 28, 2013. The markets are divided into three regions, Europe, Asia Pacific, and America. Table 1 shows the comprehensive description of these data. The descriptive statistics of the empirical data is shown in Table 2. This table reports the mean, SD, Q(.99), and Q(.01) for the daily returns of each asset, where Q(.q) is the qth quantile of data. We further divide the full-period into sub-period I (January 2, 1998–June 30, 2005) and sub-period II (July 1, 2005–June 28, 2013). The average daily return is 0.02% and the SD is 1.56% for total 20 assets. In general, America assets, excluding United States, have higher volatility whereas Europe assets have lower volatility. For these two subsidiary periods, the SD is lower in sub-period II than in sub-period I. Considering the SD, market risk decreases; however, Q(.01) increases for tail risk. Thus, investors should focus on investment risk in trading.
| ID | Country | Description |
|---|---|---|
| Panel A: Europe | ||
| AEX | Netherlands | (
 AEX)-Amsterdam AEX)-Amsterdam |
| ATX | Austrian | ATX (
 ATX)-Vienna ATX)-Vienna |
| BFX | Belgian | EURONEXT BEL-20 (
 BFX)-Brussels BFX)-Brussels |
| FCHI | France | CAC 40 (
 FCHI)-Paris FCHI)-Paris |
| FTSE | UK | FTSE 100 (
 FTSE)-FTSE FTSE)-FTSE |
| GDAXI | Germany | DAX (
 GDAXI)-XETRA GDAXI)-XETRA |
| SSMI | Switzerland | SMI (
 SSMI)-VTX SSMI)-VTX |
| Panel B: Asia Pacific | ||
| BSESN | India | BSE SENSEX (
 BSESN)-BSE BSESN)-BSE |
| HSI | HongKong | HANG SENG INDEX (
 HSI)-HKSE HSI)-HKSE |
| JKSE | Indonesia | Composite Index (
 JKSE)-Jakarta JKSE)-Jakarta |
| KLSE | Singapore | FTSE Bursa Malaysia KLCI (
 KLSE)-Kuala Lumpur KLSE)-Kuala Lumpur |
| KS11 | Korea | KOSPI Composite Index (
 KS11)-KSE KS11)-KSE |
| N225 | Japan | NIKKEI 225 (
 N225)-Osaka N225)-Osaka |
| SSEC | Shanghai | SSE Composite Index (000001.SS)-Shanghai |
| TWII | Taiwan | TSEC weighted index (
 TWII)-Taiwan TWII)-Taiwan |
| AORD | Australia | ALL ORDINARIES (
 AORD)-ASX AORD)-ASX |
| Panel C: America | ||
| BVSP | Brazil | IBOVESPA - (
 BVSP)-Sao Paolo BVSP)-Sao Paolo |
| MERV | Argentina | MERVAL BUENOS AIRES (
 MERV)-Buenos Aires MERV)-Buenos Aires |
| MXX | Mexico | IPC (
 MXX)-Mexico MXX)-Mexico |
| US | US | S&P 500 (
 GSPC)-SNP GSPC)-SNP |
- Note. Twenty indexes are selected from the website of Yahoo Finance (http://finance.yahoo.com). The sample period is from January 2, 1988 to June 28, 2013. This table shows the IDs, which is used in this paper and the corresponding descriptions. The symbols in the parentheses could be used to find the historical prices on the Yahoo Finance website.
| Full period | Sub-period I | Sub-period II | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ID | Mean | SD | Q(.99) | Q(.01) | Mean | SD | Q(.99) | Q(.01) | Mean | SD | Q(.99) | Q(.01) |
| AEX | −0.01 | 1.55 | 4.41 | −4.77 | 0.00 | 1.63 | 4.71 | −4.96 | −0.01 | 1.47 | 3.80 | −4.51 |
| ATX | 0.01 | 1.49 | 3.73 | −4.62 | 0.04 | 1.03 | 2.56 | −3.22 | −0.02 | 1.82 | 4.68 | −5.34 |
| BFX | 0.00 | 1.33 | 3.42 | −3.62 | 0.01 | 1.26 | 3.61 | −3.41 | −0.01 | 1.40 | 3.39 | −3.82 |
| FCHI | 0.01 | 1.56 | 4.06 | −4.36 | 0.02 | 1.55 | 4.08 | −4.30 | −0.01 | 1.57 | 4.02 | −4.68 |
| FTSE | 0.00 | 1.27 | 3.37 | −3.49 | 0.00 | 1.23 | 3.28 | −3.39 | 0.01 | 1.31 | 3.47 | −3.69 |
| GDAXI | 0.02 | 1.62 | 4.43 | −4.90 | 0.00 | 1.74 | 4.80 | −4.90 | 0.03 | 1.50 | 4.00 | −4.92 |
| SSMI | 0.00 | 1.27 | 3.39 | −3.86 | 0.00 | 1.33 | 3.76 | −4.17 | 0.01 | 1.21 | 3.17 | −3.60 |
| Europe | 0.01 | 1.44 | 3.83 | −4.23 | 0.01 | 1.40 | 3.83 | −4.05 | 0.00 | 1.47 | 3.79 | −4.37 |
| BSESN | 0.04 | 1.67 | 4.41 | −4.63 | 0.04 | 1.67 | 3.89 | −4.63 | 0.05 | 1.68 | 4.84 | −4.66 |
| HSI | 0.02 | 1.71 | 4.38 | −4.63 | 0.02 | 1.68 | 4.35 | −4.21 | 0.02 | 1.74 | 4.45 | −5.01 |
| JKSE | 0.06 | 1.67 | 4.87 | −4.67 | 0.05 | 1.81 | 5.35 | −4.91 | 0.07 | 1.52 | 4.17 | −4.54 |
| KLSE | 0.03 | 1.40 | 3.39 | −3.68 | 0.02 | 1.59 | 4.27 | −4.23 | 0.03 | 1.20 | 2.27 | −2.58 |
| KS11 | 0.04 | 1.91 | 5.56 | −5.57 | 0.05 | 2.29 | 6.33 | −5.93 | 0.03 | 1.48 | 3.71 | −4.33 |
| N225 | 0.00 | 1.55 | 3.77 | −4.12 | −0.01 | 1.45 | 3.71 | −3.50 | 0.01 | 1.65 | 4.06 | −5.06 |
| SSEC | 0.01 | 1.60 | 4.13 | −4.75 | −0.01 | 1.41 | 3.93 | −3.37 | 0.03 | 1.76 | 4.38 | −5.40 |
| TWII | 0.00 | 1.54 | 4.19 | −4.26 | −0.01 | 1.72 | 4.88 | −4.50 | 0.01 | 1.34 | 3.54 | −4.18 |
| AORD | 0.02 | 1.01 | 2.53 | −2.77 | 0.03 | 0.75 | 1.86 | −1.81 | 0.01 | 1.20 | 3.25 | −3.47 |
| Asia Pacific | 0.02 | 1.56 | 4.13 | −4.34 | 0.02 | 1.60 | 4.28 | −4.12 | 0.03 | 1.51 | 3.85 | −4.36 |
| BVSP | 0.04 | 2.10 | 5.32 | −5.45 | 0.05 | 2.35 | 5.97 | −5.75 | 0.03 | 1.84 | 4.86 | −5.17 |
| MERV | 0.04 | 2.15 | 5.92 | −6.41 | 0.04 | 2.42 | 7.30 | −7.09 | 0.04 | 1.86 | 5.21 | −5.49 |
| MXX | 0.05 | 1.52 | 4.49 | −4.17 | 0.05 | 1.65 | 4.71 | −4.24 | 0.05 | 1.39 | 4.26 | −4.11 |
| US | 0.01 | 1.32 | 3.75 | −3.57 | 0.01 | 1.23 | 3.48 | −3.08 | 0.01 | 1.40 | 3.96 | −4.53 |
| America | 0.04 | 1.77 | 4.87 | −4.90 | 0.04 | 1.91 | 5.36 | −5.04 | 0.03 | 1.62 | 4.57 | −4.82 |
| All | 0.02 | 1.56 | 4.18 | −4.41 | 0.02 | 1.59 | 4.34 | −4.28 | 0.02 | 1.52 | 3.97 | −4.45 |
- Note. This table reports the mean, standard deviation (SD), Q(.99), and Q(.01) for the daily returns of each asset where Q(.q) means the qth quantile of data. The sample period for the full-period, the sub-period I, and the sub-period II are January 2, 1998–June 28, 2013, January 2, 1998–June 30, 2005, and July 1, 2005–June 28, 2013, respectively. Note that all numbers are multiplied by 100 in this table.
For evaluating the benefits of trading rules, taking transaction costs into consideration is surely an important issue. Evidence demonstrating the influence of transaction costs on financial markets can be found in recent literature (Amihud, 2002; Hasbrouck, 2009). The components of transaction costs can be divided into the direct and indirect ones (Aiyagari & Gertler, 1991). The former includes brokerage commissions, exchange fees, and transaction taxes. The latter covers the market-impact costs, that is, when investors buy a large quantity of one asset, its price will be driven up. In addition, people always spend their time searching for better investment opportunities that also involves potential costs. In our empirical tests, we assume that the transaction cost is 0.3% when investors want to either buy or sell the risky asset. Although this setting ignores the complexity of the real market, we believe this setting is appropriate in our context based on the following reasons. First, in practical, trading market indexes can be easily implemented through the exchange traded funds (ETFs), which usually charge a lower transaction fee. Second, a trading rule with a lower trading frequency is usually less affected by transaction costs when its performance is measured. Averagely, the number of transactions based on our trading rules is less than 40 in the whole period, which means less than three transactions per year. Therefore, a lower trading fee and a less trading frequency could reveal that the impact of transaction costs on evaluating the economic benefits is limited in this study.
3.2 Empirical evidence: Economic benefit
For each asset, we first use the BH strategy in the entire period, followed by the sub-periods I and II, respectively. We report the value of AU (see Table 3), which is estimated by Equation 9, and the final wealth (WT) when the initial wealth of the investor is one dollar. All numbers of AU are multiplied by 104 in Table 3. In terms of WT, the average value is 2.94 dollars, and 16 assets have positive returns (WT > 1) in the entire period. We also find that America assets, excluding United States, have higher WT, whereas Europe assets have lower WT. Furthermore, the average values of WT in the two sub-periods are similar (1.52 vs. 1.54, respectively).
| Full period | Sub-period I | Sub-period II | ||||
|---|---|---|---|---|---|---|
| ID | AU | WT | AU | WT | AU | WT |
| AEX | −3.39 | 0.69 | −4.16 | 0.77 | −3.13 | 0.85 |
| ATX | −1.01 | 1.60 | 3.35 | 2.20 | −5.54 | 0.67 |
| BFX | −2.26 | 0.84 | −1.46 | 1.04 | −3.51 | 0.75 |
| FCHI | −2.40 | 1.02 | −1.66 | 1.15 | −3.57 | 0.82 |
| FTSE | −1.43 | 1.08 | −2.18 | 0.89 | −1.08 | 1.15 |
| GDAXI | −1.41 | 1.60 | −3.55 | 0.92 | 0.03 | 1.57 |
| SSMI | −1.45 | 1.06 | −2.57 | 0.87 | −1.05 | 1.10 |
| Europe | −1.91 | 1.13 | −1.75 | 1.12 | −2.55 | 0.99 |
| BSESN | 1.71 | 5.57 | 1.29 | 2.07 | 1.44 | 2.31 |
| HSI | −0.85 | 2.07 | −0.54 | 1.42 | −1.44 | 1.38 |
| JKSE | 3.65 | 10.46 | 2.21 | 2.44 | 5.32 | 4.34 |
| KLSE | 1.13 | 3.00 | 0.19 | 1.50 | 1.98 | 1.95 |
| KS11 | 0.30 | 4.29 | −0.32 | 2.32 | 0.08 | 1.56 |
| N225 | −2.80 | 0.87 | −3.81 | 0.73 | −2.78 | 1.01 |
| SSEC | −1.42 | 1.56 | −2.92 | 0.85 | −0.51 | 1.68 |
| TWII | −2.41 | 0.99 | −4.52 | 0.76 | −0.46 | 1.31 |
| AORD | 0.49 | 1.77 | 1.98 | 1.57 | −1.21 | 1.05 |
| Asia Pacific | −0.02 | 3.40 | −0.72 | 1.52 | 0.27 | 1.84 |
| BVSP | −0.22 | 4.84 | −0.20 | 2.55 | −1.08 | 1.58 |
| MERV | −0.37 | 5.02 | −1.24 | 2.31 | −0.17 | 1.90 |
| MXX | 3.51 | 9.05 | 3.50 | 3.00 | 2.87 | 2.54 |
| US | −0.73 | 1.48 | −1.02 | 1.10 | −0.67 | 1.30 |
| America | 0.55 | 5.10 | 0.26 | 2.24 | 0.24 | 1.83 |
| All | −0.57 | 2.94 | −0.88 | 1.52 | −0.72 | 1.54 |
- Note. For each asset, we use the buy-and-hold strategy in the full-period, the sub-period I, and the sub-period II, respectively. For evaluating the economic benefits of using buy-and-hold strategy, we report the average utility (AU), which is estimated by Equation 9. Furthermore, when the initial wealth of the investor is one dollar, the final wealth (WT) is also shown in this table. Note that all numbers of AU are multiplied by 104 in this table.
However,the average returns of European and American assets are lower in sub-period II (1.12 vs. 0.99 and 2.24 vs.1.83, respectively), considering investment performances from different regions and two sub-periods. However, BH return invested in the asset of Asia increases (1.52 vs. 1.84, respectively). The difference among assets is great, considering AU; for example, the AU of Jakarta Composite Index (JKSE) is 3.65, whereas that of AMSTERDAM EXCHANGE INDEX (AEX) is −3.39. However, simply observing AU value is meaningless. In the following, we explore whether AU can be improved after other trading strategies have been used.
We select 8,190 MA trading rules and 1,365 BB trading rules to determine the timing in buying or selling, thereby evaluating the use of technical analysis in producing additional economic benefit for investors. Subsequently, we use the DO and OP strategies to allocate portfolio positions. We set the maximum value of
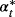 as 2Wt/Pt when using the OP strategy in deciding the OP of a risky asset (Equation 7), thereby avoiding an unreasonable level of risky asset positions. Furthermore, we assume that the expected excess return is 10%, and the γ is 2 in our empirical study.2 The average difference values of using technical analysis and only adopting BH strategy are reported in Tables 4 and 5. The results in the MA and BB trading rules are similar; thus, we discuss only the MA trading rule.
as 2Wt/Pt when using the OP strategy in deciding the OP of a risky asset (Equation 7), thereby avoiding an unreasonable level of risky asset positions. Furthermore, we assume that the expected excess return is 10%, and the γ is 2 in our empirical study.2 The average difference values of using technical analysis and only adopting BH strategy are reported in Tables 4 and 5. The results in the MA and BB trading rules are similar; thus, we discuss only the MA trading rule.
| Full period | Sub-period I | Sub-period II | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DO | OP | DO | OP | DO | OP | |||||||
| ID | AU | WT | AU | WT | AU | WT | AU | WT | AU | WT | AU | WT |
| AEX | −0.45 | 0.32 | 1.76 | 0.32 | 0.09 | 0.16 | 2.80 | 0.22 | −0.87 | 0.01 | 0.94 | 0.02 |
| ATX | 1.10 | 2.26 | 2.61 | 1.88 | 0.37 | 0.60 | 0.78 | 0.66 | 1.74 | 0.54 | 4.35 | 0.41 |
| BFX | 0.25 | 0.39 | 1.28 | 0.34 | −0.88 | −0.08 | −0.02 | −0.07 | 1.11 | 0.32 | 2.36 | 0.30 |
| FCHI | 0.20 | 0.89 | 2.29 | 0.67 | 1.79 | 0.75 | 3.38 | 0.53 | −1.34 | −0.04 | 1.29 | 0.03 |
| FTSE | −2.48 | −0.37 | −1.03 | −0.31 | −1.98 | −0.15 | −0.60 | −0.12 | −3.02 | −0.37 | −1.46 | −0.31 |
| GDAXI | −0.32 | 1.12 | 1.68 | 0.65 | 1.51 | 0.53 | 4.19 | 0.47 | −2.39 | −0.25 | −0.96 | −0.39 |
| SSMI | 0.23 | 0.42 | 1.02 | 0.39 | −1.01 | −0.07 | 0.12 | −0.06 | 0.94 | 0.31 | 1.44 | 0.29 |
| Europe | −0.21 | 0.72 | 1.37 | 0.56 | −0.02 | 0.25 | 1.52 | 0.23 | −0.55 | 0.07 | 1.14 | 0.05 |
| BSESN | −1.82 | 1.51 | 0.76 | 0.17 | −2.00 | 0.20 | 2.35 | 0.65 | −2.56 | −0.38 | −1.53 | −0.97 |
| HSI | −1.44 | 0.06 | 1.16 | 0.15 | −2.57 | −0.09 | 1.21 | 0.01 | −0.58 | 0.19 | 1.04 | 0.01 |
| JKSE | 0.33 | 24.90 | 1.45 | 6.96 | −0.69 | 1.75 | 3.04 | 1.50 | 1.54 | 4.56 | 0.19 | 0.41 |
| KLSE | 0.46 | 3.91 | 0.42 | 1.41 | 2.42 | 1.29 | 1.72 | 0.28 | −1.29 | 0.48 | −0.73 | 0.46 |
| KS11 | −2.44 | −0.32 | 0.57 | −1.76 | −2.11 | 0.32 | 2.68 | −0.53 | −3.50 | −0.50 | −1.99 | −0.54 |
| N225 | −1.91 | −0.09 | 1.89 | 0.64 | −2.52 | −0.13 | 2.26 | 0.25 | −2.37 | −0.22 | 0.67 | 0.00 |
| SSEC | 0.13 | 1.83 | 2.60 | 1.68 | −1.79 | −0.07 | 0.55 | −0.04 | 1.73 | 2.47 | 4.08 | 1.93 |
| TWII | −1.17 | 0.27 | 1.75 | 0.46 | −1.09 | 0.14 | 4.36 | 0.44 | −0.89 | 0.12 | −0.19 | −0.05 |
| AORD | −1.53 | −0.45 | −1.22 | −0.48 | −2.73 | −0.49 | −2.79 | −0.51 | −0.62 | 0.00 | 0.04 | −0.01 |
| Asia Pacific | −1.04 | 3.51 | 1.04 | 1.03 | −1.45 | 0.33 | 1.71 | 0.23 | −0.95 | 0.75 | 0.18 | 0.14 |
| BVSP | −1.69 | 2.31 | 2.02 | −1.79 | −3.37 | 0.07 | 3.71 | −0.34 | −0.87 | 0.22 | 0.42 | −0.46 |
| MERV | −2.72 | 2.14 | 2.26 | −1.43 | −5.00 | 0.11 | 4.22 | −0.24 | −0.59 | 0.60 | 0.74 | −0.34 |
| MXX | −1.75 | −0.32 | 0.16 | −2.11 | −3.42 | −0.51 | 1.41 | 0.18 | −1.32 | −0.21 | −1.94 | −1.07 |
| US | −1.49 | −0.19 | −0.31 | −0.22 | −2.53 | −0.25 | −0.69 | −0.17 | −0.20 | 0.12 | 0.42 | −0.01 |
| America | −1.91 | 0.98 | 1.03 | −1.39 | −3.58 | −0.15 | 2.16 | −0.14 | −0.75 | 0.18 | −0.09 | −0.47 |
| All | −0.92 | 2.03 | 1.16 | 0.38 | −1.38 | 0.20 | 1.73 | 0.16 | −0.77 | 0.40 | 0.46 | −0.01 |
- Note. For each asset, we use 8,190 MA trading rules in the double-or-out (DO) and the optimal-portfolio (OP) strategies. The full-period, the sub-period I, and the sub-period II are considered. For evaluating the economic benefits of using MA rules, we calculate the the average utility (AU) which is estimated by Equation 9, and the final wealth (WT) when the initial wealth of the investor is one dollar. All results reported in table are the average difference value of using MA rules and using buy-and-hold strategy. Note that all numbers of AU are multiplied by 104 in this table.
| Full period | Sub-period I | Sub-period II | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DO | OP | DO | OP | DO | OP | |||||||
| ID | AU | WT | AU | WT | AU | WT | AU | WT | AU | WT | AU | WT |
| AEX | −0.78 | 0.03 | 2.44 | 0.37 | −0.94 | −0.01 | 3.29 | 0.28 | −0.68 | −0.07 | 1.64 | 0.06 |
| ATX | 1.69 | 2.62 | 3.73 | 3.07 | 1.42 | 1.09 | 1.99 | 1.24 | 1.57 | 0.39 | 5.03 | 0.49 |
| BFX | 0.30 | 0.39 | 2.29 | 0.80 | −0.38 | 0.01 | 1.53 | 0.25 | 0.66 | 0.18 | 2.77 | 0.30 |
| FCHI | −0.89 | 0.47 | 2.26 | 0.53 | −0.22 | 0.35 | 2.71 | 0.35 | −1.65 | −0.12 | 1.76 | 0.04 |
| FTSE | −2.54 | −0.46 | −0.62 | −0.31 | −2.48 | −0.22 | −0.47 | −0.12 | −2.74 | −0.42 | −0.88 | −0.30 |
| GDAXI | −0.92 | 0.34 | 1.96 | 0.35 | 0.70 | 0.35 | 4.23 | 0.44 | −2.67 | −0.46 | −0.34 | −0.39 |
| SSMI | −0.08 | 0.37 | 1.34 | 0.52 | −0.70 | −0.04 | 1.10 | 0.05 | 0.19 | 0.15 | 1.27 | 0.22 |
| Europe | −0.46 | 0.54 | 1.91 | 0.76 | −0.37 | 0.22 | 2.05 | 0.36 | −0.76 | −0.05 | 1.61 | 0.06 |
| BSESN | −2.52 | 2.83 | 1.67 | 1.24 | −0.14 | 0.79 | 3.74 | 1.22 | −49.04 | −0.07 | −0.74 | −0.80 |
| HSI | −0.93 | 0.60 | 1.39 | 0.10 | −0.83 | 0.32 | 2.12 | 0.17 | −8.41 | −0.05 | −2.95 | −0.17 |
| JKSE | −2.53 | 23.56 | 1.72 | 6.92 | −6.06 | 3.41 | 3.88 | 1.87 | 0.29 | 1.73 | −0.19 | −0.25 |
| KLSE | 0.70 | 3.29 | 0.86 | 0.88 | 4.14 | 2.70 | 3.55 | 0.86 | −2.45 | −0.41 | −1.57 | −0.28 |
| KS11 | −0.19 | 3.62 | 1.84 | −0.89 | 1.13 | 2.46 | 3.76 | −0.23 | −1.98 | −0.37 | −0.39 | −0.34 |
| N225 | −4.07 | 0.48 | 3.28 | 1.36 | −10.31 | −0.02 | 2.69 | 0.33 | 0.95 | 0.36 | 3.63 | 0.68 |
| SSEC | 2.02 | 6.13 | 3.75 | 3.40 | −0.15 | 0.28 | 2.21 | 0.26 | 4.29 | 4.64 | 5.56 | 2.80 |
| TWII | −10.80 | 1.16 | −5.54 | 0.80 | −3.13 | 0.52 | 5.14 | 0.60 | −6.16 | 0.27 | −5.73 | 0.02 |
| AORD | −1.23 | −0.40 | −0.62 | −0.32 | −2.41 | −0.46 | −2.46 | −0.48 | −0.37 | 0.03 | 0.88 | 0.12 |
| Asia Pacific | −2.17 | 4.58 | 0.93 | 1.50 | −1.97 | 1.11 | 2.74 | 0.51 | −6.99 | 0.68 | −0.17 | 0.20 |
| BVSP | −2.22 | 0.20 | 2.06 | −1.96 | −2.48 | 0.48 | 3.95 | −0.23 | −14.69 | −0.34 | 0.40 | −0.52 |
| MERV | −3.02 | 16.75 | 3.75 | 0.70 | −8.01 | 4.25 | 5.69 | 0.43 | 1.04 | 1.13 | 1.90 | −0.07 |
| MXX | −1.50 | −0.16 | 0.21 | −2.46 | −1.10 | 0.42 | 2.09 | 0.46 | −2.43 | −0.64 | −1.94 | −1.10 |
| US | −2.33 | −0.61 | −0.36 | −0.43 | −2.97 | −0.35 | −0.63 | −0.20 | −1.66 | −0.28 | −0.02 | −0.21 |
| America | −2.27 | 4.04 | 1.41 | −1.04 | −3.64 | 1.20 | 2.78 | 0.11 | −4.43 | −0.03 | 0.09 | −0.48 |
| All | −1.59 | 3.06 | 1.37 | 0.73 | −1.75 | 0.82 | 2.51 | 0.38 | −4.30 | 0.28 | 0.50 | 0.01 |
- Note. For each asset, we use the 1,365 BB trading rules in the double-or-out (DO) and the optimal-portfolio (OP) strategies. The full-period, the sub-period I, and the sub-period II are considered. For evaluating the economic benefits of using BB trading rules, we calculate the average utility (AU) which is estimated by Equation 9, and the final wealth (WT) when the initial wealth of the investor is one dollar. All results reported in table are the average difference value of using BB trading rules and using buy-and-hold strategy. Note that all numbers of AU are multiplied by 104 in this table.
In Table 4, we find that, using either the DO or OP strategy, WT in the entire period is on averagely better than that using the BH strategy (2.03 and 0.38, respectively). Using the DO strategy cannot increase the utility of investors in terms of AU (0.92). That is, the DO strategy is possibly designed to allocate assets by a high leverage method; therefore, it will have high risks.
In terms of the OP strategy, although WT is slightly higher; however, utility of investor increases approximately 1.16 basis points. Among the 20 assets, the AU of 17 assets are better than the relevant BH strategy. America has lower WT than the BH strategy; however, this region still has larger AU. Considering both two sub-periods, two average AU are both higher than BH strategy by using the OP strategy (1.73 and 0.46, respectively). Therefore, the OP strategy in Europe and Asia creates greater wealth for investors than the BH strategy; meanwhile, using the OP strategy can bring higher utility for investors in either the entire period or in any sub-period.
3.3 The best trading rule
We report the best MA trading rules among the DO and OP strategies for each asset. We calculate the final wealth (WT) when the initial wealth of the investor is one dollar. Among the 8,190 MA trading rules, the best ones should be able to create the best AU for each asset. In Table 6, AU and WT indicate the difference between using DO (OP) strategy and BH strategy. For example, under the use of the DO strategy, AU in AEX is higher (4.41) and WT is higher (2.83) when the best MA trading rules are used than when the BH strategy is simply used. Moreover, the best MA trading rule of JKSE combined with DO strategy can create WT of up to 328.98; and the America assets, excluding United States, have 35.77 times return on average.
| Double-or-out strategy | Optimial-portfolio strategy | |||||||
|---|---|---|---|---|---|---|---|---|
| ID | Parameters | AU | WT | Num | Parameters | AU | WT | Num |
| AEX | (100, 30, 2, 20, 1) | 4.41 | 2.83 | 15.00 | (240, 100, 5, 20, 0.1) | 4.77 | 1.85 | 6.00 |
| ATX | (80, 5, 2, 5, 1) | 5.77 | 12.95 | 28.00 | (50, 5, 1, 10, 1) | 5.76 | 7.92 | 44.00 |
| BFX | (240, 25, 5, 20, 0.1) | 4.13 | 2.35 | 8.00 | (240, 10, 5, 5, 1) | 4.00 | 1.74 | 14.00 |
| FCHI | (240, 5, 2, 10, 1) | 4.44 | 4.27 | 14.00 | (240, 5, 2, 10, 1) | 5.07 | 3.42 | 14.00 |
| FTSE | (120, 100, 5, 5, 0.1) | 1.87 | 1.46 | 22.00 | (240, 120, 1, 20, 1) | 1.94 | 1.21 | 9.00 |
| GDAXI | (240, 10, 5, 10, 1) | 4.09 | 6.42 | 8.00 | (240, 40, 5, 10, 1) | 4.55 | 3.94 | 6.00 |
| SSMI | (120, 50, 5, 10, 1) | 3.90 | 3.24 | 12.00 | (120, 50, 5, 10, 1) | 4.10 | 3.00 | 12.00 |
| Europe | 4.09 | 4.79 | 15.29 | 4.31 | 3.30 | 15.00 | ||
| BSESN | (240, 100, 2, 20, 0.1) | 2.83 | 20.40 | 6.00 | (240, 100, 2, 20, 0.1) | 3.18 | 10.51 | 6.00 |
| HSI | (240, 5, 2, 10, 1) | 2.38 | 4.31 | 16.00 | (60, 15, 2, 20, 0.1) | 3.91 | 2.26 | 30.00 |
| JKSE | (25, 5, 5, 20, 0.1) | 7.59 | 328.98 | 45.00 | (25, 5, 5, 10, 1) | 6.42 | 78.83 | 49.00 |
| KLSE | (40, 5, 5, 5, 1) | 4.63 | 17.20 | 36.00 | (100, 10, 1, 10, 1) | 2.99 | 6.07 | 25.00 |
| KS11 | (50, 5, 2, 10, 0.1) | 3.08 | 16.25 | 47.00 | (80, 60, 4, 10, 1) | 3.15 | 2.75 | 27.00 |
| N225 | (120, 5, 4, 10, 1) | 2.84 | 2.28 | 22.00 | (120, 5, 4, 20, 1) | 4.71 | 3.10 | 21.00 |
| SSEC | (80, 60, 1, 5, 1) | 4.49 | 9.36 | 21.00 | (80, 30, 1, 4, 1) | 5.25 | 7.12 | 23.00 |
| TWII | (80, 5, 1, 10, 1) | 3.63 | 3.87 | 31.00 | (80, 5, 1, 20, 1) | 4.78 | 2.70 | 30.00 |
| AORD | (240, 5, 2, 10, 1) | 1.04 | 0.93 | 13.00 | (240, 5, 1, 20, 1) | 1.19 | 0.94 | 14.00 |
| Asia Pacific | 3.61 | 44.84 | 26.33 | 3.95 | 12.70 | 25.00 | ||
| BVSP | (50, 5, 3, 4, 0.1) | 4.65 | 33.28 | 51.00 | (40, 10, 1, 5, 1) | 5.08 | 3.42 | 50.00 |
| MERV | (30, 5, 2, 3, 1) | 4.45 | 47.08 | 71.00 | (100, 5, 4, 5, 1) | 5.12 | 4.32 | 25.00 |
| MXX | (50, 10, 2, 10, 0.1) | 2.65 | 26.97 | 38.00 | (240, 5, 4, 20, 0.1) | 1.37 | 2.33 | 12.00 |
| US | (240, 40, 5, 20, 1) | 3.21 | 2.77 | 6.00 | (240, 40, 5, 20, 1) | 3.20 | 2.47 | 6.00 |
| America | 3.74 | 27.52 | 41.50 | 3.69 | 3.13 | 23.25 | ||
| All | 3.80 | 27.36 | 25.50 | 4.03 | 7.50 | 21.15 | ||
- Note. For each asset, we report the best MA trading rules in the double-or-out (DO) and the optimal-portfolio (OP) strategies. We calculate the average utility (AU) which is estimated by Equation 9, and the final wealth (WT) when the initial wealth of the investor is one dollar. Both AU and WT shown in this table are the difference value of using the best MA trading rules and using buy-and-hold strategy. For each best MA trading rule, we also report the related parameters and trade numbers (num). Note that all numbers of AU are multiplied by 104 in this table.
The results relating to the best MA trading rules and trading frequency reveal that the trading frequency of the best trading rules is 51 times at most, six times at least, and about 23 times averagely. We also show the wealth differences of the investor with the best MA trading rules and with buy-and-hold strategy in Figures 1 and 2, respectively. The lower (blue) line is the results of BH strategy, and the upper (black) line is the wealth of the investor with the best MA trading rules. For example. the initial wealth of an investor is $1 in Shanghai Composite Index (SSEC) market. If the investor uses the BH strategy, his final wealth becomes $1.83 during the entire period. However, using the DO strategy with the best MA rule, the final wealth is $11.19, which is $9.36 more than the BH strategy.
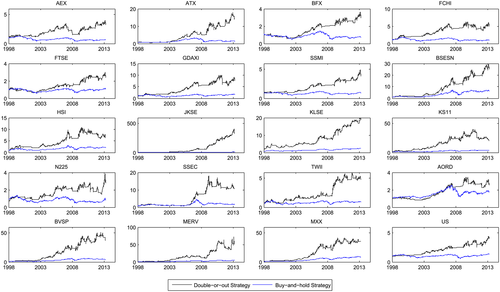
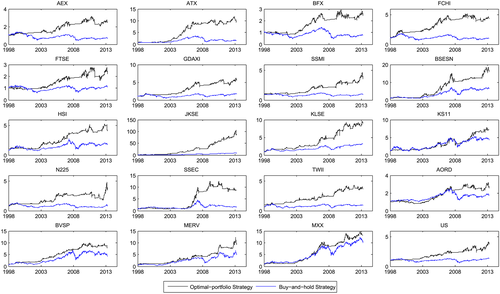
These best MA trading rules bring significantly higher wealth and better utility for investors; however, the investors only have few chances to adopt them. Therefore, we further consider the average results of the best 30, 50, and 100 MA trading rules in the DO and OP strategies in Table 7. Similar with the results in Table 4, the DO strategy averagely has much higher WT than the OP strategy; however, the OP strategy always has higher AU than the DO strategy. In terms of WT or AU, these trading rules produce considerably better performance for each asset compared with the BH strategy. Our empirical results provide the evidence in the economic benefit of technical analysis.
| DO30 | OP30 | DO50 | OP50 | DO100 | OP100 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ID | AU | WT | Num | AU | WT | Num | AU | WT | Num | AU | WT | Num | AU | WT | Num | AU | WT | Num |
| AEX | 4.27 | 2.62 | 14.9 | 4.69 | 1.75 | 10.0 | 4.20 | 2.51 | 14.0 | 4.63 | 1.70 | 11.1 | 4.04 | 2.31 | 13.8 | 4.54 | 1.66 | 10.7 |
| ATX | 5.46 | 12.23 | 30.4 | 5.52 | 6.91 | 43.0 | 5.34 | 11.88 | 31.3 | 5.46 | 6.60 | 39.0 | 5.17 | 11.30 | 33.3 | 5.33 | 6.25 | 34.3 |
| BFX | 3.82 | 2.20 | 9.5 | 3.96 | 1.67 | 14.2 | 3.77 | 2.15 | 9.4 | 3.91 | 1.61 | 14.8 | 3.71 | 2.05 | 9.4 | 3.83 | 1.61 | 11.1 |
| FCHI | 4.46 | 4.21 | 16.0 | 4.90 | 3.14 | 15.2 | 4.33 | 4.00 | 12.5 | 4.82 | 3.03 | 13.5 | 4.24 | 3.88 | 10.5 | 4.79 | 2.85 | 13.7 |
| FTSE | 1.64 | 1.31 | 19.0 | 1.92 | 1.18 | 10.9 | 1.54 | 1.23 | 15.4 | 1.87 | 1.17 | 9.8 | 1.42 | 1.12 | 12.4 | 1.81 | 1.14 | 9.0 |
| GDAXI | 4.03 | 6.22 | 8.0 | 4.51 | 3.70 | 6.8 | 3.98 | 6.09 | 7.4 | 4.52 | 3.90 | 6.8 | 3.87 | 5.77 | 7.7 | 4.56 | 3.66 | 8.0 |
| SSMI | 3.85 | 3.10 | 13.0 | 3.99 | 2.79 | 12.1 | 3.79 | 2.95 | 14.9 | 3.92 | 2.68 | 12.2 | 3.64 | 2.77 | 14.0 | 3.82 | 2.47 | 13.5 |
| Europe | 3.93 | 4.56 | 15.8 | 4.21 | 3.02 | 16.0 | 3.85 | 4.40 | 15.0 | 4.16 | 2.96 | 15.3 | 3.73 | 4.17 | 14.4 | 4.10 | 2.81 | 14.3 |
| BSESN | 2.78 | 19.88 | 6.0 | 3.16 | 10.42 | 6.0 | 2.74 | 19.52 | 6.0 | 3.15 | 10.41 | 6.0 | 2.61 | 18.58 | 6.0 | 3.12 | 10.28 | 6.6 |
| HSI | 1.95 | 3.60 | 25.8 | 3.82 | 2.41 | 30.0 | 1.88 | 3.41 | 24.7 | 3.77 | 2.29 | 30.5 | 1.82 | 3.40 | 24.0 | 3.69 | 2.16 | 31.3 |
| JKSE | 6.90 | 247.86 | 49.4 | 6.06 | 68.29 | 49.3 | 6.57 | 225.20 | 51.5 | 5.90 | 64.10 | 52.3 | 6.14 | 191.88 | 55.4 | 5.68 | 59.24 | 55.2 |
| KLSE | 4.60 | 16.98 | 37.2 | 2.84 | 5.58 | 29.1 | 4.51 | 17.36 | 39.4 | 2.87 | 5.52 | 29.5 | 4.17 | 15.45 | 38.7 | 2.75 | 5.28 | 29.3 |
| KS11 | 1.76 | 12.90 | 30.9 | 3.17 | 2.41 | 34.9 | 1.38 | 10.69 | 26.6 | 3.17 | 2.09 | 49.9 | 1.21 | 8.83 | 29.0 | 3.01 | 1.53 | 48.6 |
| N225 | 2.45 | 1.85 | 23.6 | 4.57 | 2.97 | 23.3 | 2.27 | 1.69 | 23.6 | 4.47 | 2.82 | 23.8 | 1.96 | 1.48 | 22.4 | 4.32 | 2.60 | 23.5 |
| SSEC | 4.43 | 9.37 | 21.8 | 5.08 | 5.96 | 23.5 | 4.33 | 8.92 | 21.5 | 4.98 | 5.64 | 26.7 | 4.19 | 8.35 | 21.7 | 4.85 | 5.05 | 30.2 |
| TWII | 3.42 | 3.56 | 31.7 | 4.65 | 2.52 | 32.1 | 3.30 | 3.42 | 30.7 | 4.53 | 2.37 | 31.6 | 3.12 | 3.16 | 29.9 | 4.35 | 2.16 | 31.3 |
| AORD | 1.00 | 0.89 | 14.1 | 1.13 | 0.87 | 14.1 | 0.93 | 0.87 | 16.2 | 1.01 | 0.79 | 16.2 | 0.75 | 0.85 | 20.5 | 0.75 | 0.66 | 18.3 |
| Asia Pacific | 3.26 | 35.21 | 26.7 | 3.83 | 11.27 | 26.9 | 3.10 | 32.34 | 26.7 | 3.76 | 10.67 | 29.6 | 2.88 | 28.00 | 27.5 | 3.61 | 9.88 | 30.5 |
| BVSP | 3.91 | 25.49 | 46.9 | 4.82 | 2.61 | 50.9 | 3.69 | 23.79 | 46.3 | 4.65 | 2.11 | 46.8 | 3.33 | 20.54 | 45.1 | 4.42 | 1.62 | 44.6 |
| MERV | 4.20 | 44.44 | 74.4 | 5.17 | 4.52 | 50.5 | 3.95 | 40.46 | 65.7 | 5.12 | 4.36 | 48.6 | 3.46 | 32.25 | 53.9 | 5.04 | 4.04 | 45.5 |
| MXX | 2.18 | 21.28 | 38.9 | 1.19 | 1.38 | 13.3 | 1.70 | 17.36 | 32.9 | 1.28 | 1.57 | 15.6 | 1.51 | 15.42 | 33.9 | 1.38 | 1.60 | 17.3 |
| US | 3.17 | 2.66 | 6.3 | 3.15 | 2.33 | 6.3 | 3.12 | 2.57 | 6.4 | 3.11 | 2.24 | 6.4 | 3.04 | 2.46 | 6.4 | 3.04 | 2.15 | 6.4 |
| America | 3.36 | 23.47 | 41.6 | 3.58 | 2.71 | 30.3 | 3.12 | 21.04 | 37.8 | 3.54 | 2.57 | 29.3 | 2.84 | 17.67 | 34.8 | 3.47 | 2.35 | 28.5 |
| All | 3.51 | 22.13 | 25.9 | 3.91 | 6.67 | 23.8 | 3.37 | 20.30 | 24.8 | 3.86 | 6.35 | 24.5 | 3.17 | 17.59 | 24.4 | 3.76 | 5.90 | 24.4 |
- Note. For each asset, the average results of the best 30, 50, 100 MA trading rules in the double-or-out (DO) and the optimal-portfolio (OP) strategies are reported. We calculate the average value of AU which is estimated by Equation 9, and the average final wealth (WT) when the initial wealth of the investor is one dollar. Both AU and WT shown in this table are the average difference value of using the best 30, 50, 100 MA trading rules and using buy-and-hold strategy. Note that all numbers of AU are multiplied by 104 in this table.
4 CONCLUSION
There is a heated debate concerning whether a trading strategy can produce additional economic value. The existing literature, such as Sharpe (1991), Malkiel (1995), and Fama and French (2010), showed that the active investors or trading strategies cannot bring additional profits. By contrast, Brock et al. (1992), Sullivan et al. (1999), and Lo et al. (2000) showed that technical analysis has economic value and predictive power. Therefore, this paper investigates whether trading strategies offer economic value to investors.
This paper affirms that trading strategies can produce economic benefits to investor through 20 market assets. We find that both DO and OP strategies perform better on average than the BH strategy according to WT. However, only the OP strategy has positive economic benefit; the DO strategy has negative economic benefit, although it has higher WT than the OP strategy. We also investigate the average results of the best 30, 50, and 100 MA trading rules in the DO and OP strategies. The WT is averagely greater in the DO strategy than the OP strategy; however, the OP strategy always has a higher AU. Moreover, we observe that various markets have different performances when the same trading strategies are used. This work provides a valuable reference in terms of trading strategies for academic researchers and for investors. Our empirical results cannot indicate precisely how to construct an optimal trading strategy; nevertheless, our work points to the effectiveness of technical analysis in portfolio management.
ACKNOWLEDGEMENTS
The authors would like to express their sincere appreciation to the editor and the anonymous referees for their valuable comments and suggestions, which helped improve the quality of the paper tremendously. All authors contributed equally to this manuscript. This research was supported by the National Natural Science Foundation of China (NSFC No. 71471029 and 71801117).
ENDNOTES
- 1 Some papers have explained why momentum trading strategy leads to added value. Griffin, Ji, and Martin (2003) demonstrated momentum profits through international macroeconomic risks. Li, Miffre, Brooks, and O'Sullivan (2008) revealed that momentum profits compensated for time-varying unsystematic risks.
- 2 In our empirical study, we denote the expected excess return and risk-aversion parameter as 0.1 and 2. This setting is extremely arbitrary, but this case is not the main issue of our study. This study aims to investigate the use of technique analysis in portfolio management in bringing additional economic benefits. We verify the possibility of the effectiveness of the technique analysis, but we cannot give an optimal trading strategy in all situations. Researchers can further discuss the implications of these parameters in future studies.




