Can cooperative game theory solve the low-risk puzzle?
Abstract
In this article, we illustrate that cooperative game theory may have the potential to solve the low-risk puzzle, which has become one of the most important in modern finance because its implication of a negative risk-return trade-off poses a challenge to traditional models of asset prices. Using several simulation settings, we highlight that quantifying risk by means of assets' Shapley values, that is, assets' contributions to overall portfolio risk, instead of classic measures supplies a (more) positive risk-return relationship in many practically relevant cases. This is partially attributable to the fact that the game-theoretic risk measure captures more investment-relevant information than commonly used alternatives.
1 INTRODUCTION
Empirical research has revealed an effect in the cross section of asset returns, which is now known as the low-risk puzzle. According to this phenomenon, investment opportunities with low risk consistently tend to outperform their high-risk counterparts (see Ang et al., 2006, 2009; Dutt and Humphery-Jenner, 2013; Frazzini and Pedersen, 2014). Because it holds across different markets and asset classes and seriously challenges asset pricing theory's traditional notion of a positive risk-return trade-off, the low-risk puzzle is considered to be one of the most important capital market anomalies discovered so far.
Although many authors have tried to explain the puzzle in the context of restricted borrowing, preferences for assets with lottery-like payoffs, or fund managers' mandates to beat fixed benchmarks (see Blitz et al., 2014), a more straightforward rationale might be that researchers are simply using “the wrong measure of risk” (see Baker et al., 2011, p. 43). Previous studies have relied on the standard deviation of returns (see Dutt and Humphery-Jenner, 2013), idiosyncratic volatility (see Ang et al., 2006), or beta (see Frazzini and Pedersen, 2014) to document the puzzle and to point out its relevance for investors.1 In other words, they have shown that these measures produce risk rankings of individual assets that are inconsistent with the idea that investors should be rewarded for bearing risk. However, all these measures have serious limitations because they do not fully capture the risk that is actually relevant for typical investment decisions and/or because they are bound to restrictive theoretical assumptions. For example, measures of total risk (such as the standard deviation) treat risk in an isolated fashion and thus do not consider potential diversification benefits in a portfolio context. Furthermore, popular measures of systematic risk (such as beta) can cover diversification issues (see Fama and French, 2004) but are bound to an unobservable market portfolio (see Roll, 1977), which is not held by most investors (see De Bondt, 1998). In other words, they capture how an asset contributes to the risk of a portfolio that is not relevant from a practical perspective.
We argue that a measure of risk, which can be derived from cooperative game theory, has the potential to solve the low-risk puzzle. We suggest ranking assets based on their Shapley (1953) contribution to the risk of an investment portfolio. This is because the process of portfolio formation can be interpreted as a cooperative game where the assets are the players that form coalitions to reduce risk (see Kadan, 2016; Colini-Baldeschi et al., 2017). Consequently, the corresponding Shapley values of the assets reflect their contribution to the overall portfolio risk (see Mussard and Terraza, 2008).2 They consider all possible asset coalitions and by averaging their marginal effects obtain a multidimensional contribution. Thus, in contrast to asset betas, Shapley values are more useful measures of risk for investors whose typical decision problem concerns adding or eliminating specific assets from their portfolios.
To illustrate the Shapley values' potential to produce “correct” asset rankings, we perform two simulation studies. In the first one, we look at an investor who is interested in combining individual assets in a portfolio and evaluates the riskiness of each asset based on its Shapley value with respect to the portfolio variance. We design our set-up such that the low-risk puzzle exists in the individual asset variances. We then repeatedly randomly generate the covariance matrix of the assets and consider various weighting schemes to reflect a wide spectrum of potential cases that can occur in practice. On the basis of these data, we calculate the Shapley values and the percentage of cases in which they lead to asset rankings different from the variances. Finally, calculating additional statistics helps us to characterize the cases in which the Shapley approach partially or fully eliminates the low-risk puzzle.
Because variance has also been criticized as being impacted by events with positive effects for investors (see Yan et al., 2007), our second simulation study focuses on classic downside risk measures (lower partial moments, value at risk, and drawdowns) that have become very popular in investment practice (see Lagoarde-Segot and Lucey, 2007; Ornelas et al., 2012; Stoyanov et al., 2017). Compared with variance, analytically deriving an expression for portfolio risk based on such measures can be difficult if not impossible (without highly specific return process assumptions). Therefore, we modify our first simulation study by simulating asset returns instead of only distribution parameters. That is, we generate correlated Hansen (1994) skewed-t returns, which capture empirically relevant return characteristics, in a way guaranteeing that the low-risk puzzle holds in the individual downside risks of the population. We then obtain portfolio risk and the Shapley contributions to this risk based on the simulated population returns.
The remainder of our article is organized as follows. Section 2 describes our simulation set-up in the variance case and discusses its results. Section 3 covers the approach and the findings for downside risk measures. Finally, Section 4 concludes and outlines directions for future research.
2 CONTRIBUTIONS TO PORTFOLIO VARIANCE
Suppose an investor's investment opportunity set consists of n = 3 assets with mean returns μ1 > μ2 > μ3 and variances
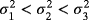.3 Thus, the low-risk puzzle occurs and asset i = 1 (i = 2, i = 3) ranks first (second and third) in terms of lowest variance risk. Instead of investing in only one of these assets, our investor is interested in combining the assets in a portfolio. Let w be a n × 1 vector of asset weights, which sum to 1, that is, w′I = 1, where I is a n × 1 vector of ones. Furthermore, denote with V the corresponding n × n covariance matrix of asset returns. Then, the variance of such a portfolio is given by
.
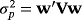We use three weighting schemes to model different kinds of investors. Type A uses personal long-only weights based on a criterion he considers suitable. To implement this kind of behaviour, we randomly select weights by stepwise drawing uniformly distributed numbers between 0 and 1 under the condition w′I = 1. Type B relies on equal weights and thus exploits findings that naive weighting performs very well in comparison with more complex weighting methods (see DeMiguel et al., 2009). Finally, type C employs the optimal weights of the minimum variance portfolio, which can be obtained by
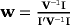and allow for short positions (see Jorion, 1985).
To evaluate how an asset i contributes to
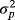, the investor uses its Shapley value φi. It can be obtained as
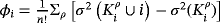, where the sum runs over all possible orders ρ of the n assets and
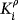is the set of assets that precede i in ρ. n! is the number of different permutations of the n assets. Thus, φi reflects the average marginal contribution of i to
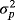.4
To identify the empirical cases in which ranking risky assets based on the Shapley values instead of variances corrects the “wrong” ranking, we perform a simulation study within this portfolio setting. That is, we simulate the covariance matrix V 100,000 times by stepwise uniform draws ensuring that the low-risk puzzle holds,5 standard deviations are between 0 and 10,6 asset correlations range from −1 to 1, and the resulting matrix is positive semidefinite. On the basis of these data, we obtain the Shapley values for each asset, derive an asset ranking based on the Shapley values, and compare this ranking to the variance ranking.
Table 1 summarizes our main results. That is, across all simulation repetitions, we report the proportions of cases, in which the game theoretic approach led to a directional correction (assets change their positions in the ranking), full correction (ranks change and all become consistent with the mean returns of the assets) or no correction (the low-risk puzzle continues to hold in full magnitude). Furthermore, we calculate the average of a simple approximate diversification measure, that is, the mean asset correlation in the investment opportunity set.7
| Directional correction | Full correction | No correction | |
|---|---|---|---|
| A. Random weights | |||
| Proportion (%) | 42.98 | 2.26 | 57.02 |
| Correlation | −0.03 | −0.09 | 0.02 |
| B. Equal weights | |||
| Proportion (%) | 37.28 | 2.69 | 62.73 |
| Correlation | −0.04 | −0.08 | 0.03 |
| C. Minimum variance weights | |||
| Proportion (%) | 35.48 | 2.71 | 64.52 |
| Correlation | −0.05 | −0.08 | 0.03 |
- Note. For our simulation of investment variances and Shapley values with 100,000 repetitions, this table reports the proportion of cases, where the Shapley ranking leads to directional, full, or no corrections of the “wrong” variance rankings. Furthermore, we report the simulation-wide average of mean asset correlations as a simple approximate measure of diversification.
The presented proportions indicate that using the Shapley value can indeed lead to partial and full ranking corrections and that this finding holds regardless of the weighting strategy. A closer look at our diversification metric reveals that the corrections mainly occur in cases where investors have access to an investment opportunity set that allows effective risk reduction via the hedging property of negative correlation. This is typical for investment universes consisting of, for example, factor-based investment funds (see Krishnan et al., 2009). Here, the Shapley value can provide asset rankings consistent with traditional asset pricing theory. However, in environments with rather positive mean correlation, such as among the constituents of high market capitalization stock indices (see Pollet & Wilson, 2010), the low-risk puzzle continues to hold even when Shapley values are used.
3 CONTRIBUTIONS TO PORTFOLIO DOWNSIDE RISK
To analyse whether our results also hold for other ways of measuring portfolio risk, we modify our previous approach by simulating 100,000 correlated skewed-t returns for each asset in each simulation repetition.8 Similar to Section 2, the correlation values for this task stem from a simulated parameter matrix V. The parameters of the skewed-t distribution controlling skewness and kurtosis are set to λ = −0.10 and ν = 5.00, respectively.9 Because the skewed-t distribution has a mean of 0 and a variance of 1 by definition, we can obtain the individual returns incorporating the low-risk puzzle via
, where we select μ1 = 1.5, μ2 = 1.0 and μ3 = 0.5 and collect the standard deviations from V.
Using this simulated data, we can calculate individual and portfolio risks as well as Shapley values. For simplification, we focus on equally weighted portfolios and three selected downside risk measures. That is, we calculate the popular lower partial moment of order θ = 0 with reference level τ = 0 (also known as shortfall probability), the value at risk with confidence level α = 99%, and the maximum drawdown (as defined in Eling & Schuhmacher, 2007).10
Analogous to Table 1, Table 2 presents our results for the downside risk measures. We find that the choice of portfolio risk measure does not qualitatively alter our conclusion. However, we can observe that the proportions of changed ranks are lower for the downside risk measures than for the variance. This suggests that the extent to which the game theoretic measure can provide a solution for the puzzle appears to depend on the implemented risk measure.
| Directional correction | Full correction | No correction | |
|---|---|---|---|
| Partial moment (θ = 0,τ = 0) | |||
| Proportion (%) | 8.82 | 0.12 | 91.18 |
| Correlation | −0.24 | −0.32 | 0.03 |
| Value at risk (α = 99%) | |||
| Proportion (%) | 28.41 | 1.50 | 71.59 |
| Correlation | −0.06 | −0.11 | 0.02 |
| Maximum drawdown | |||
| Proportion (%) | 9.04 | 0.03 | 90.96 |
| Correlation | −0.09 | −0.22 | 0.00 |
- Note. For our simulation of investment downside risk and Shapley values with 100,000 repetitions (using 100,000 returns for each asset and repetition), this table reports the proportion of cases, where the Shapley ranking leads to directional, full, or no corrections of the “wrong” downside risk rankings. Furthermore, we report the average of mean asset correlations as a simple measure of diversification. Within portfolios, assets are weighted equally.
4 CONCLUSION
We have illustrated that using Shapley contributions instead of classic measures of risk provides an interesting starting point for research seeking to solve the low-risk puzzle by more appropriate methods to quantify risk. This is because, in contrast to standalone risk measures, Shapley values can capture additional information (on favourable correlation). Furthermore, in contrast to classic beta measures focusing on a theoretical market portfolio, Shapley values can be used to evaluate real-life portfolio decision problems of investors. Although we have seen that the number of cases with directional ranking correction can be quite high, full corrections are achieved in fewer cases. Furthermore, the quality of the puzzle solution appears to depend on the nature of the underlying investment universe and the portfolio risk measure chosen by investors.
These results motivate a great deal of further research. (a) Higher correction numbers may be achieved in two ways. First, recent studies have proposed universal and objective measures of riskiness (see Foster and Hart, 2009). Analysing the Shapley contributions of assets to this kind of portfolio risk might yield valuable insights because this new class of measures does not depend on any ad hoc parameters that need to be specified (such as the value at risk confidence level) and, in contrast to other generalized measures, abstracts from the preference order of specific decision makers. Second, and probably more important, our analysis may be extended to Shapley alternatives (see Felsenthal & Machover, 2005) because they judge risk contribution in different ways. For example, although the Shapley and the Banzhaf rankings agree with three players, they can have opposite rankings with more players (see Saari & Sieberg, 2001). (b) After this research is done, that is, when a suitable combination of risk measure and contribution metric is identified, a new asset pricing model may be developed based on these findings (see Ortmann, 2016).
ENDNOTES
- 1 Others have extended the traditional capital asset pricing model by using partial moments (see Bawa and Lindenberg, 1977), the conditional value at risk (see Kaplanski, 2004), or drawdowns (see Zabarankin et al., 2014) as alternative concepts to measure risk.
- 2 Using Shapley decompositions of risk has also become quite popular in the analysis of, for example, deposit insurance premia (see Staum, 2012) and the systemic relevance of banks (see Tarashev et al., 2016; Mezei and Sarlin, 2018).
- 3 Using n > 3 does not deliver insights in addition to the ones derived for n = 3. We choose n = 3 because this setting requires less computation time and thus allows the interested reader a quick replication of our results.
- 4 For readers unfamiliar with game theory, the appendix briefly discusses the nature of cooperative games and the most important properties of the Shapley value.
- 5 For this number of repetitions, our results are stable, meaning that they do not significantly change in reruns.
- 6 These values are typical for the monthly volatility of common stocks (see Andersen et al., 2001).
- 7 Alternatively, we might use the metric of Skintzi and Refenes (2005), which is also a weighted sum of correlations but with weights tailored to the variance case and thus not applicable in our setting of Section 3. Also note that our notion of diversification (i.e., risk reduction by counter movement) is not to be confused with other definitions speaking of well-diversified portfolios if weight in the portfolio is spread reasonably evenly (see Green and Hollifield, 1992).
- 8 By simulating very large samples, that is, the entire population, changes in ranks are not related to typical sample measurement error (see Schuhmacher and Auer, 2014). Our sample size ensures closeness of simulated data and the population as measured by a negligible difference between the first four theoretical and sample moments.
- 9 These parameters determine the higher moments but do not give their actual values (see Jondeau and Rockinger, 2003). Thus, unlike a first view might suggest, our setting models typical magnitudes of large skewness and kurtosis. Also note that allowing for strong cross-sectional differences in skewness and kurtosis does not influence our main conclusions.
- 10 Similar results can be obtained for typical alternative value at risk confidence levels (e.g., α = 95%), lower partial moments of higher orders (e.g., θ = 1 and θ = 2), and other specifications of drawdowns (e.g., the ones used in the Sterling, Burke, Martin and Pain ratios; see Schuhmacher and Eling, 2011).
- 11 In cost analysis, the Shapley allocation of a player is interpreted as the player's share of the cost (see Littlechild and Owen, 1973; Littlechild and Thompson, 1977; Dubey, 1982; Young, 1994). In weighted majority games, the Shapley allocations are interpreted as voting power (see Shapley, 1953; Shapley and Shubik, 1954).
- 12 Other axiomatizations are presented by, for example, Young (1985), Myerson (1980), van den Brink (2001), Casajus, (2011, 2014), and Casajus and Yokote (2017).
APPENDIX A:
The basic idea of cooperative game theory is that players can form groups (coalitions) in order to generate worth in excess of the worth they can achieve on their own. One of the main research questions in this field is how to allocate in some fair way this worth among the group players. The answer to this question is related to a solution concept which, roughly speaking, is a vector that represents the allocation to each player.
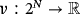such that
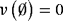. The Shapley (1953) solution concept builds on the idea that a grand coalition of all the players will form and is probably the best-known way to determine relative importance allocations. To calculate the Shapley allocation, all possible rank orders ρ of the players in N are considered. The set of these orders is denoted by RO(N) and contains n! rank orders in total.
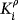is the subset of players preceding i in rank order ρ. For player i, the Shapley allocation is then obtained as the average marginal worth contribution of player i:
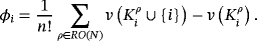
In our setting, we interpret the assets of a portfolio as players and specify the coalition function to measure portfolio risk. This way, the Shapley allocation φi to an asset i reflects i's contribution to the portfolio risk v(N).11 In our case, the advantage of forming coalitions lies in a reduction of risk via diversification.
There are different axiomatizations summarizing the properties of the Shapley solution concept. The most popular one contains four axioms (see Shapley, 1953): additivity (A), symmetry (S), null player (N), and efficiency (E).12
Axiom 1. (A)For all coalition functions v and w, we have φi(N,v) + φi(N,w) = φi(N,v + w), i ∈ N.
This first axiom states that a player's allocation in the game (N,v + w) should be the sum of the allocations he or she could achieve in the two separate games (N,v) and (N,w).
Axiom 2. (S)If i,j ∈ N are symmetric, then φi(N,v) = φj(N,v).
Two players i,j ∈ N are symmetric if
for all K⊆N, i,j∉K. More specifically, both players i and j have the same marginal contributions to coalitions that do not contain them. Thus, the second axiom says that symmetric players obtain the same allocations. Only the marginal contributions of the players, not their names or other characteristics, determine their allocations.
Axiom 3. (N)If i ∈ N is a null player, then φi(N,v) = 0.
A player i ∈ N is a null player, if
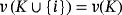for all K⊆N, i∉K. He or she does not contribute anything to any coalition. Thus, the third axiom captures that a null player obtains no allocation.
Axiom 4. (E)We have
.
Finally, the last axiom implies that the entire worth of the grand coalition is distributed among the players.
