Use of Spatially Distributed TOPMODEL to Assess the Effectiveness of Diverse Natural Flood Management Techniques in a UK Catchment
Funding: The authors received no specific funding for this work.
ABSTRACT
While natural flood management (NFM) is becoming more widely used, there remains a lack of empirical evidence regarding its effectiveness. The primary uncertainties arise from two key aspects: first, the determination of NFM effectiveness is constrained by the relatively small catchment scales studied to date; second, the combination of multiple NFM interventions within a catchment may lead to flood peak synchronisation. In this study, both instream and terrestrial NFM interventions were modelled using a spatially distributed hydrological model, Spatially Distributed TOPMODEL (SD-TOPMODEL). To demonstrate how the scale and type of interventions interact to influence flood peaks, we integrated various NFM interventions and land cover changes, including woodland planting, soil aeration, floodplain restoration, and hedgerow planting. In comparison to previous versions of SD-TOPMODEL, we improved simulation efficiency to enable grid-based modelling of up to a 200-year return period flood event for an 81.4 km2 catchment with 5 m resolution. Following extensive parameter calibration and validation, the model demonstrated stability and provided a reliable fit for flood peaks, achieving a Nash-Sutcliffe Efficiency coefficient of up to 0.93 between modelled and observed discharge. The results highlighted the effectiveness of NFM interventions in reducing flood peaks at the scale studied, particularly during single-peaked storm events and under dry pre-event catchment conditions. Moreover, the combined use of multiple interventions was more effective and resilient than single interventions, with flood peak reductions ranging from 4.2% to 16.0% in the study catchment.
1 Introduction
Natural flood management (NFM) is a flood mitigation strategy which aims to work with natural processes to restore and enhance catchment hydrological functions which limit flood risk and impact (Dadson et al. 2017; Cooper et al. 2021). In particular, NFM seeks to reduce and delay flood peaks by optimising the natural water retention function of the catchment and to mitigate the potential hazards of flood peaks (Lane 2017; Kay et al. 2019; Black et al. 2021; Ellis et al. 2021; Kumar et al. 2021; Lashford et al. 2022). For example, altering the physical properties of soil that influence water movement and storage, such as porosity and permeability, can enhance subsoil water storage capacity and encourage infiltration to delay flood peak time and/or reduce peak discharge during a storm event. Soil properties might be altered directly through aeration and other soil management interventions or indirectly by implementing afforestation, reducing grazing intensity, or delivering other ecological restoration practices (Grayson et al. 2010; Wahren et al. 2012; Palmer and Smith 2013; Marshall et al. 2014; Dixon et al. 2016; Gao et al. 2016; Alaoui et al. 2018; Gunnell et al. 2019; Wilkinson et al. 2019; Bond et al. 2022; Monger et al. 2024).
Evidence has shown that interventions such as those described above can potentially reduce and slow overland flow by locally increasing soil saturated hydraulic conductivity, the depth of the soil water table, and surface roughness. For example, results of experimental studies at the hillslope scale have shown that replacing grazed grassland with broadleaf woodland on hillslopes significantly increases saturated hydraulic conductivity and provides the soil with increased capacity to store rainfall by reducing soil compaction and bulk density and increasing depths of the soil water table (Marshall et al. 2009; Archer et al. 2013; Murphy et al. 2020), thus achieving a reduction in overland flows (Marshall et al. 2014; Bond et al. 2022). Modelling studies by Gao et al. (2016) and Goudarzi et al. (2021) highlighted that upland peat restoration, including both revegetation and gully blocking interventions, is effective in increasing static and kinematic storage of rainfall in the implementation area to reduce and delay flood peaks, and such evidence has been supported in a field experimental study (Shuttleworth et al. 2019). Critically, the reduction of overland flow velocities by increasing surface roughness can yield reduced discharge peaks (Holden et al. 2008; Roni et al. 2015; Bond et al. 2020, 2022). Soil aeration, which is the process of mechanically piercing the soil to enhance porosity, has also been shown to be effective in enhancing infiltration to reduce overland flow by increasing topsoil saturated hydraulic conductivity (Franklin et al. 2007; Alaoui et al. 2018; Wallace and Chappell 2019).
While a few NFM studies have been based on field experimental data, these have been at the plot or small catchment scale (Kay et al. 2019; Kumar et al. 2021; Zhu et al. 2024). The majority of studies of NFM effectiveness have been conducted using modelling and have focused on a specific NFM intervention. Most information from modelling studies is limited by the lack of understanding of the upscaling impacts from the local scales of intervention implementation to catchment scale, and the modelling approaches vary in accuracy and complexity (Kumar et al. 2021; Hill et al. 2023). From previous modelling studies of multiple NFM interventions, conflicting conclusions have been obtained for different modelling approaches, resolution, and catchment scale. For example, in a study of the 98 km2 Lymington River catchment in southern England, the simplified spatially distributed OVERFLOW model (20 m resolution) showed up to a 20% peak reduction by increasing mature floodplain forest to 20%–35% of the area, with greater effects from additional reforestation and sub-catchment desynchronisation (Dixon et al. 2016). Metcalfe et al. (2018) used the semi-distributed Dynamic TOPMODEL with NFM interventions which enhanced hillslope storage lumped in several hydrological response units (HRUs) for a 223 km2 catchment, reducing peak flow by a median of 5.8% and a maximum of 17.3% during one storm. The same model was coupled with the floodplain hydrodynamic model, JFlow (2 m resolution) to assess land management and peatland restoration interventions, including a runoff attenuation feature (RAF) in a 15 km2 catchment, showing a 4% ± 2% flow reduction (Hankin et al. 2019). Dynamic TOPMODEL coupled with HEC-RAS 2D (5 m resolution) showed up to 25% surface flow reduction from a combination of afforestation and in-channel barriers in an 18 km2 catchment (Ferguson and Fenner 2020). The Generalised Multistep Dynamic TOPMODEL (2 m resolution) was employed to model peatland restoration scenarios in a 25 km2 catchment, showing a high likelihood of > 5% peak discharge reduction (Goudarzi et al. 2024). Although these modelling results all demonstrate effective flood mitigation by NFM, the differences in the implementation of interventions in each catchment, such as intervention types, locations and area, and the differences in the complexity, spatial resolution and modelling scale of each model make it difficult to compare NFM benefits under the same criteria.
Using modelling to understand the impacts of types, location, and size of interventions, and the combination of interventions, is important for NFM research (Bond et al. 2022; Hill et al. 2023; Kingsbury-Smith et al. 2023; Peskett et al. 2023; Monger et al. 2024). Modelling could be used to support investment decisions, especially via the assessment of NFM from an integrated catchment perspective with single and mixed types of interventions. The number of UK NFM studies that have investigated multiple interventions and achieved valid flood mitigation results (10 articles) is less than those that have only investigated a single intervention (24 articles) (Zhu et al. 2024). Implementation of single or a combination of interventions can be effective at larger catchment scales than the evidenced 20 km2 limit proposed by Dadson et al. (2017) and increases the resilience of NFM by combining it with other forms of flood management interventions (e.g., leaky dams and runoff attenuation features) (Black et al. 2021). All NFM interventions have the potential to influence the synchronisation of flood peaks across tributaries in the catchment (Thomas and Nisbet 2007; Pattison et al. 2014). During large storms, multiple interventions yielded less peak reduction and no peak timing impacts compared to a single intervention due to the increased likelihood of peak synchronisation (Dadson et al. 2017; Kingsbury-Smith et al. 2023; Metcalfe et al. 2018). However, empirical evidence addressing positive or negative effects of the type of combined interventions, location, and area on NFM effectiveness at a large catchment scale remains very scarce.
Ideally, a modelling study for NFM effectiveness requires a model with sufficient spatial resolution to simulate all land and soil management interventions yet which is simplified enough to efficiently simulate storms with different characteristics at larger catchment scales. The Spatially Distributed TOPMODEL (SD-TOPMODEL) used in this study meets these requirements (Gao et al. 2015). SD-TOPMODEL has been used to demonstrate flood peak reductions varied across catchments for different types of NFM interventions. Peatland revegetation scenarios tested (20 m resolution) in an 84 km2 upland catchment with peatland headwaters showed a 4%–15% reduction in flood peaks (Gao et al. 2017). Hillslope grassland management scenarios achieved up to 42% reduction in overland flow peaks in a predominantly grassland-covered upland catchment (21 km2), where afforestation intervention was most effective (Bond et al. 2022). Woodland planting scenarios demonstrated up to 15.3% reduction in flood peaks in a 2.62 km2 steep upland catchment predominantly covered by unimproved grassland and semi-natural woodland (Monger et al. 2024). Kingsbury-Smith et al. (2023) used the model in a 38 km2 predominantly rural upland catchment for several single intervention scenarios, such as woodland and hedgerow planting, riparian buffer strips, soil aeration, and a combination of all these interventions. SD-TOPMODEL has been validated to effectively simulate rainfall-runoff processes in steep upland catchments with land and soil management measures (Gao et al. 2018; Bond et al. 2022), and the resolution has been improved from 20 to 5 m to enable representation of a wider variety of NFM interventions (Bond et al. 2022; Kingsbury-Smith et al. 2023). However, further testing of different combinations of NFM interventions, storm characteristics, and catchment antecedent conditions by using SD-TOPMODEL at larger catchment scales is still required, as SD-TOPMODEL has not been applied to catchment scales > 50 km2 at a fine resolution of 5 m.
Although no significant correlation between rainfall intensity and NFM effectiveness was identified in both our review and previous modelling studies, the response of different NFM intervention types to varying rainfall intensities remains variable (Gao et al. 2018; Ferreira et al. 2020; Kingsbury-Smith et al. 2023; Zhu et al. 2024). Notably, there is a research gap regarding the potential impacts of different rainfall event characteristics, such as single- versus multi-peaked events, in addition to rainfall intensity (Hankin et al. 2020). Furthermore, catchment antecedent conditions may influence NFM effectiveness (Wallace and Chappell 2019; Bond et al. 2020). The influence of these factors on NFM effectiveness has been investigated in this modelling study.
To investigate and validate whether SD-TOPMODEL can accurately represent and model soil infiltration rates, soil storage capacities, and surface roughness in the catchment as a result of NFM implementation, three main NFM interventions in the catchment were selected for this study. They are afforestation (woodland planting), soil aeration, and hedgerow planting. In this study, SD-TOPMODEL is used to simulate these NFM interventions impacting soil hydrological functions and surface roughness during high-flow events at a catchment scale. The aim is to calibrate and validate the model with parameter choices supported by evidence from previous empirical studies and improve model performance to gain a full understanding of NFM effectiveness. The land cover and NFM scenarios were applied to compare different combinations of NFM interventions and how they interacted with seven observed storms with different characteristics at a catchment scale.
2 Data and Methods
2.1 Study Site
The Upper Aire catchment is a 370.8 km2 upland catchment in northern England (Figure 1). Following extensive flooding in 2015, which exceeded a 200-year return period at the Armley gauging station (located in the city of Leeds, Figure 1b), multiple NFM interventions (woodland planting, hedgerow planting and soil aeration) have been implemented to slow runoff response to rainfall and increase surface and subsurface water storage in off-channel areas across the catchment (Figure 1c) (Leeds City Council 2024; Upper Aire Project 2024). The Upper Aire Catchment to Gargrave (~81.4 km2) was chosen as the study site, as it encompasses a significant proportion of these interventions, which also have well-documented records about their locations and nature (Yorkshire Wildlife Trust, 2022). The catchment also benefits from reliable river gauging data at Gargrave. The Gargrave station is located on the main channel of the River Aire, and its catchment area is dominated by a rural hilly landscape with a maximum elevation difference of 467 m.
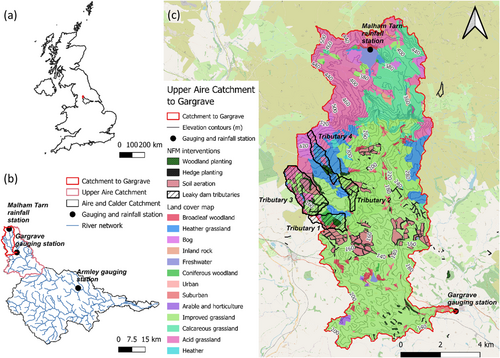
The catchment is dominated by improved grassland (49.7%), followed by calcareous grassland (18.7%), acid grassland (12.1%) and heather grassland (10.4%), bog (3.7%), broadleaf woodland (1.9%) and coniferous woodland (1.0%) (CEH 2015). Soils are mainly fine or coarse loamy, slowly permeable loamy and clayey, very shallow loamy, or well-drained silty soils over limestone (NATMAP 2016), resulting in high spatial variability in soil depth. The underlying geology is dominated by carboniferous limestone, along with sandstone, mudstone, and shale (NATMAP 2016). The area experiences a mean of 220 days of rain, with 1510 mm of mean precipitation annually (Upper Aire Project 2024).
2.2 Spatially Distributed Rainfall-Runoff Model: SD-TOPMODEL
To investigate the influence of land cover changes and NFM interventions on flood response at the catchment scale, SD-TOPMODEL was used (Gao et al. 2015). SD-TOPMODEL is a spatially distributed version of the original lumped or semi-distributed TOPMODEL (Beven and Kirkby 1979). Gao et al. (2015) developed the model by downscaling the original TOPMODEL equations from the catchment scale to grid cell equations. It has the advantage of allowing each grid cell to be saturated at different times based on the local wetness by using precipitation, slope, and soil water depth in each cell. The overland flow module uses the multiple-direction flow theory of Quinn et al. (2006) with a dynamic velocity parameter related to surface roughness to conduct overland flow directions and rates in each grid cell. This facilitates the representation of hydrological variability across the land surface and shallow subsurface conditions by adjusting parameters within each grid cell. This high-resolution capability enables the inclusion of spatially specific NFM interventions. The model is also well suited to simulate extreme rainfall events in catchments with steep topography and shallow soils (Gao et al. 2015, 2016; Bond et al. 2022; Kingsbury-Smith et al. 2023; Monger et al. 2024); thus, it is ideal for use in the Upper Aire catchment for the NFM effectiveness study.
SD-TOPMODEL can deliver three catchment outlet outputs at each timestep: overland flow, shallow subsurface flow, and the total of overland and subsurface flow outputs. Three key parameters are employed in SD-TOPMODEL to represent the catchment physical properties: overland flow velocity, Kv equals 1/n where n is the surface roughness, soil hydraulic conductivity Ks, and soil active water storage depth m (Gao et al. 2015). To increase the efficiency of SD-TOPMODEL for simulating extreme rainfall events, the model is written in C++ language and was batch run on the ARC High-Performance Computer (HPC) platform at the University of Leeds.
2.2.1 Data Sources
An Ordnance Survey 5 m digital terrain model (DTM) was used for the Upper Aire catchment (Ordnance Survey 2022). The 2015 England Land Cover Map (CEH 2015) and the National Soil Map (NATMAP) were provided as vector datasets at the same resolution (5 m) to represent land cover, vegetation, and soil types. The resolution used was the highest possible as determined by data availability and limitations of model run time (maximum 48 h of HPC platform runtime).
For rainfall data, 15-min measured precipitation (mm) from the Malham Tarn station (Figure 1) from January 2012 to January 2022was used (Environment Agency, 2022). 15-min observed river flow (m3/s) was obtained from the Gargrave and Armley gauge over the same period (Environment Agency, 2022). Within the 10-year dataset, storm events were selected using the POT method in Extreme Value Analysis (EVA) (Leadbetter 1991), identifying high-flow events, and including multiple occurrences within a year. The Python package ‘pyextremes’ (https://georgebv.github.io/pyextremes/) was utilised as a selection tool for this analysis, while return periods were calculated at the Armley station. 15 discrete flood events were initially identified, each exceeding the discharge threshold (40 m3/s) and having a time interval of more than 7 days since the preceding rainfall event. We selected seven of these flood events that occurred in different months with varying rainfall intensities, durations, and return periods for observations at the Armley gauging station (which was used due to its urban fluvial flood risk location), which covered very common, common, uncommon, and rare flood events in the catchment (Table 1). Every event was initialised with a base flow derived from discharge data, which served as the overland flow input into the model. A 5-h warmup runtime was required for each grid cell to reach water balance within the catchment. To represent base flows under different antecedent conditions, the warm-up period incorporated either 0 mm per timestep (for dry conditions) or 0.2 mm per timestep (for wet conditions). Dry and wet antecedent conditions were defined from soil moisture reports (COSMOS-UK 2020) and the Hydrological Summary for the UK (CEH 2012–2020). This helped to categorise and understand the differences in flood mitigation effectiveness of different NFM intervention types for flood events with different antecedent characteristics.
| Parameter | Lower limit | Upper limit | Intervals | Model 0 |
|---|---|---|---|---|
| Kv (−) | 20 | 40 | 5 | 30 |
| m (m) | 0.002 | 0.018 | 0.004 | 0.009 |
| Ks (m/h) | 100 | 600 | 50 | 100 |
| Event 1 (12 December 2015) | Event 2 (3 January 2012) | Event 3 (25 December 2015) | Event 4 (8 February 2020) | Event 5 (10 October 2019) | Event 6 (16 March 2019) | Event 7 (15 February 2020) | |
|---|---|---|---|---|---|---|---|
| Return period in armley station (~years) | 50 | 10 | > 200 | 100 | 1 | 20 | 20 |
| Storm duration (h) | 16 (single-peaked) | 60 (multi-peaked) | 34 (multi-peaked) | 50 (single-peaked) | 25 (multi-peaked) | 18 (single-peaked) | 23 (multi-peaked) |
| Total rainfall (mm) | 22.4 | 64.0 | 89.6 | 70.2 | 37.0 | 44.6 | 49.2 |
| Rainfall intensity (mm/h) | 1.400 | 1.067 | 2.635 | 1.404 | 1.480 | 2.478 | 2.319 |
| Maximum rainfall intensity (mm/h) | 6.4 | 4.2 | 5.6 | 7.6 | 5.6 | 4.2 | 5.2 |
| Simulation duration (h) | 45 (Wet) | 90.5 (Dry) | 65 (Wet) | 55 (Dry) | 41.25 (Dry) | 35 (Dry) | 37.5 (Wet) |
| Kv (−) | 25 | 35 | 25 | 25 | 30 | 25 | 40 |
| m (m) | 0.006 | 0.006 | 0.006 | 0.01 | 0.01 | 0.014 | 0.01 |
| Ks (m/h) | 200 | 400 | 200 | 200 | 100 | 200 | 200 |
| NSE of best fit | 0.93 | 0.80 | 0.87 | 0.84 | 0.83 | 0.96 | 0.86 |
2.2.2 Model 0 and Calibration
To establish a Model 0 (baseline model to start calibration) with optimal and spatially uniform parameter settings for the catchment, model calibration was conducted for each of the seven observed storm events. Each model run had a 5-h spin up before the rainfall event and finished after discharge observations returned to base flow levels, with a timestep of 15 min and a cell size of 5 × 5 m. To enhance efficiency by reducing the number of calibration runs and computing time, parameter spaces were selected based on prior experience with SD-TOPMODEL testing and calibration, as outlined in Table 1a (Gao et al. 2015, 2016; Kingsbury-Smith et al. 2023). For calibration, 150 simulations were conducted for each event, totalling 1050 simulations across seven events, using varying parameters with the intervals specified in Table 1. In previous studies which have applied SD-TOPMODEL, the Nash-Sutcliffe efficiency coefficient (NSE) was used as a criterion for evaluating and selecting the best performing model (Bond et al. 2022; Gao et al. 2017; Kingsbury-Smith et al. 2023; Monger et al. 2024). The best simulation and parameter setting for Model 0 were determined for each event based on the highest NSE value and minimal differences in flood peak discharge and timing compared to observations (Table 1b). Following this, despite some discrepancies in the best-fit parameters for Events 2, 6, and 7, the parameters can be constrained to the following ranges: m (0.006–0.01); Ks (100–200); Kv (25–30). A generic parameter setting that can be used to represent the entire catchment was derived through 100 Monte Carlo tests run for each of the seven events using the narrowed range. The model was considered credible when NSE values exceeded 0.5 (Moriasi et al. 2007). However, NSE has been shown to be potentially insensitive to low and peak flows in assessing model errors (Althoff and Rodrigues 2021), thus, the absolute peak error and peak error percentage were also considered. This generic parameter setting serves as Model 0 which does not account for the spatial distribution of land cover or variations between event years resulting from NFM implementation and land cover changes. Model 0, with uniform parameters, achieved NSE values exceeding 0.6 for all events, with peak discharge errors limited to no more than 32% of observed values. The best-fit model during baseline calibration attained an NSE of 0.92, aligning with the performance reported in previous studies (Bond et al. 2022; Gao et al. 2017; Kingsbury-Smith et al. 2023; Monger et al. 2024). Once the parameter setting was determined, all subsequent model runs used this set of baseline parameter values.
2.2.3 Data for Determining Parameter Values
The model was applied for different NFM interventions. This study attempts to calibrate three parameters of SD-TOPMODEL to larger catchment scales and more complex combinations of existing NFM interventions. There are two formats to input parameters in SD-TOPMODEL used in this study: (1) a parameter file which displays baseline values of each parameter conducted by Model 0 calibration (see section 2.2.2); (2) a spatially distributed map for all three parameters based on land cover and NFM interventions to apply to the baseline values.
To represent the spatially distributed parameters, each parameter was individually spatially distributed on the base map to assign the parameter to each grid cell at the same resolution as the elevation data and the entire model. During the model run, the values within each grid cell of each parameter distribution map were calculated as multipliers on the baseline values (as the improved grassland land cover, due to its dominance in the catchment) (Bond et al. 2022; Kingsbury-Smith et al. 2023; Monger et al. 2024). The calibration ranges for these values were determined with reference to previous empirical studies (Table 2). The upper and lower limits specified by the measured ratios allow the model to be more realistic, but are also constrained by the physical meaning of them.
| Class name | Modelled parameter ranges (multipliers) | Ratio of land cover type compared with improved grassland from literature | Percentage of area (2015, 25 m raster) | Percentage of area (2020, 25 m raster)b | ||||
|---|---|---|---|---|---|---|---|---|
| m (m) | Ks (m/h) | Kv | M | Ks | Kv | |||
| Broadleaf woodland | 0.0135–0.018 (1.5–2) | 200–1000 (2–10) | 12–22.5 (0.4–0.75a) | 1.5—2 (Archer et al. 2013) |
1.8 (Murphy et al. 2020) 2.4 (Marshall et al. 2009) 12 (Gonzalez-Sosa et al. 2010) 11–20 (Monger et al. 2022a) |
1.3 (Monger et al. 2022b) 2.4 (Manning's n values, Chow, 1959) |
2.09% | 1.87% |
| Coniferous woodland | 0.0135–0.018 (1.5–2) | 150–500 (1.5–5) | 12–22.5 (0.4–0.75a) |
1.2–5.6 (Archer et al. 2013) 2.1 (Gonzalez-Sosa et al. 2010) 3.9 (Kingsbury-Smith et al. 2023) ≤ 38 (Chandler et al. 2018) |
0.71% | 1.04% | ||
| Arable and horticulture | 0.009 (1) | 50 (0.5) | 22.5 (0.75) | The same as baseline (NATMAP) | 0.5 (Holden et al. 2019) | The same as Heather | 0.34% | 0.11% |
| Improved grassland (baseline) | 0.009 (1) | 100 (1) | 30 (1) | Baseline | 58.78% | 48.71% | ||
| Calcareous grassland | 0.009 (1) | 200–500 (2–5) | 15–24 (0.5–0.8) | The same as baseline (NATMAP) |
4.6 (Gonzalez-Sosa et al. 2010) ≤ 4.9 (Kingsbury-Smith et al. 2023) ≤ 10 (Monger et al. 2022b) Significantly greater (Bond et al. 2021) |
1.4 (Monger et al. 2022b) 1.2–2.8 (Bond et al. 2020) 1.4–4 (Manning's n values, Chow, 1959) |
12.07% | 18.66% |
| Acid grassland | 0.009 (1) | 200–500 (2–5) | 15–24 (0.5–0.8) | 17.54% | 12.11% | |||
| Heather | 0.009 (1) | 100 (1) | 22.5 (0.75) | The same as baseline (NATMAP) | The same as baseline | 0.75 (Manning's n values, Chow, 1959) | 0.32% | 0.00% |
| Heather grassland | 0.009 (1) | 100 (1) | 22.5 (0.75) | 7.73% | 10.41% | |||
| Bog | 0.009 (1) | 350 (3.5) | 15 (0.5) | The same as baseline (NATMAP) | 3.3–4.2 (Holden et al. 2007) |
1.9–2.3 (Holden et al. 2008) |
3.53% | 3.66% |
| Inland rock | 0.0045 (0.5) | 100 (1) | 22.5 (0.75) | 0.5 (NATMAP) | The same as baseline (Medici et al. 2019) | 1.3 (Manning's n values, Chow, 1959) | 0.74% | 0.66% |
| Freshwater | 0.0009 (0.01) | 500 (5) | 0.3 (0.01) | — | — | — | 0.96% | 0.89% |
| Urban | 0.0009 (0.01) | 1 (0.01) | 150 (5) | — | — | Set as the highest value | 0.03% | 0.07% |
| Suburban | 0.71% | 0.86% | ||||||
| NFM interventions | Parameter multipliers | Ratio of NFM interventions compared with improved grassland with references | Percentage of area | ||||
|---|---|---|---|---|---|---|---|
| m (m) | Ks (m/h) | Kv | M | Ks | Kv | ||
| Hedgerow | 0.009 (1) | 200–1000 (2–10a) | 15 (0.5) | The same as baseline |
2 (Kingsbury-Smith et al. 2023) 2–6 (Holden et al. 2019) 22.5–27.7 (Wallace et al. 2021) |
1.6–2.3 (Manning's n values, Chow, 1959) | 1.30% |
| Woodland (new planted) | 0.0135–0.018 (1.5–2) | 150–250 (1.5–2.5) | 12–22.5 (0.4–0.75) | The same as woodland land cover |
1.2 (45-yr-old woodland, (Archer et al. 2013)) 2.3 (18-month-old saplings, (Mawdsley et al. 2017)) 2.4 (7-yr-old broadleaf woodland, (Marshall et al. 2009)) |
The same as woodland land cover | 0.61% |
| Soil aeration | 0.009–0.0135 (1–1.5) | 100–500 (1–5) | 30 (1) | 1–1.5 (Willis and Klaar 2021; Kingsbury-Smith et al. 2023) |
2.5–3 (Chehaibi et al. 2010) 1–15 (Wallace and Chappell 2019) |
The same as baseline | 6.40% |
- a Bold numbers are the ranges for parameter sensitivity tests.
- b The classification of subgroups in woodlands and grasslands in CEH Land Cover Map partially changed from 2015 to 2020. Confusion and misclassification within grassland classes will also occur (CEH 2020).
2.2.4 Calibration for Land Cover, NFM Interventions and Model Validation
This section describes the process of incorporating land cover and NFM interventions into the hydrological model through the spatial distribution of parameter multipliers, which were calibrated using an observed event (Event 1) based on Model 0. Land cover (based on CEH land cover map 2015) included broadleaf woodland, coniferous woodland, calcareous grassland, and acid grassland, and NFM scenarios consisted of three implemented interventions in the research catchment: hedgerow planting, woodland planting, and soil aeration. Spatially distributed multipliers of each parameter (Table 2) were applied to Model 0 (uniform parameters) to represent these scenarios.
The multipliers summarised in Table 2 showed high variability in woodland and grassland land cover types. The range of parameter choices was informed by the results of the previous empirical studies while also considering the baseline values for the study catchment and the limit of parameter settings in the model. Event 1 from 2015 was used for parameter testing, as the shape of the hydrograph for this event is characterised by concentrated rainfall and a single flood peak and is particularly relevant for parameter testing since the model's land cover map also corresponds to 2015, making it the most representative event. Sensitivity tests using Event 1 were conducted within the valid parameter test ranges detailed in Table 2. For land cover types, the aim was to identify the most accurate set of parameter multipliers for each type, while for NFM interventions, it was to identify the most sensitive parameter set.
Sensitivity tests were conducted using fixed intervals where parameters were selected and paired within the multiplier test range for five sets of tests (Table 2): (1) in land cover tests, Ks values were tested at intervals of 2, which paired with Kv values at intervals of 0.1 and 0.15 for woodlands, with m tested at values of 1 and 1.5; (2) in grassland scenarios, Ks was tested at intervals of 1 and Kv at intervals of 0.1; (3) in NFM scenarios, Ks values were tested at intervals of 2 to represent hedgerow planting; (4) for woodland planting, Ks was tested at intervals of 0.5 and Kv at intervals of 0.1 and 0.15, while m was tested at values between 1 and 1.5; (5) soil aeration scenarios involved testing m at intervals of 0.25 and Ks at intervals of 1. The land cover tests identified parameter multipliers that optimised model accuracy for each grassland and woodland type by assessing the correlation with NSE values. After calibrating the multipliers for the 2015 land cover map to achieve the best NSE values for Event 1 (closest to 1), all calibrated values were integrated into the land cover model. For the NFM intervention tests, calibration prioritised maximum flood peak reduction with minimal NSE decrease to ensure intervention effectiveness and maintain the rainfall–runoff relationship established in Model 0, thereby preserving model reliability. Optimal multipliers were applied to represent single and combined NFM scenarios, calibrated to achieve maximum flood mitigation without compromising model accuracy. Final parameter settings are shown in Table 3. Pearson correlation analysis, conducted in SPSS after confirming the normal distribution of the dataset, was used to assess the relationship between NSE and parameter values in land cover tests, and between peak reductions and parameter values in NFM intervention tests. Correlation strength was evaluated using Cohen's guidelines (r > 0.5 = notable effect) (Cohen 1988). Correlation analysis was employed to assess the model's sensitivity to the parameters and to explore the pattern of SD-TOPMODEL's response to parameter multiplication for adding spatially distributed land cover and NFM interventions to the spatially uniform Model 0. This analysis identified parameter sensitivity patterns, reduced model uncertainty, and prevented multiple parameter choices from yielding similar model performance.
| Land cover class | Parameter multipliers | ||
|---|---|---|---|
| m | Kv | Ks | |
| Broadleaf woodland | 1.5 | 0.75 | 8 |
| Coniferous woodland | 1.5 | 0.75 | 4 |
| Improved grassland (baseline) | 1 | 1 | 1 |
| Calcareous grassland | 1 | 0.8 | 3 |
| Acid grassland | 1 | 0.8 | 3 |
| NFM interventions | |||
| Hedgerow | 1 | 0.5 | 10 |
| Woodland (new planted) | 1.5 | 0.6 | 2.5 |
| Soil aeration | 1.5 | 1 | 4 |
For model validation, discharge results after land cover was applied to the spatially uniform Model 0 were compared with observed flow rates from the Gargrave gauging station for the seven events used for calibration and three additional events (two with wet conditions and one with a dry condition) from the 15 discrete flood events identified above. Validation involved calculating NSE values (Table 4) and assessing the fit of flood peak discharge and arrival times. Following validation, NFM scenarios were applied to the land cover model, and flood peak reduction effectiveness was assessed by comparing results with the land cover model. A radar plot quantified the area and flood mitigation effects of each scenario using quantile comparisons. Results were grouped by event characteristics (single/multi-peaked and dry/wet catchment conditions) and scenario characteristics (single/multiple interventions) to evaluate their impacts on flood mitigation effectiveness.
| Scenarios | Event 1 | Event 2 | Event 3 | Event 4 | Event 5 | Event 6 | Event 7 | Mean | SD | Validation 1 (31 December 2012, wet) | Validation 2 (2 January 2015, dry) | Validation 3 (14 October 2017, wet) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NSE (Model 0) | 0.92 | 0.86 | 0.90 | 0.63 | 0.73 | 0.60 | 0.78 | 0.78 | 0.13 | 0.64 | 0.96 | 0.95 |
| NSE (Land cover model) | 0.93 | 0.77 | 0.82 | 0.68 | 0.66 | 0.59 | 0.70 | 0.74 | 0.12 | 0.61 | 0.97 | 0.91 |
| Percentage of peak differencesa of Model 0 (%) | 9% | −4% | 12% | 24% | 5% | 32% | 10% | 13% | 12% | −14% | −5% | −7% |
| Peak time difference of Model 0 (h) | 0.25 | −0.25 | 1 | −0.25 | −0.75 | −2.25 | −0.5 | −0.39 | 1.00 | −1 | −0.5 | −0.25 |
| Percentage of peak differencesa of land cover model (%) | −2% | −5% | −8% | 15% | 5% | 26% | 2% | 5% | 12% | −21% | −8% | −10% |
| Peak time difference of land cover model (h) | 0.25 | 0 | 1.25 | 0 | −3 | −3 | −0.5 | −0.71 | 1.65 | −1 | −0.5 | −0.25 |
| Overland flow peak arrival time different of land cover model (h) | 0.25 | 0.25 | 1.25 | 0 | −0.5 | −2 | −0.25 | −0.14 | 0.99 | −0.5 | −0.25 | −0.25 |
- a Peak discharge here is the sum of subsurface and overland flow. Percentages are the differences between the modelling peaks compared to the observed peaks as a percentage of observed peaks.
3 Results
3.1 Sensitivity Tests
3.1.1 Correlation Analysis for Model Calibration—Land Cover and NFM Interventions
The sensitivity of different land cover types to the three parameters' multipliers varied, and a significant correlation existed between Ks, Kv and model performance. As shown in Figure 3a, surface roughness Kv was significantly positively correlated with NSE values (r = 0.918, p < 0.001) as the NSE values increased with the increasing Kv values, but not with soil hydraulic conductivity Ks (r = 0.303, p = 0.195). NSE values increased until Ks multiplier reached 6 after which they were no longer affected by Ks. This indicates that for woodland land cover types, including broadleaf woodland and coniferous woodland, the model fit improved with a marginal increase in surface roughness. Thus, the best fit of the model (the maximum NSE values) for woodland land cover types was achieved when Kv decreased by 0.75 times and Ks increased by 8 times (as highlighted in Figure 2a). Multiplier values of 1.5 or 2 for soil active water storage depth m did not affect the correlation patterns between Ks, Kv and model fit. Choosing the multiplier of 1.5 reduced the impact of model performance caused by parameter changes, while a multiplier of 2 increased the standard deviation of NSE results in general.
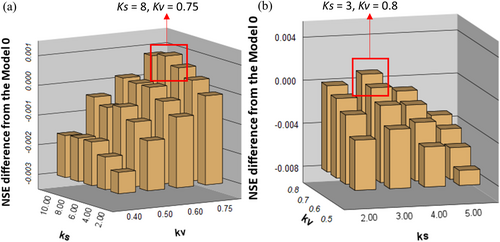
As highlighted in Figure 2b for grassland land cover types (calcareous grassland and acid grassland), Ks (r = −0.650, p < 0.01) was more strongly correlated to NSE values than Kv to NSE (r = 0.625, p = 0.01). The correlation between Ks and NSE tended to arc and had a relative peak when the Ks multiplier was 3. The relationship between Kv and NSE values was consistent with the above results of woodland tests, that is, increases in surface roughness led to better model fit. Thus, the model fit of grassland land cover types was significantly correlated with both Kv and Ks. The best model fit was achieved when Ks increased to 3 times that of Model 0 and Kv increased marginally from Model 0. Similar to the woodland results, m had no significant correlation to the model fit of grassland scenarios. Overall, the parameter multipliers for woodland and grassland scenarios were chosen using the highest NSE values achieved in the sensitivity tests.
For the NFM interventions, the same sensitivity tests were used to find the most effective combination of parameter multipliers to represent three NFM interventions. All NFM scenarios were applied to the land cover, and their test results were compared with the Model 0 results. As shown in Figure 3, none of these parameter tests caused a significant decrease in the NSE values from Model 0, indicating that the test did not affect model performance. Thus, correlation analysis for NFM scenarios was focused on comparing the effects on flood peaks.
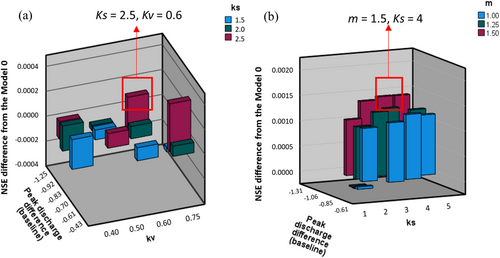
Among the three NFM interventions, there was no significant pattern among Ks, NSE values, peak discharge differences, and peak arrival time differences for hedgerow planting. The greatest flood peak reduction occurred when Ks reached 10 times the baseline value, suggesting this as the most effective multiplier for hedgerows. For woodland planting, test results were first compared between m multiplier of 1.5 and 2. While the multiplier of 2 reduced mean flood peak discharge by 0.58 m3/s and delayed mean peak arrival time by 0.02 h, it increased variability as the standard deviation increased. To maintain consistency with the land cover tests described above, the multiplier was chosen as 1.5 to represent newly planted woodlands. Kv in woodland planting was strongly correlated with peak discharge reduction (r = 0.900, p < 0.001), which indicates that the increase in surface roughness significantly reduced peak discharge, while Ks changes had no significant impacts on peak reductions (r = −0.119, p = 0.712). When the multiplier of Ks was taken as 2.5, using a Kv multiplier of 0.5, 0.6, and 0.7 all increased the NSE values, with the multiplier of 0.6 resulting in the greatest reduction in peak discharge. For woodland planting, changes in Kv and Ks had no significant impact on peak arrival delay. For soil aeration, all parameter pairs increased the NSE value. The most effective flood reduction test results were chosen (Figure 3b). An increase in m significantly reduced peak discharge (r = −0.619, p = 0.014), and an increase in Ks slightly reduced peaks (r = −0.646, p < 0.01) (Figure 3b). Finally, a parameter pair that maximised flood reduction and maximised the NSE value was chosen for soil aeration. Final parameter multipliers for land cover and NFM interventions are shown in Table 3.
3.1.2 Sensitivity of Peak Changes—Land Cover and NFM Interventions
For peak discharge reduction and arrival time delay in land cover tests, Kv was significantly correlated with peak discharge reduction for woodland (r = 0.959, p < 0.001) and grassland land cover types (r = 0.750, p < 0.001), but not with peak arrival time. Ks and m showed no correlation with peak changes. This indicates that surface roughness increases via woodland and grassland land cover significantly reduced peak discharge. For Event 1, woodland land cover attenuated mean peak discharge by 1.35% (SD = 0.84%) and delayed arrival by 0.3 h (SD = 0.1 h). Grassland land cover reduced mean peak discharge by 3.6% (SD = 1.6%) but had no peak delay (0 h; SD = 0.17 h). Therefore, woodland was more effective at delaying peaks, while grassland had a greater effect on peak discharge reduction.
Parameter test results for all three NFM interventions (section 3.1.1) revealed sensitivity in reducing peak discharge compared to the Model 0 results for Event 1. Woodland planting and soil aeration decreased flood peaks by a mean value of 0.731 m3/s (1.15%) and 0.883 m3/s (1.40%) respectively, showing greater sensitivity than hedgerows. However, none of the three NFM interventions had a significant impact on flood peak delay.
3.2 Model Performance: Robustness and Accuracy
To calibrate and validate the model, NSE values and peak fit results were evaluated for the baseline and land cover models (Table 4). While NSE values for some events in the land cover model were lower than in Model 0 with spatially uniform parameters, this did not indicate that land cover reduced model accuracy. Since the study focuses on flood peaks, the accuracy of peak fits was deemed more important. Hydrographs for Event 1 (Figure 4a) showed that the land cover model increased low flows at the start of the event and reduced peak flows, providing a better fit than Model 0.
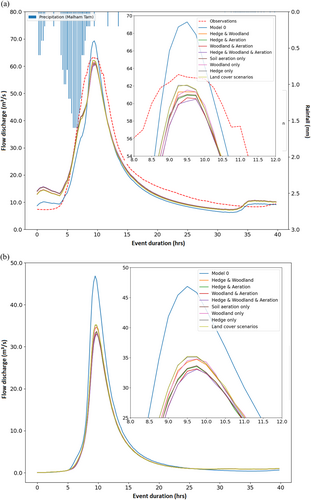
Peak fits were assessed by comparing maximum flood peaks and arrival times to observations for Model 0 and the land cover model, respectively (Table 4). The land cover model had a better fit for peak discharge but not for arrival times. When comparing the total runoff and overland flow time series data in the model results, there was a difference in peak arrival times, as illustrated in Figure 4. These biases were from 0 to 2.5 h in several events. It is likely that the bias may be due to model characteristics and does not represent an error in the model results. Moreover, it was verified that the difference between the peak arrival times of overland flow time series in the land cover model and observations was negligibly small (Table 4) and did not affect subsequent NFM scenario results. This is the reason why only overland flow discharge data were used for the analysis of the NFM scenario results.
3.3 NFM Scenarios
After obtaining all parameter expressions as shown in Table 3 through sensitivity testing, all land cover and NFM scenarios were put into the model and run for all seven storm events. There was variability in the effectiveness of the different NFM interventions for each storm event and the impact of the different events on NFM scenarios. The details of overland flow results for NFM scenarios were compared to overland flow results for the land cover model as detailed below.
3.3.1 Impacts of Single Intervention Scenarios
The soil aeration intervention was implemented across the largest proportion of the study catchment (6.40%), which is much higher than the area of the other two interventions: woodland planting (0.61%) and hedgerow planting (1.30%) (Figure 1). The axes of the radar plot (Figure 5) represent the quartiles of peak discharge reduction and area proportion. Notably, Event 4 showed the highest flood peak reduction percentage compared to other events (Figure 5a). The overland flow peak reduction effect of the single intervention scenarios varied. Discharge reduction by soil aeration was largely proportional to the increase in area of implementation. The results showed that the discharge reductions achieved by soil aeration interventions were consistently above the 50th quantile for peak reduction in Figure 5b. Woodland planting represented the smallest area yet achieved effective flood peak reduction in all events. This contrasts with the results for hedgerow planting. Although hedgerow planting increased Ks tenfold and doubled the Kv of baseline values, neither resulted in a significant reduction in flood peaks, with a maximum reduction of only 1.3% across all seven events (Table 5).
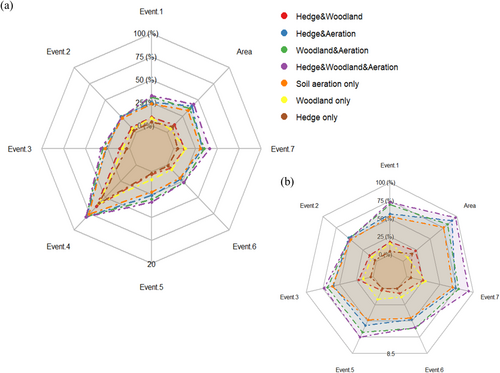
| NFM scenarios | Overland flow peak reduction (%) | Overland flow peak delay (h) | Area (%) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Event 1 (wet) | Event 2 (dry) | Event 3 (wet) | Event 4 (dry) | Event 5 (dry) | Event 6 (dry) | Event 7 (wet) | Mean | SD | SEM | Mean | SD | SEM | ||
| Soil aeration only | 4.43 | 4.02 | 5.17 | 15.00 | 4.04 | 3.79 | 5.82 | 6.04 | 3.72 | 1.41 | 0.11 | 0.23 | 0.09 | 6.40 |
| Woodland only | 1.23 | 0.66 | 1.18 | 11.79 | 1.33 | 1.05 | 2.34 | 2.80 | 3.70 | 1.40 | 0.11 | 0.18 | 0.07 | 0.61 |
| Hedgerow only | 0.31 | 0.14 | 0.23 | 11.62 | −0.09 | −0.12 | 0.49 | 1.80 | 4.02 | 1.52 | 0.00 | 0.19 | 0.07 | 1.30 |
| Hedgerow and woodland | 1.39 | 1.02 | 1.75 | 12.61 | 0.15 | 0.55 | 2.03 | 2.79 | 4.06 | 1.53 | 0.07 | 0.11 | 0.04 | 1.91 |
| Hedgerow and soil aeration | 4.75 | 4.39 | 5.04 | 15.87 | 4.81 | 4.02 | 6.20 | 6.44 | 3.90 | 1.47 | 0.04 | 0.16 | 0.06 | 7.70 |
| Woodland and soil aeration | 5.90 | 4.24 | 5.76 | 15.83 | 5.68 | 5.16 | 6.62 | 7.03 | 3.65 | 1.38 | 0.14 | 0.12 | 0.05 | 7.01 |
| Hedgerow, woodland and soil aeration | 6.17 | 4.20 | 6.21 | 15.99 | 6.36 | 5.04 | 7.91 | 7.41 | 3.66 | 1.38 | 0.18 | 0.17 | 0.07 | 8.31 |
| Mean | 3.45 | 2.67 | 3.62 | 14.10 | 3.19 | 2.78 | 4.49 | 4.75 | ||||||
| SD | 2.24 | 1.80 | 2.29 | 1.86 | 2.48 | 2.06 | 2.61 | 3.08 | ||||||
| SEM | 0.85 | 0.68 | 0.86 | 0.70 | 0.94 | 0.78 | 0.99 | 1.16 | ||||||
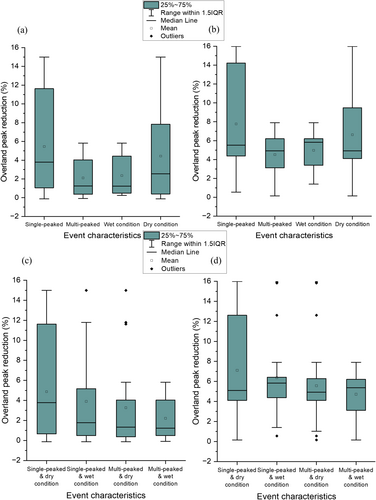
Consistent with the results of the previous parameter sensitivity tests of NFM scenarios for Event 1 (Figure 3), soil aeration was more sensitive in reducing peaks than woodland planting, but both had a greater effect than hedgerow planting (Figure 5). This was reflected in the mean values of overland flood peak reductions calculated for seven events in Table 5. While the standard deviations of peak reductions across the seven events were relatively similar, hedgerows led to slightly higher peak flow variability compared to the other two interventions. The high standard deviation values indicated that the characteristics of the events may have contributed to the increased heterogeneity in the results of NFM scenarios. To better interpret the validity of different NFM scenarios, the results were analysed by grouping according to event characteristics: the shape of hydrographs (single or multi-peaked), the wet or dry preconditions of the catchment and their combinations (Figure 6). The grouped results showed that the same NFM interventions were less effective in reducing overland flow peaks in multi-peaked flood events compared to single-peaked events. The peak reduction driven by NFM interventions in dry conditions was approximately twice as effective as in wet conditions. NFM interventions can therefore have greater effectiveness under certain conditions, such as dry antecedence in soil during a single-peaked flood event.
3.3.2 Impacts of Combinations of Scenarios
Results from the single NFM intervention scenarios were combined into pairs or with all three and tested for seven storm events. The overland flow peak reductions varied among different combinations of NFM interventions (Table 5). Comparing the mean of reductions shows that the flood mitigation effectiveness of the combined intervention scenarios is not simply equivalent to the sum of the effects of single intervention scenarios, where different combinations may have enhanced or reduced effects on the flood mitigation. For example, the mean overland flow reductions for the hedgerow & woodland planting combination and for the single woodland planting intervention were almost identical. However, for the hedgerow & soil aeration intervention combined, the mean discharge reduction increased by 0.4% compared to the single soil aeration intervention. These increases by combining hedgerow planting with another intervention are all less than the mean discharge reduction of 1.8% that can result from the hedgerow planting intervention alone. The standard deviations in Table 5 are all between 3.5% and 4%, which are relatively high compared to the mean, indicating that the impact of the interventions varies widely between events.
Although there is a clear flood mitigation effect in each combination, not all events have a stronger peak reduction by combining NFM interventions. Figure 5 shows that the effectiveness of overland flow peak reduction varies among events. For example, the hedgerow & woodland combination (red line) achieved an overland flow peak reduction effect comparable to the proportion of area implemented for all events except Event 5. This differed from the results for the woodland only scenario, where the inclusion of the hedgerow intervention significantly increased peak mitigation in Event 4 but had the opposite effect in Event 5. The soil aeration intervention was the most effective of the single interventions despite being applied to the smallest proportion of the catchment and had positive interaction effects when woodland or hedgerow planting were combined with it among all seven events. The combination of woodland and soil aeration had a more effective overland flood peak reduction effect than the combination of hedgerow and soil aeration in five events. The combination of three interventions resulted in the maximum peak reduction, except in Event 2 where the effect was slightly lower than that of hedgerow & soil aeration and woodland & soil aeration combinations and in Event 6 where the effect was slightly lower than that of the woodland & soil aeration combination. Thus, even though the addition of woodland planting and soil aeration interventions to the combinations was effective in peak reduction, there were still differences in response to different storm events. Comparing Figure 6 (a) and (b) for event groups, the increase in the median under all four groups shows that multiple interventions enhanced the overland flow peak reduction effect overall. A similar finding is shown in Figure 6 (c) and (d), where multiple interventions were effective at enhancing NFM performance under unfavourable conditions, such as multi-peaked events and wet soil conditions. Thus, the weakening of NFM effectiveness due to multi-peaked flooding and wet conditions was less pronounced under multiple interventions compared to a single intervention.
In scenario tests, overland flow peaks were delayed in arrival by up to 0.5 h. Several scenarios had overland flow peaks that were advanced by one timestep (0.25 h) in some events. Hedgerow & woodland, woodland & soil aeration, and all three interventions scenarios resulted in no advance in overland flood peak arrival time among the events. Overall, the mean delay for each scenario across the seven events ranged between 0 and 0.18 h. The mean delays for soil aeration and woodland planting were the same, but woodland planting had a smaller standard deviation, suggesting less individual variation among events. The hedgerow planting scenario had no effective peak delay compared to the other scenarios. The mean delays for various combinations of scenarios generally followed the pattern of the overland flow peak reductions: adding soil aeration and woodland planting to any interventions increased the delay slightly, while the combination of three interventions resulted in the greatest delay.
4 Discussion
This study used SD-TOPMODEL to investigate the impacts of different land cover types and NFM interventions at an 81.4 km2 catchment. These effects include impacts on model accuracy and performance, flood peak reduction and arrival time delays, and impacts on the interaction of subsurface and overland flows. In general, it was found that SD-TOPMODEL can efficiently and accurately simulate different types of NFM interventions at this catchment scale, validated against multiple storm events, while allowing high resolution (5 m) spatial distribution. The modelling results indicated that multiple interventions were not always the most effective. Event characteristics and antecedent conditions played a significant role in determining the level of flood mitigation.
4.1 Evaluating Model Parameters and Model Performance
In the parameter calibration and validation of the model, the evaluating criteria are dynamic, including model fit metrics (e.g., NSE values) and flood peak reduction, which are adapted based on the objectives of each calibration scenario. Multi-objective optimization has been justified to improve compromised solutions and enhance the hydrological consistency of parameter settings (Dung et al. 2011; Wöhling et al. 2013; Shafii and Tolson 2015; Althoff and Rodrigues 2021). A multi-objective calibration approach is needed for the accuracy of the simulation as indicated by the NSE values and the effectiveness against flood mitigation in this study, which depend on the purpose of the test (Efstratiadis and Koutsoyiannis 2010). For example, during the calibration of parameters for land cover types, results indicated that increasing surface roughness was the most effective factor in reducing peak discharge, but the multipliers with the least amount of change within the range were chosen. This is because the best model accuracy (NSE values closer to 1) was achieved when the roughness parameter was increased by the least amount. The land cover model aims to determine the best fit to the actual land cover distribution by comparing to observations; thus, NSE values were more critical criteria for the land cover model. On the contrary, in the NFM scenarios, while the NSE values were used as criteria for model stability, the determination of the parameter values depended on the best flood peak reduction that could be achieved with similar NSE values. This dual-objective approach aligns with the methods used in recent studies that emphasise balancing model stability with functional performance (e.g., flood peak reduction) (Shafii and Tolson 2015; Althoff and Rodrigues 2021). Future research could build on this strategy by exploring how different catchment characteristics influence the trade-off between stability and effectiveness, potentially leading to the development of adaptive calibration frameworks tailored to specific hydrological contexts.
4.2 Impacts of Land Cover Type and NFM Interventions on Flood Peak Reduction and Timing
Results from this study suggest that NFM interventions achieve maximum effectiveness during single-peaked storms, particularly under dry antecedence. In previous modelling studies of NFM on flood peak reduction, it has been shown that the reductions vary between events, and that this is mainly related to event characteristics (Gao et al. 2016, 2018; Ferreira et al. 2020), particularly pre-event soil moisture (Wahren et al. 2012). Some studies also considered seasonal rainfall, which could be adjusted by model parameters (Gabriels et al. 2022). The seven events used in this study occurred in winter months from October to March and were grouped based on event characteristics and catchment antecedent conditions, allowing them to be compared by their impact on overland flow peak reduction (Figure 6).
Overland flow peak reductions delivered by NFM scenarios were not significantly different for high or low rainfall intensity events when rainfall was concentrated. The most prominent of these was Event 4, which resulted in a greater peak reduction than the other events in each of the single intervention scenarios. This may be because Event 4 was a rapid flow event that occurred under dry antecedent conditions and had a much higher flood peak discharge than the other events. Overall, the results suggest that greater overland flow peak reduction occurs under dry antecedence compared to wet antecedence (Figure 6), which aligns with findings from other monitoring and modelling studies on land cover and land use (Bond et al. 2020; Breuer et al. 2009; Wallace and Chappell 2019). However, the sample size of events in this study is small, and further testing for rainfall varieties is needed in the future.
The overland flow peak reduction obtained in this study for the three combined NFM interventions was in the range of 4.20%–15.99%. We found modelling the effects of upland interventions on downstream runoff at a larger catchment scale (81.4 km2) did not yield significantly different results to other local scale modelling studies (Bond et al. 2022; Hankin et al. 2019; Kingsbury-Smith et al. 2023; Monger et al. 2024). No significant correlation was observed between the peak reduction and rainfall intensity, consistent with findings from the data synthesis by Zhu et al. (2024). The study with the closest results to ours also employed SD-TOPMODEL though at a lower resolution (20 m) and concluded that upland land management scenarios covering most of the catchment (84 km2) resulted in 3.9% to 15% flood reduction with various rainfall intensities (Gao et al. 2017). In contrast, our study used a higher resolution and covered all realistically existing land cover types, which is closer to the reality.
The closest catchment used for a published NFM simulation to that of the Upper Aire was for Bishopdale in northern England, a study which utilised SD-TOPMODEL and yielded flood peak reductions of up to 11% (Kingsbury-Smith et al. 2023). Their study concluded that the scenario combining all types of NFM interventions across a large percentage of the 38 km2 catchment achieved the smallest peak reduction for a 100-year rainfall event and suggested that such an effect may be caused by increased synchronisation between small tributaries. This is contrary to the findings of our study in our larger catchment (81.4 km2), which showed that a combination of existing interventions (covering 8.31% of the catchment) produced greater reductions in peak flow than any single intervention, including soil aeration (6.40% of the catchment), the largest and most effective individual intervention. The larger catchment scale of our study offers greater potential for a strategic distribution of multiple NFM interventions leading to desynchronisation of peak flows and achieving solid peak reductions with a lower percentage of intervention areas. However, the differences in NFM modelling results between catchments and scenarios highlight the importance of modelling potential responses on a case-by-case basis for each individual catchment (Zhu et al. 2024). This is essential for the effective planning and implementation of a portfolio of catchment-based NFM interventions both within the UK and internationally. Additionally, we tested observed rainfall events ranging from 1-year to over 200-year return periods and calibrated and validated the model using observed data, enhancing the model's credibility and realism. Another study conducted in Swindale in northern England used the Dynamic TOPMODEL combined with a 2D hydraulic model to find flow reductions of 2%–6% by NFM (Hankin et al. 2019). This suggests that even though the study is for a combination of NFM interventions and excludes differences in catchment size and rainfall intensity, the area and location of the interventions, the characteristic or precondition of the catchment, and the model used, as well as its resolution and parameter choices, all have an impact on the simulation results.
We also found that the flood reduction from different NFM combinations is not directly proportional to the sum of the areas where interventions were implemented. The hydrological response of NFM interventions is primarily attributed to the attenuation of the main flood wave travelling through the intervention area (Dixon et al. 2016). When upscaling the study area, the peak flow reduction effects from different sub-catchments did not simply accumulate at the whole catchment scale (Pattison and Lane 2012). As a result, potential synchronisation between sub-catchments means that the NFM effect on peak discharge does not increase in direct proportion to the area and number of interventions implemented. These subtle differences in peak discharge make it challenging to isolate model uncertainty.
4.3 Implications for SD-TOPMODEL and NFM
There was a bias in the flood peaks in the three outputs of the model (total runoff, subsurface flow, overland flow), which is dictated by model characteristics. A lag time exists between the peak of total runoff and the peak of overland flow (Figure 4). The arithmetic mechanism of the model is to prioritise subsurface runoff and to start generating saturation-excess overland flow when the soil is saturated, and these flows are calculated separately in each grid and each timestep (Gao et al. 2015), which allows the model to fully represent the rainfall-runoff process within the topsoil. This procedure allows the model to output the amount of runoff from the subsurface and surface at each timestep and each grid. Thus, the model produces total runoff and overland flow rising and falling limbs at different times, and their delay lengths also vary between events (Figure 4).
The scenarios in this study significantly reduced total runoff compared to the spatially uniform Model 0, while overland flow decreased and subsurface flow increased. Similarly, Monger et al. (2024) found that woodland scenarios critically affected the interactions of subsurface and overland flows in SD-TOPMODEL results and reduced total runoff. Increasing the woodland cover improved soil permeability, which increased subsurface flow and reduced its conversion to overland flow (Monger et al. 2022a, 2022b; Monger et al. 2024). Grasslands were found to have higher surface roughness and lower soil permeability than woodlands (Bond et al. 2020; Monger et al. 2022b), which may influence overland flow more than subsurface flow in SD-TOPMODEL (Bond et al. 2022). When land cover and NFM scenarios were applied, the subsurface flow increased at the beginning of storm events, which delayed the time before the onset of saturated-excess overland flow. This is because all simulated scenarios increase soil hydraulic conductivity and surface roughness in general. Higher infiltration rates and longer infiltration times allow more water to be stored in shallow soils. Moreover, the land cover and NFM scenarios increase the efficiency of the soil saturation process while increasing the active area of subsurface runoff in the catchment. Therefore, overland flow peaks are reduced by these scenarios. The simulation results of SD-TOPMODEL efficiently and accurately demonstrate the effectiveness of NFM.
5 Conclusions
Our study demonstrates a successful application of SD-TOPMODEL in a catchment (81.4 km2) at a 5 m resolution, achieving a strong fit to observed data, with NSE values reaching up to 0.93 and minimal peak flow errors. In the modelling of land cover types in the study catchment, woodland was found to be more effective in delaying peaks, whereas grassland was more effective in reducing peak discharge. Among the existing NFM interventions, soil aeration emerged as the most effective individual measure, achieving greater peak discharge reduction results than woodland planting and hedgerow planting. However, the effectiveness of NFM interventions was influenced by flood and rainfall characteristics, as well as pre-event catchment conditions (wet or dry). Notably, greater flood peak reductions were observed during single-peaked events and in dry pre-event conditions. Furthermore, multiple interventions proved more effective and resilient than single interventions in attenuating floods at the catchment scale we examined. The results also revealed that the area and number of interventions were not decisive in flood mitigation. This finding presents an opportunity to strategically plan multiple NFM interventions at the catchment scale, enabling a trade-off between intervention area and cost-effectiveness. Therefore, we recommend that high-resolution, spatially distributed modelling of more catchments be undertaken to investigate the impact of catchment characteristics on the effectiveness of NFM. This would support the optimisation of spatial planning and enhance the integration of NFM with other flood risk management measures during the planning stage.
Acknowledgements
This work was undertaken on ARC3/ARC4, part of the High-Performance Computing facilities at the University of Leeds, UK. NFM records and data in Upper Aire Catchment were provided by Yorkshire Wildlife Trust. We thank two anonymous reviewers and the editor for providing constructive feedback that imporved this manuscript.
Open Research
Data Availability Statement
Sensitivity tests and all simulations with land cover and NFM interventions/scenarios for the model are available at https://doi.org/10.5518/1628.




