Characteristics of CA1 place fields in a complex maze with multiple choice points
Funding information: Sigrid Juselius Foundation, Finland; Office of Naval Research MURI award, Grant number: N00014-10-1-0936.
Abstract
For the sake of rigorous control of task variables, hippocampal place cells have been usually studied in relatively simple environments. To approach the situation of real-life navigation in an urban-like environment, we recorded CA1 place cells while rats performance a memory task in a “Townmaze” with two start locations, three alternate paths in the maze midsection, followed by a two-way choice that determined the trial outcome, access to a goal compartment. Further, to test the ability of place cells to update their spatial representation upon local changes in the environment while maintaining the integrity of the overall spatial map to allow effective navigation, we occasionally introduced barriers in the maze mid-section to force the rat to select a nonpreferred route. The “Townmaze” revealed many new interesting features of CA1 neurons. First, we found neurons with 3–5 fields that appear to represent segments on a single common route through the maze. Second, we found neurons with 3–5 fields similarly aligned along the longitudinal or transverse maze axis. Responses to the barriers were assessed separately near and far from the barriers. Appearance of new fields in response to the barriers took place almost exclusively only locally near the barrier, whereas in-field firing rate changes occurred throughout the maze. Further, field location changes did not correlate with the task performance, whereas firing rate changes did. These findings suggest that in a complex environment with blocked distal views, CA1 neurons code for the environment as sequences of significant nodes but are also capable of extracting and associating common elements across these sequences.
1 INTRODUCTION
Hippocampal place cells of rodents have been extensively studied in walled circular arenas with a single prominent cue card. In addition, numerous experiments have employed elevated linear or circular tracks or in somewhat more complex open tracks such a figure W, O, or Phi mazes. Common to the latter group of tracks is an open view to all room cues, thus resembling navigation in open landscapes. In contrast, most human navigation nowadays takes place in an urban environment where buildings bordering the streets block the view to distant landmarks. In many cities, most buildings look the same at the first glance, forcing navigation to be based on certain prominent landmarks and an overall grid plan of the city. Virtual reality has become the gold-standard way to study navigation-related brain signaling in humans, including recordings of hippocampal single neurons. All reported evidence of hippocampal place cells in humans has been obtained in experiments with navigation in virtual towns. Human place cells appear to code for landmarks and routes (Ekstrom et al. 2003, Miller et al. 2013) rather than place in the classic sense of rodent place cells in a circular arena (Muller, Kubie, & Ranck, 1987). On the other hand, in simple elevated tracks, also rodent place cells appear to code for routes (i.e., relative position in the track and direction of movement; Jackson & Redish 2007). To make a fair comparison between rodent and human place cells, we would need similar data from the rodent hippocampus, but to our knowledge, no study so far has characterized place cell properties in an urban-like environment. To this end, we constructed the “Townmaze,” a complex but symmetric structure with winding alleys separated by high-enough walls to prevent the rat's view to the neighboring alley, and wanted to assess the place field characteristics in this large (180 cm x 140 cm) environment.
Navigation in an urban environment usually offers several alternate routes to the destination. We all probably have our preferred routes, but on special conditions such as heavy traffic or street construction, we have no problems in switching to an alternate route without losing our sense of direction. This kind of flexible use of a spatial map has been suggested to strongly depend on the hippocampus and the propensity of hippocampal place cells to show location specific firing (O'Keefe & Nadel, 1978). A conspicuous feature of rat hippocampal place cells is that their location specific firing is very stable upon repeated exposure to a constant environment (Muller et al., 1987), while in other instances even small changes in the physical appearance or geometry of the closed environment (Muller & Kubie, 1987) may induce a total rearrangement of the place fields (remapping). Furthermore, remapping can be induced by a change in task contingency in an entirely stable environment (Markus et al. 1995; Wood, Dudchenko, Robitsek, & Eichenbaum, 2000). In a classic experiment, Muller and Kubie (1987) explored the effect of a barrier that overlapped a place field on the CA1 place cell firing. In almost every case, this led to dramatically reduced firing rate. The effect was more likely due to physical obstacle for movement than the appearance of a novel object, since the low base of the barrier alone did not induce such changes (Muller & Kubie, 1987). A more recent study extended these findings by forcing a rat to make a detour in a linear maze by blocking the shortest route to goal by a transparent barrier (Alvernhe, Save, & Poucet, 2011). In this case, remapping was often observed in neurons with place field near (30–40 cm) the barrier but not in fields further away.
If introduction of barriers to the preferred route results in remapping as easily as the observations above suggest, it is easy to understand that the hippocampal spatial map is flexible and readily modifiable when changes occur in the environment. However, how can the hippocampal map at the same time maintain a stable representation of the environment that would be a prerequisite for effective navigation? To address the question of simultaneous stability and flexibility in the hippocampal spatial map, we employed the complex Townmaze in which local changes could be enforced without changing the overall structure of the environment or the task rule. In addition, we wanted to have a behavioral control to be able to relate changes in place fields with fluctuations in the task performance. To this end, we modified the Townmaze so that the rat had a free choice between three alternate routes through the maze mid-section followed by a two-way decision that determined the trial outcome. In this situation, barriers did not force the animal to take a detour through a less familiar route but only biased the choice from preferred to nonpreferred but familiar routes.
2 MATERIALS AND METHODS
2.1 Animals
Four male Long-Evans rats weighing 400–500 g during the recordings were used. During training and recording, the animals were individually housed and on a restricted diet (max 10% weight reduction) on weekdays to ensure motivation. Water was freely available all times. All procedures were approved by the Committee on Animal Care at Massachusetts Institute of Technology and followed U.S. National Institutes of Health guidelines.
2.2 Environment and behavioral tasks
Recordings took place in a complex symmetric “Townmaze” (180 cm × 140 cm) with three chambers equipped with slide doors and winding alleys separated with 20-cm high walls (Figure 1a). The maze was made of black plastic with matt surface. Three parallel alleys in the Townmaze center converged on a T-junction at the far end of the maze. This point is referred to as the Decision Point. Each trial started in the Goal chamber where the rats could consume the earned reward and rest for 1 min. Then the rat was led to the left or right Start chamber in a pseudorandom order and left there for 30 s. After a winding entrance alley, the rat had three alternate paths leading to the Decision Point, where the rat had to decide between a left and a right turn. If the choice was correct, the rat would find its way to the Goal and be rewarded with 4 minipellets (20 mg), while a wrong choice led to a blind alley, which forced the rat to backtrack to the Decision Point and choose the opposite lateral alley to reach the Goal. In this case, only one minipellet was awarded. Only fecal bullets or urine puddles were cleaned during the session, but between the sessions, the maze was cleaned carefully with 70% ethanol to remove all scent marks.
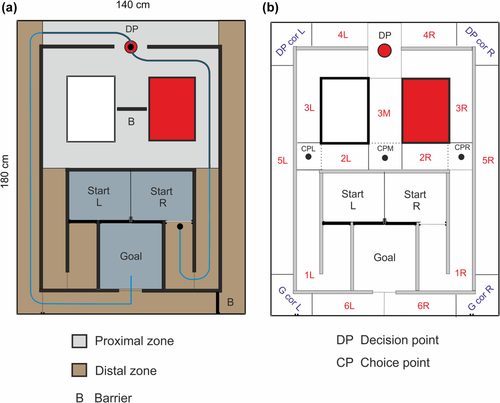
(a) Construction of the Townmaze. The blue line corresponds to a typical route during the Nonmatch task. The rat starts from the Right Start compartment and chooses the rightmost of the three alternate routes through the maze midsection. At the Decision Point (filled red circle) the rat chooses the open left route to the Goal. Note that the left lateral route is blocked by a slide door at the corner (black line and letter B). The red and white rectangles represent plastic boxes that divide the midsection into three routes. The alleys of the maze are divided into a Proximal (light gray) and Distal (light brown) zones. The open Goal and two Start compartments are further separated by a medium gray shading. The thick transverse line letter B between the red and the white rectangle depict a potential position of a barrier to bias the rat's choices. (b) Division of the Townmaze into functional segments. The segments where the animal only runs through without making decision about the direction are depicted with red labels (L = left, M = middle, R = right). When considering the geometry of the maze, 1L/1R segments are further divided into longitudinal (1La/1Ra), transverse (1Lb/1Rb) and longitudinal (1Lc/1Rc) subsegments, and 3L/3R into longitudinal (3La/3Ra) and transverse (3Lb/3Rb) subsegments. Corners where the rat makes the decision whether to continue or return are depicted with purple labels (DP cor = Decision Point corner, G cor = Goal corner). Further, points where the rat chooses between alternate routes are labels as Choice Points (CPL, CPM, CPR), and the point where the rat decides whether to choose the left or right alley to reach the goal as Decision Point (DP). [Color figure can be viewed at wileyonlinelibrary.com]
Two task rules were applied, which both required the rat to remember its starting location when it came to the Decision Point and make the choice accordingly. All rats were first trained in a Nonmatch task. If the trial started in the left Start chamber, the correct response was to turn right, while when the trial began from the right Start chamber, a left turn was required (Figure 2). The course of a typical Nonmatch task session is given in Table 1. The animals were first trained to perform the task before the electrode implantation to a criterion of 80% correct. After an initial drop in the performance close to chance level during early recordings, the rats gradually improved and reached a performance level up to 90% correct. To add difficulty to the task, occasionally (in 20% of trials on average), one or two of the paths in the maze mid-section were blocked with an opaque barrier (height 20 cm) to force the rat to take a nonpreferred route. These trials are later referred to as barrier trials in contrast to free trials. Two of the rats still attained a performance level where they rarely made mistakes. It has been demonstrated that upon repetition rats tend to switch from hippocampal-dependent spatial navigation to striatal-dependent response strategy in an attempt to solve a two-choice maze task (Packard & McGaugh, 1996). To encourage the rats' use of hippocampal spatial strategy, we introduced a second, Position task. Here the rat had to ignore its start location and repeatedly choose either left or right (predetermined by the experimenter) lateral alley (Figure 2). The course of a typical Position task session is given in Table 2. Once the rats had learned this new rule, we introduced yet another modification for the last recording sessions. Now, in the middle of the session the rule was unexpectedly changed, so that the opposite lateral alley now led to the Goal. In the Position task, the trial introducing a new rule was not counted as correct or error, only the following trials.
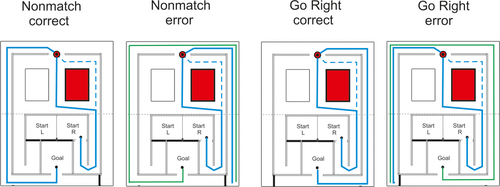
Schematic illustration of the task principles with four examples. All examples apply to a start from the Right Start compartment. In the “Nonmatch correct” case, the rat chooses the opposite lateral alley (left) at the Decision point. In the maze mid-section, theoretically the rat could choose any of the three paths, but in practice none of the rats ever chose the most distant path unless forced by barriers. The alternate path in the mid-section is shown with a dashed line. In the “Nonmatch error” case, the rats chooses the lateral alley on the start side (right) and end up facing a barrier at the Goal corner (blue line). Then it still can correct it choice and take the long route to the Goal (green line). Corresponding paths in case of a left start would be mirror images of the shown ones. The Position task could have either a “Go Right” or “Go Left” rule. Now shown is the “Go Right” rule starting from the right. During the “Go Left” rule the correct choice would be the left lateral alley at the Decision point and the path like the blue one now shown for the “Go Right error” case. [Color figure can be viewed at wileyonlinelibrary.com]
| Start | L | R | L | R | R | L | R | L | L | R | L | L | R | R | R | L | R | L | R | L | L | L | R | L | R | R | L | R | L | R | R | L |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Barr | x | x | x | x | x | x | ||||||||||||||||||||||||||
| Path | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 3 | 2 | 1 | 1 | 1 | 2 | 1 | 2 | 2 | 2 | 3 | 2 | 2 | 2 | 2 | 3 | 2 | 2 | 2 | 2 | 2 | 2 |
| Error | x | x | x | x | x | x | x | x | x | x |
- Barr = barrier.
- Path: 1 = proximal, 2 = middle, 3 = opposite.
| Start | L | R | L | R | L | R | R | L | R | R | R | L | L | R | R | L | L | L | R | L | L | L | R | R | L | L |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Barr | x | x | x | x | x | x | x | x | x | x | x | |||||||||||||||
| Path | 3 | 3 | 2 | 2 | 3 | 1 | 3 | 2 | 3 | 3 | 3 | 3 | 1 | 2 | 2 | 2 | 1 | 1 | 3 | 1 | 2 | 1 | 1 | 2 | 2 | 3 |
| Error | x | x | x | x |
- Barr = barrier.
- Path: 1 = proximal, 2 = middle, 3 = opposite.
Independent of the task rule, the rats showed a strong preference to choose either the leftmost or middle path when starting from the left, and correspondingly, the rightmost of the middle path when staring from the right. Further, this preference could vary between days. However, as expected, the rat never spontaneously chose the longest path through the opposite third middle alley. When using the barriers, we first ran at least three trials without any manipulations to identify the preferred path of a rat on that particular day.
2.3 Electrophysiology
Microdrive arrays carrying 18 independently adjustable gold-plated tetrodes aimed at area CA1 of the right dorsal hippocampus (2.4 mm lateral and 4.0 mm posterior, relative to bregma) were implanted under general anesthesia (induction: ketamine 50 mg/kg i.p. + xylazine 6 mg/kg i.p + isoflurane 3%; maintenance: isoflurane 1–2%). Postoperatively the rat received ketoprofen 5 mg/kg i.p. for pain relief. Tetrodes (Nguyen et al., 2009) and microdrives (Kloosterman et al., 2009) were constructed as described. Each tetrode consisted of a twisted bundle of four polyimide-insulated microwires (13 µm in diameter, RediOhm-800, Kanthal, Palm Coast, FL), fused and cut to create a blunt tip. Electrodes were slowly lowered into the CA1 pyramidal cell layer over the course of 1–2 weeks. Differential recordings of extracellular action potentials (sampled at 31.25 kHz per channel, filtered between 600 Hz and 6 kHz) and continuous LFP (sampled at 2 kHz per channel, filtered between 0.1 and 475 Hz) were made against a local reference electrode in overlying white matter, using patch boxes (Cheetah system) and amplifiers by Neuralynx (Boseman, MT). A screw in the skull overlying cerebellum served as ground. Position was acquired at 30 Hz by an array of diodes located above the electrode drive. Individual units were isolated by manual clustering on peak spike waveform amplitudes and spike widths across all four tetrode channels using custom software (Xclust; M.A.W.). No spike overlap was allowed between selected clusters. Spike stability was verified by plotting the peak amplitude of the tagged cluster in the tetrode with the highest amplitude across the entire 1–2 h recording session. If the amplitude dropped 25% or more during the session, the unit was considered unstable and discarded. Cluster boundaries calculated on session N were applied to session N + 1, and were never found to fully overlap even for a single tetrode, suggesting some movement with regard to the tissue. Therefore, isolated units in each session were considered separate. At the end of the recordings, the tetrode sites were marked by passing direct current through one wire in a tetrode. The rats were deeply anesthetized, perfused transcardially with 4% PFA, and the brains were cut into 50 µm coronal sections. Lesion marks were detected in cresyl violet stained sections. All tetrodes with reported units were confirmed to locate in the CA1 pyramidal cell layer.
2.4 Data analysis
Animal location and head direction were captured at 30 Hz by video tracking of two head-mounted LEDs flickering out of phase, using an overhead camera. The velocity was smoothed with a Gaussian kernel (SD = 0.25 s). Unit data were analyzed only for epochs when the movement velocity was 5 cm/s or higher. To create a firing rate map, the maze was divided into 5 cm x 5 cm bins, and the firing rate per bin was smoothed with a Gaussian filter (2 SD). Well-isolated units with a spike width > 350 ms, maximum firing rate > 1.0 Hz, mean firing rate > 0.05 Hz, and spatial information content (Markus, Barnes, McNaughton, Gladden, & Skaggs, 1994) > 1.0 displaying 1–5 identified place fields were included in the analysis as place cells. Place fields were defined as 5 or more adjacent pixels (shared at least one side with another pixel in the place field) with a firing rate ≥ 3 × unit mean rate. Further, firing rate in the place field should have only one peak. In practice, this meant that long fields in one maze alley or round fields in two adjacent alleys with continuous chain of adjacent pixels above 3 × unit mean firing rate were considered two separate fields if the firing rate distribution demonstrated two peaks. Well-isolated units with a spike width < 350 ms, mean rate ≥ 3.0 Hz displaying theta modulation were included in the analysis as interneurons.
We first calculated the mean number of place fields per pyramidal neurons considering all maze sections. However, neurons were included in this and further analyses only if they had at least one place field outside the Goal and Start compartment where the mice were mainly stationary.
Next, place field responses to barriers were categorically analyzed by subtracting the firing field map during barrier trials from the map during free trials. If the differential map showed no field after applying the “5 or more adjacent pixels with a firing rate ≥ 3 × unit mean rate” rule or showed < 25% per pixel in-field firing rate in the original place, the field was classified as Stable. If ≥ 25% of the original firing rate was present in the differential map, the field response was classified as (firing rate) Decrease. Conversely, if the rate increased by the same amount, the response was classified as (firing rate) Increase. If the in-field firing rate was stable but 20–50% of pixels did not overlap with the original field, the response was classified as field (location) Shift. If the place field in the barrier trials did not meet the “5 or more adjacent pixels with a firing rate ≥ 3 x unit mean rate” criterion any more or showed than 50% with the original field, the response was classified as field Disappearance. In contrast, if the differential map showed a “negative” field according to the “5 or more adjacent pixels with a firing rate ≥ 3 × unit mean rate” in a location with no field during free trials, the response was classified as New field. To avoid the potential confound of differential reward (4 pellets for a correct choice, 1 for incorrect), the Goal and Start chambers were excluded from the field analysis.
To assess responses to barrier manipulation more objectively, we first calculated pixel-by-pixel cross-correlations across free and barrier trial maps using Pearson rho. Then we converted the rho values to z values using Fisher transformation: z = 0.5 × ln((1 + r)/(1 - r)). The z-transformation was also done to the early vs. late trial correlations.
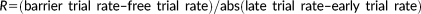
The value of R tells whether there was a net decrease or increase in the firing rate between free and barrier trials.
To compare the effect of barriers in their vicinity vs. more distal section of the Townmaze, we divided all alleys in the maze to two roughly equally large zones: a proximal zone and a distal zone (Figure 1). All barrier manipulations took place in the proximal zone. The Goal and Start chambers were not included in the comparison, since those are wide, open spaces that cannot be directly compared with long alleys. The similarity and rate scores were compared between proximal and a distal zones using paired t-tests.
Finally, to assess whether task performance affects the place field responses to the barriers, we split the sessions of each rat in two categories. Performance was consider impaired in a session if the rat made more errors in the presence of barriers than without, while unimpaired sessions included trials with similar or higher accuracy in the presence of barriers than during free trials. The performance accuracy varied between 33% and 100% correct, and there was a roughly equal number of units with acceptable place fields during both kind of trials. Then we applied ANOVA for repeated measures with maze zone and within-unit and task performance and between-unit factor.
3 RESULTS
3.1 Most place cells have many fields in the Townmaze and code for a position on a route
The place field properties were assessed on 353 well-isolated and stable CA1 pyramidal neurons that met the inclusion criteria for place cells (see Methods). Four rats provided cells for the study, and their individual contribution to the data is summarized in Table 3. On average, the cells displayed 2.44 ± 0.05 (mean ± sem) fields. To further assess the pattern of field distribution, we divided the Townmaze into 11 logical segments separated by choice points, plus the Start and Goal compartments. In addition, the Decision Point (DP) and the DP and Goal corners were considered separate segments, since many fields extended on both sides of the corner (Figure 1b). The fields were unevenly distributed, so that the left and right initial segments (1L, 1R), the left and right middle segments (3L, 3R) and the left lateral segment (5L) were overrepresented, while the corners were underrepresented (Tables 1-3). The fields were almost exclusively confined to a single alley (path) and had a mean length of 34.3 ± 0.7 cm, except on the lateral segments that were about twice as long as the remaining ones. There the mean field length was 64.0 ± 0.7 cm, suggesting scaling to the alley length (Table 4).
| Rat | Nonmatch sessions | Position task sessions | Units per session |
|---|---|---|---|
| Bibi | 7 with 27–33 trials | no | 56 – 126 |
| Gill | 2 with 32 trials | no | 18 – 21 |
| Henry | 1 with 28 trials | 3 with 30 – 42 trials | 32 – 46 |
| Ian | 4 with 19 – 46 trials | 8 with 25 – 41 trials | 33 – 60 |
| Rat | Nonmatch sessions | Position task sessions | ||
|---|---|---|---|---|
| Units included in the analysis | Pyramidal | Interneuron | Pyramidal | Interneuron |
| Bibi | 169 | 36 | 0 | 0 |
| Gill | 11 | 2 | 0 | 0 |
| Henry | 10 | 4 | 27 | 1 |
| Ian | 35 | 6 | 101 | 7 |
| Segment | Fields (exp = 42) | Mean field length (cm) | Range (cm) |
|---|---|---|---|
| Goal + Start Cs | 107 | ||
| Initial L (1L) | 84 | 37.0 | 15 – 80 |
| Initial R (1R) | 61 | 38.8 | 15 – 100 |
| Transverse L (2L) | 42 | 31.0 | 15 – 50 |
| Transverse R (2R) | 36 | 36.1 | 20 – 60 |
| Mid L (3L) | 61 | 36.1 | 15 – 60 |
| Mid M (3M) | 37 | 34.9 | 15 – 60 |
| Mid R (3R) | 61 | 35.7 | 15 – 80 |
| Decision Point | 31 | 27.9 | 15 – 50 |
| DP end L (4L) | 38 | 31.7 | 15 – 60 |
| DP end R (4R) | 30 | 32.1 | 15 – 60 |
| DP cor L | 20 | 36.5 | 20 – 70 |
| DP cor R | 4 | 33.8 | 20 – 60 |
| Lat L (5L) | 37 | 66.8 | 15 – 160 |
| Lat R (5R) | 70 | 61.3 | 20 – 150 |
| Goal cor L | 22 | 34.3 | 15 – 75 |
| Goal cor R | 21 | 35.5 | 20 – 90 |
| Goal end L (6L) | 39 | 32.7 | 15 – 60 |
| Goal end R (6R) | 28 | 35.5 | 20 – 50 |
Thus, in a large and complex environment, such as the Townmaze, most place cells display more than one well-defined field. In this set, 149 pyramidal neurons had 3–5 fields, which allowed us to investigate larger field constellations than in conventional smaller arenas. The most striking feature of these multiple fields was that they seemed to be located along the most typical paths that the rats used to traverse through the maze. The fields were dispersed along the path like scent marks that a rat would leave to mark its trail in the wild. Figure 3 illustrates some examples or these “path segment” cells. Usually these included one element in the Start compartment or initial alley (1L, 1R), one element in the mid-section (3L, 3M, 3R) and one after the Decision Point (Figure 1b). Although it appears logical to have such a representation of the path, it is essential to rule out the possibility that this can happen only by chance. To evaluate this possibility, we can consider the most typical cases (n = 22 out of 94) of fields representing a single path that is a correct choice in the Nonmatch task during free trials. A correct path from the left Start compartment until the Decision Point would include the following elements: Start compartment, 1L, left Choice Point (CPL), 2L–CPM–3M, if the rat follows the middle-mid path, or 3L directly after the CPL if the rat chooses the lateral path. (The rat never took the longest path if not forced to do so by barriers.) In both cases, the path would continue as DP, 4R, DP corner R, 5R, Goal corner R, 6R, and the Goal. This means either 13 or 11 elements in total (Figure 1b). For simplicity, we can take the average, 12 elements. Correspondingly, a correct path from the right Start would comprise the elements: Start, 1R, CPR, 2R–CPM–3M, or 3R directly from CPR, and further DP, 4L, DP corner L, 5L, Goal corner L, 6L, and the Goal (Figure 1b), again on average 12 elements. The nature of the task (advancement only in one direction, balanced number of left and right starts) ensures practically even occupancy time per segment (except for massive overrepresentation of Start and Goal compartment and 3 middle vs. 2 lateral paths, which bias is balanced by higher running speed in lateral alleys). This is further confirmed by the occupancy maps in Figure 3. Therefore, one can assume an even occupancy for all maze segments for simplicity. Since the total number of path elements in the maze is 24, the likelihood for three fields to be situated in the correct path from the left Start is thus 12/24 for the first field, 11/24 for the second field and 10/24 for the third field, because we consider only one field per element. The likelihood that all three match with the path is their product (p = 0.095). Similarly, the likelihood of having four fields in the correct path starting from left is p = 0.036 and for five fields p = 0.012. The same probabilities apply for trials starting from the right. The combined probability would then be the sum of left and right trials. Thus, the combined probability of three fields to be located on the correct path that begins either from left or right will be 2 × 0.095 = 0.191, for four fields 2 × 0.036 = 0.072, and for five fields 2 × 0.012 = 0.024. As summarized in Table 5, it appears that the observed number of 3 to 5 fields falling on a correct path was above the expected value by chance (X2(2) = 9.3, × < 0.01).
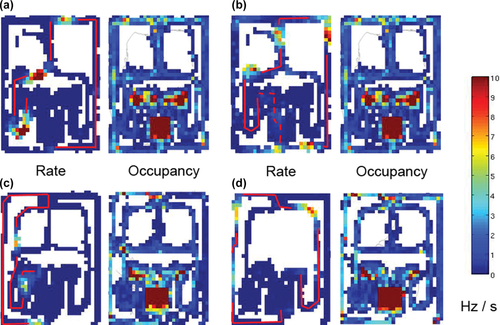
Examples of “path segment” fields. A pair of maps is shown in each case, a firing rate map on the left and an occupancy map on the right. The same scale applies to both maps, but the unit is spikes/s (Hz) for the rate and seconds (s) for the occupancy. (a) A neuron with three fields along a typical trajectory (red solid line) of one correct Nonmatch task trial starting from left. (b) A neuron with four separate fields along a similar trajectory of one correct Nonmatch task trial. The fifth field would not match with this trial, but is compatible with the end of a preceding trial starting from right (red dashed line). (c) A neuron with three fields along a typical trajectory of one correct Go Left task trial starting from left. (d) A neuron with three fields corresponding to a correct Go Left task trial starting from right. [Color figure can be viewed at wileyonlinelibrary.com]
| Fields | Bibi | Gill | Henry | Ian |
|---|---|---|---|---|
| 3 | 10 | 1 | 1 | 4 |
| 4 | 4 | 0 | 0 | 1 |
| 5 | 1 | 0 | 0 | 0 |
| Fields | Observed | Cells w N fields | P for one cell | Expected |
|---|---|---|---|---|
| 3 | 16 | 51 | 0.191 | 9.7 |
| 4 | 5 | 33 | 0.072 | 2.4 |
| 5 | 1 | 10 | 0.024 | 0.2 |
- X2(2) = 9.3, p < 0.01.
In turn, the theoretical probability of 3–5 fields to fall on the path of an erroneous choice can be calculated as follows. For instance, a path starting from left and ending with an erroneous choice would follow the correct path until the DP. Then it will contain only 3 elements (4L, DPcorL, 5L), since segments 6L and Goal are not included in the erroneous path (Figure 1b). This will leave 10 maze elements on average for trials starting from left and the same number for trials starting from right. The likelihood for three fields to be situated in the erroneous path from the left Start is thus 10/24 for the 1st field and 6/24 for the 5th field. The combined probability for three fields to be located on the erroneous path that begins either from left or right will be 2 × 0.052 = 0.104. The corresponding probabilities for four fields will be 2 × 0.015 = 0.030 and for five fields 2 × 0.004 = 0.008. In contrast to correct paths, the observed number of multiple fields that matched with the erroneous choice (n = 3 out of 94) was not different from the chance level (X2(2) = 2.1, p > 0.10; Table 6). In addition to fields that were compatible with either a correct or erroneous choice, 8 cells had a field constellation that matched with a single path up to the Decision Point, but could not be classified as either correct or erroneous paths with not fields representing the choice of the rat. The remaining 75 neurons with multiple fields had a field constellation that would only match with representation of two paths at the same time, either trials starting from both left and right or trials starting from one position but with both correct and erroneous choices.
| Fields | Bibi | Gill | Henry | Ian |
|---|---|---|---|---|
| 3 | 2 | 0 | 0 | 0 |
| 4 | 1 | 0 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0 |
| Fields | Observed | Cells w N fields | P for one cell | Expected |
|---|---|---|---|---|
| 3 | 2 | 51 | 0.104 | 5.3 |
| 4 | 1 | 33 | 0.030 | 1.0 |
| 5 | 0 | 10 | 0.008 | 0.1 |
- X2(2) = 2.1, p > 0.10.
A plausible hypothesis for the development of path-segment fields is that through hundreds of repeating passages of the rat through the maze following the same path, the route becomes represented even at the level of a single CA1 pyramidal neuron through associative learning. One way to test this hypothesis is to compare the frequency of path-segment cells during the overlearned Nonmatch task to the Position task while the rat was still learning the new rule. In total, we found 55 neurons with 3 to 5 fields during the Position task. The theoretical probability of 3 to 5 fields to fall on the path of a correct choice in this task is the same as in the Nonmatch task, since the path lengths remain the same. As summarized in Table 7, it appears that 10 neurons had 3 to 4 fields falling on a correct path (none had 5 fields), which is not different from chance distribution (X2(2) = 1.1, p > 0.10). Notably, 5 of these neurons represent the same route as in the Nonmatch task (e.g., left Start–right choice in the Go Right task) and only 5 the newly learned route. In addition, 7 cells had a field constellation that matched with a single path up to the Decision Point (again common between the two tasks). Only three neurons had three fields that would correspond specifically to an erroneous choice. These data lend tentative support to the contention that the path-segment feature of single place cells is a result of sequence learning.
| Fields | Bibi | Gill | Henry | Ian |
|---|---|---|---|---|
| 3 | N/A | N/A | 1 | 7 |
| 4 | N/A | N/A | 1 | 1 |
| 5 | N/A | N/A | 0 | 0 |
| Fields | Observed | Cells w N fields | P for one cell | Expected |
|---|---|---|---|---|
| 3 | 8 | 36 | 0.191 | 6.9 |
| 4 | 2 | 15 | 0.072 | 1.1 |
| 5 | 0 | 4 | 0.024 | 0.1 |
- X2(2) = 1.1, p > 0.10.
3.2 Some place cells with multiple fields code for general geometric features
A second conspicuous constellation of multiple place fields were “axis-aligned” fields. These were all located either on the longitudinal or transverse alleys of the Townmaze. Unfortunately, the nature of the memory task made the rats to run through most of the maze segments in only one direction. Therefore, we could not systematically test the direction specificity of these fields. Nevertheless, in several cases the aligned fields of a single cell fell on segments where the movement direction was the opposite, speaking against head-direction like coding. Figure 4 illustrates some clear examples among 32 cells of this type. If we assume that a field ∼30 cm in length can locate in three different ways—straight longitudinally, straight transversally or in an angle - there are 11 possible longitudinal segments (two counted in the long lateral alleys and two parallel in the initial segment = 1La, 1Lc, 1Ra, 1Rc, 3L, 3M, 3R, 5La, 5Lb, 5Ra, 5Rb), 10 possible transverse segments (1Lb, 1Rb, 2L, 2R, 3Lb, 3Rb, 4L, 4R, 6L, 6R) and 10 corners (1Lab, 1Lbc, 1Rab, 1Rbc, 3Lab, 3Rab, DPcorL, DPcorR, GcorL, GcorR) in the maze (Figure 1b). The likelihood of having three fields all in a longitudinal segment is thus (11/31) × (10/31) × (9/31) = 0.033 and for having them in a transverse segment correspondingly (10/31) × (9/31) × (8/31) = 0.024. As summarized in Tables 8 and 9 the observed number of either longitudinally (X2(2) = 262.0, p < 0.001) or transversally (X2(2) = 356.1, p < 0.001) aligned fields was way above the chance level.
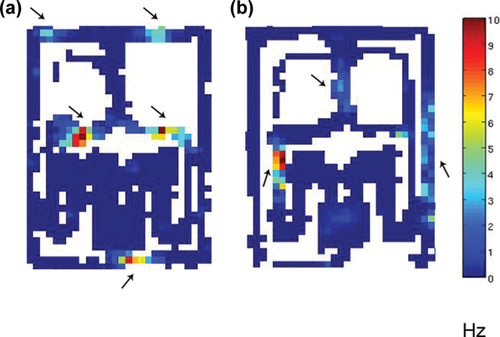
Two examples of “axis-aligned” fields. (a) A neuron with five fields, all located in transverse segments of the maze. Two almost symmetric pairs of fields on both sides of the Decision Point correspond to trajectories in the Nonmatch trials that have begun from the left and right Start compartments. The fifth field in the Goal end is compatible with correct rightward choice in trials that started from the left. (b) Three fields of one neuron on the longitudinal segments of the Townmaze. These would correspond to a single trajectory in the Go Left task with an erroneous choice to the right. The arrows point to the fields. [Color figure can be viewed at wileyonlinelibrary.com]
| Fields | Bibi | Gill | Henry | Ian |
|---|---|---|---|---|
| 3 | 3 | 1 | 0 | 6 |
| 4 | 2 | 0 | 3 | 2 |
| 5 | 1 | 0 | 0 | 1 |
| Fields | Observed | Cells w N fields | P for one cell | Expected |
|---|---|---|---|---|
| 3 | 10 | 70 | 0.033 | 2.31 |
| 4 | 7 | 49 | 0.009 | 0.44 |
| 5 | 2 | 14 | 0.002 | 0.03 |
- X2(2) = 262.0, p < 0.001.
| Fields | Bibi | Gill | Henry | Ian |
|---|---|---|---|---|
| 3 | 3 | 0 | 0 | 4 |
| 4 | 3 | 1 | 0 | 0 |
| 5 | 1 | 0 | 0 | 1 |
| Fields | Observed | Cells w N fields | P for one cell | Expected |
|---|---|---|---|---|
| 3 | 7 | 70 | 0.024 | 1.68 |
| 4 | 4 | 49 | 0.005 | 0.25 |
| 5 | 2 | 14 | 0.001 | 0.01 |
- X2(2) = 356.1, p < 0.001.
A third notable pattern of place field arrangement were “symmetric fields” that were located symmetrically on both left and right halves of the maze. Considering the left vs. right emphasis of the applied tasks, one would expect a substantial portion of cells to express such symmetry. In total, 26 pyramidal neurons out of 353 displayed at least two symmetric fields, while only two neurons had two pairs of symmetric fields. Assuming that we have the above mentioned 11 longitudinal, 10 transverse, and 10 corner segments (31 in total) in the maze, the likelihood of having two fields in symmetric segments is (31/31) × (1/31) = 0.032, and the likelihood of having two pairs of symmetric field correspondingly (31/31) × (1/31) × (29/31) × (1/31) = 0.001. Considering that 276 out of 353 analyzed pyramidal cells had two or more fields, the observed 26 cells with symmetric pairs is twice the number expected by chance (0.032 × 276 = 8.8) and the observed two cells with two symmetric field pairs 6-fold higher than by chance (0.001 × 276 = 0.3). This distribution is also significantly above chance (X2(1) = 44.1, p < 0.001).
The presence of the aforementioned three types of field constellations suggests that the CA1 place cells encode both task-relevant features and geometric aspects of the environment.
3.3 Place field responses to barriers
To assess changes in the place fields upon introduction of the barriers, we compared the place field map of all free trials to that of all barrier trials for each cell. First, to get a qualitative estimate of these changes, we divided the responses (i.e., comparison free map—barrier map) in the following categories (see Methods for definitions). A field could remain stable both in terms of firing rate and location (Stable), show a pure firing rate change (Decrease, Increase) without a change in location, or display a shift of the peak firing or field expansion with no overall change in rate (Shift). In addition, a field present during free trials could disappear (Dis) during barrier trials, or conversely, a field appears only during barrier trials (New). Figure 5 illustrates typical examples of these place field changes. One neuron with two fields shows Decrease in both fields (Figure 5a), one neuron with a single field shows Disappearance of the field together with a New field (Figure 5b), while one neurons with two fields shows Decrease of one field, Increase of a second field, and in addition, a New field (Figure 5c). As illustrated in Figures 5a and 6c, neurons with multiple fields could show discordant responses to the barriers, i.e. individual fields respond in a different way. However, this was not common, since among 211 neurons with two or more place fields, 70.9 ± 1.7% (mean ± sem) of the fields responded the same way as the majority of fields.
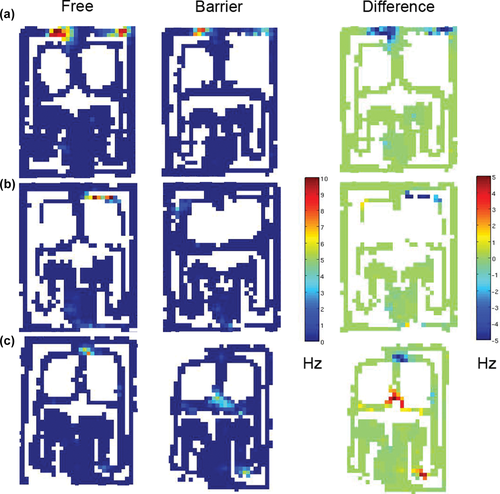
Examples of typical place cell responses to the barriers. The leftmost column shows firing rates during free trials, the middle one during barrier trials, and the rightmost column depicts the outcome of the subtraction free trials - barrier trials. The first scale bar shows the absolute mean firing rates in Hz for free and barrier trials and the second the difference in mean firing rates. (a) A neuron with two fields in the Proximal zone that decrease their firing rates coherently during the barrier trials. (b) A neuron with two fields again in the Proximal zone. During free trials, there is a field in the Middle Right segment. However, this field completely disappears during barrier trials while another smaller field appears in the Middle Left segment. (c) A neuron with one field in the Decision Point and some trace firing along the trajectory from the Right Initial segment to the DP. During barrier trials, the trace firing in the right Initial segment intensifies, while the field in the DP almost completely disappears. In addition, a new large field appears in the middle choice point. This new field would correspond to the most common detour starting from the right: while the Middle Right segment is blocked, the rat chooses the Middle Mid segment. [Color figure can be viewed at wileyonlinelibrary.com]
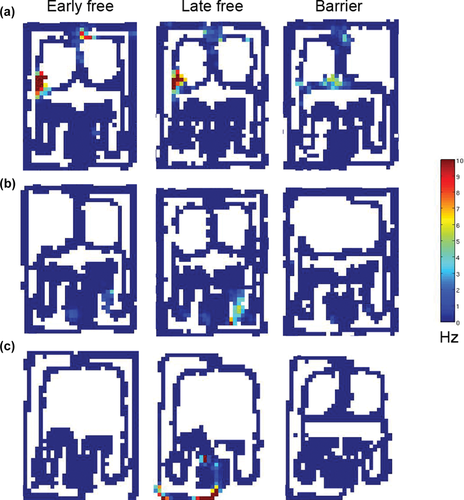
Impact of barriers on place fields during free trials. (a) A most typical example of case where no significant changes take place between early and late free trials. However, during barrier trials, firing around the leftmost choice point (CPL) substantially decreases while a new field appears on the transverse segment (2L) around the middle choice point. (b) An example of firing rate changes in free trials after barrier trials have been introduced. The field in the right Initial segment (1R) intensifies during the late free trials, although there is no firing in the corresponding location during the barrier trials. (c) Example of a new field that appears in the left Goal corner (G cor L) and end (6L) only during late free trials. Note that there is no firing in the corresponding location during any of the barrier trials. [Color figure can be viewed at wileyonlinelibrary.com]
Notably, the barrier trials were intermingled between the free trials (Table 1), so that a simple drift in firing properties of the recorded cell across time should not lead to major differences between the two maps. On the other hand, it is possible that the introduction of barriers may alter the maze representation during subsequent trials without barriers. To compare the magnitude of barrier-induced alterations in the field properties vs. changes in the firing rate during the long recording session, we divided the free trials between early and late ones, and compared the changes between free and barrier trials to those between early and late trials without barriers. Notably, this analysis could not be done on sessions where two rules were applied, like Go Left in early trials vs. Go Right in late trials. Typically, the fields remained stable across all free trials and changes were only observed during the barrier trials, as illustrated in Figure 6a. Here the neuron has two place fields, which remain stable across all free trials. However, during the barrier trial, one field remains in its original location, one field disappears while a new field appears. In addition, we sometimes also found a response type that has not been described in barrier manipulations before: a field present only during free trials substantially intensified after the barrier manipulation was introduced (Figure 6b), or in the extreme case, the field was present only during the latter half of the free trials (Figure 6c). Notably, in both cases, the response was specific to the free trials, since the corresponding field location did not show any firing during the barrier trials. Of a total of 368 place fields included in this analysis, 8 (2%) fields showed specific firing during late free trials. In the analysis of field responses to barriers, these kind of fields were categorized as Decrease or Disappear type, using the late free trials as a comparison. Table 10 summarizes the extent of field changes between free vs. barrier trials and those between early free and late free trials. Most notably, the percentage of stable fields was significantly higher between the early and late free trials than between free and barrier trials, whereas firing rate decrease was significantly more often associated with the presence of barriers.
| Stable % | Shift % | Down % | Up % | Dis % | New % | N | |
|---|---|---|---|---|---|---|---|
| Free-Barr PZ | 18.0 | 5.4 | 41.5 | 15.7 | 7.9 | 11.9 | 140 |
| Free-Barr DZ | 31.9 | 3.3 | 47.0 | 9.8 | 2.8 | 5.2 | 160 |
| FEarly-FLate PZ | 52.8 | 2.8 | 25.8 | 14.0 | 1.6 | 3.0 | 127 |
| FEarly-FLate DZ | 64.7 | 1.1 | 21.3 | 11.8 | 0.0 | 1.3 | 158 |
| ANOVA-RM, zone | NS | NS | NS | NS | NS | p < 0.01 | |
| ANOVA-RM, barrier | p < 0.001 | p = 0.02 | p < 0.001 | NS | p = 0.03 | NS |
- The stability is presented separately for the proximal (PZ) and distal zones (DZ). Statistical comparison is done for the effect of the zone and the presence of barriers
Recorded interneurons also showed firing rate changes in response to barrier manipulations. The response could be a chance in the firing rate all over the maze (Figure 7a) or a more local change in one or several maze sections (Figure 7b).
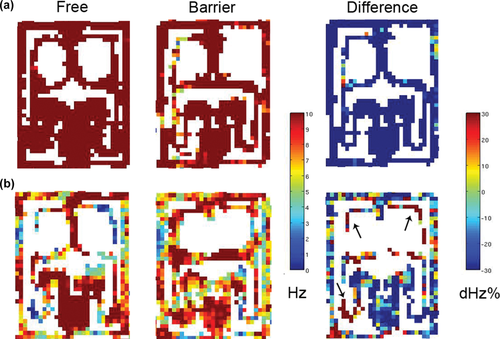
Examples of interneuron responses to barriers. The arrangement is as in Figure 5, except that the differential maps show change in firing rate in %. (a) An interneuron with general decrease in firing rate during barrier trials. (b) An interneuron with location specific firing. During free trials, there is lower than average firing in the left initial (1L), middle right (3R) and left lateral (5L) segments. During barrier trials, there is a general decrease in firing, but at the same time increase in 1L and 3L and 3R segments (arrows). [Color figure can be viewed at wileyonlinelibrary.com]
3.4 Barrier-induced new fields are largely limited to the proximal zone while firing rate changes are zone independent
To assess whether the introduction of barriers induces a global remapping of the Townmaze or more local changes near the barriers, we divided the maze into a proximal and a distal zone of approximately equal size (Figure 1a). These sections contain all the maze alleys, while the open spaces (Goal and Start compartments) were not included. Figure 8a summarizes the field changes in both zones. Overall, only 1/3 of the fields remained stable during the barrier trials. Moreover, even in the distal zone, more than half showed changes. The percentage of fields with rate changes did not differ between the distal and proximal zones, but the proportion of new fields was significantly higher in the proximal zone, while correspondingly, the proportion of stable fields was higher in the distal zone (Figure 8a). Further, in the comparison between free vs. barrier trials and early free vs. late free trials limited to the Nonmatch task, the proportion of new fields was significantly dependent on the zone while other field changes were not (Table 10).
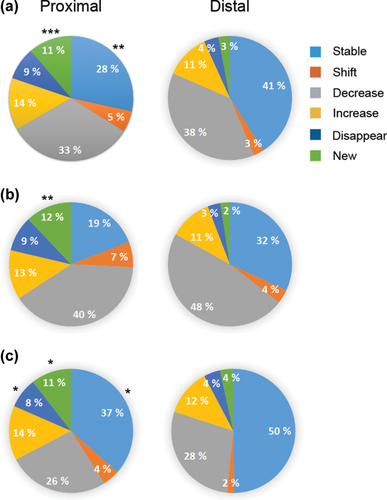
The pie diagrams illustrate categories of place field changes upon introduction of the barriers. The categories are presented in the order of increased degree of change from Stable fields to New fields. Field changes in the Proximal and Distal zone are shown in different columns. (a) Summary of all trials. (b) Trials with impaired choice accuracy due to barriers. (c) Trials with preserved choice accuracy during barrier trials. The asterisks indicate differences between Proximal and Distal zone (a significant main effect of the zone in the ANOVA, * p < 0.05, ** p < 0.01, *** p < 0.001). [Color figure can be viewed at wileyonlinelibrary.com]
Of the total 56 interneurons, 29 decreased and 8 increased their firing rate by more than 25% in the proximal zone during the barrier trials compared to free trials. The corresponding numbers in the distal zone were 34 and 8, respectively. In contrast to the pyramidal neurons, the responses of interneurons were largely zone independent, since the correlation between firing rate changes between these two zones was 0.96 (Spearman's rho).
3.5 Fields with decreased firing rate are more common during trials with impaired performance
Next, we wanted to determine how place field responses to barriers correlated with the overall task performance of the rats. The choice accuracy varied greatly (33%–100%) between sessions due to task modifications and daily fluctuation in performance. Further, in about half of the sessions, the choice accuracy dropped due to the barrier manipulation, but during some days, the rats performed even better during the barrier trials than free trials. Thus, we divided the sessions roughly into those with impaired performance due to barriers and those without such impairment. We composed an ANOVA model with impairment (present vs. absent) as between-session factor and the maze zone (proximal vs. distal) as a within-session factor, and compared the proportion of each place field response types to the barriers. Independent of the choice accuracy, New field responses were far more common in the proximal zone than in the distal zone (F1,120 = 18.4, p < 0.001; Figure 8), while Stable responses were less common in the proximal zone (F1,123 = 6.9, p = 0.010; Figure 8). In contrast, the choice accuracy significantly affected the relative proportion of Stable vs. Decrease responses. Independent of the maze zone, Stable responses were far more common during maintained choice accuracy (F1,123 = 9.1, p = 0.003; Figure 8b and c), whereas Decreased field rates were more common during impaired task performance (F1,120 = 6.5, p = 0.012; Figure 8b and c). It is not that surprising that stable fields, both in terms of location and firing rate, are associated with good task performance. However, a new finding is that appearance of new place fields (global remapping) is independent of task performance, while decrease in firing rate (rate remapping) associated with the task performance. We also assessed if concordant field responses would associate with better task performance and discordant field responses. However, the concordance was not influenced by the choice accuracy (t209 = 0.71, p = 0.48).
3.6 Global measures of field location stability are influenced by the proximity of barriers while overall firing rate reflects performance accuracy
To compare the field responses to barriers between the proximal and distal zones and their correlation with task performance in a more objective way, we calculated z-transformed Pearson correlation coefficients between free and barrier trials separately for proximal and distal maze zones. Further, to assess barrier-induced changes across time (Figure 6) we similarly calculated z-transformed Pearson rhos between early and late free trials. Finally, we composed the ANOVA model described above with impairment as the between-session and maze zone as the within-session factor.
The maze zone proved a highly significant factor for the similarity between free and barrier trials: in both pyramidal neurons (F1,321 = 52.3, p < 0.001) and interneurons (F1,54 = 36.3, p < 0.001), the z-score was highly significantly lower in the proximal than distal zone (Figure 9a). In contrast, the choice accuracy did not influence the similarity score in either pyramidal neurons (p = 0.59) or interneurons (p = 0.75). The same pattern was observed when we compared early and late free trials but only with a marginal significance: the z-score was lower in the proximal than distal zone in both pyramidal neurons (F1,298 = 5.5, p = 0.020) and interneurons (F1,54 = 4.1, p = 0.047; Figure 9b).
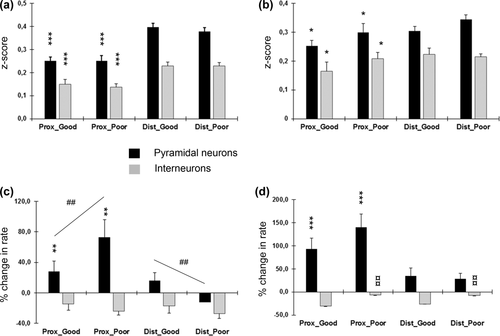
(a) Similarity scores between firing rate maps during free and barrier trials plotted separately for the two zones and two categories of impairment, and further for pyramidal neurons and interneurons. The y-axis depicts similarity in z-scores. *** Significant effect of the zone in ANOVA, p < 0.001. (b) Similarity scores between firing rate maps during early and later free trials, presented as in (A). * Significant effect of the zone in ANOVA, p < 0.001. (c) Firing rate changes between firing rate maps during free and barrier trials. The y-axis depicts change in the firing rate in %. ** Significant effect of the zone, p < 0.01; ## Significant zone × impairment interaction, p < 0.01. (d) Firing rate changes between firing rate maps during early and later free trials, presented as in (C). *** Significant effect of the zone for pyramidal neurons, p < 0.001; ¤¤ Significant effect of the impairment for interneurons, p < 0.01.
In line with the field analysis, there was an impairment × zone interaction in the firing rate of pyramidal neurons (F1,338 = 7.0, p = 0.008), such that during poor task performance the firing rate in the proximal zone tended to increase but decrease in the distal zone. In addition, firing rate increase was more robust in the proximal zone (F1,338 = 12.3, p = 0.001). No such effects were observed in the interneurons (Figure 9c). Also in the comparison between early and late free trials, the zone proved to a significant factor of pyramidal neuron firing: firing rate increase was more robust in the proximal zone (F1,326 = 17.1, p < 0.001) than in the distal zone, while the impairment factor and impairment x zone interaction were nonsignificant (p = 0.35 vs. p = 0.19). In contrast, the changes in interneuron firing rate between early and late trials were highly dependent on the task performance: the firing rate decrease was significantly smaller during poor task performance (F1,338 = 7.2, p = 0.009; Figure 9d). Overall, there were no differences in the interneuron firing between the zones.
Taken together, both the field and global analyses revealed a common pattern that robust field changes (appearance of new field and disappearance of old ones) during barrier manipulations occur mostly in the zone proximal to the barriers. However, these changes do not correlate with task performance, whereas changes in overall firing rate or both pyramidal neurons and interneurons do correlate.
4 DISCUSSION
The “Townmaze” employed in this study, with the total linear length of 13 m of its alleys, is perhaps the largest environment ever used for recording hippocampal place cells in rats. It also differs from large arenas with repeating U- or T-shaped units used in some previous studies by its varying geometry and multiple choice points. It is not a new finding that a single well-isolated CA1 place cells can have many fields in a large environment but only one in a small one (Fenton et al., 2008). However, the large number of cells with many fields and the complex structure of the maze made it possible to see some patterns of field constellations that may have gone unnoticed in simpler and smaller test environments.
To our knowledge, this is the first evidence that multiple fields of a single hippocampal place cell can code for a specific trajectory through a maze. Superficially, these “path-segment” neurons resemble path-equivalent activity as reported for CA3 place cells in closed environments with repeating U-shape elements (Singer, Karlsson, Nathe, Carr, & Frank, 2010). However, fundamentally they are different. Whereas path-equivalent neurons fire at repeating elements that are similar in shape, most of our “path-segment” neurons had fields in location with little common geometry; for instance, the open Start compartment, one straight maze segment in the middle and one corner at the Goal end. A more appropriate description would be that these “path-segment” neurons code for important elements of a route independent of their geometric similarity. However, a common feature to both types of neurons is that the representation by multiple fields probably arises through repetition and learning as discussed by Singer et al, (2010). For “path-segment” neurons this manifests as higher than chance occurrence of neurons whose multiple fields represent a single correct path to the goal, whereas the number of neurons representing the erroneous choice were close to chance level. Moreover, the occurrence of “path-segment” neurons representing the correct path dropped close to chance level when the new Position task was introduced. Notably, even during this new rule, 50% of the routes overlapped with the Nonmatch task (Go-Left from the right start and Go-Right from the left start), and correspondingly, only 5 out of 10 “path-segment” neurons in this task represented truly novel routes. The “path-segment” neurons can be one manifestation of topological rather than topographic representation of the environment (Dabaghian Brandt, & Frank, 2014). For the memory of a route in a complex maze, inclusion or exclusion of a certain segment is more important than the exact location of the field in that segment.
It is well established that hippocampal place cells can code for sequence-specific information. A good example is differential firing in the common segment of a Phi-maze on leftbound vs. rigthbound trials (Wood, Dudchenko, Robitsek, & Eichenbaum, 2000). It is possible that such trajectory-specific coding would actually involve multiple fields, one in the return segment, one in the common mid-segment and one on the choice arm, and that it has gone unnoticed due to all attention on differential coding of the mid-segment. However, there are important differences between the alternation tasks in the Townmaze and Phi-maze. First, there are two reward locations in the Phi-maze just after the Decision Point, breaking the movement pattern and adding the confounding effect of reward in the middle of the sequence. Second, whereas the Phi-maze has a single initial segment for leftbound and rightbound trials, in the Townmaze the rat could take separate routes all the way to the Decision Point. Further, the three parallel paths in the mid-section with occasional barriers made this section also relevant to be encoded into memory. Finally, the multiple U-maze and Townmaze have dividing walls blocking the rats view to distant maze segment whereas the Phi-maze is open to the room. It is not far-fetched that the rat navigates in the Townmaze similarly to humans in an urban environment. We do not pay attention to all buildings and stores on the way, only to certain conspicuous landmarks and street corners where we need to turn to reach our goal. It is possible that over dozens of repeated passages through the same route, individual CA1 pyramidal cells start to fire at those route segments that catch the rat's attention. Notably, the overrepresented Townmaze segments included the initial segments, right and left middle segments and the long lateral segment. These can summarize the essential information needed for the correct task performance: the start determines whether to turn left or right at the Decision Point, the middle segment determines which route of the three alternatives was free, and the lateral segment confirms the turning decision.
The “axis-aligned” multiple fields have not been described in the hippocampus before to our knowledge, although directional firing is a common finding in hippocampal place cells on linear tracks (Jackson & Redish 2007). However, the common element among the “axis-aligned” fields cannot be the direction, since in several cases a single neuron had fields in Townmaze segments with opposite movement directions. Rather the “axis-aligned” fields may correspond to path-equivalent fields (Singer et al., 2010) by representing a common element (alignment) among repeating segment of one route through the maze. Interestingly, a fresh article reported the presence of axis-aligned fields in subicular neurons recorded while a rat traversed through a complex elevated track made of three nesting T-mazes and lateral return pathways (Olson, Tongprasearth, & Nitz, 2017). These subicular “axis-aligned” neurons fire on most, but not all, maze segments with the same alignment independent of movement direction, while our CA1“axis-aligned” fields covered a substantially smaller proportion of the similarly aligned maze segments. One intriguing possibility is that subiculum, which is just one synapse downstream from CA1, integrates the signal of many similarly aligned CA1 neurons, and represents their common features.
The complex Townmaze also allowed us to address the old puzzle of simultaneous stability and flexibility of hippocampal spatial maps. By having three parallel alternate paths in the maze mid-section and by blocking 1–2 of them occasionally, we could bias the route selection of the rat from a preferred route to alternate nonpreferred, yet familial one. These manipulations challenged the animals' memory of its starting location that was the basis of the impending choice of turn direction, but did not provide additional relevant information for the decision. The most common response of hippocampal neurons to the introduction of barriers was a change in firing rate without a significant change in the firing location (rate remapping). This response could be seen in both place cells and interneurons, and both in the proximal zone around the barriers and the more distal zone. A less frequent response of CA1 place cells was appearance of new fields, sometime coupled with disappearance of existing fields, which was largely limited to the proximal zone. The finding that the more dramatic field changes (global remapping) takes place mainly in the vicinity of the barriers is consistent with an earlier study with the Tolman detour task (Alvernhe, Save, & Poucet, 2011). Also at the level of multiple fields of a single neuron, the fields representing the beginning and end of the route usually remained, while field changes occurred in the proximal zone (Figure 8). Collectively, these findings suggest that in a large environment, the hippocampal map can undergo location remapping only in a part of the environment. In terms of route representation, this kind of remapping implies only updating of a node in the sequence. This local remapping also explains why formation of new fields near the barriers did not correlate with the task performance.
The firing rate changes in response to the barriers were more complex and probably a result of several factors. Further, the field analysis and the global firing rate analysis applicable to both place cells and interneurons appear to give a different picture. Interestingly, both measures did correlate with the task performance. First, the net increase in pyramidal cell firing in the proximal zone, higher overall number of fields with decreased firing rate, and a lower number of stable fields during barrier trials all correlated with poor task performance. Together, this pattern is compatible with decreased signal-to-noise ratio of place cells, which typically correlates with impaired performance in memory tasks. Second, there was a significant firing rate increase in pyramidal neurons in the proximal zone from early free trials to late free trials. One possible explanation to this finding is task condition dependent rate remapping. Earlier studies employing the two-choice task in the Phi-maze have reported that behavioral context specific features, such as the type of reward (Allen, Rawlins, Bannerman, & Csicsvari 2012) or sample vs. choice phase of the task (Griffin, Eichenbaum, & Hasselmo, 2007), may be coded through rate remapping without affecting field location. It is possible that the CA1 place cells in the present task started to differentiate free vs. barrier trials through rate remapping. Another possibility is that the strategy that the rats used varied between days of good and bad performance, for instance, so that a taxon strategy (following the order and number of turns) would lead to impaired performance during barrier trials whereas a spatial strategy would be immune to these manipulations. In this case, the changes in firing rate may reflect the animal's strategy of solving the task. Of note, the rat did not know whether the trial is a barrier trial before it was advanced to the maze mid-section. Therefore, the rate remapping may happen with a delay extending over to the next trial that always was a free one. In addition, a few neurons displayed new fields toward the latter half of the session only during free trials, as if they formed a separate new representation of the free passages. Notably, these changes in firing rate did not correlate with task performance. Finally, the strongest correlation with the task performance was, a bit surprisingly, a firing rate change in interneurons. The interneurons tended to decrease firing during the barrier trials and toward the latter half of the free trials. However, during poor performance this latter change did not happen. It is tempting to speculate that the decrease in interneuron firing opens a plasticity window in the hippocampus that is beneficial for learning. This finding will be worth addressing in future studies.
The finding of neurons with multiple field representing key segments of a route is compatible with the idea that the hippocampus initially codes for episodic type of sequence information, and later associates common elements across these sequences (Eichenbaum, Dudchenko, Wood, Shapiro, & Tanila, 1999). The neurons with axis-aligned fields or symmetric fields across the longitudinal axis are just one new piece of evidence that such kind of coding for the common elements happens among CA1 place cells. Taken together, the present findings suggest that large complex environments are needed to disclose some of the multifaceted manifestations of the hippocampal neural code.
ACKNOWLEDGMENTS
The study was supported by Sigrid Juselius Foundation, Finland and Office of Naval Research MURI award N00014-10-1–0936. The authors declare no competing financial interests.




