Minimal driving of hippocampal theta by the supramammillary nucleus during water maze learning
Abstract
Previous studies have shown only modest effects of supramammillary nucleus (SuM) dysfunction on theta frequency and learning in the water maze (WM), with larger effects in other tasks. However, theta recorded from SuM, and used to trigger the production of theta-like oscillations in the hippocampus, produced reversal of the deficit in WM learning produced by theta blocking. We explored this apparent inconsistency by analyzing the relationship between SuM and hippocampal theta in the control group of this theta-blocking experiment using coherence, phase analysis, and the directed transfer function. We found little evidence of an influence of SuM on the hippocampus in the bulk of WM learning—with some possibility of SuM becoming involved briefly later in learning. A learning-related increase in coherence was observed in conjunction with gradual phase reorganization of hippocampal theta in relation to SuM theta. This change in phase dynamics between the two structures was also correlated with a relative increase of the estimated direction of theta propagation from the SuM to the hippocampus. These results are consistent with the previous weak effects of SuM lesions and suggest that the use of SuM as a source to trigger hippocampal theta and recover function is likely to be due to coherence between SuM and some other structure that normally controls hippocampal theta during WM learning. © 2010 Wiley-Liss, Inc.
INTRODUCTION
Hippocampal (HPC) theta oscillations at 4–12 Hz have long been associated with a range of brain functions (Buzsaki, 2005). Recent studies show that coherent theta oscillations between the HPC and functionally related structures are modified by experience and depend on the expression of certain behaviors (Seidenbecher et al., 2003; Jones and Wilson, 2005; Decoteau et al., 2007; Jackson et al., 2008; Hoffmann and Berry, 2009; Young and McNaughton, 2009). It is increasingly clear that theta oscillations in the HPC are not only important within the HPC but also crucial for the coordination of neuronal ensembles across areas.
The supramammillary nucleus (SuM) is located in the posterior hypothalamic area where oscillatory spike trains at theta frequencies can be recorded (Kirk and McNaughton, 1991, 1993; Kocsis and Vertes, 1994, 1997; Bland et al., 1995; Kirk et al., 1996). These observations led to the hypothesis that SuM plays a crucial role in the generation of HPC theta, which appears to be true at least in urethane-anesthetized animals (Kirk and McNaughton, 1993; McNaughton et al., 1995; Thinschmidt et al., 1995). However, in awake animals, the inactivation or destruction of SuM only decreases the ongoing HPC theta oscillations instead of abolishing them (McNaughton et al., 1995; Pan and McNaughton, 1997; Pan and McNaughton, 2002; Sharp and Koester, 2008).
The SuM is known to be involved in reward, mnemonic, and particularly emotional processes (see Pan and McNaughton, 2004 for a review). The possibility of a relatively strong contribution to mnemonic processes is raised by the fact that theta recorded from SuM, and then used to trigger electrical stimulation of HPC input, can reverse the blockade of water maze (WM) learning produced by blockade of theta via medial septal injections of local anesthetic (McNaughton et al., 2006). However, this is an isolated result and reports directly manipulating SuM function suggest that SuM may play only a minor role restricted to the later phases of WM learning (Pan and McNaughton, 1997; Shahidi et al., 2004).
In this study, we examined the relationship of field potentials recorded from the HPC and the SuM in the WM. We assessed theta coherence as an indication of the extent to which the two areas showed related activity, and we used the directed transfer function (DTF) to assess the extent to which HPC theta might depend on SuM theta as opposed to the other way round. Recent studies based on the heterogeneity of phase distributions of SuM spike trains (Kocsis and Vertes, 1994) in relation to HPC theta show that HPC-SuM interactions may be bidirectional (Kocsis, 2006; Kocsis and Kaminski, 2006). DTF is an autoregressive modeling technique based on calculating how much variance in a time series (such as EEG recordings) can be accounted for by delayed versions of another time series (Kaminski and Blinowska, 1991; Kaminski, 2005; Gourevitch et al., 2006; Young and Eggermont, 2009). The inference that one series may causally influence another is made if the past of that series can reliably predict the future of the other. This inference cannot be absolutely substantiated as the method is essentially correlational and assumes that the data are consistent with the general linear model. However, a lack of DTF predictivity suggests that one area does not exert strong and immediate control of another.
MATERIALS AND METHODS
Animals
Five male Sprague-Dawley rats were obtained from the Department of Laboratory Animal Sciences at the University of Otago. Surgery and WM testing procedures are described in detail elsewhere (McNaughton et al., 2006) where the animals analyzed in this study formed the behavioral control group. Briefly, animals were anesthetized with ketamine/medetomidine, and bipolar stainless steel electrodes were implanted in CA1/dentate layers of the hippocampus (AP −3.8 mm, ML −2.5 mm, DV −3.5 mm, tip separation 1.0 mm) and the supramammillary nucleus (AP −4.8 mm, ML −0.9 mm, DV −9.4 mm, tip separation 0.5 mm, 6.0° from vertical). A stimulating electrode aimed at the fornix and a 26 GA cannula guide aimed at the medial septum were also implanted for a different study. Antisedan (2.5 mg/kg, 5 mg/ml, Novartis Animal Health Australia Limited) was administered to facilitate recovery from anesthesia, and this was followed by postoperative analgesic administration. The rats were then allowed to recover for at least 10 days before any electrophysiological or behavioral testing. The University of Otago Animal Ethics Committee approved these manipulations, and the experimental procedures described below.
Behavior and Electrophysiology
Local field potentials (LFPs) were recorded through a source follower, amplified (Grass P511K, 1–30 Hz bandpass filter), and digitized at 100 Hz for subsequent analyses. The data were acquired and stored by Spike2 (CED, UK) for offline analysis. The WM testing followed the single-day protocol of Pan and McNaughton (1997). Briefly, the WM consisted of a rigid black plastic pool (150 cm in diameter, 35 cm high) and was filled to a 25-cm depth with 26°C (±2°C) water. A black plastic platform (15-cm square) was placed 1.5 cm beneath the water surface in the center of the southeast quadrant. Animals were prehandled and allowed 40 s to find the platform and were then guided to the platform if they failed to locate it. The animals were then left on the platform for 15 s, which also served as the intertrial interval as the next trial begins with bringing the animals to the next start location from the platform. All starting locations for a total of 16 trials were counterbalanced, and escape latency, path length, and trajectory were all acquired for offline analyses (HVS IMAGE, UK). In an open-field (OF) task, used as an analysis control, animals were left to freely explore a square (73 × 73 × 51 cm) box for 6 min.
Data Processing—General
WM data were segmented into distinct behavioral epochs for further processing based on behavioral markers generated by the HVS program. Fixed-length epochs were: (1) 2 s immediately before placing the animals in the pool; (2) 2 s immediately before the animals climbed up onto the platform; and (3) the subsequent 2 s while the animals were on the platform. In addition, recordings from the variable-length swimming period from each individual trial were separately segmented. Behavioral markers used to segment the WM data were inserted randomly into the OF recordings, and the same segmentation method was applied to generate equal-length data for WM:OF comparisons—using the randomized OF records as a statistical control. Segments of raw data with the DC component removed were exported from Spike2 (CED, UK) for further analysis in MATLAB (Mathworks, Natick, MA).
Custom-made code involving the multitaper spectral analysis (Mitra and Pesaran, 1999) and DTF (Kaminski and Blinowska, 1991; Young and Eggermont, 2009) are based on the respective cited references. Hilbert transform of zero-phase digitally filtered data (4–12 Hz) were used to calculate instantaneous phase and frequency. Raw data and examples of various analyses in time–frequency representations are shown in Figure 1.

Characteristics of recordings from a single WM trial. (A) Raw LFPs from the SuM and the HPC. The left dotted line marks the time of entry to the WM; the right line the time when the animal had found the platform. (B) The spectral properties of SuM LFP up to 20 Hz. Clear activity within the theta band can be seen between 3 and 9 Hz. (C) Spectrogram for the HPC recording, which also shows robust theta oscillations. (D) Cohereogram between HPC and SuM LFPs. Sporadic theta coherence and coherences of mainly theta harmonics can be observed. (E) The ΔDTF (taken as HPC-SuM values) showing time–frequency relationships. At theta frequencies, delta DTF is generally positive (red color), with the reverse (blue color) being true more often in the later half of the swim. (F) Unwrapped theta-phase differences between the HPC, SuM showing periods of peak-to-peak (zero-gradient) and other forms of phase locking (constant gradient).
Data Processing—Spectral Analysis
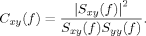
Data Processing—Directed Transfer Function
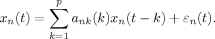
A model order of 10 was used as a compromise between computational efficiency and model accuracy for investigating the frequencies of interest. The autoregressive model was then transformed into the frequency domain. The normalized form of DTF (nDTF) was used to reduce between-subjects variation derived from electrode placement. That is, the directed coherence estimates in a particular row of the matrix were divided by the sum of all estimates in the same row of the matrix. The time–frequency representation of nDTF was also carried out with 0.9 s, 90% overlapping windows. Finally, the putative direction of control was determined by subtracting the SuM nDTF values from the HPC values to form an index for theta propagation (nDTF(HPC-SuM)), where a positive value suggests HPC LFP is predictive of SuM LFP and vice versa for a negative value.
Data Processing—Instantaneous Phase and Frequency
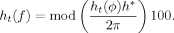
Both the instantaneous frequency and phase were averaged in 0.9 s windows.
Statistical Analysis
All statistical analyses were computed in SPSS15 (SPSS, Chicago, IL). Pearson's linear correlation coefficients and the corresponding two-tailed significance tests were calculated to determine if two variables were interdependent. One-way ANOVAs with polynomial contrasts were used to examine how measured variables changed as a function of learning. The z transform (z(x) = 0.5(log10((1 + x)/(1 − x))) was applied to the coherence and DTF values to normalize the error variance. All variables submitted to parametric tests, such as ANOVA, had approximately normal error distributions.
RESULTS
Hippocampo-Supramammillary Theta Interactions During WM Learning
To explore the relationship between the theta variables and WM acquisition, we pooled variable-length swimming epochs from all trials into four-trial blocks and spatially by pooling data obtained from a particular quadrant in the maze (Fig. 2).
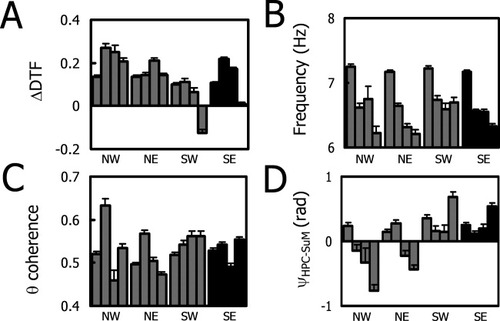
Theta parameter changes during spatial navigation in the WM as a function of time and space. (A) Different patterns of ΔDTF change across time between quadrants suggest the ΔDTF changes reflect processes that underlie spatial learning. Specifically, the changes in ΔDTF suggest an initial increase in theta propagation from HPC to SuM and the reverse trend appears toward the end of the training. (B) Changes in HPC theta frequency showed relatively uniform decrease across time between quadrants. This suggests that the decrease in HPC theta frequency is not dependent on where the animal was in the WM, but a generalized change as a function of time spent in the maze. (C) Dissimilar theta coherence changes across time and space again suggests unique contributions of both time and space in determining HPC-SuM theta synchronization. The trend in the target quadrant suggests a general increase in theta coherence, with the exception of the third trial block, which may be related to later phases of WM learning. (D) HPC-SuM theta-phase differences (radians) revealed a general dissociation between the north and south sides of the pool, where an initial decrease and a sharp increase in the final block of trials is associated with the changes in the target quadrant (SE) and one of the adjacent quadrants (SW).
The key global observations are that theta coherence between SuM and HPC is not particularly high overall, and DTF values are generally positive (indicating a potential driving of SuM by HPC rather than the reverse). The bulk of the phase differences are also more consistent with an HPC to SuM direction of propagation. There is, therefore, no evidence for any strong control of HPC by SuM and, except possibly in the later stages of training, little evidence consistent with even modest control.
Because of the large differences in numbers of data points across trials and quadrants, we performed one-way ANOVAs with polynomial contrasts to examine which polynomial fit accounted for the greatest variance (see Table 1) for each quadrant. In addition, correlations of the values from the SE quadrant (the target quadrant with the hidden platform) as a reference against the values for the rest of the quadrants were computed to assess how similar the changes across trials were across quadrants (see Table 2).
| NW | NE | SW | SE | ||||||
|---|---|---|---|---|---|---|---|---|---|
| F | P | F | P | F | P | F | P | ||
| ΔDTF | lin | 20.47 | 6E − 06 | 4.22 | 0.04 | 91.86 | 2E − 21 | 54.35 | 2E − 13 |
| quad | 28.43 | 1E − 07 | 9.68 | 0.002 | 45.02 | 2E − 11 | 292.30 | 5E − 64 | |
| cub | 1.21 | 0.27 | 15.74 | 7E − 05 | 1.63 | 0.20 | 1.23 | 0.27 | |
| Hz | lin | 131.79 | 2E − 29 | 372.19 | 1E − 79 | 59.943 | 2E − 14 | 334.76 | 8E − 73 |
| quad | 4.08 | 0.0436 | 21.219 | 4E − 06 | 19.496 | 1E − 05 | 50.978 | 1E − 12 | |
| cub | 5.88 | 0.0154 | 0.0083 | 0.9273 | 0.0847 | 0.771 | 20.106 | 7E − 06 | |
| COH | lin | 0.004 | 0.95 | 5.05 | 0.03 | 16.20 | 6E − 05 | 1.01 | 0.32 |
| quad | 32.74 | 1E − 08 | 64.94 | 1E − 15 | 1.31 | 0.25 | 4.96 | 0.03 | |
| cub | 41.66 | 1E − 10 | 31.11 | 3E − 08 | 0.09 | 0.77 | 35.17 | 3E − 9 | |
| Phi | lin | 89.36 | 1E − 20 | 70.273 | 7E − 17 | 2.4418 | 0.1183 | 17.632 | 3E − 05 |
| quad | 0.004 | 0.95 | 10.604 | 0.0011 | 17.766 | 3E − 05 | 28.553 | 9E − 08 | |
| cub | 0.40 | 0.53 | 8.9569 | 0.0028 | 0.8298 | 0.3624 | 0.0162 | 0.8988 | |
- F-statistics and their corresponding P-values from one-way ANOVA with polynomial (linear; lin, quadratic, quad; cubic; cub) contrasts. The polynomial trend with the highest F-statistics is bolded in each condition. P-values have not been Bonferroni corrected and so P < 0.001 should be taken as significant.
| ΔDTF | Hz | COH | Phi | ||
|---|---|---|---|---|---|
| SE | SE | SE | SE | ||
| NW | r | 0.54 | 0.96 | 0.71 | −0.69 |
| P | 0.46 | 0.04 | 0.29 | 0.31 | |
| NE | r | 0.32 | 0.96 | 0.02 | −0.80 |
| P | 0.68 | 0.04 | 0.98 | 0.20 | |
| SW | r | 0.86 | 0.92 | −0.13 | 0.97 |
| P | 0.14 | 0.08 | 0.87 | 0.03 |
- The target quadrant (SE) is compared to each of the nontarget quadrants.
For ΔDTF (Fig. 2A), there was a tendency for values to increase initially and then decrease later in training. However, a quadratic function accounted for the most variance (about four times that of the linear trend) in the SE (target) quadrant, which was also the case for NW (about 1.4 times the linear trend). For the SW and SE quadrants, there were decreases in ΔDTF between the start and the end of training resulting in significant linear trends (superimposed on the orthogonal quadratic trends). However, the overall trends (in terms of correlation between the mean values) were not found to be similar between SE (target) and the other quadrants, except perhaps for SW (r = 0.86, n = 4, P = 0.14). Consistent with previous findings, HPC theta frequency decreased across trials but did not show any quadrant-dependent changes (Fig. 2B), as indicated by all quadrants having the linear trend accounting for most of the variance. The means for all the other quadrants showed substantial linear correlations with SE (target), and, with the exception of SW (r = 0.92, n = 4, P = 0.08), these were significant (see Table 2). For SuM-HPC theta coherence (Fig. 2C), there was a tendency to higher coherence in the second-trial block relative to the third, giving rise to cubic trends—except in the SW quadrant. Also in the NE quadrant a quadratic trend accounted for greater variance than the cubic (Table 1). None of the nontarget quadrants demonstrated statistically significant linear correlations with SE (target) (Table 2). Finally, for HPC-SuM theta-phase differences (Fig. 2D), decreasing linear trends accounted for most of the variance on the north side of the maze, whereas quadratic trends describing an initial decrease followed by an increase in the last trial blocks were found to best account for the quadrants on the south side (Table 1). The only significant linear correlation between quadrants was found between the SE (target) and SW (r = 0.97, n = 4, P < 0.03; Table 2).
Hippocampo-Supramammillary Theta Propagation and Hippocampal Theta Frequency
A previous report (Kocsis and Kaminski, 2006) suggested that the direction of HPC-SuM theta propagation is dependent on HPC theta frequency. To explore this finding in the context of freely behaving animals, we correlated averaged instantaneous HPC theta frequency with the ΔDTF. No covariance across time can be seen between the two parameters (Fig. 3A). To further quantify this, 0.9 s bins of instantaneous HPC frequency and ΔDTF collected across all the animals tested in the WM were pooled, and an extremely weak linear relationship was found between the two (Fig. 3B, r = 0.001, n = 15163, P < 0.05), suggesting lower HPC frequency might very occasionally be associated with a HPC → SuM direction of theta propagation. To provide a degree of comparative control of this finding, we also performed the same analysis on equivalent data obtained in a separate OF test and found it to be statistically nonsignificant (r = 0.000001). There is a slight preference for higher ΔDTF values to be associated with lower HPC theta frequency during WM (Fig. 3C, left), corroborating the weak linear correlation coefficient reported in Figure 3B. There is no such trend in OF data relative to the WM, showing a skew of ΔDTF to higher values but without any HPC theta-frequency covariance (Fig. 3C, right). The ΔDTF and HPC theta-frequency distributions were further compared between the WM and OF conditions (Fig. 3D). There is an obvious skew of values to more positive values of ΔDTF in the WM compared with OF as the distributions between the conditions are statistically different (Mann-Whitney test, P < 0.001). In contrast, there appear to be more instances of higher HPC theta frequency in the OF condition compared with WM, as the distributions were also found to be statistically different (Mann-Whitney test, P < 0.001).
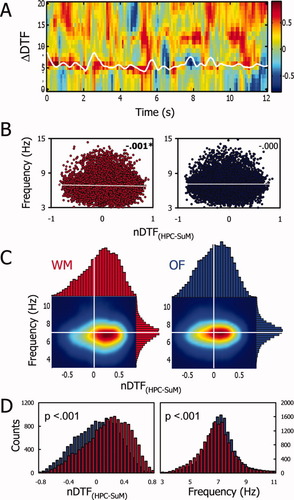
Hippocampal theta frequency is not related to ΔDTF estimates. (A) No observable relationship can be seen between the instantaneous frequency derived from bandpassed, Hilbert transformed HPC LFP (white line) overdrawn on ΔDTF time–frequency representation from a single trial of WM. (B) Instantaneous frequency and nDTF from all animals and all trials in the WM (left, in red) and the OF (right, in blue). In neither case there is a relationship between HPC theta frequency and ΔDTF values. (C) Joint distributions of HPC theta frequency and ΔDTF. The significant but weak correlation observed in the WM is supported by the observable preference of high ΔDTF values (suggesting a HPC → SuM direction of propagation) to be associated with slower HPC theta frequency. There are no obvious trends in the OF regarding the symmetry of the joint distribution. (D) Mann-Whitney test reveals neither HPC frequency nor ΔDTF have similar distributions during WM training or OF exposure.
Experience-Dependent Modification of Theta Oscillation Dynamics Between the Hippocampus and Supramammillary Nucleus
To match the length of data analyzed for each animal across trials, we analyzed three 2-s epochs. The first (handling) was the 2 s immediately before placing animals into the pool; the second (swim) was the 2 s before arriving at the platform; and the third (platform) was the 2 s immediately after the arrival on the platform (Fig. 4A; see also methods). All animals decreased their path length as a function of experience (Fig. 4B). Correlations between path lengths and ΔDTF, HPC theta frequency, HPC-SuM coherence, and HPC-SuM phase differences were carried out for each of the 2 s behavioral epochs described above. These correlations are shown in Table 3. Individual data for the swim phase are shown in Figure 4. Consistent with the analysis of the quadrant data, there appears to be a modest positive relationship between ΔDTF and path length during WM swimming, suggesting a change in theta propagation in the direction of HPC → SuM toward SuM → HPC (r = −0.56, n = 16, P < 0.05, uncorrected; Fig. 4C). There may have been a weak similar trend on the platform; but there was no sign of such changes with handling. There were no such trends in equal-length data obtained during OF exploration (Fig. 4G). Also consistent with the quadrant analysis, there were significant reductions in HPC theta frequency as a function of path length, in the handling and swim epochs with a trend to reduction in the platform epoch (r = 0.54, n = 16, P < 0.05, uncorrected; Fig. 4D). Again, no equivalent trend was seen between the same variables during OF exploration (Fig. 4H). There were indications of an experience-dependent reduction in HPC-SuM phase differences only in the “platform” epoch (Fig. 4e; see Table 3). The lack of change in handling and swim is likely to be the result of cancellation between the effects seen in the northern quadrants and those in the southern (the “handling” period involves the holding of the animal predominantly in positions that are an extension, outside the pool, of a single quadrant within the pool). Theta coherence in the swim epoch between the SuM and HPC increased as animals reduced distance traveled to the hidden platform (r = −0.57, n = 16, P< 0.05; Fig. 4F). Once again, no significant trend was seen in the OF data (Fig. 4J). There was no sign of such a change in either the handling or platform epochs.
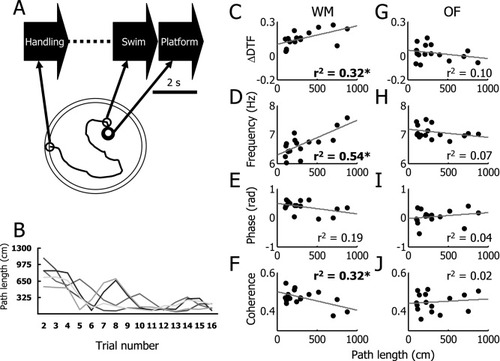
WM performance and HPC-SuM theta dynamics in the 2 s “swim” epoch, just before arriving at the platform. Simple correlations significant at P < 0.05, without Bonferroni correction, are indicated by *. For actual P values and corrected significance, see Table 3. (A) An illustration of the WM apparatus and analysis scheme. To match the length of data analyzed across trials, 2 s immediately before placing animals into the pool (handling), 2 s before arriving the platform (swim), and 2 s immediately after the arrival on the platform (platform) were extracted for analysis. (B) Clear decrease in path length can be observed from all animals, indicative of WM acquisition. (C) A significant positive linear correlation exists between ΔDTF and path length, suggesting an increase of SuM → HPC influence at theta frequencies as animals improved in the task. (D) HPC theta frequency reduced as animals improved their WM performance. (E) A suggestion of increasing HPC-SuM theta-phase differences can be seen as path length decreased, but this relationship was not found to be statistically significant. (F) A negative linear correlation exists between HPC-SuM theta coherence and path length, suggesting HPC-SuM theta oscillations became more coherent as animals improved in WM learning. (G–J) All the corresponding theta measures described previously were found to exhibit weak, nonsignificant but opposite relationships with path length in the OF.
| ΔDTF | Hz | Phi | COH | ||||||
|---|---|---|---|---|---|---|---|---|---|
| WM | OF | WM | OF | WM | OF | WM | OF | ||
| Handling | r | 0.29 | −0.33 | 0.80 | 0.31 | 0.37 | 0.19 | −0.15 | 0.28 |
| P | 0.27 | 0.22 | <0.0005 | 0.23 | 0.16 | 0.47 | 0.57 | 0.30 | |
| Swim | r | −0.56 | 0.12 | 0.73 | −0.31 | −0.44 | 0.20 | −0.57 | −0.26 |
| P | 0.03 | 0.65 | <0.002 | 0.24 | 0.09 | 0.46 | 0.03 | 0.32 | |
| Platform | r | −0.03 | 0.42 | 0.54 | −0.31 | 0.51 | −0.06 | −0.45 | −0.45 |
| P | 0.91 | 0.10 | 0.04 | 0.24 | 0.05 | 0.84 | 0.08 | 0.08 | |
- P-values have not been Bonferroni corrected and so P < 0.004 should be taken as significant.
DISCUSSION
The principal finding of this article is that the observed DTF and phase values were incompatible with a strong control of HPC by SuM in the WM. The rats acted as controls in a study in which SuM theta was used to “repair” HPC rhythmicity and was effective in restoring WM function (McNaughton et al., 2006). Our data indicate that this repair capacity was not due to SuM theta driving the HPC under normal circumstances, as estimated by DTF of field potentials.
It is known that the destruction of SuM (together with the mammillary bodies) does not impact on the size of place cell fields (Sharp and Koester, 2008)—although it decreased place cell firing rates and delayed the response to current spatial locations. Only modest pharmacologically induced acquisition deficits have been observed in the same 1-day version of the WM (Pan and McNaughton, 1997), with no effect in other WM training regimes (Pan and McNaughton, 2002; Shahidi et al., 2004). All the available evidence, then, suggests that the control of HPC theta by SuM in the WM is minimal and does not play a large functional role—despite the fact that HPC theta-like rhythmicity is important in this task.
There was some evidence for a modest relative increase in the SuM contribution to ongoing HPC theta oscillations in later stages of this 1-day version of WM learning. This is consistent with previous behavioral findings, where the injection of a benzodiazepine into the SuM decreased HPC theta frequency and modestly attenuated WM learning only in the later stages (Pan and McNaughton, 1997). This evidence was provided by changes in ΔDTF in the south part of the maze and changes in phase difference in the north part. It is not clear why these measures are uncoupled, but this emphasizes the fact that, in the WM, any evidence for control of HPC by SuM is weak.
Many previous studies have demonstrated a role for SuM in HPC-related learning (Pan and McNaughton, 1997; Shahidi et al., 2004; Aranda et al., 2008). A positive correlation between HPC theta frequency and a SuM to HPC direction of theta propagation was also reported previously with anesthetized animals (Kocsis and Kaminski, 2006). However, we found little evidence that HPC theta frequency is correlated with the direction of theta propagation in the 1-day WM task. It seems likely, then, that SuM can control HPC theta under some conditions; but that it is essentially de-efferented and other nuclei provide the main control of HPC theta in the WM.
One reason for differences between our results and previous results is that there are differences in the extent of SuM involvement in HPC theta generation and frequency in freely moving animals (McNaughton et al., 1995; Thinschmidt et al., 1995) when compared with anesthetized animals (Kirk and McNaughton, 1993; Thinschmidt et al., 1995; Jiang and Khanna, 2004).
A second source of difference is that we used field potentials, whereas other studies have usually used single-cell recordings. It is possible, then, that a population of cells in SuM that does not contribute greatly to field potentials could nonetheless be controlling theta in the WM. In particular, Kocsis and Kaminski (2006) used SuM spike train transformed surrogate LFPs in their analysis and only a subset of SuM neurons were involved in the proposed role of accelerating HPC theta, whereas another subset showed the same trend but did not demonstrate statistical significance.
A third source of difference, in this latter case, was that only theta oscillations recorded from the CA1 cell layer were used as the HPC theta reference (Kocsis and Kaminski, 2006). Here, we used a bipolar recording setup, where recorded HPC theta is the difference between stratum pyramidale and the fissure, thus maximizing the recorded theta amplitude but conflating fields from two partially distinct generators. Given that microscopic differences in coherence (Kocsis et al., 1999; Montgomery et al., 2009) and phase (Leung et al., 1982; Leung, 1984; Buzsaki et al., 1986) can occur within the HPC itself, it is unclear if data from this study and those based on single cells and more local recordings are directly comparable. Nonetheless, there are global similarities between the studies in terms of substantial positive ΔDTF values with some superimposed strengthening of the SuM-to-HPC DTF.
It remains to account for the effectiveness with which stimulation triggered by recordings of SuM theta can repair HPC function in the 1-day WM. If we assume that theta is controlled by multiple nuclei connected, via the medial septum, to the HPC in parallel, then we must also assume that these nuclei, nonetheless, do not act as independent oscillators. If they did, the HPC record would demonstrate phenomena such as beats. The simplest explanation is that these various nuclei are interlinked. They could, for example, share an inhibitory, gating network. This would result in concurrent inhibition of all the nuclei that would maintain a degree of phase consistency across them. The information flowing into each nucleus and the extent to which it contributes to current HPC theta would vary. Recordings from SuM, then, would share the rhythmicity of such nuclei as are controlling HPC theta in the WM and so allow stimulation to restore the functions lost by disconnection of these other nuclei.
Our results suggest, then, that although SuM is important for the control of some behaviors by the HPC, its influence in the WM is small and may be restricted to discrete, potentially brief, time periods. The most important feature of the system for learning and memory may, then, be the bidirectional interplay at theta frequencies between HPC, SuM, and the other nuclei with which they are connected.
Acknowledgements
The authors thank the anonymous reviewers for their detailed suggestions, which have been incorporated into the text. In particular, detailed comments by one referee have been incorporated into our discussion of Kocsis and Kaminski (2006).




