Health Economics
Volume 33, Issue 5 pp. 894-910
RESEARCH ARTICLE
Open Access

Exploring health preference heterogeneity in the UK: Using the online elicitation of personal utility functions approach to construct EQ-5D-5L value functions on societal, group and individual level

Paul Schneider, 

Corresponding Author

Paul Schneider

ScHARR, The University of Sheffield, Sheffield, UK

Valorem Health, Bochum, Germany

Correspondence

Paul Schneider.

Email: [email protected]

Search for more papers by this author
Nancy Devlin, 

Nancy Devlin

University of Melbourne, Melbourne, Victoria, Australia

Search for more papers by this author
Ben van Hout, 

Ben van Hout

ScHARR, The University of Sheffield, Sheffield, UK

Open Health, York, UK

Search for more papers by this author
John Brazier, 

John Brazier

ScHARR, The University of Sheffield, Sheffield, UK

Search for more papers by this author
First published: 20 January 2024
https://doi.org/10.1002/hec.4805

Abstract

A new method has recently been developed for valuing health states, called ‘Online elicitation of Personal Utility Functions’ (OPUF). In contrast to established methods, such as time trade-off or discrete choice experiments, OPUF does not require hundreds of respondents, but allows estimating utility functions for small groups and even at the individual level. In this study, we used OPUF to elicit EQ-5D-5L health state preferences from a (not representative) sample of the UK general population, and then compared utility functions on the societal-, group-, and individual level. A demo version of the survey is available at: https://eq5d5l.me. Data from 874 respondents were included in the analysis. For each respondent, we constructed a personal EQ-5D-5L value set. These personal value sets predicted respondents' choices in three hold-out discrete choice tasks with an accuracy of 78%. Overall, preferences varied greatly between individuals. However, PERMANOVA analysis showed that demographic characteristics explained only a small proportion of the variability between subgroups. While OPUF is still under development, it has important strengths: it can be used to construct value sets for patient reported outcome instruments such as EQ-5D-5L, while also allowing examination of underlying preferences in an unprecedented level of detail. In the future, OPUF could be used to complement existing methods, allowing valuation studies in smaller samples, and providing more detailed insights into the heterogeneity of preferences across subgroups.

1 INTRODUCTION

Preference-based measures of health, such as the EQ-5D-5L, are a widely used component of health economic evaluations. They map health states to a common currency, that is usually referred to as health state ‘utility’. Utility values are needed to compute quality-adjusted life years (QALYs) and to assess and compare the health effects of different treatment options (Drummond et al., 2015; Whitehead & Ali, 2010).

Preference-based measures of health have two components. Firstly, a descriptive system which defines a number of mutually exclusive health states. Secondly, a value set, which assigns each health state a utility value. These utility values are preference-based. They require the preferences of a target population, in most cases the general population, but occasionally also patients, as input (Brazier et al., 2017).

Health state preferences can be elicited using various different methods. Time trade-off (TTO), standard gamble (SG) and discrete choice experiments (DCE) are those most commonly used (Brazier, Ara, et al., 2017). However, for the purpose of creating value sets, these methods have a severe limitation: Since little information is obtained from each individual, data from hundreds, if not thousands of individuals are required to accurately estimate model coefficients for a value set. Work by Oppe and Van Hout (2017) suggests, for example, that the minimum sample size required to derive a main effects model (with 20 coefficients) for the EQ-5D-5L is about 1000 participants. While this may not be an issue when eliciting average preferences from the general population, the lack of statistical power limits the extent to which the heterogeneity of preferences between specific subgroups can be studied. It also makes it difficult to elicit preferences in settings where large sample sizes cannot be achieved, such as patients with rate diseases; and it is generally not feasible at all to draw inferences about the preferences of any given individual.

We recently developed a new preference elicitation method, called Online elicitation of Personal Utility Functions (OPUF) (Schneider et al., 2022). The approach is based on previous work by Devlin et al. (2019), and allows estimating preferences on the individual person-level.

Thus far, the new method has only been applied in small pilot studies. Here, we report on the results of a larger survey of the UK population, in which we used OPUF to elicit health state preferences for the EQ-5D-5L. We demonstrate how the approach's ability to construct preferences on the social, group, subgroup, and individual level can be used to study the heterogeneity of preferences. Specifically, we investigated to what extent health preferences differ between members of the UK general public, and how much of these differences can be explained by demographic characteristics.

2 METHODS

2.1 Sample

We recruited 1000 participants through Prolific (Palan & Schitter, 2018). Prolific provides a platform for researchers to recruit participants for online studies and is known for its high data quality compared to other online panels (Peer et al., 2022). The sample was selected to be broadly representative of the UK general population in terms of age, sex, and ethnicity. Since this was an exploratory study to test the OPUF method in a larger sample, rather than to estimate an official value set, we did not pre-specify any exclusion criteria. We also did not implement any checks for bots, however, the interface of the OPUF survey requires certain manual operations (dragging and dropping, clicking on specific areas on the screen) that regular bots are not able to perform. All participants completed the EQ-5D-5L OPUF survey between August 24th and 27th, 2021.

2.2 The EQ-5D-5L instrument

The EQ-5D-5L instrument is a generic preference-based measure of health-related quality of life (Herdman et al., 2011). It consists of two components: a descriptive system, which defines mutually exclusive health states and, secondly, a set of (social) values, that reflect their respective desirability.

The descriptive system defines health states along five dimensions: mobility (MO), self-care (SC), usual activities (UA), pain or discomfort (PD), and anxiety or depression (AD). Each dimension has five levels: no, slight, moderate, severe, and extreme problems or unable to do. The instrument can describe a total of 3125 health states. These states are usually referred to by a 5-digit code, representing the severity levels: ‘11111’ denotes full health, for example; ‘21111’ denotes slight mobility problems but no problems on any other dimension; and ‘55555’ denotes the (objectively) worst health state (Devlin et al., 2018; Herdman et al., 2011).

The social value set maps each health state to a utility value. Utility values range from 1, assigned to perfect health (‘11111’) to 0, assigned to dead. Health states that are considered worse than being dead have a negative utility value.

EQ-5D-5L health state preferences are most commonly represented by a linear additive model. It includes 20 coefficients, – four on each dimension – representing the disutility associated with the move from no problems to slight, moderate, severe, and extreme problems (Devlin et al., 2018).

2.3 The online elicitation of personal utility functions approach

The OPUF approach is an adaptation of the Personal Utility Function (PUF) method (Devlin et al., 2019) for use as a stand alone online survey. In contrast to traditional preference elicitation techniques (TTO, DCE, SG, etc), which are alternative-based (decompositional), the OPUF approach is attribute-based (compositional). The theoretical foundation for both, compositional and decompositional methods, lie in multi-attribute value theory. The difference between the two is the direction in which preferences are (de)constructed (Belton & Stewart, 2002; Keeney & Raiffa, 1993; Thokala et al., 2016).

Decompositional methods start with valuing health states. In a second step, the responses are decomposed into their components, using statistical methods. This means, the 20 EQ-5D-5L preference model parameter coefficients are inferred from respondents' holistic evaluation of health states.

In a compositional approach, the partial values for the different components of health states are elicited directly. The components are (1) dimension weights, which determine the relative importance of each dimension; (2) level ratings, which determine the relative position of the five severity levels (no, slight, moderate, severe, extreme) within each dimension; and (3) anchoring, which maps the dimension weights and level ratings on to the QALY scale. These components are then combined to construct values for entire health states.

2.4 The EQ-5D-5L OPUF survey

The EQ-5D-5L OPUF survey consists of nine steps, of which four are essential for the construction of PUFs. In the following, the steps will be briefly described. A more detailed description of the OPUF survey and its development is provided in Schneider et al. (2022). Much effort went into the design of an intuitive and easy-to-use interface. We thus recommend readers to consult the online demo version of the OPUF survey while reading through this section. It is available at: https://eq5d5l.me.
  • (1)

    Warm-up (own EQ-5D-5L health state, EQ VAS)

The survey began with a question asking the participants to report their own EQ-5D-5L health state and to rate their overall health status, using the EQ VAS.
  • (2)

    Level rating

Level ratings were elicited by asking participants to position ‘slight’, ‘moderate’, and ‘severe health problems’ on a visual analogue scale between 0% and 100%. The instructions stated that “a person with 100% health has no health problems”, and“a person with 0% health has extreme health problems”. Respondents are then asked "[h]ow much health does a person with slight, moderate, and severe health problems have left?”.

The level descriptions of the EQ-5D-5L are similar across dimensions. The second best level is referred to as ‘slight’ on all five dimensions, for example, We thus decided to elicit the level ratings for health problems in general, that is, without reference to any particular dimension, and then applied the level ratings to all five dimensions. However, this should be seen as a simplification. The description of the worst level differs between dimensions (extreme problems and being unable to do), and, irrespective of the wording, the ratings of levels might also differ by dimension. Ideally, level ratings should thus be obtained for each dimensions separately.
  • (3)

    Dimension ranking

Participants were asked to rank the worst levels of the five EQ-5D-5L dimensions (i.e., ‘I am unable to walk about’, ‘I am unable to wash and dress myself’, etc) from worst to less worse. Ties were not permitted. The selected rank order was used to tailor the presentation of the following task (4) to the individual participant.
  • (4)

    Dimension swing weighting

The task showed five sliders, one for each EQ-5D-5L dimension, describing an improvement from the worst (extreme problems) to the best level (no problems) on the respective dimension. The sliders were presented in the same order as the participant had ranked them before. The first slider (the most important dimension) was set to 100. Participants were asked to use this as a yardstick to evaluate the importance of the four other dimensions. The instructions for this task were personalised. If, for example, pain/discomfort was ranked first in the previous exercise, the instructions stated: “If an improvement from ‘I have extreme pain or discomfort’ to ‘I have no pain or discomfort’ is worth 100 'health points', how many points would you give to improvements in other areas?”.
  • (5)

    Validation DCE

The survey also included three DCEs. The choice sets were personalised, to cover a broad range in terms of severity (mild, moderate, severe health states) and utility differences between scenarios (easy, moderate, difficult). The choice sets always involved trade-offs, that is, dominant or dominated states were excluded. The responses were not used to construct PUFs. The task was only included to assess the consistency between PUFs and participants' DCE choices.
  • (6)

    Anchoring I: position-of-dead

Two different methods were used to anchor PUFs on the QALY scale: all participants were asked to consider a pairwise comparison between the worst health state ‘55555’ (scenario A) and being dead (scenario B). If they preferred ‘55555’ over ‘being dead’, they immediately moved on to task 7. If they preferred ‘being dead’ over ‘55555’, a binary search algorithm was initiated, during which the health state shown in scenario A changed, adaptively, depending on the participant's choices, to find the health state that they considered to be equivalent to ‘being dead’ (Devlin et al., 2019; Sullivan et al., 2020).

To enable the search algorithm, all 3125 EQ-5D-5L health states were ranked from the best to the worse, based on the participant's responses to the level rating and dimension weighting. After the first comparison (‘55555’ vs. ‘being dead’), the algorithm selects the median state (which may be different for each participant). It then jumps up or down, narrowing down to the health state that is equal to being dead. After six iterations, the search ended. At this point, the equal-to-dead state is being identified with a maximum error of +/− 49 ranks (corresponding to 1.6% of the total number of EQ-5D-5L health states).
  • (7)

    Anchoring II: dead-VAS

If participants prefer the worst health state, ‘55555’, over ‘being dead’, the utility of ‘55555’ could take any value between 1 and 0. We therefore asked those participants to locate the position of ‘55555’ on a visual analogue scale between ‘No health problems’ (=100) and ‘being dead’ (=0). The selected value was then used as the anchor point for the PUF.
  • (8)

    Demographic questionnaire

The OPUF survey included questions about personal characteristics, which were previously shown to be associated with EQ-5D-5L health preferences. These included: age, sex, having children, importance of religion or spirituality, the frequency of engaging in religious or spiritual activities, level of education, income, and experience with severe health problems – see Table 1 for more details (Feng et al., 2018; Golicki et al., 2019; MVH, 1995; Peeters & Stiggelbout, 2010).
  • (9)

    Results page

TABLE 1. Sample characteristics.
n (%)
Sex
Female 456 (52%)
Male 413 (47%)
Other/prefer not to say 5 (1%)
Age
18–29 189 (22%)
30–39 188 (22%)
40–49 162 (19%)
50–59 147 (17%)
60–69 164 (19%)
70+ 23 (3%)
Prefer not to say 1 (0%)
Children
No 410 (47%)
Yes 458 (52%)
Prefer not to say 6 (1%)
Education
without Qualifications 10 (1%)
GCSE/Standard grade 93 (11%)
A-Level/Higher grade 161 (18%)
Certificate/Diploma/NVQ 118 (14%)
Degree 305 (35%)
Post-graduate 181 (21%)
Prefer not to say 6 (1%)
Income
£0 − £20,000 207 (24%)
£20,001 − £30,000 161 (18%)
£30,001 − £50,000 216 (25%)
£50,001 − £70,000 132 (15%)
£70,001+ 99 (11%)
Prefer not to say 59 (7%)
Religious/spiritual practice
Never/practically never 545 (62%)
A few times a year 132 (15%)
A few times a month 47 (5%)
Once a week 32 (4%)
A few times a week 48 (5%)
Every day 60 (7%)
Prefer not to say 10 (1%)
Importance of religion/spirituality
Not important 476 (54%)
Slightly important 201 (23%)
Moderately important 100 (11%)
Very important 88 (10%)
Prefer not to say 9 (1%)
Experience with health problems
Health care professional 76 (9%)
Carer 86 (10%)
Family member 429 (49%)
Past own experience 199 (23%)
Present own experience 49 (6%)
No experience 285 (33%)
Prefer not to say 11 (1%)
  • a Non-exclusive categories.

As a thank-you to the participants, the last page of the survey showed a comparison between some of their own responses and aggregate results from English general population (obtained from Devlin et al., 2018).

2.5 Constructing personal utility functions

PUFs were constructed for all participants. In this section, we provide an overview of the preference construction procedure and illustrate the steps with an example.

2.5.1 Overview

  1. The level ratings for no, slight, moderate, severe, and extreme health problems were rescaled between 0 (no problems) and 1 (extreme problems).

  2. The five dimension weights were normalised to sum 1.

  3. The outer product of the dimension weights and the level ratings was taken to generate a set of 20 (un-anchored) model coefficients (+5 zero coefficients). Note that this assumes that the relative position of the intermediate levels does not vary across dimensions.

  4. Depending on whether the participants considered state ‘55555’ better or worse than dead, we either used the response from the ‘dead-VAS’ or from the ‘position-of-dead’ task to anchor the model coefficients and map them on to the QALY scale.

  5. Finally, the model coefficients were used to generate utility values for all 3125 EQ-5D-5L health states – this vector of utility values represents the PUF.

2.5.2 Example

To illustrate the procedure, suppose a participant gave the following level ratings l with l no = 100 , l slight = 90 , l moderate = 50 , l severe = 30 ${l}_{\text{no}}=100,{l}_{\text{slight}}=90,{l}_{\text{moderate}}=50,{l}_{\text{severe}}=30$ , and lextreme = 0; and the following dimension weights w with w M O = 100 , w SC = 60 , w UA = 45 , w PD = 80 ${w}_{MO}=100,{w}_{\text{SC}}=60,{w}_{\text{UA}}=45,{w}_{\text{PD}}=80$ , and wAD = 70. After rescaling the level ratings and the dimension weights, we derive the two vectors:
l ′ = 0 0.1 0.5 0.7 1 ; w ′ = 0.29 0.17 0.11 0.23 0.2 ${l}^{\prime }=\left[\begin{array}{@{}c@{}}0\\ 0.1\\ 0.5\\ 0.7\\ 1\end{array}\right];\quad {w}^{\prime }=\left[\begin{array}{@{}c@{}}0.29\\ 0.17\\ 0.11\\ 0.23\\ 0.2\end{array}\right]$
Taking the outer product provides a matrix M ˜ $\widetilde{M}$ , containing 20 (1–0 scaled) coefficients (+ zero coefficients for ‘no problems’ on each dimension).
l ' ⊗ w ' = M ˜ = w M O w S C w U A w P D w A D l n o l s l i g h t l m o d e r . l s e v e r e l e x t r e m e [ 0 0 0 0 0 0.03 0.02 0.01 0.02 0.02 0.14 0.09 0.06 0.11 0.10 0.20 0.12 0.08 0.16 0.14 0.29 0.17 0.11 0.23 0.20 ] $l\!\!{\rhook}\otimes \,w\!\!{\rhook}=\,\widetilde{M}=\begin{array}{cc}& {w}_{MO}{w}_{SC}{w}_{UA}{w}_{PD}{w}_{AD}\\ \begin{array}{c}{l}_{no}\\ {l}_{slight}\\ {l}_{moder.}\\ {l}_{severe}\\ {l}_{extreme}\end{array}& [\begin{array}{ccccc}0& 0& 0& 0& 0\\ 0.03& 0.02& 0.01& 0.02& 0.02\\ 0.14& 0.09& 0.06& 0.11& 0.10\\ 0.20& 0.12& 0.08& 0.16& 0.14\\ 0.29& 0.17& 0.11& 0.23& 0.20\end{array}]\end{array}$
Suppose the respondent considered state ‘51255’ (approximately) equivalent to being dead in the ‘Position-of-Dead’ task. To rescale and anchor M ˜ $\widetilde{M}$ on the QALY scale, we first compute the scaled disutility for the state equal to being dead with u ˜ ( 51255 ) = $\widetilde{u}(51255)=$ 0.29 + 0 + 0.02 + 0.23 + 0.2 = 0.74. Subsequently, we set the utility of that state to zero and rescale the entire matrix accordingly, by simply dividing it by that value:
M ˜ 0.74 = M = w M O w S C w U A w P D w A D l n o l s l i g h t l m o d e r . l s e v e r e l e x t r e m e [ 0 0 . 0 0 0 0.04 0.02 0.02 0.03 0.03 0.19 0.12 0.08 0.15 0.14 0.27 0.16 0.11 0.22 0.19 0.39 0.23 0.15 0.31 0.27 ] $\frac{\widetilde{M}}{0.74}=M=\begin{array}{cc}& {w}_{MO}{w}_{SC}{w}_{UA}{w}_{PD}{w}_{AD}\\ \begin{array}{c}{l}_{no}\\ {l}_{slight}\\ {l}_{moder.}\\ {l}_{severe}\\ {l}_{extreme}\end{array}& [\begin{array}{ccccc}0& 0.& 0& 0& 0\\ 0.04& 0.02& 0.02& 0.03& 0.03\\ 0.19& 0.12& 0.08& 0.15& 0.14\\ 0.27& 0.16& 0.11& 0.22& 0.19\\ 0.39& 0.23& 0.15& 0.31& 0.27\end{array}]\end{array}$

Note that the constructed preference model assigns state ‘51255’ a value of 0 (=1 – (0.39 + 0 + 0.02 + 0.31 + 0.27)); ‘11111’ is still equal to 1 (=1 – (0 + 0 + 0 + 0 + 0)), and the worst health state (‘55555’) now has a value of −0.35 (=1 − (0.39 + 0.23 + 0.15 + 0.31 + 0.27)). The model can be used to assign utility values to all EQ-5D-5L health states. The resulting vector of 3125 utility values is taken to be a representation of the participant's PUF.

2.6 Preference heterogeneity

Investigating the heterogeneity of preferences between individuals, requires a measure of dis/similarity to quantify how far apart two PUFs are. As stated above, a PUF was represented by a vector of 3125 utility values (one for each EQ-5D-5L health state). It would not be useful to compare the utility values of individual health states, nor would it provide much insight to compute means or medians in this case. Instead, we assessed the dissimilarity between PUFs using the euclidean distance (EUD) measure.

Analogous to a line between two points on a two dimensional plane, the EUD between two PUFs denotes the shortest path length in a 3125 dimensional space. It is computed as the square root of the sum of the squared differences between the PUFs of individuals i and j:
d EUD ( i , j ) = ∑ u i s 1 − u j s 1 2 + … + u i s 3125 − u j s 3125 2 ${d}_{\text{EUD}}(i,j)=\sqrt{\sum {\left({u}_{i}\left({s}_{1}\right)-{u}_{j}\left({s}_{1}\right)\right)}^{2}+\text{\ldots }+{\left({u}_{i}\left({s}_{3125}\right)-{u}_{j}\left({s}_{3125}\right)\right)}^{2}}$
with s = {11111, 21111, …, 55555}

The EUD has a lower bound of 0, which indicates that two PUFs are identical. Theoretically, it does not have an upper bound, but due to the design of the EQ-5D-5L OPUF survey, the maximum EUD between two PUFs was 1789.

2.7 Statistical analysis

After we constructed PUFs for all participants, we computed all pairwise EUD. We then performed permutational multivariate analysis of variance (PERMANOVA) to investigate the heterogeneity of preferences between subgroups.

2.7.1 PERMANOVA

PERMANOVA is a geometric partitioning of variation across a multivariate data cloud, defined in the space of any given dissimilarity measure, in response to one or more groups (Anderson, 2014; Anderson & Walsh, 2013). Originally developed to test for differences in dispersion in ecological data (e.g., Souza et al., 2013), in this study, we used it to investigate the variability in EQ-5D-5L health state preferences.

Analogous to ANOVA, PERMANOVA decomposes the total distances between observations (SST) into within-groups (SSW) and between groups sum-of-squares (SSB), with
S S T = 1 N ∑ i = 1 N − 1 ∑ j = i + 1 N d ( i , j ) 2 ; and S S W = ∑ i = 1 N − 1 ∑ j = i + 1 N d ( i , j ) 2 ϵ i j ℓ / n ℓ $\mathrm{S}{\mathrm{S}}_{T}=\frac{1}{N}\sum\limits _{i=1}^{N-1}\sum\limits _{j=i+1}^{N}d{(i,j)}^{2};\,\text{and}\,\mathrm{S}{\mathrm{S}}_{W}=\sum\limits _{i=1}^{N-1}\sum\limits _{j=i+1}^{N}d{(i,j)}^{2}{{\epsilon}}_{ij}^{\ell }/{n}_{\ell }$
where N is the total sample size (=874), d ( i , j ) 2 $d{(i,j)}^{2}$ is the squared distance between the PUFs of participants i and j, ϵij is an indicator which is 1, if participants i and j belong to the same group, and 0 if they do not, and n ℓ ${n}_{\ell }$ is the size for group ℓ. Then, SSB can then be calculated as SSB = SST – SSW, which allows calculating the pseudo F statistic for p groups:
F = S S B p − 1 S S W N − p $F=\frac{\left(\frac{\mathrm{S}{\mathrm{S}}_{B}}{p-1}\right)}{\left(\frac{\mathrm{S}{\mathrm{S}}_{W}}{N-p}\right)}$

Semiparametric inference is achieved by permutations. The data is resampled (without replacement) and each time the F statistic is recorded. The original F statistic is then compared to the F statistics of the permutations to derive a p-value. This allows robust statistical inference in situations where more response variables than participants are observed or when the data is non-normal or zero-inflated.

The null hypothesis that is investigated is that the centroids and the dispersion (however defined by the distant measure) are equivalent for all groups. The null hypothesis can be rejected either because the centroids or the spread of the distances is different.

PERMANOVA was performed on the EUD matrix. We first tested each of the group characteristics shown in Table 1 individually, and then combined them all in one model. P-values were based on 10,000 permutations and a value below 0.05 was considered statistically significant.

3 RESULTS

3.1 Sample

We recruited 1000 participants through the Prolific online platform. Data from 126 participants, who skipped one or more valuation steps, had to be excluded, because no meaningful PUF could be constructed for them. Characteristics of the 874 participants included in the study are shown in Table 1.

Although we sought to recruit a representative sample of the UK population, the included sample tended to be younger (e.g., only 3% were aged 70+ vs. 15% in the UK population), and more highly educated (e.g., 56% had a degree vs. 40% in the population).

3.2 EQ-5D-5L OPUF survey results

On average, it took participants about 9 minutes to complete the survey. The median was eight; the shortest duration was three; and the longest was 32 min.

3.2.1 Warm-up (own EQ-5D-5L health state, EQ VAS)

Most participants had no or only mild health problems: 216 (25%) were in full health and 404 (46%) reported slight problems on one or more dimensions. Overall, problems were most frequently reported for the AD (n = 470; 53%) and the PD dimension (n = 458, 52%).

The mean (SD) and median (IQR) EQ VAS score was 77.56 (15.59) and 80 (70–90), with a range of 12 to 100.

3.2.2 Level ratings

The mean (SD) ratings assigned to the ‘slight’, ‘moderate’, and ‘severe health problems’ were 80.23 (11.23); 55.61 (11.55); and 23.47 (13.18), respectively. Participants often assigned round values: 182 (21%) participants assigned a rating of 80 to the ‘slight’ level, and 112 (13%) assigned it a value of 90, for example,

3.2.3 Dimension weights

The EQ-5D-5L dimension that was, on average, considered to be most important was pain/discomfort with a mean (SD) weight of 90.05 (16.61), followed by mobility and self-care, which nearly identical weights of 82.88 (20.71) and 82.87 (20.47), and then anxiety/depression with a mean weight of 75.80 and the highest standard deviation of 24.15. The least important dimension was usual activities, with a mean (SD) weight of 73.71 (22.15).

3.2.4 Anchoring (position-of-dead and dead-VAS)

For 342 (39%) participants, who indicated that they would prefer state ‘55555’ over ‘being dead’, we took the anchor point from the dead-VAS task. For the remaining 532 (61%) participants, who considered ‘55555’ worse than dead, we anchored the PUF using their responses to the position-of-dead task. Figure 1 below shows the resulting bi-modal distribution of utility values for state ‘55555’. The mean (SD) utility of state ‘55555’ was −0.37 (0.83), and the lowest and highest values were −9.42 and 1.

Details are in the caption following the image
FIGURE 1
Open in figure viewerPowerPoint

Distribution of utility values for state ‘55555’, based on the responses from either the dead-VAS or the position-of-dead task. Values below −2 are not shown (n = 24).

3.3 Personal utility functions and an alternative EQ-5D-5L social value set for the UK

Descriptive statistics for the constructed personal EQ-5D-5L preference models are provided in Table 2. The reported mean or median model coefficients may be interpreted as a social utility function, and could be used to generate an alternative EQ-5D-5L social value set for the UK.

TABLE 2. Descriptive statistics of personal EQ-5D-5L models (n = 874).
Mean (95% CI) Median (Q1–Q3)
Mobility
Level 2 0.055 (0.053; 0.059) 0.044 (0.024; 0.071)
Level 3 0.123 (0.121; 0.130) 0.109 (0.071; 0.156)
Level 4 0.213 (0.210; 0.223) 0.193 (0.128; 0.267)
Level 5 0.283 (0.278; 0.297) 0.252 (0.168; 0.346)
Self-care
Level 2 0.055 (0.054; 0.058) 0.045 (0.026; 0.071)
Level 3 0.124 (0.122; 0.130) 0.110 (0.072; 0.158)
Level 4 0.213 (0.210; 0.222) 0.192 (0.133; 0.267)
Level 5 0.282 (0.278; 0.294) 0.256 (0.174; 0.350)
Usual activities
Level 2 0.048 (0.047; 0.051) 0.038 (0.022; 0.062)
Level 3 0.108 (0.106; 0.113) 0.096 (0.062; 0.138)
Level 4 0.186 (0.184; 0.194) 0.168 (0.110; 0.236)
Level 5 0.248 (0.245; 0.260) 0.220 (0.150; 0.317)
Pain/Discomfort
Level 2 0.060 (0.059; 0.063) 0.050 (0.029; 0.080)
Level 3 0.136 (0.134; 0.141) 0.122 (0.082; 0.171)
Level 4 0.234 (0.231; 0.243) 0.214 (0.147; 0.293)
Level 5 0.309 (0.305; 0.322) 0.275 (0.190; 0.387)
Anxiety/Depression
Level 2 0.049 (0.048; 0.052) 0.040 (0.020; 0.065)
Level 3 0.111 (0.110; 0.117) 0.099 (0.061; 0.145)
Level 4 0.192 (0.189; 0.200) 0.173 (0.114; 0.246)
Level 5 0.254 (0.250; 0.266) 0.227 (0.153; 0.322)
  • *95% CI = 95% confidence intervals, based on 10,000 bootstrap iterations; Q1 = first quartile; Q3 = third quartile.

3.4 Validation DCE

PUFs predicted participants' DCE responses between non-dominant pairs with an accuracy of 78.5%. The responses of 453 (52%) participants were fully consistent, while 299 (34%) made one, 101 (12%) made two, and 21 (2%) made three ‘mistakes’. We found that the consistency varied by difficulty of the DCE choice set. When the utility difference between the two presented health states was large (>0.3, measured on the personal 1-0 utility scale) 82% (325 of 395) choices were consistent. Yet, even when the utility difference was small (<0.1) and the choice was difficult, a participant's PUF still predicted their choices with an accuracy of 68% (143 of 209 of choices). Overall, the Cohen's Kappa statistic for the agreement between PUFs and DCE responses was 0.53 (95% CI 0.53 to 0.06), indicating moderate agreement.

3.5 Preference heterogeneity

The average utility values for the EQ-5D-5L health states ranged from 1 to −0.37. The variability of utility values increased with severity: the mean and standard deviation (SD) of states ‘22222’, ‘33333’, ‘44444’, and ‘55555’ were 0.73 (0.22), 0.40 (0.38), −0.04 (0.60), and −0.37 (0.83), respectively. (N.B.: by definition, ‘11111’ has a value of 1).

Figure 2 illustrates the substantial variation in participants' health state preferences. It shows the average utility values across all participants, that is, the social value set, for a subset of 100 health states, ranked from the best to the worst (according to the social preference). The thin lines represent the 874 individual PUFs. The colour of the line indicates the EUD from the average social value set.

Details are in the caption following the image
FIGURE 2
Open in figure viewerPowerPoint

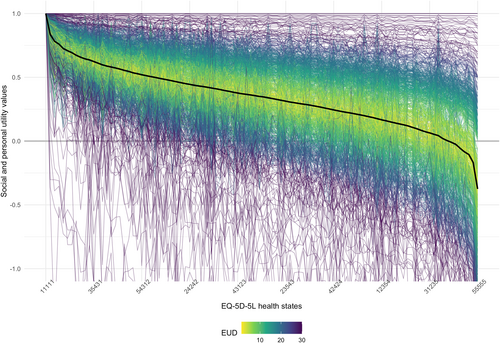
Simplified illustration of the aggregate group preference (thick black line) and the PUFs of all 874 participants. Shown are the utility values for a sample of 100 health states, ranked from the best on the left to the worst on the right (according to the aggregate group preference). The colours of the individual PUF lines indicate their euclidean distance from the average preference. Values below −1 are not shown.

We computed the EUD between the PUFs of all participants, which yielded a 874 × 874 distance matrix with 381,501 unique pairwise comparisons. The mean (SD) and median (IQR) EUD was 23.36 (23.02) and 17.95 (9.72; 29.37). The highest and lowest observed EUD were 259.93 and 0.

3.6 PERMANOVA

Table 3 provides the results of the PERMANOVA. Shown are the within-group sum-of-squares (SSW) for each group individually and for all groups combined, and the corresponding R2, pseudo F, and p values. The between groups sum-of-squares (SSB) can be computed by subtracting the SSW from the SST.

TABLE 3. Results of PERMANOVA – testing for differences in EQ-5D-5L health state preferences between groups characteristics.
Group variable SSW Df R2 F p
Sex 473 2 0.1% 0.44 0.630
Age 12180 6 2.6% 3.85 0.008*
Having children 7877 2 1.7% 7.43 0.008*
Education 4142 6 0.9% 1.29 0.238
Income 4160 5 0.9% 1.55 0.166
Importance of religion/spirituality 5708 4 1.2% 2.67 0.034*
Religious/spiritual practice 5698 6 1.2% 1.78 0.098
Experience w/health problems
Health care professional 410 1 0.1% 0.76 0.373
Carer 188 1 0.0% 0.35 0.569
Family member 146 1 0.0% 0.27 0.633
Past own experience 179 1 0.0% 0.33 0.582
Present own experience 1977 1 0.4% 3.69 0.050
No experience 180 1 0.0% 0.33 0.586
EQ VAS (quintiles) 5699 4 1.2% 2.67 0.027*
All groups together 36794 41 7.8% 1.73 0.018*
Total (SST) 469540 873
  • Abbreviations: df, degrees of freedom; F, pseudo F statistics; SST, total sum-of-squares; SSW, within-group sum-of-squares.
  • p values based on 10,000 permutations; * = p < 0.05.

Significant differences between groups were observed for four group characteristics: age, having children, importance of religion/spirituality, and own EQ VAS quintiles. In addition, the effect of currently experiencing severe health problems (‘present own experience’) was borderline significant (p = 0.0504). However, the proportions of the variance that were explained by these group characteristics individually were rather small: R2 values ranged between 2.6% (for age) and 1.2% (for importance of religion/spirituality). The effects of group characteristics that reflected experience with health problems (e.g., being a healthcare professional, carer) were not statistically significant. The model that included all group characteristics explained 8.5% of the differences between participants' PUFs.

To give some intuition for kind of differences that existed between groups, the (sub)group-specific value sets for different age groups are shown in Figure 3 as an example. The colours of the plotted group-level (thick lines) and personal utility functions (thin lines) indicate group membership. For simplicity, the ‘prefer not to say’ group is not shown.

Details are in the caption following the image
FIGURE 3
Open in figure viewerPowerPoint

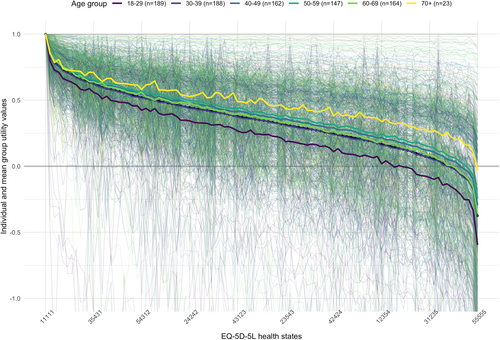
Age-group specific EQ-5D-5L health state preferences. Shown are the group level value sets (thick lines) and the underlying PUFs (thin lines), as well as the social value set (thick black line). Values below −1 and the ‘prefer not to say’ group are not shown.

The age group specific value sets differ from each other in two ways. Firstly, there appears to be some differences in scale. The curve for the youngest group (age 18–29) is the lowest. The curve then seem to move upwards with increased age, and the curve for the oldest age group (70+) is the highest. This suggests that the older the participants are, the higher they set their anchor point against dead. Secondly, the group-specific curves are not strictly decreasing, that is, they move up and down. This indicates differences in the relative importance of health state attributes, that is, groups assign different weights to the five EQ-5D-5L dimensions and/or differ in their level ratings. As a result, the rank order of the health states differs, and the graph fluctuates when compared to the overall social rank order. Due to the simplified visualisation of EQ-5D-5L utility functions (we only show 100 of the 3125 utility scores) this effect may appear smaller than it actually is.

4 DISCUSSION

This study is the first application of the newly developed OPUF approach for eliciting health state preferences in a large sample of the UK population. We constructed EQ-5D-5L value sets on the societal-, group-, and individual person level, to explore the heterogeneity of health state preferences in an unprecedented level of detail.

We found that health state preferences systematically differed between groups. Significant effects were observed in the PERMANOVA for age, having children, importance of religion/spirituality, and the EQ VAS quintile. However, the variability of preferences within groups was substantial, and individual group characteristics explained only small proportions of the EUD between PUFs. For other demographic factors (sex, education, income), we observed no systematic differences between groups. Contrary to our expectations, participants' experience with severe health problems (captured by 6 non mutually exclusive categories) were also not associated with the differences in PUFs. It should be noted though, that the participants in our sample were quite ‘healthy’ – a large majority reported no or only slight problems in any of the EQ-5D dimensions.

When all characteristics were taken into account together, group membership accounted for just 8% of the variance. This result should not be considered surprising. The formation of health preferences is a complex task, which is likely to be influenced by various emotional, cognitive, and social factors (Russo et al., 2019). The results illustrate that aggregate group-level value sets usually say little about the preferences of any given individual – in our study, preferences differed greatly between individuals within all the groups that we considered.

The ability to investigate both, aggregate social value sets, as well as the heterogeneity of preferences between subgroups and between individuals, may be particularly useful for studying diverse populations. For example, an OPUF valuation study for the EQ-5D-5L is currently ongoing in South Africa, where special attention will be given to the heterogeneity of preferences between the different population subgroups, defined by socio-economic status and race. Furthermore, decision makers in any country may well want to take into account the preferences of a specific specific population that will be affected by given decision (e.g., women in the case of a new treatment for breast cancer, or elderly people in the case of a new drug for dementia).

Another advantage of the OPUF method is that, like DCE, it can be administered as a stand-alone online survey, thereby avoiding the cost and complexity of TTO. Moreover, DCE and TTO require respondents to evaluate all dimensions (with or without a time dimension) simultaneously, while OPUF, as a compositional preference elicitation method, allows respondents to consider each dimension and level individually. For the EQ-5D-5L, this may not be a major advantage, since the number of dimensions and levels is relatively small, but for longer, more complex descriptive systems, like the EORTC QLC10 (King et al., 2016) or the EQ-HWB (Brazier et al., 2022), OPUF may significantly reduce the cognitive burden and prevent respondents from using heuristics. The fact that the OPUF survey can also be completed relatively quickly (the median completion time in our study was 8 minutes), further enhances its potential utility.

The comparison between constructed PUFs and participants' DCE choices we found a moderate agreement between the two methods. However, the observed 78% consistency between the constructed PUFs and participants' DCE choices seems comparable to the internal consistency within DCE studies: In an analysis of 16 DCE data sets, Johnson et al. (2019) found that, on average, only 70% of respondents pass stability tests (i.e., repeating a choice task to check whether the respondent chooses the same alternative).

Our study has some limitations that should be considered when interpreting the findings.

Firstly, the participants that were included in the analysis were younger and more highly educated than the general UK population. We also did not attempt to apply quality control criteria (e.g., remove participants with very fast completion times, test for response biases), but had to exclude a significant proportion of respondents, whose data could not be used to construct PUFs, because they skipped one or more valuation tasks. The reported mean EQ-5D-5L model coefficients do not yield a representative social value set for the UK. Further refinement of the technical implementation of the online survey will also prevent people from skipping essential tasks, thereby reducing the number of participants who have to be excluded.

Secondly, preference heterogeneity can be investigated in many different ways. Designing this study thus required making several, somewhat contingent methodological choices. Instead of computing the EUD between health state utility vectors, we could have assessed the differences in participants' model coefficients, or we could have computed a different distance measure – the Kendall correlation distance, for example, could be used to compare preference orderings (i.e., ordinal instead of cardinal preferences). Results may not be robust to these kinds of methodological choices.

Thirdly, we explored the variability of EQ-5D-5L health state preferences in a general sense. This means, we neither specified any hypotheses about the type or the direction of differences, nor did we test differences between subgroups. Even though the OPUF approach would have allowed us to study the health state preferences of small subgroups, in the absence of predefined hypotheses about subgroup differences, it did also not seem useful to consider the (up to 240) interaction effects between groups. For investigating more specific research questions, such as, ‘do older people with strong religious beliefs people assign higher utility values to health states than the general public?’, PERMANOVA may not be the most appropriate statistical approach.

Finally, a key consideration for the interpretation of our findings is the validity of the OPUF approach. It is a new method, based on a different paradigm (compositional approach) than other, established preference elicitation methods, such as TTO, DCE, or SG (decompositional). OPUF might introduce certain framing effects, influencing participants' preference formation, or other biases, which need to be further examined. Future studies should therefore compare OPUF to other, traditional preference elicitation methods.

It would also interesting to contrast OPUF with PAPRIKA, a patented preference elicitation method, previously used to create an EQ-5D-5L value set for New Zealand (Hernández-Ledesma et al., 2017; Sullivan et al., 2020). Despite being a decompositional method, involving pairwise ranking of partial health states, PAPRIKA supposedly allows constructing preference functions on the group as well as the individual level. However, the method is built on a number of assumptions, which deserve further examination, including non-positive anchor points (the utility of the worst state is assumed to be equal or lower than zero), the interpolation of intermediate levels, and the approximation of cardinal utility values from an ordinal scale, to name just a few. More research is needed to better understand how the OPUF approach compares to this and other methods, and, more generally, what the advantages and disadvantages of different preference elicitation methods in different settings are.

The immediate next steps in developing the OPUF approach will be to further test and validate the method in different settings. To this end, a range of studies have recently been conducted or are currently ongoing, including valuation studies for the EQ-5D-5L in South Africa, Hungary, and Germany; the EQ-5D-Y-3L in the UK; and the EQ-HWB-S in the UK and Germany (the latter will also include a test-retest sub-study). Studies involve general population as well as patient samples, and a qualitative study, to better understand the cognitive processes behind the OPUF approach, is also currently underway. These studies will help to further explore the potential and limitations of the OPUF approach. Another interesting direction of research would be to experiment with OPUF as a patient decision aid: given that OPUF can elicit health preferences on the individual level, it might be possible to use it to support the decision-making process in clinical settings, for example, by helping patient to form robust preferences for treatments, or directly facilitating the comparison of different treatment options.

5 CONCLUSION

The OPUF approach provides a flexible, conceptually attractive, alternative approach for eliciting health state preferences. The ability to construct utility functions on the individual person level opens up new and, we think, exciting avenues for research. As demonstrated in this study, the OPUF approach makes it possible to investigate the heterogeneity of health states preferences between subgroups as well as individuals in an unprecedented level of detail. It may also enable researchers to derive value sets for small groups of participants (e.g., patients with rare diseases), for which this would otherwise be practically infeasible. Even though the OPUF approach has, thus far, only been implemented for the EQ-5D-5L, in principle, it could be applied to any descriptive system or patient-reported outcome measure.

ACKNOWLEDGMENTS

We are very grateful to Siobhan Daley, Jack Dowie, Barry Dewitt, Irene Ebyarimpa, Job van Exel, Anthony Hatswell, Paul Kind, Johanna Kokot, Simon McNamara, Clara Mukuria, Monica Oliveira, Krystallia Pantiri, Donna Rowan, Erik Schokkaert, Koonal Shah, Robert Smith, Praveen Thokala, Ally Tolhurst, David Tordrup, Evangelos Zormpas, and the participants of the 2022 lolaHESG and the 2022 Summer HESG meeting for helpful comments, discussions of the ideas expressed in this paper, and/or for providing feedback on earlier versions of the EQ-5D-5L OPUF survey. We would also like to thank all participants who took part in this study. The usual disclaimer applies. This work was supported by the Wellcome Trust DTC in Public Health Economics and Decision Science (108903/Z/19/Z) and the University of Sheffield. For the purpose of open access, the author has applied a CC BY public copyright licence to any Author Accepted Manuscript version arising from this submission.

    CONFLICT OF INTEREST STATEMENT

    Ben van Hout, John Brazier, and Nancy Devlin are members of, and all authors have received research funding from the EuroQol Group.

    ETHICS STATEMENT

    The study was approved by the Research Ethics Committee of the School of Health and Related Research at the University of Sheffield (ID: 030724).

    DATA AVAILABILITY STATEMENT

    The R shiny source code for the OPUF survey tool is openly available at: https://github.com/bitowaqr/opuf_demo, and all data and an annotated version of the R source code used for this study are available at: https://github.com/bitowaqr/opuf_uk upon request.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.