Reproducibility of EEG-MEG fusion source analysis of interictal spikes: Relevance in presurgical evaluation of epilepsy
Funding information: Savoy Foundation; BioMedical Engineering Excellence Award; Natural Sciences and Engineering Research Council of Canada (NSERC); Canadian Institutes of Health Research (CIHR), Grant/Award Numbers: MOP-133619, MOP-93614; Centres of Excellence for Commercialization of Research (CECR); American Epilepsy Society Award; FRQS (The Fonds de recherche du Québec – Santé); Richard and Edith Strauss Canada Foundation
Abstract
Fusion of electroencephalography (EEG) and magnetoencephalography (MEG) data using maximum entropy on the mean method (MEM-fusion) takes advantage of the complementarities between EEG and MEG to improve localization accuracy. Simulation studies demonstrated MEM-fusion to be robust especially in noisy conditions such as single spike source localizations (SSSL). Our objective was to assess the reliability of SSSL using MEM-fusion on clinical data. We proposed to cluster SSSL results to find the most reliable and consistent source map from the reconstructed sources, the so-called consensus map. Thirty-four types of interictal epileptic discharges (IEDs) were analyzed from 26 patients with well-defined epileptogenic focus. SSSLs were performed on EEG, MEG, and fusion data and consensus maps were estimated using hierarchical clustering. Qualitative (spike-to-spike reproducibility rate, SSR) and quantitative (localization error and spatial dispersion) assessments were performed using the epileptogenic focus as clinical reference. Fusion SSSL provided significantly better results than EEG or MEG alone. Fusion found at least one cluster concordant with the clinical reference in all cases. This concordant cluster was always the one involving the highest number of spikes. Fusion yielded highest reproducibility (SSR EEG = 55%, MEG = 71%, fusion = 90%) and lowest localization error. Also, using only few channels from either modality (21EEG + 272MEG or 54EEG + 25MEG) was sufficient to reach accurate fusion. MEM-fusion with consensus map approach provides an objective way of finding the most reliable and concordant generators of IEDs. We, therefore, suggest the pertinence of SSSL using MEM-fusion as a valuable clinical tool for presurgical evaluation of epilepsy.
1 INTRODUCTION
Epilepsy is a neurological disorder caused by recurrent seizures and it affects ∼50 million people worldwide (WHO | Epilepsy, 2017). Epilepsy surgery offers the possibility of a reduction or elimination of the seizures to drug resistant patients. Candidates for epilepsy surgery undergo an extensive presurgical evaluation, which aims at localizing the brain areas where the seizures are generated (epileptogenic focus) and to determine whether surgery is feasible. Interictal epileptic discharges (IEDs) are spontaneous abnormal neuronal discharges occurring in between the seizures without any clinical manifestations. Their generators usually overlap with the region involved in the seizure onset (Hauf et al., 2012). The localization of the IEDs generator, called irritative zone, is therefore essential during the investigation of patients with intractable epilepsy (Bautista, Cobbs, Spencer, & Spencer, 1999; Hufnagel, Dümpelmann, Zentner, Schijns, & Elger, 2000; Ryvlin, Cross, & Rheims, 2014).
Electroencephalography (EEG) and magnetoencephalography (MEG) are two noninvasive electrophysiological techniques able to track IEDs at a high temporal resolution. They possess specific complementary properties, allowing their combination to be very informative in the assessment of the generators of IEDs. Simultaneously recorded EEG and MEG show that MEG is overall more sensitive to spikes but some spikes could still be detected in EEG and not in MEG (Hillebrand & Barnes, 2002; Iwasaki et al., 2005; Lin et al., 2003; Ossenblok, de Munck, Colon, Drolsbach, & Boon, 2007; Ramantani et al., 2006; Scheler et al., 2007; Yoshinaga, 2002). These differences are largely determined by EEG versus MEG sensitivity to the orientation of the anatomical sources (Haueisen, Funke, Güllmar, & Eichardt, 2012). MEG is selectively sensitive to sources that are tangential to the skull surface (fissural or sulcal walls) (Hämäläinen, Hari, Ilmoniemi, Knuutila, & Lounasmaa, 1993), whereas EEG is sensitive to both tangential and radial sources (crest of the cortical gyrus). However, EEG spikes may also be obscured by the radially oriented background ongoing “brain noise” generated in deeper regions of the brain (Ahlfors, Han, Belliveau, & Hämäläinen, 2010). Therefore, MEG and EEG signals also reflect different anatomical aspects of the activated sources because of their distinct sensitivities. As a result, epileptic spike detection can be significantly improved by analyzing simultaneously recorded EEG and MEG data; thus taking advantage of the complementarity of the two techniques.
To be detectable from scalp EEG or MEG recordings, the generators of IEDs should be synchronized over a spatially extended region of several square centimeters, thus resulting in a signal of sufficient amplitude to be visually distinguishable from the ongoing background activity (Cooper, Winter, Crow, & Walter, 1965; Ebersole, 1997; Merlet & Gotman, 1999; Mikuni et al., 1997; Oishi et al., 2002; Ramantani et al., 2014; Tao, Baldwin, Hawes-Ebersole, & Ebersole, 2007; von Ellenrieder, Beltrachini, Muravchik, & Gotman, 2014). EEG and MEG source localization techniques are used to localize the generators of epileptic discharges, but the main challenge lies not only in localizing the generators but also in accurately recovering their spatial extension. Therefore, several methods have been designed for localizing spatially extended generators (Chang, Nummenmaa, Hsieh, & Lin, 2010; Cheyne et al., 2010; Chowdhury, Lina, Kobayashi, & Grova, 2013; Chowdhury et al., 2015, 2016; Grova et al., 2016; Huiskamp, Agirre-Arrizubieta, & Leijten, 2010; Jung et al., 2013; Sohrabpour, Lu, Worrell, & He, 2016; Zhu, Zhang, Dickens, King, & Ding, 2013), and source localization with the coherent maximum entropy on the mean (cMEM) method is one such method that has been extensively studied on simulated and clinical data, and provided reliable and accurate localization of the sources of EEG and MEG discharges together with their spatial extent (Chowdhury et al., 2013, 2015; Grova et al., 2006, 2016; Heers et al., 2016; Pellegrino et al., 2017). In fact, recently we have compared cMEM with the standard dipole fitting approach on a large cohort of epilepsy patients and showed the reliability of cMEM on MEG source localization of clinical data (Pellegrino et al., 2017).
Spatial resolution of EEG and MEG influences the localization accuracy of source localization. MEG provides higher spatial resolution than EEG due to mainly two reasons. First, EEG scalp potentials are highly attenuated and smeared by the very low conductivity of the skull; whereas MEG is less distorted by the resistive properties of the skull. This leads to higher sensitivity of EEG to errors in skull modeling while MEG forward problem is more robust (Hämäläinen & Sarvas, 1989; Mosher, Leahy, & Lewis, 1999). Second, the number of MEG sensors (whole head coverage) used in relative to EEG (10–20 or 10-10 system) is typically greater (Klamer et al., 2015; Ossenblok et al., 2007). However, it has been demonstrated that improvement in EEG localization accuracy can be attained when using high-density electrodes and realistic geometry head models (Birot et al., 2014; Chowdhury et al., 2016; Hedrich, Pellegrino, Kobayashi, Lina, & Grova, 2017; Klamer et al., 2015; Lantz & Grave de Peralta, 2003; Liu, Dale, & Belliveau, 2002; Ryynanen, Hyttinen, & Malmivuo, 2006; Song et al., 2015; Wang et al., 2011). It has been shown that simultaneously acquired EEG and MEG data are super additive, that is, when combined they provide more information relevant to source localization than the sum of monomodal information (Pflieger, Simpson, Ahlfors, & Ilmoniemi, 2000). With the aim to better recover the location and the spatial extent of the generators of IEDs, we previously introduced EEG–MEG fusion source localization approach within the framework of cMEM algorithm (hereafter denoted as MEM-fusion) (Chowdhury et al., 2015). Based on realistic simulated data, we showed that MEM-fusion yields higher localization accuracy (more accurate, robust and sensitive to the spatial extent) than monomodal source localizations. In this study, we further evaluate the relevance and reproducibility of MEM-fusion on clinical data, proposing a new pipeline to improve the entire process of the source localization of interictal spikes, from single spike localization, classification up to the identification of the most reliable source imaging map.
The first and one of the most crucial steps in source analysis is the spike detection. It is a common practice to visually review EEG/MEG data and to classify and group spikes based on their morphology, topography, and signal-to-noise ratio (SNR). Reproducible transient spikes with similar spatio-temporal patterns are usually averaged to improve the SNR before applying any source localization method (Bast et al., 2004; Hara et al., 2007; Tanaka et al., 2010; Wennberg & Cheyne, 2014). Some authors have suggested to perform this task automatically by adopting automatic cluster analysis (at sensor level) to align and classify the spikes before source localization (Ossenblok et al., 2007; Van 't Ent et al., 2003). However, (Ossenblok et al., 2007) reported that this strategy often fails due to either a large variability between single spikes within one cluster or due to strong background activity leading to low SNR cluster averages. Moreover, whatever is the process chosen to classify spikes, averaging leads to some signal cancellation, which is more likely to filter out source activities that vary slightly over each individual spike (Ahlfors et al., 2009). To this end, (Aydin et al., 2015) suggested to combine bootstrap techniques and subaveraging to increase SNR while preserving some interspike variability. In this study, we propose to address this issue using a method of single spike source localization (SSSL) with subsequent clustering, to maintain a balance between SNR and inherent spike variability.
Therefore, we hypothesized that SSSL of combined EEG and MEG data using MEM-fusion method can take full benefit of the complementarities between the two modalities to characterize the underlying generators of IEDs. Following SSSL, we proposed a new method based on spatial correlation to estimate a consensus map summarizing the most reliable and consistent source maps among the reconstructed single spike sources. The consensus map was used to assess spike-to-spike reproducibility of SSSL results.
2 MATERIALS AND METHODS
2.1 Patient selection
This study was approved by the Montreal Neurological Institute (MNI) Research Ethics Board and all procedures were conducted in compliance with the Code of Ethics of the World Medical Association (1964 Helsinki declaration and its later amendments). All patients signed a written informed consent prior to participation in the EEG-MEG acquisition. Among the patients who underwent a simultaneous EEG-MEG recording for presurgical evaluation at the MNI, we retrospectively selected those patients fulfilling the following inclusion and exclusion criteria. Inclusion criteria: (a) focal neocortical epilepsy; (b) available ground truth information such as iEEG findings, well-defined epileptogenic lesion, and resection area from epilepsy surgery to define the epileptogenic focus; (c) good-quality anatomical MRI to obtain an accurate segmentation of head surfaces, which is required for realistic individual head modeling; and (d) sufficient number of spikes (at least 10 spikes). Exclusion criteria: (a) multifocal or widespread epileptic focus; (b) deep generators; and (c) large magnetization artefacts.
Acquisitions were done at the Psychology Department of the University of Montreal from September 2006 until July 2012 and later at Montreal Neurological Institute and Hospital. We selected 26 patients, from whom 34 studies consisting of different types of markers involving spikes, spike and wave discharges (spike-wave), or sharp waves were marked.
2.2 MEG–EEG data acquisition and preprocessing
Simultaneous EEG–MEG recordings were performed using a CTF MEG system (MISL, Vancouver, Canada) with 275 axial gradiometers and 54 EEG electrodes arranged on a cap according to the 10–20 system, plus additional electrodes according to the 10-10 system (F1, FPZ, F2, AF7, AF3, AFZ, AF4, AF8, FT9, FC5, FC3, FC1, FCZ, FC2, FC4, FC6, FT10, C1, C2, CP5, CP3, CP1, CPZ, CP2, CP4, CP6, P9, P1, P2, P10, PO7, PO3, POZ, PO4, PO8—Easy-cap, Herrsching, Germany). Note that in the CTF MEG system, most of the recordings were done using 272 MEG sensors since 3 channels were bad. Additional electrodes were used to record electrocardiogram and electro-oculograms. EEG electrode positions and the head shape were digitized using a Polhemus 3D localizer (Colchester, NH). The CTF system is equipped with reference sensors that were used to calculate synthetic third-order gradients to reduce the influence of magnetic background interferences. During the acquisition, the head position of the subject was tracked using localization coils placed on three fiducial points (nasion, left and right periauricular points). Sampling rates for EEG/MEG acquisitions were 1200 or 2400 Hz. To minimize head movements, all recordings were done with subjects lying down in a supine position. Recording at rest lasted for about 1 hr, divided into 10 runs of 6 min each. Brainstorm software (Tadel, Baillet, Mosher, Pantazis, & Leahy, 2011) was used to preprocess the EEG/MEG data offline. Data were downsampled to 600 Hz, synthetic third-order gradient noise correction was applied to MEG data, DC offset was removed, EEG was re-referenced to average montage, and 60 Hz notch filter (and its harmonics) was applied (Heers et al., 2016; Pellegrino et al., 2016, 2017). EEG and MEG data were visually inspected and inter-ictal spikes were marked using the DataEditor software (MISL, Vancouver, Canada) by two experienced neurophysiologists (GP and EK). The spikes were marked at their peak. EEG/MEG spikes were further filtered at 0.3–70 Hz bandpass filter (butterworth, fourth order) prior to source localization.
2.3 MRI data acquisition, analysis, and head modeling
High-resolution anatomical 3T MRI (Siemens Tim Trio 3T scanner) were acquired at the Brain Imaging Center of the MNI, using a T1W MPRAGE sequence (1 mm isotropic 3D images; 192 sagittal slices; 256 × 256 matrix; TE (echo time), 52.98 ms; TR (repetition time), 52.3 s). The MRI was processed using BrainVISA-4.2.1 software,1 allowing the segmentation of the surfaces of the skin and the gray–white matter interface which was then used as the source space for source imaging (Mangin, Frouin, Bloch, Régis, & López-Krahe, 1995). The MRI, the skin surface, and the cortical mesh tessellated from the gray–white matter interface were imported to the Brainstorm software for subsequent processing. MRI–MEG co-registration was performed by surface fitting between the skin surface derived from the MRI and the head shape points digitized using the Polhemus system at the time of the EEG–MEG acquisition. Individual three-layer boundary element method (BEM) surfaces (inner skull, outer skull, and skin) were constructed. The EEG and MEG forward models were computed using the OpenMEEG BEM (Gramfort, Papadopoulo, Olivi, & Clerc, 2011; Kybic, Clerc, Faugeras, Keriven, & Papadopoulo, 2006) implementation in Brainstorm software, using a three-layer BEM model consisting of the inner skull, outer skull, and the scalp surfaces, with conductivity values of 0.33, 0.0165, and 0.33 S/m, respectively (Ferree, Eriksen, & Tucker, 2000; Gonçalves et al., 2003; Hoekema et al., 2003; Lai et al., 2005).
2.4 EEG–MEG distributed source localization method
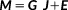 (1)
(1) τ signal matrix acquired on q EEG/MEG channels at τ time samples. E models the additive measurement noise (q
τ signal matrix acquired on q EEG/MEG channels at τ time samples. E models the additive measurement noise (q
 τ matrix). J is a r
τ matrix). J is a r
 τ unknown matrix of the current density of the r dipolar sources along the tessellated cortical surface. G indicates the q
τ unknown matrix of the current density of the r dipolar sources along the tessellated cortical surface. G indicates the q
 r lead field matrix obtained by solving the forward problem, by estimating the contribution of each dipolar source on the sensors. The objective of the inverse solution is to estimate J from the measured data M and the estimated lead field matrix G.
r lead field matrix obtained by solving the forward problem, by estimating the contribution of each dipolar source on the sensors. The objective of the inverse solution is to estimate J from the measured data M and the estimated lead field matrix G.2.4.1 cMEM inverse solution
Every source localization approach consists in solving an ill-posed inverse problem (Baillet, Mosher, & Leahy, 2001). Therefore, some a priori knowledge should be incorporated within a regularization framework to estimate a unique solution. In the MEM framework, we consider the amplitude of the sources J to be estimated as a multivariate random variable j of dimension r, with a probability distribution
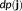 . To regularize the inverse problem, the MEM framework incorporates prior information on j in the form of a reference distribution
. To regularize the inverse problem, the MEM framework incorporates prior information on j in the form of a reference distribution
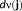 (Amblard, Lapalme, & Lina, 2004). This reference distribution is a realistic spatial model that assumes brain activity to be organized into K (K ≪ r) cortical parcels, where each parcel is associated to a hidden state variable controlling whether the parcel is active or not, when contributing to a specific activity. This type of spatial clustering of the cortical surface into K nonoverlapping parcel was obtained using a data driven parcellization (DDP) technique (Lapalme, Lina, & Mattout, 2006). DDP consisted in first applying a projection method, the multivariate source prelocalization (MSP) technique (Mattout, Pélégrini-Issac, Garnero, & Benali, 2005), estimating a probability-like coefficient (MSP score) between 0 and 1 for each dipolar source on the cortical mesh, characterizing the contribution of each source to the data, followed by region growing around local MSP maxima.
(Amblard, Lapalme, & Lina, 2004). This reference distribution is a realistic spatial model that assumes brain activity to be organized into K (K ≪ r) cortical parcels, where each parcel is associated to a hidden state variable controlling whether the parcel is active or not, when contributing to a specific activity. This type of spatial clustering of the cortical surface into K nonoverlapping parcel was obtained using a data driven parcellization (DDP) technique (Lapalme, Lina, & Mattout, 2006). DDP consisted in first applying a projection method, the multivariate source prelocalization (MSP) technique (Mattout, Pélégrini-Issac, Garnero, & Benali, 2005), estimating a probability-like coefficient (MSP score) between 0 and 1 for each dipolar source on the cortical mesh, characterizing the contribution of each source to the data, followed by region growing around local MSP maxima.
In the MEM reference model, a hidden variable is associated to each of these parcels in order to model the probability of the parcel to be active. Note that this probability was initialized using the median of the MSP scores of all the sources within the parcel. Based on the state of activation of the parcels, MEM inference is able to specifically switch these parcels on or off and to estimate a contrast of source intensities within the selected active parcels. The cMEM method, which is a variant within the MEM framework, further imposes a spatial smoothness constraint in the reference distribution
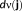 to model locally spatially smooth cortical parcels (Harrison, Penny, Ashburner, Trujillo-Barreto, & Friston, 2007). Then, the MEM principle aims at estimating the distribution
to model locally spatially smooth cortical parcels (Harrison, Penny, Ashburner, Trujillo-Barreto, & Friston, 2007). Then, the MEM principle aims at estimating the distribution
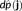 that maximizes the amount of information brought by the data, with respect to the reference distribution
that maximizes the amount of information brought by the data, with respect to the reference distribution
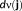 (Amblard et al., 2004; Jaynes, 1957). The resulting current density distribution
(Amblard et al., 2004; Jaynes, 1957). The resulting current density distribution
 is estimated using MEM regularization, iteratively for each time sample, as the first moment of the distribution
is estimated using MEM regularization, iteratively for each time sample, as the first moment of the distribution
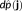 , (i.e.,
, (i.e.,
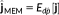 ). For more details on MEM framework and its implementation, please refer to Chowdhury et al. (2013).
). For more details on MEM framework and its implementation, please refer to Chowdhury et al. (2013).
In our previous studies, using simulations and clinical data, quantitative assessment of the cMEM methods demonstrated the benefits of whole cortex parcellization (DDP) in localizing sources at different spatial extents, demonstrating notably that the method is able to adapt the localization of generators of different spatial extents ranging from 3 to 30 cm2 (Chowdhury et al., 2013, 2015, 2016; Grova et al., 2016; Hedrich et al., 2017; Heers et al., 2014, 2016). Such a sensitivity to the source spatial extent was found to be relatively independent of the number and size of parcels considered in the reference model
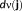 (Chowdhury et al., 2013), resulting in the ability of cMEM to also provide less spurious distant secondary generators than other source localization methods (Grova et al., 2016; Heers et al., 2016).
(Chowdhury et al., 2013), resulting in the ability of cMEM to also provide less spurious distant secondary generators than other source localization methods (Grova et al., 2016; Heers et al., 2016).
2.4.2 MEM-fusion
 (2)
(2)MEM-fusion consists of a three step fusion process where the first level of fusion involves the concatenation of the data and the lead field matrices of each modality. To integrate the two modalities efficiently, it was important to scale them to a common basis since they have different units. To do so, we applied SNR transformation of the data and the lead field, using the mean standard deviation of their respective background activity (
 ,
,
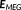 ) over all sensors of a modality as suggested in (Ding & Yuan, 2011; Fuchs et al., 1998), thus creating unit-less measures of EEG and MEG. The superscript “s” in Equation 2 represents the corresponding scaled data, lead field matrices, and noise.
) over all sensors of a modality as suggested in (Ding & Yuan, 2011; Fuchs et al., 1998), thus creating unit-less measures of EEG and MEG. The superscript “s” in Equation 2 represents the corresponding scaled data, lead field matrices, and noise.
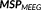 ) are used for the whole cortex parcellization and for the initialization of the probability of each parcel to be active. This was possible due to the inherent flexibility of MEM framework to incorporate several constraints regarding the source model through the definition of the reference model
) are used for the whole cortex parcellization and for the initialization of the probability of each parcel to be active. This was possible due to the inherent flexibility of MEM framework to incorporate several constraints regarding the source model through the definition of the reference model
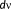 . This feature allows incorporating the complementary information provided by EEG and MEG data through the reference model. To do so, MSP scores were first computed from each modality separately to assign a coefficient of activation of the sources for each modality. These coefficients assess the contribution of each dipolar source to the corresponding EEG and MEG data. By using a logical OR operation on the EEG and MEG MSP scores, we consider the contribution of the dipolar sources to EEG or MEG or both data as follows:
. This feature allows incorporating the complementary information provided by EEG and MEG data through the reference model. To do so, MSP scores were first computed from each modality separately to assign a coefficient of activation of the sources for each modality. These coefficients assess the contribution of each dipolar source to the corresponding EEG and MEG data. By using a logical OR operation on the EEG and MEG MSP scores, we consider the contribution of the dipolar sources to EEG or MEG or both data as follows:
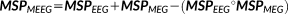 (3)
(3) denotes the Schur (Hadamard) product of the two matrices leading to element-wise multiplication of their elements. Here,
denotes the Schur (Hadamard) product of the two matrices leading to element-wise multiplication of their elements. Here,
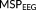 ,
,
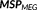 , and
, and
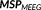 correspond to scores for all the “r” dipoles along the cortical surface and for “τ” time samples around the IED peak, leading to a (r × τ) matrix. A more detailed justification of the rationale leading to Equation 3 has been provided in Appendix A. These
correspond to scores for all the “r” dipoles along the cortical surface and for “τ” time samples around the IED peak, leading to a (r × τ) matrix. A more detailed justification of the rationale leading to Equation 3 has been provided in Appendix A. These
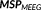 fusion scores then impacted both the estimation of the parcels through DDP and the initialization of their probability of being active, putting forward cortical parcels for which the median of the fusion MSP scores was high. This type of fusion during the definition of the reference model leads to an efficient way to integrate complementary information from the two modalities. This is a modeling particularity and originality of the MEM model when compared to other fusion approaches. Then starting from this fusion reference model, the MEM regularization technique was used to find the MEM solution for fusion data. It is also important to note that during the MEM regularization process, we estimated a more accurate noise covariance model taking into account the noise level of each individual channel in a diagonal matrix as opposed to the prewhitening models usually considered in MNE, sLORETA, and dSPM. For further details on the MEM-fusion implementation and evaluation, the reader is referred to Chowdhury et al. (2015).
fusion scores then impacted both the estimation of the parcels through DDP and the initialization of their probability of being active, putting forward cortical parcels for which the median of the fusion MSP scores was high. This type of fusion during the definition of the reference model leads to an efficient way to integrate complementary information from the two modalities. This is a modeling particularity and originality of the MEM model when compared to other fusion approaches. Then starting from this fusion reference model, the MEM regularization technique was used to find the MEM solution for fusion data. It is also important to note that during the MEM regularization process, we estimated a more accurate noise covariance model taking into account the noise level of each individual channel in a diagonal matrix as opposed to the prewhitening models usually considered in MNE, sLORETA, and dSPM. For further details on the MEM-fusion implementation and evaluation, the reader is referred to Chowdhury et al. (2015).2.5 EEG–MEG source analysis
Our standard clinical investigation involves averaging spikes with similar morphology and topography to improve the SNR of the EEG/MEG signals and then applying cMEM source localization method (Heers et al., 2014, 2016; Pellegrino et al., 2017). We first presented a comparison between standard EEG and MEG source localization of averaged spike for all 34 studies (range, 10–287 spikes per study) from the 26 selected patients. Source localization was performed on the averaged spike signals along a window of −100 to 100 ms around the peak of the spike, whereas a 2 s baseline window was selected for noise covariance estimation. In this study, source localization results only at the peak of the spikes were considered. Following this standard investigation, we performed a qualitative and individual evaluation of the possible reasons leading to the failure of EEG and MEG source localization of averaged spikes.
The same approach was then applied to individual spikes (SSSL) which were localized using either EEG, MEG, or fusion data.
2.6 Estimation of a consensus map assessing spike-to-spike reproducibility
SSSL using cMEM method is suitable for retrieving important information available at the individual spike level. The purpose of estimating a consensus map was then to assess the reproducibility of a reliable and consistent source map across the reconstructed single spike source maps. To do so, a similarity index between all SSSL source maps based on spatio-temporal correlation around the peak of the spike was first estimated. The source maps were then clustered using a hierarchical clustering approach (Ward's hierarchical clustering followed by thresholding of the dendrogram to obtain the optimal number of clusters, refer to Step 3 in Appendix B). All single spike source maps associated with the same cluster were averaged to obtain the most characteristic source map of each cluster, further denoted as cluster map. Finally, the most reproducible and reliable cluster map, further denoted a consensus map, was chosen as the one with highest number of spikes and with source concordant with the clinical ground truth information. Moreover, any other cluster map that also presented concordant source with the clinical ground truth information was also considered for the analysis of reproducibility. This procedure for the estimation of the consensus map is explained further in details in Appendix B.
As we included spikes, spike-wave, and sharp waves in our analysis, the temporal window considered for spatio-temporal correlation during the estimation of the consensus map subjectively varied, to recover similar spatio-temporal patterns of the discharges. This time window was selected as 50 ms around the peak of the spikes and 100 ms around the peak of the spike-wave and sharp waves.
2.7 Comparison of the consensus map approach on EEG, MEG, and fusion data
To evaluate SSSL results obtained from EEG alone, MEG alone, and EEG–MEG fusion, we considered both qualitative and quantitative evaluation against the available ground truth, denoted as the clinical reference. Definition of the clinical reference (CR) for the source localization results was based on the available clinical information for each patient. This information consisted of (in the order of priority, not all factors were available for every patient): resected region, iEEG ictal, and interictal findings, epileptic lesions such as focal cortical dysplasia (FCD) detected on MRI. Refer to Table 1 for details. Note that, whenever the resection did not lead to seizure freedom, information based on iEEG findings or lesion were considered, as resections could have been constrained by proximity to eloquent cortex to avoid deficits. Based on such information, two expert neurophysiologists (GP and EK) manually drew the CR on each patient's MRI-based cortical mesh. This CR was used for both qualitative and quantitative assessments.
| EEG averaged spike source localization | MEG averaged spike source localization | iEEG | Lesion | Surgery | Markers (patients) |
|---|---|---|---|---|---|
| N/A | Postcentral region | N/A | M1 (P1) (76 spikes) | ||
| N/A | Postcentral region | N/A | M2 (P1) (85 spikes) | ||
| IED: L Hc and L fronto-mesial; Ictal: L OF mesial and L mesial T; F > T | L F | L OF mesial encephalocele removed | M3 (P2) (11 spikes) | ||
| IED: L Hc and L fronto-mesial; Ictal: L OF mesial and L mesial T; F > T | L F | L OF mesial encephalocele removed | M4 (P2) (59 spikes) | ||
| IED: R lesion; Ictal: R lesion | R F parasagittal | Small cortical resection of the RF lobe near its upper convexity | M5 (P3) (23 spikes) | ||
| IED: Diffuse bil. F L>R; Ictal: Bil. F, max L SMA | Normal | L mesial F | M6 (P4) (127 spikes) | ||
| IED: L perilesion and lesion, bil. F; Ictal: Bil. F max lesion and perilesion | L ant. F, parasagittal | L F lesion | M7 (P5) (30 spikes) | ||
| N/A | R ant. | N/A | M8 (P6) (40 spikes) | ||
| IED: R T and post. T and precuneus; Ictal:R precuneus, R Superior Occ | Normal | R Occ lobe, extension of resection | M9 (P7) (86 spikes) | ||
| IED: L mesial T >> R. - Ictal: no focus identified | L Hippocampal malrotation | N/A | M10 (P8) (60 spikes) | ||
| IED: R OF, lat. and ant. Insula, R Am and Hc; Ictal: R OF and ant. Insula, also opercular region | R hemimegalencephaly | R OF | M11 (P9) (13 spikes) | ||
| IED: R OF, lat. and ant. Insula, R Am and Hc; Ictal: R OF and ant. Insula, also opercular region | R hemimegalencephaly | R OF | M12 (P9) (13 spikes) | ||
| IED: R OF, lat. and ant. Insula, R Am and Hc; Ictal: R OF and ant. Insula, also opercular region | R hemimegalencephaly | R OF | M13 (P9) (20 spikes) | ||
| IED: R OF, lat. and ant. Insula, R Am and Hc; Ictal: R OF and ant. Insula, also opercular region | R hemimegalencephaly | R OF | M14 (P9) (14 spikes) | ||
| IED: ROF, mid F convexity and ant. T neocortex, Ictal: R OF | R 0F | R OF resection | M15 (P10) (287 spikes) | ||
| IED: L. Post. Rolandic mid convexity; Ictal: L. Post. Sensory cortex | Normal | L sensory hand and face | M16 (P11) (18 spikes) | ||
| IED: L. Post. Rolandic mid convexity; Ictal: L. Post. Sensory cortex | Normal | L sensory hand and face | M17 (P11) (37 spikes) | ||
| IED: R Hc>SMA>mid cingulate gyrus>mesial OF; Ictal: R T, R SMA followed by rapid propagation | Normal | R frontomesial | M18 (P12) (12 spikes) | ||
| IED: R Hc > SMA > mid cingulate gyrus > mesial OF; Ictal: R T, R SMA followed by rapid propagation | Normal | R frontomesial | M19 (P12) (10 spikes) | ||
| IED: superficial contact SMAa, SMAm or SMAp, R CP; Ictal: R SMA overlapping with structural lesion | R F | R F lesion | M20 (P13) (12 spikes) | ||
| IED: Bil. F R > L; Ictal: Bil. F R > L, R F or bil. F widespread changes | R mesial and ant. F | N/A | M21 (P14) (19 spikes) | ||
| IED: R parasagittal central (deep contacts RSMAP, RCP); Ictal: R parasagittal central | Normal | N/A | M22 (P15) (10 spikes) | ||
| IED: mid portion R F convexity; Ictal: same contacts | R mid F convexity | R mid F | M23 (P16) (97 spikes) | ||
| IED: L neocortical and mesial T; Ictal: LT, neocortical and mesial | Cerebral herniation of the L OF region through orbital bone, left hippocampus malrotation | L amygdalohippocampectomy | M24 (P17) (40 spikes) | ||
| N/A | R F pole | R F pole | M25 (P18) (60 spikes) | ||
| IED: multifocal and widespread T, P ,neocortex, Hc and lingual gyrus; Ictal:diffuse changes and nonlocalizing | Normal | R post. neocortex, Inf. P | M26 (P19) (19 spikes) | ||
| IED: multifocal and widespread T, P ,neocortex, Hc and lingual gyrus; Ictal:diffuse changes and nonlocalizing | Normal | R post. neocortex, Inf. P | M27 (P19) (32 spikes) | ||
| IED: R mesial T lobe, hippocampus > amygdala, Ictal: likely R mesial T lobe | L OF | L F resection at the level of the lateral O gyrus | M28 (P20) (16 spikes) | ||
| N/A | R T hippocampal atrophy and gliosis. L middle cranial fossa meningoencephalocele. | R ant. T lobectomy | M29 (P21) (13 spikes) | ||
| IED: L FT(max. ant. Cingulate + T pole), L post. Hc+Am; Ictal: L ant. Cingulate and ant. T | L ant. Cingulate OF | R ant. T, R OF and and extension in the R OF | M30 (P22) (32 spikes) | ||
| IED: multifocal temporomesial bil. independent ( > R); Ictal: from the R and the L T structures | Bil. Hippocampal atrophy | N/A | M31 (P23) (24 spikes) | ||
| N/A | L opercular F | N/A | M32 (P24) (24 spikes) | ||
| N/A | L F cortex (deep precentral gyrus) | N/A | M33 (P25) (21 spikes) | ||
| IED: R OF; Ictal: R OF | R OF | R OF resection | M34 (P26) (26 spikes) |
- Note. For each of the 34 studies, the averaged spike source localization results using EEG and MEG data have been provided in the last two columns. Based on visual inspection, the results that were concordant with the clinical reference (CR) have been marked in blue color, the sublobar concordant results in orange, and the discordant results in gray color. L, left; R, right; T, temporal; F, frontal; P, parietal; Occ, occipital; O, orbital; ant., anterior; post., posterior; Inf., inferior; bil., bilateral; Hc, hippocampus; Am, amygdala; N/A, Not Available.
2.7.1 Qualitative assessment
- A cluster map was assessed as concordant with the CR whenever the vertex of the cluster map exhibiting the maximum source amplitude (source maximum) was inside the CR.
- A cluster map was assessed as sublobar concordant with the CR whenever the source maximum was within the sublobar region of the CR. We identified 10 sublobar regions per hemisphere based on anatomical atlas (Agirre-Arrizubieta, Huiskamp, Ferrier, van Huffelen, & Leijten, 2009; de Gooijer-van de Groep, Leijten, Ferrier, & Huiskamp, 2013; Heers et al., 2016; Pellegrino et al., 2016). The sublobar region classifications were based on the anatomical atlas proposed in (Agirre-Arrizubieta et al., 2009), which consisted of subdivisions of the different lobes, resulting in a total of 10 regions per hemisphere. The frontal lobe was divided into the frontal superior, medial, inferior, and fronto-orbital regions, the temporal lobe into the lateral and mesial regions. The central, occipital, and parietal lobes were not further subdivided (de Gooijer-van de Groep et al., 2013). Such a qualitative evaluation was made visually using anatomical landmarks as used in two of our previous studies (Heers et al., 2016; Pellegrino et al., 2016).
- A cluster map was assessed as discordant with the CR whenever the source maximum was outside the sublobar region.
2.7.2 Spike-to-spike reproducibility rate (SSR)
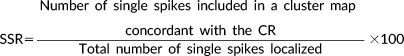 (6)
(6)2.7.3 Quantitative assessment
- Minimum distance (Dmin): minimum Euclidean distance expressed in mm between the dipolar source showing the global maximum of reconstructed source activity at the peak of the spike and the closest vertex belonging to the CR. This represents the localization error.
- Spatial dispersion (SD): This metric (Molins, Stufflebeam, Brown, & Hämäläinen, 2008) was used in our previous studies based on clinical and simulation data (Chowdhury et al., 2015; Grova et al., 2016; Heers et al., 2016; Pellegrino et al., 2016). It measures both the spatial spread of the estimated source distribution around the CR and the localization error between the estimated source distribution and CR. SD values close to zero means that the estimated source is inside the CR. A high value of SD means there are sources far away from the CR that are contributing to the estimated solution or the reconstructed source map is spatially spread around the CR.
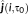 as the amplitude of the current density distribution estimated for a dipolar source i on the cortical surface at the main peak of the spike (
as the amplitude of the current density distribution estimated for a dipolar source i on the cortical surface at the main peak of the spike (
 ).
).
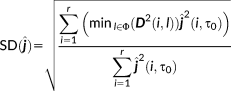 (7)
(7)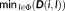 provides the minimum Euclidean distance between the source i anywhere in the cortical surface and the sources l belonging to the CR.
provides the minimum Euclidean distance between the source i anywhere in the cortical surface and the sources l belonging to the CR.
 denotes the set of indices of the dipoles in the CR and this minimum distance is zero when the source i belongs to
denotes the set of indices of the dipoles in the CR and this minimum distance is zero when the source i belongs to
 .
.2.7.4 Statistical analysis
-
Does fusion provide an overall improved performance when compared to EEG alone and MEG alone?
To test this, for each of the modality, we pooled together the metric (SD or Dmin) values obtained for all the clusters including concordant, sublobar concordant, and discordant clusters from the 34 studies.
-
Does the cluster involving the highest number of spikes exhibit the most concordant result with the CR?
To test this, for each modality, we pooled together the metric (SD or Dmin) values for only the cluster involving the highest number of spikes from the 34 studies.
2.8 Impact of the number of EEG electrodes in fusion
In our previous study based on realistic simulations, interestingly we showed that the addition of only 20 EEG electrodes to the high-density MEG sensors was sufficient to bring additional information missed by MEG in fusion (Chowdhury et al., 2015). To further validate these findings on clinical data, we assessed the impact of fusion source localization on the 34 markers when using either the whole 54 EEG electrodes (following the 10-10 system of electrode placement) and two downsampled montages involving 32 EEG electrodes and 21 EEG electrodes (following the standard 10–20 system of electrode placement) with the 272 MEG sensors. We also assessed one configuration involving the whole 54 EEG electrodes setup with only 25 MEG sensors. MEG subsampling was done by maintaining a full spatial coverage, using regularly placed sensors. For each study, only the single spikes involved in the consensus map estimated using the full fusion configuration (54 EEG + 272 MEG) were selected. These spikes were then averaged, and four fusion configurations were considered: (1) 54 EEG + 272 MEG, (2) 32 EEG + 272 MEG, (3) 21 EEG + 272 MEG, and (4) 54 EEG + 25 MEG. Source localization results of the averaged spike were obtained for each configuration and their concordance with CR was qualitatively evaluated.
3 RESULTS
3.1 EEG and MEG averaged spike localization—Standard approach
Table 1 summarizes the 34 different selected studies together with clinical details. For each study, results of our standard approach consisting in localizing EEG and MEG averaged spike are also reported. Based on visual assessment, we found 8/34 (23%) cases in MEG and 11/34 (32%) cases in EEG that were discordant with the CR and considered as a failure of the standard approach. There were 4/34 (12%) cases that were discordant with the CR in both EEG and MEG. Therefore, neither EEG nor MEG averaged spike localization brought clinically relevant information for 12% of the cases studied.
We first provide a qualitative report on the source localization results to understand the reasons for the failure of standard averaged spike localization on our dataset. We found out that one of the most common reason for the failure of standard source localization (markers M3, M4, M5, M29, M32, and M33 for EEG; M5, M10, and M32 for MEG) was due to the fact that EEG or MEG were not sensitive to the orientation and/or the location of the generators of spikes, especially for generators located in too deep structures for which recorded scalp signals represented mainly propagated activity. In addition, since no depth-weighting compensation is involved in cMEM source localization, sometimes the method found an alternative superficial source related to the underlying deep generator. The second common reason for failure was found to be due to noisy data, resulting in low SNR conditions even after spike averaging (markers M11, M18, and M24 for EEG; M4, M11, and M33 for MEG). Low SNR conditions were notably observed when involving noisy background data or high impedances of the EEG electrodes. Low SNR was also noticed when the patient was not well-placed inside the MEG helmet, thus some sensors were far from the region of interest. The SNR was measured as the standard deviation ratio between the signal around the peak and some background activity. M4, M11, M18, and M33 data exhibited SNR values <2. For M24, the impedance between many EEG electrodes and the scalp were very high resulting in noisy EEG signals. Next most common reasons for source localization failures were found to be due the complex nature of scalp topographies leading to spurious localizations (M28 and M33 for EEG; M9 for MEG). Finally, failure for EEG averaged spike source localization in M16 was probably due to spike-to-spike variability. All these possible reasons clearly suggest some limitations of the standard approach of EEG or MEG averaged spike source localization. Our objective was to overcome such limitations by combining SSSL and EEG–MEG fusion.
3.2 Application of the consensus map approach on EEG alone, MEG alone, and EEG–MEG fusion
Figure 1 illustrates an example of the application of consensus map approach on a patient (M23) for whom 97 spikes were marked on EEG and MEG data. The presumed CR has been marked in the right mid frontal region based on the surgical resection (postsurgical outcome was Engel 1), outlined in white color on the cortical surface. In this figure, for each modality, the dendrogram obtained from Ward's hierarchical clustering and the plot of the standardized cluster linkage as a function of the number of clusters (see Step 3 in Appendix B) are presented. The first break in this plot provided the threshold to consider for the dendrogram. For EEG, the first break in the plot was noticed at 2, indicating that there were two distinct clusters among the 97 SSSL results. From these two clusters, cluster 1 containing 26 spikes and cluster 2 containing 71 spikes were both sub-lobar concordant with the CR (Figure 1a). For MEG, the first break was noticed at 3 indicating three distinct clusters. Cluster 1 containing 21 spikes was discordant with the CR, presenting a distant source in the left fronto-mesial region. More spikes were actually included in cluster 2 (43 spikes) and cluster 3 (33 spikes), both concordant with the CR (Figure 1b). For fusion, we identified 3 distinct clusters. The cluster exhibiting the lowest number of spikes (cluster 2 with 15 spikes) presented sublobar concordance, whereas cluster 1 (39 spikes) and cluster 3 (43 spikes) involving higher number of spikes were both concordant with the CR (Figure 1c). Overall, the highest number of spikes presenting concordance with CR was found in fusion with a total of 82 spikes, whereas MEG provided concordance with CR for 76 spikes. This result suggests higher spike-to-spike reproducibility in fusion when compared to MEG or EEG alone.
Example of consensus map estimation. On a patient (M23) with the CR in mid frontal region, as outlined in white color on the cortical surface. A total of 97 spikes have been marked in both EEG and MEG data. Results on EEG, MEG, and fusion have been presented. Column 1 shows the dendrogram obtained from Ward's hierarchical clustering, x-axis (object number) and y-axis (cluster linkage value). Column 2 shows the plot of the standardized cluster linkage against the number of clusters, red arrow points toward the first break or elbow in the plot indicating the number of clusters; x-axis (number of clusters) and y-axis (cluster linkage value). In this plot, only the first 10 hierarchical levels are shown. The next columns represent the cluster maps displayed over the inflated cortical surface obtained through the Brainstorm software toolbox. (a) EEG consensus map approach presenting 2 clusters with Cluster 1 containing 26 spikes and Cluster 2 containing 71 spikes. Clusters 1 and 2 are sublobar concordant with the CR. (b) MEG consensus map approach presenting 3 clusters with Cluster 1 containing 21 spikes, Cluster 2 containing 43 spikes, and Cluster 3 containing 33 spikes. Cluster 1 is discordant with the CR and Clusters 2 and 3 are concordant with the CR. (c) Fusion consensus map approach presenting 3 clusters with Cluster 1 containing 39 spikes, Cluster 2 containing 15 spikes, and Cluster 3 containing 43 spikes. Clusters 1 and 3 are concordant with the CR. Cluster 2 is sublobar concordant with the CR. The consensus map was defined as the one with highest number of spikes and with source concordant with the clinical ground truth information [Color figure can be viewed at wileyonlinelibrary.com]
3.3 Comparison of averaged spike localization and consensus map approach on single spike localizations
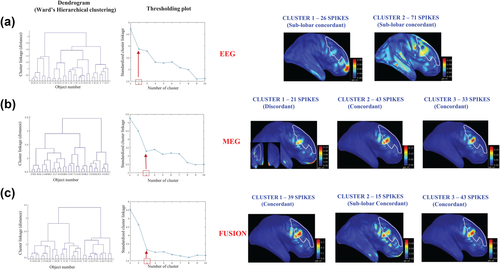
Figure 2 illustrates the results of averaged spike source localization and SSSL results using the consensus map approach on a patient (M8), for whom the CR was identified in the right anterior frontal region with the presence of a FCD lesion visible in the MRI. In total, 40 spikes were marked. EEG averaged spike localization was successful in localizing the CR (Figure 2a). However, MEG averaged spike localization found the source in the sublobar region, anterior to the lesion (Figure 2b). After applying the consensus map approach on EEG, MEG, and fusion, we were able to find at least one cluster in all three modalities that was fully concordant with the CR. In all three modalities, this concordant cluster was the one exhibiting the highest number of spikes (Figure 2c-e) and considered to be the consensus map in this case.
Comparison of averaged spike localization results with consensus map approach on the single spike localization results. Example on a patient (M8) with FCD in the right anterior region (CR), outlined in white color on the cortical surface. A total of 40 spikes have been marked on EEG and MEG data. (a) EEG source localization on average of 40 spikes, showing the averaged EEG signal with SNR = 2.4, the topography at the peak of the spike, and the source localization result which is concordant with the CR, presented on the inflated cortical surface. (b) MEG source localization on average of 40 spikes, showing the averaged MEG signal with SNR = 1.6, the topography at the peak of the spike, and the source localization result which is sublobar concordant with the CR, presented on the inflated cortical surface. (c) Consensus map approach applied on EEG single spike source localizations presenting 2 clusters. Cluster 1 containing 13 spikes that is discordant with the CR. Cluster 2 containing 27 spikes that is concordant with the CR. (d) Consensus map approach applied on MEG single spike source localizations presenting 2 clusters. Cluster 1 containing 12 spikes that is discordant with the CR. Cluster 2 containing 28 spikes that is concordant with CR. (e) Consensus map approach applied on fusion single spike source localizations presenting 2 clusters. Cluster 1 containing 12 spikes that is discordant with the CR. Cluster 2 containing 28 spikes that is concordant with the CR [Color figure can be viewed at wileyonlinelibrary.com]
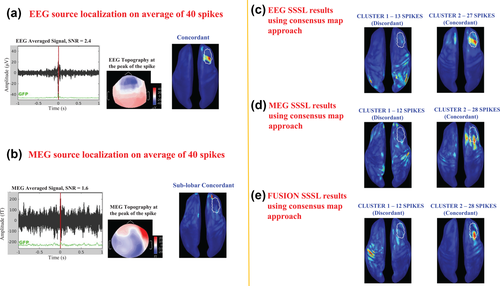
Figure 3 illustrates the results of averaged spike localization and SSSL results using the consensus map approach on a patient (M16) who underwent surgical resection of the posterior rolandic mid convexity region (CR, outlined in white color on the cortical surface in Figure 3). A total of 18 spikes were marked on EEG and MEG data. EEG averaged spike localization failed to localize the CR, while MEG averaged spike localization found the source in sublobar concordance with the CR. Here again, the consensus map approach was able to help find at least one cluster of spikes fully concordant with the CR, indicating the advantage of applying the consensus map approach on single spike localizations over averaged spike localizations. It is worth noting that the other clusters found for the three modalities were also sublobar concordant with the CR. The concordant cluster was the one that exhibited the highest number of spikes in EEG (cluster 1 with 11 spikes) (Figure 3c) and in fusion (cluster 2 with 12 spikes) (Figure 3e), whereas in MEG, only the smallest cluster involving 6 spikes was concordant with the CR (Figure 3d).
Comparison of averaged spike localization results with consensus map approach on the single spike localization results. Example on a patient (M16) with resection in the left posterior rolandic region (CR), outlined in white color on the cortical surface. A total of 18 spikes have been marked on EEG and MEG data. (a) EEG source localization on average of 18 spikes, showing the averaged EEG signal with SNR = 6.5, the topography at the peak of the spike, and the source localization result which is discordant with the CR, presented on the inflated cortical surface. (b) MEG source localization on average of 18 spikes, showing the averaged MEG signal with SNR = 2.9, the topography at the peak of the spike, and the source localization result which is sublobar concordant with CR, presented on the inflated cortical surface. (c) Consensus map approach applied on EEG single spike source localizations presenting 2 clusters. Cluster 1 containing 11 spikes that is concordant with the CR. Cluster 2 containing 7 spikes that is sublobar concordant with the CR. (d) Consensus map approach applied on MEG single spike source localizations presenting 2 clusters. Cluster 1 containing 6 spikes that is concordant with the CR. Cluster 2 containing 12 spikes that is sublobar concordant with the CR. (e) Consensus map approach applied on fusion single spike source localizations presenting 2 clusters. Cluster 1 containing 6 spikes that is sublobar concordant with the CR. Cluster 2 containing 12 spikes that is concordant with the CR [Color figure can be viewed at wileyonlinelibrary.com]
In summary, in all three examples illustrated in Figures 1-3, fusion identified a concordant cluster that was always the one exhibiting the highest number of spikes, thereby suggesting higher spike-to-spike reproducibility rate in fusion when compared to EEG alone and MEG alone.
3.4 Consensus map approach—Qualitative assessment
We performed SSSL on a total of 1435 spikes from the 34 studies. We categorized these 1435 spikes’ source maps into concordant, sublobar concordant, or discordant results with the CR. To do so, we proceed as follows: all spikes classified in a concordant cluster were categorized as concordant spikes, and similarly for all spikes classified in a sublobar concordant or discordant cluster were categorized as sublobar concordant or discordant spikes, respectively. Figure 4a illustrates a pie chart of the percentage of spikes that provided concordant, sublobar concordant, and discordant results with the CR when considering SSSLs of EEG alone, MEG alone, and fusion data. While EEG yielded the lowest percentage of spikes that provided concordant results with the CR (SSR = 55%), MEG outperformed EEG with a SSR = 71% of spikes exhibiting concordant results. On the other hand, fusion showed the highest spike-to-spike reproducibility and reliability with SSR = 90% of spikes providing concordant results with the CR. This was the case when considering all studies together. Interestingly, when studying the distribution of SSR values for each study (Figure 4b), we also noticed that overall fusion provided higher SSR when compared to EEG alone or MEG alone. Fusion provided 100% SSR in 18/34 markers, whereas 100% SSR was observed in 9/34 markers for MEG and 6/34 markers for EEG. On the other hand, 0% SSR (complete source localization failure) was observed for 8/34 cases in EEG and 6/34 cases in MEG, whereas for fusion the lowest SSR value was 42%. This suggests an overall high reliability of fusion SSSL results using the consensus map when compared to EEG or MEG alone. We noticed that the SSR of fusion was lower than either EEG or MEG in only 4/34 markers. Those were marker number 19 (EEG had higher SSR), 28 (both EEG and MEG had higher SSRs), 31 (EEG had higher SSR), and 32 (MEG had higher SSR). Note that the order of the markers was sorted in descending order based on SSR values, therefore, the marker numbers in Figure 4b do not match with the marker numbers reported in Table 1.
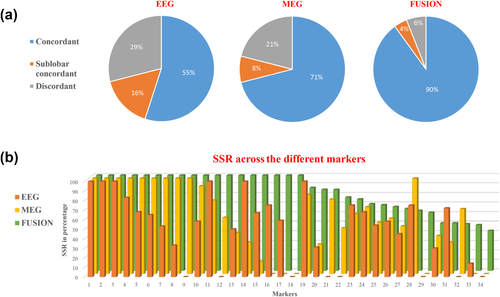
Qualitative assessment of consensus map approach. (a) Pie charts illustrating the comparison of location of source with respect to the CR in EEG, MEG, and fusion single spike localization. The values in the charts represent the percentage of spikes that provided concordant (in blue color), sublobar concordant (in orange color), and discordant (in gray color) results in each modality from the total number of 1435 spikes that were localized in the 34 studies. EEG presented 55% spike-to-spike reproducibility rate (SSR), MEG with 71% SSR, and fusion presented the highest SSR of 90%. (b) Chart comparing the SSR across the three modalities (EEG, MEG, and fusion) for each study. EEG in orange, MEG in yellow and fusion in white color: x-axis, markers; y-axis, SSR in percentage. For each study, fusion provided an overall higher SSR than EEG alone and MEG alone [Color figure can be viewed at wileyonlinelibrary.com]
With reference to Section 3.1, we also observed that by applying the consensus map approach on SSSL results, out of the 11 cases of averaged spike localization failure in EEG, 9 of them were correctly localized within the CR. The localization remained unsuccessful for 2 of them. Out of the 34, there were 3 additional cases (M10, M26, and M27) that failed to localize the CR after applying the consensus map approach in EEG. In MEG, out of the 8 cases of averaged spike localization failure, the consensus map approach improved the localization for 7 of them, resulting in either concordant or sub-lobar concordant results. Finally, for fusion, we noticed that the consensus map approach improved the localization in 100% of the cases, exhibiting at least one cluster fully concordant with the CR for each study. Note that in 33/34 cases the cluster involving the highest number of spikes was indeed the one concordant with the CR.
3.5 Consensus map approach—Quantitative assessment
3.5.1 Does fusion provide an overall improved performance when compared to EEG alone and MEG alone?
Figure 5a shows the boxplot representation of the localization errors, Dmin values, pooled together from all the clusters of the 34 studies in EEG alone, MEG alone, and fusion. We found an overall significant effect of the modality over Dmin values (Kruskal–Wallis H(2) = 10.6, p = 0.005). Post-hoc paired comparison showed that fusion provided significantly lower Dmin than EEG (p = 0.004), whereas the differences in Dmin between fusion and MEG (p = 0.054), and EEG and MEG (p = 0.6) were not statistically significant. Figure 5b shows the boxplot representation of the spatial dispersion metric, SD values, pooled together from all the clusters of the 34 studies in EEG alone, MEG alone and fusion. We found an overall significant effect of the modality over SD values (Kruskal–Wallis H(2) = 8.68, p = 0.013). Post-hoc paired comparison showed that fusion provided SD values significantly lower than EEG (p = 0.009) but not significantly different from MEG (p = 0.24). We found no statistically significant differences in SD between EEG and MEG (p = 0.3).
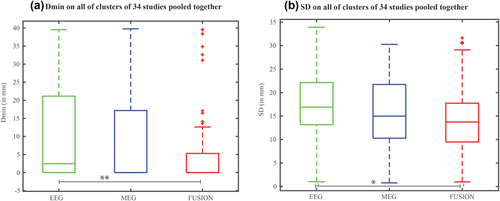
Quantitative assessment to compare the performances of monomodal SSSL with fusion SSSL using the quantitative metrics SD and Dmin. Boxplot representation of the (a) Dmin values and (b) SD values pooled together from all the clusters (including concordant, sublobar concordant and discordant clusters) of the 34 studies in EEG alone, MEG alone and fusion. ** represents statistically significant difference with p < 0.005; * represents statistically significant difference with p < 0.0167 (Bonferroni corrected) [Color figure can be viewed at wileyonlinelibrary.com]
3.5.2 Does the cluster involving the highest number of spikes exhibit the most concordant result with the CR?
When considering only the cluster that exhibited the highest number of spikes for each study, fusion results showed Dmin values of zero for all clusters involving the highest number of spikes (Figure 6a), except for two clusters: one cluster was sublobar concordant (within 3 mm distance) with the CR, and another cluster that was discordant with the CR. MEG also provided concordant results with the CR (Dmin = 0mm) for most of the clusters with the highest number of spikes. Only few cases (6/34 cases) provided either sublobar concordant or discordant results with the CR. For EEG, the cluster with the highest number of spikes did not exhibit concordant results with the CR in 14/34 cases (median Dmin = 0.6mm). When considering quantitative metrics selecting only the clusters with the highest number of spikes, we also found an overall significant effect of the three modalities on Dmin distribution (Kruskal–Wallis H(2) = 15.6, p < 0.001). Post-hoc paired comparison showed that fusion provided Dmin values significantly lower than EEG (p < 0.001), whereas no statistically significant differences were found between fusion and MEG (p = 0.364) or EEG and MEG (p = 0.03). When considering SD values from the clusters with the highest number of spikes (Figure 6b), we found no statistically significant effect of SD distribution on the three modalities (H(2) = 5.2, p = 0.07).
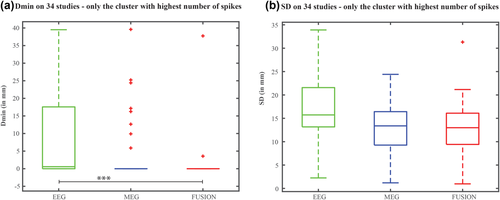
Quantitative assessment using the metrics Dmin and SD to find if the cluster with the highest number of spikes exhibited the concordant result with the CR. Boxplot representation of the (a) Dmin values and (b) SD values pooled together for only the cluster with highest number of spikes from each study in EEG alone, MEG alone, and fusion. *** represents statistically significant difference with p ≪ 0.001 [Color figure can be viewed at wileyonlinelibrary.com]
To summarize the qualitative and quantitative assessments, the radar chart in Figure 7 shows that MEG performed better than EEG by presenting lower SD, lower Dmin, and lower discordance rate but the smallest triangle corresponded to fusion indicating the advantage of combining EEG and MEG for the localization of single interictal spikes.
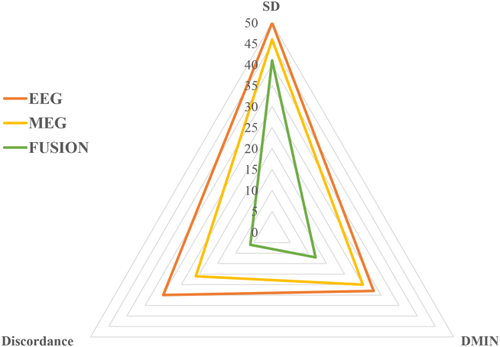
Radar chart summarizing the qualitative and quantitative assessments of EEG alone, MEG alone, and fusion in terms of the average SD, average Dmin, and the percentage of discordant spikes from the 1435 spikes in the 34 studies. EEG (in orange) with averaged SD = 50 mm, Dmin = 28 mm, and percentage of discordant spikes = 29%. MEG (in yellow) with averaged SD = 46 mm, Dmin = 25 mm, and percentage of discordant spikes = 21%. Fusion (in white color) with averaged SD = 41 mm, Dmin = 12 mm, and percentage of discordant spikes = 6%. Fusion exhibits the smallest triangle indicating the advantage of combining EEG and MEG for the localization of interictal spikes [Color figure can be viewed at wileyonlinelibrary.com]
3.6 Impact of the number of EEG electrodes in fusion
We also tested the impact of three EEG electrode setup and one subsampled MEG sensors set-up in fusion for all 34 studies, but only when applied on averaged signals corresponding to the consensus map obtained with the complete set up (54 EEG and 272 MEG sensors). Overall, all four configurations achieved similar level of accuracies for most studies. Of 34 cases, 33 presented concordant results with the CR when considering the full fusion 54 EEG + 272 MEG setup (Section 3.5.2). When subsampling the number of sensors from one of the two modalities, concordant or sub-lobar concordant results with the CR were found in 31/34 cases (19 concordant) for the 32 EEG + 272 MEG setup, in 30/34 cases (21 concordant) for the 21 EEG + 272 MEG setup, and in 30/34 cases (26 concordant) for the 54 EEG + 25 MEG setup. These results are suggesting a good stability of fusion results, even when lowering the number of EEG electrodes or MEG sensors while covering the whole head surface.
Figure 8 illustrates two examples (M25 and M8) of the source localization results obtained for the four fusion configurations. Figure 8a presents the source localization results on a patient (M25) with surgical resection in the right fronto-polar region (CR, outlined in white color in the figure) with an Engel 1A outcome. All four configurations provided sources concordant with the CR, however, recovered slightly different aspects of the active cortical patch. Figure 8b, presents the source localization results on a patient with an FCD in the right anterior frontal region, as outlined in white color in the figure. All four configurations showed concordance with the CR, while being sensitive to slightly different aspects of the active cortical patch.
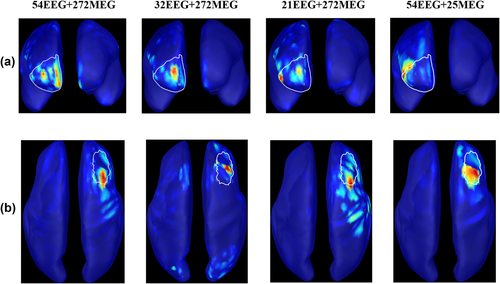
Impact of the number of EEG electrodes in fusion: two examples illustrating the performance of the four fusion configurations with different number of EEG electrodes and MEG sensors: (1) 54 EEG + 272 MEG, (2) 32 EEG + 272 MEG, (3) 21 EEG + 272 MEG, and (4) 54 EEG + 25 MEG. (a) Source localization results on M25, a patient with surgical resection in the right fronto-polar region (CR, outlined in white color) with an Engel 1A outcome. (b) Source localization results on (M8), a patient with an FCD in the right anterior region, as outlined in white color. All the four configurations recovered the source that was concordant with the CR [Color figure can be viewed at wileyonlinelibrary.com]
4 DISCUSSION
The objective of this study was to demonstrate the relevance of EEG–MEG fusion source analysis for presurgical evaluation of epilepsy. The advantage of performing single spike localization of fusion EEG–MEG data is twofold. Combining EEG and MEG data can help bring additional information missed by either modality, and localizing single spikes can bring important information that may be lost during averaging of the spikes. The advantage of performing single spike localization within the MEM-fusion framework is two folds as well. First, MEM-fusion can provide superior localization accuracy as it is sensitive to the spatial extent of the generators of epileptic activity. Second, MEM-fusion was proved to be robust in low SNR conditions such as single spike localization (Chowdhury et al., 2015). Whereas, applying source localization to the averaged signal provides only one source localization result, performing single spike source localization allows bringing more statistics, by building a consensus map to find the most reliable and reproducible source maps. In this study, we proposed and evaluated a systematic approach for clustering single spike source localization results to provide a consensus map. Applying the consensus map approach on fusion SSSL results, we were able to provide successful localization of the CR in all 34 markers studied here, where standard localization of averaged spikes resulted in failures in 8/34 cases for MEG and 11/34 cases for EEG. More importantly, we showed that fusion significantly improved the spike-to-spike reproducibility when compared to EEG or MEG SSSL, that is, from 55% in EEG and 71% in MEG to 90% in fusion. Finally, we demonstrated that using the consensus map approach on fusion data, the cluster exhibiting the highest number of spikes provided consistently concordant results with the CR; thus, suggesting an automatic way to find the most reliable, reproducible, and concordant source localization result in clinical investigations.
As mentioned in Section 1, spike clustering at sensor level has already been explored by several studies (Aydin et al., 2015; Ossenblok et al., 2007; Van 't Ent et al., 2003) demonstrating its pros and cons. In this study, we demonstrated the benefits of applying spike clustering at source level, which preserves the individual spike level variabilities by avoiding spike averaging at sensor level. We believe that preserving the complementarity of EEG and MEG recording at the single spike level is actually essential to take full benefit of EEG–MEG fusion approaches. Comparison of sensor and source level spike clustering techniques using the same dataset remains of great interest, but this was out of the scope of this study and this should be further explored in a prospective work. In the proposed consensus map approach, it is important to note that choosing an appropriate distance metric and linkage method to apply on the data that is being investigated plays a crucial role. For example, we chose the Ward's linkage method as it performs well with noisy data and we dealt with clustering of source maps from single spike localizations with low SNR (Marrelec, Messé, & Bellec, 2015). Consequently, results may vary by changing the type of distance and linkage method but investigating such influence was not in the scope of this article as our main objective was to test spike-to-spike reproducibility.
There are several fusion source localization methods that have been proposed to evaluate the advantage of combining EEG and MEG data (Aydin et al., 2015; Bast et al., 2007; Cohen & Cuffin, 1983; Ebersole & Ebersole, 2010; Pataraia, Lindinger, Deecke, Mayer, & Baumgartner, 2005; Pflieger et al., 2000; Yoshinaga, 2002; Zijlmans et al., 2002) including dipole fitting (Diekmann et al., 1998; Fuchs et al., 1998; Huang et al., 2007), beamformer (Hong, Ahn, Kim, & Jun, 2013), minimum norm estimate (Babiloni et al., 2001, 2004) and its noise normalized variants (Liu et al., 2002; Molins et al., 2008; Sharon, Hämäläinen, Tootell, Halgren, & Belliveau, 2007), sparse source imaging (Ding & Yuan, 2013), and Bayesian approach (Henson, Mouchlianitis, & Friston, 2009). Most of them were evaluated using simulations of focal activity (Babiloni et al., 2004; Ding & Yuan, 2013; Fuchs et al., 1998; Huang et al., 2007; Liu et al., 2002) or coherent sources (Hong et al., 2013). Other fusion studies were evaluated on experimental data such as auditory responses (Hong et al., 2013), face evoked responses (Henson et al., 2009), visual evoked responses (Sharon et al., 2007), or responses elicited by electrical median nerve stimulation (Fuchs et al., 1998; Molins et al., 2008) and on epilepsy data (Diekmann et al., 1998). To the best of our knowledge, MEM-fusion seems the only fusion approach designed and evaluated for localizing spatially extended generators of epileptic activity (Chowdhury et al., 2015), thus making it more appropriate for this clinical application.
In the context of localizing epileptic activity, SSSL of fusion data has been done with a dipole fitting approach, however, only on a small number of patients (6 patients) and with a limited MEG/EEG coverage (32 EEG and 22 MEG channels) (Diekmann et al., 1998). This dipole fitting fusion strategy involved only one level of fusion, consisting in concatenating the normalized EEG and MEG data and the corresponding lead field. In the MEM-fusion strategy, fusion of EEG and MEG data actually took place at three levels. At the first level, the data and the lead field matrices of each modality were normalized by the standard deviation of the respective background activity and then concatenated. The second and third level involved the use of fusion MSP scores for the whole cortex parcellization and for the initialization of the probability of each parcel to be active. These steps, which are specific to the MEM framework, actually play an important role in combining the complementary information from EEG and MEG within the fusion process (Section 2.4.2).
Reliability of the source localization methods when performing SSSL is crucial. Wennberg and Cheyne (2014) studied the reliability of dipole fitting approach when performing single spike localization. They reported that dipole fitting can result in different source solution even when localizing the same single spike. This was mainly attributed to the limitations in reliability of the dipole fitting method when dealing with low SNR data (Ossenblok et al., 2007). In addition, the single dipole solutions, leading to the delineation of a “dipole cluster,” were mainly driven by noise and not necessarily reflecting an extended region. On the other hand, we demonstrated the sensitivity of cMEM method to the spatial extent of the generators of epileptic activity (Chowdhury et al., 2013, 2015; Heers et al., 2014, 2016). In our previous study, we also demonstrated that cMEM method was showing less distant spurious sources, when compared to other conventional techniques (MNE, dSPM, and sLORETA), probably because of the ability of cMEM to switch off parcels that are less likely to contribute to the data (Heers et al., 2016). Therefore, cMEM seems more suitable for the localization and decomposition of simultaneously active sources; thus, offering the possibility to separate accurately spike and background activity. Moreover, the high spike-to-spike reproducibility rate (90%) in MEM-fusion (Figure 4) suggests an excellent reliability of the consensus map approach using MEM-fusion SSSL.
Spike averaging has been adopted in most studies (Bast et al., 2004; Hara et al., 2007; Heers et al., 2014, 2016, Pellegrino et al., 2016, 2017; Tanaka et al., 2010; Wennberg & Cheyne, 2014) to increase the SNR and improve the reliability of the source localization solutions. However, it is well known that waveforms of individual spikes might actually be quite variable in epileptic patients (Aydin et al., 2015; Köhling et al., 2000). Therefore, averaging effect is more likely to filter out source activities, which slightly vary over each individual spike, by inducing signal cancellation and consequently possible localization errors. According to standard averaged spike localizations results reported in this study (Section 3.1), we noticed that in many cases averaging did not increase the SNR nor did it diminish the noisy background data; thus, resulted in localization errors. We found 11/34 cases in EEG and 8/34 cases in MEG that actually failed, resulting in source localization results discordant with the CR. Moreover, there were 4/34 cases that were discordant with the CR for both EEG and MEG. In contrast, after applying the consensus map approach on SSSL results of EEG or MEG data, we noticed an overall improvement in the localization accuracy of EEG (discordant, 5/34; sublobar concordant, 3/34) and MEG (discordant, 1/34; sublobar concordant, 3/34). This shows that SSSL combined with consensus map estimate created a balance between spike variability and SNR. The consensus map approach proposed in this study serves as a promising way of overcoming the limitations of averaged spike localizations and extracting the most reliable and reproducible source among the single spike sources. It is also important to emphasize that by applying the consensus map approach on the MEM-fusion results, we were able to achieve excellent spike-to-spike reproducibility and reliability for all studied cases. We were able to find at least one cluster that was fully concordant with the CR, resulting in successful localization in all the 34 cases. Moreover, in 33/34 cases, the cluster involving the highest number of spikes was indeed the one showing full concordance with the CR. We also verified that the range of number of spikes involved in each study (10–287) was not biasing the resulting SSR scores reported in Figure 4b (results not shown).
In the literature, it has been often suggested that MEG provides a higher localization accuracy than EEG, which is mainly attributed to considerably lower effects of the skull resistivity in MEG forward problem and to the dense sampling of MEG sensors (Klamer et al., 2015; Ossenblok et al., 2007; Vorwerk et al., 2014). However, to further improve the localization accuracy of MEG, our study suggests that it is recommended to fuse EEG with the high-density MEG to bring the complementary information missed by MEG (e.g., involvement of radial sources or deeper generators). In the quantitative analysis using Dmin, we found lowest localization error in fusion. Based on spatial dispersion metric (SD), we noticed that fusion localization results presented an overall less spatial spread of the solution around the true extent of the source or less spurious activity distant from the true source than EEG results. On the other hand, MEG results provided comparable spatial dispersion values when compared to fusion results.
Whole head coverage can be achieved with the high-density MEG sensors, but MEG can mainly bring information about the tangential component of the underlying neuronal sources. In our previous study (Chowdhury et al., 2015) based on realistic simulations, we suggested that the addition of only 20 or 32 EEG electrodes would be sufficient to bring additional information about the source within an MEM fusion framework. This in turn would help reduce the preparation time required for EEG electrodes setup during simultaneous EEG–MEG recordings and patient's discomfort inside the MEG helmet. Another previous study based on simulations (Babiloni et al., 2004) showed that the use of simultaneous 29 EEG sensors during the MEG measurements carried out with 153 sensors results in an accuracy of the cortical source estimate statistically similar to the one obtained by combining 64 EEG and 153 MEG sensors. In this study, we further validated on clinical data, the concept that MEM fusion remains stable even when lowering the number of EEG electrodes. For the first time, we also considered the reversed configuration of keeping all EEG and lowering the MEG spatial sampling. We found that the localization accuracy was overall comparable for all four configurations of fusion involving 21, 32, and 54 EEG electrodes combined with 272 MEG sensors, and 25 MEG sensors combined with 54 EEG electrodes. We have explored the sub-sampling of EEG electrodes according to the standard montages such as 10–20 or 10-10 system. Furthermore, exploring the fusion of 54 electrodes EEG system with few MEG sensors (25 MEG sensors) was interesting considering the advent of the next generation of non-SQUID-based individual MEG sensors (Boto et al., 2017; Öisjöen et al., 2012). These results indicate that by combining even only few EEG or few MEG sensors, to a complete MEG or EEG setup, we can achieve a good spatial sampling of the head while bringing complementary information from both EEG and MEG to ensure accurate fusion. However, there was some clinical rationale for subsampling EEG according to standard well-recognized montages (10–20 system), but MEG sensors were subsampled randomly while taking into account a good spatial coverage of the anatomical locations as per the standard EEG montage. Therefore, we recommend subsampling only one modality while keeping a dense sampling of the other modality. We recently demonstrated similar level of spatial accuracy obtained with MEM using either MEG or high-density EEG (256 electrodes) during electrical median nerve stimulation (Hedrich et al., 2017). A comparison of the fusion between high-density EEG and several subsampled MEG setups would be of interest but was out of the scope of this study. This would further open avenues for exploring optimal fusion montages with well-placed and densely sampled electrodes and sensors to benefit from the fusion of the two modalities. Although, we addressed a similar issue in the context of near infrared spectroscopy (exploiting the forward model and defining some a prior target areas to place sensors in an optimal manner) (Machado, Marcotte, Lina, Kobayashi, & Grova, 2014), we believe that such an analysis was out of the scope of this study.
In this study, we excluded deep generators as it is still an open question whether deep generators are detectable by EEG and MEG as their sensitivities decrease rapidly as the neural sources are located deeper inside the brain (Ahlfors et al., 2010; Attal & Schwartz, 2013; Hunold, Funke, Eichardt, Stenroos, & Haueisen, 2016; Liu et al., 2002; Mikuni et al., 1997; Stephen, Ranken, Aine, Weisend, & Shih, 2005). However, by combining EEG and MEG, we can improve the sensitivity to deep generators, by taking benefit from the better sensitivity to deep generators of EEG when compared to MEG gradiometers notably. Improvement of sensitivity to deep generators when using EEG–MEG fusion was indeed shown previously using simulation studies by (Huizenga, van Zuijen, Heslenfeld, & Molenaar, 2001) and by our team in (Chowdhury et al., 2015), as well as for epileptic data by (Aydin et al., 2015). In fact, we were able to show that EEG–MEG fusion using cMEM method improves the sensitivity to depth despite the fact that no depth weighting strategy was considered in cMEM.
The clinical references considered in this study were manually drawn on the cortical surface based on the available clinical information (i.e., resected region, intracranial EEG ictal/interictal findings, and/or lesion visible on MRI). The largest CRs with approximately 200 cm2 surface (S6, S21, and S30) were smaller than the size of a lobe, assuming the total surface area of the cerebral cortex to be equal to 2,500 cm2 (Peters & Jones, 1984) and the percentage of total cerebral cortex volume in human are frontal lobe = 41%; temporal lobe = 22%; parietal lobe = 19%; occipital lobe = 18% (Al-Chalabi, Delamont, & Turner, 2008; Kennedy et al., 1998). Although manual drawing of CRs along the cortical surface was subjective, we can still assume our quantitative analysis using CR to be more accurate than most qualitative evaluations done at the sublobar level, which is the level of choice considered in many clinical studies (Lantz, de Peralta Menendez, Andino, & Michel, 2001; Park et al., 2015).
Finally, whereas we only evaluated source localization results at the peak of the spike, the consensus map approach provides a spatio-temporal source map, which is well-suited for the study of propagation patterns or other complex epileptic patterns. In our recent study (Chowdhury et al., 2016), we have shown the accuracy of MEM methods on high-density EEG and MEG data, when localizing complex patterns of epileptic discharges, including propagation patterns. Therefore, the combination of consensus map approach within the MEM-fusion algorithm as proposed in this study is ideal to further investigate the spatio-temporal features of epileptic discharges and their reproducibility, but this was out of scope of this study.
5 CONCLUSION
We proposed and validated a systematic approach for clustering single spike source localization results at the source level using hierarchical clustering to provide a consensus map of the most reproducible and clinically reliable source localization result. While, the consensus map approach leads to an improvement in the analysis of EEG or MEG source localization results, when compared to standard averaged spike source localization, it is its combination with MEM-fusion that provided successful localization in all the studied cases. MEM-fusion with consensus map yielded excellent spike-to-spike reproducibility. Moreover, the consensus map obtained from MEM-fusion showed that the most consistent and clinically relevant findings were the ones corresponding to the cluster involving the highest number of spikes. Therefore, when dealing with clinical data without any available ground truth information, this study suggests applying SSSL using MEM-fusion and estimating the consensus map as the cluster exhibiting with the highest number of spikes is likely to provide the most reproducible and reliable findings and should be considered in clinical practice. In conclusion, we demonstrated that SSSL using MEM-fusion with the help of consensus map approach can be used as a valuable noninvasive tool during presurgical investigation of patients with epilepsy.
ACKNOWLEDGMENTS
This work was supported by studentship and postdoctoral fellowship from Savoy Foundation, BioMedical Engineering Excellence Award, Natural Sciences and Engineering Research Council of Canada (NSERC) Discovery grant and grant from Canadian Institutes of Health Research (CIHR) (MOP-133619). The EEG-MEG acquisitions on patients were funded by CIHR (MOP-93614), Centres of Excellence for Commercialization of Research (CECR), the American Epilepsy Society Award, and the FRQS (The Fonds de recherche du Québec – Santé) postdoctoral fellowship (UA). GP was supported by funding from Richard and Edith Strauss Canada Foundation.
Footnote
APPENDIX A
EXPLANATION OF THE LOGICAL OR OPERATION IN EQUATION 3
 and
and
 ) by probabilities (p(EEG) and p(MEG)), respectively, in Equation 3. Using such a notation, Equation 3 can be rewritten as
) by probabilities (p(EEG) and p(MEG)), respectively, in Equation 3. Using such a notation, Equation 3 can be rewritten as
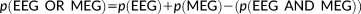
The last term p(EEG AND MEG) = p(EEG, MEG) is a joint probability that can factorize as p(EEG|MEG) p(MEG). Assuming that the activity from EEG occurs “independently” from what we observe from MEG, we obtain
p(EEG|MEG) = p(EEG), therefore leading to p(EEG AND MEG) = p(EEG)p(MEG) and Equation 3 using Hadamard product. This assumption of EEG to be independent from MEG is moderately true as we can say that the two modalities rely on two different physical processes (Ohmic current propagation within the volume versus magnetic fields elicited by neuronal currents) while they are produced by the same neuronal activity. Secondary volume conduction currents yield potential differences on the scalp of the head that can be measured by EEG, whereas MEG measures magnetic fields induced mainly by primary currents.
Moreover, this step is specific to the MEM-fusion framework and was not proposed in other fusion approaches, where the final fusion probability, that is, p(EEG OR MEG) provides an efficient way of combining the complementary information from both EEG and MEG. For example, if we have strong contribution from EEG but poor contribution from MEG such as
 = 0.8 and
= 0.8 and
 = 0.3, then
= 0.3, then
 = 0.8 + 0.3 − 0.8 × 0.3 = 1.1 − 0.24 = 0.86, where we have the contribution from EEG being carried forward. Or when both modalities are contributing equally such as
= 0.8 + 0.3 − 0.8 × 0.3 = 1.1 − 0.24 = 0.86, where we have the contribution from EEG being carried forward. Or when both modalities are contributing equally such as
 = 0.7 and
= 0.7 and
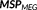 = 0.75, then
= 0.75, then
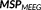 = 0.7 +0.75 − 0.7 × 0.75 = 1.45 − 0.525 = 0.925, where we have the strong contribution from both EEG and MEG being carried forward.
= 0.7 +0.75 − 0.7 × 0.75 = 1.45 − 0.525 = 0.925, where we have the strong contribution from both EEG and MEG being carried forward.
Consequently, we believe that such an approximation could be fair, especially as it is mainly used as an initialization of our reference (prior) model, thus introducing a second level of fusion of the two modalities at the level of a priori model definition.
APPENDIX B
ESTIMATION OF A CONSENSUS MAP
Step 1. Normalization of the reconstructed source maps
cMEM reconstructed current density distributions, or source maps estimated for each single spike are denoted
 , a r
, a r
 τ matrix, where r is the number of dipolar sources and τ is the number of time samples. The mean of the estimated source map was first subtracted to obtain zero-mean maps. Then, the source maps were normalized between 0 and 1 using the Frobenius norm as follows:
τ matrix, where r is the number of dipolar sources and τ is the number of time samples. The mean of the estimated source map was first subtracted to obtain zero-mean maps. Then, the source maps were normalized between 0 and 1 using the Frobenius norm as follows:
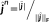 . The Frobenius norm computes the square root of the sum of the square of the coefficients of a matrix. The purpose of this normalization is to retrieve the spatio-temporal shape of all the source maps within a selected time window, thus recovering typical dynamic patterns. These normalized source maps
. The Frobenius norm computes the square root of the sum of the square of the coefficients of a matrix. The purpose of this normalization is to retrieve the spatio-temporal shape of all the source maps within a selected time window, thus recovering typical dynamic patterns. These normalized source maps
 were then used for calculating the absolute correlation measure between source maps.
were then used for calculating the absolute correlation measure between source maps.
Step 2. Estimation of the similarity index based on absolute correlation measure
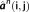 and
and
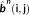 is given by,
is given by,
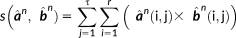 (A.1)
(A.1) N matrix with
N matrix with
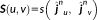 for u and v = 1, …, N.
for u and v = 1, …, N.Then, the dissimilarity matrix given by Ð = 1 − S, is used for hierarchical clustering.
Step3. Hierarchical clustering of source maps
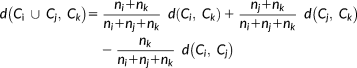 (A.2)
(A.2)This procedure yields a hierarchy of clusters represented as a binary tree, denoted as a dendrogram. A dendrogram is a tree diagram that shows the nested structure of the partitions and how the various clusters are linked at each level of the hierarchy. Each level of the hierarchy where two branches (i.e., clusters) join is associated to a numerical value, called linkage value, which usually represents the distance d(Ci, Cj) between the two fused clusters. The scale of this linkage value is represented along the vertical axis of the dendrogram as illustrated in Figure 1. Hierarchical clustering was implemented using MATLAB R2015 Linkage function.
To threshold the dendrogram to obtain the optimal classification of the objects, Martinez and Martinez (2004) recommended the visual inspection of a break in the evolution of the standardized cluster linkages
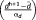 as a function of the number of clusters (Martinez & Martinez, 2004). Here, d h+1 is the linkage value at (h + 1) hierarchy level,
as a function of the number of clusters (Martinez & Martinez, 2004). Here, d h+1 is the linkage value at (h + 1) hierarchy level,
 and
and
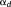 are the average and standard deviation of the linkages for h previous levels of hierarchy, respectively. An elbow or a break in the plot is therefore interpreted as an indication of the number of clusters. See Figure 1 for an example where the break at “2” indicates 2 clusters.
are the average and standard deviation of the linkages for h previous levels of hierarchy, respectively. An elbow or a break in the plot is therefore interpreted as an indication of the number of clusters. See Figure 1 for an example where the break at “2” indicates 2 clusters.
Step 4. Generation of a consensus map
With the help of the hierarchical clustering, we were able to group the source maps that were spatially similar into clusters. At this stage, we performed an average of the source maps within each cluster to provide a cluster map. This type of averaging helped in avoiding some signal cancellation or loss of information, problems often faced during averaging at the signal level. We obtained spatio-temporal cluster maps; however, for this study, we focused only on the results at the peak of the averaged cluster spike. From all the cluster maps, the consensus map was defined as the most reproducible and reliable cluster map, which was chosen as the one involving the highest number of spikes and with source concordant with the clinical ground truth information.




