Rolandic alpha and beta EEG rhythms' strengths are inversely related to fMRI-BOLD signal in primary somatosensory and motor cortex
Abstract
Similar to the posterior alpha rhythm, pericentral (Rolandic) EEG rhythms in the alpha and beta frequency range are referred to as “idle rhythms” indicating a “resting state” of the respective system. The precise function of these rhythms is not clear. We used simultaneous EEG-fMRI during a bimanual motor task to localize brain areas involved in Rolandic alpha and beta EEG rhythms. The identification of these rhythms in the MR environment was achieved by a blind source separation algorithm. Rhythm “strength”, i.e. spectral power determined by wavelet analysis, inversely correlated most strongly with the fMRI-BOLD signal in the postcentral cortex for the Rolandic alpha (mu) rhythm and in the precentral cortex for the Rolandic beta rhythm. FMRI correlates of Rolandic alpha and beta rhythms were distinct from those associated with the posterior “classical” alpha rhythm, which correlated inversely with the BOLD signal in the occipital cortex. An inverse correlation with the BOLD signal in the respective sensory area seems to be a general feature of “idle rhythms”. Hum Brain Mapp 2009. © 2008 Wiley-Liss, Inc.
INTRODUCTION
Rhythms in the alpha and beta frequency bands are a dominant feature of the resting EEG in human subjects [Berger,1929; Niedermeyer and Lopes da Silva,2004]. Some of the well-known rhythms are functionally related to major sensory systems. Most notably, the posterior alpha rhythm is thought to be functionally related to the visual system, based on its occipital origin and its modulation by visual input [Berger,1929]. Similar rhythms are found in the sensorimotor system [Salmelin and Hari,1994a]: one of them has a peak frequency in the alpha band (around 10 Hz), and has been termed the “mu” or “Rolandic alpha rhythm” [Gastaut,1952; Kuhlman,1978], while the other has a peak frequency in the beta band (around 20 Hz), and is usually referred to as the “central” or “Rolandic beta rhythm” [Pfurtscheller,1981,1992; Salmelin and Hari,1994b]. A functional relationship of these rhythms to the sensorimotor system is strongly suggested by (i) their pericentral (pre- and postcentral gyrus) location (“Rolandic rhythms”) and (ii) their modulation by hand movements and somatosensory input. This relationship is further supported by (iii) the dependence of motor cortex excitability on the strength of these rhythms, e.g. facilitation of the motor response during beta desynchronization after somatosensory stimulation [Deletis et al.,1992] and a decreased motor cortex excitability during β-rebound [Chen et al.,1999].
- 1
Given the subtlety of the Rolandic rhythms, is it possible to identify these rhythms based on EEG during MRI data acquisition despite the artifact-prone MR environment that necessitates extensive artifact reduction?
And if so
- 2
Is it possible to identify correlates of these rhythms in fMRI?
And if so
- 3
Are these fMRI correlates spatially different for the two Rolandic rhythms as suggested by the findings of previous MEG studies [Cheyne et al.,2003; Salmelin et al.,1995; Salmelin and Hari,1994a]?
And finally
- 4
What are the directions of the BOLD-signal changes, specifically, is the inverse correlation noted for the occipital alpha rhythm a general feature of idle rhythms?
SUBJECTS, MATERIALS, AND METHODS
Subjects
Fifteen healthy subjects (mean age 28 years, range 25-30, 4 males/11 females) with no history of neurological or psychiatric disorder participated in the study. All subjects gave written informed consent prior to the investigation. The experiments were performed in compliance with the relevant laws and institutional guidelines and were approved by the local ethics committee.
Experimental Task
To modulate Rolandic rhythms, subjects performed a motor task. This task consisted of self-paced effortless synchronous opening and closing of the hands at a frequency of about 1 Hz (trained before the experiment) for 20 s alternating with rest periods of equal duration. In previous studies, such grip tasks have been shown to induce robust activation in fMRI [Jancke et al.,1998]. The task blocks were acoustically cued by “start” and “stop” commands presented via MR compatible headsets using the software Presentation v0.71 (Neurobehavioral Systems, Albany, NY). As Rolandic rhythms are known to be enhanced by complex visual input [Koshino and Niedermeyer,1975], the subjects were instructed to keep their eyes open during the entire experiment to maintain a low level of posterior alpha rhythm strength and to focus on a fixation cross in the middle of the screen that was embedded in a colored picture (N = 9) or in a cartoon (N = 6) during the experiment. All subjects were asked neither to move their eyes beyond normal eye-blinking nor their bodies beyond the motor task.
Simultaneous EEG-fMRI Recordings
Simultaneous EEG-fMRI recordings were performed with a 1.5-T scanner (Magnetom Vision, Siemens, Erlangen, Germany) and a 32-channel MR-compatible EEG (Brain Products, Munich, Germany). Functional imaging was performed using a T2*-weighted BOLD [Bandettini et al.,1992; Frahm et al.,1992; Kwong et al.,1992; Ogawa et al.,1992] sensitive gradient echo planar imaging sequence (repetition time TR = 2.5 s, acquisition time TA = 2.1 s, echo time TE = 60 ms, flip angle 90°, matrix 64 × 64, voxel size 3.3 × 3.3 × 6 mm3, interslice distance 1.5 mm, 20 slices, 200 scans). For EEG recordings, a customized 32-channel EEG cap was used including six electromyography (EMG) electrodes for bipolar recordings from chin and bilateral hand muscles, three electrooculogram (EOG) electrodes for vertical and horizontal EOG, and two electrocardiogram (ECG) electrodes (Easy cap, Falk Minow Services, Herrsching-Breitbrunn, Germany). The resolution of the MR-compatible 16-bit EEG amplifier was set to 0.5 μV giving a large dynamic range of ±16.384 mV to capture both low-amplitude EEG/EMG signals in the range of 50 μV and large MR-artifacts in the range of 5,000 μV. The sampling frequency was 5,000 Hz. The amplifier was equipped with an analog 1,000 Hz low-pass/0.1 Hz high-pass hardware filter. The EEG was recorded from 21 electrode positions (International 10-20 system) referenced to a point at the vertex at position FCz. This reference was selected as others seemed less appropriate for the following reasons: “Neutral” nose reference in the fMR setup proved to be unreliable since the nose-electrode happened to become loose, possibly due to vibrations during MR acquisition. “Mastoid” reference seemed unsuitable due to the likely occurrence of laterality effects. The average reference proved to be more artifact afflicted than a single-electrode reference, possibly due to residual artifacts in single channels included in the average reference. After acquisition, EEG data were MR-artifact corrected using artifact-template subtraction according to the approach proposed by Allen et al. [2000] using BrainAnalyzer Software (V. 1.03 BrainProducts, Munich, Germany). This approach has been shown to be capable of recovering physiological signal content from artifact-afflicted EEG periods [Becker et al.,2005] and to restore EEG rhythms in the spectral alpha and beta range with sufficient quality [Ritter et al., 2007]. Subsequently, a 70 Hz low-pass filter was applied.
Analysis of EEG Data
Identification of Rolandic alpha and beta rhythms (see Fig. 1)
- (i)
Rolandic alpha (“mu”) and beta rhythms have peak frequencies of around 10 and 20 Hz respectively [Tiihonen et al.,1989].
- (ii)
During finger movements, Rolandic rhythms are known to be suppressed [Arroyo et al.,1993; Jasper and Penfield,1949]. To identify Rolandic alpha and beta rhythms, we performed frequency analysis of the EEG recordings and searched for components that were suppressed during hand movements.
- (iii)
Both Rolandic alpha and beta rhythms occur most prominently in pericentral regions.
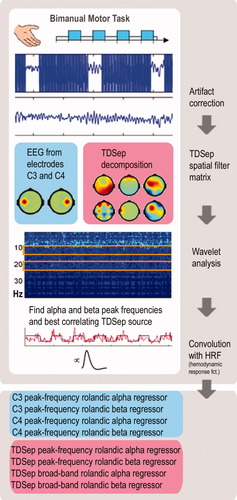
Schematic illustration of data analysis. EEG and fMRI were acquired simultaneously when subjects performed a bimanual motor task. MR-related artifacts were removed from the EEG data. Blind source separation was applied to the EEG data using Temporal Decorrelation Source Separation (TDSep). EEG of channels C3 and C4 and of all identified TDSep sources were frequency decomposed using wavelet analysis. TDSep sources with α- and β-spectral power correlating best with the motor task were identified. For the C3 and C4 EEG signals and for the previously determined TDSep sources, individual (subject-specific) peak frequencies in the alpha and beta band were estimated. Peak frequency and broad-band (α-2 and β-2) power time courses of C3, C4, and TDSep sources were convolved with the hemodynamic response function and used as predictors for the BOLD signal in subsequent fMRI analysis. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
C3 and C4 Rolandic alpha and beta rhythms
EEGs of the C3 and C4 channels (the channels located most closely to the pericentral/Rolandic brain areas) were time-frequency decomposed at a bandwidth of ∼1 Hz using wavelet analysis to obtain power time courses for all frequencies (see Fig. 1). Since reactivity to the motor task was one criterion for the identification of Rolandic rhythms, for each subject, a two-sample Student's t-test (task vs. rest condition) was calculated for the following eight frequency bands: delta (1.5–6 Hz), theta (6–8 Hz), α-1 (8–10 Hz), α-2 (10–12 Hz), β-1 (12–18 Hz), β-2 (18–21 Hz), β-3 (21–30 Hz), and gamma (30–60 Hz). In the alpha and beta range, the respective bands which correlated best with on/off periods of hand movement (over all subjects) were identified (α-2 and β-2, see Results) and further referred to as Rolandic alpha band and Rolandic beta band respectively. As Rolandic frequency components vary across subjects [Pfurtscheller and Lopes da Silva, 1999], individual peak frequencies were determined for each subject by separately correlating spectral time courses at a resolution of 0.5 Hz with the motor task. Since the peak Rolandic frequencies correlated more strongly with the motor task than the broad-band Rolandic alpha and beta rhythms (see Results), individual peak frequencies in the previously determined Rolandic alpha and beta bands were operationally defined as “C3 (C4) Rolandic alpha rhythm” and “C3 (C4) Rolandic beta rhythm” respectively.
We further determined whether potential hemispheric side differences in the modulation of Rolandic rhythms during a motor task [Niedermeyer and Koshino,1975] could be picked up by EEG-recordings. To this end we tested for a difference in modulation between C3 and C4 electrode positions, respectively, across all subjects using a paired Student's t-test.
For correlation with fMRI data, power time courses of individual Rolandic rhythms were convolved with the canonical hemodynamic response function (HRF) provided by SPM2 (www.fil.ion.ucl.ac.uk/spm/software/spm2/) and were down-sampled to the temporal resolution of the fMRI data TR = 2.5 s (one datapoint every 2.5 s was sampled; data were not averaged over 2.5 s).
Blind source separation
In a parallel approach, we attempted to separate the Rolandic rhythms from other contaminating biological and measurement-induced signals such as the volume-conducted classical alpha rhythm or residual MR-artifact traces. To this end, we used a blind source separation algorithm TDSep (temporal decorrelation source separation) [Ziehe et al.,2000] http://www.old.first.fhg.de/∼ziehe/download.html). This algorithm uses an approximate simultaneous diagonalization of time-delayed second order correlation matrices assuming distinctive spectral and temporal characteristics of the sources, and thereby exploits the inherent time structure of signals as found in neurophysiological recordings. It also allows the definition of a set of several time delays (between the signals of different channels) to circumvent the problem of selecting the optimal (mostly unknown) time delay. In this study, time delays were set from 0 to 30 ms in six discrete steps, which is approximately in the range of autocorrelations of EEG signals. The method has been described in detail elsewhere and its capability to successfully extract the signal of interest by eliminating disturbances originating from biological and technical noise sources has been demonstrated before [Ziehe et al.,2000].
After blind-source separation of EEG signals, all resulting sources were wavelet analyzed to obtain power time courses for all frequencies (see Fig. 1). As described above, a two-sample Student's t-test (task vs. rest condition) was calculated for determination of individual peak frequencies within the previously determined Rolandic alpha and beta bands. For the blindly separated sources, the broad-band rhythms at times correlated better with the motor task than rhythm at individual peak frequencies (see Results), so we used both the broad band and individual peak frequencies for subsequent MR analysis.
Thus, for each subject, broad-band alpha and beta rhythms of the respective TDSep sources exhibiting strongest modulations by the motor-task were used as operational definitions for broad-band Rolandic alpha/beta rhythms (“TDSep broad-band Rolandic alpha/beta rhythm”) and peak-frequency alpha and beta rhythms of the respective TDSep sources exhibiting strongest modulations by the motor-task were used as operational definitions for peak-frequency Rolandic alpha/beta rhythms (“TDSep peak-frequency Rolandic alpha/beta rhythm”).
Power time courses of Rolandic rhythms were then convolved with the HRF and down-sampled to the temporal resolution of the fMRI data as described above. In addition, we operationally defined the posterior alpha rhythm (“TDSep posterior alpha”) as the average (8–12 Hz) power of the TDSep source whose alpha (8–12 Hz) power maximally correlated with the alpha power derived from electrode position O2.
Validation of blind source separation
Before applying the TDSep algorithm to experimental EEG data, the algorithm was tested on surrogate data. Artificial EEG data were created as follows (see Fig. 2): 21 data channels with individual random noise plus “posterior alpha rhythm” consisting of a 10-Hz sinus wave with highest strength in posterior channels and “bilateral Rolandic rhythms”, consisting of a 11-Hz and a 19-Hz sinus wave and being modulated in strength every 20 s. Both posterior alpha and Rolandic rhythms gradually declined in channels adjacent to the site of maximum strength. As shown in Figure 2, by means of TDSep, Rolandic rhythms were reliably identified. The temporal and spatial characteristics of these rhythms were more accurately reconstructed than by any single EEG electrode signal, demonstrating the superiority of this method.
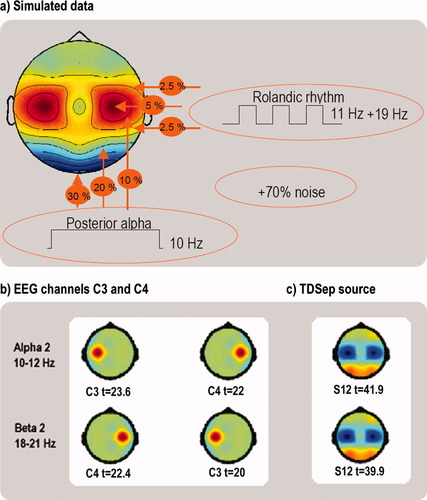
Temporal decorrelation source separation (TDSep) of simulated and real data. TDSep algorithm for blind source separation was tested on simulated EEG data. (a) The 21 simulated EEG channels consisted of individual noise, posterior alpha rhythm, and block-modulated Rolandic rhythms. (b) Correlation analysis (Student's t-test) between α-2/β-2 bands of all 21 simulated EEG channels and the modulating block function reveal C3 and C4 as the best correlating channels. C3 and C4 positions are depicted color-coded in scalp maps, and the respective t-values are given underneath. (c) By means of blind source separation using the TDSep algorithm, Rolandic rhythms were reliably identified. Depicted are the scalp maps of the best correlating TDSep source (S12) for both frequency bands (weighting of single channels is color-coded). The temporal and spatial characteristics of these rhythms were reconstructed in a more superior way than by any single EEG channel signal, e.g. from positions C3 or C4 as can be observed from the scalp maps and the higher t-values. Rolandic rhythm's source as obtained by TDSep is higher correlated with the motor task than the best correlating EEG channel signal in the respective alpha and beta frequency bands. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
This superiority was confirmed on the experimental data. Rolandic alpha and beta power in sources identified by TDSep mirrored the motor task more closely than the power of both rhythms measured by the C3 or C4 EEG channels (see Results). This indicates higher functional specificity of signals from TDSep sources. Furthermore, regressors obtained from TDSep sources accounted for more BOLD signal variance than regressors obtained from EEG channels (see Results).
Overview of EEG rhythms used for fMRI correlation
- 1
“C3 Rolandic alpha/beta rhythm” and “C4 Rolandic alpha/beta rhythm” (the power of the respective rhythms at individual peak frequencies at electrode positions C3 and C4 respectively).
- 2
“TDSep broad-band Rolandic alpha/beta rhythm” and “TDSep peak-frequency Rolandic alpha/beta rhythm” (the broad-band/individual peak-frequency power of the respective rhythms in EEG sources identified with a TDSep filter).
- 3
The “classical” “posterior alpha rhythm” (the power of the broad-band (8–12 Hz) alpha rhythm derived at electrode position O2 and the respective rhythm identified with a TDSep filter).
Analysis of fMRI Data
SPM2 was used for fMRI data analysis. Functional MR images were realigned, normalized to the MNI standard brain, smoothed with double voxel size, and high-pass filtered (512 s). Serial correlations were estimated using an autoregressive model to subsequently correct for non-sphericity during inference [Friston et al.,1995]. Because of the covariance between the two rhythms' power and the motor task, a fraction of the BOLD signal variance cannot be ascribed unambiguously to one particular regressor [Andrade et al.,1999]. In such a situation, a variety of model configurations can be proposed, each addressing distinct hypotheses and hence allowing for different conclusions. There is no single “perfect” model to unambiguously explain all effects. We employed three different modeling strategies each addressing different questions. In our opinion each of the approaches has its validity, as we will explicate below. Figure 3 schematically illustrates differences between the three approaches based on a hypothetical data set.
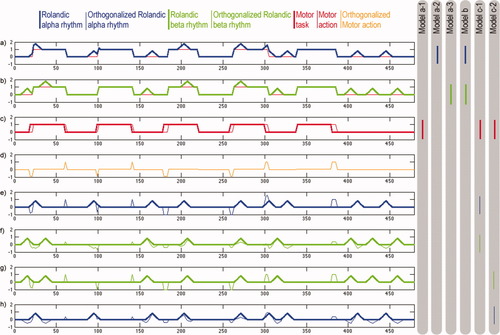
Schematic illustration of differences between the employed modeling approaches based on a surrogate data set. X- (time) and Y- (amplitude) axes are scaled in arbitrary units. On the right, regressors are indicated that were utilized for the three modelling approaches. (a, b) Surrogate data representing the Rolandic alpha rhythm amplitude (blue) and the Rolandic beta rhythm amplitude (green). Each data set was calculated by summing two signal time courses, one block-function reflecting motor-task induced fluctuations and one individual signal reflecting rhythm specific motor-task independent fluctuations. The thin red line indicates the motor task - as performed by the subject (“real” motor task). (c) Motor-task as defined by markers of the “start” and “stop” acoustic signals presented to the subjects (bold red line) and the “real” motor task as performed by the subject (thin red line). The real motor task function slightly deviates from the motor-task function defined by markers because of performance differences, accordingly motor-action related rhythm-modulations differ from the task. (d) Signal time course of the real motor-task after orthogonalization to the motor-task defined by markers. Such artificial signal changes can also occur when Rolandic rhythm amplitudes are orthogonalized to the “theoretical” motor task. (e, f) Rolandic alpha rhythm amplitude after orthogonalization to the theoretical motor-task (blue thin line) and Rolandic beta rhythm amplitude after orthogonalization to the motor-task and to the Rolandic alpha rhythm amplitude (green thin line). Bold lines indicate the original task-independent signal time course of both rhythms. (g, h) The orthogonalization order has been changed here by swapping Rolandic alpha (blue) and beta (green) rhythms. Again thin lines indicate signal time courses after orthogonalization and bold lines indicate original task-independent fluctuations. Orthogonalization order slightly affects the resulting signal time courses of both rhythms. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
In the first approach (a), a separate model was estimated for each regressor. In this case, the regressors' weights reflect correlation of a single, distinct effect with the BOLD signal. However, because there are redundancies between the regressors, the identified BOLD signal changes could also be caused by a correlating covariate. With this approach, however, we were interested in (1) exploratively describing differences resulting from different definitions of Rolandic rhythms, i.e. rhythms directly obtained from electrodes, rhythms obtained from TDSep sources, rhythms at individual peak-frequencies and rhythms at fix spectral bands, and (2) the differences of the results for Rolandic alpha versus beta rhythms as assessed in a second level analysis. A correlating covariate may diminish the estimated differences of any true underlying effect, but not create spurious differences (hence avoiding type I error). Subsequent inferences regarding the differences of the results for Rolandic alpha and beta rhythms were exclusively based on significant differences between the fMRI correlates of the respective regressors. A disadvantage of this analysis strategy is that the model accounts only for the BOLD signal variance explained by a single effect. The BOLD signal variance due to other effects not within the model leads to residual error. An advantage, however, is that no bias from other regressors (see below) is introduced into the model, i.e. the “pure” and physiological rhythm strength, as measured by EEG (Fig. 3a,b), is used as a predictor for the BOLD signal.
In the second approach (b), both Rolandic alpha and beta regressors were integrated in a single model. An advantage of this approach over approach (a) is that the individual weights reflect BOLD signal changes that are specific for the respective regressor. Effects caused by the redundant parts of the regressors (thin red lines in Fig. 3a,b), however, will be missed. In approach (b) the motor-task is not included into the model due to the imprecision of its timing. The motor-task is a block-function defined by the start and stop markers recorded when acoustic commands are presented (Fig. 3c, bold red line). Thus, the “real” timing of motor action can slightly deviate from the task function (Fig. 3c, thin red line), which would lead to additional error variance where the motor-task function to be integrated into the model. Given that the Rolandic rhythms are weak and, therefore, the BOLD signal changes will be small, we sought to avoid such confounding effects in approach (b).
In the third approach (c), redundancies between the motor-task, Rolandic alpha and beta regressors were removed by a Gram-Schmidt orthogonalization procedure (SPM2 MATLAB code), which computes the projection of a unit vector x onto another vector y and then subtracts the projection from x, such that what remains is orthogonal to y. For two orthogonal vectors, the sum of element-wise multiplications of both vectors equals zero. Subsequently, one model was estimated including all orthogonalized regressors. As with approach (b), individual weights in approach (c) reflect BOLD signal changes that are specific for the respective regressor. However, in approach (c) effects caused by the redundant parts of the regressors will be attributed to the hierarchically higher regressor (in terms of the orthogonalization order). Since we were interested in specific effects of the two Rolandic rhythms, we first removed redundant variance caused by the motor-task, i.e. the rhythms were orthogonalized to the motor task. The order of the orthogonalization of the regressors of the Rolandic alpha and beta rhythm is slightly arbitrary and cannot be justified in terms of functionality. Therefore we estimated models for both orders and chose the one with the smallest residual error. An advantage of approach (c) is that including all three regressors in a single model would be expected to minimize residual BOLD signal variance. As mentioned earlier, however, the motor-task function may not perfectly reflect the real motor-action. In Figure 3d we show how orthogonalization based on a slightly imprecise motor-task function may artificially change regressors representing Rolandic rhythms. Figure 3e–h illustrates how the orthogonalization order slightly modifies regressors for Rolandic alpha and beta rhythms.
- a
Ten linear correlation (fixed effects) models within approach (a) were estimated, each including one of the following regressors: (1) motor-task protocol, (2) C3 Rolandic alpha rhythm, (3) C3 Rolandic beta rhythm, (4) C4 Rolandic alpha rhythm, (5) C4 Rolandic beta rhythm, (6) TDSep peak-frequency Rolandic alpha rhythm, (7) TDSep peak-frequency Rolandic beta rhythm, (8) TDSep broad-band Rolandic alpha rhythm, (9) TDSep broad-band Rolandic beta rhythm and (10) TDSep posterior alpha rhythm. Additionally, the respective first derivatives and realignment parameters were included in each model.
- b
One model was calculated including both TDSep broad-band Rolandic alpha rhythm and TDSep broad-band Rolandic beta rhythm as effects of interest. Additionally, the respective first derivatives and realignment parameters were included in each model. Contrast images were generated for the effects of interest and for the difference between both effects of interest.
- c
One model was calculated including motor-task protocol, orthogonalized TDSep Rolandic alpha rhythm, orthogonalized TDSep Rolandic beta rhythm, and realignment parameters. The orthogonalization algorithm removed (1) signal components of both alpha and beta Rolandic rhythms which were correlated to the motor task and (2) signal components of the Rolandic beta rhythm which were correlated to the Rolandic alpha rhythm. In a second model, the orthogonalization order of Rolandic rhythms was changed, i.e. signal components of the Rolandic alpha rhythm which were correlated to the Rolandic beta rhythm were removed. The residual error was calculated for both models.
Group effects were computed for all models by a random effects analysis (one-sample Student's t-test), which allows for assignment of the observed effects to the general population. Contrasts were calculated for single effects as well as for the differences between effects of Rolandic alpha and beta rhythms for analysis strategy (a) and (b).
Depending on our hypotheses two types of statistical evaluations were performed. In order to test our anatomically specified hypotheses “right versus left pericentral cortex” and “precentral versus postcentral cortex” statistical maps were small volume corrected (SVC). For anatomically open hypotheses whole-brain false discovery rate (FDR) correction was performed on voxel and cluster levels. Coordinates of activation sites are given in MNI (Montreal Neurological Institute) space.
RESULTS
Rolandic Rhythms in the EEG Data
Two representative examples of the EEG before and after gradient artifact correction are shown in Figure 4. The correlation between Rolandic alpha as well as beta rhythms with the motor task was much stronger for rhythms identified by blind source separation as compared to Rolandic rhythms extracted from single electrode signals (see Fig. 5) in each individual subject as well as for the entire group. Furthermore, Figure 5 illustrates that the Rolandic beta rhythm is stronger modulated by the motor task than the Rolandic alpha rhythm.
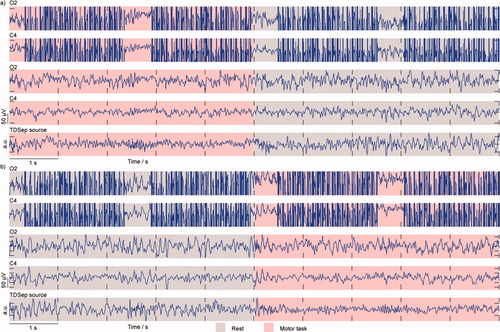
Two representative EEG epochs of a single subject before and after artifact correction. EEG is depicted for channels C4 and O2. In addition, the signal time course of this subject's TDSep source with highest correlation between alpha/beta band power and the motor task is shown. Sections of motor task and rest are indicated by red and gray color respectively. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
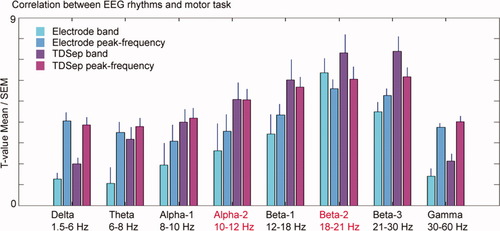
Correlation between rhythms and motor task. T-scores (mean and SEM) obtained by paired Student's t-testing rest versus motor task periods of the power of different frequency bands or the power of individual peak frequencies of best correlating EEG-channels (i.e. with highest t-score in the respective frequency band) and of best correlating TDSep sources. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
Rolandic rhythms derived from selected electrodes correlate better with the motor task at individual peak frequencies (except for the β-2 band), whereas Rolandic rhythms obtained from blind source separation (TDSep) correlate best in the beta range when defined by spectral bands (see Fig. 5).
Modulation of Rolandic rhythms by the motor task was more pronounced over the right hemisphere than over the left hemisphere, indicated by higher mean t-scores as well as higher mean TDSep weights at right versus left positions C4/C3: α-2 band: 0.83 (left), 2.62 (right); β-2 band: 1.36 (left), 1.85 (right); paired Student's t-test: P = 0.0004/P = 0.26 (see Fig. 6).
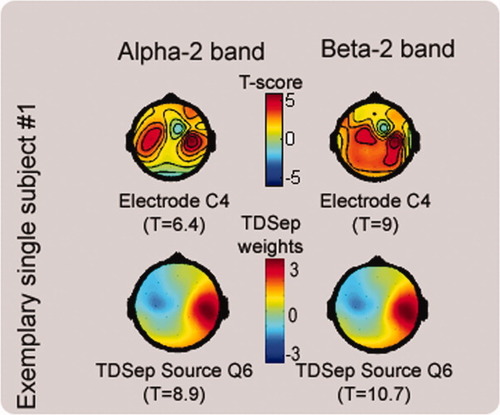
Topographies of correlation between motor task and rhythms. Exemplary single subject: upper row shows color-coded t-scores indicating the degree of correlation between motor task and the power of α-2 and β-2 bands. Highest correlation is found in pericentral areas. The best correlating electrode position with its respective t-score is printed below the scalpmap. Lower row: Color-coded are the weighting matrices of the TDSep sources best correlating with the motor task in the α-2 and β-2 band. In this subject for both bands the same source was identified. Source names and the respective t-scores are given below the scalpmaps. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
FMRI Correlates of “Rolandic Alpha Rhythm” and “Rolandic Beta Rhythm”
Subjects performed a bimanual motor task in a block design to modulate Rolandic rhythms. In all 15 subjects, a clear modulation of the 10- and 20-Hz Rolandic rhythms “during bilateral hand movement versus rest” was detected. As expected, both rhythms were suppressed during hand movement and reappeared during rest. This approach, however, implies that the three parameters “motor task”, “Rolandic alpha rhythm”, and “Rolandic beta rhythm” are highly intercorrelated. Specifically, the power of the two pericentral rhythms is most likely inversely correlated to the motor task. Because of this presumable inverse covariance between the rhythms' power and the motor paradigm, the BOLD signal variance, which correlates with the motor task, is also inversely correlated with Rolandic rhythms. As a consequence, voxels that are “activated” during hand movement will tend to be “deactivated” during periods of high “rhythm activity”. We addressed this issue by using the three different approaches as described above. The first approach implied calculation of one separate model for each regressor, thus testing whether each regressor correlates with the BOLD signal irrespective of the others. In this type of analysis, differences between the respective functional maps can indicate characteristics of the respective regressor. For example, in addition to movement-induced modulations of Rolandic rhythms, there are also spontaneous fluctuations. These fluctuations differ slightly between the hemispheres [Niedermeyer and Koshino,1975]. While it is not entirely clear whether such fluctuations represent the same phenomena as the movement-correlated events, they offer a continuous “additional signal”, which goes beyond the mere on-off dichotomy of the bilateral movement task. The EEG recordings at C3 versus C4 positions, respectively, may be able to pick up such lateralized fluctuations of Rolandic rhythms.
fMRI Correlates of Left Versus Right (C3/C4) Rolandic Beta Rhythms During a Motor Task
Whether BOLD correlates are specific for left versus right Rolandic rhythms was tested for C3/C4 Rolandic beta rhythms. TDSep sources were not used for this question since they are spatially distributed over both hemispheres. Rolandic beta rhythm was chosen since it was most intensely modulated by the motor task (see Fig. 5) and since it was clearly identified over both hemispheres (see Fig. 6). Statistical t-maps of fMRI correlates of Rolandic beta rhythm at left central electrode position C3 are depicted in Figure 7. Negative correlations between Rolandic beta rhythms and the BOLD signal in the pericentral cortex were maximal in the left hemisphere (MNI x, y, z: −53, −26, 55; P = 0.0001 voxel level; P = 0.001 SVC voxel level FDR-corrected) for Rolandic rhythms derived from the left central electrode position C3 and in the right hemisphere (MNI x, y, z: 39, −23, 66; P = 0.00003 voxel level; P = 0.002 SVC voxel level FDR-corrected) for Rolandic rhythms derived from the right central electrode position C4. For a better illustration, a lower statistical threshold of 0.01, uncorrected for multiple comparisons was chosen in Figure 7
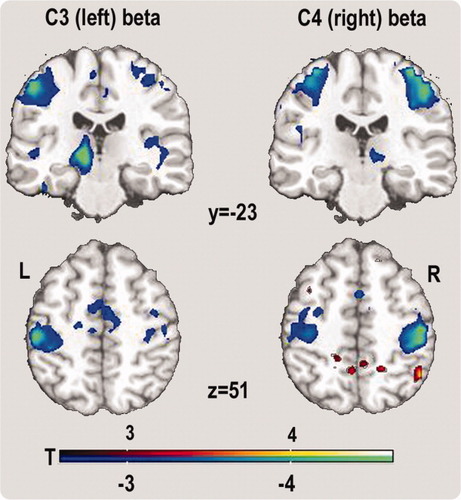
fMRI correlate of the Rolandic beta rhythm. Correlations between the BOLD signal and the Rolandic beta rhythm obtained from electrode positions C3 and C4 (random effects group analysis N = 15, P ≤ 0.01, uncorrected). One can see lateralized negative correlations dependent on the electrode position (C3: left/C4: right). T-values are color-coded. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
Thus, in general, there is an inverse correlation between the power of the Rolandic beta rhythm and the BOLD signal in cortical bilateral sensorimotor structures; however, there is a clear hemispheric dominance corresponding to the side of the electrode, i.e. the Rolandic beta rhythm obtained from the left hemisphere (“C3 Rolandic beta”) has a much stronger (inverse) correlation with the BOLD signal in the left hemisphere, and vice versa for the right side (see Fig. 7).
Pre- Versus Postcentral Distribution of fMRI Correlates of Rolandic Alpha and Beta Rhythms
There is no single optimal analysis addressing the question of whether there is a differential distribution within pericentral cortex between fMRI correlates of Rolandic alpha and beta rhythms. Therefore, different approaches were chosen as described in the Methods section. Results are listed in Table I and illustrated in Figure 8.
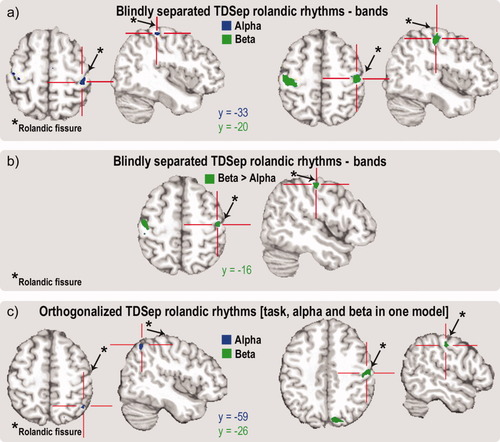
Maximum negative fMRI correlates of Rolandic alpha and beta rhythms in the pericentral cortex. All results are based on a random effects group analysis (N = 15). MNI y coordinates, indicating locations on the anterior-posterior axis are given in blue (Rolandic beta rhythm) and green (Rolandic alpha rhythm). For further details on location and statistics see Table I. (a) fMRI correlates of TDSep broad-band Rolandic alpha and beta rhythms based on separate models. (b) TDSep broad-band Rolandic beta contrasted against broad-band Rolandic alpha rhythm (based on separate models). Green areas exhibit significantly stronger inverse correlation for the Rolandic beta rhythm. (c) fMRI correlates of orthogonalized TDSep peak-frequency Rolandic alpha and beta rhythms based on a single model comprising motor task, Rolandic alpha and Rolandic beta rhythm. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
| Model | Contrast (negative if not stated otherwise) | MNI coordinate | Voxel level z-score | Voxel level P uncorrected | Voxel level SVC FDR-corrected |
|---|---|---|---|---|---|
| Separate models for alpha and beta | C4 alpha peak-frequency | 43, −23, 55 | 2.75 | 0.003 | 0.096 |
| C4 beta peak-frequency | 39, −23, 66 | 4.0 | 0.00003 | 0.002 | |
| TDSep alpha peak-frequency | 43, −36, 61 | 2.29 | 0.02 | 0.2 | |
| TDSep beta peak-frequency | 46, −20, 61 | 3.94 | 0.00005 | 0.001 | |
| TDSep alpha band | 43, −33, 61 | 3.6 | 0.00016 | 0.004 | |
| TDSep beta band | 49, −20, 55 | 4.39 | 0.0000056 | 0.00025 | |
| TDSep beta band > alpha band | 49, −16, 55 | 3.6 | 0.00016 | 0.005 | |
| Motor task (pos) | 36, −26, 61 | 5.07 | 0.0000002 | 0.000007 | |
| Alpha and beta in one model | TDSep alpha band | 43, −33, 61 | 2.72 | 0.003 | 0.1 |
| TDSep beta band | 49, −20, 55 | 4.99 | 0.00000030 | 0.000014 | |
| TDSep beta band > alpha band | 49, −16, 55 | 4.12 | 0.000019 | 0.001 | |
| Orthogonalized task/alpha/ beta in one model | TDSep alpha peak-frequency | 46, −59, 55 | 2.5 | 0.006 | 0.237 |
| TDSep beta peak-frequency | 59, −26, 50 | 3.11 | 0.001 | 0.033 | |
| Motor task (pos) | 36, −26, 50 | 5.41 | 0.00000003 | 0.00005 |
- All results are based on random effects group analyses (N = 15).
In addition to the results of our anatomically restricted hypothesis, additional loci within the entire brain are reported in Tables II and III.
| Model | Contrast | MNI coordinate | Voxel level z-score | Voxel-level p uncorrected | Voxel-level p FDR-corrected | Cluster level corrected | Anatomical label |
|---|---|---|---|---|---|---|---|
| Separate models for alpha and beta | TDSep beta band | −20, −53, −28 | 4.6 | 2 × 10−6 | 0.021 | 0.0005 | Left cerebellum |
| 49, −20, 55 | 4.39 | 2 × 10−6 | 0.025 | 0.00003 | Right pericentral cortex | ||
| −53, −23, 50 | 4.33 | 7 × 10−6 | 0.025 | 0.0001 | Left pericentral cortex | ||
| 20, −53, −28 | 3.71 | 0.0001 | 0.028 | 0.095 | Right cerebellum | ||
| 3, −7, 55 | 3.61 | 0.0002 | 0.032 | 0.534 | SMA | ||
| −13, −13, −22 | 3.50 | 0.0002 | 0.036 | 0.725 | Left brain stem/hippocampal gyrus | ||
| −46, −23, 17 | 3.48 | 0.0002 | 0.037 | 0.725 | Left insula | ||
| Motor task | −10, −39, 55 | 4.59 | 2 × 10−6 | 0.011 | 1 × 10−10 | Left/right paracentral lobule | |
| 39, 7, 55 | 4.28 | 9 × 10−6 | 0.011 | 1 × 10−7 | Right frontal lobe (BAs 6, 8, 9) | ||
| 20, −69, 50 | 3.54 | 0.0002 | 0.026 | 0.036 | Right precuneus/superior parietal lobe | ||
| Alpha and beta in one model | TDSep beta band | 49, −20, 55 | 4.99 | 3 × 10−7 | 0.007 | 0.00003 | Right pericentral cortex |
| −39, −23, 55 | 4.43 | 5 × 10−6 | 0.017 | 0.0004 | Left pericentral cortex | ||
| 7, −82, −22 | 3.89 | 0.00005 | 0.022 | 0.014 | Right cerebellum | ||
| −16, −53, −28 | 3.85 | 0.00006 | 0.023 | 0.167 | Left cerebellum | ||
| 0, −10, 61 | 3.72 | 0.0001 | 0.029 | 0.566 | SMA | ||
| −46, −23, 17 | 3.36 | 0.0004 | 0.047 | 0.738 | Left insula | ||
| TDSep beta (neg) > alpha (neg) | −53, −13, 50 | 4.07 | 0.00002 | 0.130 | 0.049 | Left pericentral cortex | |
| Orthogonalized task/alpha/ beta in one model | Motor task | 7, −39, 55 | 4.32 | 8 × 10−6 | 0.032 | 6 × 10−8 | Right/left paracentral lobule |
| 43, 10, 55 | 4.29 | 6 × 10−9 | 0.032 | 0.0001 | Right frontal lobe (BA 6,8) | ||
| 23, −69, 61 | 3.82 | 0.00007 | 0.036 | 0.0004 | Right precuneus/superior parietal lobe | ||
| −16, −66, 61 | 3.59 | 0.0002 | 0.043 | 0.067 | Left precueus/superior parietal lobe | ||
| Occipital classical alpha rhythm | O2 alpha band | −39, 7, 28 | 4.36 | 6 × 10−6 | 0.046 | 2 × 10−9 | Left frontal lobe |
| 59, −46, 39 | 4.27 | 0.00001 | 0.046 | 0.025 | Right supramarginal gyrus/inferior parietal lobule | ||
| −62, −36, 44 | 3.70 | 0.0001 | 0.046 | 0.013 | Left supramarginal gyrus/inferior parietal lobule | ||
| 30, −95, 11 | 3.65 | 0.0001 | 0.046 | 0.025 | Right occipital lobe | ||
| TDSep occipital alpha band | 30, −92, 6 | 4.05 | 0.00003 | 0.1 | 0.001 | Right occ. cortex | |
| −43, −56, 61 | 3.88 | 0.00005 | 0.1 | 0.014 | Left inf. parietal lobule | ||
| −7, 23, 44 | 3.71 | 0.0001 | 0.1 | 0.004 | R/L cingulated/medial frontal gyrus |
- All results are based on random effects group analyses (N = 15) and a significance threshold of P < 0.05 whole brain FDR corrected voxel level or corrected cluster level.
| Model | Contrast | MNI coordinate | Voxel level z-score | Voxel-level P uncorrected | Voxel-level P FDR-corrected | Cluster level corrected | Anatomical label |
|---|---|---|---|---|---|---|---|
| Separate models for alpha and beta | TDSep beta peak-frequency | −10, −43, 66 | 4.46 | 0.000004 | 0.094 | 4 × 10−6 | L/R paracentral lobule |
| TDSep beta band | −7, −33, 61 | 4.48 | 0.000004 | 0.067 | 0.00003 | L/R paracentral lobule | |
| Motor task | −16, −53, −28 | 5.44 | 3 × 10−8 | 0.0002 | 2 × 10−13 | Left/right cerebellum | |
| −46, −33, 61 | 5.31 | 6 × 10−8 | 0.0002 | 1 × 10−7 | Left pericentral cortex | ||
| 36, −26, 61 | 5.07 | 2 × 10−7 | 0.0003 | 4 × 10−7 | Right pericentral cortex | ||
| −13, −23, −6 | 5.03 | 3 × 10−7 | 0.0003 | 7 × 10−6 | Left thalamus | ||
| 16, −20, 0 | 4.84 | 6 × 10−7 | 0.0004 | 0.012 | Right thalamus | ||
| 30, −3, −11 | 4.44 | 4 × 10−6 | 0.001 | 0.005 | Right lentiform nucleus | ||
| 53, 13, −11 | 4.29 | 9 × 10−6 | 0.001 | 0.004 | Right temporal lobe (BAs 22, 38) | ||
| −46, −20, 17 | 4.04 | 0.00003 | 0.003 | 0.145 | Left insula | ||
| 3, −7, 50 | 4.00 | 0.00003 | 0.003 | 0.145 | Right/left medial frontal/cingulate gyrus (BAs 6, 24, 31) | ||
| −49, 7, −6 | 3.5 | 0.0002 | 0.009 | 0.036 | Left temporal lobe (BAs 13, 22) | ||
| Orthogonalized task/alpha/ beta in one model | TDSep alpha | 13, −92, 22 | 4.07 | 0.00002 | 0.104 | 0.036 | Left/right occipital lobe |
| −7, 53, 17 | 3.79 | 0.00008 | 0.104 | 0.015 | Left medial frontal gyrus/anterior cingulated (BAs 10, 32, 42) | ||
| Motor task | −16, −53, −28 | 5.41 | 3 × 10−8 | 0.0004 | 7 × 10−16 | Left/right cerebellum | |
| −43, −33, 61 | 5.11 | 2 × 10−7 | 0.0005 | 2 × 10−7 | Left pericentral cortex | ||
| 36, −26, 50 | 4.71 | 1 × 10−6 | 0.001 | 1 × 10−7 | Right pericentral cortex | ||
| 53, 13, −11 | 4.61 | 2 × 10−6 | 0.001 | 0.001 | Right temporal lobe (BAs 13, 22, 38, 44) | ||
| −43, −20, 17 | 4.29 | 9 × 10−6 | 0.002 | 0.049 | Left insula | ||
| −7, −3, 44 | 4.25 | 0.00001 | 0.002 | 0.026 | Right/left medial frontal/cingulate gyrus (BAs 24, 31) | ||
| −10, −23, −22 | 4.18 | 0.00001 | 0.002 | 0.001 | Left thalamus | ||
| −56, 10, −6 | 3.7 | 0.0001 | 0.006 | 0.079 | Left temporal lobe (BA 22) |
- All results are based on a random effects group analyses (N = 15) and a significance threshold of P < 0.05 whole brain FDR corrected voxel level or corrected cluster level.
Since we were interested in topographic differences of the BOLD correlates of both Rolandic rhythms in primary sensorimotor cortex, we looked for maximal (de-) activation sites (the tip of the iceberg) within the right pericentral cortex where rhythms had their strongest correlates in the EEG. Results are similar throughout all analyses. Maximum negative fMRI correlates of the Rolandic alpha rhythm were located posterior to the maximum negative fMRI correlates of the Rolandic beta rhythm throughout all analyses. Representative results yielded by two different methodological approaches are shown in Figure 8.
Figure 8a shows fMRI correlates of TDSep broad-band Rolandic alpha and beta rhythms based on separate models. Negative correlation in the right pericentral region was noted for the TDSep alpha rhythm to be located more posterior (MNI x, y, z: 46, −33, 61; P = 0.00016 voxel level uncorrected, P = 0.004 SVC voxel level FDR-corrected) as compared to the negative correlate of the TDSep beta rhythm (MNI x, y, z: 49, −20, 55; P = 0.0000056 voxel level uncorrected, P = 0.00025 SVC voxel level FDR-corrected. When contrasting alpha and beta effects in a group analysis on the second level (paired t-test), negative BOLD correlates of the TDSep Rolandic beta rhythms are significantly stronger in a precentral area (MNI x, y, z: 49, −16, 55; P = 0.00016 voxel level uncorrected; P = 0.005 SVC voxel level FDR-corrected) as compared to the effects of the TDSep Rolandic alpha rhythm (Fig. 8b).
As described under point “c” in “Analysis of fMRI data”, we also employed a fMRI-data modeling approach in which the three orthogonalized functional regressors “motor task”, “TDSep peak-frequency Rolandic alpha”, and “TDSep peak-frequency Rolandic beta” were included in one model. Two models were calculated with differing orthogonalization order of Rolandic alpha and beta rhythm regressors. Mean residual error was 857 when the Rolandic alpha rhythm regressor preceded the Rolandic beta rhythm regressor. In the converse case mean residual error was 872. Anatomical correlates were exactly the same for both models with slightly different statistical z-values. In the following we report the results of the model with the lower residual error. Results for the “motor task” (which are not the focus of this work) changed only slightly as compared to the separate-models approach given above (Table I). The posterior-anterior topographical distribution of FMRI responses to Rolandic alpha versus beta rhythms persisted, with the response to the Rolandic alpha rhythm, however, shifting backwards to the posterior parietal cortex (Fig. 8c). Pericentral negative fMRI correlates of the orthogonalized TDSep Rolandic alpha rhythm (MNI x, y, z: 46, −59, 55; P = 0.006 voxel level uncorrected; P = 0.237 SVC voxel level FDR-corrected) were located posterior to those of the orthogonalized TDSep Rolandic beta rhythm (MNI x, y, z: 59, −26, 50; P = 0.001 voxel level uncorrected; P = 0.033 SVC voxel level FDR-corrected). For this modeling approach, single subject analyses revealed topographically similar effects, i.e. precentral fMRI correlates versus posteroparietal fMRI correlates, in 14 subjects for the Rolandic alpha rhythm and in 12 subjects for the Rolandic beta rhythm (all P < 0.05, uncorrected).
Positive fMRI correlates of Rolandic rhythms in pericentral cortex
No positive fMRI correlates of Rolandic alpha or beta rhythms were identified in the right pericentral region throughout all analysis-approaches.
FMRI correlates of Rolandic rhythms beyond our anatomically restricted hypothesis
Negative and positive fMRI correlates of Rolandic rhythms exceeding the conservative statistical threshold of P < 0.05 at the whole brain FDR corrected voxel level or corrected cluster level occurring outside of the right pericentral cortex are listed in Tables II and III. Significant negative correlates were only found for the TDSep Rolandic broad-band beta rhythm, predominantly in both pericentral areas, bilateral cerebellum, medial frontal cortex (SMA) and left insula. Additional significant negative correlates were neither found for Rolandic rhythms obtained from single electrode positions nor for rhythms at individual peak frequencies. Positive fMRI correlates were identified for the TDSep peak-frequency and broad-band Rolandic beta rhythms in the bilateral paracentral lobule and for the TDSep peak-frequency alpha rhythm in the model comprising orthogonalized Rolandic rhythms and motor task in the occipital lobe and left medial frontal gyrus.
fMRI correlates of the posterior (classical) alpha rhythm during a motor task
For both the broad-band (8-12 Hz) alpha rhythm of the right occipital electrode position O2 and the TDSep posterior alpha rhythm, we found negative fMRI correlates in the right occipital cortex (Table II; Fig. 9c,d). For the O2 posterior alpha rhythm, additional negative correlates were located in the left frontal and bilateral supramarginal/inferior parietal cortex whereas for the TDSep posterior alpha rhythm additional negative fMRI correlates were found in the left inferior parietal lobule and the bilateral medial frontal gyrus. No significant positive fMRI correlates have been found for the posterior alpha rhythm during a motor task at the given conservative statistical threshold.
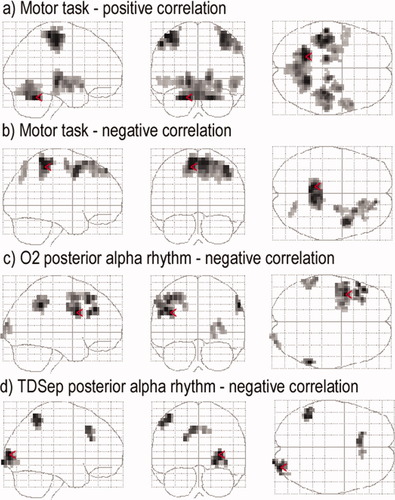
FMRI correlates of the bimanual motor task and the posterior (classical) alpha rhythm. All results are based on a random effects group analysis (N = 15, P < 0.05 FDR corrected voxel level or corrected cluster level). Red arrows indicate global maxima. (a) Positive fMRI correlates of the motor task obtained from a separate model not including Rolandic rhythms. (b) Negative fMRI correlates of the motor task obtained from separate model analysis. (c) Negative fMRI correlates of the posterior alpha rhythm derived at electrode position O2. (d) Negative fMRI correlates of the TDSep posterior alpha rhythm. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
fMRI correlates of the bimanual motor task
Positive and negative fMRI correlates of the bimanual motor task based on a separate model are shown in Table III/Figure 9a. Positive correlation was found in the bilateral cerebellum, bilateral pericentral cortex, bilateral thalamus, right lentiform nucleus, bilateral medial frontal and cingulated gyrus and left temporal lobe. Negative correlation (Fig. 9b) was found in the bilateral paracentral lobule, right frontal lobe and right precuneus/superior parietal lobe.
DISCUSSION
We employed simultaneous EEG-fMRI recordings for the functional assessment of Rolandic EEG rhythms during a bimanual motor task in healthy human subjects. We showed that: (1) Even subtle sensorimotor rhythms such as Rolandic alpha and Rolandic beta rhythms can be recovered from EEG recordings obtained during MRI data acquisition; (2) fMRI correlates of these rhythms can be identified via correlation with BOLD-sensitive MR image series; (3) Rolandic alpha and beta rhythms differ with respect to their fMRI correlates located in the postcentral gyrus (SI) for the former and in the precentral gyrus (MI) for the latter; (4) Finally, the strengths of Rolandic alpha and beta rhythms, respectively, are inversely related to the fMRI BOLD signal in the pericentral cortex.
Rolandic EEG Rhythms
Rolandic rhythms were first described by Jasper and Andrews [Jasper and Andrews,1936], and since then the nomenclature has varied among researchers, e.g. the term “mu rhythm” has sometimes been applied to the Rolandic alpha rhythm, and sometimes to both rhythms [Tiihonen et al.,1989]. Here, we use the terms “Rolandic alpha rhythm” and “Rolandic beta rhythm” respectively.
Both rhythms are suppressed during tactile stimulation [Cheyne et al.,2003] or voluntary phasic muscle activity [Jasper and Andrews,1936; Jasper and Penfield,1949; Pfurtscheller and Aranibar,1980; Pfurtscheller and Berghold,1989] and are enhanced by visual stimulation [Brechet and Lecasble,1965; Jasper and Andrews,1938; Koshino and Niedermeyer,1975]. However, Rolandic alpha and beta rhythms are not always modulated in parallel and their spatial distribution differs, with the beta rhythm being spatially more widespread distributed than the alpha rhythm [Magnus,1954]. In MEG studies during phasic motor activity [Salmelin and Hari,1994a] and tactile stimulation [Cheyne et al.,2003], the reactive sources of Rolandic beta rhythm were localized in MI and for Rolandic alpha rhythm in SI [Salmelin et al.,1995].
The precise function of these rhythms is not clear. Similar to the posterior alpha rhythm they are frequently referred to as “idle rhythms” indicating a “resting state” of the respective (sensory) system [Pfurtscheller,1992]. Apart from the suppression during somatosensory stimulation or during a motor action, this notion is in agreement with modulations of motor cortex excitability with Rolandic rhythms' strength as shown in transcranial magnetic stimulation (TMS) studies: Motor responses evoked by TMS have been shown to be facilitated during event-related desynchronization (ERD), i.e. during a decrease in Rolandic rhythm strength of up to 200 ms after somatosensory stimulation [Deletis et al.,1992; Deuschl et al.,1991; Hirashima and Yokota,1997; Komori et al.,1992; Maertens de Noordhout et al.,1992; Rossini et al.,1991; Terao et al.,1995] and reduced motor cortex excitability has been shown during event-related synchronization (ERS), i.e. an increased power of Rolandic rhythms following 200-1,000 ms after somatosensory stimulation [Chen et al.,1999].
EEG Rhythms Obtained During MRI Data Acquisition: Technical/Methodological Issues
The relationship of brain electrical activity and perfusion/metabolism has been studied by combined EEG and positron emission tomography (PET) [Leuchter et al.,1999; Oakes et al.,2004]. FMRI has the advantage of having a faster time resolution than PET, but artifacts due to electro-magnetic interference are inherent with this technique. Several studies have now shown that EEG can be recovered from recordings obtained within the MR environment [Bonmassar et al.,2002; Lemieux et al.,2001] and even from segments obtained during MRI data acquisition [Becker et al.,2005; Salek-Haddadi et al.,2003]. Few studies, however, have systematically evaluated the quality of the EEG after artifact removal [Becker et al.,2005; Goncalves et al.,2007; Grouiller et al.,2007; Ritter et al.,2007; Sammer et al.,2005], and the issue of its full validity is still not finally resolved. It clearly would constitute a further argument for the validity of the EEG-fMRI approach if even very subtle EEG features can be recovered that behave in a “meaningful” way, e.g. showing the expected (previously described) reaction to certain stimuli. Previous studies have shown that the posterior alpha rhythm can be obtained from EEG recorded during and/or between MRI data acquisition, and that the signal-to-noise ratio of the EEG is sufficient to use the power of the alpha rhythm as a regressor for modeling of the fMRI data [Feige et al., 2005]. In this study, we extend this approach to Rolandic rhythms with amplitudes markedly smaller than those of the posterior alpha rhythm (8-25 μV when compared to 20-60 μV [Jasper and Andrews,1936]. Nevertheless, gradient artifact correction made it possible to recover these rhythms with their major features, such as pericentral topography, motor-task reactivity and spectral predominance in the alpha and beta band. Further the EEG signal was strong enough to act as a regressor in BOLD correlation analysis, i.e. it explained a significant portion of the BOLD-signal variance.
There Is Distinct Laterality of the fMRI Response to Right Versus Left Rolandic Rhythms
There are strong and clearly lateralized correlations between Rolandic rhythms that were recorded from the right or from the left hemisphere (“C3/C4 Rolandic rhythms”) and the BOLD signal. The lateralization of the BOLD signal, particularly for the Rolandic areas (MI, SI), clearly corresponded to the site of the EEG electrode, i.e. there was a left hemispheric dominance in fMRI signal for C3 and right hemispheric dominance for C4 respectively. These findings indicate that spontaneous fluctuations of the Rolandic rhythms, occurring in addition to the block-wise modulations by the bimanual motor task, have distinct fMRI correlates in the respective hemisphere (see Fig. 7).
Rolandic Alpha and Beta Rhythms Differ with Respect to Their fMRI Correlates
With all employed modeling approaches, we found spatial differences in the sites of fMRI correlation between the Rolandic alpha versus beta rhythm. The fMRI correlates of the Rolandic alpha rhythm meet our strict significance criteria only in the case of the blind-source separated broad-band Rolandic alpha rhythm. The consistency of the anatomical locus in the postcentral cortex (as compared to the precentral correlate of the Rolandic beta rhythm, see Table I), adds to the credibility of this finding and exemplifies the utility of separating various EEG signatures.
Our findings are in agreement with previous MEG studies in which reactive sources of the Rolandic alpha rhythms were localized in the SI and the Rolandic beta rhythms in the MI [Salmelin et al.,1995] during phasic motor activity [Salmelin and Hari,1994a] and tactile stimulation [Cheyne et al., 2003].
There are electrocorticographic studies reporting rather widespread and individually variable cortical desynchronization during movement in both the precentral and postcentral cortex [Crone et al., 1998]. These authors are in favor of the view that oscillatory suppression reflects a synaptic network of a distributed cortical system rather than a locally isolated phenomenon, such that activation of a subset of the network will result in suppression of oscillations elsewhere in the network. Also in intracortical recordings, both the Rolandic alpha and beta rhythms are found in pre- and postcentral areas in human [Jasper and Penfield,1949] and in monkey [Rougeul et al.,1979]. Thus, the association of the Rolandic beta rhythm with motor cortex and the Rolandic alpha with somatosensory cortex is not definitive. Nevertheless, in these intracranial recordings, the maximal beta rhythm tends to be found more anterior and the alpha rhythm more posterior to the Rolandic fissure. These findings are supported by our results. In a recent combined EEG-fMRI study a temporary post-movement beta synchronization (“beta rebound”) was paralleled by a BOLD signal increase in the primary sensorimotor cortex [Parkes et al.,2006]. In this study the most significant “β-rebound” related BOLD signal change was located in the postcentral sulcus. Another recent study employing synthetic aperture magnetometry localized the post-movement beta rebound to the precentral gyrus whereas movement related desynchronization of Rolandic alpha (mu) and beta rhythms was localized to the postcentral gyrus [Jurkiewicz et al., 2006]. In our present study the continuous time course of Rolandic beta and alpha band desynchronization and synchronization across a motor-task was correlated to the BOLD signal. Thus, we identified regions where the BOLD signal followed the time course of both motor-task related synchronization and desynchronization of Rolandic alpha and beta rhythms.
Interestingly, although our results show a maximal cortical fMRI response to the (bimanual) motor task in the left SMI (Fig. 9a, Table III), the maximum fMRI correlate of the “TDSep Rolandic rhythms” was throughout in the right sensorimotor cortex. This is in concordance with our EEG findings of stronger motor-task related modulations of Rolandic rhythms in the right hemisphere. A slightly stronger Rolandic alpha rhythm in the right hemisphere has also been found independent of the handedness of the subject [Niedermeyer and Koshino,1975]. There are EEG reports showing stronger desynchronization in the left sensorimotor cortex during unimanual hand movements irrespective of the side of movement. However, these EEG data are associated with a stronger β-rebound in the right hemisphere [Stancak and Pfurtscheller,1996,1997]. Probably the latter effect outweighs the former resulting in a stronger modulation in the right hemisphere in our data.
The direct comparison of the maximal negative BOLD response to the Rolandic alpha rhythm versus beta rhythm indicates a motor cortex association of the beta rhythm (precentral activations) and a somatosensory association (postcentral/parietal activation) for the Rolandic alpha rhythm (Fig. 8, Table I).
In addition we found a positive correlation between the Rolandic beta rhythm and the BOLD signal in the bilateral paracentral lobule, i.e. an increasing strength of the rhythm was associated with an fMRI signal increase in this region. This contradictory behavior of the BOLD signal in the bilateral paracentral lobule and the primary sensorimotor hand area might be linked with the finding of bilateral increase of oscillations in hand sensorimotor cortices during foot movements [Pfurtscheller and Neuper,1994]. The hand movement task may induce short lasting idling states in the neuronal representation of other body parts as discussed by Pfurtscheller and Neuper and thus also lead to an inverse hemodynamic behavior in respect to somatomotor hand areas.
Functional Implications for Rolandic Rhythms
While above we emphasized the maximal inverse correlation between the Rolandic beta rhythm and the BOLD signal in MI, it is equally notable that when looking at the whole brain, the inverse correlation to Rolandic beta is seen to be almost identical to the activation pattern for the bimanual motor task. Since it is not possible to distinguish between only correlating brain activations and those which are directly attributable to beta synchronization, one should nevertheless mention that previous work has suggested a role of beta oscillations in widespread somatosensory and motor areas during premovement maintenance behavior [Donoghue et al.,1998; MacKay and Mendonca,1995; Rougeul et al.,1979; Sanes and Donoghue,1993]. A beta synchronized large-scale network that links pre- and postcentral areas during premovement motor maintenance behavior has been identified in monkey [Brovelli et al.,2004]. It has also been proposed that voluntary movement depends on a corticoperipheral cortical sensorimotor loop [Favorov et al.,1988] and that this loop is supported by oscillatory neuronal activity [MacKay,1997]. Different rhythms are known to employ different dynamic mechanisms to synchronize based on different ionic currents [Bibbig et al.,2002; Kopell et al.,2000] and beta rhythm tends to indicate synchronization over long conduction delays. Thus, oscillations may bind sensorimotor areas into a functional loop during premovement motor maintenance behavior [Brovelli et al.,2004]. A dynamic beta range (16–28 Hz) synchronization has also been demonstrated between activity in primary and premotor cortex and muscle activity, starting after termination of phasic voluntary movement, during a period of tonic muscle activity [Feige et al.,2000]. Feige et al. reported a low frequency (2–14 Hz) synchronization of the same cortical areas and medial premotor cortex with the EMG signal during movement execution. They also suggested that beta synchronization may reflect transition of the motor network into a new equilibrium state, while the low frequency synchronization may be related to movement execution.
In addition to inverse correlations to the BOLD signal, there are also positive correlations of the TDSep Rolandic beta rhythm in the bilateral paracentral lobule. It seems likely that these represent an attentional network which (at first glance rather counter-intuitively) is activated during the rest period. An explanation may be derived from a previous study [MacKay and Crammond,1987] in which the posterior parietal cortex, BA 5, bilaterally has been shown to be activated during expectation of an event. As described above, the positive hemodynamic behavior in the bilateral paracentral lobule could also be induced by short lasting idling states in the neuronal representation of other body parts than the functionally activated hand area. Lastly, a potential explanation is given by Gusnard et al. [Gusnard et al.,2001] who proposed an involvement of these areas in self-referential mental activity that becomes attenuated during an attention demanding motor task itself.
We also investigated the fMRI correlates of the posterior (classical) alpha rhythm as a control. Confirming previous findings [Feige et al.,2005; Goldman et al.,2002; Moosmann et al.,2003], the BOLD-fMRI signal in the occipital cortex was inversely related to the strength of the posterior alpha rhythm (Fig. 9c,d, Table II). The inverse relationship is more pronounced (see also Table II) for the blindly separated (TDSep) posterior alpha rhythm, which may be attributed to the separation of the posterior alpha rhythm from other rhythms and EEG signatures. The clear anatomical separation of fMRI correlates between Rolandic rhythms on the one side and occipital alpha on the other side confirms the regional specificity of the EEG-fMRI approach.
Lauf's group has proposed that MR correlates of the occipital alpha and beta band also reflect global mental states [Laufs et al.,2003a,b,2006]. While this seems to be plausible given the fact that alpha and beta spectral content indexes mental activities, it also highlights the challenge to functionally separate the multiplicity of cortical rhythms superimposed in the EEG. In this study, the finding that the strength of each of the three different background rhythms (Rolandic alpha, Rolandic beta, and posterior alpha) inversely correlates with the fMRI signal in “its cortical area” indicates that (1) functional segregation of the rhythms was sufficient and (2) this relation between rhythms and blood oxygenation in the underlying cortex is possibly a general feature presumably due to similar fundamental physiological mechanisms.
CONCLUSION AND PERSPECTIVES
On the basis of the assessment of Rolandic alpha and beta EEG rhythms during a bimanual motor task with simultaneous EEG and fMRI, we identified distinct patterns of brain areas presumably involved in these rhythms. Our data suggest that the Rolandic alpha rhythm is linked predominantly to the somatosensory system, while the Rolandic beta rhythm is more related to motor processing. We anticipate more information on the functional role of Rolandic rhythms to come from future simultaneous EEG-fMRI studies based on other types of tasks and by investigating the interaction of these background rhythms with evoked activity. Furthermore, we expect the EEG-fMRI approach to be useful for studying other types of EEG rhythms [Niessing et al.,2005], such as gamma rhythms or high frequency (>600 Hz) oscillations as shown by our current work [Ritter et al.,2006].
Acknowledgements
We thank Robert Becker, Michael Breakspear, Frank Freyer, Hauke Heekeren, Randy McIntosh, Martin Stemmler, and Birol Taskin for helpful comments.




