A W-test collapsing method for rare-variant association testing in exome sequencing data
ABSTRACT
Advancement in sequencing technology enables the study of association between complex disorder phenotypes and single-nucleotide polymorphisms with rare mutations. However, the rare genetic variant has extremely small variance and impairs testing power of traditional statistical methods. We introduce a W-test collapsing method to evaluate rare-variant association by measuring the distributional differences between cases and controls through combined log of odds ratio within a genomic region. The method is model-free and inherits chi-squared distribution with degrees of freedom estimated from bootstrapped samples of the data, and allows for fast and accurate P-value calculation without the need of permutations. The proposed method is compared with the Weighted-Sum Statistic and Sequence Kernel Association Test on simulation datasets, and showed good performances and significantly faster computing speed. In the application of real next-generation sequencing dataset of hypertensive disorder, it identified genes of interesting biological functions associated to metabolism disorder and inflammation, including the MACROD1, NLRP7, AGK, PAK6, and APBB1. The proposed method offers an efficient and effective way for testing rare genetic variants in whole exome sequencing datasets.
1 BACKGROUND
Sequencing technology development in recent years allows deep DNA sequencing to be done at lower cost, and has made available the study of extremely low-frequency variants in the Next-Generation Sequencing (NGS) dataset. One main challenge in studying rare-variant association is the lack of statistical power due to low minor allele frequency (MAF). A number of statistical methods for rare-variant association testing have been proposed, which can be generally divided into two categories, the burden tests including the Weighted Sum Statistic (WSS; Madsen & Browning, 2009) and Combined Multivariate Collapsing (Li & Leal, 2008), and the variance component tests such as the C-alpha test (Neale et al., 2011) and the Sequence Kernel Association Test (SKAT; Ionita-Laza et al., 2013). Both types of methods increase the power by pooling adjacent genetic markers to conduct the tests. In this article, we introduce a W-test collapsing method to evaluate rare-variant data. The method tests for distributional differences in cases and controls using a retrospective design after aggregating allele frequencies within a genomic region. The power and type I error rate of W-test collapsing is compared with the WSS and the SKAT using simulated datasets; it shows better performance and faster in computing speed. The proposed method is also applied on real exome sequencing data set of hypertensive disorder, and genes with meaningful biological function related to metabolic disorder have been found.
2 METHOD
2.1 The W-test
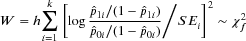
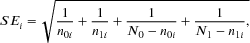
is the proportion of cases in cell-i out of total case number N1, and 
is the proportion of controls in cell-i out of total control number N0. SEi is the standard error of log odds ratio of cell-i, in which n1i and n0i are the number of cases and controls in the ith cell. The scalar h and the degrees of freedom parameter f are obtained by estimating the covariance matrix from bootstrapped data under null hypothesis. The statistic inherits a chi-squared distribution with f degrees of freedom. Empirical studies give h ≈ (k−1)/k and f ≈ k−1. Because the parameters are estimated from the data, they could reduce bias in testing probability distribution arose from complex data structures (Wang et al., 2016).2.2 The W-test collapsing method
The W-test collapsing method is a direct extension of the original W-test main effect evaluation on rare variants. Suppose a genomic region contains m rare SNPs; each SNP forms a contingency table. The m contingency tables of SNPs in the genomic region are summed cell by cell, and a combined contingency table is formed for this region. The W-test collapsing applies the original W-test on top of the combined table as a new statistic, which still follows a chi-squared distribution with f degrees of freedom. The h and f are estimated from bootstrapped collapsing region under the null hypothesis (Supporting Information).
2.3 Comparison with other rare-variant methods
Two representative rare-variant methods are considered as alternative approaches, namely, the SKAT and the WSS (Ionita-Laza et al., 2013; Madsen & Browning, 2009). The SKAT is a kernel machine regression method that incorporates a variance component score for coefficient evaluation, which has the advantage of dealing with both continuous and discrete phenotypes, and can test genetic effect in opposite directions (Wu et al., 2011). The WSS first gives each individual a weighted sum score of mutations counts, and then test for excess of mutations in cases compared to null hypothesis through a rank-sum statistic. The testing statistic is then permutated to calculate P-values (Sung et al., 2014).
2.4 Simulation data I
- Scenario I: In a causal gene, 12 causal SNPs cluster together in the same effect direction.
- Scenario II: In a causal gene, eight causal SNPs cluster together in opposite effect directions, with six SNPs of risk effect and two SNPs of protective effect.
There are 37.5% causal variants in Scenario I, and 25% in Scenario II. Scenario I model favors burden-like test, and scenario II is suitable to apply the variance component test (Sung et al., 2014). A gene is positive if its P-value is smaller than Bonferroni corrected alpha of 5% in 60 genes, namely, 0.00083. Power is the averaged true positive proportion in 500 replicated datasets, and type I error rate is the averaged false positive proportion.
2.5 GAW18 simulated and real data sets
The proposed method is applied on the simulated and real data set of the Genetic Analysis Workshop 18 (GAW18). The subjects are unrelated Mexican Americans who are enriched in type 2 diabetes, drawn from the T2D-GENES consortium project 2 (Cordell, 2014). The GAW18 simulated data contains real genetic data and predefined systolic and diastolic blood pressure (SBP and DBP) generated from a linear regression model (Cordell, 2014). Hypertension is defined at SBP > 90 mmHg or DBP > 140 mmHg. The total number of causal SNPs is 164. The simulated datasets consist of 330 cases, 1,600 controls, and 42,825 rare SNPs; 200 replicated phenotypes are used for power and type I error rate calculation. The rare-variant methods need to be applied based on a certain genomic region, while the optimal regions can be nonidentical for different methods. We estimate optimal collapsing window for each method at which they have the best power for the GAW18 simulated dataset. The list of window size considered is {5, 10, 15, 30, 50}. The optimal window for the SKAT and the W-test is 15 SNPs, and for WSS is 10 SNPs. A causal region is defined as the genomic area containing at least one causal SNP. Receiver operating characteristic (ROC) curve is plotted using the top number of collapsed regions. For real data analysis, there are 398 hypertensive individuals and 1,453 controls. Quality control (QC) is conducted to remove variants with missing value percentage over 5% and inconsistent genotyping format. Odd numbered chromosomes are evaluated and the total number of rare SNPs passed QC is 308,722 in the real dataset. The collapsing window size for real data is 15, so the number of multiple tests is 308,722/15 = 25,385, and Bonferroni corrected significance level at 5% alpha is 1.97 × 10−6.
3 RESULTS
3.1 Comparison of alternative methods in simulation data
In Scenario I where causal SNPs in a gene have the same effect direction, the W-test's power is 66.6%, slightly better than WSS's 66.3%. Both burden tests outperform the SKAT's power 55.9% under this scenario (Table 1). For Scenario II, where the causal markers show different effect directions, the SKAT's power is the highest, 93.0%, followed by W-test's 47.1% and WSS's 39.6%. All methods’ type I error rates are conservative: 0.13% for W-test, 0.13% for SKAT, and 0.17% for WSS (Table 1). The W outperforms WSS in both scenarios. Importantly, the W-test takes 0.06 seconds to evaluate one gene; it is 235 times faster than SKAT, and 393 times faster than the WSS. The W-test benefits from its intrinsic probability distribution estimated from the small bootstrapped samples to calculate P-values, compared to other rare-variant association tests that require complete permutation or Monte Carlo estimation.
| Statistical Tests | Power Scenario Ia | Power Scenario IIb | Type I Error Rate | Speedc (sec) |
|---|---|---|---|---|
| WSS | 66.3% | 39.6% | 0.17% | 23.59 |
| SKAT | 55.9% | 93.0% | 0.13% | 14.13 |
| W-test | 66.6% | 47.1% | 0.13% | 0.06 |
- a Scenario I: causal SNPs clustered together with the same effect direction.
- b Scenario II: causal SNPs clustered together, with opposite effect directions.
- c Speed is the averaged elapsed time of evaluating one gene.
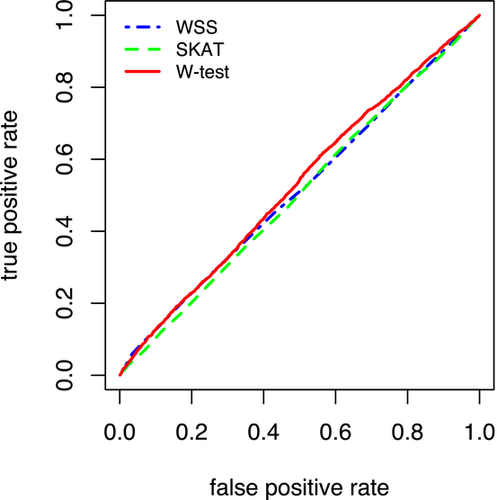
3.2 Application to GAW18 simulation study
The ROC curves of the W-test, SKAT, and the WSS are plotted in Figure 1. The figure shows that in the GAW18 dataset, all methods have low power and high false-positive rates. Similar lack of power has been observed by other studies on the same data (Cordell, 2014; Rui Sun, Hu, Zee, & Wang, 2015; Sung et al., 2014). Nevertheless, the W-test performs the best among the three methods. At false-positive rate 52.5%, the W-test collapsing has true positive rate (TPR) 57.3%, which is 52% for the SKAT and 52.8% for the WSS. The causal SNPs’ distribution in the top-ranked causal genes is exhibited in Table 2. All methods are able to find extremely rare variants with MAF 0.0003 and SNPs of very small effect sizes. The characteristics of identified causal markers are also intriguing: except for one gene ZBTB38 that is identified by all three methods, the regions short-listed by SKAT and WSS share no similarities, while the W-test found common regions to the other two methods (Table 2). The causal regions identified by SKAT are mostly composed of a single SNP with very large effect sizes (coefficients with absolute value ranges from 0.06 to 20); and the WSS identified regions containing two or more causal SNPs of moderate effect size (coefficients in the linear regression with absolute magnitude under 1.5). Interestingly, the W-test collapsing identified both the moderate effect sizes genes SEMA3F and MUC13, and the unique genes SENP5 of a large effect size. These results showed that the W-test collapsing has slight power advantage than the SKAT and WSS in the GAW18 data; it shares common properties of the other two methods, and also has unique finding of its own.
| Causal SNPs in the Gene | |||||||
|---|---|---|---|---|---|---|---|
| Method | Rank | Gene | Number of Causal SNPs | Position | MAF | SBP Effect | DBP Effect |
| SKAT | 1 | ZBTB38 | 1 | 141164276 | 0.0003 | –0.007 | –0.002 |
| 2 | ARHGEF3 | 2 | 56835799 | 0.0003 | –0.067 | –0.062 | |
| 56835795 | 0.0008 | –0.059 | –0.055 | ||||
| 3 | MAP4 | 1 | 48040284 | 0.0003 | –20.808 | –9.682 | |
| 4 | FLNB | 1 | 58134409 | 0.0005 | 1.687 | 0.249 | |
| 5 | MUC13 | 1 | 124646631 | 0.0003 | 0 | –2.178 | |
| WSS | 1 | ZBTB38 | 1 | 141164276 | 0.0003 | –0.007 | –0.002 |
| 2 | SEMA3F | 3 | 50222143 | 0.0008 | 0.706 | 0.505 | |
| 50214207 | 0.0005 | 0.00002 | 0.00001 | ||||
| 50222178 | 0.0010 | 0.00007 | 0.00005 | ||||
| 3 | SEMA3F | 3 | 50222879 | 0.0010 | 1.361 | 0.973 | |
| 50223334 | 0.0003 | 1.010 | 0.722 | ||||
| 50223764 | 0.0010 | 1.101 | 0.787 | ||||
| 4 | MLH1 | 2 | 37048495 | 0.0005 | 0 | –0.454 | |
| 37045960 | 0.0008 | 0 | –0.280 | ||||
| 5 | MLH1 | 2 | 37061893 | 0.0003 | 0 | –0.00004 | |
| 37061929 | 0.0005 | 0 | –0.00001 | ||||
| W-test | 1 | ZBTB38 | 1 | 141164276 | 0.0003 | –0.007 | –0.002 |
| 2 | SEMA3F | 3 | 50222879 | 0.0010 | 1.361 | 0.973 | |
| 50223334 | 0.0003 | 1.010 | 0.722 | ||||
| 50223764 | 0.0010 | 1.101 | 0.787 | ||||
| 3 | MUC13 | 2 | 124632448 | 0.0005 | 0 | –1.244 | |
| 124639097 | 0.0008 | 0 | –0.476 | ||||
| 4 | SENP5 | 5 | 196612750 | 0.0003 | –4.336 | 0 | |
| 196612959 | 0.0062 | –3.169 | 0 | ||||
| 196613022 | 0.0003 | –1.697 | 0 | ||||
| 196613096 | 0.0003 | –4.271 | 0 | ||||
| 196613191 | 0.0008 | –0.635 | 0 | ||||
| 5 | SEMA3F | 4 | 50225153 | 0.0003 | 1.418 | 1.013 | |
| 50225255 | 0.0003 | 0.00003 | 0.00002 | ||||
| 50225285 | 0.0003 | 1.391 | 0.994 | ||||
| 50225454 | 0.0003 | 0.254 | 0.182 | ||||
3.3 Application to real hypertension exome sequencing data
We applied the W-test collapsing method on real exome data of hypertensive disorder. One region reached Bonferroni corrected significance level. Not surprisingly, SNPs in this region were not discoverable by single marker test as they are individually nonsignificant. The identified chromosome position contained the gene MACROD1/LRP16 (11q11, average MAF = 0.001, odds ratio for collapsed marker = 3.84, W-test P-value 6.1 × 10−7), which is a ubiquitous protein module that binds ADP-ribose derivatives, and supports many different protein functions and pathways. It was reported that the LRP16 is overexpressed in tissues of colorectal and gastric carcinoma patients (Li, Zhao, & Han, 2009; Xi, Zhao, & Han, 2010). The top 17 regions that have large-to-moderate effect are listed in Table 3. These include genes NLRP7, AGK, PAK6, and APBB1, which have potential association to hypertension: The NLRP7 (MAF = 0.0027, OR = 2.23, W-test P-value = 8.3 × 10−6) encodes a protein that is implicated in the activation of proinflammatory caspases through multiprotein complexes inflammasones. Studies reported that this gene is associated with molar pregnancy and other pregnancy complications (Sebire et al., 2013; Ulker et al., 2013). The acylglycero kinase (AGK) is involved in lipid and glycerolipid metabolism, and it was found to have a significant overexpression in retinas of diabetic rats (Abu El-Asrar et al., 2013), and may play a role in the development of cataract (Aldahmesh et al., 2012). The gene PAK6 is a p21-activated kinase that is central to signal transduction and cellular regulation. Previous cell-line, tissue, and gene expression studies reported that this gene may play essential roles in the initiation and progression of hepatocellular carcinoma (Chen et al., 2014; Fang et al., 2014). The protein encoded by APBB1 is a member of the Fe65 protein family, and interacts with the transcription factor LBP1 and the low-density lipoprotein receptor-related protein (Davidson & Shelness, 2000).
| Rank | Position | Gene | Chr | MAF | OR | W-test P-Value |
|---|---|---|---|---|---|---|
| 1 | 64122856-64127883 | MACROD1/LRP16 | 11 | 0.0010 | 3.84 | 6.1 × 10−7 |
| 2 | 149520895-149521591 | — | 7 | 0.0012 | 3.09 | 5.2 × 10−6 |
| 3 | 54947030-54947395 | NLRP7 | 19 | 0.0027 | 2.23 | 8.3 × 10−6 |
| 4 | 5809248-5809272 | — | 11 | 0.0007 | 1.92 | 9.3 × 10−6 |
| 5 | 40843119-40843343 | — | 17 | 0.0004 | 8.64 | 9.9 × 10−6 |
| 6 | 115091763-115091808 | — | 13 | 0.0035 | 0.31 | 1.1 × 10−5 |
| 7 | 91732176-91746400 | — | 7 | 0.0006 | 4.44 | 2.0 × 10−5 |
| 8 | 67103877-67109739 | HELZ | 17 | 0.0003 | 14.8 | 3.0 × 10−5 |
| 9 | 141619479-141635585 | AGK | 7 | 0.0015 | 2.55 | 3.6 × 10−5 |
| 10 | 141618669-141619479 | AGK | 7 | 0.0012 | 2.80 | 3.9 × 10−5 |
| 11 | 6328839-6413690 | — | 9 | 0.0017 | 2.22 | 4.1 × 10−5 |
| 12 | 40268764-40290931 | PAK6 | 15 | 0.0022 | 2.14 | 5.0 × 10−5 |
| 13 | 58102391-58111521 | ZSCAN18 | 19 | 0.0006 | 4.20 | 5.2 × 10−5 |
| 14 | 41113238-41131622 | KRTAP9-7 | 17 | 0.0014 | 2.52 | 5.5 × 10−5 |
| 15 | 7794026-7797451 | — | 17 | 0.0010 | 2.63 | 6.6 × 10−5 |
| 16 | 2435288-2435470 | — | 11 | 0.0011 | 2.75 | 9.3 × 10−5 |
| 17 | 6341489-6411783 | APBB1, SMPD1 | 11 | 0.0007 | 3.00 | 9.9 × 10−5 |
- MAF, average minor allele frequency in the collapsing region; OR, odds ratio for minor allele of the collapsed marker.
4 DISCUSSION
We propose a W-test collapsing method to test the association between a dichotomous phenotype and rare genetic variants. It is model-free, fast, and tests the distributional differences in cases and controls through integrated log odds ratios. Because of the odds ratio core, it has a unique retrospective design that is suitable to be applied on both prospective and retrospective data sets. The proposed method can be categorized as a burden test; therefore, it is more advantages under the scenario when the SNPs effect directions are the same, compared to variance component test. It outperforms another burden test WSS under different effect scenarios. The advantage of the proposed method, apart from power and controlled type I error rate, is its P-value calculation free from large permutations. There are two major benefits: the first one is the computing speed, while almost all rare-variant tests have heavy computing burden, which prohibits possible optimization of collapsing region in whole exome sequencing data. Second, the proposed test inherits a data-dependent probability distribution. The method makes use of small bootstrapped samples under null hypothesis to estimate degrees of freedom (noninteger) for the testing probability distribution. Because the estimation considers data covariance structure, the resulting chi-squared distribution reduces potential bias due to complex data structures and therefore gives more-accurate P-values at minimum computing cost.
In the GAW18 simulation dataset, we compared different methods at their optimized collapsing region, which is usually not performed in the literature. The optimal bin size is related to the number of causal markers in a region, their effect size, effect direction, weighting scheme, and the distribution of mutations in cases and controls. This study demonstrated that the optimal window sizes are not the same for different methods; and the best collapsing bin is smaller than the commonly adopted range, such as a gene or pathway (Ionita-Laza et al., 2013; Madsen & Browning, 2009). Further study is needed to explore how to locate the best collapsing region in real exome sequencing data.
The W-test collapsing method shared similarities with the WSS that they both identified the regions populated with many causal variants in the GAW18 simulation data. There are differences in the two burden methods as well: the WSS mainly found variants with moderate effect size, but the W-test collapsing also identified large protective effect variants. The reason can be explained from the formulation of the two statistics. The WSS adds the number of mutated alleles in a genomic region and weight them inversely by the proportion of mutations in the unaffected subjects. A critical assumption of the WSS is that the minor alleles are mutations and contribute to disease risk (Madsen & Browning, 2009); therefore, if the minor allele with protective effect is concentrated in the unaffected, the WSS will down weight the variants and may miss them. As a result, the causal gene SENP5 that contains five large negative effects SNPs is not shortlisted by the WSS in the GAW18 simulation study, in which most of the mutations in this gene occur in the unaffected (Table 2). On the contrary, the W-test collapsing does not make assumption on mutation effect; it directly tests for the distributional differences between the affected and unaffected; therefore, it is more general to identify protective effect rare variants. The SKAT performs a kernel regression using variance component in each region, and variants with small MAF are given heavier weights. The SKAT method tends to select a region that includes a few rare variants with large effect sizes, and it allows variants within a region to adopt opposite effect directions. In the GAW18 simulation study, four of the five top regions identified by SKAT contain only one causal marker, and the other gene ARHGEF3 contains two SNPs of the same effect direction. Except for gene ZBTB38, the SKAT does not share common identified regions with the WSS and the W-test collapsing method. The three tests explored in this study all have distinct properties and strength. In real data analysis, when the underlying genetic model is unknown, the methods may need to be considered jointly to obtain a complete picture. There are existing combined tests such as the SKAT-O and Fisher's method, which pool individual tests by some tuning parameters (Derkach, Lawless, & Sun, 2013; Lee, Wu, & Lin, 2012). The W-test collapsing method can be naturally pooled with the SKAT by the Fisher's method, which we might explore in future study.
To conclude, we proposed the W-test collapsing method for rare-variant analysis with good power, controlled type I error rate, and fast computing speed. The efficiency and effectiveness of the method provide opportunities to improve exome-sequencing analysis strategy such as locating dataset-specific optimal collapsing region, and enable the analysis of the whole genome sequencing data under an integrated statistical framework.
ACKNOWLEDGMENTS
MHW conceived the study and wrote the article; RS and HW processed the data and performed the analysis; JG wrote part of the program; IH and WKKW commented and proved the article; and BZ contributed and coordinated the study.
This work has been supported by the Chinese University of Hong Kong Direct Grant (4054169), Research Grant Council – General Research Fund (476013), and National Science Foundation of China (81473035, 31401124); all to MHW. This research was conducted using the resources of the High Performance Cluster in Li Ka Shing Institute of Health Sciences, the Chinese University of Hong Kong; and the High Performance Cluster Computing Centre, Hong Kong Baptist University, which receives funding from Research Grant Council, University Grant Committee of the HKSAR, and Hong Kong Baptist University. We thank Tony Liu, Sammy Tang, and Morris Law for their technical help in the cluster usage, and Genetic Analysis Workshop 18 for providing the datasets.
CONFLICT OF INTEREST
The authors declare no competing interest.
