TARV: Tree-based Analysis of Rare Variants Identifying Risk Modifying Variants in CTNNA2 and CNTNAP2 for Alcohol Addiction
Contract grant sponsor: National Institute on Drug Abuse; Contract grant number: R01 DA016750; Contract grant sponsor: NIH; Contract grant numbers: U01 HG004422, U01 HG004446, U10 AA008401, P01 CA089392, R01 DA013423, U01 HG004438, and HHSN268200782096C.
ABSTRACT
Since the development of next generation sequencing (NGS) technology, researchers have been extending their efforts on genome-wide association studies (GWAS) from common variants to rare variants to find the missing inheritance. Although various statistical methods have been proposed to analyze rare variants data, they generally face difficulties for complex disease models involving multiple genes. In this paper, we propose a tree-based analysis of rare variants (TARV) that adopts a nonparametric disease model and is capable of exploring gene–gene interactions. We found that TARV outperforms the sequence kernel association test (SKAT) in most of our simulation scenarios, and by notable margins in some cases. By applying TARV to the study of addiction: genetics and environment (SAGE) data, we successfully detected gene CTNNA2 and its 43 specific variants that increase the risk of alcoholism in women, with an odds ratio (OR) of 1.94. This gene has not been detected in the SAGE data. Post hoc literature search also supports the role of CTNNA2 as a likely risk gene for alcohol addiction. In addition, we also detected a plausible protective gene CNTNAP2, whose 97 rare variants can reduce the risk of alcoholism in women, with an OR of 0.55. These findings suggest that TARV can be effective in dissecting genetic variants for complex diseases using rare variants data.
Introduction
Over the past decade, genome-wide association studies (GWAS) have been widely applied in biomedical researches and successfully identified many common variants associated with complex human diseases [Hindorff et al., 2009]. However, for most diseases, the reported common variants explain only a small proportion of the risk. This phenomenon is sometimes referred to as missing inheritance, and some believe that it may be explained, at least in part, by variants with low minor allele frequencies (MAFs) or rare variants (MAF lower than 1% or 5%) [Manolio et al., 2009].
In the recent years, the next generation sequencing (NGS) technology has been developed and introduced to the genetic analysis. The NGS technology is a low-cost, high-throughput, and parallelized sequencing technology, which can produce thousands or millions of sequences concurrently [Metzker, 2009]. With this technology, it becomes affordable for researchers to sequence the whole human genome or exons. A major advantage of the NGS technology is the de novo sequencing which is not based on any known variants, allowing novel and rare variants to be identified alongside the common ones.
Analysis of rare variants gives rise to two obvious challenges. First, the variants are so rare that even a large scale GWAS does not have enough statistical power to detect the association between a single rare variant and a trait beyond a reasonable chance. Furthermore, rare variants are much more abundant than common variants in the human genome, and controlling for type I errors becomes an even severe problem for any single-variant-based analysis. Therefore, multiple variants are usually grouped and tested together to avoid this problem. The grouping is generally based on the chromosomal positions of the variants; for example, variants on the same gene can be tested together as a group.
Various methods have been proposed to simultaneously test multiple variants. Current methods can be roughly categorized into three major strategies. The first strategy is represented by the burden test that directly or indirectly collapses specific rare variants and then focuses on the created variant. For example, cohort allelic sums test (CAST) collapses multiple rare variants into one “supervariant” and tests this supervariant instead of the individual ones [Morgenthaler and Thilly, 2007]. The supervariant is a dummy variable (1 or 0) indicating whether any minor allele in a group of rare variants is present or not. The combined multivariate and collapsing (CMC) method also uses this supervariant, although it is in a multiple regression setting in which the supervariant is considered as a predictor along with common variants [Li and Leal, 2008]. There are also more sophisticated methods to collapse rare variants. Specifically, dummy variables can be defined for each rare variant in a group and then a new variable can be created from a linear combination of the dummy variables. For example, we can use 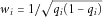 as the linear coefficient for the ith variant, where
as the linear coefficient for the ith variant, where  is the MAF of the ith variant [Madsen and Browning, 2009]. Because the effects of various variants may have different directions, methods have been proposed to use both positive and negative coefficients [Hoffmann et al., 2010].
is the MAF of the ith variant [Madsen and Browning, 2009]. Because the effects of various variants may have different directions, methods have been proposed to use both positive and negative coefficients [Hoffmann et al., 2010].
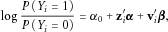 (1)
(1) is the disease status for sample i (
is the disease status for sample i ( for controls and
for controls and  for cases),
for cases), 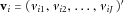 are the genotypes for the J variants to be tested together (generally codes as
are the genotypes for the J variants to be tested together (generally codes as 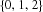 ),
), 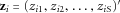 are the confounding covariates to adjust, α0 and
are the confounding covariates to adjust, α0 and  are the intercept and coefficients for the confounders, and
are the intercept and coefficients for the confounders, and  are the coefficients for the variants of interest. Then the goal is to test the null hypothesis
are the coefficients for the variants of interest. Then the goal is to test the null hypothesis  .
.Because the number of variants, J, tested simultaneously may be large, which may decrease the statistical power, SKAT also considers random effects by assuming that  , where
, where  and F is a distribution function with mean 0 and variance τ2. Then the null hypothesis becomes
and F is a distribution function with mean 0 and variance τ2. Then the null hypothesis becomes  .
.
The third strategy is based on functional analysis. Let 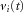 be the genotype of the rare variant of sample i at chromosome position t. Despite that
be the genotype of the rare variant of sample i at chromosome position t. Despite that 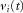 can only take discrete values at discrete position t,
can only take discrete values at discrete position t, 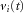 is treated as a continuous function defined on continuous t. Then
is treated as a continuous function defined on continuous t. Then 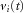 can be decomposed as
can be decomposed as  , where
, where 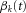 with
with  is a functional basis. In general when
is a functional basis. In general when  , the problem reduces to testing the distribution of
, the problem reduces to testing the distribution of  between cases and controls [Luo et al., 2011]. In this method, various types of functional basis can be adopted, such as the functional principal component basis [Luo et al., 2011], the B-spline basis [Luo et al., 2012; Fan et al., 2013], and the Fourier basis [Fan et al., 2013]. Although the interpretation of the result may be complicated, this method enjoys good statistical power and deals with the dependence structures among the variants.
between cases and controls [Luo et al., 2011]. In this method, various types of functional basis can be adopted, such as the functional principal component basis [Luo et al., 2011], the B-spline basis [Luo et al., 2012; Fan et al., 2013], and the Fourier basis [Fan et al., 2013]. Although the interpretation of the result may be complicated, this method enjoys good statistical power and deals with the dependence structures among the variants.
The burden test and the quadratic test have their pros and cons under different disease models: the burden test is more powerful when most of the variants are causal and have the same direction of effect, whereas the quadratic test is more powerful if just a few of the variants are causal or the variants have both positive and negative effects. Unfortunately, in practice, we do not know the true effects in real data analysis. As a result, the more neutral variants are included in the analysis, the lower the statistical power will be. Therefore the functional analysis based method serves as a useful dimensional reduction method when many rare variants are included. In addition, variable selection has been proposed to remove the neutral variants based on the linkage disequilibrium structure [Talluri and Shete, 2013].
In this paper, we propose tree-based analysis of rare variants (TARV) and evaluate its use to select rare variants for subsequent analysis. The software is available at http://c2s2.yale.edu/software. This method has unique features as opposed to many existing ones. Not only can it consider multiple variants, but also incorporate potential interactions among them. We should note that tree-based methods have been successfully applied in GWAS to identify gene–gene and gene–environmental interactions [Chen et al., 2011; Zhang et al., 2000, 2001]. This work is to extend the application of the tree based methods into the analysis of rare variants.
Methods
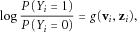 (2)
(2) is not limited to a linear function, and
is not limited to a linear function, and  includes all the genotyped variants (not limited to the variants in a certain gene). The tree-based method provides a nonparametric fit to the unknown
includes all the genotyped variants (not limited to the variants in a certain gene). The tree-based method provides a nonparametric fit to the unknown  which allows potential nonlinear relations and high-order interactions. We refer to Zhang and Singer [Zhang and Singer, 2010] for a detailed presentation of the method.
which allows potential nonlinear relations and high-order interactions. We refer to Zhang and Singer [Zhang and Singer, 2010] for a detailed presentation of the method.Despite these appealing features, directly applying trees onto the rare variants does not produce useful information because a tree structure is determined by its node splits which in turn depends on selected predictors. In our setting, the predictors include rare variants with very low MAFs. Such low frequencies yield very unbalanced, unstable, and unreliable tree structures. We overcome this problem by transforming the original variants and create predictors before applying the tree methods. Our idea is different from the collapsing of rare variants as introduced above, but is also related in light of the creation of new variables.
Transformation
As discussed above, it is important to consider variants with or without effects and whether those effects are positive or negative while we create new variables. We propose an adaptive transformation as follows.
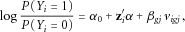 (3)
(3) is the marginal effect size for the jth variant in gene g with
is the marginal effect size for the jth variant in gene g with  variants, and
variants, and  . Then we use the t-test statistic for
. Then we use the t-test statistic for  , denoted by
, denoted by  , to order the variants both descendingly and ascendingly so that variants with positive or negative effects are accounted for. Let
, to order the variants both descendingly and ascendingly so that variants with positive or negative effects are accounted for. Let 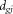 and
and  be the indices of the variants with the jth largest and smallest t-statistic, respectively. Define
be the indices of the variants with the jth largest and smallest t-statistic, respectively. Define
 (4)
(4) . Similarly, define
. Similarly, define
 (5)
(5) is the dummy variable indicating whether the minor allele of variant j in gene g is present in subject i. Our adaptive transformation is related to some existing collapsing methods. For example, if we use the indicator variable
is the dummy variable indicating whether the minor allele of variant j in gene g is present in subject i. Our adaptive transformation is related to some existing collapsing methods. For example, if we use the indicator variable  as the created variable, it is the same as collapsing the top k variants with positive effects. Figure 1 displays the transformation process for a hypothetical gene.
as the created variable, it is the same as collapsing the top k variants with positive effects. Figure 1 displays the transformation process for a hypothetical gene.
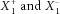 .
.When there exist missing data in some of the variants, we can still calculate the marginal effects and order the variants accordingly. Then  and
and  can be calculated in the same way by treating the missing genotype as 0.
can be calculated in the same way by treating the missing genotype as 0.
Tree Model
After defining  and
and  , we include them as predictors together with the environment variables and common variants in tree-based analysis.
, we include them as predictors together with the environment variables and common variants in tree-based analysis.
We use the RTREE [Zhang and Singer, 2010] program to grow trees. Like other tree-growing programs, RTREE begins with the root node containing all learning samples. Then those samples are recursively split into daughter nodes based on queries about the predictors. The queries are selected such that for each split, the derived daughter nodes have the lowest impurity. A common measure of impurity is the entropy function. For a node with n samples, without loss of generality, assume the disease status of these n samples are 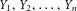 . Denote
. Denote  . The entropy is defined as
. The entropy is defined as  .
.
After a tree is grown, nodes are pruned to prevent overfitting. In our method, the pruning is carried out based on the Chi-squared test. During the pruning procedure, Chi-squared tests are performed on the end splits. If the P-value is larger than the given cutoff (e.g., 10−6), the split is pruned. The pruning is repeatedly carried out until all the splits yield P-values smaller than the cutoff. In the RTREE program, the users can also choose to intervene the splitting and pruning procedure manually. Also, considering the reality that most studies do not have enough power to identify many causal genes, we pay our attention to top few splits, which also greatly simplifies our computation by avoiding a full-blown pruning, which may not be necessary for our purpose.
Simulation
 . To take into account diverse situations that may be common in real studies, we simulated 500 cases and 500 controls in six disease models. The simulation was repeated for 100 times for each model. The specifications of the seven disease models are listed below.
. To take into account diverse situations that may be common in real studies, we simulated 500 cases and 500 controls in six disease models. The simulation was repeated for 100 times for each model. The specifications of the seven disease models are listed below.
- Disease model 1: In this disease model, we first randomly sampled 2 genes (A and B) as being causal. Then within either gene, each variant was randomly selected as a causal variant with a probability depending on the region of the variant. Specifically, this probability was 0.9 for coding regions, 0.8 for other exon regions, 0.4 for intron regions, 0.5 for 5′-untranslated regions (UTRs), 0.3 for 3′-UTRs, 0.2 for other transcribed regions, and 0.1 for the upstream and downstream flanking regions. A gene is regarded as being mutated in sample i if any of its causal variants was mutated in this sample. We introduce
 if gene A is mutated in sample i, and
if gene A is mutated in sample i, and  otherwise.
otherwise.  is similarly defined for gene B. The penetrance probabilities were designed such that having only one gene (either gene A or gene B) mutated elevated the probability of having disease only slightly (from 0.7% to 1.8%), but having both genes mutated increased the probability dramatically (to 99.9%).
is similarly defined for gene B. The penetrance probabilities were designed such that having only one gene (either gene A or gene B) mutated elevated the probability of having disease only slightly (from 0.7% to 1.8%), but having both genes mutated increased the probability dramatically (to 99.9%). - Disease model 2: The second disease model is the same as model 1 except the penetrance. The penetrance probabilities in this model were designed such that mutated gene A increased the disease risk, whereas the effect of gene B depended on whether gene A was mutated. Specifically, when gene A was not mutated, the penetrance was 0.7%, no matter if gene B was mutated; when gene A was mutated, the penetrance increased to 26.9% or 73.1% depending on whether gene B was normal or also mutated, respectively.
- Disease model 3: The setting of this model follows the previous two. The penetrance probabilities were designed such that mutating gene A increased the risk, whereas mutating gene B decreased the risk. Specifically, mutated gene B would decrease the penetrance probability from 10% to 0.2% if gene A was normal, or from 80% to 30% if gene A was mutated.
- Disease model 4: In this model, we allowed variants in the same gene to have opposite effects. First, we randomly selected one gene. A variant within this gene has a 40% of chance to have a positive effect, 40% to have a negative effect, and 20% neutral. Define
 if any of the risk variants is mutated, and
if any of the risk variants is mutated, and  otherwise; and similarly define
otherwise; and similarly define  on the basis of the protective variants. The penetrance probability was 10% if
on the basis of the protective variants. The penetrance probability was 10% if  , 0.2% if
, 0.2% if  and
and  , 80% if
, 80% if  and
and  , or 30% if
, or 30% if  .
. - Disease model 5: In this model, we selected gene A and derived
 as above. In addition, we simulated another gene in LD with gene A. Specifically, we introduced
as above. In addition, we simulated another gene in LD with gene A. Specifically, we introduced  such that
such that  and
and  . As a matter of fact,
. As a matter of fact,  can be viewed as any covariate whose distribution depends on gene A. The penetrance probabilities are designed such that the marginal effect of
can be viewed as any covariate whose distribution depends on gene A. The penetrance probabilities are designed such that the marginal effect of  is diminished by its negative correlation with gene A. This phenomenon is known as the Simpson's paradox [Wagner, 1982]. In this model, the penetrance probability was 1% if
is diminished by its negative correlation with gene A. This phenomenon is known as the Simpson's paradox [Wagner, 1982]. In this model, the penetrance probability was 1% if  , 75% if
, 75% if  and
and  , 25% if
, 25% if  and
and  , or 80% if
, or 80% if  .
. - Disease model 6: In this model, we simulated the disease status based on five genes randomly selected on chromosome 22. Similarly to model 1, within each gene, variants were sampled as causal in probability of 30%.
 are dummy variables indicating whether the minor allele is present in any causal variants for sample i. The disease status for each sample i was simulated using the logistic model
We see that genes 1, 2, and 3 have positive coefficients and are risk genes, whereas genes 4 and 5 have negative coefficients and have protective effects.
are dummy variables indicating whether the minor allele is present in any causal variants for sample i. The disease status for each sample i was simulated using the logistic model
We see that genes 1, 2, and 3 have positive coefficients and are risk genes, whereas genes 4 and 5 have negative coefficients and have protective effects.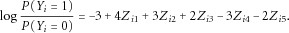 (6)
(6) - Disease model 7: In this model, to demonstrate the effects of missing values, we adopted exactly the same model as in model 1, but with a 10% no-call rate for the genotype of each variant in each sample.
Real Data Application
In order to demonstrate the potential of the tree method in real data, we applied TARV into the study of addiction: genetics and environment (SAGE) [Bierut et al., 2010] data. The rare variant in this dataset was imputed by GENEVA on the 1000 Genome reference panels using software BEAGLE. The data were made available by dbGaP. Our trait is alcohol-addiction. We used European samples only (1,151 cases and 1,336 controls) and restricted our attention to variants with MAF  .
.
Results
Simulation Results
In the simulation analysis, we compare the performance of TARV with SKAT. Because these methods are designed differently and have different emphases, to make the comparison fair, we focus on the top genes identified by each method. Although gene discoveries have been primarily based on significance level and/or false discovery control, it is a common practice for investigators to select a number of top candidates. In this regard, we believe our strategy is not only appropriate but also practical.
For disease models 1–5, we examined the tree structure up to the third layer involving three splitting variables, and up to three genes may be used in the three splits. Accordingly, the three genes with the smallest P-values from SKAT were chosen for the comparison. For disease model 6, because there were five causal genes in the underlying model, we examined the tree structure to the fourth layer, requiring seven splitting variables, and up to seven genes. In parallel, we selected the top seven genes detected by SKAT. We should note that in practice, we do not know how many genes are causal, and it may be a good idea to consider four layers in general. Here, we made some use of the underlying disease models to simplify the comparison and this information is utilized equally for the two methods.
For disease model 1, TARV detected both genes A and B in 99 out of 100 runs and detected at least one gene in all 100 runs. In contrast, SKAT detected both genes in 80 out of 100 runs and detected at least one gene in 98 runs. Thus, TARV clearly outperformed SKAT in identifying the two genes.
For disease model 2, TARV detected both genes in 29 runs, and detected at least one gene in 97 runs. SKAT detected both genes in 35 runs, and detected at least one gene in 97 runs. Here, SKAT was slightly better than TARV in detecting the presence of both genes.
For model 3, TARV detected the risk gene in all of the 100 runs and the protective gene in 72 out of 100 runs. SKAT detected the risk gene in 99 runs, and detected the protective gene in 53 runs. TARV clearly outperformed SKAT in detecting the protective gene.
In disease model 4, we had one causal gene with both risky and protective variants. SKAT detected this gene in 86 runs. To the contrary, TARV detected a risk variant in every run, and a protective variant in 96 runs. TARV had a clear advantage for this model, not only identifying the gene more often but also the directions of the effects.
Because of the Simpson's paradox in disease model 5, it is not surprising that SKAT failed to detect  completely. To the contrary, TARV detected both the gene and
completely. To the contrary, TARV detected both the gene and  in all runs.
in all runs.
In the more complex disease model 6, TARV detected all five genes in 28 runs, four genes in 54 runs, and three genes in 18 runs. In comparison, SKAT detectedfive5 genes in 35 runs, four genes in 40 runs, three genes in 21 runs, and two genes in four runs. These results are comparable.
In model 7 with missing data, TARV detected both genes in 95 out of 100 runs and detected at least one gene in 96 runs. SKAT, which automatically imputed missing data, detected both genes in 78 out of 100 runs and detected at lease one gene in 99 runs. We see that both methods are robust against excessive (10%) missing data, and TARV still outperforms SKAT in this scenario with missing data.
To examine and compare the sensitivity and specificity of the two methods, we summarized the average number of detected genes, the true discoveries, as well as the false discovery rate (FDR) of TARV and SKAT while controlling the detection criteria for each method. In TARV, we adjusted the tree layer, whereas in SKAT, we varied the P-value cutoff. The results of these two methods for disease models 1-4, 6, and 7 are presented side-by-side in Tables 1-6. We can see that TARV was always more sensitive and specific than SKAT. When a similar number of genes were detected, TARV always detects more true discoveries.
| TARV | SKAT | ||||||
|---|---|---|---|---|---|---|---|
| Depth | #Detected | #True | FDR | P-value | #Detected | #True | FDR |
| 1 | 1.00 | 1.00 | 0 | 1e-8 | 12.02 | 1.87 | 0.84 |
| 2 | 2.53 | 1.99 | 0.21 | 1e-6 | 23.29 | 1.94 | 0.92 |
| 3 | 5.99 | 1.99 | 0.67 | 1e-4 | 51.93 | 1.96 | 0.96 |
| 4 | 13.10 | 1.99 | 0.85 | 1e-2 | 120.07 | 2.00 | 0.98 |
| TARV | SKAT | ||||||
|---|---|---|---|---|---|---|---|
| Depth | #Detected | #True | FDR | P-value | #Detected | #True | FDR |
| 1 | 1.00 | 0.97 | 0.03 | 1e-8 | 5.43 | 1.31 | 0.76 |
| 2 | 2.74 | 1.26 | 0.54 | 1e-6 | 10.51 | 1.49 | 0.86 |
| 3 | 6.36 | 1.34 | 0.79 | 1e-4 | 24.26 | 1.67 | 0.93 |
| 4 | 13.30 | 1.39 | 0.90 | 1e-2 | 73.97 | 1.92 | 0.97 |
| TARV | SKAT | ||||||
|---|---|---|---|---|---|---|---|
| Depth | #Detected | #True | FDR | P-value | #Detected | #True | FDR |
| 1 | 1.00 | 1.00 | 0 | 1e-5 | 2.65 | 1.39 | 0.48 |
| 2 | 2.69 | 1.72 | 0.36 | 1e-4 | 4.49 | 1.56 | 0.65 |
| 3 | 6.14 | 1.79 | 0.71 | 1e-3 | 8.88 | 1.70 | 0.81 |
| 4 | 13.10 | 1.83 | 0.86 | 1e-2 | 23.88 | 1.89 | 0.92 |
| TARV | SKAT | ||||||
|---|---|---|---|---|---|---|---|
| Depth | #Detected | #True | FDR | P-value | #Detected | #True | FDR |
| 1 | 1.00 | 1.00 | 0 | 1e-5 | 1.00 | 0.75 | 0.25 |
| 2 | 2.77 | 1.96 | 0.29 | 1e-4 | 1.39 | 0.79 | 0.43 |
| 3 | 6.52 | 1.98 | 0.70 | 1e-3 | 3.17 | 0.84 | 0.74 |
| 4 | 13.84 | 1.98 | 0.86 | 1e-2 | 10.90 | 0.88 | 0.92 |
| TARV | SKAT | ||||||
|---|---|---|---|---|---|---|---|
| Depth | #Detected | #True | FDR | P-value | #Detected | #True | FDR |
| 1 | 1.00 | 1.00 | 0 | 1e-8 | 5.92 | 3.31 | 0.44 |
| 2 | 2.77 | 2.76 | 0.004 | 1e-6 | 10.36 | 3.98 | 0.62 |
| 3 | 4.69 | 4.10 | 0.13 | 1e-4 | 24.39 | 4.54 | 0.81 |
| 4 | 10.23 | 4.75 | 0.54 | 1e-2 | 77.42 | 4.88 | 0.94 |
| 5 | 22.50 | 4.88 | 0.78 | ||||
| TARV | SKAT | ||||||
|---|---|---|---|---|---|---|---|
| Depth | #Detected | #True | FDR | P-value | #Detected | #True | FDR |
| 1 | 1.00 | 0.96 | 0.04 | 1e-10 | 6.34 | 1.86 | 0.71 |
| 2 | 2.31 | 1.91 | 0.17 | 1e-8 | 11.16 | 1.90 | 0.83 |
| 3 | 5.92 | 1.92 | 0.68 | 1e-6 | 22.01 | 1.94 | 0.91 |
| 4 | 12.85 | 1.93 | 0.85 | 1e-4 | 48.91 | 1.96 | 0.96 |
Real Data Application Results
We applied TARV on the SAGE data to find genes that may be associated with alcohol addiction in white population. We first generated a tree using the variant-derived variables with positive coefficients only. The tree was pruned at P-value of 10−6 as displayed in Figure 2. For practical purpose, we recommend to pay closer attention to the top three splits, because it is much less likely to replicate the splits that appears further in the downstream.
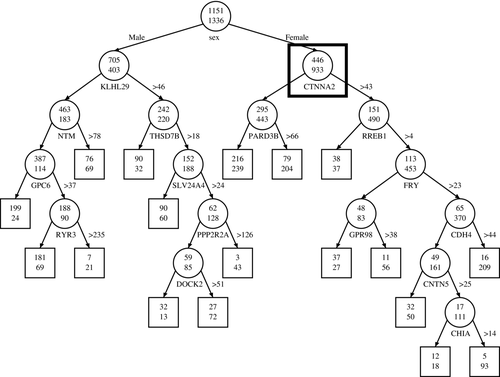
We should note that the first splitting variable is gender, which is a well-documented factor for alcoholism. Of great importance is the third split using the CTNNA2 gene. The cutoff value of 43 implies that having minor allele in any of the top 43 rare variants with positive coefficients in this gene may increase the risk of alcohol addiction in women. The details of the 43 variants are given in Table 7. Using a post hoc logistic regression analysis, we found that the odds ratio (OR) for having any of the 43 variants is 1.94, with a 95% confidence interval (CI) of (1.64, 2.30).
| Chromosome | Position | Alteration | Frequency | rsSNP ID |
|---|---|---|---|---|
| 2 | 79414140 | G→ C | 0.0325282431 | |
| 2 | 79440921 | C→ T | 0.0323334632 | |
| 2 | 79583819 | C→ T | 0.0313595637 | |
| 2 | 79618395 | G→ A | 0.0268796260 | |
| 2 | 79678697 | A→ G | 0.0054538372 | |
| 2 | 79702781 | T→ C | 0.0019477990 | |
| 2 | 79703081 | A→ T | 0.0019477990 | |
| 2 | 79704003 | A→ G | 0.0019477990 | |
| 2 | 79711967 | T→ G | 0.0019477990 | |
| 2 | 79720449 | A→ G | 0.0377873004 | |
| 2 | 79813928 | G→ A | 0.0089598753 | rs11899508 |
| 2 | 79814436 | G→ A | 0.0015582392 | |
| 2 | 79828985 | A→ C | 0.0009738995 | |
| 2 | 79854979 | G→ A | 0.0072068563 | rs11900109 |
| 2 | 79928873 | A→ G | 0.0031164784 | |
| 2 | 79956168 | G→ A | 0.0247370471 | |
| 2 | 79968624 | C→ T | 0.0319439034 | rs7564458 |
| 2 | 80116325 | C→ T | 0.0407089988 | rs12986588 |
| 2 | 80119494 | T→ G | 0.0407089988 | rs13034462 |
| 2 | 80129506 | G→ A | 0.0163615115 | |
| 2 | 80130025 | A→ T | 0.0410985586 | rs12992230 |
| 2 | 80130310 | T→ A | 0.0410985586 | rs13024343 |
| 2 | 80132996 | T→ G | 0.0407089988 | |
| 2 | 80135517 | G→ A | 0.0405142189 | rs34044554 |
| 2 | 80137537 | T→ C | 0.0414881184 | rs12987105 |
| 2 | 80146869 | G→ A | 0.0414881184 | |
| 2 | 80164612 | T→ C | 0.0430463576 | rs35502473 |
| 2 | 80175881 | C→ T | 0.0333073627 | rs7568815 |
| 2 | 80207455 | C→ T | 0.0093494351 | |
| 2 | 80237164 | A→ C | 0.0225944683 | |
| 2 | 80278302 | T→ G | 0.0239579275 | |
| 2 | 80427250 | C→ T | 0.0241527074 | |
| 2 | 80443327 | G→ T | 0.0410985586 | |
| 2 | 80513810 | A→ G | 0.0037008181 | |
| 2 | 80558293 | C→ T | 0.0231788079 | rs310784 |
| 2 | 80694931 | T→ C | 0.0044799377 | rs59527500 |
| 2 | 80695839 | C→ T | 0.0044799377 | |
| 2 | 80695894 | A→ G | 0.0044799377 | |
| 2 | 80696657 | A→ G | 0.0040903779 | |
| 2 | 80697114 | G→ A | 0.0040903779 | |
| 2 | 80697779 | G→ A | 0.0040903779 | |
| 2 | 80697892 | A→ G | 0.0040903779 | rs11899864 |
| 2 | 80709515 | G→ A | 0.0023373588 |
We also generated a tree using variant-derived variables for both positive and negative coefficients. The resulting tree is presented in Supplementary Figure S1. This tree indicates that 97 rare variants in the gene CNTNAP2 is protective against alcohol-addiction in female. The details of the 97 variants are given in Supplementary Table S1. Using a post hoc logistic regression analysis, we found that the OR for having any of the 97 variants is 0.55, with a 95% CI of (0.46, 0.66).
Discussion
We proposed TARV to detect rare variants associated with certain diseases. Our method is novel in several ways and possesses unique strengths. Because the tree-based method is nonparametric and flexible, it can be used to explore complex gene–gene interactions. By simulation, we demonstrated that TARV outperforms SKAT when multiple genes are included in the disease model. This is an important strength of our method because complex diseases do involve multiple genes.
Furthermore, we applied TARV for SAGE data to demonstrate its usage and successfully detected gene CTNNA2 that increases the risk of alcohol addiction in White women. According to the UniProt database, CTNNA2 may regulate the cell–cell adhesion and differentiation in the nervous system, and also regulate morphological plasticity of synapses and cerebellar and hippocampal lamination during development, which is very likely to be related to the addiction behavior. This hypothesis is supported by a number of existing studies. For example, CTNNA2 is reported to be related to excitement-seeking [Terracciano et al., 2011], ability to quit [Uhl et al., 2008], schizophrenia and nicotine addiction [Mexal et al., 2008].
We also identified gene CNTNAP2 that decreases the risk of alcohol addiction in female. This gene functions in the nervous system as cell adhesion molecules and receptors and is found to be associated with numerous psychiatric disorders such as autism [Alarcón et al., 2008; Arking et al., 2008; Bakkaloglu et al., 2008], language disorders [Vernes et al., 2008], schizophrenia, and depression [Ji et al., 2013]. To our knowledge, there is no study reporting a protective effect of this gene for addiction behaviors.
Our findings for both CTNNA2 and CNTNAP2 underscore the great potential of TARV in unraveling disease related genes that are otherwise difficult to find by existing methods. Neither gene could have been identified as a significant risk factor in the SAGE data by the existing methods.
The findings from TARV can have intuitive interpretation. For example, the split based on “CTNNA2 ” corresponds to a biological query: “whether the sample has at least one mutation in any of the top 43 variants with positive effect in CTNNA2.” Not only can we identify important genes, but also a set of important variants for the genes.
” corresponds to a biological query: “whether the sample has at least one mutation in any of the top 43 variants with positive effect in CTNNA2.” Not only can we identify important genes, but also a set of important variants for the genes.
It is worth noting that the purpose of the tree model is different from the hypothesis testing procedure which can test the variables one by one. In the tree model, the predictors are analyzed together to model the relationship between the predictors and the outcome, which enables the user to explore the interactions between the predictors nonparametrically. The predictors selected by the tree in the top tend to be important variables for the outcome. One caveat with our method is that it is much more challenging to understand its theoretical properties. It serves as a needed, powerful alternative to existing methods in gene hunting, but replication of the findings is warranted.
To overcome the difficulties arising from the low MAFs of the rare variants, we proposed an adaptive collapsing method to combine the rare variants in a gene. During this process, we rank the variants according to their marginal effects and then perform the collapsing. Because the marginal effect sizes are estimated from the data, the rankings are not independent of the outcome. As a result, the genes with more rare variants are more likely to be selected as a split than the genes with fewer rare variants if both genes are noncasual. This phenomenon is also observed in other tree-based method such as classification and regression trees (CART) [Breiman et al., 1984] when binary splits are made on nominal variables with multiple levels, in which case the variables with more levels are more likely to be selected. One solution is to use an unbiased test to select the splitting variables [Loh, 2009], which however will make the algorithm overcomplicated and reduce the overall statistical power. Because the tree-based method is exploratory, we can afford the potential variable selection bias, and call for the need to validate the findings. Alternatively, if biological evidence or an independent dataset presents, we can order the variants accordingly instead of using the marginal effect estimated from the training data. When this is feasible, the splitting variable selection will become unbiased.
In summary, TARV enjoys several critical and unique strengths that are necessary in analyzing rare variants (as well as common variants) for high throughput data. We have also made some cautionary remarks for the use of our method.
Acknowledgments
This research is supported in part by grants R01 DA016750 from the National Institute on Drug Abuse. The dataset used for the analyses described in this manuscript was obtained from dbGaP at http://www.ncbi.nlm.nih.gov/projects/gap/cgi-bin/study.cgi?study_id=phs000092.v1.p1 through dbGaP accession number phs000092.v1.p.




