Estimating and Testing Pleiotropy of Single Genetic Variant for Two Quantitative Traits
ABSTRACT
Along with the accumulated data of genetic variants and biomedical phenotypes in the genome era, statistical identification of pleiotropy is of growing interest for dissecting and understanding genetic correlations between complex traits. We proposed a novel method for estimating and testing pleiotropic effect of a genetic variant on two quantitative traits. Based on a covariance decomposition and estimation, our method quantifies pleiotropy as the portion of between-trait correlation explained by the same genetic variant. Unlike most multiple-trait methods that assess potential pleiotropy (i.e., whether a variant contributes to at least one trait), our method formulates a statistic that tests exact pleiotropy (i.e., whether a variant contributes to both of two traits). We developed two approaches (a regression approach and a bootstrapping approach) for such test and investigated their statistical properties, in comparison with other potential pleiotropy test methods. Our simulation shows that the regression approach produces correct P-values under both the complete null (i.e., a variant has no effect on both two traits) and the incomplete null (i.e., a variant has effect on only one of two traits), but requires large sample sizes to achieve a good power, when the bootstrapping approach has a better power and produces conservative P-values under the complete null. We demonstrate our method for detecting exact pleiotropy using a real GWAS dataset. Our method provides an easy-to-implement tool for measuring, testing, and understanding the pleiotropic effect of a single variant on the correlation architecture of two complex traits.
Introduction
Pleiotropy is a biological phenomenon where a single genetic variant affects two or more phenotypic traits. The term was introduced into the literature a century ago, and since then, has had an important influence on the fields of evolutionary biology, physiology, and genetics [Stearns, 2010]. In recent years, increasing numbers of polymorphic variants across the human genome have been associated with many complex traits, and there is growing interest in the identification of pleiotropic effects, especially in understanding genetic and molecular basis of the correlated architecture among complex traits.
Genome-wide association studies (GWAS) have produced very rich data on both genotypes and phenotypes, providing unprecedented opportunities for investigation of pleiotropy. However, statistical methods for identifying and characterizing pleiotropy are still quite insufficient and limited. A variety of multitrait analysis methods, such as principal components based methods [Bensen et al., 2003; Klei et al., 2008], FBAT-GEE [Lange et al., 2003], EGEE [Liu et al., 2009], canonical correlation analysis (CCA) [Ferreira and Purcell, 2009], combined multivariate (CMV) analysis [Medland and Neale, 2010], univariate-statistic combined test [Yang et al., 2010], PRIMe [Huang et al., 2011], parameterized multitrait mixed model (MTMM) [Korte et al., 2012], and correlated meta-analysis [Province and Borecki, 2013], have been proposed and can be used for initial screen of potential pleiotropy, such methods, however, are not strictly designed for testing exact pleiotropy. The presence of pleiotropy may increase the power of these methods in detecting overall association, but a significant test may not necessarily indicate pleiotropy, because most of these methods are based upon the null hypothesis that a variant affects none of the traits and do not include the incomplete null in which the variant affects only one of the traits. Therefore the null is not correctly specified. A proper pleiotropy test should answer the question whether a variant contributes to two or more traits. Another limitation of most existing methods is the lack of well-defined parameter and estimator for the pleiotropic effect, thus they help very little in assessing the magnitude of pleiotropy and understanding how pleiotropy influences the relationship between traits.
We propose in this paper a novel, easy-to-implement approach for estimating and testing exact pleiotropy of a variant on two correlated traits, in which the pleiotropic effect of a variant is estimated as the portion of between-trait correlation that can be explained by the variant, and then tested under the proper null hypothesis of no pleiotropy (i.e., the variant does not contribute to both traits), against the proper alternative hypothesis of pleitropy (i.e., the variant contributes to both traits). We investigate statistical properties of our method through simulation and demonstrate its application using real data. Referred to as pleiotropy estimation and test (PET), the proposed method provides a novel tool for clearly characterizing and properly testing pleiotropy between two traits. We compare its performance to other possible approaches and assess power and sample size requirements.
Methods
Definitions and Models
(1)
(2)
). Assuming the covariances between X and ε1 and between X and ε2 are 0, the covariance between Y1 and Y2 (denoted by 
) can be decomposed into two components (Appendix A):
(3)The first component, 
, is the covariance between residuals of the two models; the second, 
, is the covariance caused by pleiotropy. Here 
is the variance of X.
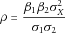(4)To estimate and test ρ, we have developed two approaches, a regression approach and a bootstrap approach, described below.
A Regression Approach
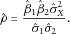(5)When 
, 
, and 
can be estimated from the sample data, the estimation of β1 and β2 may be biased if they are simply obtained by separate regressions of Y1 and Y2 on X, especially when Y1 and Y2 are strongly correlated. For example, even if β1 = 0, a simple regression coefficient of Y1 on X will not be 0 if β2 ≠ 0 and 
≠ 0, because of the indirect effect produced by β2 and passed to Y1 from Y2 through the correlation between Y1 and Y2.
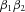as one parameter in a composite model of the product of Y1 and Y2.
(6)This model is obtained through a multiplication of models (1) and (2), where 
, 
, 
, 
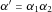, and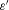 
is the composite residual (Appendix B). The composite parameter 
can be estimated by a regression of 
on X and X2.
Significance of PPC can be determined by testing the null hypothesis, H0: ρ = 0, vs. the alternative hypothesis, HA: ρ ≠ 0. According to the definition of ρ, HA is equivalent to the hypothesis of 
≠ 0 (i.e., β1 ≠ 0 and β2 ≠ 0) and H0 equivalent to 
= 0 (i.e., β1 = 0 and/or β2 = 0). Here H0 is a compound null involving two types of possible null hypotheses, the complete null 
:β1 = β2 = 0, and the incomplete null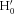 
(including 
:β1 = 0, β2 ≠ 0 and 
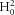: β1 ≠ 0, β2 = 0). Instead of testing these nulls separately, we propose to perform a universal test for all the nulls (
, 
, and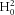 
) against the alternative (
≠ 0 and β2 ≠ 0) through a test of 
= 0 vs. 
≠ 0 based on the model (6).
Because some features of the composite model (6) may not strictly satisfy the assumptions of regular regression (such as normality and homogeneity of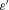 
and independence between parameters), we chose a robust regression to estimate and test 
, which is based on Huber's method [Huber, 1981] and implemented in the R package MASS.
A Bootstrap Approach
Alternatively, based on Equation 3, we propose to estimate 
(denoted by δ) as 
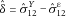and then estimate ρ using Equation 5. When 
is calculated as the sample covariance between two traits, 
can be obtained through a bivariate model (Appendix C).
Similar to the test of 
, significance of PPC can be determined by testing the null hypothesis, H0:δ = 0, vs. the alternative hypothesis, HA:δ ≠ 0. According to the composition of δ(i.e., δ = 
), HA is equivalent to the hypothesis of β1 ≠ 0 and β2 ≠ 0, whereas H0 includes both the complete null 
and the incomplete null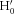 
. Because the analytical distribution of 
under compound null is unknown and commonly used permutation test is not applicable, we propose to calculate P-value via bootstrapping. Given the data of X, Y1, and Y2, a two-tailed P-value is defined as two times the minimum of P(
> 0) and P(
< 0), where 
is a set of 
values obtained by bootstrapping and P means the observed percentage. For the convenience of discussion, we refer to the proposed method as pleiotropy estimation and test (PET) and refer to the regression version as PET-R and the bootstrap version as PET-B.
Simulation
To investigate statistical properties of the PET methods, we simulated data under a variety of parameter configurations based on the models (1) and (2). For a given sample size N, we first simulated genotype data (X) of N subjects for a variant under Hardy-Weinberg equilibrium with a fixed or random minor allele frequency (MAF), and then generated two quantitative traits based on the models (1) and (2) with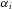 
= 0 and different combinations of β1 and β2 for different hypotheses (i.e. 
, 
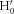, and HA). To simulate the correlation between Y1 and Y2, ε1 and ε2 were sampled from a bivariate normal distribution with a mean vector of (0,0) and a 2 × 2 variance-covariance matrix, in which the variance components were set to 1 and the covariance components (r) were set to nonzero (fixed or random) values.
Methods for Comparison
As a comparison, we included in this paper other two multiple-trait analysis methods, canonical correlation analysis (CCA) and correlated meta-analysis (CMA). CCA is a multivariate approach for analyzing correlation between two groups of variables. We utilized it to test the overall association between a variant and two traits, by calculating Wilk's statistic through an eigenanalysis of raw data and obtaining P-value based on a simplified F-approximation [Ferreira and Purcell, 2009]. CMA is a meta-analysis approach that takes between-trait correlation into account and combines statistics from individual traits into a summarized statistic and tests its significance through a correlated multivariate normal distribution [Province and Borecki, 2013]. Although CCA and CMA test the same statistical hypothesis of potential pleiotropy (i.e., 
vs.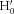 
and HA), they require different data as input. When CCA requires individual subjects’ data and is performed for each single variant with no use of data from other variants, CMA uses summarized data (P-values) from each trait and requires large number of variants to estimate the between-trait correlation.
In addition, to understand the difference in power between single-trait and multiple-trait analyses, we also include in the paper two other simple tests based on single-trait regression analysis, one testing the association between a variant and a trait (based on one P-value, denoted by P1), another testing the association between a variant and both two traits (based on two separate P-values, denoted by P2). The P2 test is a commonly used, simple approach for detecting pleiotropy, however, a significant P2 test (i.e., both two P-values are less than a given cutoff) may not indicate exact pleiotropy, because when both two P-values are significant, one of them can be caused by indirect effect of a variant through between-trait correlation, not by pleiotropy.
Because the statistical hypotheses to be tested in CCA, CMA, P1, and P2 are different from PET, we have no intention to make a competitive comparison between them. Our purpose of including these methods is to help understanding some important features of pleiotropy testing through a contrast.
Results
Type-I Error
We applied CCA, CMA, PET-R, and PET-B to the data simulated under both complete null (
) and incomplete null (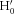
), and investigated their type-1 error characteristics by Q-Q plots showing the comparison between the observed and expected, uniformly distributed P-values. The two existing methods, CCA and CMA, produce uniformly distributed P-values under 
(Fig. 1A and C) but are significantly inflated when testing exact pleiotropy under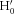 
(Fig. 1B and D). This is because, as mentioned earlier on most existing multiphenotype analysis methods, that they are originally proposed to test potential pleiotropy (i.e., 
against both 
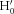and HA), not exact pleitropy (i.e., 
and 
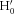against HA). The PET-R method produces expected, noninflated P-values under both 
(Fig. 1E) and 
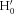(Fig. 1F), when PET-B produces expected P-values under 
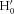(Fig. 1H) and conservative P-values under 
(Fig. 1G). The results indicate that PET has a good control for false positives and is more appropriate for testing exact pleiotropy.
Q-Q plots of P-values under the null hypotheses obtained by different methods. In each plot, x-axis represents expected P-values and y-axis represents observed P-values, both in the negative log10 scale. The P-values are obtained by applying CCA, CMA, PET-R, and PET-B to 2,000 replications of data simulated for a sample size of N = 5,000, under complete null 
and incomplete null 
, separately. In each replication of simulation, MAF is randomly drawn between 0.2∼0.5, r between 0.2∼0.8; when β1 = 0 is used for all simulations, β2is set to 0 (for 
) or randomly drawn between −0.3 to 0.3 (for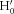 
). The results presented here include(A) CCA under 
, (B) CCA under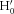 
, (C) CMA under 
, (D) CMA under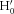 
, (E) PET-R under 
, (F) PET-R under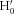 
, (G) PET-B under 
, and (H) PET-B under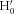 
.
Power
We estimated the statistical power of CCA, CMA, PET-R, PET-B, P1, and P2 tests through simulation under the alternative hypothesis (HA: β1 ≠ 0 and β2 ≠ 0) of exact pleiotropy. The estimation (Table 1) shows that when β1 ≠ 0 and β2 ≠ 0, in terms of detecting association, two-trait based testing methods (CCA and CMA) have higher power than single-trait based methods (P1 and P2); potential pleiotropy tests (CCA, CMA, and P2) and single-trait association test (P1) higher than exact pleiotropy tests (PET-R and PET-B). These results indicate that detecting exact pleiotropy is more difficult and requires larger sample size than detecting potential pleiotropy or single-trait association. This property is due to the nature of PET, because it needs to distinguish H0, 
, and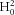 
from HA, which is different from other methods.
| α | N | CCA | CMA | P1 | P2a | PET-R | PET-B |
|---|---|---|---|---|---|---|---|
| 0.05 | 500 | 0.684 | 0.780 | 0.655 | 0.503 | 0.079 | 0.472 |
| 1,000 | 0.946 | 0.974 | 0.919 | 0.846 | 0.083 | 0.844 | |
| 5,000 | >0.99 | >0.99 | >0.99 | >0.99 | 0.111 | >0.99 | |
| 10,000 | >0.99 | >0.99 | >0.99 | >0.99 | 0.208 | >0.99 | |
| 50,000 | >0.99 | >0.99 | >0.99 | >0.99 | 0.444 | >0.99 | |
| 0.01 | 500 | 0.445 | 0.565 | 0.422 | 0.244 | 0.019 | 0.215 |
| 1,000 | 0.826 | 0.907 | 0.775 | 0.640 | 0.029 | 0.618 | |
| 5,000 | >0.99 | >0.99 | >0.99 | >0.99 | 0.058 | >0.99 | |
| 10,000 | >0.99 | >0.99 | >0.99 | >0.99 | 0.130 | >0.99 | |
| 50,000 | >0.99 | >0.99 | >0.99 | >0.99 | 0.220 | >0.99 |
- Power for each method at different sample sizes and α levels are estimated through 2,000 replications of simulation for a variant with MAF = 0.5 and two traits with r = 0.5, under an exact pleiotropy hypothesis HA of β1 = β2 = 0.15 (resulting in an approximate heritability of 0.01 for each traits).
- a Significance is determined when both two single-trait test P-values are equal to or less than the α level.
Comparing the two PET approaches, PET-R's power is significantly lower and thus requires very large sample size, making its application to real data unpractical; PET-B has a better power, which is acceptable in practice. For example, when sample size N = 1,000, a pleiotropic effect resulting in an approximate heritability of 1% for each traits (i.e., β1 = β2 = 0.15) can be detected by PET-B with a power of 0.844 or 0.618 at a significance level of 0.05 or 0.01 (Table 1).
Besides sample size (N), many other factors can affect the power of PET. Among these factors, correlation (r) between traits, MAF of variant, variant effects on traits (β1 and β2) and the difference between variant effects (|β1 − β2|) are four major ones. We investigated the power of PET-B through simulations with varied factors and observed that the power of PET increases with the increase of r, MAF, β1, and β2 (Fig. 2A–C); however, when the product of β1 and β2 is fixed, the power of PET increases with the decrease of 
(Fig. 2D) and reaches its maximum when β1 = β2, indicating that it is relatively easier to detect a pleiotropy when a variant has similar effects on two traits.
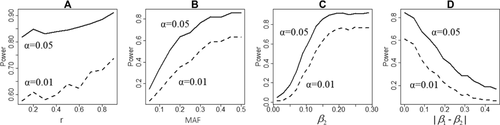
Power curves of PET-B at the 0.01 and 0.05 significance levels under different scenarios. Power for each scenario is estimated from 10,000 replications of simulation with N = 1,000, and (A) β1 = β2 = 0.15, MAF = 0.5, r = 0.1∼0.9; (B) β1 = β2 = 0.15, MAF = 0.01∼0.5, r = 0.5; (C) β1 = 0.15, β2 = 0.01∼0.3, MAF = 0.5, r = 0.5; (D)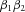 
= 0.152, |β1-β2| = 0∼0.5, MAF = 0.5, r = 0.5.
Estimation of PCC
To investigate the performance of the estimation of PCC, we used simulation to compare the expected PCC values (calculated by Equation 4 based on known parameters used in data simulation) and the estimated PCC values (estimated from simulated data using the PET-R and PET-B methods, respectively). We observed that PET-B produces significantly more accurate estimation of PCC than PET-R does. In our simulation, the PCC values estimated by PET-B have a strong correlation (r = 0.991) with their expected values, and the correlation is much lower (r = 0.879) when PCC is estimated by PET-R (Fig. 3). Overall, the PCC is underestimated by PET-R, probably due to some features in model (6) that violate the assumptions usually required in regression analysis. For example, in model (6), 
, 
, and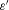 
all include the components β1 and β2 (see Appendix B), which may cause the underestimation of 
. These results, combined with the power analysis (Table 1), suggest that PET-B should be a better choice over PET-R in practice.
Scatter plots of expected PCC and the PCCs estimated by PET-R and PET-B. The PCC values are based on 1,000 replications of simulation with N = 5,000, β1 and β2 randomly drawn between 0∼0.5, MAF between 0.2∼0.5 and r between 0.1∼0.9. For each replication, the expected PCC is calculated using the theoretical Equation 4 in METHODS with known β1 and β2 (they are used for simulation); the estimated PCCs are obtained by applying (A) PET-R and (B) PET-B to the simulated data.
Application
To demonstrate how to detect pleiotropy in practice using the proposed method, we applied CMA and PET-B to a set of real GWAS data from the Family Heart Study (FamHS) [Higgins et al., 1996]. The dataset contains 2,705 subjects, about 2.5 million typed and imputed SNPs and we focus on two quantitative traits: waist circumference (WC) and the homeostatic model assessment (HOMA) which is an indicator of insulin resistance. The correlation coefficient between the two traits is 0.542 (P < 10−16).
Because bootstrapping in the PET-B test is computationally intensive, we did not perform the PET-B analysis on all SNPs. Instead, we first computed P-values for all SNPs using the CMA method and then calculated the false discovery rates (FDRs) using the Benjamini-Hochberg procedure [Benjamini and Hochberg, 1995]. Applying a cutoff of FDR < 0.05, we identified 76 significant SNPs with potential pleiotropy. Because CMA is only for testing 
against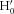 
and HA, most of the 76 SNPs are expected to be associated with at least one of the two traits. To further distinguish exact pleiotropy from potential pleiotropy (i.e., distinguish the SNPs contributing to only one trait from those contributing to both traits), we performed the PET-B test (with a bootstrap N = 10,000) on the 76 SNPs and identified 43 significant ones at a cutoff P-value < 0.01 (Supplementary Table S1). Because PET is appropriate for testing 
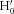against HA, most of the 43 SNPs are expected to have pleiotropic effects on the two traits. We investigated single-trait test P-values of these SNPs and found that most of the 43 SNPs significant in the PET-B test have closer P-values in separate tests of WC and HOMA (Fig. 4), suggesting a significant PET test requires a SNP has similar effects on two traits. A large effect on a trait and a small (or zero) effect on another trait may result in very different single-trait test P-values and will be less likely identified by PET, as the smaller effect could be more likely explained as the indirect effect of the larger effect passed through trait correlation.
Single-trait association test P-values for 43 pleiotropic and 33 nonpleiotropic SNPs. P-values (in the–log10 scale) in the scatter plot are calculated from separate association tests of two traits, WC and HOMA. The plot includes a total of 76 SNPs with potential pleiotropy identified by CMA, among which 43 SNPs are identified by PET-B to be pleiotropic and 33 nonpeiotropic.
The estimated PCC values of the 43 SNPs vary in the range of 0.183%∼0.28%, indicating that individual SNPs have small pleiotropic effects on WC and HOMA. These SNPs are located on chromosomes 6, 11, 12, 15, and 18, falling in five genes (GMDS, APIP, PDHX, CACNB3, and FAM174B) and an upstream region near the CDH19 gene (see Supplementary Table S1 for more details). Some of these genes have obvious connection to both WC and HOMA. For example, GMDS is involved in glucose-metabolism pathway and expressed in a variety of tissues (including adipocyte and skeletal muscle). It has been reported to be associated with obesity-related traits testosterone [Derese, 2011] and echocardiography [Imai et al., 2011]. There is also evidence that the SNP rs9503038 (P = 0.0086 in the PET test) in GMDS is an expression quantitative trait locus (eQTL) of gene EXOC4 (according the SCAN annotation [Levy et al., 2011]). EXOC4 is involved in insulin-stimulated glucose transport and a candidate for the association with type 2 diabetes and fasting glucose levels [de Heus, 2012]. These facts strongly suggest a very possible pleiotropic effect of GMDS on WC and HOMA. Although these results still need a validation using more data, this application demonstrates that the PET analysis can provide more detailed and clearer information on pleiotropy.
Discussion
We have developed a novel method, PET, for estimating and testing pleiotropic effect of a variant on two complex traits. Compared with most existing multiple-trait analysis methods, the PET method has two unique features. A key and important feature is that, unlike most multiple-trait analysis methods testing a potential pleiotropy (i.e., the association between a variant and at least one trait), PET directly tests an exact pleiotropy (i.e., a variant has effects on both two traits). Therefore, when most multiple-trait analysis methods may provide an initial screen for potential pleitropy, PET provides a more detailed test for distinguishing exact pleiotropy from potential pleiotropy, which is clearer and more helpful in answering the question of whether a variant contributes to both two traits or not.
One of the most challenging issues of testing pleiotropy is the compound property of the null hypothesis. The pleiotropy test for a variant and two traits involves one alternative hypothesis of exact pleiotropy (HA: β1 ≠ 0 and β2 ≠ 0), one complete null (
: β1 = β2 = 0), and two incomplete nulls (
: β1 = 0, β2 ≠ 0 and 
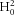: β1 ≠ 0, β2 = 0). Because the complete null can be tested by most existing multiple-trait analysis methods, there is more interest in testing the incomplete nulls vs. the alternative hypothesis. In practice there is no clear rule for choosing a particular null from 
, 
, and 
, making it hard to construct a test for HA. Although it is possible to construct likelihood ratio or generalized least squares (GLS) based procedures for separate tests of 
vs. HA, 
vs. HA, and 
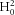vs. HA, it will introduce an extra ambiguity when making decision based on multiple P-values. An example of the ambiguity can be seen from a recently developed MTMM method [Korte et al., 2012], in which common effect and interaction effects of a variant on multiple traits are tested separately and can be used to infer pleiotropy; however, when common effect is not significant but interaction is significant, no clear conclusion can be drawn on pleiotropy. Similarly, Flutre et al. have recently developed a Bayesian statistical framework for joint eQTL analysis in multiple tissues [Flutre et al., 2013], which is featured by both joint and separate hypothesis testing and can be used for the identification of pleiotropy. However, when using such a separate testing strategy to detect pleiotropy, because of the screening of all alternative hypotheses (e.g., HA, 
, and 
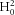) against the same null (
), it will introduce the similar multiple testing and ambiguity issue, sometimes making the inference on pleiotropy difficult (especially when more than one P-values are significant with a conflict, for example, both tests of 
vs. HA and 
vs. 
are significant, but a further test of HA vs. 
is not significant). To avoid such issues, we have proposed the PET test, which allows a universal test of an alternative hypothesis (HA) against multiple nulls (
, 
, and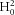 
), thus provides a single P-value for clearer testing of pleiotropy.
Another unique feature of PET is that it provides an estimation of the size of pleiotropy, which is clearly defined as the portion of between-trait correlation that can be explained by a variant and is measured by PPC. The estimation of PPC is very useful for understanding how and to what extent a pleiotropic variant affects the correlation structure of complex traits. The value of PPC can be positive or negative. A positive PPC indicates the same direction of the effects of a variant on traits and negative indicates different directions.
It should be noted that there are many different biological types of pleiotropy [Hodgkin, 1998; Solovieff et al., 2013], and thus statistical definitions of pleiotropy could be different, and different definitions may result in very different statistical methods. For example, pleiotropy can be defined by variant, gene or region. A pleitropic variant is a single variant that contribute to two (or more) traits and a pleiotropic gene (or region) may contribute to multiple traits through different variants but each individual variant may not be pleiotropic. The PET method is developed only for testing pleiotropic variants. Detecting pleitropic gene (or region) will need a different method. In addition, the PET method itself may need a modification to answer some more complicate and delicate questions regarding pleitropic variants. For example, if there are two variants with strong linkage disequilibrium (LD), if the two variants contribute to two different traits separately (i.e., both are nonpleiotropic variants), direct application of PET to either variant may lead a significance of pleiotropy due to the LD between them. Another challenging issue is how to test pleiotropy when trait number increases (far more than two). From these facts and questions, we can see that our current version of PET is still limited. When pleiotropy test involves more variants and more traits, it needs to be improved through modification or incorporation with other techniques. A recently published Bayesian method for testing colocalization between pairs of genetic associations has touched such questions [Giambartolomei et al., 2013]. This method uses summary statistics to assess different association hypotheses for pairs of traits and variants (e.g., hypotheses of no association with either trait, association with trait 1 but not with trait 2, association with two trait via two independent variants, or one shared variant, etc.). Of course, when this type of method is of great potential to be extended for more complicated pleiotropy analyses, there are some challenging issues that need to be improved, for instance, how to reduce the false positives and increase the power of detecting a true hypothesis when an inference is made based on multiple possible hypotheses, and how to improve a Bayes factor based test when the posterior probabilities of multiple hypotheses are not independent (due to the correlation between traits and/or LD between variants).
Finally, we want to point out that the PET analysis is different from another two widely used analyses, mediation model (MM) [MacKinnon et al., 2007; Richiardi et al., 2013] and Mendelian randomization (MR) [Smith and Ebrahim, 2003; Thomas and Conti, 2004]. Although they all are about modeling and interpreting the relationship between three (or more than three) variables (for the convenience of comparison, here we refer to three variables as A, B, and C), they have different application goals. When PET is developed for detecting pleiotropy (i.e., whether A has direct effects on both B and C), MM tests mediation effect of A between B and C (i.e., whether B has a causal effect on A and then A has a causal effect on C) and MR investigates the casual effect of B on C by introducing an instrumental variable A (i.e., whether B has causal effect on C, given extra association information from A). In terms of model, a major difference is that both MM and MR require the definition of causality direction (from B to C, or from C to B) before analysis, but PET does not, because the focus of PET is to assess how much correlation between B and C can be explained by A, regardless of the causality direction between B and C. Because they all are based on linear models, some statistical features of them are related and/or interacted. For example, in the presence of pleiotropic effects (of A on both B and C), the MR causality inference (on B and C) will be biased [Solovieff et al., 2013]. Such interaction may suggest the use of a combination of these methods in practice. For example, before MR analysis, we can perform a PET test to make sure there is no pleiotropy and thus the MR result will be more likely to be unbiased. Of course, how these models and methods are connected to and interacted with each other is still an open question and requires more theoretical work.
Software
The R program for PET analysis is available. Please contact Dr. Qunyuan Zhang at [email protected] to request it.
Acknowledgments
This work was supported by the National Institute of Health (NIH) grants 1R01DK8925601 (to I.B.B.) and 5R01DK075681 (I.B.B.). We thank Dr. Lihua Wang for assistance in SNP and gene annotation and interpretation.
Appendix A
Decomposition of Covariance of Two Traits
and 
, the covariance between Y1 and Y2, 
, can be decomposed as
= 0 and 
= 0,
Appendix B
Multiplication of Two Regression Models
and 
, we have
= 
, 
= 
, 
= 
, 
= 
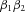, and the sum of all components carrying ε1 or ε2 be a composite residual 
= 
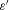, the model of 
can be rewritten as
Appendix C
Estimation of Residual Covariance of Two Traits
) in Equation 3, Y1 and Y2 are simultaneously fitted in a bivariate model
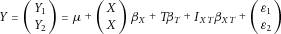
is a trait-by-variant interaction design vector, constructed by taking the combination of X and T. μ, 
, 
, and εi are grand mean, main effect of X, interaction effects between X and traits, and residuals, respectively. Because Y1 and Y2 are two correlated traits, the residual ε is a random, two-segment vector with a mean of (0,0)T and a 2 × 2 covariance matrix of
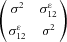
The covariance component 
can be estimated using a maximum likelihood method (or other methods such as GLS and simplified regression). In this article, we chose the maximum likelihood method implemented in the R lme function).
