X-Chromosome Genetic Association Test Accounting for X-Inactivation, Skewed X-Inactivation, and Escape from X-Inactivation
ABSTRACT
X-chromosome inactivation (XCI) is the process in which one of the two copies of the X-chromosome in females is randomly inactivated to achieve the dosage compensation of X-linked genes between males and females. That is, 50% of the cells have one allele inactive and the other 50% of the cells have the other allele inactive. However, studies have shown that skewed or nonrandom XCI is a biological plausibility wherein more than 75% of cells have the same allele inactive. Also, some of the X-chromosome genes escape XCI, i.e., both alleles are active in all cells. Current statistical tests for X-chromosome association studies can either account for random XCI (e.g., Clayton's approach) or escape from XCI (e.g., PLINK software). Because the true XCI process is unknown and differs across different regions on the X-chromosome, we proposed a unified approach of maximizing likelihood ratio over all biological possibilities: random XCI, skewed XCI, and escape from XCI. A permutation-based procedure was developed to assess the significance of the approach. We conducted simulation studies to compare the performance of the proposed approach with Clayton's approach and PLINK regression. The results showed that the proposed approach has higher powers in the scenarios where XCI is skewed while losing some power in scenarios where XCI is random or XCI is escaped, with well-controlled type I errors. We also applied the approach to the X-chromosomal genetic association study of head and neck cancer.
Introduction
X-chromosome inactivation (XCI) on female X-chromosome loci, which was originally hypothesized by Lyon in 1961 [Lyon, 1961], states that in females during early embryonic development one of the two copies of the X-chromosome present in each cell is randomly inactivated to achieve the dosage compensation of X-linked genes in males and females [Chow et al., 2005; Gendrel and Heard, 2011; Hickey and Bahlo, 2011; Loley et al., 2011; Minks et al., 2008; Starmer and Magnuson, 2009; Willard, 2000; Wong et al., 2011]. Because of this random XCI, two copies of the X-chromosome in females do not have twice the effect of a single copy of the X-chromosome in males. Clayton's approach [Clayton, 2008] was the first statistical method taking the random XCI into account when analyzing the X-chromosome genetic data. He proposed two chi-squared tests, including the 1-degree-of-freedom and 2-degrees-of-freedom chi-squared tests, where the males were treated as homozygous females in the models. Specifically, three genotypes of females are coded as 0, 1, or 2, while two genotypes of males are coded as 0 or 2. With this coding strategy, the heterozygous genotype in females falls midway between two homozygous genotypes on the linear predictor scale [Clayton, 2008], which is appropriate because in heterozygous females about 50% of cells have the deleterious allele active while the other 50% of cells have the normal allele active due to random XCI. The 1-degree-of-freedom chi-squared test proposed by Clayton has been shown to be more powerful in previous studies [Hickey and Bahlo, 2011; Loley et al., 2011]. Clayton's approach is also implemented in other software programs for genetic analysis, such as IMPUTE [Howie et al., 2009; Marchini et al., 2007] and MaCH [Li et al., 2010].
The XCI process is in general random; however, studies have suggested that skewed or nonrandom XCI is a biological plausibility [Amos-Landgraf et al., 2006; Belmont, 1996; Busque et al., 2009; Chagnon et al., 2005; Minks et al., 2008; Plenge et al., 2002; Struewing et al., 2006; Willard, 2000; Wong et al., 2011]. In this study, we denote this phenomenon of skewed XCI as XCI-S. The skewness of XCI has been defined using an arbitrary threshold as inactivation of one of the alleles in more than 75% of cells [Abkowitz et al., 1998; Chabchoub et al., 2009; Minks et al., 2008; Naumova et al., 1998; Renault et al., 2013; Sharp et al., 2000; Wong et al., 2011]. Extreme or severe skewness, which is defined as inactivation of one of the alleles in more than 90% of cells, has also been observed [Amos-Landgraf et al., 2006; Busque et al., 1996; Champion et al., 1997; Gale et al., 1997; Hatakeyama et al., 2004; Minks et al., 2008; Sharp et al., 2000; Tonon et al., 1998; Willard, 2000; Wong et al., 2011]. In a population of phenotypically unaffected females, the percentage of cells with one X-chromosome active can range from 50% (i.e., random XCI) to 100% (i.e., same X-chromosome is active in all cells) [Amos-Landgraf et al., 2006; Belmont, 1996]. Skewed XCI has been observed in young children, but the skewness increases with age [Amos-Landgraf et al., 2006; Busque et al., 2009; Chagnon et al., 2005; Minks et al., 2008; Sharp et al., 2000; Wong et al., 2011].
Multiple studies of complex disorders have shown that the skewed XCI pattern could be more common in affected females than in unaffected females. For example, Plenge et al. [2002] reported that XCI-S pattern is a relatively common feature in women with X-linked mental retardation disorders. They found that approximately 50% of affected women demonstrated a markedly XCI-S pattern, compared with only 10% of female control subjects. Talebizadeh et al. [2005] showed that the XCI-S pattern was observed in a larger proportion of females in the autism group (33%) than in the control group (11%). Chabchoub et al. [2009] found that the XCI-S pattern was observed in 34% of rheumatoid arthritis patients and 26% of autoimmune thyroid disease patients, compared to 11% of controls. Two other studies have suggested that the XCI-S pattern is more common in patients with invasive ovarian cancer and young patients with breast cancer than in controls [Buller et al., 1999; Kristiansen et al., 2002]. Therefore, it is important to account for XCI-S when testing the association between X-chromosome genetic markers and diseases. In such association studies, special consideration is needed because one cannot assume that the genotypic effects for heterozygous females will be midway between two homozygous genotypes. To our knowledge, no statistical test has been developed to account for the skewed XCI.
Another complexity in analyzing X-chromosome data is the escape from XCI (denoted as XCI-E) outside the pseudo-autosomal regions on the X-chromosome. It is estimated that about 75% of X-linked genes undergo silencing of one copy of the female X-chromosomes as the result of XCI; however, the remaining genes may escape inactivation, and in those genes both alleles will be active (i.e., no dosage compensation) [Brown et al., 1997; Carrel and Willard, 2005; Carrel et al., 2006; Miller and Willard, 1998; Willard, 2000]. The XCI-E regions can be analyzed using the standard association tests for autosomal loci, such as allele-counting approaches [Zheng et al., 2007] and the regression approach used by PLINK [Purcell et al., 2007]. Zheng et al. [2007] proposed six association tests for X-chromosome genetic markers, using different combinations of tests for male and female samples based on the genotypic counts and allelic counts in cases and controls. PLINK is the most popular software for genome-wide association (GWA) studies and has been widely used in association studies of the X-chromosome [Carrasquillo et al., 2009; Chung et al., 2011; Wise et al., 2013]. PLINK performs the association tests for X-chromosome loci in two ways: using only females or using all samples in regression models (linear or logistic) that include sex as a covariate. The first approach might lead to a loss of power for the analysis because of the smaller sample size due to the exclusion of males from the analyses. For the regression models, PLINK codes the genotypes assuming the effect of the deleterious allele in males is the same as the effect of the heterozygote genotype in females, that is, three genotypes of females are coded as 0, 1, or 2, while two genotypes of males are coded as 0 or 1. Both the PLINK and Zheng et al. approaches account for escape from XCI but ignore biologically plausible random and skewed XCI mechanisms. On the other hand, Clayton's approach accounts for random XCI but ignores escape from XCI and skewed XCI.
Because the true underlying XCI process is unknown and differs across different regions on the X-chromosome, we proposed a unified approach that maximizes the likelihood ratio over all such biological possibilities: random XCI, XCI-S, and XCI-E. A permutation-based procedure was developed to assess the significance of the proposed association test. We conducted simulation studies to investigate the performance of the proposed approach and compared it to the 1-degree-of-freedom chi-squared test proposed by Clayton and the PLINK regression approach. The results showed that the proposed association test had higher power than the other two approaches in the scenarios where XCI was skewed while losing some power in scenarios where XCI was random or XCI escape occurred. The type I errors of all three methods were well controlled. We also applied all three approaches to investigate X-chromosome genetic association in head and neck cancer.
Methods
We considered a single-nucleotide polymorphism (SNP) on the X-chromosome with two alleles: deleterious allele A and normal allele a. We assumed a binary random variable for the disease of interest and denoted it as Y = {0, 1}, with 0 representing individuals without the disease and 1 representing individuals with the disease. As discussed above, the true underlying XCI process is unknown and differs from region to region on the X-chromosome; therefore, at any given locus on the X-chromosome it is possible to observe one of four biological models: XCI, XCI-S in the direction of the deleterious allele, XCI-S in the direction of the normal allele, and XCI-E. We aimed to account for all of these biological models in our statistical approach for the X-chromosome association test. Particularly, for random and nonrandom XCI, i.e., XCI and XCI-S, we used a random variable X = {0, 2} to denote alleles a and A, respectively, for males and a random variable X = {0, γ, 2} to denote genotypes (a, a), (A, a), and (A, A), respectively, for females, where γ∈ [0, 2]. Because we considered both random and nonrandom XCI in the model, we would not know the true underlying percentage of skewness with certainty. Therefore, instead of using a fixed number for γ (i.e., 1 as denoted in Clayton's approach), we used a number for γ that varied between 0 and 2 to denote the level of skewness in the heterozygous females. Note that when γ = 1, this coding is the same as in Clayton's additive genetic model, which assumes a random XCI. When γ takes a value between 1 and 2, this coding assumes a nonrandom XCI-S skewed toward the deleterious allele. For example, γ = 1.5 represents a scenario where 75% of the cells have the deleterious allele active and the other 25% of the cells have the normal allele active. When γ takes a value between 0 and 1, this coding assumes a nonrandom XCI-S skewed toward the normal allele. For example, γ = 0.5 represents a scenario where 25% of the cells have the deleterious allele active and the other 75% of the cells have the normal allele active. To account for XCI-E, we used the same coding as the one used by PLINK: for males, we used a binary random variable X = {0, 1} to denote alleles a and A, respectively; for females, we used a categorical random variable X = {0, 1, 2} to denote genotypes (a, a), (A, a), and (A, A), respectively. In this scenario, both copies of the X-chromosome in females are active, so the males carrying the deleterious allele were treated as heterozygous females.

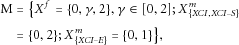
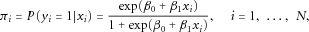
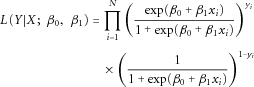
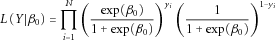
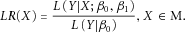 (1)
(1)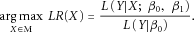 (2)
(2)In the above maximization scheme, we performed a grid search in which the γ value ranged from 0 to 2. Given the fixed coding of X, we can estimate the regression coefficients β0 and β1 by maximizing the likelihood ratio LR as in equation 1, and the corresponding LR can be calculated. Thus, the maximum LR, or LR*, corresponding to the optimal coding strategy X* given the sample data, can be obtained by enumerating all the coding strategies X ∈ M. Moreover, the effect size (or odds ratio [OR] for the logistic model) of the association between the disease and the SNP can be obtained using the  (OR* = exp(
(OR* = exp( )) corresponding to LR*.
)) corresponding to LR*.
Based on the simulation studies, we found that we do not need to perform a grid search using a small step function as it has very little impact on the LR values and grid search strategy typically leads to loss of statistical power because of the multiple testing corrections. Therefore, we considered only four coding strategies: one coding for XCI-E and three coding for XCI and XCI-S. Particularly, the value for γ was set as 0, 1, or 2 to represent XCI-S toward the normal allele, random XCI, or XCI-S toward the deleterious allele, respectively.
Permutation-based Calculation of Empirical P Value
- We randomly permuted the values of disease status for B times and kept all the other variables unchanged (i.e., SNP). By permuting the disease status values, we ensured that there would be no association between the disease and the SNP.
- For each permuted disease status, we evaluated the association between the disease and SNP and obtained permuted
 , u = 1, 2,…, B, corresponding to the optimal strategy
, u = 1, 2,…, B, corresponding to the optimal strategy  .
. - The empirical P value of LR* was estimated from the proportion of
 , u = 1, 2,…, B, resulting from permutations greater than the observed LR*: (number of
, u = 1, 2,…, B, resulting from permutations greater than the observed LR*: (number of  )/B.
)/B.
Simulation Approach

In the logistic model, X1 and X2 represent associated SNP1 and unassociated SNP2, and Xsex represents the sex covariate. The minor allele frequency (MAF) for both SNPs was assumed to be 40%. We fixed the regression coefficients at β1 = 0.2624 and β2 = 0, which correspond to ORs of 1.3 and 1, respectively. We assumed that sex was associated with the disease of interest (βs = 0.4055). We used a binary random variable for sex, Xsex = {0, 1}, with either female or male being at increased risk for disease (i.e., coded as 1). The intercept coefficient β0 was set as −2.55. Note that allowing sex to be an independent risk factor, we are considering scenarios with different male and female proportions in cases and controls. Across different scenarios listed in Table 1, the proportions of females in cases varied from 40% to 60%. We also investigated different MAFs in males and females, which has been shown to have an impact on different statistical approaches for X-chromosome genetic association in previous studies [Hickey and Bahlo, 2011; Loley et al., 2011]. We observed that the largest estimated difference in MAFs of males and females was ∼13% based on the head and neck X-chromosomal genetic data. Thus, in some simulation scenarios, we set the MAF as 30% (or 40%) for males and 40% (or 30%) for females, respectively.
| Median OR (95% CI) | |||||||
|---|---|---|---|---|---|---|---|
| PLINK | Clayton | Our Approach | |||||
| Biological Models | Increased riska | SNP1 | SNP2 | SNP1 | SNP2 | SNP1 | SNP2 |
| XCI-S to deleterious allele | Male | 1.47 (1.27–1.71) | 1.00 (0.86–1.16) | 1.32 (1.19–1.46) | 1.00 (0.90–1.11) | 1.32 (1.20–1.44) | 1.00 (0.89–1.12) |
| Female | 1.46 (1.26–1.69) | 1.00 (0.86–1.16) | 1.32 (1.19–1.47) | 1.00 (0.90–1.11) | 1.32 (1.20–1.45) | 0.99 (0.89–1.12) | |
| XCI-S to normal allele | Male | 1.40 (1.21–1.63) | 1.00 (0.86–1.16) | 1.29 (1.16–1.42) | 1.00 (0.90–1.11) | 1.31 (1.19–1.45) | 0.99 (0.89–1.12) |
| Female | 1.37 (1.19–1.58) | 1.00 (0.86–1.16) | 1.28 (1.16–1.42) | 1.00 (0.90–1.11) | 1.31 (1.18–1.45) | 0.99 (0.89–1.12) | |
| Random XCI | Male | 1.44 (1.24–1.67) | 1.00 (0.86–1.16) | 1.30 (1.17–1.44) | 1.00 (0.90–1.11) | 1.31 (1.18–1.45) | 0.99 (0.89–1.12) |
| Female | 1.41 (1.22–1.63) | 1.00 (0.87–1.16) | 1.30 (1.17–1.44) | 1.00 (0.90–1.11) | 1.31 (1.18–1.46) | 1.01 (0.90–1.12) | |
| XCI-E | Male | 1.30 (1.12–1.51) | 1.00 (0.86–1.16) | 1.19 (1.07–1.32) | 1.00 (0.90–1.11) | 1.25 (1.11–1.43) | 1.01 (0.89–1.12) |
| Female | 1.30 (1.13–1.50) | 1.00 (0.86–1.16) | 1.20 (1.08–1.33) | 1.00 (0.90–1.11) | 1.26 (1.11–1.44) | 1.00 (0.89–1.12) | |
- XCI, X-chromosome inactivation; XCI-S, skewed X-chromosome inactivation; XCI-E, escape from X-chromosome inactivation.
- a male or female implies the gender for which the disease risk was higher.
Given these parameters, we first randomly generated the sex for each subject on the basis of the prevalence of males in the general population (i.e., 50%). Because males are hemizygous, the genotypes were simulated conditional on sex according to the different biological models discussed in the Methods section. The disease statuses were then generated based on SNP genotypes and sex. Using this approach, we simulated a large amount of data on the population of interest and then randomly selected 1,000 cases (subjects with the disease) and 1,000 controls (subjects without the disease). We employed the permutation procedure described above to evaluate the empirical P values for our approach based on B = 100,000 permutations. The results for the PLINK regression approach were obtained using PLINK software, version 1.07 [Purcell et al., 2007]. Clayton's 1-degree-of-freedom test was performed with the use of R package “snpStats” software developed by Clayton [2011]. The powers and type I error rates reported for the simulation studies were based on 100,000 replicate datasets.
Furthermore, to investigate the potential bias in OR estimates obtained using different approaches, we performed additional simulations. Particularly, we simulated a range of ORs from 1.0 to 3.0 at 0.1 grid values resulting in a total of 21 ORs for each of the four biological models: random XCI, XCI-S toward either the deleterious or normal allele, and XCI-E. As in the previous simulations, we used an SNP MAF of 40%, with males coded as 1 and females coded as zero and a corresponding beta coefficient (βs = 0.4055). We reported median estimated ORs based on 500 replicates, each with 1,000 cases and 1,000 controls.
Results
In Table 1, we report the median estimated ORs and their 95% confidence intervals (CIs) for testing the association between X-chromosome SNPs and the disease of interest using PLINK regression, Clayton's 1-degree-of-freedom test, and the proposed approach. For all four biological models, all three approaches provided accurate OR estimates with comparable 95% CIs when the SNP was not associated with the disease (i.e., SNP2). When the SNP was associated with the disease (i.e., SNP1), the PLINK regression highly overestimated ORs for most of the scenarios. For example, the estimated median ORs for the XCI-S to the deleterious allele model in males and females at increased risk, respectively, were 1.47 and 1.46, compared to the true OR of 1.3. As expected, the only scenario in which PLINK regression provided accurate ORs was when the simulated biological model was XCI-E. In contrast, our approach and Clayton's 1-degree-of-freedom test provided accurate OR estimates for most scenarios except for the XCI-E biological model. However, our approach was less biased for the XCI-E biological model compared to Clayton's approach. In this scenario, compared to the true OR of 1.3, Clayton's approach provided estimated median ORs of 1.19 and 1.20, respectively, for males and females at increased risk, whereas our approach provided estimated median ORs of 1.25 and 1.26, respectively. We also investigated the 95% coverage probabilities for the CIs using the three approaches and observed similar trends (supplementary Table S1).
To further investigate the bias in OR estimates, we performed simulations for a range of ORs. Figure 1 shows the estimated ORs obtained using the different approaches compared to the true ORs used for the simulation of these datasets. Panels (A) to (D) correspond to different biological models. Each panel shows the median ORs based on 500 replicates. For all four of the biological models, our approach provided accurate OR estimates for the entire simulated range of ORs, except when the true model was XCI-E and ORs were relatively small (1.2–1.5) because in these scenarios the different XCI models have very close likelihood ratio values limiting ability of our approach to select the true XCI-E model, which in turn leads to underestimation of the estimated ORs (Fig. 1D). PLINK regression provided highly overestimated ORs except for the XCI-E model, and the magnitude of bias increased as the true ORs increased. For example, when the true OR was 3, PLINK regression gave OR estimates close to 5 for the random and skewed XCI models (Fig. 1, panels (A–C)). Clayton's approach provided highly under-estimated ORs for the XCI-E model, and the magnitude of bias increased as the true ORs increased. For example, when the true OR was 3, Clayton's approach gave an OR estimate close to 2 (Fig. 1, panel (D)). Clayton's approach also provided a slightly overestimated OR for the scenario of XCI-S toward the deleterious allele when the true ORs were higher than 2 (Fig. 1, panel (A)). The proposed approach was thus found to be mostly robust for estimating ORs in different biological models.

We conducted further simulations to investigate the robustness of our approach, which considered only four coding strategies: one coding for XCI-E and three coding for XCI and XCI-S (see Methods section). Specifically, when generating the data for females, we used X = {0, 1.5, 2} to denote genotypes (a, a), (A, a), and (A, A), respectively, a scenario where 75% of the cells have the deleterious allele active and the other 25% of the cells have the normal allele active. We also considered another scenario where female was coded as X = {0, 0.5, 2}, reflecting 25% of the cells having the deleterious allele active and the other 75% of the cells having the normal allele active. We used two SNPs as we defined previously: associated SNP1 and unassociated SNP2 with MAFs of 40%. The true underlying ORs were set as 1.3 and 1, respectively. The median of ORs and 95% CIs were reported in supplementary Table S2 based on 100,000 replicates, each with 1,000 cases and 1,000 controls. As can be seen from supplementary Table S2, the four coding strategies that we had used for our approach remained robust with either male or female as the factor increasing the disease risk.
We also investigated the type I error rates for the different approaches using SNP2, which was not associated with the disease. The type I error rates were estimated at nominal significance levels of 0.001 and 0.0005 (Table 2). We observed that, for all scenarios, all three approaches controlled the type I error rates at both nominal significance levels, and the type I error rates were similar for the three approaches. For example, when the underlying biological model was XCI-S toward the deleterious allele and females were at increased risk for the disease, the type I error rates were 0.0008, 0.0011, and 0.0012 at the 0.001 significance level and 0.0004, 0.0005, and 0.0006 at the 0.0005 significance level for PLINK regression, Clayton's 1-degree-of-freedom test, and our approach, respectively. When the MAFs were different for males (30%) and females (40%), we considered two permutation strategies: permute case-control status using combined male and female data, and permute case-control status within sex-specific strata. Both permutation approaches provided controlled type I error rates (supplementary Table S3).
| Type I Errors | ||||
|---|---|---|---|---|
| Biological models | Increased riska | PLINK | Clayton | Our Approach |
| α = 0.001 | ||||
| XCI-S to deleterious allele | Male | 0.0010 | 0.0007 | 0.0008 |
| Female | 0.0008 | 0.0011 | 0.0012 | |
| XCI-S to normal allele | Male | 0.0008 | 0.0009 | 0.0014 |
| Female | 0.0011 | 0.0012 | 0.0011 | |
| Random XCI | Male | 0.0010 | 0.0012 | 0.0011 |
| Female | 0.0009 | 0.0009 | 0.0012 | |
| XCI-E | Male | 0.0011 | 0.0010 | 0.0013 |
| Female | 0.0010 | 0.0010 | 0.0010 | |
| α = 0.0005 | ||||
| XCI-S to deleterious allele | Male | 0.0004 | 0.0004 | 0.0003 |
| Female | 0.0004 | 0.0005 | 0.0006 | |
| XCI-S to normal allele | Male | 0.0003 | 0.0004 | 0.0008 |
| Female | 0.0006 | 0.0007 | 0.0007 | |
| Random XCI | Male | 0.0006 | 0.0005 | 0.0003 |
| Female | 0.0006 | 0.0004 | 0.0006 | |
| XCI-E | Male | 0.0005 | 0.0006 | 0.0008 |
| Female | 0.0005 | 0.0006 | 0.0005 | |
- XCI, X-chromosome inactivation; XCI-S, skewed X-chromosome inactivation; XCI-E, escape from X-chromosome inactivation.
- a male or female implies the gender for which the disease risk was higher.
Power Comparisons
We also investigated the statistical power of each approach using SNP1, which was associated with the disease. The powers were assessed at nominal significance levels of 0.001 and 0.0005 (Table 3). When the true underlying biological model for the simulation was assumed to be XCI-S to either the deleterious or normal allele, our approach had the highest power to identify the associated SNP. For example, when the underlying model was XCI-S to the normal allele and females were at increased risk, the powers were 80.67, 89.73, and 93.72% for PLINK regression, Clayton's approach, and our approach, respectively, at a significance level of 0.0005. The power loss for PLINK regression was highest when the true biological models were XCI-S.
| Powers | ||||
|---|---|---|---|---|
| Biological models | Increased riska | PLINK | Clayton | Our Approach |
| α = 0.001 | ||||
| XCI-S to deleterious allele | Male | 96.02% | 97.52% | 98.59% |
| Female | 95.37% | 96.63% | 98.23% | |
| XCI-S to normal allele | Male | 88.73% | 94.42% | 96.98% |
| Female | 85.43% | 92.79% | 95.56% | |
| Random XCI | Male | 92.92% | 96.12% | 94.95% |
| Female | 91.32% | 94.91% | 94.08% | |
| XCI-E | Male | 58.03% | 50.21% | 54.98% |
| Female | 60.90% | 53.23% | 55.41% | |
| α = 0.0005 | ||||
| XCI-S to deleterious allele | Male | 94.06% | 95.99% | 97.40% |
| Female | 93.21% | 94.99% | 97.09% | |
| XCI-S to normal allele | Male | 84.65% | 91.90% | 95.50% |
| Female | 80.67% | 89.73% | 93.72% | |
| Random XCI | Male | 89.87% | 94.24% | 91.36% |
| Female | 87.94% | 92.62% | 92.15% | |
| XCI-E | Male | 50.51% | 42.43% | 47.94% |
| Female | 53.38% | 45.76% | 47.65% | |
- XCI, X-chromosome inactivation; XCI-S, skewed X-chromosome inactivation; XCI-E, escape from X-chromosome inactivation.
- a male or female implies the gender for which the disease risk was higher.
As expected, when the underlying true biological model for simulation was assumed to be random XCI, Clayton's 1-degree-of-freedom test always had the highest power, whereas PLINK regression had the lowest power to identify the associated SNP. In this situation, our approach had higher power than PLINK regression but lower power than Clayton's approach. For example, when females were at increased risk, the powers were 87.94, 92.62, and 92.15% for PLINK regression, Clayton's approach, and our approach, respectively, at a significance level of 0.0005.
As expected, when the underlying true biological model was assumed to be XCI-E, the PLINK regression approach always had the highest power to detect the associated SNP, whereas Clayton's 1-degree-of-freedom test always had the lowest power. In this scenario, our approach had higher power than Clayton's approach but lower power than PLINK regression. For example, when females were at increased risk, the powers were 53.38, 45.76, and 47.65% for PLINK regression, Clayton's approach, and our approach, respectively, at a significance level of 0.0005.
We also investigated the statistical power of each approach when the MAF for female was higher than MAF for male (40% vs. 30%). Once again the powers were assessed at nominal significance levels of 0.001 and 0.0005 (supplementary Table S4). The results from this scenario showed similar patterns as in Table 3. Furthermore, we once again considered two strategies for permutation for our approach: permute case-control status using combined male and female data, and permute case-control status within sex-specific strata. Both permutation approaches provided similar powers (supplementary Table S4). The scenario where the MAF for female was lower than MAF for male (30% vs. 40%) provided similar results (data not shown).
Head and Neck Cancer X-Chromosome Association Test
Next, we applied our approach to a case-control association study of head and neck cancer and X-chromosome genetic variants using data from a head and neck GWA study. The phase 1 analysis included 2,718 individuals, with 1,161 head and neck cancer patients and 1,557 controls frequency-matched to the cases by age (±5 years), sex, residency (by county), and ethnicity. There were 902 males and 259 females in the cases and 986 males and 571 females in the controls. The phase 2 analysis included 3,996 individuals, with 1,031 patients and 2,965 controls. There were 786 males and 245 females in the cases and 1,507 males and 1,458 females in the controls. The head and neck cancer cases were accrued at The University of Texas MD Anderson Cancer Center (UT MD Anderson) and were patients with newly diagnosed, histologically confirmed, previously untreated head and neck cancer, including cancers of the oral cavity, pharynx, and larynx. In both phases, genotyping of cases was conducted using Illumina HumanOmniExpress-12v1 BeadChip. For phase 1 analysis, after removing the individuals with discordant sex information, genotypes were available for 1,155 cases. For controls, we used Illumina HumanOmniExpress-12v1 BeadChip genotypes on 531 individuals recruited by UT MD Anderson for the study of head and neck cancers and Illumina Omni1-Quad_v1-0_B BeadChip genotypes on 1,026 individuals also recruited at UT MD Anderson for the study of cutaneous melanoma previously [Amos et al., 2011]. After removing the individuals with discordant sex information, genotypes were available for 1,547 individuals. The phase 2 analysis was based on genotyping 1,031 cases ascertained by UT MD Anderson. For phase 2 controls, we used Illumina HumanOmniExpress-12v1 BeadChip genotypes on 643 individuals recruited by UT MD Anderson and Illumina Human1Mv1 BeadChip genotypes on 2,322 European-descendent-only individuals from the Study of Addiction: Genetic and Environment provided by the National Center for Biotechnology Information and downloaded from dbGaP [Mailman et al., 2007]. From the second phase data, no individual was removed due to discordant sex information. This case-control study was approved by the institutional review board at UT MD Anderson, and all participants provided written informed consent. In the phase 1 analysis, 14,169 tagging SNPs were genotyped on the X-chromosome; in the phase 2 analysis, 14,371 tagging SNPs were genotyped on the X-chromosome. We excluded SNPs that were missing in more than 10% of the study population. To assess the empirical P values for our approach, we used 1,000,000 permutations in both phases. The fixed and random effect model analyses in the meta-analysis were conducted using PLINK software, version 1.07 [Purcell et al., 2007].
In the phase 1 study, we selected the top 50 SNPs based on the most significant P values obtained using the PLINK regression approach and another top 50 SNPs based on the most significant P values obtained using Clayton's 1-degree-of-freedom test. In the phase 2 data, a total of 33 SNPs were available from the list of SNPs that were significant using PLINK regression and Clayton's 1-degree-of-freedom test in phase 1. We then performed meta-analysis of the 33 SNPs based on the results from the phase 1 and phase 2 data using Fisher's method and the fixed and random effects models. The resulting combined P values for the three approaches, as well as the corresponding P values for Cochrane's Q statistic and heterogeneity indexes I, are reported in Table 4 (ranked using Fisher's method P values based on our approach). We also showed the −log10(meta-analysis P values) for the 33 SNPs with respect to their base-pair positions on the X-chromosome (Fig. 2). Given that there are 14,169 SNPs in phase 1 and 14,371 SNPs in phase 2, the chromosome-wide significance level should be approximately 3.5 × 10−6. Using the proposed approach, SNP rs12388803 had meta-analysis-based P values of 2.04 × 10−6, 2.83 × 10−6, and 2.83 × 10−6 using the Fisher's, fixed effect, and random effect models, respectively, which reached the chromosome-wide significance threshold. Using Clayton's approach, the corresponding meta-analysis P values were 3.74 × 10−5, 8.58 × 10−6, and 8.58 × 10−6, and using PLINK regression, the corresponding meta-analysis P values were 3.22 × 10−3, 9.16 × 10−4, and 9.16 × 10−4. The P values using Clayton's method approached chromosome-wide significance, whereas the PLINK regression method gave P values that were much less significant.
| PLINK | Clayton | Our approach | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| rs number | bp | Fisher | Fixed | Random | Q | I | Fisher | Fixed | Random | Q | I | Fisher | Fixed | Random | Q | I |
| rs12388803 | 94862551 | 3.22 × 10−03 | 9.16 × 10−04 | 9.16 × 10−04 | 0.904 | 0.00 | 3.74 × 10−05 | 8.58 × 10−06 | 8.58 × 10−06 | 0.889 | 0.00 | 2.04 × 10−06 | 2.83 × 10−06 | 2.83 × 10−06 | 0.624 | 0.00 |
| rs1554987 | 48621514 | 4.19 × 10−05 | 1.52 × 10−04 | 1.27 × 10−01 | 0.012 | 84.07 | 8.50 × 10−05 | 2.25 × 10−04 | 1.19 × 10−01 | 0.018 | 82.06 | 8.38 × 10−06* | 1.31 × 10−05 | 6.41 × 10−03 | 0.192 | 41.15 |
| rs2075837 | 48676839 | 6.81 × 10−05 | 1.13 × 10−04 | 6.35 × 10−02 | 0.035 | 77.50 | 1.53 × 10−04 | 2.05 × 10−04 | 5.75 × 10−02 | 0.049 | 74.32 | 1.71 × 10−04 | 1.14 × 10−04 | 6.34 × 10−02 | 0.035 | 77.45 |
| rs4824286 | 145929424 | 1.54 × 10−04 | 1.17 × 10−03 | 2.22 × 10−01 | 0.005 | 87.30 | 8.35 × 10−04 | 2.23 × 10−03 | 1.72 × 10−01 | 0.020 | 81.45 | 1.83 × 10−04 | 3.17 × 10−03 | 2.13 × 10−01 | 0.001 | 90.37 |
| rs5906714 | 48684646 | 7.28 × 10−05 | 1.34 × 10−04 | 7.25 × 10−02 | 0.031 | 78.47 | 1.58 × 10−04 | 2.23 × 10−04 | 6.30 × 10−02 | 0.045 | 75.10 | 3.22 × 10−04 | 1.33 × 10−04 | 7.20 × 10−02 | 0.031 | 78.41 |
| rs5905706 | 48619002 | 1.40 × 10−04 | 6.67 × 10−04 | 1.86 × 10−01 | 0.009 | 85.46 | 2.82 × 10−04 | 8.63 × 10−04 | 1.64 × 10−01 | 0.016 | 82.90 | 3.32 × 10−04 | 3.43 × 10−03 | 2.22 × 10−01 | 0.002 | 90.13 |
| rs760393 | 48612615 | 1.19 × 10−04 | 3.64 × 10−04 | 1.33 × 10−01 | 0.016 | 82.85 | 2.55 × 10−04 | 5.40 × 10−04 | 1.17 × 10−01 | 0.026 | 79.86 | 3.39 × 10−04 | 2.46 × 10−03 | 2.02 × 10−01 | 0.002 | 89.43 |
| rs4824284 | 145929326 | 1.20 × 10−04 | 9.15 × 10−04 | 2.16 × 10−01 | 0.005 | 87.31 | 7.27 × 10−04 | 3.00 × 10−03 | 2.23 × 10−01 | 0.011 | 84.55 | 4.09 × 10−04 | 9.00 × 10−04 | 2.15 × 10−01 | 0.005 | 87.32 |
| rs5906709 | 48646906 | 1.51 × 10−04 | 5.24 × 10−04 | 1.53 × 10−01 | 0.014 | 83.60 | 3.41 × 10−04 | 8.16 × 10−04 | 1.39 × 10−01 | 0.022 | 80.92 | 5.43 × 10−04 | 3.57 × 10−03 | 2.18 × 10−01 | 0.002 | 89.72 |
| rs2579849 | 11949003 | 1.01 × 10−03 | 4.01 × 10−02 | 4.75 × 10−01 | 0.001 | 90.14 | 1.89 × 10−03 | 8.12 × 10−02 | 5.37 × 10−01 | 0.002 | 89.78 | 9.06 × 10−04 | 3.61 × 10−02 | 5.18 × 10−01 | 0.000 | 91.92 |
| rs10521783 | 136444480 | 6.00 × 10−04 | 2.38 × 10−01 | 6.75 × 10−01 | 0.000 | 92.48 | 2.76 × 10−04 | 2.79 × 10−01 | 7.33 × 10−01 | 0.000 | 93.30 | 9.24 × 10−04 | 2.77 × 10−01 | 7.33 × 10−01 | 0.000 | 93.28 |
| rs5904897 | 145939528 | 4.11 × 10−04 | 2.03 × 10−03 | 2.16 × 10−01 | 0.009 | 85.51 | 1.93 × 10−03 | 3.76 × 10−03 | 1.62 × 10−01 | 0.032 | 78.23 | 1.03 × 10−03 | 4.53 × 10−03 | 2.06 × 10−01 | 0.003 | 88.91 |
| rs5975918 | 136446557 | 8.47 × 10−04 | 2.24 × 10−01 | 6.61 × 10−01 | 0.000 | 92.03 | 3.52 × 10−04 | 2.66 × 10−01 | 7.23 × 10−01 | 0.000 | 93.06 | 1.23 × 10−03 | 2.65 × 10−01 | 7.23 × 10−01 | 0.000 | 93.03 |
| rs2239477 | 123545077 | 9.70 × 10−04 | 5.19 × 10−03 | 2.39 × 10−01 | 0.009 | 85.50 | 9.55 × 10−04 | 5.84 × 10−03 | 2.66 × 10−01 | 0.007 | 86.32 | 1.23 × 10−03 | 2.11 × 10−03 | 2.10 × 10−01 | 0.008 | 85.93 |
| rs3373 | 48567295 | 6.97 × 10−04 | 9.03 × 10−02 | 6.06 × 10−01 | 0.001 | 91.50 | 1.69 × 10−03 | 1.07 × 10−01 | 6.12 × 10−01 | 0.001 | 90.24 | 1.33 × 10−03 | 6.72 × 10−01 | 5.41 × 10−01 | 0.000 | 93.41 |
| rs16995035 | 148268501 | 1.13 × 10−03 | 1.39 × 10−01 | 5.77 × 10−01 | 0.001 | 91.29 | 5.85 × 10−03 | 1.37 × 10−01 | 5.61 × 10−01 | 0.004 | 87.88 | 2.15 × 10−03 | 1.22 × 10−02 | 7.12 × 10−01 | 0.006 | 86.76 |
| rs6417935 | 55960724 | 5.98 × 10−03 | 6.71 × 10−02 | 4.41 × 10−01 | 0.006 | 86.68 | 3.94 × 10−03 | 1.55 × 10−02 | 2.95 × 10−01 | 0.012 | 84.05 | 2.96 × 10−03 | 1.49 × 10−03 | 9.70 × 10−02 | 0.070 | 69.55 |
| rs5935185 | 11930465 | 2.27 × 10−03 | 5.12 × 10−03 | 1.86 × 10−01 | 0.027 | 79.67 | 2.15 × 10−03 | 6.59 × 10−03 | 2.34 × 10−01 | 0.017 | 82.50 | 3.24 × 10−03 | 5.68 × 10−04 | 7.76 × 10−02 | 0.111 | 60.68 |
| rs2105910 | 57778934 | 5.19 × 10−03 | 3.50 × 10−03 | 3.66 × 10−02 | 0.159 | 49.52 | 1.40 × 10−03 | 1.13 × 10−03 | 4.27 × 10−02 | 0.108 | 61.34 | 3.26 × 10−03 | 1.04 × 10−03 | 4.60 × 10−02 | 0.087 | 65.82 |
| rs7888207 | 11916455 | 7.06 × 10−03 | 1.56 × 10−02 | 2.52 × 10−01 | 0.027 | 79.62 | 7.10 × 10−03 | 1.62 × 10−02 | 2.57 × 10−01 | 0.026 | 79.76 | 3.47 × 10−03 | 4.64 × 10−03 | 2.18 × 10−01 | 0.015 | 83.18 |
| rs16993411 | 136486358 | 3.84 × 10−03 | 1.38 × 10−01 | 5.68 × 10−01 | 0.003 | 89.00 | 1.63 × 10−03 | 1.55 × 10−01 | 6.34 × 10−01 | 0.001 | 90.74 | 4.14 × 10−03 | 1.51 × 10−01 | 6.65 × 10−01 | 0.001 | 90.89 |
| rs1231461 | 12042112 | 2.02 × 10−03 | 2.03 × 10−02 | 3.75 × 10−01 | 0.005 | 87.55 | 4.80 × 10−03 | 5.18 × 10−02 | 4.47 × 10−01 | 0.006 | 86.66 | 4.21 × 10−03 | 2.09 × 10−01 | 4.24 × 10−01 | 0.001 | 91.74 |
| rs5935181 | 11923987 | 3.78 × 10−03 | 1.11 × 10−02 | 2.72 × 10−01 | 0.017 | 82.52 | 4.09 × 10−03 | 2.04 × 10−02 | 3.56 × 10−01 | 0.010 | 84.96 | 5.07 × 10−03 | 2.32 × 10−02 | 4.17 × 10−01 | 0.005 | 87.64 |
| rs708467 | 11846155 | 4.66 × 10−03 | 1.52 × 10−01 | 5.85 × 10−01 | 0.003 | 88.64 | 2.96 × 10−03 | 3.14 × 10−01 | 7.15 × 10−01 | 0.001 | 90.40 | 5.76 × 10−03 | 7.62 × 10−01 | 5.98 × 10−01 | 0.001 | 91.69 |
| rs7876455 | 107260683 | 6.96 × 10−03 | 1.07 × 10−02 | 1.68 × 10−01 | 0.050 | 73.88 | 6.95 × 10−03 | 7.41 × 10−03 | 1.09 × 10−01 | 0.084 | 66.42 | 6.63 × 10−03 | 1.31 × 10−02 | 1.69 × 10−01 | 0.029 | 78.96 |
| rs5978730 | 15495233 | 6.19 × 10−03 | 1.01 × 10−02 | 1.87 × 10−01 | 0.044 | 75.39 | 3.89 × 10−03 | 7.62 × 10−03 | 2.00 × 10−01 | 0.032 | 78.27 | 6.83 × 10−03 | 4.73 × 10−03 | 1.75 × 10−01 | 0.031 | 78.39 |
| rs1415124 | 145949281 | 5.79 × 10−03 | 3.75 × 10−02 | 3.89 × 10−01 | 0.009 | 85.38 | 1.14 × 10−02 | 2.15 × 10−02 | 2.57 × 10−01 | 0.035 | 77.57 | 8.37 × 10−03 | 1.49 × 10−02 | 1.99 × 10−01 | 0.015 | 83.21 |
| rs844971 | 140439277 | 2.38 × 10−02 | 4.31 × 10−02 | 3.08 × 10−01 | 0.038 | 76.80 | 6.52 × 10−03 | 1.50 × 10−02 | 2.66 × 10−01 | 0.025 | 80.20 | 9.00 × 10−03 | 1.45 × 10−02 | 2.64 × 10−01 | 0.015 | 83.27 |
| rs12394374 | 135076147 | 5.20 × 10−03 | 1.69 × 10−01 | 5.68 × 10−01 | 0.003 | 88.59 | 2.18 × 10−02 | 4.72 × 10−01 | 6.50 × 10−01 | 0.008 | 85.76 | 1.05 × 10−02 | 6.05 × 10−01 | 5.45 × 10−01 | 0.001 | 90.82 |
| rs5935986 | 15498034 | 1.01 × 10−02 | 1.29 × 10−02 | 1.68 × 10−01 | 0.064 | 70.92 | 6.40 × 10−03 | 9.77 × 10−03 | 1.82 × 10−01 | 0.047 | 74.72 | 1.12 × 10−02 | 1.83 × 10−03 | 3.86 × 10−02 | 0.200 | 39.02 |
| rs10856171 | 145878179 | 5.05 × 10−03 | 7.36 × 10−03 | 1.58 × 10−01 | 0.050 | 74.06 | 1.56 × 10−02 | 1.68 × 10−02 | 1.54 × 10−01 | 0.085 | 66.31 | 1.26 × 10−02 | 3.62 × 10−02 | 2.48 × 10−01 | 0.010 | 85.10 |
| rs5929779 | 136040115 | 8.32 × 10−03 | 1.70 × 10−02 | 2.32 × 10−01 | 0.033 | 78.07 | 5.93 × 10−03 | 1.22 × 10−02 | 2.15 × 10−01 | 0.032 | 78.27 | 1.30 × 10−02 | 9.17 × 10−03 | 1.90 × 10−01 | 0.042 | 75.73 |
| rs3761543 | 48554637 | 8.79 × 10−03 | 3.91 × 10−02 | 3.86 × 10−01 | 0.014 | 83.46 | 4.02 × 10−02 | 7.13 × 10−02 | 3.59 × 10−01 | 0.047 | 74.66 | 1.60 × 10−02 | 2.98 × 10−01 | 4.32 × 10−01 | 0.002 | 89.38 |
- *The phase 1 P value was less than 1.00 × 10−06. The meta-analysis P value was calculated using a P value of 1.00 × 10−06 for phase 1.
- bp, base-pair position; Q, P value for Cochrane's Q statistic; I, heterogeneity index.

For this SNP rs12388803, we also investigated potential heterogeneity between phase 1 and phase 2 data using Cochrane's Q statistic and the heterogeneity index, I. The P values of Cochrane's Q statistic were 0.904, 0.889, and 0.624 for PLINK regression, Clayton's approach, and our approach, respectively, and the heterogeneity index values were 0 for all three approaches, implying that there is no heterogeneity for this SNP between the phase 1 and phase 2 studies.
Discussion
The biological process for XCI is complex. In addition to the random XCI process, nonrandom, or skewed, XCI has been shown to be a biological plausibility associated with complex disorders. Furthermore, some of the X-linked genes altogether escape XCI. Currently, to our knowledge, there is no method of association testing that accounts for all of the different plausible biological models. To overcome this limitation, we proposed a unified approach for maximizing the likelihood ratio that accounts for the unknown underlying XCI process, including random XCI, skewed XCI toward either the deleterious or normal allele, and escape from XCI. We also developed a permutation procedure to obtain P values for the proposed approach. We conducted simulation studies to investigate the performance of the proposed approach and compared it to PLINK regression and Clayton's 1-degree-of-freedom test. We examined multiple scenarios with different plausible biological models (random XCI, XCI-S toward either allele, and XCI-E) and different sexes at increased risk for the disease.
Power comparisons showed that Clayton's 1-degree-of-freedom test was the most powerful approach when the true underlying biological model was random XCI, but it lost some power when the true underlying biological models were escape from or skewed in XCI. On the other hand, PLINK regression was the most powerful approach when the true underlying biological model was XCI-E but would lose power when the true underlying biological models were random or skewed XCI. Finally, the proposed approach was the most powerful when the true underlying biological model was XCI-S (toward either the deleterious or normal allele), and it lost a small amount of power when the true underlying biological models were random or escape from XCI.
We also investigated the potential bias in the OR estimations for the three approaches. PLINK regression provided upward biased ORs for random XCI and XCI-S models, and the magnitude of overestimation increased when the true ORs were higher; Clayton's approach provided underestimated ORs for the XCI-E model and slightly overestimated ORs for XCI-S to the deleterious allele model, and the magnitude of bias increased as the true OR values increased. Our approach provided accurate estimations for ORs for all four biological models, except when the true model was XCI-E and ORs were relatively small (1.2–1.5). We also conducted simulation studies using other parameters, including different ORs for the association between sex and disease of interest, different ORs for the disease-associated SNP1, and different MAFs such as 10%, and obtained similar results and conclusions (data not shown).
In addition to reporting our new approach developed for testing the association between X-chromosome SNPs and the disease of interest, we also have compared, for the first time to our knowledge, PLINK regression and Clayton's approach under scenarios of XCI-S toward either the deleterious or normal allele. We found that in our simulation studies, PLINK regression had more loss of power than Clayton's approach in general.
We also applied our approach to the case-control association study of head and neck cancer and X-chromosome genetic variants. Based on the meta-analysis outcomes combining results from both phases, we found that, using our approach, SNP rs12388803 reached the chromosome-wide significance threshold. Clayton's test provided P values approaching chromosome-wide significance, and PLINK regression gave P values that were much less significant. The optimal biological model identified for this SNP is XCI-S toward to deleterious allele. This SNP does not belong to any gene region and is not functional. Additional studies are needed to externally validate our findings.
We considered two permutation strategies: permute case-control status using combined male and female data, and permute case-control status within sex-specific strata. Both permutations strategies provided similar results in the simulation studies and head and neck X-chromosomal genetic data analysis. However, these findings could be due to the fact that the differences in MAFs in males and females were not very large (≤10%). There could be a scenario where this difference could be much higher. Therefore, we recommend performing the permutations within males and females separately. A computer program that analyzes X-chromosomal SNP association with the use of the proposed approach is available at website https://sites.google.com/site/jianwangswebsite/xchrom. The computation time of the program highly depends on the number of permutations conducted and the number of clusters used. For example, to obtain the results reported in Table 4, the program took about 9 hr to conduct 1,000,000 permutations (at approximate X-chromosome-wide significance level), using multiple high-performance clusters with 3.07 GHz CPU and 96 GB memory available in UT MD Anderson, which showed that it is feasible to use our approach for the X-chromosome-wide genetic association study.
There are several advantages to the approach proposed in this article. First of all, the approach was developed based on biologically plausible models. Not only does this approach account for random XCI and escape from XCI as do Clayton's approach and PLINK regression, respectively, it also accounts for the skewed XCI pattern, which, to our knowledge, has not been considered in previous X-chromosomal genetic variant association tests. As we have discussed in the Introduction section, the skewed XCI pattern is a special phenomenon that is more common in affected females in certain complex diseases, whereas random XCI is more common in unaffected females [Buller et al., 1999; Chabchoub et al., 2009; Kristiansen et al., 2002; Plenge et al., 2002; Talebizadeh et al., 2005]. Therefore, accounting for this phenomenon of skewed XCI will increase the power of detecting X-chromosome disease-associated genetic variants. If the genetic association test is conducted within the pseudo-autosomal regions or within the genes that have been identified to escape XCI, one may choose to employ PLINK regression for the study. However, for most of the X-chromosomal regions, the true underlying XCI process is not known with certainty and could differ from region to region; our approach is therefore more robust than Clayton's approach or PLINK regression.
In genetic association studies, there might be differences in the genetic architecture between females and males. For example, there might be different MAFs, effect sizes, or prevalence values for males and females, different numbers of males and females in the study sample, and different sex ratios in cases and controls [Hickey and Bahlo, 2011; Loley et al., 2011]. Therefore, we recommend always including sex as a covariate when conducting X-chromosomal genetic association study using our proposed approach. Also, studies have shown that the prevalence of the skewed XCI pattern increases in females with increasing age [Amos-Landgraf et al., 2006; Busque et al., 2009; Chagnon et al., 2005; Minks et al., 2008; Sharp et al., 2000; Wong et al., 2011], which might be included in the analysis as an interaction between genetic variant and age.
In conclusion, the new approach we propose in this study was developed based on biological plausibility and accounts for all possibilities of the XCI process. The proposed approach controls the type I error rate and compared with current approaches has higher powers in the scenarios where XCI is skewed with some loss of power in scenarios where XCI is random or XCI is escaped. Finally, the approach is more robust to different XCI processes, including random XCI, XCI-S toward the deleterious or normal allele, and XCI-E, than the existing popular approaches of PLINK regression and Clayton's 1-degree-of-freedom test for testing the association between X-chromosome SNPs and the disease of interest.
Acknowledgments
This work was supported by National Institutes of Health grant 1R01CA131324 (to S.S.), R01DE022891 (to S.S.), and R25DA026120 (to S.S.) and by a faculty fellowship from The University of Texas MD Anderson Cancer Center Duncan Family Institute for Cancer Prevention and Risk Assessment (to J.W.). Funding support for the Study of Addiction: Genetics and Environment (SAGE) was provided through the NIH Genes, Environment and Health Initiative (GEI) (U01 HG004422). SAGE is one of the genome-wide association studies funded as part of the Gene Environment Association Studies (GENEVA) under GEI. Assistance with phenotype harmonization and genotype cleaning, as well as with general study coordination, was provided by the GENEVA Coordinating Center (U01 HG004446). Assistance with data cleaning was provided by the National Center for Biotechnology Information. Support for collection of datasets and samples was provided by the Collaborative Study on the Genetics of Alcoholism (COGA; U10 AA008401), the Collaborative Genetic Study of Nicotine Dependence (COGEND; P01 CA089392), and the Family Study of Cocaine Dependence (FSCD; R01 DA013423). Funding support for genotyping, which was performed at the Johns Hopkins University Center for Inherited Disease Research, was provided by the NIH GEI (U01HG004438), the National Institute on Alcohol Abuse and Alcoholism, the National Institute on Drug Abuse, and the NIH contract "High-throughput genotyping for studying the genetic contributions to human disease" (HHSN268200782096C). The datasets used for the analyses described in this manuscript were obtained from dbGaP at http://www.ncbi.nlm.nih.gov/projects/gap/cgi-bin/study.cgi?study_id=phs000092.v1.p1 through dbGaP accession number phs000092.v1.p.




