Power in the phenotypic extremes: a simulation study of power in discovery and replication of rare variants
Abstract
Next-generation sequencing technologies are making it possible to study the role of rare variants in human disease. Many studies balance statistical power with cost-effectiveness by (a) sampling from phenotypic extremes and (b) utilizing a two-stage design. Two-stage designs include a broad-based discovery phase and selection of a subset of potential causal genes/variants to be further examined in independent samples. We evaluate three parameters: first, the gain in statistical power due to extreme sampling to discover causal variants; second, the informativeness of initial (Phase I) association statistics to select genes/variants for follow-up; third, the impact of extreme and random sampling in (Phase 2) replication. We present a quantitative method to select individuals from the phenotypic extremes of a binary trait, and simulate disease association studies under a variety of sample sizes and sampling schemes. First, we find that while studies sampling from extremes have excellent power to discover rare variants, they have limited power to associate them to phenotype—suggesting high false-negative rates for upcoming studies. Second, consistent with previous studies, we find that the effect sizes estimated in these studies are expected to be systematically larger compared with the overall population effect size; in a well-cited lipids study, we estimate the reported effect to be twofold larger. Third, replication studies require large samples from the general population to have sufficient power; extreme sampling could reduce the required sample size as much as fourfold. Our observations offer practical guidance for the design and interpretation of studies that utilize extreme sampling. Genet. Epidemiol. 35: 236-246, 2011. © 2011 Wiley-Liss, Inc.
INTRODUCTION
Whole-genome association studies have identified hundreds of common genetic variants associated with complex human traits and diseases [Hindorff et al., 2009]. While successful in identifying novel genetic loci contributing to each disease, these findings have prompted three key questions: (i) what is the full contribution of genetic variation (common and rare) at each locus? (ii) what gene or genes are responsible for the association signal in each region? (iii) what risk genes have yet to be found, because they carry neither rare Mendelian mutations detectable by linkage, nor common variants detectable by genome-wide association studies (GWAS) [Bodmer and Bonilla, 2008]?
Next-generation sequencing makes it increasingly practical to comprehensively assess low-frequency polymorphisms and rare mutations, both in candidate genes such as those found by GWAS (to answer the first two questions) [Ahituv et al., 2007; Cohen et al., 2004, 2006; Ji et al., 2008; Kathiresan et al., 2009; Nejentsev et al., 2009; Romeo et al., 2007] and genome-wide (to answer all three) [Ng et al., 2009, 2010]. The search for rare variants is motivated both by the long history of Mendelian genetics in families, and by population-based sequencing that has implicated rare variants (in genes previous discovered via Mendelian genetics) influencing blood pressure [Ji et al., 2008] and high-density lipoprotein (HDL) cholesterol levels [Cohen et al., 2004].
This paper addresses three features related to the design of studies using DNA sequencing to study rare variants: the samples used for variant discovery, selection of specific genes and variants for follow-up, and replication of putative genotype-phenotype relationships in independent samples. We focus on one widely discussed design feature: the ascertainment of samples from the extremes of a population distribution [Ahituv et al., 2007; Bell et al., 2007; Cohen et al., 2004; DeAngelis et al., 2004; Kryukov et al., 2009; Mohammadi et al., 2009; Nebert 2000; Perez-Gracia et al., 2002; Risch and Zhang, 1995, 1996; Romeo et al., 2007] (previously referred to as “selective genotyping”) [Lander and Botstein, 1989; Van Gestel et al., 2000]. Intuitively, ascertainment of samples from the extremes of phenotype should enrich for the burden of alleles influencing a trait, thus improving power to discover risk variants and to detect their association to phenotype. One such example is the extreme discordant sib-pair design, which results in a substantial increase in statistical power when compared to other sib-pair designs [Risch and Zhang, 1995, 1996]. Similarly, ascertainment of extremes of quantitative traits from large population cohorts has also been shown to increase the power to identify associated variants [Kryukov et al., 2009; Lander and Botstein, 1989; Van Gestel et al., 2000].
Many quantitative and methodological issues remain regarding extreme sampling. These include (a) selection of extremes for dichotomous traits influenced by multiple risk factors (such as type 2 diabetes (T2D) or myocardial infarction), (b) impact on power to discover variants of different sampling strategies, (c) how to select, from the numerous variants discovered via sequencing, a set of variants to be followed-up in independent cohorts (i.e. replication), and (d) design of studies for replication in extended samples.
In this report, we first propose a model in which samples from the phenotypic extremes of a dichotomous trait in the presence of multiple clinically relevant risk factors. We apply this model to quantify the impact of different sampling procedures on the power to discover casual variants. We evaluate strategies for the selection of variants for follow-up, and of design for replication studies. The results provide practical guidance for design of next-generation sequencing studies and their follow-up to confirm valid and reproducible discoveries.
METHODS
SIMULATED POPULATION
Our primary simulated population consisted of 27,500 individuals whose simulated characteristics were based on empirical summary statistics obtained from the combination of three prospective cohorts: the Malmö Preventive Project, the Scania Diabetes Registry, and the Botnia Study (details of these populations are described elsewhere) [Bakhtadze et al., 2008; Cervin et al., 2008; Lyssenko et al., 2008]. We additionally simulated smaller (n = 5,000) and larger (n = 100,000) cohort sizes. The populations were simulated with a logistic regression model in which T2D status (37% affected and 63% unaffected) was predicted from three known risk factors—age, body mass index (BMI), and gender—and a di-allelic low-frequency variant. This genetic effect could represent a single polymorphic DNA variant, or a collection of rare variants that sum to a given frequency and pooled effect size. Age and BMI were assumed to follow normal distributions with mean and standard deviations estimated from empirical data; gender was dichotomized in simulations. Age, BMI, and gender were transformed to be correlated using the Cholesky decomposition of the covariance matrix. Effect sizes and inter-correlations used in the simulations are presented in Supplementary Table 1. We varied the frequency and effect size of the genetic effect across a grid of parameter values. Specifically, the allele frequency and effect size (odds ratio (OR)) of the genetic variant were allowed to vary from 0.001–0.01 and 1.0–6.0, respectively. Protective variants were also simulated (OR range: 0.16–0.67); results for protective variants are symmetrical (data not shown). This “spiked-in” genetic perturbation contributes little to the population variability of the trait overall and is not included in the liability model. In an attempt to map a portion of parameter space that is expected to be revealed by next-generation sequencing studies, we focused on low-frequency variation and moderate effect sizes. We avoided scenarios of higher allele frequencies (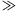
1%) and larger odds ratios (
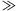6) as they would have been likely to be uncovered by previous linkage studies or existing genome-wide approaches in appropriately sized samples (∼2,000 affected sib pairs for linkage or 2,000 cases/2,000 controls for association studies), even assuming imperfect single-nucleotide polymorphism (SNP) tagging in the case of association [Purcell et al., 2003; Risch and Merikangas, 1996]. We performed 5,000 replications for each MAF/OR combination.
DEFINITION OF LIABILITY SCORES
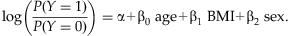
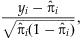
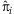is the predicted model probability for individual i. For large sample, Pearson residuals can approximate a standard normal distribution [Agresti and Wiley InterScience (Online service), 2002]. Positive residuals indicate model deviations exclusively for affected individuals while negative residuals indicate deviations exclusively for unaffected individuals. Simulated phenotypic extremes were selected at the tails of the liability score, where the highest liability scores correspond to the largest model deviations for affected individuals and the lowest liability scores correspond to the largest model deviations for unaffected individuals. We note that, although we have defined liability scores from a logistic regression model in our study, our framework could be easily generalized to time-to-event data by using the Cox proportional hazards model by selecting the tails of model residuals.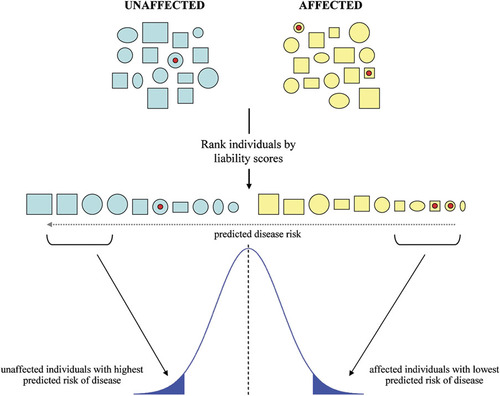
Graphical representation of the ascertainment of individuals with extreme liability scores. Individuals are ranked according to their liability scores in a multivariable risk model. Squares and circles represent males and females, respectively. The size of each shape is proportional to the individual's predicted disease risk. The red circles represent a low-frequency genetic mutation present in the general population. Individuals at the extremes of the liability distribution are then selected for the sequencing study.
Recently, an approach was described that estimates the proportion of genetic and environmental variance contributing to an outcome variable, per individual, using Monte Carlo simulation with Gibbs or Rejection Sampling within pedigree data [Campbell et al., 2010]. The information of focus in our work (identifying phenotypic extremes given a set of risk factors) and the information estimated broadly in that work are similar in spirit. While not explicitly described, their model could be used to identify individuals with large residual genetic contributions that have unexpected outcomes given estimates of environmental effects. However, there are still differences between both approaches in their implementation. First, the model is conceptualized for pedigrees and uses information from families to estimate parameters for their model, and a description for application to unrelated population-based collections was not described. Second, our approach does not require a specific assumption about the model for environmental or genetic contributions to the outcome; rather, we empirically measure departures from the predicted effect of risk factors included in the model. Third, in our model, we treat age of onset as a predictor for disease rather than a latent variable which “reveals” disease status over time. Finally, Campbell et al. requires a specific assumption about the heritability for the outcome variable; our assumption is that the heritability for the outcome variable is nonzero.
Variants were prioritized and examined for association to disease status using a two-tailed Fisher's exact test. A stringent significance level of 0.001 was used, as it is often the case that researchers will sequence thousands of variants simultaneously. The power to detect a genetic association presented throughout the text was estimated using two-tailed Fisher's exact test; specifically, it was computed as the proportion of simulations the null hypothesis was rejected given a specified significance level.
DETAILS OF THE LIABILITY MODEL FOR EXAMINED COHORTS
A liability score was generated which measured risk to T2D in the context of three known risk factors (age, BMI, and gender) in 27,500 individuals drawn from three prospective cohorts: the Malmö Preventive Project (MPP), the Scania Diabetes Registry, and the Botnia Study [Bakhtadze et al., 2008; Cervin et al., 2008; Lyssenko et al., 2008]. Risk model estimates are shown in Supplementary Table 1, distribution of liability scores are shown in Supplementary Figure 1.
GENOTYPING OF THE TCF7L2 VARIANT (rs7903146)
Genotyping of rs7903146 in TCF7L2 has been described previously [Bakhtadze et al., 2008; Cervin et al., 2008; Lyssenko et al., 2008]. Briefly, in the MPP, genotyping was performed with the use of matrix-assisted laser desorption-ionization time-of-flight (MALDI-tof) mass spectrometry on the MassARRAY platform (Sequenom, San Diego, CA). The genotype call rate was >95% and the genotyping accuracy was >99%, which was estimated by re-genotyping 11% of the samples using the Sequenom platform. In Botnia and Scania Diabetes Registry, the variant was genotyped with an allelic discrimination assay-by-design method on the ABI 7900 platform (Applied Biosystems, Carlsbad, CA).
RESULTS
A MODEL TO DEFINE EXTREMES FOR A DICHOTOMOUS OUTCOME USING MULTIPLE RISK FACTORS
A simple approach to ascertain phenotypic extremes of a dichotomous trait is to apply a threshold to a given risk factor, and to select individuals exceeding that threshold. Such an approach by design does not weight individuals by the extremity of phenotype, nor does it model the contributions to risk of multiple factors. We propose a liability score for each individual, derived from the Pearson residuals estimated in a risk model for a set of known epidemiological risk factors (such as BMI and age). The details of the model are presented in the Methods. The liability score is defined as a continuous distribution, from which phenotypic extremes can be selected at the tails of the distribution, similar to the selection of extremes from a quantitative trait [Kryukov et al., 2009; Lander and Botstein, 1989; Risch and Zhang, 1995, 1996; Van Gestel et al., 2000]. Specifically, the liability score is a quantitative measure of the discordance between an individual's observed disease status (e.g. affected = 1/unaffected = 0) and predicted risk score (values ranging from 0 to 1). Thus, the highest liability scores correspond to individuals who are affected, despite low predicted risk; conversely the lowest liability scores correspond to unaffected individuals with the largest predicted risk (Fig. 1). Indeed such liability scores estimated from disease status, risk factors, and residual heritability have already been proposed for pedigrees [Campbell et al., 2010; Falconer, 1965].
To evaluate empirically whether this approach resulted in the expected increase in power, we implemented the model in a large cohort (n = 27,500, see Methods) [Bakhtadze et al., 2008; Cervin et al., 2008; Lyssenko et al., 2008], in which T2D status was known, along with multiple quantitative measures. Liability scores were calculated for T2D according to disease status and three conventional T2D risk factors: age, BMI, and gender. We evaluated the allele frequency of an intronic SNP near the transcription factor 7-like 2 gene (TCF7L2: Entrez GeneID = 6934, rs7903146), which has been previously shown to contribute susceptibility to T2D [Florez et al., 2006; Frayling, 2007].
The frequency of the TCF7L2 SNP minor allele is higher in cases (32%) than in controls (24%) as previously reported (Table I) [Florez et al., 2006; Frayling, 2007]. The risk allele frequency rose with increasing liability score, from 32% in all cases to 44% in cases drawn from the highest 90th percentile of liability scores. This translated into inflation of the allelic OR from 1.44 in the total population to 2.47. Conversely, the MAF of the TCF7L2 SNP decreased in controls selected based on the liability score (Table I). Furthermore, our simulated data yielded similar effect sizes, albeit slightly attenuated, in phenotypic extremes as the observed data.
| Ascertainment | CC | CT | TT | N | Risk allele frequency | Nonrisk allele frequency | Comparison group | OR (95% CI) | Simulated OR (95% CI) |
|---|---|---|---|---|---|---|---|---|---|
| All controls [No ascertainment] | 5,081 | 3,104 | 576 | 8,761 | 0.243 | 0.757 | All cases | – | – |
| All cases [No ascertainment] | 483 | 417 | 112 | 1,012 | 0.317 | 0.683 | All controls | 1.44 (1.31–1.60) | 1.44 (1.33–1.58) |
| Highest 50-percentile cases | 378 | 358 | 96 | 832 | 0.331 | 0.669 | All controls | 1.54 (1.38–1.71) | 1.50 (1.35–1.64) |
| Highest 75-percentile cases | 177 | 189 | 62 | 428 | 0.366 | 0.634 | All controls | 1.80 (1.56–2.07) | 1.75 (1.53–2.00) |
| Highest 90-percentile cases | 29 | 48 | 18 | 95 | 0.442 | 0.558 | All controls | 2.47 (1.85–3.30) | 1.98 (1.62–2.39) |
| Lowest 50-percentile controls | 275 | 147 | 16 | 438 | 0.204 | 0.796 | All cases | 1.80 (1.49–2.18) | 1.52 (1.28–1.78) |
- The allelic ORs are calculated from the subset of the n = 27,500 prospective cohort data (obtained from the Malmö Preventive Project, the Scania Diabetes Registry, and the Botnia Study) where genetic data for rs7903146 were available. We applied the proposed liability model to the data for increasing extremes in cases (50-percentile, 75-percentile, and 90-percentile) and controls (the top 50-percentile). As expected, we note that the frequency of the risk allele increases as a function of ascertainment of cases from extreme liabilities, which results in an increasingly higher OR when compared to control frequencies. Furthermore, our simulated data yield similar effect sizes to the observed data. OR, odds ratio.
With a model in place, we investigated the power of extreme phenotypic sampling for rare variant discovery.
POWER TO DISCOVER VARIANTS USING PHENOTYPIC EXTREME SAMPLING
Simulations show that higher liability thresholds systematically increased the frequency of the genetic effect in affected individuals and decreased the frequency in unaffected individuals (Table II). Alleles with larger effects are more likely to be enriched in the tails of the liability distribution, similar to behavior observed in quantitative traits [Van Gestel et al., 2000]. For example, a variant with a 1% MAF with a twofold effect in the general population (similar to the cumulative frequency and effect size for hypertension of rare variants in Mendelian blood pressure genes) [Ji et al., 2008] has only a 2.7-fold enrichment in the 5% tails of the liability distribution. In comparison, a variant with a 1% MAF with a fivefold effect in the general population is enriched 68% to 8.4-fold in the 5% most extreme individuals for liability score. This enrichment was not observed for a simulated set of null alleles, and is independent of the size of the cohort (data not shown).
| Phenotypic extremeness (based on Liability)a | ||||||||
|---|---|---|---|---|---|---|---|---|
| MAF | OR | Population average | Top/bottom 10% | Top/bottom 5% | Top/bottom 2.5% | Top/bottom 1% | Top/bottom 0.1% | Top/bottom 0.01% |
| 0.001 | 1 | 1.001 | 0.969 | 1.063 | 1.018 | 0.975 | 0.972 | 0.994 |
| 2 | 1.997 | 2.217 | 2.516 | 3.071 | 2.860 | 2.951 | 3.468 | |
| 5 | 4.979 | 6.178 | 10.457 | 10.176 | 13.258 | 17.134 | 22.493 | |
| 0.002 | 1 | 1.000 | 0.966 | 0.970 | 0.978 | 0.976 | 0.973 | 0.951 |
| 2 | 1.999 | 2.298 | 2.675 | 2.849 | 2.869 | 3.399 | 3.562 | |
| 5 | 4.974 | 6.556 | 9.378 | 12.155 | 13.280 | 15.859 | 19.848 | |
| 0.005 | 1 | 1.000 | 1.039 | 1.058 | 0.928 | 0.992 | 1.039 | 1.013 |
| 2 | 1.991 | 2.308 | 2.568 | 3.065 | 3.140 | 3.313 | 3.339 | |
| 5 | 4.947 | 7.335 | 9.118 | 11.384 | 13.242 | 15.572 | 18.286 | |
| 0.010 | 1 | 1.000 | 0.993 | 1.012 | 0.990 | 0.968 | 0.973 | 1.014 |
| 2 | 1.984 | 2.376 | 2.740 | 2.918 | 3.117 | 3.357 | 3.484 | |
| 5 | 4.989 | 6.801 | 8.396 | 10.928 | 13.391 | 15.840 | 18.650 | |
- The ratio of allele frequency in affected and unaffected individuals is shown for individuals across a range of liability scores and in the entire population. These ratios approximate ORs due to the low allele frequencies considered. OR, odds ratio.
- a aData are presented as ratio of affected allele frequency to unaffected allele frequency.
Relative to a random sample, the enrichment of variant alleles in extreme samples translates into higher power to discover genetic variation contributing to the trait (Table III). For example, consider the case in which 900 individuals (450 cases/450 controls) are ascertained from a total of 27,500 individuals. Consider furthermore a true causal mutation with frequency 0.1% in the general population. If the individuals were sampled at random, the OR of that risk mutation would have to be sixfold or greater before the power to discover the mutation by sequencing is 95%. In contrast, if the 900 samples were selected from the extremes of the liability score, one has the same power (95%) to discover a risk variant with an effect less than half as large (OR = 2.9).
| Fixed MAF | Random sampling | Phenotypic extremes |
|---|---|---|
| Lowest OR where power = 95% to discover | ||
| 0.010 | <1.5 | <1.5 |
| 0.005 | <1.5 | <1.5 |
| 0.001 | >6 | ∼2.9 |
| Fixed OR | Random sampling | Phenotypic extremes |
| Lowest MAF where power = 95% to discover | ||
| 6 | 0.0013 | 0.00075 |
| 4 | 0.0014 | 0.00100 |
| 2 | 0.0015 | 0.00135 |
- The lowest MAFs and ORs for fixed genetic model parameters in which the power to discover a low-frequency variation is at least 95% are presented for a sequencing cohort of 450 cases and 450 controls ascertained from a larger population of 27,500. Results are shown for both a phenotypically extreme sample and a randomly selected sample. OR, odds ratio.
The size of the cohort from which a sample is drawn influences the degree of “extremeness” of a fixed number of individuals (Table IV). The degree of “extremeness,” consequently, directly influences the power to discover a variant as well as the power to detect a genetic association. Intuitively, a given number of samples selected from the extreme of a small cohorts have less power to discover variants than one sampled from a larger cohort.
| n = 5,000 | n = 27,500 | n = 100,000 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Ascertainment sample size | MAF | OR | Minimum liability | Power to discover | Power to associate | Minimum liability | Power to discover | Power to associate | Minimum liability | Power to discover | Power to associate |
| 50 | 0.001 | 2 | 3.06 (0.016) | 0.215 | 0.000 | 5.03 (0.23) | 0.219 | 0.000 | 6.99 (0.33) | 0.209 | 0.000 |
| 50 | 0.005 | 2 | 0.697 | 0.000 | 0.715 | 0.000 | 0.711 | 0.000 | |||
| 50 | 0.010 | 2 | 0.917 | 0.000 | 0.913 | 0.000 | 0.912 | 0.000 | |||
| 50 | 0.001 | 5 | 0.352 | 0.000 | 0.389 | 0.000 | 0.415 | 0.000 | |||
| 50 | 0.005 | 5 | 0.888 | 0.000 | 0.906 | 0.000 | 0.918 | 0.000 | |||
| 50 | 0.010 | 5 | 0.986 | 0.002 | 0.988 | 0.003 | 0.995 | 0.004 | |||
| 100 | 0.001 | 2 | 2.41 (0.086) | 0.371 | 0.000 | 4.15 (0.143) | 0.392 | 0.000 | 5.88 (0.206) | 0.401 | 0.000 |
| 100 | 0.005 | 2 | 0.911 | 0.000 | 0.908 | 0.000 | 0.929 | 0.000 | |||
| 100 | 0.010 | 2 | 0.992 | 0.001 | 0.995 | 0.000 | 0.992 | 0.000 | |||
| 100 | 0.001 | 5 | 0.551 | 0.000 | 0.607 | 0.000 | 0.625 | 0.000 | |||
| 100 | 0.005 | 5 | 0.978 | 0.001 | 0.991 | 0.004 | 0.997 | 0.004 | |||
| 100 | 0.010 | 5 | 0.999 | 0.053 | 1.000 | 0.157 | 0.999 | 0.198 | |||
| 450 | 0.001 | 2 | 1.26 (0.032) | 0.883 | 0.000 | 2.59 (0.046) | 0.852 | 0.000 | 3.90 (0.067) | 0.894 | 0.000 |
| 450 | 0.005 | 2 | 1.000 | 0.010 | 1.000 | 0.029 | 1.000 | 0.033 | |||
| 450 | 0.010 | 2 | 1.000 | 0.063 | 1.000 | 0.173 | 1.000 | 0.220 | |||
| 450 | 0.001 | 5 | 0.928 | 0.000 | 0.968 | 0.001 | 0.975 | 0.001 | |||
| 450 | 0.005 | 5 | 1.000 | 0.314 | 1.000 | 0.747 | 1.000 | 0.871 | |||
| 450 | 0.010 | 5 | 1.000 | 0.877 | 1.000 | 1.000 | 1.000 | 0.999 | |||
| 1,000 | 0.001 | 2 | 0.73 (0.026) | 0.986 | 0.000 | 1.92 (0.021) | 0.996 | 0.000 | 3.05 (0.037) | 0.987 | 0.000 |
| 1,000 | 0.005 | 2 | 1.000 | 0.039 | 1.000 | 0.179 | 1.000 | 0.250 | |||
| 1,000 | 0.010 | 2 | 1.000 | 0.120 | 1.000 | 0.524 | 1.000 | 0.721 | |||
| 1,000 | 0.001 | 5 | 0.993 | 0.002 | 1.000 | 0.047 | 0.999 | 0.143 | |||
| 1,000 | 0.005 | 5 | 1.000 | 0.641 | 1.000 | 0.994 | 1.000 | 1.000 | |||
| 1,000 | 0.010 | 5 | 1.000 | 0.978 | 1.000 | 1.000 | 1.000 | 1.000 |
- The minimum liability scores are presented as median (median absolute deviation). For a fixed sequencing cohort size, the minimum liability score increases as a function of the total population size, indicating that the sequencing cohort is more “extreme” when ascertained from a larger population as expected. The “power to discover” columns show the probability of observing at least a singleton in a given sequencing cohort size ascertained from a given total population size. The “power to associate” columns show the power to detect a genetic association given a significance level of 0.001 across variable cohort sizes. OR, odds ratio.
IMPLICATIONS OF EXTREME PHENOTYPIC SAMPLING ON VARIANT PRIORITIZATION FOR FOLLOW-UP EFFORTS
To determine which variants robustly associate to the phenotype of interest, a two-stage design (discovery of associated genes/variants followed by replication sequencing/genotyping in independent samples) will often be necessary [Nejentsev et al., 2009]. Often the number of discovered variants will, in general, be large (and will continue to increase with the number of sequenced individuals); therefore, it will be important to prioritize genes and variants for follow-up. Three questions include: (a) how to estimate power not only to discover a risk variant via sequencing but also to observe a distortion in frequency between cases and controls, (b) how to interpret associations in an initial sequencing experiment based on extreme sampling, and (c) how to design replication samples that follow-up extreme sampling.
First, we observe that the power to discover a variant is much greater than the power to observe a significant association in cases vs. controls (Table IV). This is true even for alleles of strong effect. For example, consider the case of 100 affected and 100 unaffected samples drawn from the extremes of a cohort of 5,000 individuals (this is similar to the studies for lipid traits in the Dallas Heart Study) [Cohen et al., 2004; Kotowski et al., 2006]. For variants with 1% frequency and a fivefold effect, the power is >99% to discover the variant, but only 5% to detect a significant difference in frequency between cases and controls. Thus, false negatives of association will be a major problem in small discovery samples, even if the effects are large. Similar results hold across various genetic model parameters (Table IV).
Conversely, effect sizes will be systematically over-estimated in samples drawn from phenotypic extremes relative to the true effect size in the general population [Lander and Botstein, 1989; Van Gestel et al., 2000], even when the association is real (Table V). For example, rare variants in multiple genes were collectively shown to be more frequent (16 vs. 2%) in individuals with low HDL (<5th percentile) compared to individuals with high HDL cholesterol (>95th percentile) [Cohen et al., 2004]. Although the estimated effect size in this phenotypically extreme sample is eightfold, this is over-estimated due to the extreme sampling design. Numerically, we estimate the true effect size in the total population to be closer to 4.5. Similar results hold for other rare variant distributions (Table V). The inflation of estimated effect size will be even greater in genome-wide exome sequencing, where studies with smaller sample sizes, underpowered to detect even strong effect will be subjected to winner's curse and will also contribute to over-estimation of effect sizes relative to the true effect in the general population.
| Distribution of variant counts [case to control]a | Sample ascertainment | Estimated OR in discovery cohort | Expected OR in general population |
|---|---|---|---|
| 2 to 2 | Random | 1.0 | 0.954 |
| Liability | — | 1.059 | |
| 3 to 1 | Random | 3.0 | 3.273 |
| Liability | — | 1.462 | |
| 4 to 0 | Random | ≥4.0 | 5.627 |
| Liability | — | 1.973 |
- ORs estimated directly from phenotypic extremes will be systemically over-estimated compared to the ORs expected in the general population. Listed are the estimated ORs in the discovery cohort and expected ORs in the general population given a total of four observed variants counts assuming a population MAF of 0.5% for a liability and random sample ascertainment of 450 cases/450 controls from a cohort of 27,500 individuals. The expected ORs in the general population were estimated over a grid of effect sizes (OR ranging from 0.1 to 10) simulated in the total population as the weighted mean OR of a particular variant count distribution observed in the discovery cohort. For example, for a variant observed twice in cases and twice in controls, the mean OR is weighted by the probabilities of each OR for those simulations where a 2:2 case:control variant count was observed. The estimated OR in the discovery cohort is based solely on the observed counts, and note that in the case of 4 to 0, the OR is not calculable. In that case, the closest approximation is that the estimated OR is at least 4, but could be much larger. OR, odds ratio.
- a aFor n = 4 variant observations (MAF = 0.005), assuming 450 cases and 450 controls.
As expected, the systematic inflation in effect size due to extreme sampling results in increased power to detect genetic associations (Fig. 2) [Kryukov et al., 2009; Lander and Botstein, 1989; Risch and Zhang, 1995, 1996; Van Gestel et al., 2000]. Power increases dramatically for low-frequency polymorphisms with population frequency 0.1–1% and effect sizes two- to sixfold, given a significance level of 0.05 (Fig. 2, Supplementary Figure 2), for a sample of 450 cases and 450 controls drawn from the liability extremes of 27,500 individuals compared to a random sampling of the same size. The distribution of variant effect sizes and frequencies is exactly those that might have been missed by Mendelian genetics (because the effect sizes were too modest) and by GWAS (because they were too rare for the first generation of GWAS arrays) [Purcell et al., 2003; Risch and Merikangas, 1996].
Difference in power of Fisher's exact test between liability and random ascertainment. The difference between power of Fisher's exact test for a liability and random ascertainment given a significance level of 0.05 is shown. The MAF and OR refer to parameters in the larger population (n = 27,500) from which the subsample of 450 affected and 450 unaffected individuals was selected. The mean liability scores (standard deviation in parentheses) in affected and unaffected individuals were 3.68 (1.37) and − 2.54 (0.83), respectively, under a liability ascertainment and 0.99 (0.83) and − 0.60 (0.50), respectively, under a random ascertainment. OR, odds ratio.
Similarly, the power to detect a genetic association is substantially enriched for other risk models with varying degrees of variance explained (Table VI). The amount of variance explained is presented here by Nagelkerke's R2 [Nagelkerke, 1991], a generalized form of the coefficient of determination which scales its range to be from 0 to 1. Power is enriched substantially even for risk models with 5% of the variability explained, suggesting that our method would be useful for most significant covariates that explain a fraction of the variability. The enrichment in power becomes greater as the amount of variance explained increases. Thus, the addition of meaningful and clinically relevant covariates into the risk model could provide additional increases in power. However, we caution against over-saturation of risk models with irrelevant covariates.
| Power of Fisher's exact test | ||||
|---|---|---|---|---|
| OR = 2 | OR = 5 | |||
| Nagelkerke R2 | MAF = 0.005 | MAF = 0.01 | MAF = 0.005 | MAF = 0.01 |
| 0.00 | 0.004 | 0.019 | 0.074 | 0.382 |
| 0.05 | 0.013 | 0.067 | 0.348 | 0.881 |
| 0.10 | 0.015 | 0.105 | 0.504 | 0.959 |
| 0.15 | 0.018 | 0.110 | 0.582 | 0.975 |
| 0.20 | 0.021 | 0.126 | 0.616 | 0.981 |
| 0.25 | 0.028 | 0.133 | 0.654 | 0.989 |
| 0.30 | 0.027 | 0.152 | 0.709 | 0.992 |
| 0.35 | 0.026 | 0.153 | 0.715 | 0.993 |
| 0.40 | 0.030 | 0.169 | 0.738 | 0.997 |
| 0.45 | 0.027 | 0.169 | 0.757 | 0.996 |
- Power estimates are shown for a sequencing cohort of 450 cases and 450 controls ascertained from a larger population of 2,75,000 individuals in risk models with varying degrees of variance explained (Nagelkerke R2 [Nagelkerke, 1991]), given a signficance level of 0.001. OR, odds ratio.
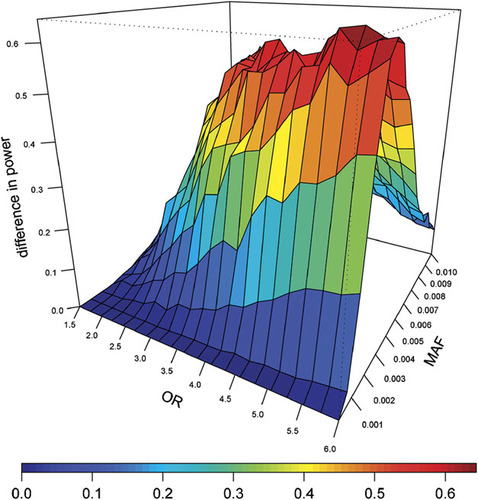
Finally, even where a modest enrichment is seem between cases and controls, it is much more likely to be due to chance than a true association. Figure 3 shows a representative example of the distribution of variant counts for a null variant and a risk variant that has been observed a total of four times in a sequencing cohort sampled from the extremes of liability. Specifically, under the alternative hypothesis (OR = 2), the variant is, on average, more likely to be observed disproportionally in affected individuals compared to unaffected individuals. However, some fraction of variants under the null hypothesis (OR = 1) will also be similarly distorted, and since there will be many more null variants than causal variants, it is likely that a large fraction of alleles will be phenotypically neutral, rather than risk-inducing.
Distribution of variant counts in affected and unaffected individuals. The distribution of variant counts in affected and unaffected individuals is shown under the null hypothesis (OR = 1) and alternative hypothesis (OR = 2) for a variant observed a total of four times in a liability ascertained sequencing cohort of 900 individuals (450 cases; 450 controls) given a MAF of 0.001. OR, odds ratio.
In summary, it is relatively straightforward to design sequencing samples with excellent power to discover causal variants (if they exist); much larger sample sizes are required before power is obtained to observe enrichment of risk (or protective) variants in cases as compared to controls. Moreover, where enrichment is observed, it will likely represent an over-estimate of the true effect size in the total population, which can lead to false-negative replication studies.
IMPLICATIONS OF EXTREME PHENOTYPIC SAMPLING ON REPLICATION OF ASSOCIATION
As discussed above, ascertainment from the phenotypic extremes is intended to increase the frequency of risk alleles in cases, and by inflating the frequency distortion between cases and controls increase statistical power [Kryukov et al., 2009; Lander and Botstein, 1989; Risch and Zhang, 1995, 1996; Van Gestel et al., 2000]. The most powerful approach for replication would be to select an independent cohort in which similar phenotypic extremes could be obtained (Table VII). However, to obtain an unbiased estimate of the genetic effect size, a random (or complete) sample of the population is needed, even though the statistical power to prove a statistical association would be lessened. Alternatively, follow-up could be performed in the same population as the discovery sequencing cohort, either by continuing deeper sampling based on liability score rankings or by sampling random individuals—but power to detect the effect would be reduced.
| Simulation parameters | Number case/control pairs | OR | |||||
|---|---|---|---|---|---|---|---|
| MAF | OR | Phenotypic extreme | Random | Phenotypic extreme | Random | Expected [Extreme] | Expected [Random] |
| Follow-up in same population as discovery cohort | |||||||
| 0.001 | 2 | a | >36,630 | a | a | a | a |
| 0.005 | 2 | 7,200 | 7,200 | 2.09 (0.24) | 2.06 (0.29) | 2.04 (0.31) | 1.97 (0.35) |
| 0.010 | 2 | 2,000 | 3,550 | 2.63 (0.46) | 2.08 (0.25) | 2.51 (0.51) | 2.01 (0.30) |
| 0.001 | 5 | 8,050 | 8,050 | 6.13 (2.16) | 5.67 (1.74) | 5.47 (2.38) | 5.24 (2.09) |
| 0.005 | 5 | 675 | 2,000 | 17.2 (11.6) | 5.31 (2.19) | 10.6 (8.38) | 5.16 (2.03) |
| 0.010 | 5 | 350 | 950 | 18.4 (12.9) | 5.23 (1.91) | 12.9 (10.6) | 4.85 (2.11) |
| Follow-up in independent population from discovery cohort | |||||||
| 0.001 | 2 | a | 36,630 | a | a | a | a |
| 0.005 | 2 | 7,100 | 7,160 | 2.09 (0.29) | 2.19 (0.35) | 2.05 (0.35) | 2.05 (0.42) |
| 0.010 | 2 | 1,750 | 3,510 | 3.03 (0.75) | 2.06 (0.26) | 2.88 (0.81) | 1.98 (0.31) |
| 0.001 | 5 | 8,000 | 8,030 | 5.90 (2.25) | 5.67 (1.74) | 5.18 (2.34) | 5.00 (2.10) |
| 0.005 | 5 | 500 | 1,630 | 22.4 (18.9) | 5.63 (1.82) | 19.3 (16.3) | 5.23 (1.95) |
| 0.010 | 5 | 225 | 830 | 23.6 (20.4) | 5.38 (1.95) | 20.8 (17.9) | 4.88 (1.96) |
- Number of case/control pairs required to achieve 80% power to detect a genetic association assuming a significance level of 0.001 in a phenotypically extreme sample and a randomly ascertained sample. The replication sample sizes were determined for studies, which sampled from the same population as the discovery cohort (total n = 27,500) and a completely independent population of the same size. ORs are presented as median (median absolute deviation). The expected ORs were estimated across all simulations while the observed ORs were estimated only for significant simulations (P<0.001). OR, odds ratio.
- a aRequired sample size exceeds the size of the total population and thus, parameters were not estimated for these scenarios.
To estimate the power of each of these replication approaches, we determined the number of case/control pairs required to demonstrate statistical association (P<0.001) by simulation over a collection of genetic models. As expected, the smallest sample size required was in an extreme phenotypic sampling from an independent cohort (Table VII). For example, given a 0.5% variant with a fivefold effect in the general population, a sample size of 500 cases and 500 controls would be required to achieve 80% power in an independent, phenotypically extreme sample. If random samples were used, four times as many samples (2,000 cases and controls) would be needed to achieve comparable power. If the replication samples were chosen from the initial cohort (i.e. the next-most extreme samples), power is only slightly reduced compared to those obtained from a completely independent cohort (675 cases and 675 controls for 80% power). Of course, if extreme samples are used in replication, systematic over-estimation of effect sizes compared to the true effect size in the general population will ensue. Additionally, winner's curse will heighten the effect size estimates, and this augments the expected effect size for both random and phenotypic extreme sampling replication efforts.
DISCUSSION
We present a quantitative framework to ascertain phenotypic extremes of a dichotomous trait, and using simulations, evaluate statistical power, prioritization of variants for follow-up, and design of replication samples. Our approach simultaneously ascertains “hypernormal” controls, samples which may be the most likely to carry alleles conferring protection, as well as extreme cases, which may be the most likely to carry a high-risk allele burden. As expected, selection of individuals for a dichotomous trait based on extremes of nongenetic risk factors increases the difference in risk variant allele frequencies in cases as compared to controls, which results in an increase in power. We also observe that for a given design, power to discover genetic variation is much greater than the power to detect association between cases and controls—with the implication that true variants may be missed if only those with association in the discovery samples are carried forward into replication. We observe that the effect sizes estimated in phenotypic extremes effect sizes are systematically larger than those estimated in random samples; thus, replication studies will either need to be performed in independent samples from the extremes, or in much larger samples from the general population to have sufficient power. Finally, while follow-up in phenotypic extremes will have improved power, it will also return inflated estimates of the effect size. Our quantification of this intuitively powerful sampling strategy reported here offers some practical guidance for future phenotypically driven genetic studies, including but not limited to resequencing efforts.
Our model to characterize liability given risk factors, though similar in spirit, differs in implementation. In contrast to Campbell et al., whose aim is to directly model and estimate the proportion of genetic and environmental variance contributions to an outcome variable using Monte Carlo simulations, our strategy focuses simply on each individual's unexplained disease liability conditional on a set of risk factors, which does not make a specific assumption about genetic or environmental variance explained. However, the specific information, which is the focus of this work, could potentially be extracted from Campbell et al.
Inflated effect sizes due to extreme sampling could be corrected for with likelihoods that condition on the ascertainment process [Clayton, 2003]. Such conditional likelihoods have been used to adjust effect sizes estimated in highly ascertained pedigrees (enriched for having multiple affected relatives) with retrospective likelihoods that condition the joint distribution of genotypes of pedigree members on their disease status [Carayol and Bonaiti-Pellie, 2004; Clayton, 2003; Kraft and Thomas, 2000; Schaid et al., 2010]. A similar conditional likelihood can be envisioned for our ascertainment method, which would consider the likelihood for inference conditioning on liability scores. Such a correction would be valuable for future studies that intend on sampling in phenotypic extremes.
Our results generalize to other risk models with varying degrees of variance explained (Table VI), with the amount of enrichment dependent on the extent of variance explained by covariates entered in the risk model. Although the magnitude of enrichment increases as the proportion of variance explained increases, we caution against over-saturation of the risk model or the inclusion of inappropriate covariates. The addition of covariates that are statistically uninformative could dilute the efficacy of the scoring method, leading to misclassification and error or a reduction in power. Alternatively, caution should be exercised including variables as covariates, which are part of the phenotypic definition (e.g. covariates for glucose impairment in the context of type-2 diabetes as the outcome variable). These types of inclusions might cause counter-intuitive extreme liability definitions. Genetic factors could be easily incorporated into the liability score [Plomin et al., 2009], although it is unclear how much power would be gained with this approach. Family history could improve estimates of disease risk and liability scores [Campbell et al., 2010; Falconer, 1965; Feng et al., 2009]; however, researchers should a priori decide how family history should be incorporated in the liability model. If the ascertainment strategy is to select cases that have little to no risk but have a family history of disease (and conversely controls who are at high risk of being affected but have no family history of disease), then the directionality of family history should be reversed in the risk model. Additionally, disease severity was not considered explicitly here but in principal could be included in the liability model in a straightforward way. Further research is warranted regarding the incorporation of family history, genetic factors, and severity into the liability model with respect to rare variants.
Similar to all simulations, our work is limited by assumptions about the underlying population model. First, the simulations assumed that there was a genetic variant that conferred an additional risk (or protection) independent of other factors entered into the risk model. The proposed strategy would decrease power to discover genetic variants that indirectly influence the disease through the risk factors included in the liability model. However, this may be attractive as the strategy could potentially reveal new biological mechanisms that act independently of well-established risk factors. Second, we did not consider interactions between risk factors; if the trait were influenced by one or more nonadditive interaction terms (and these are known a priori), including them in the risk model would improve the sensitivity and specificity of the liability scores. Third, our power/sample size estimates regarding replication samples do not consider the impact of founder populations, wherein the value of conducting the follow-up study in the same population could be substantially greater.
Fourth, we assumed no misclassification of cases and controls and no sequencing errors. Selecting unaffected individuals with the highest liability may result in misclassification which would decrease power. This problem can be alleviated if one imposes additional criterion that ensures “disease-free” status for the unaffected individuals. For example, if nondiabetics are selected that carry many or all risk factors for T2D, one could constrain the sampling to euglycemic individuals with the highest liability. Sequencing errors (i.e. false positives and false negatives) will undoubtedly have deleterious effects for the prioritization of variants for follow-up.
Fifth, we did not explicitly examine the impact of liability sampling on mis-matching of ancestry or other nonmeasured confounders. It is clear that appropriate case/control matching will remain essential to minimize false-positive associations due to population stratification. This may be especially important for ascertainment of extreme phenotypes, which are known to vary across ancestry and geography (for example, stature, which shows a North–South gradient in Europe). Sampling from extremes of phenotypes might amplify population stratification.
Sixth, we did not explicitly discuss the use of external information (such as biological plausibility and allele frequency in public datasets) in prioritizing candidate variation for follow-up. Strategies which encompass biological or functional information on sequence characteristics (e.g. coding mutations) could also be employed separately [Ng and Henikoff, 2003; Ramensky et al., 2002; Sunyaev et al., 2001] or in conjunction with statistical information to prioritize candidate variants for follow-up.
Finally, we employed a very simple model of association (in which the collective frequency of a variant class is compared between cases and controls with Fisher's exact test) and considered a stringent significance level of 0.001. Fisher's test in combination with a stringent significance level will be substantially underpowered for rare variant analysis and thus, alternative tests and methods will need to be developed. More sophisticated association statistics that analyze rare variants in aggregate [Li and Leal, 2008; Madsen and Browning, 2009; Morgenthaler and Thilly, 2007] need to be evaluated in simulations such as these. Although the absolute value of the power calculations will no-doubt be influenced by the choice of statistical test, we imagine that the conceptual results will likely be consistent: i.e. that extreme sampling increases power, that power will be much greater to discover variation than it is to detect an association, and that replication studies will face a choice of using extremes (thereby over-estimating true effect sizes in the general population), or of requiring much larger samples. These principles may prove of value in the next couple of years as advances in next-generation sequencing technology make possible dramatic increases in sequencing studies of rare variants.
Acknowledgements
The authors thank David Cox, Shaun Purcell, and Mark Daly for their helpful comments on the manuscript. O. M. acknowledges support from the Marianne and Marcus Wallenberg Foundation. L. G. is supported by grants from the Swedish Research Council (Scania Diabetes Registry) and from The Sigrid Juselius Foundation and Folkhälsan Foundation (Botnia Study).
