Meta-analysis of gene-environment interaction: joint estimation of SNP and SNP × environment regression coefficients
Abstract
Introduction: Genetic discoveries are validated through the meta-analysis of genome-wide association scans in large international consortia. Because environmental variables may interact with genetic factors, investigation of differing genetic effects for distinct levels of an environmental exposure in these large consortia may yield additional susceptibility loci undetected by main effects analysis. We describe a method of joint meta-analysis (JMA) of SNP and SNP by Environment (SNP × E) regression coefficients for use in gene-environment interaction studies. Methods: In testing SNP × E interactions, one approach uses a two degree of freedom test to identify genetic variants that influence the trait of interest. This approach detects both main and interaction effects between the trait and the SNP. We propose a method to jointly meta-analyze the SNP and SNP × E coefficients using multivariate generalized least squares. This approach provides confidence intervals of the two estimates, a joint significance test for SNP and SNP × E terms, and a test of homogeneity across samples. Results: We present a simulation study comparing this method to four other methods of meta-analysis and demonstrate that the JMA performs better than the others when both main and interaction effects are present. Additionally, we implemented our methods in a meta-analysis of the association between SNPs from the type 2 diabetes-associated gene PPARG and log-transformed fasting insulin levels and interaction by body mass index in a combined sample of 19,466 individuals from five cohorts. Genet. Epidemiol. 35:11–18, 2011. © 2010 Wiley-Liss, Inc.
INTRODUCTION
Genome-wide association studies have facilitated discovery of associations between genetic variants and complex phenotypes. After discovery and replication of the strongest association signals, weaker associations are discoverable only with the increased power of larger samples [McCarthy et al., 2008]. Therefore, individual research groups have formed consortia and meta-analyzed their GWAS of complex diseases to find such signals [Ioannidis et al., 2007; Lindgren et al., 2009; Prokopenko et al., 2009; Psaty et al., 2009]. For commonly used analyses, this approach is as efficient as combining individual participant data [Lin and Zeng, 2010]. However, the SNP associations identified by these consortia explain little heritability in the quantitative traits being studied. Many quantitative traits are influenced by environmental factors, which may interact with the genetic loci being tested. As a way to incorporate environmental factors, identify other genetic contributors to the trait of interest, explain the remaining heritability, and to further characterize the genetic architecture of the trait, we now wish to look beyond SNP main effect associations to SNP-environment interaction associations.
In this paper, we propose a method to jointly meta-analyze the regression coefficients for a SNP's main effect and its interaction with an environment variable (SNP × E). This method provides meta-analytic estimates of these coefficients, as well as a joint test of significance and a test of heterogeneity. We present a simulation study to compare the joint meta-analysis (JMA) to four other meta-analytic methods for detecting SNP associations in quantitative traits. Other methods have been proposed in the context of phenotypes tested in case-control designs [Chatterjee and Wacholder, 2008; Murcray et al., 2009]; here we focus on a quantitative trait as the outcome.
As an example illustrating our method, the Meta-Analysis of Glycemic and Insulin-related traits Consortium (MAGIC) has recently published the discovery of 16 loci associated with fasting glucose but only two loci associated with fasting insulin [Dupuis et al., 2010]. The low number of SNPs associated with insulin resistance measures, as compared to those associated with insulin secretion indices, remains an intriguing empiric observation in the field. The MAGIC meta-analysis of 21 studies contributing up to 38,238 individuals to the discovery sample failed to detect associations between log-transformed fasting insulin and SNPs near PPARG, a known type-2 diabetes gene [Altshuler et al., 2000]. Fasting insulin, a surrogate indicator of insulin resistance, is highly associated with body mass index (BMI), and it has been suggested that BMI interacts with the PPARG locus in influencing type 2 diabetes risk [Florez et al., 2007; Ludovico et al., 2007; Tonjes et al., 2006]. Consequently, we explored methods for identifying main effect of SNPs in PPARG on levels of log(fasting insulin), and their interactions with BMI, in a meta-analysis of five cohorts comprising 19,466 individuals.
METHODS
For all strategies we assume that association results are gathered from k studies where N SNPs are genotyped and the trait Y and environmental factor E are also measured. From these studies, summary statistics are available from single-SNP regressions assessing the association between Y and each SNP. Two regressions will be considered: the main effects regression, in which the association between the SNP and Y is tested while adjusting for E, and the interaction regression with both SNP and SNP × E regression terms.
MAIN EFFECTS REGRESSION MODEL
The mean model used in linear regression for main effects is
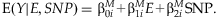
INTERACTION REGRESSION MODEL
A mean model used in linear regression for interaction effects is
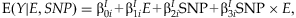
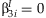.JOINT META-ANALYSIS OF SNP AND SNP × E
We propose to apply the method of Becker and Wu [2007] to simultaneously summarize the SNP and SNP × E regression coefficients from fitted interaction models. This method provides a joint test of significance of the estimates and a test of homogeneity of the regression estimates across the k studies. The benefit of the JMA is two-fold: first, it can act as a screening tool to find SNPs which may have significant main or interaction effects and second, SNPs may only show significant associations when interaction is considered.
For each study, linear unbiased estimators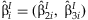 
and 
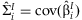are computed. We assume that the 
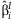are asymptotically normally distributed with mean β and variance Σ. The purpose of this method is to estimate β and Σ.
A vector, b, is formed with the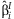 
from each cohort. This vector has block-diagonal covariance under the assumption of independence among cohorts:
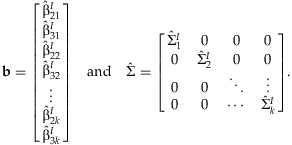
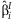estimates β, we can rewrite the vector b as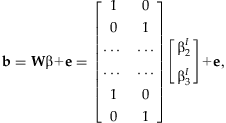
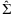.The estimate of β and its covariance are obtained from generalized least squares, accounting for the unequal variances contributed to the estimate from studies of different sizes: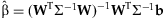 
and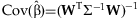 
.
Confidence intervals of the regression estimates can be obtained with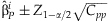 
where 
is the pth element of 
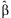and Cpp is the pth diagonal element of 
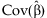. Additionally, 
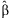and 
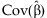can be used to calculate a joint confidence region of 
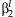and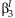 
.
A Wald statistic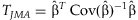 
follows a two degree of freedomχ2 distribution under the null hypothesis that β = 0 and can be used to test the joint significance of 
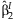and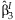 
.
A test of homogeneity of regression coefficients, analogous to the Cochran's Q-test [Cochran, 1954; Higgins and Thompson, 2002], can be performed using the statistic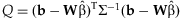 
. Under the null hypothesis that 
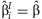for all i, the test statistic Q = 0.
The summary regression estimates obtained from the JMA are used for the interpretation of the SNP effect for varying levels of the environmental variable. Gathering terms from the model, 
, the effect of the SNP can be written as:
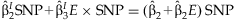
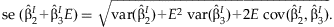
SIMULATION STUDY
We designed a simulation study to compare the JMA strategy to four other meta-analytic methods. The first two produce meta-analyzed summaries of a single term: in the main effects meta-analysis, we summarize the estimate of the SNP term from the main effects regression model and in the interaction meta-analysis, we summarize the estimate of the interaction term from the interaction regression model. The third method, screening by main effects, restricts the interaction test to the subset of SNPs with main effects p-values lower than a prespecified threshold αM. Finally, the fourth method, the meta-analysis of the two degree of freedom test, jointly tests the SNP and SNP × E regression coefficients.
META-ANALYSIS OF SNP MAIN EFFECTS
In the study of SNP associations, the main effect of a SNP will often be assessed prior to performing interaction regressions. The estimates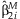 
can be summarized across the k studies using an inverse-variance weighted meta-analysis [Petitti, 2000]. We define 
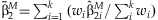, where 
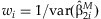, as a weighted average of the 
from each study. Here, the weights are inversely proportional to the estimated variance of the regression estimates.
The estimated standard error of 
is:
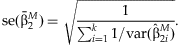
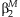is equal to zero, the test statistic, TMAIN, can be constructed:
META-ANALYSIS OF INTERACTION EFFECTS
The simplest approach to detect possible interaction effects is to summarize the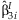 
from the k studies. This method identifies SNPs with significant interaction effects regardless of whether or not there is a main effect of the SNP. We perform the same meta-analysis as described above with the 
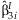obtaining: 
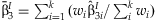with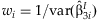 
and the estimated standard error:
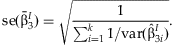
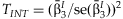can be compared it to a one degree of freedom χ2 distribution to test if 
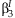is equal to zero.SCREENING BY MAIN EFFECTS
One strategy for detecting SNP × E interactions when many SNPs are being tested is to assess interaction in the subset of SNPs with significant main effects [Kooperberg and Leblanc, 2008]. Here, we perform the meta-analysis of the main effects and carry out the meta-analysis of the interaction term on those SNPs with a main effects p-value less than a prespecified threshold αM. This limits the number of interaction tests performed, and therefore permits the use of a less stringent α-level correction. This approach has the theoretical advantage of increasing power under the assumption that the SNPs with strong interaction effects will also have marginal effects, which pass the screening step. Two values of αM will be considered: 0.01 and 0.05.
To control the type I error rate, a critical assumption is that the tests at the first stage are independent of the tests at the second stage. A proof of this appears in Kooperberg and Leblanc [2008]. The type I error rate of α of all N SNPs is preserved by allowing NM = αM × N SNPs to pass to the second stage. The number of null SNPs reaching statistical significance at the second stage, with significance threshold of α/NM, is then NM × α/NM = N×α.
META-ANALYSIS OF TWO DEGREE OF FREEDOM TEST
Kraft et al. [2007] proposed a two degree of freedom (2 df) test of main and interaction effects in the context of genome-wide association studies (GWAS), which detects SNPs with main effects and SNPs with heterogeneity in genetic effects across different levels of the environmental variable.
Within each study, the 2 df test statistic can be constructed: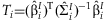 
, where 
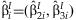and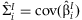 
. This statistic is compared to a 2 df χ2 distribution to test if both 
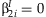and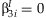 
.
The p-value of this test, pi, can then be meta-analyzed using Fisher's method [Hedges and Olkin, 1985], which provides a summarized χ2 statistic with 2k degrees of freedom:
SIMULATED DATA
We simulated data from five studies with 1,000 participants each. The simulated data included a continuous environmental variable, E, a SNP with minor allele frequency of 0.30, and a quantitative trait, Y, whose mean value is a function of E and the SNP. The effect of the SNP was additive so that the mean value of Y is higher for those with more copies of the minor allele. The continuous environmental variable, E, explained 10% of the variation in Y, while the main effect of the SNP explained between 0 and 1% of the variation in Y and the interaction between E and the SNP explained between 0 and 1% of the variation in Y. In addition to the SNP associated with Y, 999 nonassociated SNPs with minor allele frequencies uniformly distributed between 0.05 and 0.5 were generated. A total of 15 scenarios were considered, with 1,000 simulations each.
In the context of multiple independent tests, a standard α-level correction can be used to determine statistical significance. If N denotes the number of SNPs tested, a Bonferroni correction of α/N can be used to define the significance threshold for an overall type I error rate of α. This controls the family-wise error rate, defined as the probability of having one or more false-positive associations in each simulation, at nominal level α. For the screening method, a threshold αM must be defined. For these simulations, we set αM to 0.01 and 0.05, which translates to carrying forward 10 or 50 null SNPs to the second stage. If NM denotes the number of SNPs passing the first stage, a Bonferroni correction of α/NM can be used to define statistical significance at the second stage.
TYPE I ERROR AND POWER
The empirical type I error rate of each method was assessed by first observing the proportion of significant null SNPs within each simulation, using a corrected significance threshold of 0.01/999 = 1.001 × 10−5 for each set of 999 null SNPs. These proportions are averaged across all simulations. The theoretical type I error rate for each simulation is 0.01. The power of each method was determined by observing the proportion of simulations in which the associated SNP was statistically significant.
RESULTS
TYPE I ERROR
The comparison of the empirical type I error rates in 15,000 simulations is displayed in Figure 1A. The theoretical error rate is 0.01, as each of the simulations had 999 null SNPs with a Bonferroni corrected significance level of 0.01/999 = 1.001 × 10−5. The empirical type I error rate of all 14,985,000 null SNPs and the breakdown of empirical type I error rates by minor allele frequency category are displayed in Figures 1B and C, respectively. These rates are reported on the SNP level, where the theoretical type I error rate is 1.001 × 10−5. All five methods had an empirical type I error rate with 95% confidence intervals overlapping the theoretical type I error rate indicated by a horizontal line, except the JMA in the 0.20–0.25 minor allele frequency category, which had a slightly inflated empirical type I error rate.
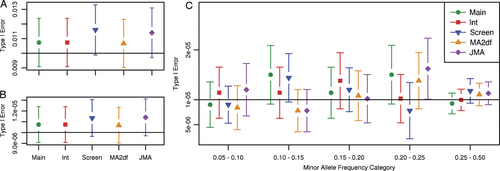
(A) Empirical type I error rate in 15,000 simulations of 999 null SNPs, empirical type I error rates for (B) 14,985,000 null SNPs and (C) 14,985,000 null SNPs broken into minor allele frequency categories. A horizontal line is drawn at the theoretical type I error rate in each plot.
POWER
The five methods described here have different null hypotheses, resulting in differences in power when the effects of the SNP and the SNP × E terms are varied. The meta-analysis of the main effect tests the null hypothesis that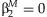 
, and the meta-analysis of the interaction effect tests the null hypothesis that 
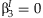. The screening approach tests the null hypothesis that 
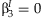for SNPs whose main effect meta-analysis p-value is less than αM. Finally, both the meta-analysis of the 2 df test and the JMA test the null hypothesis that 
and 
, although the meta-analytic methods differ.
A comparison of the power of the five methods is presented in Figure 2. When there is no interaction effect, the main effects meta-analysis, the meta-analysis of the 2 df test, and the JMA can be compared in terms of power, as these methods test the main effect of the SNP. Figure 2A describes the scenario where the percent variance in Y explained by the SNP is increased from 0 to 1% and the percent of variances of Y explained by SNP × E is 0%. The meta-analysis of the main effect has the highest power, with the JMA having slightly less power.
Power of the five methods of meta-analysis compared in the simulation study. Both the percent of the variance in the outcome explained by the SNP and the SNP × E terms vary between 0 and 1%.
When there is an interaction effect, the interaction meta-analysis and the screening approach can be added to the power comparison. Figures 2B and C show scenarios where the percent of variance of Y explained by SNP × E is 0.5 and 1%, respectively. In these situations, the JMA has the highest power, except in the situation where there is no main effect (i.e. the percent variance explained by the SNP is zero), in which case the meta-analysis of the interaction alone has the highest power. When αM was set to 0.05, a more generous screening threshold, power for the screening method was decreased (data not shown) as more SNPs passed the screening and the significance threshold for the interaction analysis was lowered.
IMPLEMENTATION IN A LARGE GENETIC CONSORTIUM
The missense P12A variant within the PPARG gene has been found to be associated with type 2 diabetes [Altshuler et al., 2000], a phenotype related to insulin resistance and impaired β-cell function. PPARG encodes the peroxisome proliferator activated receptor gamma2, a transcription factor involved in adipocyte differentiation and the target of thiazolidinedione medications. It is believed that the risk allele at PPARG P12A increases risk of type 2 diabetes by reducing insulin sensitivity. The covariate BMI is strongly associated with type 2 diabetes; individuals with higher BMI are at higher risk of the disease, and BMI may modify the risk conferred by the PPARG P12A variant [Florez et al., 2007; Ludovico et al., 2007; Tonjes et al., 2006]. We assessed the association of 60 tagSNPs within 1,000 kb of PPARG with the diabetes-related quantitative trait of fasting insulin levels (as a surrogate of insulin resistance) in five cohorts, with sample sizes ranging between 561 and 8,367 nondiabetic participants, resulting in a sample size of 19,466 individuals. The cohorts, described in Table I, are as follows: the Framingham Heart Study [Meigs et al., 1998] (FHS), the Family Heart Study [Coon et al., 2004; Higgins et al., 1996] (FamHS), the Cardiovascular Heart Study [Cushman et al., 1995; Fried et al., 1991; Psaty et al., 2009] (CHS), the Atherosclerosis Risk in Communities Study [ARIC, 1989] (ARIC), and the Dynamics of Health, Aging and Body Composition Study [Simonsick et al., 2001] (Health ABC). The outcome trait, fasting insulin, was naturally log-transformed in order to reduce the skewness of its distribution.
| Cohort | Sample size | Age mean (SD) | % Female | Body mass index mean (SD) | Fasting insulin (pmol/l) mean (SD) |
|---|---|---|---|---|---|
| CHS | 2,854 | 72.3 (5.4) | 57 | 26.0 (4.3) | 93.9 (49.1) |
| ARIC | 8,367 | 54.1 (5.7) | 54 | 26.7 (4.6) | 72.1 (53.9) |
| FamHS | 561 | 53.4 (11.9) | 47 | 27.7 (5.1) | 69.1 (43.8) |
| FHS | 6,023 | 46.2 (11.6) | 54 | 27.0 (5.0) | 29.9 (16.5) |
| HealthABC | 1,661 | 73.8 (2.8) | 47 | 26.6 (4.1) | 57.0 (40.6) |
| Total | 19,466 |
The − log 10 (p-values) of the meta-analysis of each of the 60 tagSNPs within 1,000 kb of the PPARG gene are presented in Figure 3. The regression estimates and p-values for SNPs reaching statistical significance are listed in Table II for all methods except the screening approach. The significance threshold was α/N = 0.01/60 = 1.67 × 10−4. We did not detect significant heterogeneity in the regression slopes among the five samples (p>0.01). Significant associations were seen with both the meta-analysis of the 2 df test and the JMA. The most significant SNP, rs1801282 (PPARG P12A), had a p-value of 1.15 × 10−6 with the meta-analysis of the 2 df test and 8.29 × 10−9 with the JMA. Neither the main effects meta-analysis nor the interaction meta-analysis produced tests with p-values less than the corrected significance threshold of 0.01/60 = 0.000167. For the screening approach, even though the main effects meta-analysis would have allowed the SNP to pass to the second stage with a p-value below αM = 0.01, the p-value of the interaction meta-analysis would not have been below the corrected p-value threshold of α/NM.
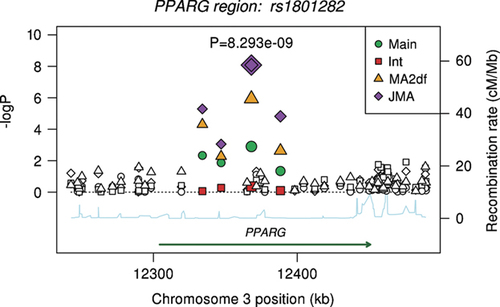
Single SNP associations of SNPs in the PPARG gene with log(fasting insulin) in a meta-analysis of five studies of 19,466 nondiabetic individuals, after taking into account a putative interaction with BMI. The PPARG P12A SNP is indicated by a double-diamond and annotated with the p-value from the joint meta-analysis (JMA). The shading represents SNPs with R2 greater than 0.2 with P12A.
| Main effects meta-analysis | Interaction meta-analysis | Meta-analysis of the 2 df test | Joint meta-analysis | Test of homogeneity | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| SNP |  |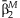
p |  |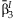
p | T2 df (8 df) | p |  |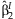
 |
TJMA (2 df) | p | p (8 df) |
| rs1801282 | 0.0293 | 0.001 | 0.0013 | 0.44 | 46.52 | 1.15 × 10−6 | 0.0009 | 0.0016 | 37.22 | 8.3 × 10−9 | 0.317 |
| rs2067819 | −0.0205 | 0.005 | 0.0002 | 0.86 | 37.34 | 4.94 × 10−5 | −0.0237 | −0.0002 | 24.37 | 5.1 × 10−6 | 0.113 |
| rs2120825 | 0.0216 | 0.050 | 0.0005 | 0.80 | 27.33 | 2.31 × 10−3 | 0.0232 | 0.0006 | 22.2 | 1.5 × 10−5 | 0.743 |
The effect of the SNP rs1801282 (PPARG P12A) on log(Insulin) for BMI values of 25, 30, and 35 are displayed in Table III. For a BMI of 25, the effect of the minor allele of rs1801282 on log(Insulin) is 0.041 (se = 0.0073), while for a BMI of 35, the effect is 0.057 (se = 0.016), demonstrating the synergistic effect of BMI on the association between PPARG P12A and log(Insulin).
| BMI | Effect | SE (effect) |
|---|---|---|
| 25 | 0.041 | 0.0073 |
| 30 | 0.049 | 0.0094 |
| 35 | 0.057 | 0.0160 |
DISCUSSION
We have shown that the JMA has higher power than the other methods when both main and interaction effects are present. Most of the difference in power between the methods can be attributed to the different hypotheses and to the different degrees of freedom in the tests. The main effects meta-analysis and the interaction meta-analysis have one degree of freedom, the meta-analysis of the 2 df test has 2k degrees of freedom and the JMA has two degrees of freedom. As demonstrated in Figure 2A, when comparing the ability of the three methods to detect the main effect in the absence of interaction, the main effects meta-analysis has the highest power, followed closely by the JMA. The meta-analysis of the 2 df test has 10 degrees of freedom, resulting in lower power than the other two methods.
The JMA strategy simultaneously tests and estimates the SNP and SNP × E regression coefficients of an interaction regression model. This method accounts for the covariance between the SNP regression estimate and the SNP × E regression estimate. A joint test of significance is available, testing the null hypothesis that both the SNP regression coefficient and SNP × E regression coefficient are equal to zero. A confidence region of the regression estimates can be constructed using the covariance matrix of the meta-analyzed regression estimates. Finally, we provide a test of heterogeneity of the regression estimates. The meta-analyzed regression coefficients and the joint test fully characterize the association between the SNP and the outcome, allowing for a possible interaction between the SNP and the environmental variable. We have confirmed that PPARG P12A interacts with BMI in increasing insulin resistance, a phenomenon which may be extended to other putative insulin resistance loci.
The JMA method has been implemented in METAL (http://www.sph.umich.edu/csg/abecasis/Metal). Individual studies can obtain the required regression and covariance estimates for interaction regression models using QUICKTEST version 0.95 (http://toby.freeshell.org/software) and ProbABEL version 0.1–3 (http://mga.bionet.nsc.ru∼yurii/ABEL/) [Aulchenko et al., 2007].
We hope that the use of this method in appropriately sized consortia with relevant environmental variables will lead to both the identification of novel associations with complex quantitative traits and a more refined characterization of existing signals. When an environmental variable is known or suspected to contribute to the expression of complex quantitative traits and phenotypes, a greater proportion of the heritability of complex traits may be explained by accounting for the joint effects of the SNP and the SNP-environment interaction.
Acknowledgements
The authors acknowledge Han Chen for his programming support in adding the Joint Meta-Analysis method to METAL as well as his work modifying QUICKTEST and ProbABEL to produce the statistics required by the Joint Meta-Analysis.
FHS
This research was conducted in part using data and resources from the Framingham Heart Study of the National Heart Lung and Blood Institute of the National Institutes of Health and Boston University School of Medicine. The analyses reflect intellectual input and resource development from the Framingham Heart Study investigators participating in the SNP Health Association Resource (SHARe) project. This work was partially supported by the National Heart, Lung and Blood Institute's Framingham Heart Study (Contract No. N01-HC-25195) and its contract with Affymetrix, Inc for genotyping services (Contract No. N02-HL-6-4278). A portion of this research utilized the Linux Cluster for Genetic Analysis (LinGA-II) funded by the Robert Dawson Evans Endowment of the Department of Medicine at Boston University School of Medicine and Boston Medical Center. Also supported by National Institute for Diabetes and Digestive and Kidney Diseases (NIDDK) R01 DK078616 to Drs. Meigs, Dupuis and Florez, NIDDK K24 DK080140 to Dr. Meigs, and NIDDK Research Career Award K23 DK65978, a Massachusetts General Hospital Physician Scientist Development Award and a Doris Duke Charitable Foundation Clinical Scientist Development Award to Dr. Florez.
HealthABC
The Health ABC Study research reported in this article was supported by NIA contracts N01AG62101, N01AG62103, and N01AG62106. Research was also supported in part by the Intramural Research Program of the NIH, National Institute on Aging. The genome-wide association study was funded by NIA grant 1R01AG032098-01A1 to Wake Forest University Health Sciences, and genotyping services were provided by the Center for Inherited Disease Research (CIDR). CIDR is fully funded through a federal contract from the National Institutes of Health to The Johns Hopkins University, contract number HHSN268200782096C. Also supported by NIDDK K01 DK083029.
ARIC
The Atherosclerosis Risk in Communities Study (ARIC) is carried out as a collaborative study supported by National Heart, Lung, and Blood Institute contracts N01-HC-55015, N01-HC-55016, N01-HC-55018, N01-HC-55019, N01-HC-55020, N01-HC-55021, N01-HC-55022, R01HL087641, R01HL59367 and R01HL086694; contract U01HG004402; and National Institutes of Health contract HHSN268200625226C. The authors thank the staff and participants of the ARIC study for their important contributions.
CHS
The CHS research reported in this article was supported by contract numbers N01-HC- 85079 through N01-HC-85086, N01-HC-35129, N01 HC-15103, N01 HC-55222, N01-HC-75150, N01-HC-45133, grant numbers U01 HL080295 and R01 HL087652 from the National Heart, Lung, and Blood Institute, with additional contribution from the National Institute of Neurological Disorders and Stroke. A full list of principal CHS investigators and institutions can be found at http://www.chs-nhlbi.org/pi.htm. DNA handling and genotyping was supported in part by National Center for Research Resources grant M01RR00069 to the Cedars Sinai General Clinical Research Center Genotyping core and National Institute of Diabetes and Digestive and Kidney Diseases grant DK063491 to the Southern California Diabetes Endocrinology Research Center.
FamHS
The Family Heart Study (FamHS) work was supported in part by NIH grants 5R01 HL08770003, 5R01 HL08821502 (Michael A. Province) from NHLBI, and 5R01 DK07568102, 5R01 DK06833603 from NIDDK (Ingrid B. Borecki).
