Combining machine learning and domain decomposition methods for the solution of partial differential equations—A review
Abstract
Scientific machine learning (SciML), an area of research where techniques from machine learning and scientific computing are combined, has become of increasing importance and receives growing attention. Here, our focus is on a very specific area within SciML given by the combination of domain decomposition methods (DDMs) with machine learning techniques for the solution of partial differential equations. The aim of the present work is to make an attempt of providing a review of existing and also new approaches within this field as well as to present some known results in a unified framework; no claim of completeness is made. As a concrete example of machine learning enhanced DDMs, an approach is presented which uses neural networks to reduce the computational effort in adaptive DDMs while retaining their robustness. More precisely, deep neural networks are used to predict the geometric location of constraints which are needed to define a robust coarse space. Additionally, two recently published deep domain decomposition approaches are presented in a unified framework. Both approaches use physics-constrained neural networks to replace the discretization and solution of the subdomain problems of a given decomposition of the computational domain. Finally, a brief overview is given of several further approaches which combine machine learning with ideas from DDMs to either increase the performance of already existing algorithms or to create completely new methods.
1 INTRODUCTION
Scientific machine learning (SciML) is a new, rapidly developing field of research within the field of artificial intelligence in which techniques of scientific computing and machine learning are combined and further developed 2. One major aspect in SciML is the integration of domain knowledge into ML algorithms to obtain more accurate algorithms with a better interpretability. Here, the term domain knowledge contains, for example, physical laws or physical principles, expert knowledge, results of computational simulations, or certain constraints. For example, including the residual of a differential equation representing certain physical principles into the loss of a neural network can be used to discretize and solve the differential equation.
Another important aspect of SciML is enhancing numerical algorithms with ML techniques. The machine learning techniques often replace parts of the method where the domain knowledge is not sufficient to, for example, choose appropriate parameters or models. In general, this results in hybrid methods, which can be faster and more robust solvers or new model order reduction models.
In the present article, as an example of SciML, we provide a brief overview of the combination of machine learning and domain decomposition methods (DDMs) for the solution of partial differential equations (PDEs). DDMs are highly scalable and robust iterative solution methods for discretized nonlinear or linear PDEs. The excellent scalability results from a divide and conquer principle, based on the decomposition of the computational domain into overlapping or nonoverlapping subdomains and thus on the spatial decomposition of the PDE into smaller subproblems. These subproblems can be processed independently and in parallel. Synchronization and communication are first necessary on the interface of neighboring subdomains—or small overlapping regions of it—in order to obtain the correct solution at convergence and, second, during the solution of a global coarse problem. The coarse problem guarantees robustness if defined appropriately. Successful DDMs are, among others, overlapping Schwarz methods 12, 13 or nonoverlapping finite element tearing and interconnecting-dual primal (FETI-DP) 18, 19, 49, 50 and balancing domain decomposition by constraints (BDDC) 10, 11, 51, 58 methods.
In general, one can divide the approaches combining ML and DDMs into three classes: the first one consists of approaches where ML techniques are used within a classical DDM in order to improve the convergence properties or the computational efficiency. In the second class, deep neural networks (DNNs) are used as discretization methods and solvers for differential equations replacing classical approaches based on finite elements or finite differences. In combination with DDMs these DNN-based methods are used as subdomain solvers. In the third class, which will not be further described in the present review article, ideas from the area of DDMs are used to improve ML algorithms, among others, the parallelization properties and convergence speed of the training procedure of a neural network. Here, we can further distinguish the distribution of data sets and features. Among these are the overlapping areas of distributed and parallel learning 5, 67, 68, 79, 82 as well as collaborative and federated learning 35, 53, 74. We will not describe these here and refer to the given references and the references therein. Let us remark that these classes are not disjoint and some approaches can be assigned to more than one. Here, we will clearly focus on the first two classes and provide a detailed description of two very specific and very different approaches in Sections 2 and 3, respectively.
A very specific combination of ML and adaptive DDMs was presented by the authors in 30, where neural networks were trained to predict the location of important coarse space constraints in adaptive FETI-DP; see Section 2. This can be used to reduce the computational effort in the setup phase of adaptive FETI-DP methods. In the present article, we will not only review our own existing results on adaptive FETI-DP but also expand this approach to the completely different class of overlapping adaptive Schwarz methods for the first time.
Physics-constrained neural networks, among others, physics-informed neural networks (PINNs) 54 and Deep Ritz methods 52, have been used to replace the discretization and solution of the subdomain problems in a classical Schwarz DDM. The main idea of both PINNs and Deep Ritz is to integrate a priori knowledge in the form of physical laws or domain expertise into a deep learning model; see, for example, 16, 69 for more details. In particular, PINNs can be applied to solve forward as well as inverse problems and are completely mesh-free since the optimization of their respective loss function is based on the evaluation of selected collocation points. Thus, PINNs and Deep Ritz are an excellent example for the combination of ML techniques and domain knowledge. Hence the deep domain decomposition approaches introduced in 52, 54 are again excellent examples for the combination of SciML and DDMs. We will present the DeepDDM method 54 and the similar D3M method 52 within a unified framework in Section 3.
Finally, in Section 4, we give a brief overview of several further approaches combining ML with DDMs and describe the main ideas of 8, 15, 36, 39, 57, 61, 77, 81 in a few sentences each.
2 MACHINE LEARNING IN ADAPTIVE DOMAIN DECOMPOSITION
In 27, 30, 31 we proposed an approach to reduce the computational cost in the setup of adaptive FETI-DP solvers using DNNs—without deteriorating the robustness and convergence behavior of adaptive FETI-DP. This machine learning-finite element tearing and interconnecting-dual primal (ML-FETI-DP) method is thus a hybrid method combining machine learning and DDMs.
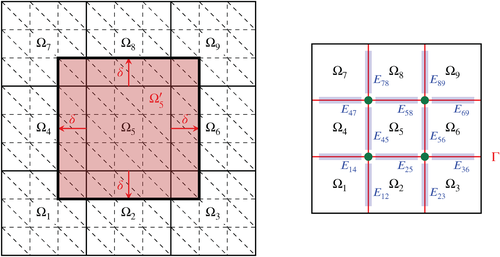
In general, adaptive DDMs are designed for challenging problems with bad parameters, for example, for composites in solid and structural mechanics, where the performance of standard preconditioners will depend strongly on the contrast of the coefficient function. In contrast, the condition number bound of adaptive DDMs is independent of the coefficient function. To achieve this desirable property, the coarse problem or second level of the DDM has to be enhanced with specific and problem dependent constraints which altogether build the adaptive coarse space. The adaptive coarse space is always computed automatically, which is typically done by solving many local eigenvalue problems on smaller parts of the interface between the subdomains—often faces or edges. In the description in this section, we restrict ourselves to two-dimensional problems and all eigenvalue problems which are considered are associated with edges. A drawback of adaptive DDMs is the substantial computational cost which is involved in the setup and solution of all these local eigenvalue problems. Both are part of the setup of the adaptive DDM and this cost is difficult to amortize, especially in parallel computations, and currently makes adaptive domain decomposition (DD) most suitable for problems where standard methods fail to converge at all. In Table 1 we present an illustrating example where the standard FETI-DP method fails to converge within 300 iterations. The adaptive method converges fast and has a small condition number. To achieve this fast convergence, 112 eigenvalue problems have to be solved, each one associated with an edge and its two adjacent subdomains. We will provide details on the specific adaptive coarse space and the associated eigenvalue problem later on.
| Model problem | Algorithm | cond | it | evp | |
|---|---|---|---|---|---|
| Standard | — | >300 | 0 | Cheap setup/bad convergence | |
| Microsection problem | Adaptive | 15.86 | 36 | 112 | Expensive setup/fast convergence |
| ML | 15.86 | 36 | 44 | Reasonable setup/fast convergence |
- Note: We show the condition number (cond), the number of CG iterations (it), and the number of solved eigenvalue problems (evp).
Obviously, there is a big potential to save computational cost and to make adaptive DDMs more competitive by omitting eigenvalue problems on certain edges which are unnecessary as they do not add any important constraint to the coarse problem. Indeed, for many practical and realistic model problems, only a small number of adaptive constraints are necessary at all to retain a robust algorithm. In particular, this means that a large number of the eigenvalue problems can actually be omitted. For our specific example from Table 1, actually only 39 of the 112 eigenvalue problems result in any adaptive constraints and thus approximately 65% of the eigenvalue problems are solved for nothing in adaptive FETI-DP; see also Figure 1 (middle) where all unnecessary edges are marked in yellow. For remarks on ongoing research with regard to the evaluation of computational cost of the new approach compared to traditional approaches, see Section 2.7.

However, in general it is difficult to predict for which edges the eigenvalue problem is necessary or not before actually solving it. The approach proposed in 27, 30, 31 is to train a neural network to make this decision automatically and in advance, that is, in a preprocessing phase before even solving the local eigenvalue problems. For our specific example, we can omit most of the unnecessary edges a priori and still preserve the robustness of adaptive FETI-DP; see Table 1 and Figure 1 (right), where all edges for which an eigenvalue problem was solved are marked in green (necessary) and yellow (unnecessary). These results exactly show the desired property: a lower setup cost to make adaptive DD competitive while preserving its robustness and low condition number. In the remainder of this chapter, we will describe the methodology used to reach both objectives in detail.
Let us remark that the basic procedure is the same for all adaptive DDMs which rely on the solution of localized eigenvalue problems on edges or, in three dimensions, on edges and faces. Hence, we describe the approach independently of the specific DDM and show numerical results for two very different examples, that is, adaptive FETI-DP and adaptive generalized Dryja-Smith-Widlund (GDSW) 26. Let us remark that we combine an overlapping adaptive DDM with our machine learning approach for the first time in this article and thus also show the generality of our approach. We will first describe the machine learning approach to classify all local eigenvalue problems or all edges, respectively, as necessary or not for the robustness of the algorithm. Afterwards we will describe the two specific adaptive DD approaches we consider here.
Let us finally emphasize a further important property of all our hybrid machine learning based adaptive DD approaches: The validation if the DNN worked appropriately is pretty simple by checking the condition number and convergence behavior. There is no uncertainty involved and also the quality of the solution of the discretized PDE is thus not depending on the quality of the DNN. This is different to many machine learning approaches and a big advantage of the ML-DD approach.
2.1 General domain decomposition and model problems
2.2 Machine learning approach
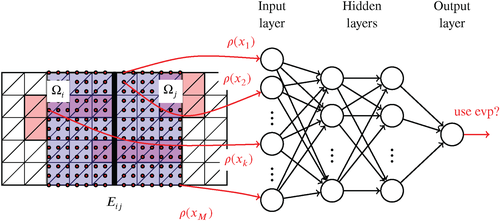
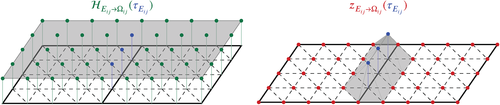
As input data for the neural network, we use samples, that is, point-wise evaluations of the coefficient function or the material distribution within the two subdomains adjacent to an edge Eij; see Figure 4. As output data for the neural network, we save the classification whether the corresponding eigenvalue problem is necessary for a robust algorithm (class 1) or not (class 0); see also Figure 4. In particular, this means that we solve the corresponding eigenvalue problem for each configuration within our training and validation data set and save the related classification based on the number of selected constraints as the ground truth for the DNN; see also [30, section 3.2]. Let us remark that we also suggested a classification with three different classes in 27, 30, 31 for adaptive FETI-DP. In that case, class 1 is again split into eigenvalue problems resulting in exactly a single constraint (class 1a) and eigenvalue problems resulting in more than one constraint (class 1b). This can be useful if, for example, an appropriate approximation for the first adaptive constraint is known which can be computed at a low cost. In 27, 30, 31, we always use a frugal constraint 29 instead of solving an eigenvalue problem for each edge from class 1a. This further reduces the setup cost due to a higher percentage of eigenvalue problems saved compared with the fully adaptive approach. For simplicity, we will not discuss the three-class classification approach in the present review article in detail. As we can also observe from Figure 4, the described classification problem is, in principle, an image recognition problem. However, whereas in image classification the resolution of an image needs to be the same for all image samples, we use an approach that is independent of the finite element distribution. This is achieved by computing a sampling grid which is especially independent of the resolution of the underlying finite element grid. For all the sampling points in the computed sampling grid, we evaluate the coefficient function and use these evaluations as input data for the neural network. The only assumption that we make is that the sampling grid is fine enough to resolve all geometric details of the coefficient function within each subdomain. Let us remark that, for rectangular subdomains, the sampling grid can be chosen such that it completely covers both subdomains adjacent to an edge. For irregular decompositions obtained by, for example, METIS, small areas might not be covered by the sampling grid, but typically these areas are further away from the edge. This usually does not affect the performance of the algorithm. It also motivates the use of smaller sampling grids on areas solely around the edge to save computational cost; see also 31. Let us note that for the classification of an edge Eij we solely use coefficient values within the neighboring subdomains and .
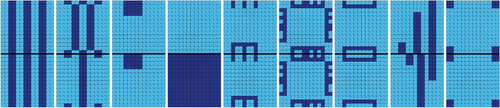
Training data. To arrange a representative training data set consisting of a number of different coefficient distributions on two neighboring subdomains, two different strategies have been tested so far. First, in 30, we have used a set of carefully designed training data, that is, specific coefficient distributions. Later on, in 27, 31, we also denote this set by smart data in contrast to training data sets obtained by a randomized approach. For the smart data, the basic coefficient distributions shown in Figure 5 are used as a basis to create the full set of training data for the numerical experiments in 30. For this specific purpose all of these nine coefficient distributions are mirrored, rotated, and shifted within a subdomain. Second, in 27, we have used randomized coefficient distributions which in principle can be designed without any a priori knowledge. Nevertheless, some structure has to be enforced to obtain satisfactory results. For the first part of this random data training set, we randomly generate the coefficient for each pixel, consisting of two triangular finite elements, independently and only control the ratio of high and low coefficient values. Here, we use 30%, 20%, 10%, and 5% of high coefficient values. For the second part, we also control the distribution of the coefficients to a certain degree by randomly generating either horizontal or vertical stripes of a maximum length of four or eight pixels, respectively; see Figure 6. Additionally, we generate new coefficient distributions by superimposing pairs of horizontal and vertical coefficient distributions.

Sampling on slabs. We now describe how we reduce the number of sampling points used as input data for the neural network. In 30, the computed sampling grid covers both neighboring subdomains of an edge entirely—at least in case of a regular domain decomposition. Let us remark that in case of irregular domain decompositions, our sampling strategy might miss small areas further away from the edge; see, for example, [30, fig. 4]. However, this does not affect the performance of our algorithm. Although the preparation of the training data as well as the training of the neural network can be performed in an offline-phase, we try to generate the training data as efficient and fast as possible. For all sampling points, we need to determine the corresponding finite element as well as to evaluate the coefficient function for the respective finite element. Therefore, there is clearly potential to save resources and compute time in the training as well as in the evaluation phase by reducing the number of sampling points used as input data for the neural network. In general, the coefficient variations close to the edge are the most relevant, that is, the most critical for the condition number bound of FETI-DP. Therefore, to reduce the total number of sampling points in the sampling grid, reducing the density of the grid points with increasing distance to the edge is a natural approach. More drastically, one could exclusively consider sampling points in a neighborhood of the edge, that is, on slabs next to the edge. We consider the latter approach here; see also Figure 4 for an illustration of the sampling points inside slabs.
2.3 Adaptive FETI-DP
The description of standard as well as adaptive FETI-DP is essentially taken from 30. For more details on standard FETI-DP see, for example, 46, 49, 78 and for a detailed description of adaptive FETI-DP see 43, 44, 59.
2.3.1 Standard FETI-DP
Let us first describe the standard FETI-DP domain decomposition method and introduce some relevant notation. We denote by W(i) the local finite element space associated with . The finite element nodes on the interface are either vertex nodes, belonging to the boundary of more than two subdomains, or edge nodes, belonging to the boundary of exactly two subdomains. All finite element nodes inside a subdomain are denoted as interior nodes.
2.3.2 Condition number bound for standard FETI-DP
However, as already mentioned, for arbitrary and complex coefficient distributions, as, for example, shown in Figure 5, Equation (6) does not hold anymore. In recent years, adaptive coarse spaces have been developed to overcome this limitation 4, 7, 9, 14, 17, 20-22, 25, 26, 37, 40-44, 59, 60, 64, 65, 75, 76 and we will especially consider two of them in the following sections.
2.3.3 Adaptive constraints
In the following, we give a very brief description of the algorithm introduced in 59 for the convenience of the reader. First, we introduce the relevant notation and the eigenvalue problem on an edge. Second, in Section 2.3.4, we give an estimate of the condition number for two-dimensional problems where all the vertex variables are primal in the initial coarse space. Let us remark that the adaptive constraints additionally enhance the original set of primal constraints described above. There are several possibilities in the literature to implement such additional constraints, but this is not in the focus of this review article.
As already mentioned, for each edge Eij, a single eigenvalue problem has to be solved. We first restrict the jump matrix B to this edge. Let be the submatrix of with the rows that consist of exactly one 1 and one −1 and are zero otherwise. Let be obtained by taking the same rows of . Let , where S(i) and S(j) are the Schur complements of K(i) and K(j), respectively, with respect to the interface variables. We further define the operator .
2.3.4 Condition number bound of adaptive FETI-DP
2.4 Adaptive GDSW
In this section, we will briefly introduce the standard GDSW preconditioner as well as the AGDSW preconditioner. The presentation follows the original work introducing the AGDSW coarse space for overlapping Schwarz methods 26. As for the adaptive FETI-DP method and in contrast to 26, we will only consider the two-dimensional case here.
2.4.1 The GDSW preconditioner
To define the coarse basis , we consider a partition of the interface of the nonoverlapping domain decomposition into vertices and edges . Then, the discrete characteristic functions of the vertices and edges form a partition of unity on . Now, let the columns of the matrix be the coefficient vectors corresponding to the characteristic functions corresponding to all vertices and edges. Then, the matrix has only entries 0 and 1.
2.4.2 Condition number bound for the GDSW preconditioner
2.4.3 AGDSW coarse basis functions
In order to extend the GDSW preconditioner to be robust for arbitrary coefficient distributions, we construct edge basis functions based on local generalized eigenvalue problems. In particular, the coarse basis functions are constructed as discrete harmonic extensions of the corresponding edge eigenmodes.
We note that the computation of the AGDSW coarse space, based on local eigenvalue problems associated with edges, is similar to the adaptive FETI-DP approach. This is sufficient to apply the same machine learning strategy to predict the location of AGDSW coarse basis functions, despite strong differences in the specific formulation of the eigenvalue problem. Nevertheless, there is one important difference when applying the machine learning approach: as already mentioned, in AGDSW, the first coarse basis function is always necessary, but it can be computed without actually solving the eigenvalue problem. Hence, an eigenvalue problem will only be marked as necessary in our machine learning based AGDSW if more than one coarse basis function corresponds to an eigenvalue lower than the chosen tolerance. This is different to ML-FETI-DP.
2.4.4 Condition number bound for AGDSW
2.5 Numerical results for FETI-DP
In order to be competitive, the ML-FETI-DP algorithm, that is, the combination of adaptive FETI-DP and ML as described above, has to have two important properties or, in other words, there are two main objectives in the design of the ML-FETI-DP and the underlying DNN. First, ML-FETI-DP has to be robust and has to have a similar condition number as adaptive FETI-DP. Second, a lower setup cost than for the fully adaptive approach is desirable, that is, a large part of the local eigenvalue problems has to be omitted. Unfortunately, both objectives are sometimes contradictory and a good trade-off has to be found in the design of the classification network which is used within ML-FETI-DP. As already mentioned, a cheap setup can be reached by a strong reduction in the number of eigenvalue problems but also by reducing the number of sampling points in the sampling grid.
In contrast, to obtain a small condition number and a robust algorithm, it is essential that the DNN delivers no false negative edges, that is, does not falsely classify edges to class 0. To set up the neural network properly and to obtain satisfactory results, many technical details have to be considered. Before we discuss all those details of different training data sets and the reduction of sampling points, we will first concentrate on a single parameter which illustrates the balancing act between robustness and efficiency of the method. The simplest adjustment of the DNN is the ML threshold for the decision boundary between critical edges (class 1) and uncritical edges (class 0), which can be varied between zero and one. Choosing a high value for implies that we set a high priority on a low setup cost as edges are more likely classified as uncritical. In that case, the risk of having false negative edges is very high. In contrast, choosing a small implies that we set a high priority on a robust ML-FETI-DP algorithm and solve some unnecessary eigenvalue problems in the setup phase—one for each false positive edge. We usually prefer the latter choice. Choosing an appropriate ML threshold, the ML-FETI-DP algorithm can be as robust as adaptive FETI-DP with a reduced setup cost; see Table 2 for a first comparison with standard FETI-DP and adaptive FETI-DP. Here, proved to be a good choice while choosing a threshold of deteriorates the robustness by adding false negative edges; see Figure 8. We further provide the receiver operating characteristic (ROC) curve and a precision-recall plot for the optimized neural network model in Figure 9. Here, the threshold is varied between zero and one and the considered thresholds are indicated as circles.
| Alg. | cond | it | evp | fp | fn | acc | |
|---|---|---|---|---|---|---|---|
| Standard | — | — | >300 | 0 | — | — | — |
| Adaptive | — | 11.0 (15.9) | 34.6 (38) | 112.0 (112) | — | — | — |
| ML | 0.5 | 8.6e4 (9.7e4) | 39.5 (52) | 45.0 (57) | 1.6 (2) | 1.9 (3) | 0.97 (0.96) |
| 0.45 | 11.0 (15.9) | 34.6 (38) | 46.9 (59) | 4.4 (6) | 0 (0) | 0.96 (0.94) |
- Note: We show the ML threshold (), the condition number (cond), the number of CG iterations (it), the number of solved eigenvalue problems (evp), the number of false positives (fp), the number of false negatives (fn), and the accuracy in the classification (acc). We define the accuracy (acc) as the number of true positives and true negatives divided by the total number of edges. We show the average values as well as the maximum values (in brackets). Taken from [30, Table 4].Values in bold indicate the best results in terms of robustness.
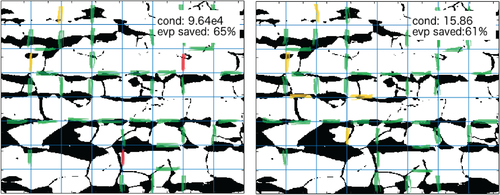

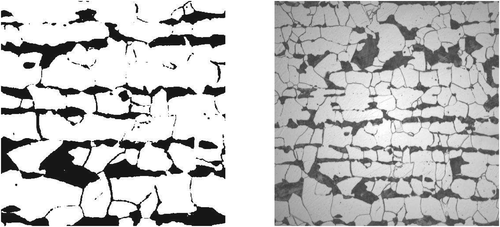
In the remainder of this section we will discuss all the technical details which underlie the excellent performance of ML-FETI-DP shown in Tables 1 and 2. First, we show comparison results for the ML-FETI-DP algorithm using different sets of training data, as described in Section 2.2, for both stationary diffusion and linear elasticity problems. Second, we summarize the obtained numerical results when reducing the sampling effort, that is, computing a reduced number of sampling points for input data of the neural network. As realistic test problems for our algorithm, we use 10 different and randomly chosen subsections of the microsection of a dual-phase steel in Figure 10 (right); see also Figures 10 (left) and 1 for examples of a specific subsection used as the coefficient distribution in our computations. Let us note that these specific coefficient distributions are explicitly not included in the training and validation data. Additionally, we provide the resulting accuracy values and percentages of false negative and false positive edges for the different training and validation data sets to prove that all trained neural networks provide a reliable model. All computations in this section have been performed using the machine learning implementations in TensorFlow 1 and Scikit-learn 66 as well as our Matlab implementation of the adaptive FETI-DP method.
Different training data sets. We now summarize the numerical results from 27, 30, where the performance of the proposed machine learning based adaptive FETI-DP algorithm was tested for different choices of training and validation data sets to train our neural network. As described in detail in 27, we use a set of 4500 smart data configurations (denoted by “S”) and sets of 4500 and 9000 random data configurations (denoted by “R1” and “R2,” respectively) each individually as well as a combination of 4500 smart and 4500 random data configurations, which will be denoted by “SR.” Let us note that we did not observe a significant improvement for a larger number of 18 000 random data configurations.
As already mentioned, we deliberately investigated the performance of the trained DNNs for the different training data sets for different coefficient distributions, which were explicitly not included in the training data. In particular, we applied the respective trained networks to 10 different randomly chosen subsections of a microsection as shown in Figure 10 (right). In all presented computations, we consider in the black part of the microsection and elsewhere in case of a stationary diffusion problem and E1 = 1e6, E2 = 1, and a constant in case of a linear elasticity problem, respectively. For the discretization of this model problem we use a regular decomposition of the domain into 64 square subdomains and a subdomain size of H/h = 64. For the selection of the adaptive coarse constraints we use a tolerance of TOL = 100. For the test data, that is, the microsection subsections, we will only compute the local eigenvalue problems on edges which are classified as critical (class 1) by the neural network. On all uncritical edges (class 0), we do not enforce any constraints. For the respective ML classification, we use a ML threshold of 0.5 and 0.45 for the classification for the decision boundary between critical and uncritical edges. Let us note that a lower threshold decreases the false negative rate of the predictions and thus increases the robustness of our algorithm; cf. also the explanations on the balancing act of our algorithm at the beginning of this section. For the 10 microsections and the stationary diffusion problem (see Table 3) all four different training data sets result in a robust algorithm when using an ML threshold . For all these approaches, we obtain no false negative edges, which are critical for the convergence of the algorithm. However, the use of 4500 and 9000 random data (see R1 and R2) results in a higher number of false positive edges compared to the sole use of 4500 smart data, resulting in a larger number of computed eigenvalue problems. For linear elasticity and the 10 microsections, see Table 4, the results are fairly comparable. Again, the use of the smart data training set provides the best trade-off between robustness and computation cost since we obtain no false negative edges and only 4.8 false positive edges on average. Additionally, also using 9000 random data (R2) as well as the combined training data set (SR) provides no false negative edges when choosing the ML threshold . However, for both cases we have a slightly increased number of false positive edges compared to S which results in a slightly higher computational effort. On the other hand, the advantage of the randomized training data lies in the random generation of the coefficient distributions which is possible without any specific problem-related knowledge. Let us also remark that setting up a smart data set in three dimensions is very complicated and we thus prefer a randomly generated set in this case. Given the relatively low share of additional false positive edges compared to the number of saved eigenvalue problems, we can conclude that we can achieve comparable results using the randomized training data when generating a sufficient amount of coefficient configurations.
| Alg. | T-Data | cond | it | evp | fp | fn | acc | |
|---|---|---|---|---|---|---|---|---|
| Standard | — | — | — | >300 | 0 | — | — | — |
| Adaptive | — | — | 11.0 (15.9) | 34.6 (38) | 112.0 (112) | — | — | — |
| ML | S | 0.5 | 8.6e4 (9.7e4) | 39.5 (52) | 45.0 (57) | 1.6 (2) | 1.9 (3) | 0.97 (0.96) |
| S | 0.45 | 11.0 (15.9) | 34.6 (38) | 46.9 (59) | 4.4 (6) | 0 (0) | 0.96 (0.94) | |
| R1 | 0.5 | 1.3e5 (1.6e5) | 49.8 (52) | 43.2 (44) | 7.4 (8) | 3.8 (4) | 0.88 (0.87) | |
| R1 | 0.45 | 11.0 (15.9) | 34.6 (38) | 53.8 (58) | 14.6 (16) | 0 (0) | 0.86 (0.84) | |
| R2 | 0.5 | 1.5e5 (1.6e5) | 50.2 (51) | 40.4 (41) | 5.6 (6) | 3.4 (4) | 0.91 (0.89) | |
| R2 | 0.45 | 11.0 (15.9) | 34.6 (38) | 50.4 (52) | 11.2 (12) | 0 (0) | 0.90 (0.87) | |
| SR | 0.5 | 9.6e4 (9.8e4) | 45.8 (48) | 38.2 (39) | 1.8 (2) | 1.6 (2) | 0.96 (0.95) | |
| SR | 0.45 | 11.0 (15.9) | 34.6 (38) | 43.4 (44) | 4.8 (5) | 0 (0) | 0.96 (0.94) |
| Alg. | T-Data | cond | it | evp | fp | fn | acc | |
|---|---|---|---|---|---|---|---|---|
| Standard | — | — | — | >300 | 0 | — | — | — |
| Adaptive | — | — | 79.1 (92.8) | 87.4 (91) | 112.0 (112) | — | — | — |
| ML | S | 0.5 | 9.3e4 (1.3e5) | 92.2 (95) | 44.0 (56) | 2.2 (3) | 2.4 (3) | 0.96 (0.95) |
| S | 0.45 | 79.1 (92.8) | 87.4 (91) | 48.2 (61) | 4.8 (7) | 0 (0) | 0.95 (0.93) | |
| R1 | 0.5 | 1.4e5 (1.6e5) | 96.6 (98) | 47.2 (48) | 7.6 (8) | 4.0 (5) | 0.90 (0.88) | |
| R1 | 0.45 | 1.7e3 (2.1e4) | 90.4 (91) | 53.6 (57) | 13.4 (16) | 0.8 (1) | 0.87 (0.86) | |
| R2 | 0.5 | 1.1e5 (1.3e5) | 96.2 (97) | 46.8 (48) | 7.0 (8) | 3.6 (5) | 0.91 (0.89) | |
| R2 | 0.45 | 79.1 (92.8) | 87.4 (91) | 52.8 (57) | 11.6 (12) | 0 (0) | 0.90 (0.87) | |
| SR | 0.5 | 9.7e4 (9.9e4) | 94.8 (97) | 45.8 (47) | 5.8 (6) | 3.0 (4) | 0.92 (0.93) | |
| SR | 0.45 | 79.1 (92.8) | 87.4 (91) | 50.6 (61) | 8.8 (10) | 0 (0) | 0.92 (0.90) |
- Note: We denote by 'S' the training set of 4500 smart data, by “R1” and “R2” a set of 4500 and 9000 random data, respectively, and by 'SR' the combination of 4500 smart and 4500 random data. See Table 2 for the column labeling. Taken from [31, Table 1].Values in bold indicate the best results in terms of robustness.
Reducing the computational effort. In addition to the performance of different training data sets, we have also investigated the effect of using a reduced number of sampling points as input data for the neural network by sampling in slabs of different width; see also Figure 4. As the smart data as well as an increased number of randomized training data showed comparable results in the previous experiments, we solely have used the smart data for this investigation. Moreover, we focus on the ML threshold which led to the most robust results for the full sampling approach.
We show comparison results for the original approach with full sampling as introduced in 30 and for further, different sampling approaches on slabs. In particular, for subdomains of width H, we consider the cases of sampling in one half and one quarter, that is, H/2 and H/4, as well as the extreme case when sampling only inside minimal slabs of the width of one finite element, that is, h. As already mentioned, our machine learning problem is, in principle, an image recognition task. Thus, the latter sampling approaches correspond to the idea of using only a fraction of pixels of the original image as input data for the neural network. We have focused on linear elasticity problems for the remainder of this paragraph.
As we can observe from Table 5, using again the microsection problem in Figure 10 (left) as a test problem, both sampling in slabs of width H/2 and H/4 results in a robust algorithm in terms of the condition number and the iteration count when using the ML threshold . For both approaches, we obtain no false negative edges which are critical for the convergence of the algorithm. However, using fewer sampling points results in a higher absolute number of false positives edges and therefore in a larger number of computed eigenvalue problems with a higher computational effort. When applying the extreme case of sampling only in slabs of width h, we do not obtain a robust algorithm for the microsection problem since the convergence behavior clearly deteriorates. Hence, it is questionable if the latter sampling approach does provide a reasonable machine learning model. The weak performance of the latter sampling approach can also be observed for the training data; see the following discussion on the training and validation data. With respect to our model problems we can summarize that reducing the size of the sampling grid in order to reduce the effort in the training and evaluation of the neural network still leads to a robust algorithm. However, we can also observe that the slab width for the sampling cannot be chosen too small and a sufficient number of finite elements close to the edge have to be covered by the sampling.
| Model problem | Algorithm | cond | it | evp | fp | fn | acc | |
|---|---|---|---|---|---|---|---|---|
| Standard | — | — | >300 | 0 | — | — | — | |
| Microsection problem | Adaptive | — | 84.72 | 89 | 112 | — | — | — |
| ML, full sampling | 0.5 | 9.46e4 | 91 | 41 | 2 | 2 | 0.96 | |
| ML, full sampling | 0.45 | 84.72 | 89 | 46 | 5 | 0 | 0.95 | |
| ML, sampling in H/2 | 0.45 | 84.72 | 89 | 47 | 6 | 0 | 0.95 | |
| ML, sampling in H/4 | 0.45 | 85.31 | 90 | 48 | 7 | 0 | 0.94 | |
| ML, sampling in h | 0.45 | 10.9e5 | 137 | 50 | 19 | 10 | 0.74 |
Finally, we present results for the whole set of training data using cross-validation and a fixed ratio of 20% as validation data to test the generalization properties of our neural networks. Please note that due to different heterogeneity of the various training data, the accuracies in Table 6 are not directly comparable with each other. However, the results in Table 6 serve as a sanity check to prove that the specific trained model is able to generate appropriate predictions. Let us further note that we always have to generate a separate training data set for stationary diffusion and linear elasticity problems, respectively, since the number of necessary adaptive constraints can differ for the two aforementioned model problems. However, as the performance for the different sets of training data is comparable for both types of model problems, we exclusively show the results for the training data for linear elasticity problems in Table 6. As we can observe from the results in Table 6 training the neural network with the set of smart data as well as with a combination of the smart and randomized coefficient distributions leads to the highest accuracy values, that is, the highest numbers of true positive and true negative edges in relation to the total number of edges. However, also training the neural network with solely the randomly generated coefficient functions leads to an appropriate model while we can observe the tendency that a higher number of training data is needed to obtain comparable accuracy values. Moreover, when using the smart training data, both sampling with a width of H/2 and H/4 leads to accuracy values in the classification that are only slightly lower than for the full sampling approach. In particular, we obtain slightly increased false positive values, corresponding to an increased computational effort in terms of the solution of eigenvalue problems. For the extreme case of sampling only in slabs of minimal width h, thus, using the minimal possible width in terms of finite elements, the accuracy value drops from 88.4% to 71.7% for the two-class model for the threshold . Thus, also for the training data, it is questionable whether this extreme case does still provide a reliable machine learning model. This is also supported by the weak performance of the respective trained neural network for the test problem in form of the microsection; see also Table 5.
| two-class | three-class | |||||||
|---|---|---|---|---|---|---|---|---|
| training configuration | fp | fn | acc | fp | fn | acc | ||
| S, full sampling | 0.45 | 8.9% | 2.7% | 88.4% | 0.4 | 5.2% | 2.0% | 92.8% |
| 0.5 | 5.5% | 5.6% | 88.9% | 0.5 | 3.3% | 3.3% | 93.4% | |
| S, sampling in H/2 | 0.45 | 8.0% | 2.6% | 89.4% | 0.4 | 9.6% | 4.3% | 86.1% |
| 0.5 | 5.9% | 4.0% | 90.1% | 0.5 | 7.4% | 5.0% | 87.6% | |
| S, sampling in H/4 | 0.45 | 8.2% | 2.7% | 89.1% | 0.4 | 10.4% | 3.9% | 85.7% |
| 0.5 | 5.7% | 4.5% | 89.8% | 0.5 | 8.1% | 4.8% | 87.1% | |
| S, sampling in h | 0.45 | 20.8% | 7.5% | 71.7% | 0.4 | 22.4% | 9.2% | 68.4% |
| 0.5 | 15.4% | 12.9% | 72.3% | 0.5 | 15.0% | 15.3% | 69.7% | |
| S, full sampling | 0.45 | 8.9% | 2.7% | 88.4% | 0.4 | 5.2% | 2.0% | 92.8% |
| 0.5 | 5.5% | 5.6% | 88.9% | 0.5 | 3.3% | 3.3% | 93.4% | |
| R1, full sampling | 0.45 | 12.9% | 6.4% | 80.7% | 0.4 | 10.7% | 8.0% | 81.3% |
| 0.5 | 8.6% | 9.1% | 82.3% | 0.5 | 8.9% | 9.3% | 81.8% | |
| R2, full sampling | 0.45 | 9.9% | 5.5% | 84.6% | 0.4 | 9.8% | 4.8% | 85.4% |
| 0.5 | 7.0% | 7.2% | 85.8% | 0.5 | 7.2% | 6.4% | 86.4% | |
| SR, full sampling | 0.45 | 8.7% | 3.1% | 88.2% | 0.4 | 6.7% | 2.9% | 90.4% |
| 0.5 | 5.3% | 5.4% | 89.3% | 0.5 | 4.5% | 4.4% | 91.1% | |
- Note: See Table 2 for the column labeling.
2.6 Numerical results for GDSW
In this section, for the first time, we will apply our machine learning framework to an overlapping adaptive DDM, the AGDSW method; see also Section 2.4. The AGDSW algorithm is also based on the solution of localized eigenvalue problems on edges in 2D and on faces and edges in 3D. Thus, we can extend our machine learning techniques to the classification of critical edges for the GDSW coarse space. In particular, the presented results have not yet been published in previous works and are an extension of the already existing publications 27, 30, 31 for the FETI-DP algorithm. As the classification of critical edges can be different for AGDSW than for adaptive FETI-DP, we have generated a separate training data set for the GDSW approach. As for FETI-DP, we generated 4500 randomized coefficient distributions using the techniques described in Figure 6 to build the training and validation data set. We denote this training data set by R1'. For each pair of neighboring subdomains sharing an edge we solved the respective eigenvalue problem and saved the classification whether at least one adaptive constraint is necessary for the respective edge or not for the robustness of the algorithm. In particular, we used the overlap and the tolerance for the generation of the training data. Let us briefly comment on the classification of edges for the GDSW approach. As already mentioned in Section 2.4.3, in AGDSW, the first coarse basis function is always necessary for robustness. It corresponds to the constant function on the edge and can thus be computed without actually solving the eigenvalue problem. Therefore, for ML-AGDSW all critical edges where more than the single constant constraint is necessary are classified as class 1. Let us note that this is different to class 1 for ML-FETI-DP.
To prove that the described machine learning framework can successfully be applied to other domain decomposition approaches than the FETI-DP method, we show comparison results for standard GDSW, using exclusively one constant constraint per edge, the AGDSW, and our new ML-AGDSW algorithm. Since these are the first results obtained for GDSW, here, we focus on stationary diffusion problems and regular domain decompositions. As a test problem for our ML-AGDSW method we use again subsections of the microsection problem in Figure 10. However, we explicitly use different decompositions of the domain , that is, different discretizations as for the FETI-DP method in Section 2.5. For all presented computations we set in the black parts of the microsections and elsewhere.
As a first test problem, we use a decomposition of the microsection in Figure 10 (left) into 4 × 4 subdomains and 6272 finite elements per subdomain. The obtained results for the different GDSW coarse spaces are presented in Table 7. As we can observe from Table 7, using the standard GDSW coarse space clearly fails to provide a robust algorithm since 297 iterations are needed until convergence and the condition number bounds has the magnitude of the coefficient contrast. Thus, using exclusively constant constraints for each edge is not sufficient for this model problem and additional coarse constraints are necessary. Using our ML-AGDSW approach and the ML threshold we are able to achieve nearly the same performance as the AGDSW. Even though we obtain a single false negative edge the respective condition number estimate is clearly independent of the coefficient contrast and the iteration number is sufficient. As a second test problem we use a domain decomposition with 8 × 8 subdomains and again 6272 finite elements per subdomain for the microsection problem in Figure 10 (left); see Table 8. Here, using the ML threshold we obtain no false negative edges and four false positive edges. As a result we observe almost the same convergence properties and condition number estimate as for the AGDSW while we only have to solve 27 instead of 112 eigenvalue problems on edges. Let us note that we have used the same ML thresholds for the decision boundary between the two classes of edges as for the ML-FETI-DP approach. As the presented results are the first obtained results for the ML-AGDSW approach, we have not yet fully optimized the decision threshold for the ML-AGDSW approach. This will be done in future research on the ML-AGDSW method. Finally, we provide the results, that is, the accuracy values and the percentages of false positive and false negative edges for the training and validation data in Table 9. These results serve as a sanity check that our trained neural network provides a reliable model. Let us remark that we have slightly modified the network architecture compared to the networks used for ML-FETI-DP to achieve comparable results on the training and validation data.
| Model problem | Algorithm | cond | it | evp | fp | fn | acc | |
|---|---|---|---|---|---|---|---|---|
| Standard GDSW | — | 1.61e6 | 297 | 0 | — | — | — | |
| Microsection problem | Adaptive GDSW | — | 182.89 | 84 | 24 | — | — | — |
| ML-AGDSW | 0.5 | 5.47e4 | 91 | 14 | 2 | 2 | 0.96 | |
| ML-AGDSW | 0.45 | 201.42 | 86 | 16 | 3 | 1 | 0.83 |
- Note: See Table 2 for the column labeling.
| Model problem | Algorithm | cond | it | evp | fp | fn | acc | |
|---|---|---|---|---|---|---|---|---|
| Standard GDSW | - | 3.66e6 | 500 | 0 | - | - | - | |
| Microsection problem | Adaptive GDSW | — | 162.60 | 95 | 112 | — | — | — |
| ML-AGDSW | 0.5 | 9.64e4 | 98 | 25 | 2 | 2 | 0.95 | |
| ML-AGDSW | 0.45 | 163.21 | 95 | 27 | 4 | 0 | 0.95 |
- Note: See Table 2 for the column labeling.
| Training configuration | Threshold | fp | fn | acc |
|---|---|---|---|---|
| R1', full sampling | 0.45 | 11.3% | 3.3% | 85.4% |
| 0.5 | 6.7% | 7.1% | 86.2% |
- Note: See Table 2 for the column labeling.
2.7 Ongoing and future research
The techniques described above can also be adapted such that they can be applied in three dimensions; see 28. In 28, we describe the central difficulties and the necessary extensions and show numerical results for ML-FETI-DP in three dimensions. Let us briefly describe the main differences from the two-dimensional case. First, the essential eigenvalue problems are no longer related to edges, but to faces between two neighboring subdomains. Second, we only considered randomly generated training data, since generating a smart, that is, manually selected set of coefficient distributions containing all the necessary phenomena, is a complicated task in three dimensions. Third, building an appropriate grid of sampling points with a consistent ordering of the sampling points is more difficult in three dimensions when considering irregular domain decompositions obtained by, for example, the graph partitioning software METIS. To obtain such an ordering, we first project each face onto a two-dimensional plane, optimize the triangulation of the projection, define a consistently ordered sampling grid on the optimized projection, and finally project this sampling grid back to three dimensions. Using these modifications, the ML-FETI-DP approach can successfully be used in three dimensions as well; see 28 for details.
In addition to the three-dimensional ML-FETI-DP approach, there are various possibilities for future research considering the combination of ML and adaptive DDMs. First, it is our goal to include ML-FETI-DP and ML-AGDSW into our parallel software packages based on PETSc and, respectively, Trilinos. This is important to prove that both approaches can actually save computation time compared to the adaptive methods in a parallel computation. Second, a three-dimensional version of ML-AGDSW is planned 32. Third, we plan to investigate the opportunity to predict the adaptive coarse constraints or coarse basis functions directly using a machine learning approach, that is, a method without the need for solving any eigenvalue problems in the online stage.
3 Physics-informed deep neural networks in domain decomposition methods
A completely different approach to combine ML with DDMs was suggested in 52, 54. In 54, Li et al. replaced the subdomain solvers of a classical Schwarz domain decomposition approach by PINNs. Here, PINNs replace the discretization of the local subdomain problems and the training of PINNs replaces the solution process. The resulting new deep-learning-based DDM is named DeepDDM and applied to two-dimensional elliptic PDEs as a proof of concept.
In 52, Li et al. presented a very similar approach. Here, the authors use the Deep Ritz method 16 to replace the subdomain solvers of a classical overlapping Schwarz approach. This means that, in contrast to 54, the trained neural networks (NNs) are based on the variational formulation of the underlying PDEs. In particular, the loss functions used in the optimization process are different from the ones in 54 and the approach corresponds to a discretization of the variational formulation of the PDEs. The corresponding variational deep learning approach is named D3M. In this review article, we will first briefly introduce the concept of PINNs as well as the Deep Ritz method and then the use of physics-constrained neural networks as subdomain solvers in DDMs as suggested in 52, 54.
3.1 Physics-informed neural networks
3.2 The Deep Ritz method
3.3 Deep domain decomposition methods—using PINNs and Deep Ritz as subdomain solvers
Having defined a solver for the boundary value problem in Equation (12) by training the neural network with certain collocation points and the loss function given in Equation (13) or Equation (19), respectively, it can also be used to solve the subdomain problems in DDMs. This approach has been applied to a parallel overlapping Schwarz method using PINNs 54 and the Deep Ritz method 52. Both resulting algorithms are denoted as Deep Domain Decomposition method and abbreviated as DeepDDM in 53 and D3M in 51. To better distinguish them, we will make use of the acronyms DeepDDM and D3M in the following. Although a neural network in this subsection can be either defined using PINNs or the Deep Ritz method, to avoid a proliferation of notation, we do not distinguish here between them in the notation.
Algorithm 1. Brief sketch of the DeepDDM and D3M algorithms; see [54, Algorithm 2] and [52, Algorithms 1 and 2], respectively, for details
Let us finally summarize some important findings and remarks on the training of the introduced physics-constrained NNs. First, when using a stochastic gradient descent method and dividing the total set of collocation points into mini-batches, it is important for the performance that all boundary and interface collocation points or at least a sufficient share of them are redundantly part of each mini-batch. Only the interior collocation points can be divided in mini-batches as usual in the training of DNNs. This is based on the observation that for solving a general PDE, the boundary information is quite essential. For a further analysis of the respective numbers of collocations points, we refer to 52, 54. Second, both DeepDDM and D3M inherit the parallelization capacities from the underlying DDM since the physics-constrained NNs local to the subdomains can be trained in parallel. The only synchronization point is the exchange of information on the overlap.
3.4 Ongoing and future research
There are several opportunities to extend the aforementioned deep domain decomposition methods; some of these approaches are already subject to ongoing research.
Within each iteration in Algorithm 1, the local PINNs on the subdomains are trained from scratch with new boundary data in the collocation points on the interface. However, as this overlapping Schwarz method is a fixed point iteration, it may be a reasonable assumption that the local solutions in two successive iterations are rather similar. Therefore, in the sense of transfer learning, the trained neural network from the previous iteration can be used as a good initial guess for the training of the current neural network on the same subdomain.
In order to improve the numerical scalability and accuracy of the one-level algorithm, a coarse correction can be added, resulting in a two-level deep domain decomposition methods. Recently, this approach has been presented by Hyea Hyun Kim at the 26th International Domain Decomposition Conference 38. In particular, an additional PINN on the whole domain has been added to enable fast transport of global information in the Schwarz iteration. In order to keep the load between the local and the global models in balance, the complexity of the coarse PINN has to be chosen accordingly, for example, the same as for the local PINNs.
Moreover, instead of an overlapping Schwarz DDM, nonoverlapping DDMs can be employed, for instance, based on Dirichlet-Neumann, Neumann-Neumann, or Dirichlet-Dirichlet (FETI) methods. In addition to Dirichlet data, all these approaches require the transfer of Neumann boundary data on the interface. Therefore, the normal derivatives of the local neural networks have to be evaluated and trained, respectively, on the interface. The normal derivatives can be easily computed for neural networks using the backpropagation algorithm. A related approach for solving a boundary value problem using a partitioned deep learning algorithm based on direct substructuring has also recently been presented by Hailong Sheng at the 26th International Domain Decomposition Conference 72. In particular, the problem is partitioned into local Dirichlet problems and a Schur complement system on the interface. This approach could also be extended to a multilevel direct substructuring or nested dissection approach, respectively; cf. 73.
4 FURTHER WORK ON COMBINING MACHINE LEARNING AND DDMs
To provide a broader overview, we collect and briefly describe some more approaches combining the idea of domain decomposition and machine learning. We divide the approaches in three different classes. In general, many methods combining domain decomposition ideas and machine learning are based on neural networks with loss functions enhanced by the physical laws that govern the data, as modeled by PDEs. Similar to the two approaches which we described in detail in Section 3 the loss function which is minimized in the training of physics-constrained NNs can be based on the strong or the variational form of the underlying PDEs. Therefore, we subdivide the approaches based on NNs used for the discretization with respect to the constructed type of loss function. As a third class we consider related work which is based on different machine learning techniques other than physics-informed or theory-guided neural networks. Let us note that we do not claim nor attempt to provide an exhaustive list of all related work combining domain decomposition ideas and machine learning since this is beyond the scope of this paper. Instead, we aim to present a number of different related approaches to provide a broad overview of the ongoing work within this field of research.
Machine learning based discretization of the strong form of the PDEs. In 15, the authors introduce the concept of distributed PINNs (DPINNs) for the efficient solution of PDEs. In contrast to standard PINNs, DPINNs benefit from an improved distribution of the data and can provide more accurate solutions with the same or less effort. The approach is motivated by the finite volume method and thus the authors decompose the computational domain into nonoverlapping cells, which can also be interpreted as the subdomains in a DDM. Then, for each cell a separate, local PINN with a loss function based on collocation points from the interior of the cell is installed; see Section 3.1 for a description of PINNs. Additionally, again motivated by the flux conditions of the finite volume method, a loss term for the interface conditions is introduced which is associated with collocation points located on the boundary of the cells. Finally, the DPINN approach is based on training all local PINNs together by minimizing the sum of all local losses plus the interface loss. In difference to the approaches described in Section 3, some interface information has to be communicated in each step of the optimization approach used in the training of the network.
In 77, the authors interpret PINNs (see Section 3.1) as neural solvers in the sense that trained PINNs predict time-dependent solutions of a system of PDEs at any point in space and time. The authors especially focus on the reduction of computational effort within the training process of PINNs and propose to learn a domain decomposition which steers the number of neurons per layer within a PINN. The main idea is to incorporate conditional computing into the PINNs framework in order to learn an arbitrary decomposition of the computational domain, that is, the neural network, which is adaptively tuned during the training process. Here, conditional computing denotes an approach that activates only certain neurons or units of a neural network depending on the network input; see 6, 71 for more details. Based on this concept the authors introduce GatedPINNs which rely on a number of experts which decompose the neural network and are each modeled by a simple MLP; see [77, section 3.2] for further details. The authors show comparative results for the GatedPINN and standard PINN approach and are able to reduce the training time significantly.
In 61, the authors present a different type of decomposition of PINNs used for the solution of time-dependent systems of PDEs in a given spatio-temporal domain. Here, the main idea is to split a long-time computational domain into many independent temporal slices and train a separate PINN for each obtained time interval. The obtained NN is denoted by parareal physics-informed neural network (PINN) as it is inspired by the original parareal algorithm 56. When implementing PPINNs, two different propagators have to be employed: a serial CG solver representing the coarse correction of the solution and a number of fine PINNs for the different time intervals. In each iteration, all fine PINNs can be trained completely in parallel and only after the fine solutions at all time-dependent collocation points have been obtained, the discrepancy between the coarse and fine solution can be computed. Then, the serial CG PINN is run on the coarse grid, that is, on the boundary between the different time intervals, to update the solution at all collocation points between two neighboring subdomains.
A domain decomposition-based approach for the discretization of arterial trees using PINNs was proposed in 39. In order to predict arterial blood pressure from non-invasive 4D flow MRI, the authors decompose the arterial tree into artery segments, which can be regarded as the subdomains of a nonoverlapping domain decomposition, and which are connected at the bifurcations of the tree. Each artery segment is modeled by a one-dimensional fluid-structure interaction system of PDEs, which is then discretized by a PINN. Now, all these PINNs discretizing the whole arterial tree are trained monolithically by minimizing a single loss function. In order to ensure conservation of momentum and mass of the global solution, corresponding residual terms coupling the local PINNs at the interfaces are added to the loss function.
Machine learning based discretization of the variational formulation of the PDEs. In 36, the authors introduce hp-variational PINNs (hp-VPINNs) which are based on the variational formulation of the residuals of the considered PDEs, similar to the variational NN used in 52. In particular, they use piecewise polynomial test functions within the variational formulation. This corresponds to a domain decomposition of the underlying neural network since each test function vj is always a polynomial of a chosen order over the subdomain j and zero otherwise. Let us note that with respect to the implementation of this approach, the authors employ a single DNN to approximate the solution over the whole computational domain despite virtually decomposing the domain into several subdomains. Different numerical examples of function approximation for continuous and discontinuous functions as well as for solving the Poisson equation are presented.
In 81, the authors develop theory-guided neural networks (TgNN) which are also based on the weak, that is, variational formulation of a given system of PDEs (TgNN-wf). The idea of TgNN-wf is to integrate the weak formulation of the PDE in the loss function as well as data constraints and initial or boundary conditions; see also Section 3.2. In contrast to the use of automatic differentiation when integrating the strong form of the PDE into the loss function (see also Section 3.1), the authors transfer high-order derivatives in the PDE to the test functions by performing integration-by-parts. This has the potential to increase the accuracy of the network predictions since the test functions are usually relatively simple analytical functions such as polynomials of a given order. In particular, similar to 36, the authors use locally defined test functions to perform a domain decomposition of the computational domain to accelerate the training process. As a further novelty the authors formulate the original loss minimization problem into a Lagrangian duality problem in order to optimize the weights of the different components of the loss function within the training process. The authors provide comparative results for the strong form TgNN and TgNN-wf for an unsteady-state 2D single-phase flow problem and a 1D two-phase flow problem in terms of accuracy, training time, and robustness with respect to noise in the training data.
Other approaches. An early work on the combination of DD and machine learning is presented in 57 and has many similarities with the approaches described in Section 3. The authors combine different types of radial basis function networks (RBFNs) with the philosophy of domain decomposition to approximate nonlinear functions or to solve Poisson's equation on a rectangular domain. Each nonoverlapping subdomain is discretized by a shallow RBFN and then an algorithm similar to Algorithm 1 is suggested. In each iteration of the proposed algorithm all local subproblems are solved using the RBFNs and then the interface condition is estimated and updated using boundary integral equations. Hence, the method distinguishes from the approaches in Section 3 by the choice of the local networks, the nonoverlapping domain decomposition, and the treatment of the interface conditions.
Finally, in 8, a method is suggested to optimize the width of the overlap in Schwarz methods using a machine learning approach. The authors consider two-dimensional diffusion problems with jumps in the coefficient function. The input for the learning approach consists of certain features collected for each subdomain individually—together with its neighbors. The features are, for example, the maximal or minimal coefficient within certain sets of rows and columns of degrees of freedom in the surrounding of the boundary of the overlapping subdomain. Hence, for the training set, several coefficient distributions are combined with domain decompositions choosing different overlaps. For all these combinations the features are collected and as an output for the machine learning based regression the number of floating point operations is chosen which is needed by the Schwarz method to converge. In the online stage of the method suggested in 8, all features are extracted for different overlaps and thus different domain decompositions of the same problem. Then, evaluating the regression model, the number of expected floating point operations necessary until solution can be minimized.
Acknowledgments
Open Access funding enabled and organized by Projekt DEAL.





