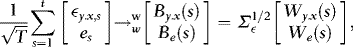Testing the Efficient Market Hypothesis in Conditionally Heteroskedastic Futures Markets
Abstract
Most empirical evidence suggests that the efficient market hypothesis, stating that spot and futures prices should cointegrate with a unit slope on futures prices, does not hold. These results have recently motivated researchers to start looking for more “informative” tests, and the current paper takes a step in this direction. However, unlike existing tests, the test proposed here exploits the information contained in the heteroskedasticity of the data, which is expected to lead to more accurate inference, a result that is confirmed by our findings. © 2013 Wiley Periodicals, Inc. Jrl Fut Mark
1. INTRODUCTION
The issue of whether commodity markets are efficient has produced a voluminous literature. Market efficiency is based on the principle that asset prices reflect all publicly available information. Under the joint assumptions of risk neutrality and rationality, the expected returns to speculative activity in an efficient market should be zero. Thus, in a futures (or forward) market, the current price of an asset for delivery at a specified date should be an unbiased predictor of the future spot rate.
Despite the wide acceptance of the efficient market hypothesis (EMH) in theory, the postulated long-run one-for-one relationship between spot and futures prices has proven very difficult to verify empirically, in spite of the recent advances in econometric methodology for testing long-run relationships using cointegration techniques. In fact, most studies tend to reject the EMH as a long-run cointegrating relationship (see, e.g., Coleman, 1990; Copeland, 1991; Diebold, Gardeazabal, & Yilmaz, 1994; Hakkio & Rush, 1989; Lajaunie & Naka, 1992; Lajaunie, McManis, & Naka, 1996; MacDonald & Talyor, 1989; Rapp & Sharma, 1999). Other studies, including Chowdhury (1991), Lai and Lai (1991), Schwarz and Szakmary (1994), and Moosa and Al-Loughani (1994), do not reject cointegration, but find the estimated slope on futures prices significantly different from one.
Most attempts to reconcile these results have taken the empirical evidence more or less at face value, and have then modified the theoretical arguments. Some of the explanations offered include, among other factors, the inefficiency of agents in conveying new information to the market (Kaminsky & Kumar, 1990), the inability of futures prices to reflect all publicly available information (Beck, 1994), the existence of a risk premium (He & Hong, 2011; Kellard, Newbold, Rayner, & Ennew, 1999), the definition of market efficiency as a lack of arbitrage opportunities (Crowder & Hamed, 1993; Dwyer & Wallace, 1992), and the existence of arbitrage (Brenner & Kroner, 1995).
Peroni and McNown (1998) take an alternative route, and focus on the cointegration-based methodology used for testing the EMH. They argue that the existing empirical evidence concerning the EMH is lacking in one important respect, and that this may well at least partially explain the weak results previously obtained. It therefore seems reasonable to investigate this issue before embarking on further revisions of economic theory.
The econometric workhorse of the industry is an ordinary least squares (OLS) regression of the current spot rate, yt, onto a constant and one lag of the corresponding future rate, xt–1. The main finding of such regressions is that the t-statistic of the hypothesis of a unit slope coefficient is typically greater than 2. Most earlier studies, which tended to rely on normal critical values, were therefore able to reject the hypothesized unit slope coefficient. However, as Peroni and McNown (1998) argue, the presence of a risk premium may well introduce a correlation between the first-differenced regressor and the error term, leading to a violation of one of the basic OLS assumptions of (weakly) exogenous regressors. The standard distribution theory for cointegrated processes can therefore be quite misleading, suggesting that some of the rejections of the unit slope hypothesis might actually be due to size distortions. The authors therefore refer to the OLS-based tests as “non-informative,” whereas tests that are robust to endogeneity are referred to as “informative.”
The question is how “informative” these tests really are? In particular, as is well known, robustness is not for free, but comes at a cost in terms of efficiency/precision. Thus, although correctly sized, robust tests are expected to suffer from low power when compared to the corresponding (non-robust) OLS-based test. This means that a non-rejection of the unit slope null need not be interpreted as providing evidence in favor of the EMH, but could just as well be due to a lack of power. This leaves us with an intricate dilemma: we would like to be able to exploit the power that becomes available when using conventional OLS; however, when we do this we run the risk of obtaining spurious results due to endogeneity.
The current paper can be seen as an attempt to resolve the above dilemma. The idea is to use a robust test that is truly “informative” in the sense that it is based on a relatively large information set. Specifically, where conventional robust approaches only exploit the sample information regarding the conditional mean, the approach considered here also exploits the sample information regarding the conditional variance, a well-documented feature of spot and futures prices data (see, e.g., Franses, Kofman, & Moser, 1994; Fujihara & Mongoue, 1997). Although the asymptotic distribution of OLS is invariant with respect to heteroskedasticity of this kind, the estimator does not make use of the information contained therein. Recognizing this deficiency, Seo (2007) proposes full maximum likelihood (ML) estimation of both the conditional mean and variance equations. As this estimator accounts for the information contained in the conditional heteroskedasticity, it is relatively efficient, suggesting that the resulting ML-based t-test should be relatively more powerful, a result that is verified by Monte Carlo simulations.
Full ML estimation has at least four major drawbacks, though. First, in small samples the ML estimator is known to exhibit Cauchy-like tails and therefore infinite moments, which can generate extreme outliers with misleading inference as a result (Phillips, 1994). Second, because of the poor behavior in small samples, successful maximization of the log-likelihood can be quite difficult, and in some cases borderline impossible (see, e.g., Brüggemann & Lütkepohl, 2005; Herwartz & Lütkepohl, 2011). Third, although the ML estimator has been around for quite some time now, it has not yet been implemented in any econometric software package, making it quite unattractive from an applied point of view.
Therefore, as an alternative to using ML, the current paper proposes weighted least squares (WLS). This estimator is not only computationally very convenient, requiring nothing but simple OLS operations, but is also relatively robust in the sense that it is not subject to any numerical optimization difficulties.
In the theoretical part of the paper we show, both analytically and using Monte Carlo simulations, that the information contained in the heteroskedasticity is useful when estimating and testing cointegrated relationships, and that the power of the new WLS-based t-test for a unit slope can be increased, well above that achievable by the existing tests that do not make use of this information. In the empirical part we consider a sample comprised of daily data for the period 2005–2011 for four commodities, crude oil, gold, silver, and platinum. Crude oil is the most commonly traded commodity and together with gold, silver, and platinum constitute around 76% of total commodities trading (see Narayan, Huson, & Narayan, 2012). The results suggest that the errors driving the observed spot and futures price data are indeed heteroskedastic, and also that futures prices are endogenous. This leads us to the conclusion that the new WLS estimator should be well suited for the sample at hand. The results further suggest that although spot and futures prices for all four commodities are cointegrated, the slope coefficient is one for gold, silver, and platinum, but not for oil, and this is true even when considering subsamples corresponding to the pre- and post-global financial crisis periods. We also find that although the estimated equilibrium errors for gold, silver, and platinum are only mildly serially correlated, those for oil are highly correlated. Therefore, although gold, silver, and platinum appear to be efficient markets, crude oil is inefficient.
The rest of the paper is organized as follows. Section 1. presents the model, whereas Section 1. introduces the WLS estimator and its asymptotic distribution, which is evaluated using Monte Carlo simulations in Section 1.. Section 1. reports the results of the empirical application. Section 1. concludes.
2. MODEL AND ASSUMPTIONS
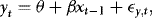 (1)
(1)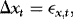 (2)
(2)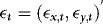 ,
, 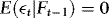 ,
, 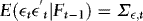 ,
, 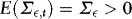 and
and 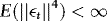 , with
, with 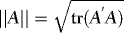 and Ft denoting the Euclidean norm of the (generic) matrix A and sigma-field generated by
and Ft denoting the Euclidean norm of the (generic) matrix A and sigma-field generated by 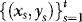 , respectively.
, respectively.The EMH implies that β = 1. This restriction is based on a definition of market efficiency that argues that price changes from one period to the next should be unpredictable given current information. If the futures price at time t–1, xt–1, contains all relevant information to forecast the next period's spot price, yt, as this definition of market efficiency implies, then xt–1 should be an unbiased predictor of the future spot price.
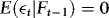 implies that
implies that  is serially uncorrelated, and hence stationary, suggesting that
is serially uncorrelated, and hence stationary, suggesting that 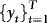 and
and 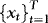 are cointegrated with cointegrating vector
are cointegrated with cointegrating vector 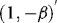 . The model given by 1 and 2 is therefore nothing but the conventional “triangular system” (Phillips, 1991), which, following the seminal article of Baillie (1989), has been used extensively for testing rational expectations restrictions. The fact that the elements of
. The model given by 1 and 2 is therefore nothing but the conventional “triangular system” (Phillips, 1991), which, following the seminal article of Baillie (1989), has been used extensively for testing rational expectations restrictions. The fact that the elements of 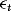 are allowed to be correlated is in agreement with the results of Zivot (2000), showing how neglected endogeneity can lead to deceptive inference. However, there is at least one empirical regularity that is not captured here, namely, heteroskedasticity. Indeed, as demonstrated by, for example, Franses et al. (1994) the residuals of cointegrated spot–futures regressions tend to be characterized by conditional heteroskedasticity. However, strangely enough this information is almost always ignored in the estimation of the cointegrating vector. As a response to this, following Seo (2007), the current paper assumes that
are allowed to be correlated is in agreement with the results of Zivot (2000), showing how neglected endogeneity can lead to deceptive inference. However, there is at least one empirical regularity that is not captured here, namely, heteroskedasticity. Indeed, as demonstrated by, for example, Franses et al. (1994) the residuals of cointegrated spot–futures regressions tend to be characterized by conditional heteroskedasticity. However, strangely enough this information is almost always ignored in the estimation of the cointegrating vector. As a response to this, following Seo (2007), the current paper assumes that 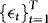 follows a constant-correlation autoregressive conditional heteroskedasticity (ARCH) process (see Bollerslev, 1990). Formally, letting
follows a constant-correlation autoregressive conditional heteroskedasticity (ARCH) process (see Bollerslev, 1990). Formally, letting 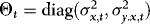 and
and
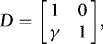
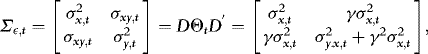 (3)
(3)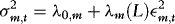 (4)
(4) , where
, where 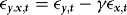 ,
, 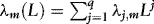 is a polynomial in the lag operator L, q < ∞,
is a polynomial in the lag operator L, q < ∞, 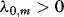 ,
,  and
and 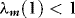 . The unconditional covariance matrix,
. The unconditional covariance matrix, 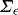 , is partitioned conformably with
, is partitioned conformably with 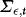 , and in view of 3 the elements of this matrix are given by
, and in view of 3 the elements of this matrix are given by 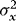 ,
, 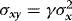 and
and 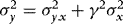 .
.
Remarks 1.The assumption of a finite-order ARCH structure is not particularly restrictive, because any model with stationary conditional heteroskedasticity, such as a generalized ARCH (GARCH) model, can be approximated arbitrarily well by taking q sufficiently large (see Andrews & Guggenberger, 2009, section 7). In fact the results of this paper are general enough to accommodate also other predetermined stationary variables in 4. For example, setting 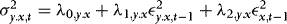 gives the “X–ARCH” of Brenner, Harjes, and Kroner (1996). Models of known non-linear functions can also be accommodated. For example,
gives the “X–ARCH” of Brenner, Harjes, and Kroner (1996). Models of known non-linear functions can also be accommodated. For example, 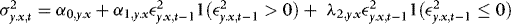 , where 1(x) is the indicator function, gives the asymmetric threshold ARCH of Glosten et al. (1993). The only requirement for the results of this paper (see Section 3) to go through also in these cases is that the estimated conditional variance has to be changed so as to mimic the assumed model (see Remark 3 of Section 1.).
, where 1(x) is the indicator function, gives the asymmetric threshold ARCH of Glosten et al. (1993). The only requirement for the results of this paper (see Section 3) to go through also in these cases is that the estimated conditional variance has to be changed so as to mimic the assumed model (see Remark 3 of Section 1.).
2. The requirement that 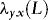 and
and 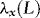 are of the same order q is not a restriction. If the orders are different, then we simply set q equal to the maximum of the two orders. In Section 1. we describe how to proceed in practice when the order of
are of the same order q is not a restriction. If the orders are different, then we simply set q equal to the maximum of the two orders. In Section 1. we describe how to proceed in practice when the order of 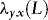 is unknown and has to be estimated.
is unknown and has to be estimated.
3. As long as x0 is Op(1), the initiation does not affect the results. Hence, we can just as well set x0 = 0.
3. THE WLS ESTIMATOR
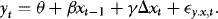
As 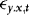 is per construction uncorrelated with
is per construction uncorrelated with 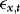 , the DOLS estimator
, the DOLS estimator 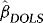 of β is unbiased and therefore robust to endogeneity. It is also robust to conditional heteroskedasticity. In particular, although endogeneity makes it biased, the OLS estimator is unaffected by the heteroskedasticity, at least asymptotically. Unattended ARCH will therefore not interfere with inference. The same is true for the DOLS estimator. However, there might still be important efficiency gains to be made by accounting for the ARCH information. Indeed, one of the most well-known results from classical regression theory is that OLS/DOLS is inefficient in the presence of heteroskedasticity. Our approach is therefore based on WLS.
of β is unbiased and therefore robust to endogeneity. It is also robust to conditional heteroskedasticity. In particular, although endogeneity makes it biased, the OLS estimator is unaffected by the heteroskedasticity, at least asymptotically. Unattended ARCH will therefore not interfere with inference. The same is true for the DOLS estimator. However, there might still be important efficiency gains to be made by accounting for the ARCH information. Indeed, one of the most well-known results from classical regression theory is that OLS/DOLS is inefficient in the presence of heteroskedasticity. Our approach is therefore based on WLS.
The above WLS estimator is similar in spirit to the one recently considered by Herwartz and Lütkepohl (2011). The idea is to exploit the information contained in the ARCH, while at the same time not having to sacrifice the simplicity and robustness of OLS. Let us denote by 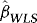 and
and 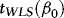 the WLS estimator of β in 4 and the associated t-statistic for testing
the WLS estimator of β in 4 and the associated t-statistic for testing 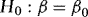 . Theorem 1 provides the asymptotic distributions of
. Theorem 1 provides the asymptotic distributions of  and
and 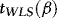 .
.
Theorem 1 1.Under the conditions laid out in Section 2.1, as 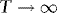 ,
,
(a) 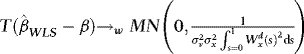 ,
,
(b) 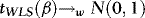 ,where
,where 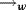 signify weak convergence, MN denote the mixed normal distribution function,
signify weak convergence, MN denote the mixed normal distribution function,  ,
,  is a standard Brownian motion, and
is a standard Brownian motion, and 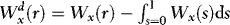 .
.
Remarks 2.1. According to Theorem 1 (a), 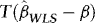 converges to a normal variate with mean zero and random variance. The asymptotic distribution is therefore a mixture of normals, suggesting that
converges to a normal variate with mean zero and random variance. The asymptotic distribution is therefore a mixture of normals, suggesting that 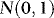 inference is possible, and this is verified in (b). Moreover, as the distribution has a mean of zero,
inference is possible, and this is verified in (b). Moreover, as the distribution has a mean of zero, 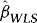 is asymptotically median unbiased. Hence, with this estimator there is no second-order bias.
is asymptotically median unbiased. Hence, with this estimator there is no second-order bias.
2. Because of the differing orders of magnitude of xt and Δxt, the WLS estimators of β and γ are asymptotically uncorrelated. Unreported results (available upon request) further show that if 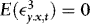 , the estimators of β and λ are also asymptotically uncorrelated, suggesting that asymptotically there are no efficiency gains to be made by iterating between the two.1 Another implication is that we do not lose generality by considering separate hypothesis tests for β, γ, and δ. The estimators of the two latter coefficients are asymptotically normal (a proof is available upon request), suggesting that inference regarding these can be carried out in the usual manner using conventional t- and F-tests. Pretesting for the presence of endogeneity and/or ARCH is therefore very simple.
, the estimators of β and λ are also asymptotically uncorrelated, suggesting that asymptotically there are no efficiency gains to be made by iterating between the two.1 Another implication is that we do not lose generality by considering separate hypothesis tests for β, γ, and δ. The estimators of the two latter coefficients are asymptotically normal (a proof is available upon request), suggesting that inference regarding these can be carried out in the usual manner using conventional t- and F-tests. Pretesting for the presence of endogeneity and/or ARCH is therefore very simple.
3. The estimation of the conditional variance is based on rewriting (4) as 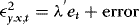 , where
, where 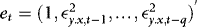 , which is just a stationary q-order autoregression in
, which is just a stationary q-order autoregression in 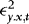 . In the Appendix we show that the effect of replacing
. In the Appendix we show that the effect of replacing 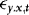 with
with 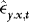 is negligible, suggesting that the fitted value from this regression can be used as an estimator of
is negligible, suggesting that the fitted value from this regression can be used as an estimator of 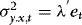 . This illustrates that as long as they are stationary and predetermined (and therefore also independent of the error term), there is nothing here that prevents the inclusion of additional regressors. Thus, in terms of the types of conditional variances that can be allowed, the ARCH assumption is just a simplification.
. This illustrates that as long as they are stationary and predetermined (and therefore also independent of the error term), there is nothing here that prevents the inclusion of additional regressors. Thus, in terms of the types of conditional variances that can be allowed, the ARCH assumption is just a simplification.
4. In the Appendix we show that as long as q is large enough to capture the true underlying ARCH structure, 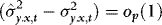 . This means that in the absence of ARCH (such that
. This means that in the absence of ARCH (such that 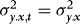 ) WLS and DOLS have the same asymptotic distribution, which in turn implies that the asymptotic “price” of accounting for ARCH is zero. In Section 1., we use simulations to assess this price in small samples.
) WLS and DOLS have the same asymptotic distribution, which in turn implies that the asymptotic “price” of accounting for ARCH is zero. In Section 1., we use simulations to assess this price in small samples.
5. Although researchers have appreciated the importance of allowing for ARCH/GARCH when analyzing the spot–futures relationship (see, e.g., Franses et al., 1994; Fujihara & Mongoue, 1997), as far as we are aware, this is the first paper that uses it as a source of information when inferring the cointegrating slope. For example, Koutmos and Tucker (1996) use a bivariate error correction model with exponential GARCH (EGARCH) errors, which is estimated using ML. Like most studies in the literature, the authors do not exploit the information contained in the EGARCH, but rather just impose a unit cointegrating slope.
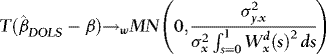
 . By the Cauchy–Schwarz inequality,
. By the Cauchy–Schwarz inequality,  with equality only if there is no ARCH, in which case
with equality only if there is no ARCH, in which case 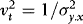 . It follows that
. It follows that
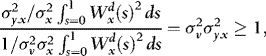
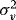 ) leads to a larger gain. The only exception is when
) leads to a larger gain. The only exception is when 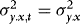 , in which case efficiency is equalized.
, in which case efficiency is equalized.4. MONTE CARLO SIMULATIONS
In this section, we investigate briefly the small-sample performance of the WLS estimator, and also when compared to the OLS and DOLS estimators. The DGP is given by a restricted version of 1–4 that sets θ = 1, q = 1, 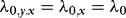 ,
, 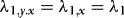 ,
,  (to ensure that
(to ensure that 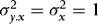 are kept fixed) and
are kept fixed) and 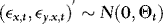 .
.
By setting λ1 and γ, we can control the extent of ARCH and endogeneity. As a measure of the latter we use the correlation between 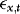 and
and 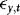 , which in the current DGP can be written as
, which in the current DGP can be written as 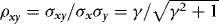 . In the simulations, by calibrating γ, we control
. In the simulations, by calibrating γ, we control 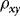 . As for the ARCH effect, there is no obvious measure; however, we know that it is increasing in λ1. All results are based on 5,000 replications.
. As for the ARCH effect, there is no obvious measure; however, we know that it is increasing in λ1. All results are based on 5,000 replications.
In constructing the WLS estimator, we need to determine the appropriate ARCH order, q. We experimented with several rules, but opted for the Schwarz Bayesian information criterion (BIC) with the maximum number of lags set to 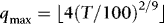 , where
, where 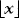 denoted the integer part of x. Another important issue in practice is that the estimated variance is bounded away from zero. One way to ensure this is to use a trimmed estimator such as
denoted the integer part of x. Another important issue in practice is that the estimated variance is bounded away from zero. One way to ensure this is to use a trimmed estimator such as 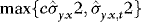 , where
, where 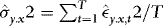 and
and 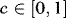 (see Hansen, 1995). The value of c is of course arbitrary, and it is difficult to see any convincing argument for one value over another. In this paper we set c = 0.1.2
(see Hansen, 1995). The value of c is of course arbitrary, and it is difficult to see any convincing argument for one value over another. In this paper we set c = 0.1.2
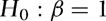 . Although Table I reports the size, RMSE and absolute bias results for the case when β = 1, Table II contains the power results. The information content of these tables may be summarized as follows:
. Although Table I reports the size, RMSE and absolute bias results for the case when β = 1, Table II contains the power results. The information content of these tables may be summarized as follows:
- With β = 1 and
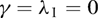 (Table I) all four estimators and their associated t-statistics perform very similarly, both in terms of size accuracy and RMSE. Being based on the true restrictions of no ARCH and no endogeneity, the OLS estimator is expected to perform best, and this is also what we see in Table I. However, the results change quite dramatically as endogeneity is introduced, in which case the relative performance of OLS deteriorates substantially. By contrast, as expected, the size of the tests is not affected by the value taken by λ1.
(Table I) all four estimators and their associated t-statistics perform very similarly, both in terms of size accuracy and RMSE. Being based on the true restrictions of no ARCH and no endogeneity, the OLS estimator is expected to perform best, and this is also what we see in Table I. However, the results change quite dramatically as endogeneity is introduced, in which case the relative performance of OLS deteriorates substantially. By contrast, as expected, the size of the tests is not affected by the value taken by λ1. - As expected, as λ1 goes from zero to 0.6 (Table I), the relative RMSE of WLS decreases. The infeasible WLS estimator (denoted IWLS) based on knowing
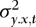 performs best, with feasible WLS ending up at second place. If γ = 0, the worst performance is obtained by using DOLS, whereas if γ > 0, then OLS performs worst.
performs best, with feasible WLS ending up at second place. If γ = 0, the worst performance is obtained by using DOLS, whereas if γ > 0, then OLS performs worst. - The results reported in Table II reveal that the greater efficiency of OLS in the case when
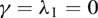 need not translate into relatively high power, which is somewhat unexpected. What is expected, however, is the tendency for power to increase as both T and the deviation from the null (as measured by |β – 1|) increase.
need not translate into relatively high power, which is somewhat unexpected. What is expected, however, is the tendency for power to increase as both T and the deviation from the null (as measured by |β – 1|) increase. - The highest power is generally obtained by using WLS, and this is true even if λ1 = 0, suggesting that in terms of power nothing is lost by using WLS. We also see that the gain in power obtained by using WLS rather than OLS or DOLS can be quite sizable. For example, when β = 1.01, λ1 = 0.6, γ = 0, and T = 400 the (feasible) WLS test rejects in about 43% of the times, whereas the OLS and DOLS tests reject in only 35% of the times.
- The power advantage of using WLS is larger the closer we are to the null, suggesting that the ARCH information become more “valuable” in cases when the deviation from the null is relatively difficult to discern. Conversely, as the deviation from the null becomes larger, the ARCH information become less important. But then power is very high anyway.
| ρxy | T | 5%s Size | Absolute bias | RMSE | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| OLS | DOLS | WLS | IWLS | OLS | DOLS | WLS | IWLS | OLS | DOLS | WLS | IWLS | ||
| λ1 = 0 | |||||||||||||
| 0.00 | 100 | 5.1 | 5.4 | 5.8 | 4.9 | 1.0000 | 1.0209 | 1.0320 | 1.0334 | 1.0000 | 1.0268 | 1.0391 | 1.0416 |
| 0.00 | 200 | 5.3 | 5.3 | 5.5 | 5.1 | 1.0000 | 1.0119 | 1.0189 | 1.0179 | 1.0000 | 1.0161 | 1.0235 | 1.0214 |
| 0.00 | 400 | 5.3 | 5.2 | 5.3 | 5.2 | 1.0000 | 1.0036 | 1.0063 | 1.0028 | 1.0000 | 1.0056 | 1.0088 | 1.0040 |
| 0.50 | 100 | 10.6 | 5.4 | 5.8 | 4.9 | 1.4694 | 1.0000 | 1.0109 | 1.0122 | 1.4825 | 1.0000 | 1.0120 | 1.0145 |
| 0.50 | 200 | 11.3 | 5.3 | 5.5 | 5.1 | 1.5195 | 1.0000 | 1.0069 | 1.0060 | 1.5472 | 1.0000 | 1.0073 | 1.0052 |
| 0.50 | 400 | 10.3 | 5.2 | 5.3 | 5.2 | 1.5048 | 1.0007 | 1.0034 | 1.0000 | 1.5537 | 1.0016 | 1.0048 | 1.0000 |
| 0.95 | 100 | 27.8 | 5.4 | 5.8 | 4.9 | 6.4647 | 1.0000 | 1.0109 | 1.0122 | 6.1190 | 1.0000 | 1.0120 | 1.0145 |
| 0.95 | 200 | 27.7 | 5.3 | 5.5 | 5.1 | 6.5981 | 1.0000 | 1.0069 | 1.0060 | 6.3716 | 1.0000 | 1.0073 | 1.0052 |
| 0.95 | 400 | 26.4 | 5.2 | 5.3 | 5.2 | 6.6466 | 1.0007 | 1.0034 | 1.0000 | 6.4822 | 1.0016 | 1.0048 | 1.0000 |
| λ1 = 0.6 | |||||||||||||
| 0.00 | 100 | 5.7 | 6.0 | 5.8 | 5.0 | 1.1537 | 1.1780 | 1.0702 | 1.0000 | 1.1599 | 1.1955 | 1.0795 | 1.0000 |
| 0.00 | 200 | 5.3 | 5.6 | 5.9 | 5.0 | 1.1940 | 1.2041 | 1.0689 | 1.0000 | 1.1973 | 1.2084 | 1.0793 | 1.0000 |
| 0.00 | 400 | 5.2 | 5.3 | 6.3 | 5.5 | 1.2356 | 1.2424 | 1.0687 | 1.0000 | 1.2511 | 1.2563 | 1.0825 | 1.0000 |
| 0.50 | 100 | 12.1 | 6.0 | 5.8 | 5.0 | 1.7960 | 1.1780 | 1.0702 | 1.0000 | 1.8197 | 1.1955 | 1.0795 | 1.0000 |
| 0.50 | 200 | 12.0 | 5.6 | 5.9 | 5.0 | 1.8789 | 1.2041 | 1.0689 | 1.0000 | 1.8932 | 1.2084 | 1.0793 | 1.0000 |
| 0.50 | 400 | 11.0 | 5.3 | 6.3 | 5.5 | 1.8901 | 1.2424 | 1.0687 | 1.0000 | 1.9432 | 1.2563 | 1.0825 | 1.0000 |
| 0.95 | 100 | 29.9 | 6.0 | 5.8 | 5.0 | 7.8305 | 1.1780 | 1.0702 | 1.0000 | 7.5444 | 1.1955 | 1.0795 | 1.0000 |
| 0.95 | 200 | 28.8 | 5.6 | 5.9 | 5.0 | 8.1627 | 1.2041 | 1.0689 | 1.0000 | 7.8620 | 1.2084 | 1.0793 | 1.0000 |
| 0.95 | 400 | 28.4 | 5.3 | 6.3 | 5.5 | 8.3497 | 1.2424 | 1.0687 | 1.0000 | 8.1261 | 1.2563 | 1.0825 | 1.0000 |
Note
- ρxy and λ1 refer to the correlation between the regression errors and the differenced regressor, and the ARCH coefficient, respectively. IWLS refers to the infeasible WLS estimator based on the true weight. The RMSE and absolute bias results are relative to the best performing estimator.
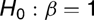
| ρxy | T | β = 1.01 | β = 1.05 | β = 1.1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| OLS | DOLS | WLS | IWLS | OLS | DOLS | WLS | IWLS | OLS | DOLS | WLS | IWLS | ||
| λ1 = 0 | |||||||||||||
| 0.00 | 100 | 7.5 | 7.7 | 8.2 | 7.1 | 46.7 | 46.7 | 47.0 | 45.0 | 85.7 | 85.3 | 85.3 | 84.5 |
| 0.00 | 200 | 13.2 | 13.5 | 13.7 | 12.7 | 85.6 | 85.5 | 85.5 | 84.6 | 99.6 | 99.5 | 99.5 | 99.5 |
| 0.00 | 400 | 34.6 | 34.9 | 34.8 | 34.0 | 99.5 | 99.5 | 99.5 | 99.5 | 100.0 | 100.0 | 100.0 | 100.0 |
| 0.50 | 100 | 7.5 | 7.7 | 8.2 | 7.1 | 20.9 | 46.7 | 47.0 | 45.0 | 60.0 | 85.3 | 85.3 | 84.5 |
| 0.50 | 200 | 6.5 | 13.5 | 13.7 | 12.7 | 59.9 | 85.5 | 85.5 | 84.6 | 93.9 | 99.5 | 99.5 | 99.5 |
| 0.50 | 400 | 14.1 | 34.9 | 34.8 | 34.0 | 93.2 | 99.5 | 99.5 | 99.5 | 99.9 | 100.0 | 100.0 | 100.0 |
| 0.95 | 100 | 24.3 | 7.7 | 8.2 | 7.1 | 13.9 | 46.7 | 47.0 | 45.0 | 11.2 | 85.3 | 85.3 | 84.5 |
| 0.95 | 200 | 20.7 | 13.5 | 13.7 | 12.7 | 10.4 | 85.5 | 85.5 | 84.6 | 26.3 | 99.5 | 99.5 | 99.5 |
| 0.95 | 400 | 15.7 | 34.9 | 34.8 | 34.0 | 26.0 | 99.5 | 99.5 | 99.5 | 68.0 | 100.0 | 100.0 | 100.0 |
| λ1 = 0.6 | |||||||||||||
| 0.00 | 100 | 7.9 | 8.0 | 8.9 | 8.4 | 46.6 | 46.2 | 51.6 | 54.8 | 81.8 | 81.7 | 86.2 | 89.3 |
| 0.00 | 200 | 13.5 | 13.8 | 16.6 | 17.1 | 83.5 | 83.1 | 88.8 | 91.0 | 99.0 | 98.9 | 99.4 | 99.7 |
| 0.00 | 400 | 34.7 | 34.7 | 42.7 | 45.7 | 99.0 | 98.9 | 99.6 | 99.9 | 100.0 | 100.0 | 100.0 | 100.0 |
| 0.50 | 100 | 8.5 | 8.0 | 8.9 | 8.4 | 21.3 | 46.2 | 51.6 | 54.8 | 57.5 | 81.7 | 86.2 | 89.3 |
| 0.50 | 200 | 7.4 | 13.8 | 16.6 | 17.1 | 57.6 | 83.1 | 88.8 | 91.0 | 91.7 | 98.9 | 99.4 | 99.7 |
| 0.50 | 400 | 14.5 | 34.7 | 42.7 | 45.7 | 91.7 | 98.9 | 99.6 | 99.9 | 99.9 | 100.0 | 100.0 | 100.0 |
| 0.95 | 100 | 26.6 | 8.0 | 8.9 | 8.4 | 16.3 | 46.2 | 51.6 | 54.8 | 13.2 | 81.7 | 86.2 | 89.3 |
| 0.95 | 200 | 21.9 | 13.8 | 16.6 | 17.1 | 12.6 | 83.1 | 88.8 | 91.0 | 26.9 | 98.9 | 99.4 | 99.7 |
| 0.95 | 400 | 16.4 | 34.7 | 42.7 | 45.7 | 26.7 | 98.9 | 99.6 | 99.9 | 66.7 | 100.0 | 100.0 | 100.0 |
Note
- See Table I for an explanation.
In sum, we find that the information contained in the ARCH is useful when estimating and testing the cointegrating slope, and that the use of WLS can lead to substantial gains in performance when compared to DOLS and in particular OLS. Interestingly, the use of WLS seems to have little or no “cost” to it, leading to relatively good performance even when there is no ARCH. The result is a robust test with good power properties, and, as such, it should be a valuable addition to the already existing menu of estimators of cointegrated regressions.
5. EMPIRICAL RESULTS
In the spot–futures relationship, the EMH holds if the following three conditions are satisfied: (i) spot and futures prices are cointegrated; (ii) the slope coefficient in this cointegrating equation equals one; and (iii) the errors in this equation are not predictable using information available in any prior period (Peroni & McNown, 1998). In this section, while all three conditions are tested, we focus on (ii).
Our empirical analysis is based on four commodities, namely, crude oil, gold, silver, and platinum. The data are daily and span the period July 5, 2005 to November 22, 2011. We also consider sub-samples, motivated by the global financial crisis: the pre-crisis sample covers the period from July 5, 2005 to September 12, 2008, whereas the post-crisis sample covers the September 13, 2008–November 22, 2011 period. The full sample period has a total of 2,332 daily observations, whereas for the pre- and post-crisis samples we have 1,254 and 1,079 observations, respectively. All data are downloaded from BLOOMBERG.
Typically, the empirical analysis is based on either daily data (see, e.g., Baillie & Myers, 1991; Bessler & Covey, 1991; Schroeder & Goodwin, 1991) or monthly data (see Chowdhury, 1991; Krehbiel & Adkins, 1993; Quan, 1992; Chow, 1998). We use daily data, which are more likely to be characterized by ARCH. As for the span of data, although the BLOOMBERG data stretch all the way back to the 1970s, we focus on a relatively recent, and hence also more relevant, period that includes, among other events, the global financial crisis. Therefore, in order to gauge against the effects of a potential structural break due to the financial crisis, we split our sample size into a pre- and a post-crisis period. In order to ensure accurate inference in both pre- and post-crisis regimes, one should have a reasonable balance in the number of observations in the two sub-sample periods. Our focus on the 2005–2011 period is motivated in part by this consideration.
Before testing conditions (i)–(iii), we provide some descriptive statistics of the data. These are reported in Table III. As is typical with spot and futures prices, we see that the prices of the commodities considered here behave very similarly. Spot prices are generally higher than futures prices in the case of gold, silver and oil, but not for platinum. The coefficient of variation (denoted “CV”) suggests that silver prices are the most volatile, followed by gold, and then oil. Platinum prices are least volatile. All prices are positively skewed, with silver and oil prices being relatively more skewed. Similarly, oil and silver prices tend to have relatively thicker tails than do platinum and gold, as suggested by the estimated kurtosis. The estimated autocorrelations reported at lag 12 are all close to one, which is suggestive of non-stationarity, and the results of the Ljung–Box test suggest that the null of no autocorrelation must be strongly rejected for all commodities.
| Variable | Mean | CV | Skewness | Kurtosis | AC | ARCH | ADF |
|---|---|---|---|---|---|---|---|
| Gold spot | 939.431 | 0.368 | 0.679 | 2.667 | 0.97 (0.00) | 609.83 (0.00) | 0.060 (0.96) |
| Gold futures | 939.058 | 0.368 | 0.675 | 2.659 | 0.97 (0.00) | 504.81 (0.00) | 0.058 (0.96) |
| Silver spot | 17.328 | 0.499 | 1.491 | 4.471 | 0.97 (0.00) | 1151.81 (0.00) | −1.077 (0.73) |
| Silver futures | 17.304 | 0.497 | 1.487 | 4.453 | 0.97 (0.00) | 1044.94 (0.00) | −0.990 (0.76) |
| Platinum spot | 1388.659 | 0.238 | 0.298 | 2.198 | 0.97 (0.00) | 709.76 (0.00) | −1.859 (0.35) |
| Platinum futures | 1391.649 | 0.238 | 0.305 | 2.227 | 0.97 (0.00) | 669.38 (0.00) | −1.895 (0.34) |
| Oil spot | 79.289 | 0.2839 | 0.667 | 2.690 | 0.97 (0.00) | 509.59 (0.00) | −1.446 (0.56) |
| Oil futures | 77.497 | 0.259 | 0.766 | 3.733 | 0.96 (0.00) | 397.08 (0.00) | −1.891 (0.34) |
Note
- CV and AC refers to the coefficient of variation and the estimated 12-order autocorrelation coefficient, respectively. The ARCH LM test includes 12 lags. The values within parentheses are the p-values.
We also test whether prices exhibit ARCH. To do this, we run an autoregressive (AR) model with 12 lags for each of the prices (to eliminate possible serial correlation), and then conduct a Lagrange multiplier (LM) test of the null hypothesis of no ARCH in the resulting residuals. The test is conducted at lag 12. The results reveal that the null can be strongly rejected, even at the 1% level. Hence, all prices seem to be characterized by ARCH, suggesting that our WLS-based approach should be appropriate. In the final column of Table III, we present the results obtained by applying the augmented Dickey–Fuller (ADF) test to each of the price series. The test regression is fitted with both intercept and trend, and the lag augmentation is chosen by the Schwarz information criterion (SIC) (with a maximum of eight lags). The results suggest that all price series are unit root non-stationary, at least at the 5% level, thus corroborating the preliminary evidence based on the estimated autocorrelations (Table III).
Having found that prices are unit root non-stationary we proceed to test for cointegration, the first of the three necessary conditions for the EMH. In this case, we apply the same ADF test as before but to the residuals of the level regression where the estimated parameters are obtained by applying OLS to the same regression in first differences. The reason for doing the testing in this particular way is that it makes the asymptotic distribution of the test independent of the regressor (see Westerlund & Edgerton, 2007), which means that the usual ADF critical values can be used. The test is implemented as before, but without a linear trend. The range of the test values for gold, silver, platinum and oil (across the three samples) are [−35.52, −24.40], [−36.66, −23.42], [−33.25, −17.57] and [−23.73, −16.67], respectively, which are all way out in the left tail of the ADF test distribution. The null of no cointegration is therefore rejected for all commodities in all samples considered.
The results from the estimated cointegrated regressions are reported in Table IV. We begin by looking at some results from the estimation of γ in (5), which measures the extent of endogeneity. If γ = 0, then the error terms in 1 and 2 are uncorrelated and therefore xt is exogenous, whereas if γ ≠ 0, then the error terms are correlated and so xt is endogenous. The estimates of γ are all close to one and are significantly different from zero, suggesting that futures prices are indeed endogenous, thereby invalidating inference by OLS. In view of this and the evidence of ARCH, WLS stands out as the most suitable estimator, and in Table IV we therefore only consider this estimator. Consider first the evidence for gold. In all three samples, the estimate of β is almost exactly one, and the null hypothesis that β = 1 cannot be rejected in the pre- and post-crisis samples. The results for silver are even stronger with no evidence against the unit slope null regardless of the sample period considered. The results for platinum are more mixed; although the null is rejected in the full and pre-crisis samples, it is not rejected in the post-crisis sample. However, the estimates are still very close to one, suggesting that while statistically significant, the difference from one might not be “economically significant.” Thus, in case of gold, silver, and platinum there is really not much evidence against the unit slope hypothesis. The results for oil are, however, quite different with the estimates being much further away from one, and the null of a unit slope is rejected in all three samples.
| Coefficient | Full sample | Pre-crisis | Post-crisis |
|---|---|---|---|
| Gold | |||
| β | 1.001*** | 1.000 | 1.000 |
| γ | 1.001*** | 1.031*** | 0.996*** |
| Silver | |||
| β | 1.001 | 1.000 | 0.999 |
| γ | 1.032*** | 1.036*** | 1.031*** |
| Platinum | |||
| β | 1.002*** | 0.999*** | 1.001 |
| γ | 0.984*** | 0.987*** | 0.976*** |
| Oil | |||
| β | 1.047*** | 0.996*** | 1.126*** |
| γ | 0.937*** | 0.896*** | 0.997*** |
Note
- β and γ are the coefficients of the level and first-differenced predictor, respectively. ***, ** and * denote significance at the 1%, 5%, and 10% levels, respectively.
Considering the existing evidence on the cointegration between spot and futures prices, to our surprise, despite crude oil being the most heavily traded commodity, there is only one study that tests for cointegration and estimates the slope coefficient. Quan (1992) do, and find the slope coefficient to be 0.48, which is substantially lower than our (full-sample) estimate of 1.047. As for the other commodities, although Krehbiel and Adkins (1993) estimate the slope coefficient to be 1.005 for gold and silver, and 1.009 for platinum, Chow (1998) estimates the slope coefficients of gold, silver, and platinum to be 0.997, 0.999, and 0.990, respectively. Thus, although our estimate for oil differs markedly from previous results, the results for gold, silver, and platinum are largely consistent with the existing evidence. As for the reason for the observed differences for oil, the difference in sample size and the accounting of ARCH stand out as natural candidates.
While stationary, the residuals from 1 need not be serially uncorrelated. Absence of serial correlation is the third and final test of the EMH. The estimated first-order autocorrelations of the equilibrium errors for gold, silver, platinum and oil are 0.111, 0.118, 0.165, and 0.918, respectively, and they are all significantly different from zero. Hence, there is indeed some serial correlation left unaccounted for in the predictive regressions. However, except for oil, where the correlation is very high, for the other commodities the autocorrelations are quite small, suggesting that there are no major violations of the no serial correlation condition.
Hence, in sum, although the EMH seems to provide an accurate description of the gold, silver, and platinum markets, this is not the case for oil. This is not surprising, though. A recent study by Narayan et al. (2012) estimates profits using momentum trading strategies in the crude oil, gold, silver, and platinum spot and futures markets. They find that gold is unprofitable and oil is the most profitable commodity. They show that while silver and platinum are also profitable, profits are small compared to oil, suggesting that the oil market is relatively inefficient. For example, they estimate that investors in the crude oil market make at least twice as much profits compared to silver and platinum markets. The results reported here, based obviously on a completely different approach, corroborate the findings of Narayan et al. (2012).
6. CONCLUDING REMARKS
The EMH is a central concept in financial economics. The commodity spot and futures markets are no exception. The conventional way in which researchers have been trying to test this hypothesis is to examine if spot and futures prices are (i) cointegrated and (ii) with a unit slope on the latter. Moreover, the equilibrium errors should be (iii) serially uncorrelated. However, although widely accepted in theory, such tests of the EMH hypothesis have met with limited success in commodity futures markets. In this paper, we focus specifically on the failure of the unit slope condition. In particular, it is argued that existing OLS-based approaches have low power and that the use of the additional information contained in the heteroskedasticity of the equilibrium errors should lead to more powerful tests. Our approach is therefore based on WLS, which is shown, both analytically and using Monte Carlo simulations, to be more efficient than OLS. We then apply the new WLS approach to test the slope restriction in four commodity spot and futures markets, namely, gold, silver, platinum and oil. Using daily data for the period 2005–2011 we find that spot and futures prices are cointegrated with a slope equal to one in all markets but oil.
APPENDIX: PROOF OF THEOREM 1
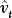 . We now show that
. We now show that 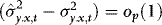 . The proof begins by noting that although
. The proof begins by noting that although  ,
, 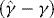 ,
, 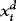 and
and 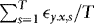 are
are 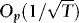 , where
, where 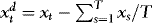 with a similar definition of
with a similar definition of  and
and 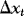 . It follows that
. It follows that
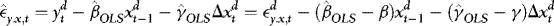
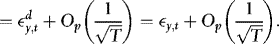
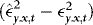 and hence also
and hence also 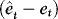 are
are 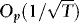 . This implies
. This implies
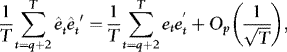
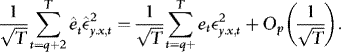
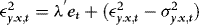 , by Taylor expansion,
, by Taylor expansion,
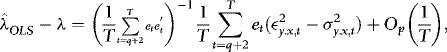
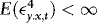 , by the ergodic theorem,
, by the ergodic theorem, 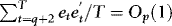 , the order of
, the order of 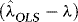 is determined by that of
is determined by that of 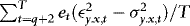 . If
. If 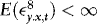 , then by a central limit theorem for martingale difference sequences,
, then by a central limit theorem for martingale difference sequences, 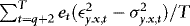 is
is 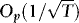 , and therefore so is
, and therefore so is 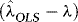 . On the other hand, if
. On the other hand, if 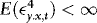 , as in Section 1., then by the ergodic theorem,
, as in Section 1., then by the ergodic theorem, 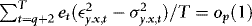 . It follows that
. It follows that 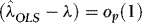 , and therefore
, and therefore
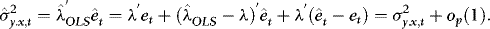
The effect of the estimation of 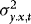 is therefore negligible. In what follows we therefore assume that
is therefore negligible. In what follows we therefore assume that 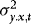 and hence also
and hence also 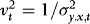 are known.
are known.
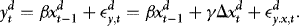
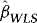 and
and 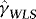 the WLS estimators of β and γ in the above regression. Since
the WLS estimators of β and γ in the above regression. Since
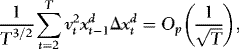
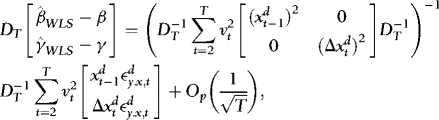
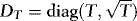 . Thus, although
. Thus, although 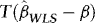 and
and 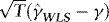 are asymptotically uncorrelated, we do not lose generality by focusing on the first term.
are asymptotically uncorrelated, we do not lose generality by focusing on the first term.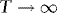 , where We(s) and
, where We(s) and  are independent of each other, and
are independent of each other, and
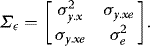
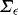 , by the law of iterated expectations,
, by the law of iterated expectations,
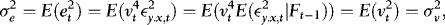
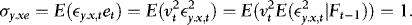
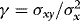 ,
, 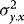 can be written as
can be written as 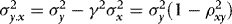 , where
, where 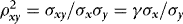 and
and 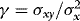 . Write
. Write 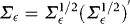 . The Cholesky decomposition of
. The Cholesky decomposition of 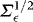 is given by
is given by
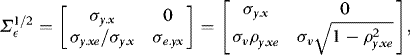
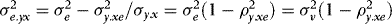 and
and 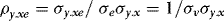 . It follows that
. It follows that
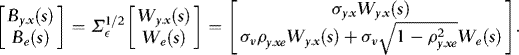
 satisfies an invariance principle. By using this and the above results,
satisfies an invariance principle. By using this and the above results,
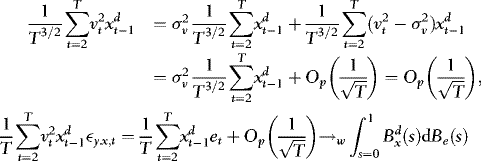
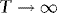 , where
, where 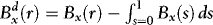 , which in turn implies
, which in turn implies
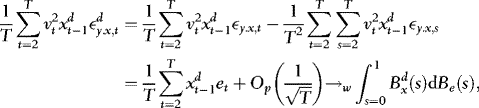
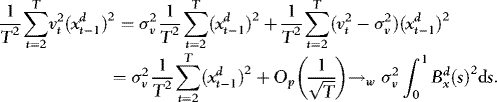
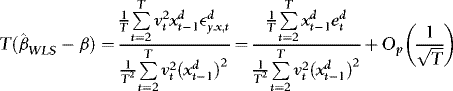
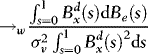
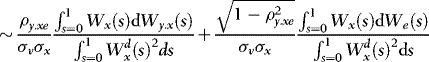
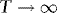 . Since Wx(s),
. Since Wx(s), 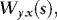 , and We(s) are independent, using F to denote the sigma-algebra generated by Wx(s) for
, and We(s) are independent, using F to denote the sigma-algebra generated by Wx(s) for 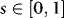 ,
, 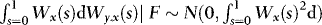 and
and 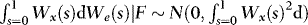 , from which it follows that
, from which it follows that 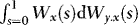 and
and 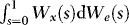 are mixed normal with the same mixing variate
are mixed normal with the same mixing variate  . Thus, using MN to denote a mixed normal distribution function,
. Thus, using MN to denote a mixed normal distribution function,
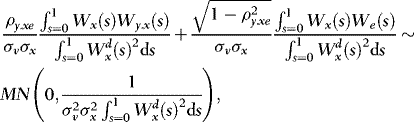
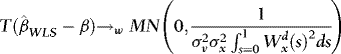
 , as required for (a).
, as required for (a).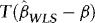 and
and 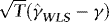 are asymptotically uncorrelated, without loss of generality, we focus on the t-statistic for β, which we write as
are asymptotically uncorrelated, without loss of generality, we focus on the t-statistic for β, which we write as
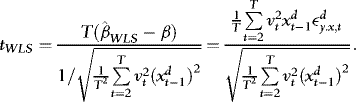
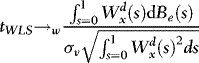
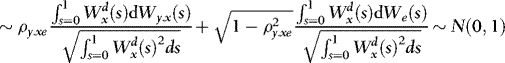
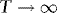 , as required for (b), and therefore the proof is complete.
, as required for (b), and therefore the proof is complete.
BIBLIOGRAPHY
Notes
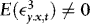 , then the estimators of β and γ become correlated, suggesting that there might be efficiency gains to be made by using WLS to construct the residuals to be used in the second-step estimation of γ.
, then the estimators of β and γ become correlated, suggesting that there might be efficiency gains to be made by using WLS to construct the residuals to be used in the second-step estimation of γ.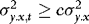 , by the consistency of
, by the consistency of 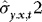 (see the proof of Theorem 1), we have that for each
(see the proof of Theorem 1), we have that for each 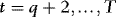 ,
, 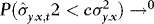 as
as 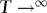 . The asymptotic results are therefore unaffected by trimming.
. The asymptotic results are therefore unaffected by trimming.


 . Then estimate the vector of ARCH coefficients,
. Then estimate the vector of ARCH coefficients, 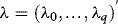 , from a regression of
, from a regression of 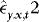 onto
onto 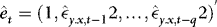 . Compute
. Compute 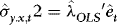 , where
, where 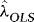 is the OLS slope estimator of λ.
is the OLS slope estimator of λ. .
.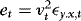 . By using the same arguments as in Seo (
. By using the same arguments as in Seo (