A Markowitz Optimization of Commodity Futures Portfolios
We thank a reviewer for numerous useful suggestions that have improved the quality of this study. We thank David Nawrocki for his help with the Portfolio Management Software Package (PMSP) program. All portfolio results are generated using PMSP.
Abstract
We examine the diversification benefits of using individual futures contracts instead of simply a commodity index. We determine the ex-ante, ex-post, and stability results for optimal Markowitz portfolios, investigate the instability between the ex-ante and ex-post results, and compare our results to traditional and naïve portfolios. The ex-ante complete futures portfolio dominates the traditional and naive portfolios and the ex-post portfolio outperforms the naïve portfolio. The instability between the ex-ante and ex-post results is primarily driven by the time-varying returns of the individual assets rather than by risk. Finally, the Sharpe portfolio results are essentially identical to the Markowitz results. © 2012 Wiley Periodicals, Inc. Jrl Fut Mark 33:343-368, 2013
I. INTRODUCTION
Modern finance owes its origin to the introduction of Markowitz portfolio theory, which subsequently became a basic tenet of finance. Furthermore, Johnson (1960) and Levy (1987) state that in principle, purchasing and selling futures is similar to purchasing and selling stocks; therefore, portfolio theory is also applicable to futures markets. However, studies on applying portfolio theory to commodity futures to determine the optimal risk-return portfolio, as well as the related commodity correlation diversification studies, are limited in scope (Fuertes, Miffre, & Rallis, 2010; Kaplan & Lummer, 1997; Satyanarayan & Varangis, 1996).1 In particular, few commodity articles consider the potential benefits of adding individual commodity futures contracts to a portfolio (Erb & Harvey, 2006; You & Daigler, 2010), or examine the (in)consistency between the ex-ante and ex-post results (Dye & Groth, 2000). In fact, the dearth of commodity futures studies in these areas is puzzling, especially given that the literature shows that commodity futures possess positive skewness, high liquidity, low trading costs, low correlations with traditional assets, and abnormal returns, all of which potentially make them ideal securities to aid diversification (Chong & Miffre, 2010; Gorton & Rouwenhorst, 2006, Miffre & Rallis, 2007).
In this study, we remedy the above omissions by examining whether it is beneficial to diversify with individual commodity futures by using mean-variance optimization techniques. More specifically, we apply the Markowitz portfolio optimization models to a comprehensive set of individual commodity and financial futures contracts, examine the ex-ante optimal portfolios results, and study the associated ex-post outcomes and resultant stability issue.2 We then analyze the effects of the risk-return factors (the return, the risk, and the correlations between instruments) on the stability results. Finally, we compare the optimal portfolios generated by the Markowitz model to those of the Sharpe model to determine the robustness of the optimal results to the Sharpe approach of setting the cross correlations between assets to zero. In general, the high return, high risk, and low pairwise correlations of commodity futures make them an ideal test for the potential risk-return benefits of employing portfolio models over time. In turn, examining portfolio model results provide a means to examine the benefits of employing commodity futures as part of an optimal portfolio.
We find that the low correlations across the different types of futures contracts lead to optimal ex-ante mean-variance commodity portfolios significantly dominating individual futures contracts, the traditional portfolio of stocks and bonds, and the naïvely weighted futures portfolio. However, when we examine the portfolio stability over time we find that the portfolio weights are not stable, especially for the high-risk/high return portfolios. As a result, the ex-post mean-variance portfolios perform substantially worse than the optimal ex-ante ones. On the other hand, the ex-post portfolios still provide superior results relative to the naïvely constructed futures portfolio on a return-risk basis. In addition, we find that the ex-post portfolio results are relatively consistent with the ex-ante results on a risk basis, although not on a return basis. Consequently, an investigation of the stability issues of the results shows that applying the Markowitz model over time is much more sensitive to changes in returns than to changes in risks. Finally, the Sharpe model provides results that are essentially equivalent to the Markowitz results and there is little difference between two-moment and four-moment value-at-risk (MVaR) results.
Our results show the benefits of adding individual commodity futures to a traditional portfolio of stocks and bonds, examine the difference between ex-post and ex-ante performance, and provide evidence for managers employing a mean-variance optimization approach rather than a pure naïve approach to market selection. More generally, these findings provide insights into the application of portfolio models, as well as to the use of commodity futures for diversification purposes, including the shortcomings of these applications.
This study is structured as follows: in the literature section, we discuss the key issues associated with commodity futures diversification; in Section III., we present the data and outline the methodology; the empirical results are presented in Section IV.; and in the final section, we conclude the study.
II. LITERATURE REVIEW REGARDING COMMODITY DIVERSIFICATION
In this section, we review issues related to commodity diversification. In particular, we examine diversifying with individual futures contracts rather than indexes, the low correlation between commodities and equities, portfolio stability, and ex-post portfolio results.
The increasing correlations among international equity markets during the last several decades motivated investors to include alternative investment vehicles in their portfolios.3 Subsequent studies report that it is beneficial to include commodity futures as part of a traditional portfolio due to their low correlations with equities. For example, Lintner (1983) shows a low correlation between 15 commodity trading advisors (CTAs) performance relative to a stock and bond portfolio. Kaplan and Lummer (1997) find that the Goldman Sachs Commodity Index's (GSCI) total return is negatively correlated with stocks and bonds, and Schneeweis and Georgiev (2002) show that futures accounts managed by CTAs are negatively correlated with the S&P 500 index, especially during market downturns.
Other studies examine the direct effect of adding commodity futures to the return/risk of a portfolio. For example, Bodie and Rosansky (1980) find that a portfolio with a 40% investment in commodity futures reduces risk by 30% compared to an all-equity portfolio, without lowering returns. Greer (1994) shows that investing 50% in the Daiwa Physical Commodity Index and 50% in the S&P 500 leads to a lower standard deviation than simply owning the S&P 500 portfolio alone. Satyanarayan and Varangis (1996) find that allocating only 3% of one's investment to the GSCI can reduce an international equity portfolio's monthly risk as much as 3.67%. Anson (1998) finds that including commodity index futures into a well-diversified portfolio of stocks and bonds can improve the Sharpe ratio. Other studies supporting the diversification benefit of adding a commodity index include Garrett and Taylor (2001) and Schneeweis and Georgiev (2002).
Issues do exist for previous commodity studies. First, most of the previous commodity diversification studies focus on adding one commodity index to a traditional portfolio of stocks and bonds. One problem with this approach is that the index is typically overweighted in one area, such as the GSCI's emphasis on energy; thus, employing a commodity index creates a bias. In addition, only employing an index obscures the benefits of using different types of futures as well as excluding individual futures contracts. Erb and Harvey (2006) and You and Daigler (2010) employ individual futures, but the former focuses on the return of individual futures and indexes, and the latter focuses on naïve portfolios. The other important issue ignored by most commodity diversification papers is the stability of the risk and return characteristics of the relevant portfolios, as well as the stability of the component assets in the optimal portfolio. More specifically, portfolio theory prescribes optimization in an ex-ante setting, with ex-post outcomes rarely examined by previous studies. Of course, employing Markowitz-optimized portfolios as an investment model assumes stable ex-ante to ex-post results. If the results are unstable over time then investors could be better off holding naïve portfolios or not diversifying at all.
III. DATA AND METHODOLOGY
We employ weekly prices for the 39 most actively traded commodity and financial futures contracts in the U.S. futures markets from the Commodity Research Bureau (CRB) database for the period 1994–2010.4 The data include all major futures contracts traded on U.S. markets, as determined by their daily trading volume.5 These futures include contracts on two commodity indexes (the GSCI and the CRB), five stock index futures (SIFs),6 six interest rate contracts, seven currencies, and 21 commodity futures. The commodity futures include three metals, four energy contracts, and 14 agricultural products. The naive portfolio is generated by equally weighting the returns for each of the futures in our sample. The data are then divided into ten annual periods in order to examine the portfolio performance and the stability of the portfolios over time. We also construct the traditional benchmark portfolio by including SIF and interest rate futures only; such a portfolio tracks the traditional benchmark institutional portfolio of stocks and bonds.7
 be a 1 × n vector of portfolio weights, whose ith element is the proportion of a particular asset relative to the entire portfolio. The mean-variance efficient set of weights
be a 1 × n vector of portfolio weights, whose ith element is the proportion of a particular asset relative to the entire portfolio. The mean-variance efficient set of weights  can be found by
can be found by
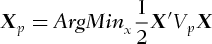 (1)
(1)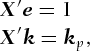 (2)
(2)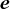 is a vector of 1 and
is a vector of 1 and  and
and  are the portfolio's mean and variance, respectively.
are the portfolio's mean and variance, respectively. (3)
(3) (4)
(4)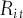 and Rmt are the return on the individual asset and market, respectively; ɛi is the error or residual return of the ith security; and Var(ɛi) and Var(ɛi, ɛj) are the variance of the ith security and the covariance between the ith and jth securities, respectively. In this study, we employ the Sharpe model to check the robustness of our results to possible instability of the individual correlations used by the Markowitz model.
and Rmt are the return on the individual asset and market, respectively; ɛi is the error or residual return of the ith security; and Var(ɛi) and Var(ɛi, ɛj) are the variance of the ith security and the covariance between the ith and jth securities, respectively. In this study, we employ the Sharpe model to check the robustness of our results to possible instability of the individual correlations used by the Markowitz model.Computer programs implementing the Markowitz/Sharpe model report the ex-ante corner portfolios on the efficient set.8 A corner portfolio differs from its adjacent corner portfolio by the addition or deletion of one asset. Ex-post portfolios are obtained by applying the weights of the optimal portfolio at time t to data at time t + 1. According to Tobin's two-fund separation theorem, investors will choose to invest in a risk-free asset and a tangent optimal portfolio of the risky asset. Therefore, we also provide the Sharpe ratios of tangent portfolios to evaluate the optimal results. In addition, the Sortino ratio and the VaR and MVaR measures at three standard deviations are calculated for the tangent portfolios to complement the Sharpe ratio analysis.9
IV. EMPIRICAL RESULTS
A. Basic Statistics
In Table I>, we provide the basic statistics for the 39 futures contracts and the equally weighted naïve portfolio over the period 1994–2010. We find that SIF and commodity futures both have high returns and high standard deviations, whereas currency and interest rate futures have low returns and low standard deviations, which is consistent with previous studies on the distribution of futures returns. The equally weighted naïve portfolio possesses an average return and a low risk compared to most of the individual futures contracts, showing the potential diversification benefit of investing in different types of futures contracts.
| Security Number | Mean (%) | Geometric Mean | Standard Deviation | Skewness | Kurtosis |
|---|---|---|---|---|---|
| Naïve portfolio | 0.06 | 0.05 | 1.30 | −1.23 | 8.83 |
| GSCI | 0.03 | −0.02 | 3.09 | −0.75 | 3.09 |
| CRB index | 0.10 | 0.09 | 1.69 | −0.93 | 5.24 |
| S&P 500 | 0.09 | 0.06 | 2.53 | −0.83 | 8.05 |
| Dow Jones | 0.04 | 0.01 | 2.64 | −0.79 | 7.32 |
| NADAQ 100 | 0.09 | 0.00 | 4.14 | −0.65 | 4.73 |
| S&P 400 | 0.11 | 0.06 | 2.84 | −0.53 | 6.33 |
| Nikkei | −0.04 | −0.09 | 3.18 | −1.00 | 11.61 |
| T-bond 30 years | 0.06 | 0.05 | 1.43 | 0.01 | 2.39 |
| T-note 10 years | 0.05 | 0.05 | 0.93 | −0.32 | 1.01 |
| T-note 5 years | 0.05 | 0.04 | 0.60 | −0.28 | 1.27 |
| T-note 2 years | 0.02 | 0.02 | 0.27 | −0.18 | 2.82 |
| U.S. dollar | −0.02 | −0.03 | 1.14 | 0.11 | 0.99 |
| British pound | 0.03 | 0.02 | 1.28 | −0.53 | 3.79 |
| Japanese yen | −0.02 | −0.03 | 1.56 | 1.37 | 10.28 |
| Swiss franc | 0.02 | 0.00 | 1.49 | 0.23 | 0.98 |
| Australian dollar | 0.08 | 0.07 | 1.78 | −1.40 | 12.07 |
| Canadian dollar | 0.02 | 0.02 | 1.16 | −0.91 | 8.73 |
| Mexican peso | 0.11 | 0.10 | 1.44 | −1.50 | 16.24 |
| Copper | 0.34 | 0.27 | 3.77 | −0.92 | 4.82 |
| Gold | 0.13 | 0.10 | 2.21 | −0.19 | 3.00 |
| Silver | 0.23 | 0.15 | 3.88 | −0.77 | 3.22 |
| Crude oil | 0.23 | 0.10 | 4.87 | −0.74 | 2.80 |
| Heating oil | 0.22 | 0.10 | 4.85 | −0.27 | 2.05 |
| Natural gas | −0.24 | −0.49 | 6.99 | −0.09 | 0.91 |
| Unleaded gasoline NY | 0.39 | 0.25 | 5.13 | −0.58 | 2.80 |
| Cocoa | 0.21 | 0.13 | 4.14 | −0.21 | 2.54 |
| Coffee | 0.18 | 0.06 | 4.90 | 0.22 | 2.04 |
| Corn | −0.04 | −0.10 | 3.52 | 0.22 | 2.23 |
| Cotton | −0.06 | −0.13 | 3.69 | −0.01 | 2.51 |
| Feeder cattle | 0.02 | 0.00 | 1.98 | −0.08 | 1.14 |
| Live cattle | 0.03 | 0.01 | 2.13 | 0.04 | 0.63 |
| Lean hog | −0.18 | −0.24 | 3.60 | −0.43 | 2.60 |
| Orange juice | −0.05 | −0.14 | 4.38 | 0.37 | 2.67 |
| Soybeans | 0.20 | 0.15 | 3.33 | −0.45 | 1.69 |
| Soybean meal | 0.25 | 0.18 | 3.78 | −0.21 | 1.90 |
| Soybean oil | 0.00 | −0.06 | 3.30 | −0.17 | 1.38 |
| Sugar #11 | 0.16 | 0.05 | 4.51 | −0.96 | 4.59 |
| Wheat | −0.55 | −1.01 | 8.39 | −1.76 | 31.60 |
| KC wheat | 0.10 | 0.03 | 3.65 | 0.07 | 1.67 |
| Average | 0.06 | 0.00 | 3.08 | −0.41 | 4.76 |
Note
- The basic statistics for the returns of 39 futures contracts and the equally weighted naive portfolio for the period 1994–2010 are provided in this table.
B. Correlation Analysis
In Table II, we summarize the within- and between-group average correlations over the 17 annual periods from 1994 to 2010 (more comprehensive correlation results are available upon request). The within-group correlations are calculated by averaging the pairwise correlations among all the futures in each futures group over each of the 17 annual periods (e.g., all agricultural futures); the between-group correlation for any pair of groups is obtained by averaging the correlations between individual futures in the two groups over the individual 17 years (e.g., correlating an agricultural future with a SIF).10 In Table II, we show that all of the within-group correlations are high, except for currency and agricultural futures.11 The SIFs within-group correlation ranks the highest, with a value of 0.74, confirming previous findings that the equity markets are more integrated than in past decades. Compared to the within-group correlations, the correlations between different groups are exceptionally low, ranging from −0.21 to 0.20.12 Overall, the correlation analysis shows that diversifying among different groups of futures helps to reduce risk.
| Stock Index | Interest Rate | Currency | Metal | Energy | Agricultural | |
|---|---|---|---|---|---|---|
| Stock index | 0.74 | |||||
| Interest rate | −0.21 | 0.67 | ||||
| Currency | 0.15 | 0.00 | 0.04 | |||
| Metal | 0.16 | −0.03 | 0.17 | 0.42 | ||
| Energy | 0.12 | −0.01 | 0.10 | 0.20 | 0.57 | |
| Agricultural | 0.12 | −0.04 | 0.08 | 0.13 | 0.11 | 0.16 |
| Average | 0.07 | −0.06 | 0.10 | 0.13 | 0.10 | 0.08 |
Note
- Correlations are averaged within (numbers on the diagonal) and among (off-the-diagonal) the different groups of futures contracts for the 17 annual periods from 1994 to 2010. “Indices” are the futures based on the commodity indices. The last row provides the average correlation between that group and all other groups.
C. Ex-ante Optimal Portfolios
In this section, we examine the diversification benefits of commodity futures by employing the optimal mean-variance Markowitz portfolio technique. Two sets of efficient frontiers are constructed using the Markowitz model: the traditional benchmark portfolio (consisting of SIFs and interest rate contracts) and the complete portfolio (consisting of all individual futures contracts). In order to examine the stability and diversification benefits of the portfolios over time, we rebalance the portfolios each year.13 For evaluation purposes, the Sharpe ratios, Sortino ratios, and the VaR and MVaR values of the tangent portfolios are determined over each of the 17 annual periods.
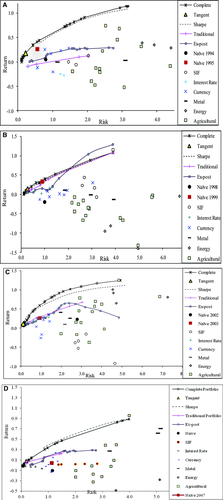
The efficient frontiers of the traditional and complete portfolios are constructed for each year, as well as the risk and return values of the naive portfolio and each individual futures contract. Figure 1A–D illustrates the 1994, 1998, 2002, and 2006 efficient frontiers (the others are omitted due to space considerations). Figure 1A–D shows that the interest rate and currency futures contracts typically have low risk and low return, SIFs possess medium risk and return, agricultural futures generate medium to high risk and return, and energy futures are associated with high risk and high return. The naïve equally weighted portfolio for year t (i.e., the year of the ex-ante portfolio) has a lower risk value than most individual futures contracts, but the naïve portfolio only dominates about half of the individual futures contracts on a risk-return basis. For each year in our study the traditional benchmark efficient frontier (logically) dominates the individual SIF and interest rate futures, showing its diversification benefits relative to individual SIF and interest rate futures contracts on an ex-ante basis. Similarly, the efficient frontier of the ex-ante complete portfolio dominates all of the individual futures contracts for each year. In addition, the complete efficient set dominates the naïve portfolio and the traditional benchmark frontier for all of the 17 years, except 1998.14 Moreover, the shape and position of the complete portfolio efficient frontier is very similar from one year to the next. However, the traditional benchmark efficient frontier changes from year to year. Thus, in an ex-ante sense, adding commodity futures to a traditional stock and bond portfolio provides superior diversification and risk-return portfolio benefits over only using a stock and bond portfolio; moreover, the stability of the location of the efficient set improves when commodities are added to the stock and bond only portfolio.15
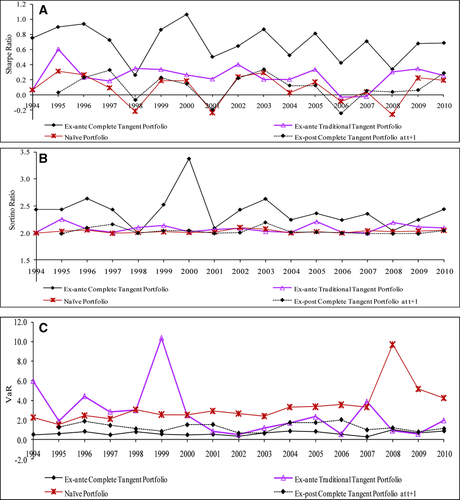
The tangent portfolio is often considered to be the most important optimal portfolio, because it possesses the highest Sharpe ratio among all of the optimal portfolio choices. In Figure 2A, we provide the Sharpe ratios for the tangent portfolios for each year based on the ex-ante complete and traditional benchmark efficient frontiers, as well as the complete ex-post and the naively weighted portfolios. The Sharpe ratios for the ex-ante complete tangent portfolio are considerably larger than those for the ex-ante traditional tangent portfolios. On average, the Sharpe ratio for the complete tangent portfolio is 8.05 times the traditional tangent portfolio, with this difference being statistically significant.16 Thus, these results show that a significant benefit can be achieved by adding commodities to the traditional portfolio on an ex-ante basis. However, the Sharpe ratio is more variable over time for the complete tangent portfolio than for the traditional tangent portfolio. This is mainly due to commodity futures being more volatile than interest rate futures. Figure 2B and C, in which we provide the Sortino ratios and the potential VaR losses (at three standard deviations for a $100 investment), also support a similar conclusion of the superiority of the ex-ante complete portfolio.17 The MVaR results are very similar to the VaR results (for all different portfolios); therefore, they are not reported here.18
If a portfolio's composition and individual component weights are stable from year to year, then an investor benefits from the reduced risk of investing in the complete portfolio. Here we examine the weights of the components of the Markowitz ex-ante portfolios from year to year as one measure of stability. In Tables III-V, we provide the asset weights of the portfolio's components for the high-, medium-, and low-risk levels for each of the 17 years of the study. The risk levels are chosen based on the standard deviations of the optimal portfolios.19 The results show that the portfolios’ component assets, as well as theirs weights, generally change drastically from year t to year t + 1, especially for the high-risk level portfolio. For the low-risk portfolios approximately half of the component assets for year t remain in the optimal portfolio for year t + 1, although the weights can vary considerably.20 Thus, if the stability of the component assets (and the resultant risk-return performance over time) is the primary goal, then the low-risk portfolio is preferable.
| Year | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Standard deviation (%) | 2.94 | 2.35 | 3.04 | 3.04 | 5.17 | 3.16 | 4.30 | 4.99 | 3.78 | 3.47 | 3.03 | 3.33 | 3.53 | 2.89 | 2.16 | 3.46 | 3.16 |
| NASDAQ | 74.21 | 43.36 | 12.59 | 2.82 | |||||||||||||
| T-bond 30 years | 100 | ||||||||||||||||
| Japanese yen | 25.39 | ||||||||||||||||
| Copper | 93.13 | 48.89 | 10.75 | 54.05 | |||||||||||||
| Silver | 0.41 | 18.01 | |||||||||||||||
| Crude oil | 45.41 | 56.64 | 2.35 | ||||||||||||||
| Heating oil | 11.63 | ||||||||||||||||
| Natural gas | 62.75 | ||||||||||||||||
| Unleaded gasoline NY | 27.54 | 13.84 | 32.14 | ||||||||||||||
| Cocoa | 33.72 | 95.47 | 67.86 | ||||||||||||||
| Coffee | 54.59 | 32.61 | 40.49 | ||||||||||||||
| Corn | 38.67 | ||||||||||||||||
| Cotton | 6.87 | ||||||||||||||||
| Live cattle | 4.99 | ||||||||||||||||
| Lean hog | 97.65 | ||||||||||||||||
| Orange juice | 4.53 | 84.01 | |||||||||||||||
| Soybeans | 33.66 | 0.01 | 55.46 | ||||||||||||||
| Soybean meal | 94.99 | ||||||||||||||||
| Sugar | 11.78 | 5.74 | 21.02 | ||||||||||||||
| KC wheat | 72.46 | 45.37 | 5.24 | 44.54 | 12.35 | ||||||||||||
| Sum | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
Note
- The weights for the Markowitz optimal portfolios at a high-risk level are presented in this table. Futures contracts that do not appear in any of the portfolios are not presented. The standard deviations and weights are percentage numbers.
| 94 | 95 | 96 | 97 | 98 | 99 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Standard deviation | 1.50 | 1.48 | 1.90 | 1.47 | 1.81 | 1.68 | 1.51 | 1.50 | 1.56 | 1.65 | 1.70 | 1.50 | 1.44 | 1.41 | 1.35 | 1.58 |
| S&P 500 | 0.00 | 5.14 | ||||||||||||||
| NASDAQ | 29.92 | 34.55 | 20.45 | 11.56 | ||||||||||||
| Nikkei | 42.34 | |||||||||||||||
| T-bond 30 years | 48.38 | 23.13 | 13.65 | 33.08 | ||||||||||||
| T-notes 10 years | 66.92 | |||||||||||||||
| U.S. dollar | 51.75 | 16.70 | ||||||||||||||
| British pound | 56.36 | |||||||||||||||
| Japanese yen | 21.58 | 12.65 | ||||||||||||||
| Swiss franc | 13.98 | |||||||||||||||
| Canadian dollar | 36.09 | |||||||||||||||
| Mexican peso | 1.66 | |||||||||||||||
| Copper | 33.64 | 0.00 | 1.87 | 13.40 | 18.36 | 20.63 | ||||||||||
| Gold | 24.65 | |||||||||||||||
| Silver | 9.05 | 0.13 | 7.44 | 9.64 | 9.04 | |||||||||||
| Crude oil | 3.66 | 33.19 | 21.52 | 0.34 | 3.46 | |||||||||||
| Heating oil | 0.55 | 3.77 | 12.49 | |||||||||||||
| Natural gas | 11.98 | 17.74 | 5.14 | |||||||||||||
| Unleaded gasoline | 20.93 | 8.73 | 12.01 | |||||||||||||
| Cocoa | 20.06 | 26.61 | 19.56 | |||||||||||||
| Coffee | 27.01 | 12.92 | 2.99 | 9.08 | 0.86 | 19.71 | ||||||||||
| Corn | 37.57 | 15.71 | ||||||||||||||
| Cotton | 23.60 | 6.74 | ||||||||||||||
| Feeder cattle | 0.00 | 30.97 | 22.63 | |||||||||||||
| Live cattle | 15.62 | 15.51 | 1.74 | |||||||||||||
| Lean hog | 2.96 | 38.14 | 4.03 | 3.22 | 46.47 | |||||||||||
| Orange juice | 0.00 | 8.77 | 4.85 | 35.54 | ||||||||||||
| Soybeans | 17.35 | 33.50 | 6.02 | |||||||||||||
| Soybean meal | 22.35 | |||||||||||||||
| Soybean oil | 0.00 | 29.62 | 5.61 | |||||||||||||
| Sugar #11 | 24.56 | 35.47 | 8.43 | 0.31 | 23.48 | 14.73 | ||||||||||
| Wheat | 15.82 | 2.84 | ||||||||||||||
| KC wheat | 38.54 | 8.10 | 15.78 | 1.36 | ||||||||||||
| Sum | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
Note
- The weights for the Markowitz optimal portfolio at a medium-risk level are presented in this table. Futures that do not appear in any of the portfolios are not presented. The standard deviations and weights are percentage numbers.
| 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Standard deviation (%) | 0.61 | 0.48 | 0.64 | 0.52 | 0.49 | 0.44 | 0.47 | 0.55 | 0.58 | 0.57 | 0.59 | 0.50 | 0.38 | 0.45 | 0.37 | 0.46 | 0.58 |
| S&P 500 | 35.10 | 0.68 | 22.49 | ||||||||||||||
| Dow Jones | 1.76 | 4.25 | 5.51 | 2.88 | |||||||||||||
| NASDAQ | 8.58 | 7.80 | 5.85 | 4.74 | 1.51 | 7.68 | 6.13 | ||||||||||
| S&P 400 | 3.25 | ||||||||||||||||
| Nikkei | 3.08 | 8.38 | |||||||||||||||
| T-bond 30 years | 6.33 | 13.68 | 20.35 | 1.95 | 5.67 | ||||||||||||
| T-notes 10 years | 3.65 | 3.37 | 55.23 | 26.01 | 6.40 | 29.08 | |||||||||||
| T-notes 5 years | 13.73 | 0.00 | 58.16 | 7.05 | |||||||||||||
| T-notes 2 years | 29.70 | 43.20 | 0.01 | 82.64 | 30.39 | ||||||||||||
| U.S. dollar | 25.63 | 15.66 | 12.54 | 23.68 | 18.12 | 27.27 | 7.75 | 30.37 | 32.97 | 0.00 | 7.10 | 23.16 | 15.91 | ||||
| British pound | 9.50 | 21.04 | 13.82 | 10.31 | 23.38 | 6.80 | 5.18 | 45.66 | |||||||||
| Japanese yen | 11.92 | 8.50 | 11.01 | 3.15 | 10.18 | ||||||||||||
| Swiss franc | 16.28 | 6.15 | 0.00 | 0.00 | 12.22 | ||||||||||||
| Australian dollar | 24.58 | 8.97 | 30.70 | 8.71 | |||||||||||||
| Canadian dollar | 16.95 | 4.57 | 20.55 | ||||||||||||||
| Mexican peso | 46.92 | 6.95 | 0.56 | 8.04 | 13.15 | 16.20 | |||||||||||
| Copper | 2.61 | 3.25 | 4.19 | 6.89 | 0.26 | 6.73 | 1.97 | 5.09 | 6.21 | ||||||||
| Gold | 3.68 | 1.19 | 10.44 | ||||||||||||||
| Silver | 8.34 | 0.03 | 0.42 | 6.49 | 4.23 | ||||||||||||
| Crude oil | 1.25 | 5.65 | 4.62 | 2.12 | 2.39 | 1.12 | 3.90 | 2.40 | |||||||||
| Heating oil | 0.76 | 4.63 | |||||||||||||||
| Natural gas | 3.12 | 3.84 | 3.74 | 3.24 | 2.04 | ||||||||||||
| Unleaded gasoline NY | 2.55 | 3.57 | 2.67 | 4.02 | |||||||||||||
| Cocoa | 0.78 | 2.45 | 5.81 | 8.90 | 3.26 | 2.54 | 0.71 | ||||||||||
| Coffee | 5.60 | 3.76 | 0.63 | 1.61 | 4.37 | 2.76 | 7.85 | ||||||||||
| Corn | 13.11 | 4.74 | |||||||||||||||
| Cotton | 0.42 | 0.56 | 1.65 | 4.52 | |||||||||||||
| Feeder cattle | 3.72 | 15.55 | 0.00 | 0.00 | 0.98 | 13.27 | 16.18 | 13.57 | |||||||||
| Live cattle | 12.48 | 18.03 | 10.11 | ||||||||||||||
| Lean hog | 4.34 | 10.10 | 2.06 | 1.41 | 13.99 | ||||||||||||
| Orange juice | 0.53 | 0.35 | 1.68 | 2.98 | 1.84 | 6.83 | 4.19 | ||||||||||
| Soybeans | 4.78 | 9.87 | 5.89 | 5.83 | |||||||||||||
| Soybean meal | 7.27 | ||||||||||||||||
| Soybean oil | 1.73 | 2.59 | 1.68 | 2.82 | |||||||||||||
| Sugar #11 | 4.36 | 2.20 | 1.18 | 14.85 | 0.65 | 2.54 | 0.70 | 10.69 | 5.40 | ||||||||
| Wheat | 5.21 | 0.97 | |||||||||||||||
| KC wheat | 2.13 | 7.30 | 1.48 | 2.47 | 2.62 | 3.60 | 0.87 | ||||||||||
| Sum | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
Note
- The weights for the Markowitz optimal portfolio at a low-risk level are provided in this table. The standard deviations and weights are in percentages.
D. Ex-post Results
Relative to the stability of the weights of the ex-ante portfolio, investors are even more concerned about the stability of the realized return and risk measures between the ex-ante and ex-post portfolios. This section examines these ex-post stability results.
Investors should prefer a Markowitz diversification with commodity futures only if the ex-post Markowitz results provide return and risk diversification benefits that are superior to a naïve diversification approach. In Figure 1A–D, we provide the ex-post as well as the ex-ante efficient frontier results for years 1994, 1998, 2002, and 2006. Figure 1A–D shows that the ex-post optimal portfolio results significantly underperform relative to the ex-ante portfolios (as expected, except for the high-risk portfolio for 1998), and even underperform relative to the original year's performance of some of the individual futures contracts.
More interesting is the comparison of the ex-post results to the traditional benchmark ex-ante portfolio results and to the naïve portfolio. In order to examine the resultant ex-post “optimal” portfolios at time t + 1, we apply the optimal weights at year t to the data in year t + 1 to obtain the ex-post “optimal” year t results (e.g., the component weights of the optimal portfolios from 1994 are applied to data from 1995 to obtain what we call the 1994 ex-post results).21 An important conclusion for the portfolio comparison is that the ex-post optimal portfolio resultant frontiers lie above the traditional stock and bond ex-ante efficient frontiers for the majority of optimal portfolios on the frontiers, suggesting that adding commodity futures to a portfolio can provide important ex-post risk-return benefits. Moreover, comparing the naïve portfolio's return and risk for year t + 1 to the ex-post efficient frontier (which typically occurs at the low-risk end of the efficient frontier) we find the ex-post t + 1 resultant frontier possesses as good as, if not better than, risk-return combinations for 10 of the 16 years studied. Finally, the higher risk portfolios on the ex-post efficient frontier portfolios typically do not possess substantially higher ex-post returns (again, 1998 is the exception). Overall, benefits from using the Markowitz portfolios in an attempt to achieve superior risk-return results do appear to be limited to the lower risk portfolios.
Another approach to evaluate the ex-post results is to compare the Sharpe ratios of portfolios. Theoretically, investors desire the portfolio providing the highest Sharpe ratio. Therefore, we obtain the return and risk of the ex-post tangent portfolio by applying the weights of the tangent portfolio for year t to the data for year t + 1.22 The ex-post tangent portfolio for year t + 1 is compared to the naive portfolio results for year t + 1. The ex-post tangent portfolios’ Sharpe ratios in Figure 2A are larger than the naïve portfolios’ Sharpe ratios for eight of the 16 years of this study, although the differences are generally small.23 However, the Sharpe ratio has several problems. First, when negative returns exist, ranking portfolios by their negative ratios provides incorrect information, because highly volatile markets will possess “better” (smaller negative) ratios. Second, Brooks and Kat (2002) point out that the Sharpe ratio substantially overestimates the true performance of portfolios when significant skewness and excess kurtosis exist. In order to overcome these issues we complement the Sharpe ratio with the Sortino ratio, as well as address the VaR and MVaR (four-moment) measures.
Figure 2B presents the Sortino ratio. The results are very similar to those of the Sharpe ratio. Figure 2C shows the VaR values for three standard deviations for a $100 investment, illustrating that the ex-post tangent portfolio has less potential loss than the naive portfolio for every year in our sample except 1995. The MVaR results are not given here because they are very similar to the VaR results. Thus, although the ex-post tangent portfolio provides a similar reward to standard deviation performance to the naïve portfolio, it has less downside risk. Consequently, we conclude that ex-post optimal commodity futures portfolios can provide risk-return benefits relative to the naïve portfolio, at least based on the VaR and MVaR criteria.
Now let us directly compare the stability between the ex-ante and ex-post results via the differences in return and risk from year t to year t + 1. We examine this issue by employing the optimal ex-ante and subsequent ex-post portfolios chosen for the three different risk levels: high, medium, and low. Figure 3A shows the differences in risk and return between the ex-ante and ex-post outcomes. The ex-ante portfolios all have higher returns than the ex-post portfolios, because the ex-ante returns minus the ex-post returns are almost all positive. This shows that the Markowitz optimal portfolio weights contain a substantial upward bias when used to forecast out-of-sample portfolio returns. On the risk side, the risk of the ex-ante portfolio results are somewhat smaller on average than the ex-post portfolio risk, because the majority of the differences between the ex-ante and the ex-post risk values are negative; however, for some periods/portfolios the risk is reduced from year t to year t + 1. The relative stability in the risk values is encouraging for the Markowitz procedure; on the other hand, the reduced returns from the ex-ante portfolio to ex-post results, especially for the high-risk portfolios, suggest a difficulty in using the Markowitz method for optimal forecasting purposes. Our findings in this section are generally in line with a number of studies that only employ equities (Chopra & Ziemba, 1993; Fisher & Statman, 1997; Mailer, Durand, & Lee, 2005). Our results support the conclusion of these studies that the Markowitz model has an upward bias in estimating or forecasting returns and is very sensitive to errors in parameters estimation.

E. The Driving Factor for Instability
 (5)
(5) , and
, and  are the ranks for the return, the risk, and the average correlation of the futures contract relative to all the other futures,24 respectively.
are the ranks for the return, the risk, and the average correlation of the futures contract relative to all the other futures,24 respectively. 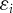 is the error term. In order to control for the effect of the risk level of the optimal portfolio, we estimate separate regressions at the high-, medium-, and low-risk portfolios. The high-, medium-, and low-risk Markowitz portfolios are obtained from each year and the regressions are executed using these pooled portfolios. The White and Breusch-Pagan tests show heteroskedastic error terms. After adjusting for heteroskedasticity, the regression results are reported in Table VI.
is the error term. In order to control for the effect of the risk level of the optimal portfolio, we estimate separate regressions at the high-, medium-, and low-risk portfolios. The high-, medium-, and low-risk Markowitz portfolios are obtained from each year and the regressions are executed using these pooled portfolios. The White and Breusch-Pagan tests show heteroskedastic error terms. After adjusting for heteroskedasticity, the regression results are reported in Table VI.| Variable | Parameter Estimate | Standard Error | t-Value | Pr > |t| | R2 | F-Value |
|---|---|---|---|---|---|---|
| Panel A: High-Risk Portfolios (43 Observations) | ||||||
| Intercept | 72.55 | 25.11 | 2.89 | 0.01 | 0.22 | 3.75** |
| Return (r) | 1.59 | 0.77 | 2.07* | 0.04 | ||
| Risk (σ) | −0.22 | 0.71 | −0.31 | 0.76 | ||
| Correlation (ρ) | −0.85 | 0.43 | −1.01 | 0.17 | ||
| Panel B: Medium-Risk Portfolios (91 Observations) | ||||||
| Intercept | 40.18 | 7.33 | 5.48** | <.0001 | 0.23 | 8.48** |
| Return (r) | 0.69 | 0.18 | 3.65** | 0.00 | ||
| Risk (σ) | −0.62 | 0.22 | −2.86* | 0.01 | ||
| Correlation (ρ) | −0.02 | 0.15 | −0.13 | 0.91 | ||
| Panel C: Low-Risk Portfolios (120 Observations) | ||||||
| Intercept | 23.90 | 3.70 | 6.46** | <.0001 | 0.27 | 21.41** |
| Return (r) | 0.25 | 0.09 | 2.82* | 0.01 | ||
| Risk (σ) | −0.55 | 0.13 | −4.28** | <.0001 | ||
| Correlation (ρ) | −0.01 | 0.08 | −0.10 | 0.93 | ||
Note
- The regressions of the component weights of the optimal portfolios on the rank of the return and the risk of the chosen futures and the average correlation of these futures contracts with all other futures are provided in this table. The resultant coefficients, R2, and F-values are reported in this table. Panels A, B, and C report the regression results for the high-, medium-, and low-risk portfolios. Values with *, and ** show significance at 5% and 1% levels, respectively.
The regression at each risk level possesses significant F-values at the 1% or better level, with the R2 equaling 22%, 23%, and 27% for the high, medium, and low portfolio risk levels. Among the three variables, the return variable is significant at the 5% level or better for all three regressions. The risk variable is significant for the medium- and low-risk portfolios, whereas correlation is not significant at any risk level. We conclude that the return is more important than the risk and correlation factors in determining the asset weights in the optimal portfolios. Consequently, the Markowitz model is more sensitive to returns than to either the risk or correlation factors; therefore, the time-varying returns are associated with the inconsistency between the ex-ante and ex-post results. These results support the graphical results in Figure 3A.
F. Robustness Check
In order to determine whether the Markowitz model results presented here are robust to a less parameter sensitive mean-variance optimization model, we compare the Markowitz results to the Sharpe optimization model results. Figure 1A–D shows both the Sharpe and Markowitz efficient frontier sets. These figures illustrate that the two models generate almost identical ex-ante risk-return efficient frontiers, with the Markowitz results slightly dominating the Sharpe results in most cases. Both efficient frontiers clearly dominate the ex-ante individual futures contracts. In Table VII, we present the weights of the asset components for the Sharpe optimal portfolios across time for the high-risk portfolios. (Due to space limitations, we do not present the weights of the components assets for the low- and medium-risk levels for the Sharpe results.) The portfolios in Table VII> are very similar to the Table III portfolios (the Markowitz results) in terms of the component assets and their weights. In addition, Figure 3B presents the ex-ante versus ex-post Sharpe optimal portfolios for different risk levels. The results in Figure 3B are also similar to the Markowitz results in Figure 3A. Therefore, we conclude that our results are invariant to the use of the Sharpe versus Markowitz models. Because the difference between the Sharpe and Markowitz models is that the former ignores the correlations between individual assets while the later takes them into consideration, this also shows that the correlations between the pairs of individual instruments are not an important factor affecting stability.
| 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Standard deviation (%) | 2.50 | 2.50 | 3.54 | 6.46 | 6.82 | 4.04 | 4.83 | 4.97 | 3.75 | 2.41 | 2.51 | 3.03 | 3.12 | 3.12 | 2.14 | 4.88 | 3.29 |
| NASDAQ | 85.27 | 15.77 | |||||||||||||||
| T-bond 30 years | 9.35 | 100 | |||||||||||||||
| T-notes 10 years | |||||||||||||||||
| Mexican peso | |||||||||||||||||
| Copper | 76.41 | 49.19 | 15.51 | 15.51 | 57.22 | ||||||||||||
| Silver | 5.37 | 3.96 | 10.16 | 10.16 | 7.89 | ||||||||||||
| Crude oil | 40.33 | 84.23 | 8.71 | ||||||||||||||
| Heating oil | 23.02 | ||||||||||||||||
| Natural gas | 74.53 | ||||||||||||||||
| Unleaded gasoline NY | 35.84 | 10.45 | |||||||||||||||
| Cocoa | 96.05 | 64.16 | |||||||||||||||
| Coffee | 59.67 | 75.30 | |||||||||||||||
| Corn | 41.3 | 46.06 | |||||||||||||||
| Cotton | |||||||||||||||||
| Feeder cattle | 11.85 | 46.06 | |||||||||||||||
| Lean hog | 79.45 | ||||||||||||||||
| Orange juice | 74.33 | 74.33 | |||||||||||||||
| Soybeans | 24.70 | 53.73 | |||||||||||||||
| Soybean meal | 46.27 | ||||||||||||||||
| Sugar #11 | 23.59 | 2.45 | 4.71 | ||||||||||||||
| Wheat | 46.10 | 32.33 | |||||||||||||||
| KC wheat | 58.7 | ||||||||||||||||
| Sum | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
Note
- The weights for the Sharpe optimal portfolios at the high-risk level are presented in this table. Futures that do not appear in any of the portfolios are not presented. The standard deviations and weights are percentage numbers.
V. CONCLUSIONS
Previous studies on commodity diversification typically focus on the risk and/or return benefits of adding a commodity index to a portfolio of stocks and bonds. Moreover, other studies employ an equally weighted naïve portfolio instead of generating optimal portfolios, and they typically ignore both the ex-post out-of-sample portfolios and the resultant (in)stability of the optimal portfolio weights over time. This study provides alternative ways to examine diversification and risk-return results by employing the mean-variance optimization model.
In this study, we employ a wide variety of types of futures contracts to study the potential portfolio benefits of adding individual commodity futures to a traditional portfolio. Correlation analysis reveals high correlations between futures in the same category but low correlations for futures in different categories, implying diversification benefits of including futures contracts from different categories of assets. Examination of the ex-ante mean-variance optimal portfolios shows that they dominate individual futures contracts, as well as the efficient frontier of the traditional stock and bond benchmark portfolio, for each year in our sample period. Moreover, the potential VaR losses for the complete portfolios are smaller than the potential losses from the traditional portfolios. On an ex-ante basis, it is beneficial to diversify with commodity futures.
When we examine the components of the Markowitz portfolios, we find that the optimal portfolios are less stable at the high risk-return level than at the low risk-return level over time. Moreover, the ex-post portfolios perform much worse than the ex-ante optimal portfolios. However, when the ex-post portfolios are compared to the naive portfolio, the results show that optimizing the structure of the portfolio with commodity futures still provides ex-post benefits over a simple naïve strategy. Further analysis shows that the instability associated with the ex-post results are due to the return factor rather than the risk factor. Finally, the Sharpe optimization model provides nearly equivalent results to the Markowitz model results, showing the robustness of the Markowitz approach to pairwise correlations.
The results here show the benefits and problems in applying the Markowitz model. In particular, the use of volatile futures contracts emphasizes both the advantages of a superior ex-ante portfolio, and the disadvantage of changing weights and assets (and therefore risk and return) over time. However, the potential for ex-post portfolios (generally the lower risk ones) providing superior results to a naively weighted portfolio suggests further work in applying the Markowitz model to futures data could provide useful results. For portfolio managers, the use of the mean-variance optimization technique still provides better results than using an indexing approach, where the index is typically naively weighted. In conclusion, improvements to model application that would provide more consistent weights for the ex-post versus ex-ante portfolios (and thus reduce the resultant bias in the expected return between the ex-ante and ex-post portfolios) would make optimal portfolio models more useful in practice.
 where
where 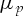 and
and  are the mean and standard deviation of the portfolio. The MVaR is calculated as follows:
are the mean and standard deviation of the portfolio. The MVaR is calculated as follows:
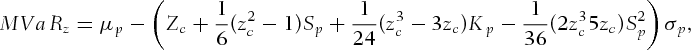 (6)
(6)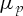 ,
,  ,
, 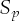 , and
, and  are the first four moments of portfolio p, and
are the first four moments of portfolio p, and  is the number of standard deviations that specifies the probability level associated with the MVaR. When skewness and kurtosis is ignored, the MVaR collapses to the VaR.
is the number of standard deviations that specifies the probability level associated with the MVaR. When skewness and kurtosis is ignored, the MVaR collapses to the VaR.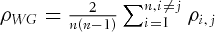 , where assets i and j belong to the same group of futures (e.g., both are agricultural futures), and n is the number of assets in that group. The between-group correlation for groups 1 and 2 is defined as
, where assets i and j belong to the same group of futures (e.g., both are agricultural futures), and n is the number of assets in that group. The between-group correlation for groups 1 and 2 is defined as 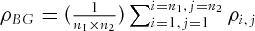 , where asset i is from group 1 with n1 number of assets, and asset j is from group 2 with n2 number of assets.
, where asset i is from group 1 with n1 number of assets, and asset j is from group 2 with n2 number of assets.



