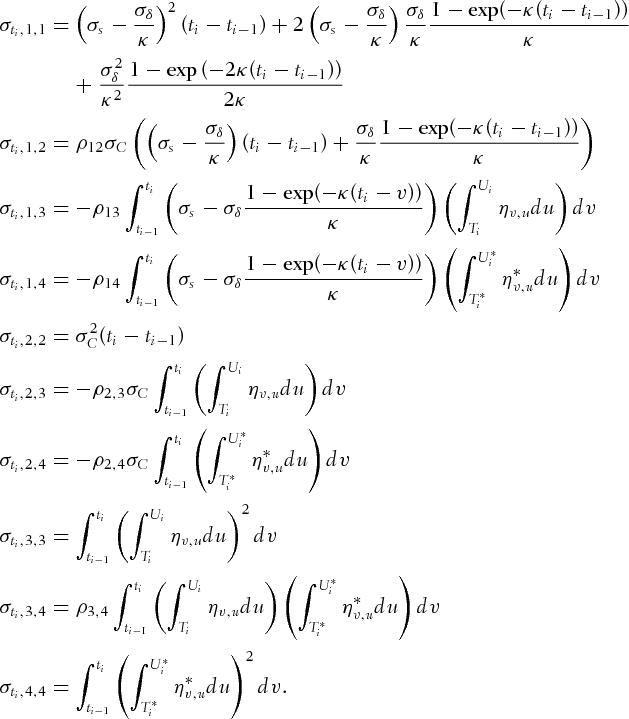Risk Management of Nonstandard Basket Options with Different Underlying Assets
The authors acknowledge the financial support of the Institut de Finance Mathématiques de Montréal (IFM2), the National Science and Engineering Research Council of Canada (NSERC), and the Fonds Québécois de Recherche sur la Société et la Culture, (FQRSC). This study extends N. Ouertani's Ph.D. thesis on which Phelim P. Boyle, Michel Denault, and Pascal François have made very helpful suggestions. We also thank Nabil Tahani and Jean-Guy Simonato for their comments.
Abstract
Basket options are among the most popular products of the new generation of exotic options. They are particularly attractive because they can efficiently and simultaneously hedge a wide variety of intrinsically different financial risks and are flexible enough to cover all the risks faced by firms. Oddly, the existing literature on basket options considers only standard baskets where all underlying assets are of the same type and hedge the same kind of risk. Moreover, the empirical implementation of basket-option models remains in its early stages, particularly when the baskets contain different underlying assets. This study focuses on various steps for developing sound risk management of basket options. We first propose a theoretical model of a nonstandard basket option on commodity price with stochastic convenience yield, exchange rate, and domestic and foreign zero-coupon bonds in a stochastic interest rate setting. We compare the hedging performance of the extended basket option containing different underlying assets with that of a portfolio of individual options. The results show that the basket strategy is more efficient. We apply the maximum likelihood method to estimate the parameters of the basket model and the correlations between variables. Monte Carlo simulations are conducted to examine the performance of the maximum likelihood estimator in finite samples of simulated data. A real-data study for a nonfinancial firm is presented to illustrate ways practitioners could use the extended basket option. © 2012 Wiley Periodicals, Inc. Jrl Fut Mark 33:299-326, 2013
1. INTRODUCTION
The vast majority of firms face various financial risks (interest rates, exchange rates, commodity prices, etc.) and would like more efficient and cheaper ways to hedge these risks. Traditionally, these firms have used derivative securities to hedge each of these risks separately. A portfolio approach (such as the basket option) allows the inclusion of correlations between these risks. Usually traded over the counter, the basket option is designed to meet firms’ specific needs, and when the underlying basket is well diversified, its theoretical price is lower than the price of a basket of individual options. However, in practice, it may be difficult to find a counterpart (usually a bank), which usually demands high premiums for these options due to the potential lack of liquidity.
The literature on basket options proposes different ways to price a standard basket. The underlying portfolio contains assets of the same type (such as exchange rates or equities) usually modeled with multidimensional geometrical Brownian motions with a constant spot interest rate. Such pricing contributions include Gentle (1993), Curran (1994), Brigo, Mercurio, Rapisarda, and Scotti (2004), Deelstra, Liinev, and Vanmaele (2004), and Zakamoulie (2008). Other works present numerical pricing techniques based on Monte Carlo and quasi-Monte Carlo simulation methods (Barraquand, 1995; Dahl, 2000; Dahl & Benth, 2001; Wan, 2002). Some researchers propose closed-form solutions for different distribution functions (Datey, Gauthier, & Simonato, 2003; Henriksen, 2008; Milevsky & Posner, 1998a, 1998b, 1998c; Pellizzari, 2001; Posner & Milevsky, 1999). Further, Flamouris and Giamouridis (2007) explore the use of a jump diffusion process, Ju (2002) describes the Taylor expansion for an analytical approximation of the option price, and Vanmaele, Deelstra, and Liinev (2004) and Laurence and Wang (2004) examine the determination of bounds for the option price or premium. Nonetheless, these types of basket pricing models do not necessarily correspond to firms’ needs because they consider only assets of the same type and do not cover risk management functions other than pricing.
Reaching beyond the existing literature, our work focuses on the risk management of basket options. Our main contribution consists in proposing different steps for developing a sound risk management of nonstandard basket options: a theoretical model, parametric estimations, and a performance analysis. In the same basket, we combine commodity prices, exchange rates, and zero-coupon bonds in a stochastic interest rate setting. The basket option we propose allows firms to cover some of their financial exposure with a single hedge and at a lower cost than if the company were to hedge each of these risks separately. We treat many aspects related to the risk management of basket options, which makes our contribution very practical, especially for practitioners who use this kind of product for hedging. In our extended framework, the estimation of the model's parameters is non-trivial and is required for a practical use of these options.
First, we develop a theoretical model for a basket option under the equivalent martingale measure. As justified below, we presume that the commodity price and the convenience yield share the same source of risk, which allows us to work with a complete market and adopt a single price for the basket option. This simplification frees us from having to define and estimate a functional form for the market-price risk associated with the stochastic convenience yield.
Second, we compare the performance of a basket option to that of a portfolio of individual plain vanilla options by computing option prices and profits. We show empirically that the basket option, composed of different underlying assets, costs less and is more efficient. Given that our model depends on several underlying assets with different stochastic processes, we do not obtain a closed-form solution for the price of the basket option. Hence, we carry out a Monte Carlo simulation to price the basket option.
One of the main difficulties with the empirical implementation of the basket-option model is that some variables, such as the convenience yield and the instantaneous forward rates, are not directly observable. A technique well suited to such situations is the maximum likelihood method. The main advantage of using the maximum likelihood approach to estimate basket parameters is linked to the asymptotic properties of its estimator. These properties, which include consistency and normality, are necessary for statistical inference because they make it possible to build confidence intervals when applying maximum likelihood to real data. We use this technique to estimate all the parameters of the basket model and the correlations between the underlying assets comprising the basket. This estimation procedure is implemented empirically on simulated data, and its performance is analyzed using a Monte Carlo study. We also apply the model to real data on commodity prices, exchange rates, and futures on zero-coupon bonds to estimate the parameters of the basket model. This application to a nonfinancial firm should provide practitioners with ways to use the extended basket option effectively.
The remainder of the study is organized as follows. Section 2. presents the model including the commodity with stochastic convenience yield, exchange rate, and stochastic domestic and foreign interest rates chosen among the Heath, Jarrow, and Morton (1992) (hereafter HJM) family. In Section 3., the performances of the basket option and a portfolio of individual options are compared numerically. Section 4. presents the maximum likelihood estimation of the parameters. A Monte Carlo study analyzes the performance of the estimators. An application using real data is also presented. Section 5. concludes the study.
2. THE MODEL
 denote the commodity price at time t expressed in the domestic currency, whereas
denote the commodity price at time t expressed in the domestic currency, whereas 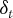 represents its stochastic convenience yield.1 Our model is inspired from Schwartz (1997), with the difference that, here, both processes share the same source of risk. Indeed, allowing for stochastic convenience yield with an extra source of noise will lead to an incomplete model, as the convenience yield is not a tradable asset. Our simplification solves this problem and may be justified with a highly positive correlation between the commodity return and its convenience yield (see Brennan, 1991). The exchange rate
represents its stochastic convenience yield.1 Our model is inspired from Schwartz (1997), with the difference that, here, both processes share the same source of risk. Indeed, allowing for stochastic convenience yield with an extra source of noise will lead to an incomplete model, as the convenience yield is not a tradable asset. Our simplification solves this problem and may be justified with a highly positive correlation between the commodity return and its convenience yield (see Brennan, 1991). The exchange rate 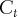 is the value at time t of one unit of the foreign currency expressed in the domestic currency. The instantaneous forward rates’ models (
is the value at time t of one unit of the foreign currency expressed in the domestic currency. The instantaneous forward rates’ models ( denotes the domestic rate and
denotes the domestic rate and 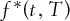 stands for the foreign rate) are chosen among the HJM family where the volatility parameters
stands for the foreign rate) are chosen among the HJM family where the volatility parameters  and
and  are deterministic functions2 of time t and maturity T. Under the objective measure
are deterministic functions2 of time t and maturity T. Under the objective measure  , the model is
, the model is
 (1a)
(1a)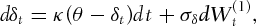 (1b)
(1b) (1c)
(1c)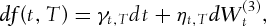 (1d)
(1d) (1e)
(1e)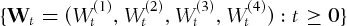 is a four-dimensional
is a four-dimensional  -Brownian motion with a constant correlation matrix
-Brownian motion with a constant correlation matrix  The parameters
The parameters  are unknown and need to be estimated. The deterministic functions
are unknown and need to be estimated. The deterministic functions  will be specified and estimated as well in Section 4.1.. Note that both instantaneous forward rates are Gaussian processes allowing for potential negative interest rates.
will be specified and estimated as well in Section 4.1.. Note that both instantaneous forward rates are Gaussian processes allowing for potential negative interest rates. values of the domestic and foreign zero-coupon bonds follow, respectively:
values of the domestic and foreign zero-coupon bonds follow, respectively:
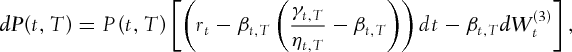 (1f)
(1f)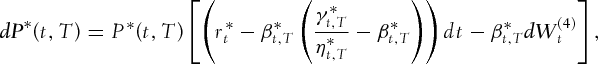 (1g)
(1g) and
and  are, respectively, the domestic and the foreign spot interest rates at time t and
are, respectively, the domestic and the foreign spot interest rates at time t and  ,
,  . Finally, the time t value of the domestic and foreign bank accounts are characterized, respectively, by
. Finally, the time t value of the domestic and foreign bank accounts are characterized, respectively, by  and
and 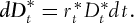
 :
:
 (2a)
(2a)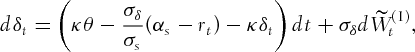 (2b)
(2b)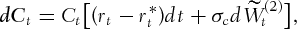 (2c)
(2c) (2d)
(2d)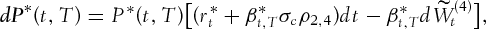 (2e)
(2e) is a four-dimensional
is a four-dimensional  -Brownian motion with a constant correlation matrix
-Brownian motion with a constant correlation matrix  .
.3. PERFORMANCE OF THE EUROPEAN BASKET OPTION: A MONTE CARLO STUDY
Whenever the underlying assets are not perfectly and positively correlated, the portfolio is partially diversified and its volatility reduced. We can apply this reasoning to a basket option that gives to its owner the right to buy or sell the portfolio at a predetermined exercise price at a prespecified date. Hence, the basket option allows for the simultaneous hedging4 of different financial risks at a potentially lower cost than the one associated with the individual hedge of each of these risks. The advantage of the basket option is obtained when the basket increases the shareholders’ wealth. Like entreprise risk management (Hoyt & Linbenberg, 2011), the basket option is a structure that incorporates all risk management activities in an integrated framework that creates synergies between different risk management activities by taking into account the dependences between the various risks of the firm. Consequently, it integrates the natural hedging opportunities that reduce duplication costs. In this section, we will demonstrate numerically that the basket option is cheaper than a portfolio of standard options, and then analyze its performance. However, this analysis does not account for the basket option's possible lack of liquidity.
 a portfolio comprising the commodity, a domestic zero-coupon bond (with maturity
a portfolio comprising the commodity, a domestic zero-coupon bond (with maturity  ), and a foreign zero-coupon bond (with maturity
), and a foreign zero-coupon bond (with maturity  ) converted to the domestic currency. We assume that w1, w2, and w3 correspond, respectively, to the number of shares initially invested in the commodity, the domestic bond, and the foreign bond. The time t value of this option is
) converted to the domestic currency. We assume that w1, w2, and w3 correspond, respectively, to the number of shares initially invested in the commodity, the domestic bond, and the foreign bond. The time t value of this option is
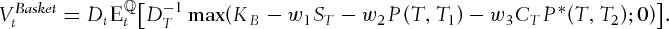
We now analyze the performance of basket option empirically as a risk management instrument. To avoid the possibility of the results being influenced by the choice of model parameters, we compute option prices over a wide range of parameters.6 Like Broadie and Detemple (1996), we use 1, 000 parameter combinations generated randomly from a realistic set of values and assuming a continuous uniform distribution as presented in Table I.
| Drift Coefficients | Volatilities | Correlations |
|---|---|---|
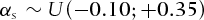 |
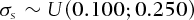 |
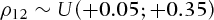 |
 |
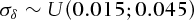 |
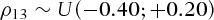 |
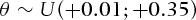 |
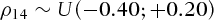 |
|
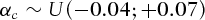 |
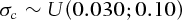 |
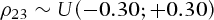 |
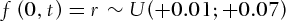 |
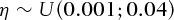 |
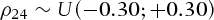 |
 |
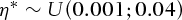 |
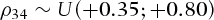 |
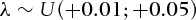 |
||
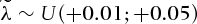 |
Note
 means that x has been simulated using a uniform distribution on the interval
means that x has been simulated using a uniform distribution on the interval  . For this study, the volatility parameters of both instantaneous forward rates models is set to some constants, that is, for any
. For this study, the volatility parameters of both instantaneous forward rates models is set to some constants, that is, for any 
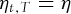 and
and  . The parameters λ and
. The parameters λ and  are required for the bonds’ price dynamics under the probability measure
are required for the bonds’ price dynamics under the probability measure  and are defined in Section 4.1..
and are defined in Section 4.1..
We consider a gold mining firm that, in six months from now  , will sell
, will sell 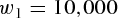 ounces of gold, sell
ounces of gold, sell  domestic zero-coupon bonds (with maturity
domestic zero-coupon bonds (with maturity  ), and convert
), and convert 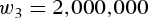 of foreign currency into the domestic currency. To reduce its risk, this firm may choose between buying a basket put option or buying a portfolio of individual options. We assume that the firm holds the risky assets. The determination of the optimal composition of the basket that accounts for the correlations between the assets is beyond the goals of this study.
of foreign currency into the domestic currency. To reduce its risk, this firm may choose between buying a basket put option or buying a portfolio of individual options. We assume that the firm holds the risky assets. The determination of the optimal composition of the basket that accounts for the correlations between the assets is beyond the goals of this study.
 and for each parameter set, 10, 000 scenarios of possible gold prices, exchange rates, and domestic bond prices are simulated. For each generated scenario, the profit and the return of both hedging strategies are computed. More precisely, let
and for each parameter set, 10, 000 scenarios of possible gold prices, exchange rates, and domestic bond prices are simulated. For each generated scenario, the profit and the return of both hedging strategies are computed. More precisely, let

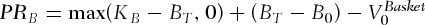
 of the basket option. The basket-option strike price is chosen to meet the risk management needs of the firm. In Table II, we present various scenarios for this strike price, identified with
of the basket option. The basket-option strike price is chosen to meet the risk management needs of the firm. In Table II, we present various scenarios for this strike price, identified with  The profit
The profit
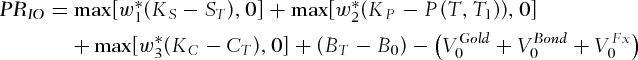
 ,
,  ,
,  of the individual options.
of the individual options.  ,
,  ,
,  , and
, and  correspond, respectively, to the exercise prices of the basket option, the gold price option, the domestic bond option, and the exchange rate option. Because it is possible that the portfolio of individual options is weighted differently from the basket, the weights
correspond, respectively, to the exercise prices of the basket option, the gold price option, the domestic bond option, and the exchange rate option. Because it is possible that the portfolio of individual options is weighted differently from the basket, the weights 

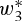 may differ from w1, w2, and w3, respectively. All option prices are computed under the risk-free measure
may differ from w1, w2, and w3, respectively. All option prices are computed under the risk-free measure  using a Monte Carlo simulation with 10, 000 trajectories with antithetic variable. The profit associated with a nonhedging strategy is simply
using a Monte Carlo simulation with 10, 000 trajectories with antithetic variable. The profit associated with a nonhedging strategy is simply

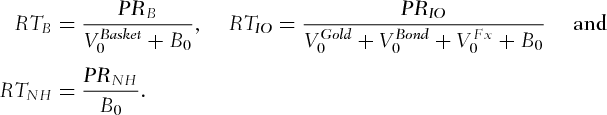
 of the simulated prices. In a second step, we use the Pellizzari (2005) procedure to optimize the strike prices
of the simulated prices. In a second step, we use the Pellizzari (2005) procedure to optimize the strike prices  ,
,  , and
, and  as well as the weights
as well as the weights 
 , and
, and 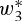 of the individual options so that the cash flow of the portfolio of individual options is as close as possible to the cash flow generated by the basket option.
of the individual options so that the cash flow of the portfolio of individual options is as close as possible to the cash flow generated by the basket option. |
 |
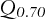 |
 |
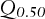 |
|
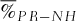 |
56.7% | 52.2% | 47.7% | 42.8% | 37.1% |
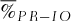 |
95.1% | 91.0% | 87.8% | 86.4% | 85.2% |
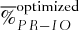 |
88.6% | 79.7% | 75.1% | 71.1% | 69.7% |
 |
$312,226 | $312,226 | $312,226 | $312,226 | $312,226 |
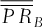 |
$500,811 | $459,996 | $428,513 | $402,272 | $378,569 |
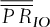 |
$460,090 | $418,571 | $388,277 | $360,674 | $338,745 |
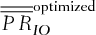 |
$478,679 | $440,764 | $410,702 | $387,494 | $365,630 |
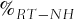 |
56.1% | 51.6% | 47.1% | 42.2% | 36.6% |
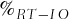 |
94.4% | 90.5% | 87.9% | 86.5% | 85.8% |
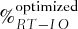 |
85.1% | 81.4% | 77.6% | 73.5% | 71.3% |
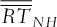 |
3.7% | 3.7% | 3.7% | 3.7% | 3.7% |
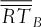 |
5.7% | 5.3% | 5.0% | 4.7% | 4.5% |
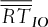 |
5.2% | 4.8% | 4.5% | 4.2% | 4.0% |
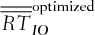 |
5.3% | 5.0% | 4.7% | 4.5% | 4.3% |
 |
$667,484 | $481,854 | $369,683 | $286,766 | $218,152 |
 |
$800,867 | $586,443 | $461,844 | $361,241 | $286 913 |
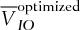 |
$895,118 | $667,376 | $533,688 | $409,736 | $300 534 |
Note
- A total of 10,000 scenarios for each of the 1, 000 parameters sets have been simulated.
 means that the different exercise prices,
means that the different exercise prices,  and
and  are set to the
are set to the  quantile of
quantile of  and
and  respectively (these
respectively (these  vary with the parameter sets). The initial values are
vary with the parameter sets). The initial values are  ,
,  ,
,  .
. 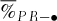
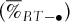 is the percentage of the 107 scenarios for which the profits (returns) associated with the basket option strategy is larger than the profits (returns) of the other strategy.
is the percentage of the 107 scenarios for which the profits (returns) associated with the basket option strategy is larger than the profits (returns) of the other strategy. 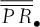
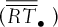 are the average profits (returns) based on the 107 scenarios.
are the average profits (returns) based on the 107 scenarios. 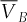 and
and 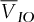 represent, respectively, the average basket option price and the sum of the average individual option prices. Whenever the superscript “optimized” is present, it indicates that the exercise prices of individual options no longer correspond to their quantiles, but that they have been optimized at the same time as the weights
represent, respectively, the average basket option price and the sum of the average individual option prices. Whenever the superscript “optimized” is present, it indicates that the exercise prices of individual options no longer correspond to their quantiles, but that they have been optimized at the same time as the weights  ,
,  , and
, and 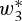 of the individual options so that the cash flows of the options’ portfolio are as similar as possible to those of the basket option.
of the individual options so that the cash flows of the options’ portfolio are as similar as possible to those of the basket option.
For each parameter set, we have calculated the percentages ( ) of the 1, 000 × 10, 000 scenarios for which the profit
) of the 1, 000 × 10, 000 scenarios for which the profit 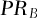 associated with the basket-option strategy is larger than the profit
associated with the basket-option strategy is larger than the profit  of the individual options strategy. A similar procedure is implemented to compare the returns associated with the two strategies.
of the individual options strategy. A similar procedure is implemented to compare the returns associated with the two strategies.
At first glance in Table II, the nonhedging strategy seems to dominate the basket strategy, as the profits associated with the basket strategy are larger than the nonhedging strategy's profits in certain moderate proportions ranging between 37% and 57% of the simulated scenarios. However, looking at the average profits and returns, the basket-option strategy surpasses the nonhedging strategy. The introduction of the basket-option shifts the portfolio distribution to the left (because of the initial cost), but increases the right tail of the distribution as the protection comes into play (see Figure 1). In this sense, risk management enables the firm to increase its value that corresponds to higher expected return in our model. The benefits of the basket option enlarge the right tail of the distribution much more significantly than the option price contributes to the left tail of the distribution. The asymmetric effect leads to the basket portfolio's distribution, which has a larger mean than the nonhedging strategy.
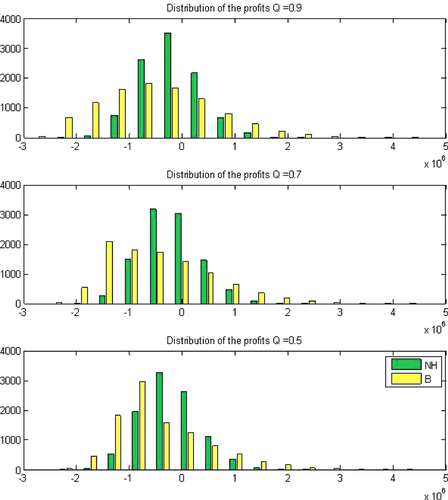
Compared to the individual options strategy (even in the optimized case), the basket option dominates in each of the considered measures reported in Table II. However, a couple of other aspects of basket options should be mentioned. In practice, investment banks that issue these options tend to factor high margins into their pricing, as the contracts are difficult to hedge. Furthermore, some options are very sensitive to the correlations, and correlations are often unstable and difficult to estimate, which tends to increase their price.
4. ESTIMATION RESULTS
4.1. Parameter Estimation
 be the points in time where the sample is observed and note that
be the points in time where the sample is observed and note that  depends on the convenience yield
depends on the convenience yield 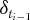 :
:
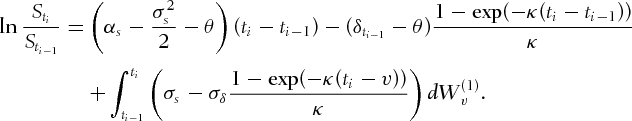 (3a)
(3a)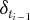 . Let
. Let 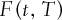 denote the time t value of a forward contract on the commodity with maturity date T. As shown in Appendix A, if the contract's time-to-maturity
denote the time t value of a forward contract on the commodity with maturity date T. As shown in Appendix A, if the contract's time-to-maturity  is small, then the convenience yield may be approximated by:
is small, then the convenience yield may be approximated by:
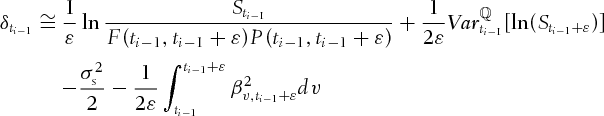 (3b)
(3b)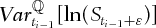 , given in the appendix (equation A.1), is a function of time and the maturity date. Note that it is possible to find the exact expression for
, given in the appendix (equation A.1), is a function of time and the maturity date. Note that it is possible to find the exact expression for  using the forward contract
using the forward contract  with an arbitrary maturity date
with an arbitrary maturity date  but it involves the instantaneous forward rates
but it involves the instantaneous forward rates  ,
,  that would have to be estimated at each sampling date (a sample of size n requires the estimation of n term structures of instantaneous forward rates).
that would have to be estimated at each sampling date (a sample of size n requires the estimation of n term structures of instantaneous forward rates). where λ(3) is a certain risk premium and
where λ(3) is a certain risk premium and  . This relationship appears in the construction of the risk-neutral measure
. This relationship appears in the construction of the risk-neutral measure  . Because the domestic zero-coupon bond satisfies the relationship
. Because the domestic zero-coupon bond satisfies the relationship
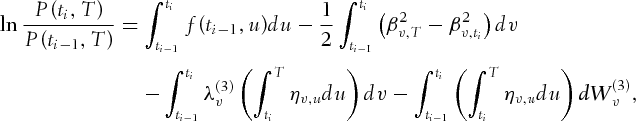 (3c)
(3c) is required at each sampling date. However, these rates are not directly observable and, to avoid estimating them, we rely on forward contracts on zero-coupon bonds. Indeed, if
is required at each sampling date. However, these rates are not directly observable and, to avoid estimating them, we rely on forward contracts on zero-coupon bonds. Indeed, if  denotes the time
denotes the time  value of some forward contract on a zero-coupon bond, where
value of some forward contract on a zero-coupon bond, where  is the maturity date of the contract and
is the maturity date of the contract and  is the maturity date of the underlying zero-coupon bond, then7 for
is the maturity date of the underlying zero-coupon bond, then7 for  ,
,
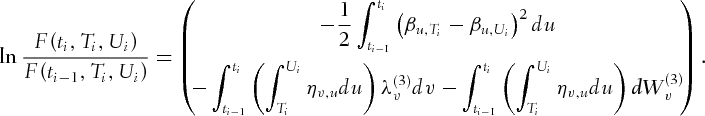 (3d)
(3d)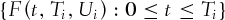 is a Gaussian Markovian process under the objective measure
is a Gaussian Markovian process under the objective measure  and depends only on the diffusion coefficient
and depends only on the diffusion coefficient  and the risk premium
and the risk premium  .
.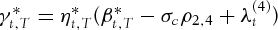 where λ(4) is a risk premium and
where λ(4) is a risk premium and  . The foreign zero-coupon bond requires the unobserved term structure of the instantaneous forward rates
. The foreign zero-coupon bond requires the unobserved term structure of the instantaneous forward rates  . Let
. Let  denote the time t value of some forward contracts on a foreign zero-coupon bond, where
denote the time t value of some forward contracts on a foreign zero-coupon bond, where  is the maturity date of the contract and
is the maturity date of the contract and  is the maturity date of the underlying zero-coupon bond. The forward contract value satisfies
is the maturity date of the underlying zero-coupon bond. The forward contract value satisfies
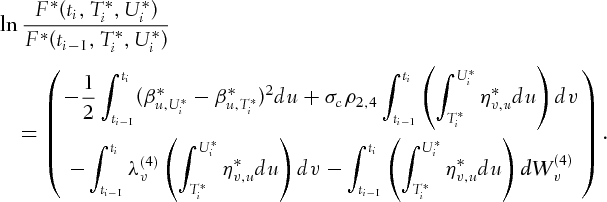 (3e)
(3e)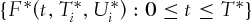 is Markovian and normally distributed under the objective measure
is Markovian and normally distributed under the objective measure  and depends only on the diffusion coefficients
and depends only on the diffusion coefficients 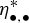 and
and  , the correlation coefficient ρ2, 4 and the risk premium
, the correlation coefficient ρ2, 4 and the risk premium 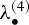 .
.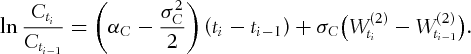

 and
and  . Let
. Let  denote the set of parameters that will be estimated where
denote the set of parameters that will be estimated where  contains the parameters needed in the pricing of the basket option, whereas
contains the parameters needed in the pricing of the basket option, whereas  are some parameters that will be estimated but not used in the pricing procedure:
are some parameters that will be estimated but not used in the pricing procedure:

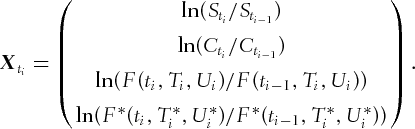
 is
is
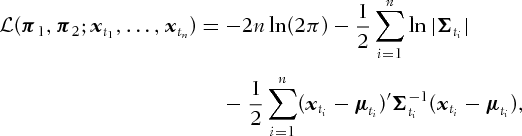 (4)
(4)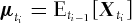 and covariance matrix
and covariance matrix 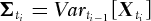 are given in Appendix B.
are given in Appendix B.-
Step 1. We estimate the parameters
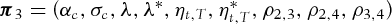 associated with the exchange rate and the domestic and foreign interest rates using the log-likelihood function
where
associated with the exchange rate and the domestic and foreign interest rates using the log-likelihood function
where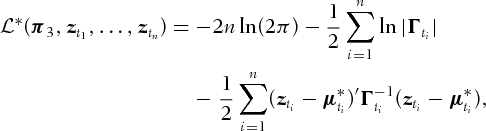
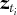 contains the three last components of
contains the three last components of  ,
, 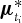 is formed with the last three components of
is formed with the last three components of  and
and 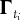 is the 3 × 3 matrix
is the 3 × 3 matrix  .
.
Note that in the case8 where
 and
and  , that is, the two first moments are constant through time, it is possible to find analytically the maximum likelihood estimates
, that is, the two first moments are constant through time, it is possible to find analytically the maximum likelihood estimates 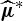 and
and 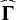 that maximize the log-likelihood function
that maximize the log-likelihood function 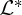 . The parameters estimates
. The parameters estimates 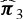 are chosen such that
are chosen such that  and
and 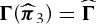 .
. - Step 2. Assuming that
 , then the log-likelihood
, then the log-likelihood  is maximized to get estimates for
is maximized to get estimates for 
The numerical optimization routine used to maximize these two log-likelihood functions is the quadratic hill-climbing algorithm of Goldfeld, Quandt, and Trotter (1966) with a convergence criterion based on the absolute values of the variations in parameter values and functional values between successive iterations. When both of these changes are smaller than 10−5, we attend convergence.
Maximum likelihood methods not only produce point estimates, but allow for the computation of precision measures through the estimators’ standard deviation estimations. Because in the second stage some parameters are not optimized, being fixed to the values obtained in the first step, some potential variability that could affect the estimates of standard deviations is eliminated. We therefore perform a Monte Carlo study to assess numerically the quality of our estimates.
4.2. Monte Carlo Study
We conduct a Monte Carlo study to evaluate the quality of the coefficients estimated using the maximum likelihood method. We verify numerically that the two-step procedure does not produce biased point estimates. Moreover, we assess numerically how well the asymptotic normal distribution proposed by the theory approximates the empirical distributions for a reasonable sample size. More precisely, we generate daily observations for two different sampling periods: four and ten years. For each time series, maximum likelihood estimates are computed, as are their associated estimated standard error and confidence intervals based on the Gaussian distribution. We repeat the simulation run 2,000 times and report averages of the point estimates and the proportions of the simulated scenarios producing confidence intervals that contain the true parameter value. If the Gaussian distribution and the estimation of the estimator's standard errors are appropriate, then the proportions should be close to their corresponding confidence level. The forward contracts on the commodity have a time-to-maturity of one day.
As shown in Tables III, IV, V, and VI, for all the parameters, the maximum likelihood estimators are asymptotically unbiased. However, the standard deviations of the risk premium estimators as well as those of the convenience yield's parameters are large, which means that the point estimation is imprecise for these parameters. The coverage rates associated with these parameters indicate that either the estimator's standard deviation estimates are incorrect or the asymptotic distribution has not been reached, even with the ten-year sample. For all other parameters, the standard errors indicate that we are in the presence of precise point estimators and that the Gaussian distribution is appropriate for inference.
 |
 |
λ |  |
η |  |
 |
 |
 |
|
|---|---|---|---|---|---|---|---|---|---|
| True | 0.0900 | 0.0300 | 1.2000 | 1.2000 | 0.0200 | 0.0150 | 0.1500 | 0.2000 | 0.8500 |
| Mean | 0.0911 | 0.0299 | 1.2589 | 1.2649 | 0.0199 | 0.0149 | 0.1501 | 0.2010 | 0.8497 |
| Median | 0.0911 | 0.0299 | 1.2325 | 1.2515 | 0.0200 | 0.0150 | 0.1515 | 0.2016 | 0.8502 |
| Std | 0.0218 | 0.0013 | 0.6215 | 0.6098 | 0.0016 | 0.0022 | 0.0538 | 0.0464 | 0.0127 |
| 25 % cvr | 0.2460 | 0.2405 | 0.2980 | 0.3115 | 0.2655 | 0.2695 | 0.2510 | 0.2745 | 0.2450 |
| 50 % cvr | 0.4910 | 0.4960 | 0.5315 | 0.5465 | 0.5090 | 0.5065 | 0.4930 | 0.5085 | 0.5000 |
| 75 % cvr | 0.7435 | 0.7435 | 0.7470 | 0.7515 | 0.7520 | 0.7525 | 0.7625 | 0.7475 | 0.7590 |
| 90 % cvr | 0.8910 | 0.9000 | 0.8575 | 0.8600 | 0.8990 | 0.9035 | 0.9080 | 0.9060 | 0.8970 |
| 95 % cvr | 0.9430 | 0.9490 | 0.8930 | 0.8965 | 0.9450 | 0.9475 | 0.9480 | 0.9445 | 0.9415 |
| 99 % cvr | 0.9850 | 0.9880 | 0.9315 | 0.9365 | 0.9835 | 0.9850 | 0.9830 | 0.9810 | 0.9820 |
Note
- Mean, median, and std are the descriptive statistics based on the simulated sample of 2,000 parameter estimates obtained from the two-step procedure. The coverage rates (cvr) represent the proportion of the confidence intervals (based on the Gaussian distribution and the estimator's standard deviation estimate) that contain the true parameter's value. The estimates written in bold differ significantly from their theoretical counterpart (at a confidence level of 95%). Std, standard deviation.
 |
 |
κ | θ |  |
 |
 |
 |
|
|---|---|---|---|---|---|---|---|---|
| True | 0.2500 | 0.1200 | 0.2000 | 0.1000 | 0.1500 | −0.1000 | −0.2500 | −0.3000 |
| Mean | 0.2715 | 0.1197 | 0.1605 | 0.1089 | 0.1676 | −0.0976 | −0.2493 | −0.2997 |
| Median | 0.2677 | 0.1197 | 0.1622 | 0.1058 | 0.1260 | −0.0991 | −0.2499 | −0.3008 |
| Std | 0.0871 | 0.0043 | 0.1337 | 0.0578 | 0.1831 | 0.0498 | 0.0412 | 0.0405 |
| 25 % cvr | 0.2590 | 0.2535 | 0.4420 | 0.6695 | 0.2135 | 0.2505 | 0.2600 | 0.2440 |
| 50 % cvr | 0.5090 | 0.4935 | 0.5385 | 0.8300 | 0.4065 | 0.4815 | 0.4860 | 0.4960 |
| 75 % cvr | 0.7450 | 0.7390 | 0.5815 | 0.8965 | 0.4870 | 0.7375 | 0.7410 | 0.7505 |
| 90 % cvr | 0.8875 | 0.8920 | 0.6120 | 0.9325 | 0.5255 | 0.8640 | 0.8955 | 0.8865 |
| 95 % cvr | 0.9345 | 0.9460 | 0.6255 | 0.9435 | 0.5345 | 0.9080 | 0.9425 | 0.9315 |
| 99 % cvr | 0.9735 | 0.9860 | 0.6475 | 0.9525 | 0.5500 | 0.9445 | 0.9835 | 0.9850 |
Note
- Mean, median, and std are the descriptive statistics based on the simulated sample of 2,000 parameter estimates obtained from the two-step procedure. The coverage rates (cvr) represent the proportion of the confidence intervals (based on the Gaussian distribution and the estimator's standard deviation estimate) that contain the true parameter's value. The estimates written in bold differ significantly from their theoretical counterpart (at a confidence level of 95%). Std, standard deviation.
 |
 |
λ |  |
η |  |
 |
 |
 |
|
|---|---|---|---|---|---|---|---|---|---|
| True | 0.0900 | 0.0300 | 1.2000 | 1.2000 | 0.0200 | 0.0150 | 0.1500 | 0.2000 | 0.8500 |
| Mean | 0.0898 | 0.0300 | 1.1986 | 1.1994 | 0.0200 | 0.0150 | 0.1499 | 0.1998 | 0.8499 |
| Median | 0.0900 | 0.0300 | 1.2087 | 1.1941 | 0.0200 | 0.0150 | 0.1503 | 0.2000 | 0.8501 |
| Std | 0.0093 | 0.0004 | 0.3136 | 0.3209 | 0.0003 | 0.0002 | 0.0186 | 0.0185 | 0.0055 |
| 25 % cvr | 0.2618 | 0.2495 | 0.2811 | 0.2781 | 0.2663 | 0.2623 | 0.2825 | 0.2781 | 0.2505 |
| 50 % cvr | 0.4985 | 0.5030 | 0.5148 | 0.5059 | 0.5118 | 0.5049 | 0.5286 | 0.5350 | 0.5108 |
| 75 % cvr | 0.7456 | 0.7392 | 0.7130 | 0.7106 | 0.7510 | 0.7623 | 0.7766 | 0.7771 | 0.7579 |
| 90 % cvr | 0.9078 | 0.8955 | 0.8402 | 0.8269 | 0.8881 | 0.9073 | 0.9083 | 0.8999 | 0.9019 |
| 95 % cvr | 0.9443 | 0.9487 | 0.8802 | 0.8787 | 0.9487 | 0.9551 | 0.9443 | 0.9433 | 0.9512 |
| 99 % cvr | 0.9768 | 0.9882 | 0.9285 | 0.9334 | 0.9852 | 0.9877 | 0.9808 | 0.9798 | 0.9887 |
Note
- Mean, median, and std are the descriptive statistics based on the simulated sample of 2,000 parameter estimates obtained from the two-step procedure. The coverage rates (cvr) represent the proportion of the confidence intervals (based on the Gaussian distribution and the estimator's standard deviation estimate) that contain the true parameter's value. The estimates written in bold differ significantly from their theoretical counterpart (at a confidence level of 95%). Std, standard deviation.
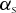 |
 |
κ | θ |  |
 |
 |
 |
|
|---|---|---|---|---|---|---|---|---|
| True | 0.2500 | 0.1200 | 0.2000 | 0.1000 | 0.1500 | −0.1000 | −0.2500 | −0.3000 |
| Mean | 0.2527 | 0.1199 | 0.1930 | 0.0977 | 0.1400 | −0.1006 | −0.2500 | −0.2999 |
| Median | 0.2528 | 0.1199 | 0.1899 | 0.0977 | 0.1448 | −0.1010 | −0.2497 | −0.3004 |
| Std | 0.0528 | 0.0017 | 0.0486 | 0.0437 | 0.0532 | 0.0194 | 0.0187 | 0.0184 |
| 25 % cvr | 0.2489 | 0.2696 | 0.4634 | 0.4643 | 0.2873 | 0.2573 | 0.2602 | 0.2420 |
| 50 % cvr | 0.4786 | 0.5224 | 0.6916 | 0.6950 | 0.4771 | 0.5027 | 0.5007 | 0.4988 |
| 75 % cvr | 0.7004 | 0.7560 | 0.8190 | 0.8077 | 0.6449 | 0.7368 | 0.7304 | 0.7290 |
| 90 % cvr | 0.8396 | 0.8977 | 0.8819 | 0.8603 | 0.7467 | 0.8770 | 0.8849 | 0.8869 |
| 95 % cvr | 0.8859 | 0.9474 | 0.9026 | 0.8844 | 0.7821 | 0.9188 | 0.9356 | 0.9385 |
| 99 % cvr | 0.9415 | 0.9902 | 0.9297 | 0.9051 | 0.8259 | 0.9661 | 0.9818 | 0.9848 |
Note
- Mean, median, and std are the descriptive statistics based on the simulated sample of 2,000 parameter estimates obtained from the two-step procedure. The coverage rates (cvr) represent the proportion of the confidence intervals (based on the Gaussian distribution and the estimator's standard deviation estimate) that contain the true parameter's value. The estimates written in bold differ significantly from their theoretical counterpart (at a confidence level of 95%). Std, standard deviation.
To determine whether the two-step procedure produces different estimates from those obtained if the complete likelihood function is used, we compare estimates obtained from both procedures. Even though the numerical results are not presented herein, we can still draw two main conclusions. First, there are no significant differences between the point estimates generated by the two procedures. Second, the standard deviations based on 2,000 parameter estimates differ slightly from one procedure to another when the sample is for the four-year term, but their differences are shrinking for the ten-year sample length. This indicates that the precision of both procedures converges to the same values as the length of the sampling period increases.
In conclusion, we obtain reasonable point estimates despite some problems with the dispersion of some parameters.
4.3. Real-Data Study
In the following, we apply the procedure outlined in Section 4.1. to real data.
Both algorithms in one and two steps may remain trapped in a local optimum. For this reason, the optimization algorithm is initiated with many initial points. These are obtained by a lattice based on plausible ranges for each parameter. Obviously, the dimension of this lattice increases exponentially with the number of parameters to be estimated. This is one reason why the two-step procedure is potentially more effective.
In the real-data study presented below, we adopt a three-step procedure to benefit from the computational gain of the two-step procedure as well as consistent standard deviation estimates of the parameters’ estimators arising from the one-step procedure. Indeed, the estimates obtained with the two-step procedure (using a multistart heuristic) is used as initial value in the optimization routine of the complete likelihood function (one-step procedure). We refer to this approach as the three-step procedure. A simulation study not reported herein has shown that, using a single initial point, the three-step procedure is four times faster than the one-step procedure with an average computation time of 9.5 minutes (with a standard deviation of 4 minutes), compared with 39 minutes and a standard deviation of 4.5 minutes. Intuitively, it is because the two-step procedure converges faster as the dimension of the objective function is smaller and, starting with a good initial point, the one-step procedure converge much more faster. Moreover, the quality of the optimum found with the three-step procedure is better in all cases, that is to say, the likelihood is larger.
4.3.1. Data

 , and
, and  we use the three-month Eurodollar Time Deposit futures contracts traded on the Chicago Mercantile Exchange (CME), and the three-month Canadian Bankers’ Acceptance (BAX) futures contracts traded on the Montréal Exchange.9 Both BAX and Eurodollar futures contracts are settled in cash and have the same delivery date on the second London bank business day immediately preceding the third Wednesday of the contract month. Although the Eurodollar contract is chosen for its extreme liquidity, the less liquid BAX contract represents the more tradable contract on a riskless zero-coupon bond available in Canada. Our sample consists of daily prices for both contracts ranging from January 1, 2001 to December 31, 2010. It should be noted that both futures contracts are traded on an index basis, meaning that the contract price is calculated by subtracting the annualized implied yield of the underlying asset from 100. For example, a December BAX (Eurodollar) contract quoted as 97.30 on the exchange floor implies a 2.70% (i.e., 100 − 97.30) annual yield for the BAX (Eurodollar) issued in December. To carry out the estimation, we need the futures prices under the physical measure
we use the three-month Eurodollar Time Deposit futures contracts traded on the Chicago Mercantile Exchange (CME), and the three-month Canadian Bankers’ Acceptance (BAX) futures contracts traded on the Montréal Exchange.9 Both BAX and Eurodollar futures contracts are settled in cash and have the same delivery date on the second London bank business day immediately preceding the third Wednesday of the contract month. Although the Eurodollar contract is chosen for its extreme liquidity, the less liquid BAX contract represents the more tradable contract on a riskless zero-coupon bond available in Canada. Our sample consists of daily prices for both contracts ranging from January 1, 2001 to December 31, 2010. It should be noted that both futures contracts are traded on an index basis, meaning that the contract price is calculated by subtracting the annualized implied yield of the underlying asset from 100. For example, a December BAX (Eurodollar) contract quoted as 97.30 on the exchange floor implies a 2.70% (i.e., 100 − 97.30) annual yield for the BAX (Eurodollar) issued in December. To carry out the estimation, we need the futures prices under the physical measure  ; hence, we must convert the quoted prices using the equations:
; hence, we must convert the quoted prices using the equations:
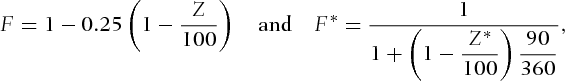
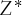 represent the quoted prices for the Eurodollar and BAX futures contracts, respectively.
represent the quoted prices for the Eurodollar and BAX futures contracts, respectively.We also use daily gold prices as well as the CAD/USD exchange rate covering the same period as above to estimate the parameters related to the commodity price and the exchange rate: the drifts 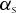 and
and  the volatilities
the volatilities  and
and  , and the correlation coefficient ρ12. Finally, we use gold futures contracts to estimate the convenience yield and its parameters.
, and the correlation coefficient ρ12. Finally, we use gold futures contracts to estimate the convenience yield and its parameters.
The data are obtained from Datastream. The summary statistics for the various data used are provided in Table VII.
| Assets | Mean | Median | Standard Deviation |
|---|---|---|---|
| Gold prices | 617.40 | 528.10 | 308.02 |
| Exchange rates CAD/USD | 0.8208 | 0.8315 | 0.1235 |
| Eurodollar futures contracts | 0.9934 | 0.9947 | 0.0044 |
| BAX contracts | 0.9931 | 0.9929 | 0.0033 |
| Gold futures contracts | 617.99 | 527.90 | 308.21 |
 |
|||
Note
- The descriptive statistics are based on a sample of daily observations over ten years.
4.3.2. Empirical results
We proceed with a two-step estimation in order to avoid any convergence problems. First, we estimate the exchange rate, the domestic, and foreign zero-coupon bonds parameters as well as the correlation coefficients between these three variables  . Then, we use these estimates to determine the parameters related to the commodity and the convenience yield
. Then, we use these estimates to determine the parameters related to the commodity and the convenience yield  that maximize the global likelihood function given in Equation (4). We apply the quadratic hill-climbing algorithm of Goldfeld et al. (1966), and we use different starting points to increase the probability of reaching a global maximum.10 To ensure that the two-step procedure does not create a bias, we use the results of the latter to initiate the optimization of the complete likelihood function.
that maximize the global likelihood function given in Equation (4). We apply the quadratic hill-climbing algorithm of Goldfeld et al. (1966), and we use different starting points to increase the probability of reaching a global maximum.10 To ensure that the two-step procedure does not create a bias, we use the results of the latter to initiate the optimization of the complete likelihood function.
The results from the maximum likelihood estimation are reported in Table VIII. First, note that the point estimates obtained by the two procedures are similar. However, the estimated standard deviation of the estimators are different in the case of risk premiums, the mean reversion parameter θ, and some of the correlations. This may be because the two-step procedure neglects the variation of some parameters when estimating the second set of parameters. This means that the two-step procedure produces good point estimates, but inferences should be handled with care.
| Two-Step Procedure | |||||
|---|---|---|---|---|---|
| Estimate | Std | Estimate | Std | ||
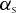 |
−0.1266 | 0.0589 | κ | −0.0175 | 0.0019 |
 |
0.0460 | 0.0083 | θ | 0.0261 | 0.0292 |
 |
0.1698 | 0.0023 |  |
0.2007 | 0.0717 |
 |
0.1014 | 0.0014 | ρ12 | 0.2293 | 0.0189 |
| η | 0.0056 | 0.0001 | ρ13 | −0.0202 | 0.0078 |
 |
0.0050 | 0.0001 | ρ14 | −0.0452 | 0.0302 |
| λ | −0.7731 | 0.1640 | ρ23 | −0.0602 | 0.0129 |
 |
−0.6006 | 0.3032 | ρ24 | 0.1122 | 0.0175 |
| ρ34 | 0.3549 | 0.0319 | |||
| Likelihood = 67,586.30 | |||||
| Three-Step Procedure | |||||||
|---|---|---|---|---|---|---|---|
| Estimate | Std | p-value | Estimate | Std | p-value | ||
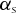 |
−0.1349 | 0.0267 | 0.0000 | κ | −0.0152 | 0.0037 | 0.0000 |
 |
0.0461 | 0.0126 | 0.0001 | θ | 0.0059 | 0.0048 | 0, 1096 |
 |
0.1698 | 0.0023 | 0.0000 |  |
0.1856 | 0.0346 | 0.0000 |
 |
0.1014 | 0.0014 | 0.0000 | ρ12 | 0.2291 | 0.0183 | 0.0000 |
| η | 0.0056 | 0.0001 | 0.0000 | ρ13 | −0.0211 | 0.0052 | 0.0000 |
 |
0.0050 | 0.0001 | 0.0000 | ρ14 | −0.0447 | 0.0196 | 0, 0114 |
| λ | −0.7731 | 0.1897 | 0.0000 | ρ23 | −0.0601 | 0.0059 | 0.0000 |
 |
−0.5998 | 0.0958 | 0.0000 | ρ24 | 0.1125 | 0.0207 | 0.0000 |
| ρ34 | 0.3549 | 0.0170 | 0.0000 | ||||
| Likelihood = 67,586.31 | |||||||
Note
- The estimates and their standard deviations are obtained from daily observations over a ten-year sample, extending from January 1, 2001 to December 31, 2010. The p-values are computed using the Gaussian distribution. The relative value of the gradient norm with respect to the objective function at the optimum point is
 .
.
The results show that both risk premiums, the instantaneous returns estimate of the commodity 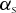 and the exchange rate
and the exchange rate  are rather imprecise. However, three of these four parameters are not used in the pricing of the basket option. The convenience yield mean reversion parameters estimates,
are rather imprecise. However, three of these four parameters are not used in the pricing of the basket option. The convenience yield mean reversion parameters estimates,  and
and 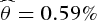 , are small. This result is in line with the finding in Schwartz (1997) that mean reversion for convenience yields does not seem to hold for gold. On the other hand, the volatility parameters for commodity, exchange rate, domestic, and foreign zero-coupon bonds are estimated fairly accurately and differ very significantly from zero. We will not comment on the risk premium as the Monte Carlo study indicates that the point estimates are imprecise and that inference is meaningless (the coverage rates being false, even with a ten-year sample).
, are small. This result is in line with the finding in Schwartz (1997) that mean reversion for convenience yields does not seem to hold for gold. On the other hand, the volatility parameters for commodity, exchange rate, domestic, and foreign zero-coupon bonds are estimated fairly accurately and differ very significantly from zero. We will not comment on the risk premium as the Monte Carlo study indicates that the point estimates are imprecise and that inference is meaningless (the coverage rates being false, even with a ten-year sample).
The correlation coefficients are between the different Brownian motions. However, from the nature of the model, they are also related to the correlations among the logarithm of the forward contracts, gold prices, and exchange rate as established in Appendix B. As expected, the correlation ρ34 between the Canadian and American zero-coupon bonds’ noise terms is high and statistically different from zero. We observe a small negative correlation between the Brownian motions involved in the gold prices and futures contracts on both Eurodollars,  and BAX,
and BAX,  . We also note a highly significant positive correlation between gold price and foreign exchange noises
. We also note a highly significant positive correlation between gold price and foreign exchange noises  . The correlations between the exchange rate and futures contracts noises on both domestic
. The correlations between the exchange rate and futures contracts noises on both domestic  and foreign
and foreign  bonds are relatively small.
bonds are relatively small.
5. CONCLUSION
This study describes various steps for developing a sound risk management of a nonstandard basket option based on a commodity price with stochastic convenience yield, exchange rate, and domestic and foreign zero-coupon bonds in a stochastic interest rate environment. Our main contribution is the consideration of many risk management aspects of basket options: modeling, performance analysis, econometric estimation of parameters, and the application of the model to real data of a nonfinancial firm. The empirical implementation of our model raises several problems that are successfully solved. Many of the variables prove to be unobservable, such as the commodity convenience yield, the market price of convenience-yield risk, and the market-price risk related to zero-coupon bonds. To overcome these problems, we assume that the process describing the convenience yield has the same source of risk as the commodity process. This simplification frees us from having to estimate the market-price risk related to the convenience yield. Second, we view the futures contract as a derivative instrument based on the instantaneous forward rate. It thus derives its uncertainty from the same source of risk as the forward rate. We empirically compare the performance of a basket-option strategy and that of a portfolio of individual plain vanilla options using a large variety of parameter values. Our results show that the nonstandard basket option dominates the individual option strategy. Compared with the nonhedging strategy, the profit distributions have fatter tails with positive skewness, meaning that the probability of larger profits is augmented. The basket option also dominates the individual options strategy. Consequently, the basket option is a superior risk management strategy for maximizing shareholders’ profits. We estimate our theoretical model empirically, using both simulated and real data. Application of the maximum likelihood method to estimate the parameters of risky assets yields satisfactory results. Our contribution should be very useful for practitioners who use this kind of product for hedging.
 and
and  will be set to some constants (η and
will be set to some constants (η and  ) or some exponential functions (
) or some exponential functions (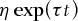 ) and
) and 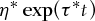 ) at the estimation stage.
) at the estimation stage. , one needs to constitute the self-financing assets expressed in the domestic currency. These four assets are (1) the value
, one needs to constitute the self-financing assets expressed in the domestic currency. These four assets are (1) the value 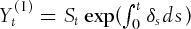 of a portfolio initially formed with the commodity S0, and, whenever they are perceived, the profits are reinvested to buy more of the commodity; (2) the value
of a portfolio initially formed with the commodity S0, and, whenever they are perceived, the profits are reinvested to buy more of the commodity; (2) the value  of the foreign bank account expressed in the domestic currency; (3) the domestic zero-coupon bond; and (4) the value
of the foreign bank account expressed in the domestic currency; (3) the domestic zero-coupon bond; and (4) the value 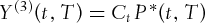 of the foreign zero-coupon bond converted to the domestic currency. Using the standard methodology,
of the foreign zero-coupon bond converted to the domestic currency. Using the standard methodology, 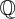 is constructed such that the four relevant assets have the risk-free rate as return. Details are available from the authors upon request.
is constructed such that the four relevant assets have the risk-free rate as return. Details are available from the authors upon request. is a
is a  -martingale. Therefore,
-martingale. Therefore, 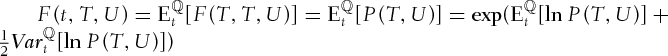 where
where 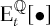 denotes the conditional expectation with respect to the information available at time t:
denotes the conditional expectation with respect to the information available at time t: 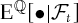 . The last equality is justified by the log-normal distribution of
. The last equality is justified by the log-normal distribution of  . The final result is obtained from the evaluation of the conditional moments of
. The final result is obtained from the evaluation of the conditional moments of 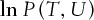 under the risk-neutral measure
under the risk-neutral measure  .
.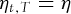 and
and  of the instantaneous forward rates are constant, the time between two sample observations
of the instantaneous forward rates are constant, the time between two sample observations  is constant, and the differences between the maturity date of the underlying bond and the maturity date of the forward contract
is constant, and the differences between the maturity date of the underlying bond and the maturity date of the forward contract  and
and  are constant, then
are constant, then

Appendix A
Forward Contract on Commodity
 . Therefore,
. Therefore,
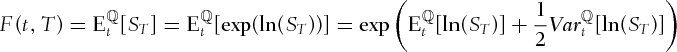
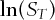 is normally distributed under the measure
is normally distributed under the measure  and where
and where 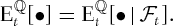 Recall that
Recall that
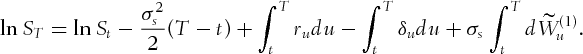
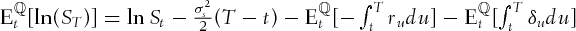 . Since
. Since

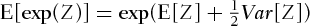 implies that
implies that 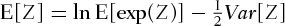 ,
,
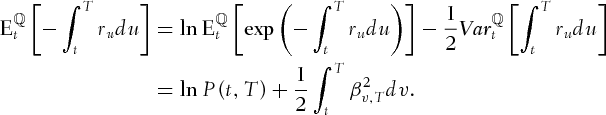
 is small,
is small, 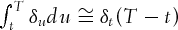 and
and
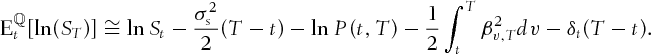
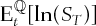 . Second, we evaluate
. Second, we evaluate 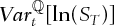 . Since
. Since
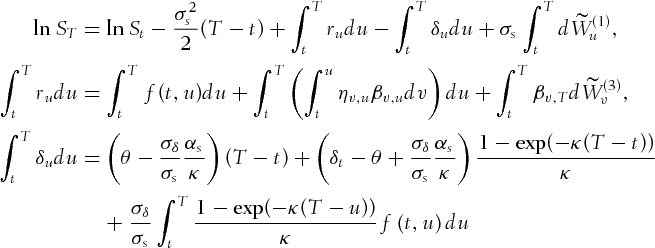
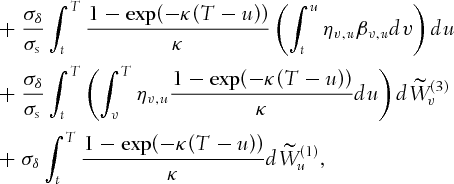
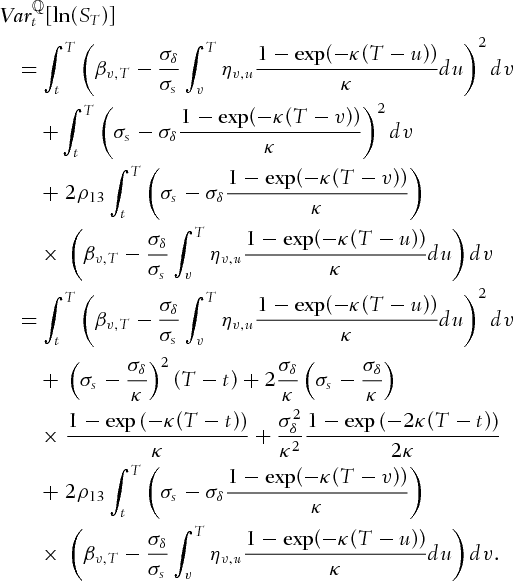 (A.1)
(A.1)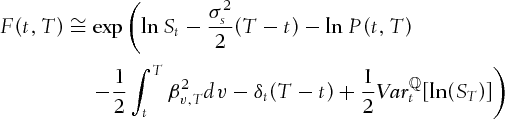
 is small,
is small,
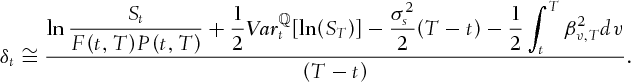
Appendix B
The Log-Likelihood Function
In this section, we determine the log-likelihood function (4).
 and let
and let 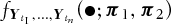 denote the joint density of the random vectors
denote the joint density of the random vectors  and
and  stands for the conditional density of
stands for the conditional density of 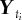 given
given  . The log-likelihood function associated with the observed sample
. The log-likelihood function associated with the observed sample 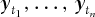 is
is
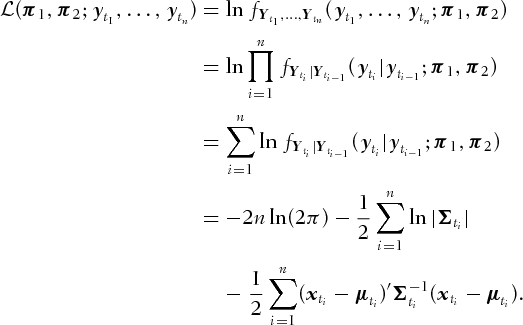
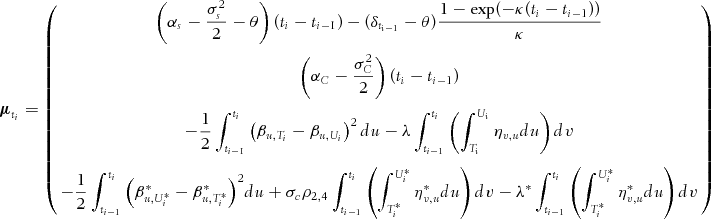
 where
where