New numerical schemes based on a criterion for constructing essentially stable and accurate numerical schemes for convection-dominated equations

In order to obtain stable and accurate numerical solutions for the convection-dominated steady transport equations, we propose a criterion for constructing numerical schemes for the convection term that the roots of the characteristic equation of the resulting difference equation have poles.

By imposing this criterion on the difference coefficients of the convection term, we construct two numerical schemes for the convection-dominated equations. One is based on polynomial differencing and the other on locally exact differencing.

The former scheme coincides with the QUICK scheme when the mesh Reynolds number (Rm) is \documentclass{article}\pagestyle{empty}\begin{document}$\mathop \[{\textstyle{{\rm 8} \over {\rm 3}}}\] $\end{document}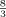, which is the critical value for its stability, while it approaches the second-order upwind scheme as Rm goes to infinity. Hence the former scheme interpolates a stable scheme between the QUICK scheme at Rm = \documentclass{article}\pagestyle{empty}\begin{document}$\mathop \[{\textstyle{{\rm 8} \over {\rm 3}}}\] $\end{document} 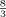and the second-order upwind scheme at Rm = ∞. Numerical solutions with the present new schemes for the one-dimensional, linear, steady convection-diffusion equations showed good results.