Modeling the toxicity of polar and nonpolar narcotic compounds to luminescent bacterium Shk1
Abstract
Luminescent bacterium Shk1 was created for the purpose of testing and screening the toxicity of activated sludge wastewater treatment plant influent to avoid toxic shock to the wastewater treatment plant microorganisms. The toxicity of a number of organic compounds was tested using an assay employing Shk1. Because these compounds exhibit toxicity by mechanisms of both polar and nonpolar narcosis, their toxicity cannot be properly modeled together using a quantitative structure-activity relationship model based on the logarithm of the octanol-water partition coefficient (log Kow). A solvation parameter model was developed to describe and predict the nonspecific (i.e., polar and nonpolar narcosis) toxicity of organic compounds to Shk1, which does not depend on the discrimination between polar and nonpolar narcotic compounds. The statistically significant model descriptors were the McGowan's characteristic volume (VX) and the hydrogen-bond basicity (∑βH). The model was similar to the solvation parameter model developed for Vibrio fischeri, but it did not include an excess molar refraction (R) term.
INTRODUCTION
Bioassays have been widely used for toxicity testing in various compartments of the environment, such as water/ wastewater, sediment, and soil. An ideal bioassay for toxicity testing should be inexpensive, easy to perform, accurate, reproducible, and both relevant and appropriate for on-line or in situ toxicity monitoring [1]. Luminescent bacteria-based bioassays have an additional advantage in that they usually have a short response time. The commercial basis for a luminescent bacteria-based assay was first described by Bulich [2]. The assay employed the marine luminescent bacterium Vibrio fischeri (also known as Photobacterium phosphoreum). This assay was later marketed by Azur Environmental (Carlsbad, CA, USA) and is commonly applied as the Microtoxr̀ assay, which has become a standardized method for assessing possible ecotoxicological effects of water samples [3].
In recent years, interest has been increasing in regard to testing and estimating the toxicity of influent to activated sludge wastewater treatment plants to prevent upsets in plant operations caused by influent toxicity. Whereas V. fischeri has been used for the toxicity monitoring of effluent discharges [4, 5], studies in the literature have frequently concluded that V. fischeri is not well suited for predicting the possible toxic effects of influent wastewater on the activated sludge [6-9], because V. fischeri is not an indigenous activated sludge microorganism.
The continuous Shk1 assay was developed at the Center for Environmental Biotechnology at the University of Tennessee for the purpose of influent wastewater toxicity monitoring and has been described previously [10]. The bacterium used in this assay, Shk1, is a genetically modified luminescent bacterium whose host strain was isolated from the activated sludge in an industrial wastewater treatment plant [11]. When applied to influent wastewater toxicity assessment, the continuous Shk1 assay has the advantage of being relevant to the activated sludge compared to other assays that use luminescent organisms not native to activated sludge. In our previous study [10], we demonstrated that compared to the Microtox assay, the results of the continuous Shk1 assay for phenols are more similar to those of activated sludge respiration or growth-inhibition assays.
The number of chemical compounds in industrial use is huge; currently, more than 100,000 chemical compounds are used worldwide [12]. A significant number of environmental pollutants are eventually discharged into wastewater. However, due to cost and other constraints, testing the toxicity of all compounds that can eventually exist in wastewater is difficult. A quantitative structure-activity relationship (QSAR) can be developed and used to predict toxicity when little or no experimental data are available. We have developed QSAR models based on the logarithm of the octanol-water partition coefficient (log Kow) for phenols in our previous study [10]. The continuous Shk1 assay can be applied to compounds other than phenols, but we limited the scope of that previous study to phenols because of their distinct mechanism of toxicity.
Several mechanisms of aquatic toxicity have been identified, such as polar and nonpolar narcosis, respiratory uncoupling, etc. [13]. These mechanisms of toxicity can be broadly categorized as general or specific [14]. General toxicity refers to polar and nonpolar narcosis, which act by nonspecific disruption of the functioning of the cell membrane, and specific toxicity refers to reactive toxicity, which occurs through disruption of the function of a defined receptor site in the cell [14]. Most industrial organic chemicals have a narcotic mode of toxic action [15]. The correlation of the observed toxicity of nonpolar narcotic compounds with log Kow has been used to define a baseline toxicity [13]. Polar narcotic compounds, which include phenols and anilines, exhibit toxicity slightly greater than that predicted by the baseline toxicity, whereas reactive compounds can exhibit toxicity orders of magnitude higher than that predicted by baseline toxicity [16].
Because of the deviations from the baseline toxicity of polar narcotic compounds, properly modeling the toxicity of polar and nonpolar narcotic compounds together using log Kow usually is difficult. For example, when Tang et al. [17] modeled the toxicity of both nonpolar and polar narcotic (namely, phenols) compounds with log Kow, a low r2 (coefficient of determination) of 0.11 was obtained. As those authors noted, two groups of data points were present; consequently, the authors developed separate QSAR models. After separating the two classes of compounds, the r2 values increased to 0.88 and 0.79 for nonpolar narcotic compounds and polar narcotic phenols, respectively.
The fact that the toxicity of polar and nonpolar narcotic compounds cannot be satisfactorily modeled together using log Kow as the single model descriptor reflects the failure of octanol to adequately model the polar interactions associated with the partition of polar narcotic compounds into the cell membrane [14]. Separate QSAR models can be developed for polar and nonpolar narcotic compounds, as was done by Tang et al. [17], but a single model for both classes of compounds is desirable. The solvatochromic method developed by Kamlet et al. [18, 19] has been successfully used to model the aquatic toxicity to several organisms. In particular, the use of solvation parameters appears to provide a promising alternative for modeling the toxicity of polar and nonpolar narcotics together [14]. In the present study, we investigated the use of solvation parameters in modeling the toxicity of polar and nonpolar narcotic compounds to Shk1 simultaneously.
MATERIALS AND METHODS
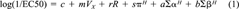 (1)
(1)The Shk1 luminescence EC50 values of 40 organic compounds were obtained in our laboratory following an assay procedure described and reported previously [10, 21]. These compounds included both polar narcotic phenols and nonpolar narcotic compounds. The organic compounds, their log (1/EC50) values, and solvation parameters are shown in Table 1. Extrapolated EC50 values (50% Shk1 luminescence repression was not observed at saturation) are indicated in the table as well. The solvation parameters were taken from the study of Gunatilleka and Poole [14]. A multiple regression of log (1/ EC50) values on the solvation parameters was performed using JMP 4.0 software (SAS Institute, Cary, NC, USA).
RESULTS
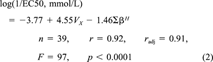 (2)
(2)As Neter et al. [22] pointed out, a fairly close agreement between PRESS and SSE would suggest that MSE may be a reasonably valid indicator of the selected model's predictive capability. Because the PRESS and SSE values of the model shown by Equation 2 were judged to be close, the MSE value of 0.14 was used to indicate the predicting capacity of the model. Taking the square root of 0.14, a value of 0.37 is obtained, which means that an error of 0.37 is expected when predicting log (1/EC50) using the model. As Blum [23] pointed out, the achievable accuracy of a QSAR for predicting toxicity to bacteria is approximately one order of magnitude. Therefore, the prediction accuracy of the model shown by Equation 2 is acceptable.
DISCUSSION
As Gunatilleka and Poole [14] pointed out, the approach of the solvation parameter model provides an interpretation of nonspecific toxicity in terms of the characteristic membrane sorption properties. The results of the multiple regression showed that three variables (R, πH, and ∑αH) were not statistically significant. Equivalently, their regression coefficients (i.e., r, s, and a) were all taken to be zero in Equation 2. As mentioned in Materials and Methods, the coefficients in the product terms of Equation 1 characterize the differences in the aqueous phase and the site of toxic action. Those regression coefficients in Equation 2 that equal zero indicate the following: The capacity of the site of toxic action in Shk1 to interact with lone-pair electrons is the same as water (the r constant), the site of toxic action in Shk1 is as dipolar or polarizable as water (the s constant), and the site of toxic action in Shk1 is as hydrogen-bond basic as water (the a constant). Consequently, the existence of lone-pair electrons in the toxicants, the dipolarity, and the hydrogen-bond acidity of the toxicants do not contribute to the nonspecific toxicity of organic compounds to Shk1.
| Compound | Shk1 log (1/EC50, mM) (5-min data) | Vibrio fischeri log (1/EC50, mM)b (5-min data unless otherwise specified) | Vx | R | πH | παH | πβH |
|---|---|---|---|---|---|---|---|
| Methanol | −3.1 | −3.69c | 0.308 | 0.278 | 0.44 | 0.43 | 0.47 |
| Ethanol | −2.83 | −2.70c | 0.449 | 0.246 | 0.42 | 0.37 | 0.48 |
| Acetone | −2.59 | −2.44c | 0.547 | 0.179 | 0.70 | 0.04 | 0.51 |
| Cyclohexanone | −0.076 | 0.72 | 0.861 | 0.403 | 0.86 | 0.00 | 0.56 |
| Ethyl acetate | −1.29 | −1.82c | 0.747 | 0.106 | 0.62 | 0.00 | 0.45 |
| tert-Butyl methyl ether | −0.2 | 1.03c | 0.872 | 0.024 | 0.11 | 0.00 | 0.63 |
| Chloroform | −0.77 | −0.75c | 0.617 | 0.425 | 0.49 | 0.15 | 0.02 |
| 1,2-Dichloroethane | −1.15 | −0.20d | 0.635 | 0.416 | 0.64 | 0.10 | 0.11 |
| 1,1,1-Trichloroethane | 0.43 | 1.22 (15 min) | 0.758 | 0.369 | 0.41 | 0.00 | 0.09 |
| 1,1,2,2-Tetrachloroethane | 0.62 | 1.49e | 0.880 | 0.595 | 0.76 | 0.16 | 0.12 |
| 1,2-Dichloropropane | −0.39 | 0.28 | 0.776 | 0.371 | 0.60 | 0.10 | 0.11 |
| 1,3-Dichloropropane | −0.59 | 0.20 | 0.776 | 0.408 | 0.74 | 0.00 | 0.17 |
| 1-Chlorobutane | −0.48 | −0.72 | 0.795 | 0.210 | 0.40 | 0.00 | 0.10 |
| 1,4-Dichlorobutane | −0.33 | 0.31 | 0.917 | 0.413 | 0.95 | 0.00 | 0.17 |
| Trichloroethylene | −0.16 | 0.13 | 0.715 | 0.524 | 0.40 | 0.08 | 0.03 |
| Tetrachloroethylenef | −0.11 | 0.98 | 0.837 | 0.639 | 0.28 | 0.00 | 0.00 |
| Chlorobenzene | 0.03 | 1.08c | 0.839 | 0.720 | 0.65 | 0.00 | 0.07 |
| 1,2-Dichlorobenzene | 0.26 | 1.73 | 0.961 | 0.872 | 0.78 | 0.00 | 0.04 |
| 1,3-Dichlorobenzene | 0.36 | 1.68 | 0.961 | 0.847 | 0.73 | 0.00 | 0.02 |
| 1,4-Dichlorobenzene | 0.15 | 1.53 | 0.961 | 0.825 | 0.75 | 0.00 | 0.02 |
| Hexanef | 0.16 | −0.082 | 0.954 | 0.000 | 0.00 | 0.00 | 0.00 |
| Octane | −0.15 | −0.81d | 1.236 | 0.000 | 0.00 | 0.00 | 0.00 |
| Benzene | −0.41 | 1.59 | 0.716 | 0.610 | 0.52 | 0.00 | 0.14 |
| Toluenef | −0.004 | 0.73 | 0.857 | 0.601 | 0.52 | 0.00 | 0.14 |
| p-Xylene | 0.27 | 1.27 (30 min) | 0.998 | 0.663 | 0.56 | 0.00 | 0.16 |
| Ethylbenzene | 0.27 | 1.21c | 0.998 | 0.613 | 0.51 | 0.00 | 0.15 |
| Cyclohexane | −0.048 | −0.0069 | 0.845 | 0.305 | 0.10 | 0.00 | 0.00 |
| Nitrobenzene | −0.22 | 0.84 (15 min) | 0.891 | 0.871 | 1.11 | 0.00 | 0.28 |
| Benzaldehyde | −0.35 | 1.24 | 0.873 | 0.820 | 1.00 | 0.00 | 0.39 |
| 4-Chlorobenzaldehyde | 0.48 | 1.14 | 0.995 | 0.930 | 1.08 | 0.00 | 0.36 |
| Phenol | −0.71 | 0.50c | 0.775 | 0.810 | 0.89 | 0.60 | 0.30 |
| m-Cresolf | −0.24 | 1.16c | 0.916 | 0.822 | 0.88 | 0.57 | 0.34 |
| 1-Nathphol | 0.43 | 1.81c | 1.144 | 1.520 | 1.05 | 0.60 | 0.37 |
| 2-Chlorophenolf | −0.07 | 0.54c | 0.898 | 0.853 | 0.88 | 0.32 | 0.31 |
| 4-Chlorophenol | 0.81 | 1.18c | 0.898 | 0.920 | 1.08 | 0.67 | 0.20 |
| 4-Chloro-3-methylphenol | 0.9 | 2.71c | 1.038 | 0.920 | 1.02 | 0.65 | 0.23 |
| 2,4-Dichlorophenol | 0.74 | 1.51c | 1.020 | 0.960 | 0.99 | 0.58 | 0.14 |
| 4-Nitrophenol | 0.51 | 1.11 | 0.949 | 1.070 | 1.72 | 0.82 | 0.26 |
| Salicylaldehyde | −0.22 | 0.87 | 0.932 | 0.962 | 1.15 | 0.11 | 0.31 |
| Anilinef | −1.13 | 0.16c | 0.816 | 0.960 | 0.96 | 0.26 | 0.41 |
The nonzero regression coefficients for Vx and ∑βH in Equation 2 indicate that forming a cavity at the site of toxic action in Shk1 is relatively easier than in water (the m constant) and that the site of toxic action in Shk1 is more hydrogen-bond acidic than water (the b constant). In Equation 2, the regression coefficient for Vx is positive and that for ∑βH is negative, which indicates that toxicity increases as the McGowan's characteristic volume, or size (discussed later), of the toxicants increases and that toxicity decreases as the hydrogen-bond basicity decreases.
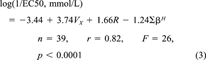 (3)
(3)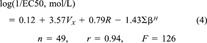 (4)
(4)The regression coefficients in Equations 3 and 4 are essentially the same (noting the difference in the units of the EC50 values mentioned previously) except for the coefficient multiplying R. Comparing Equation 2 and Equations 3 and 4 it can be seen that the site of toxic action in Shk1 interacts less easily with lone-pair electrons of the toxicant molecules compared to the site of toxic action in V. fischeri, as indicated by the absence of a term containing R in Equation 2 and the presence of such a term in Equations 3 and 4. The site of toxic action in Shk1 is approximately as hydrogen-bond acidic as that in V. fischeri, as indicated by similar regression coefficients for ∑βH in Equations 2, 3, and 4. Finally, the site of toxic action in Shk1 is less cohesive than that of V. fischeri, and cavities can be more easily formed, both of which are indicated by a larger regression coefficient for Vx in Equation 2 than those in Equations 3 and 4.
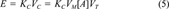 (5)
(5)Some researchers have used both hydrophobicity (log Kow) and hydrogen-bonding descriptors to model the toxicity of polar and nonpolar narcotic compounds [20, 29, 30]. We did not include log Kow in our model, because a preliminary multiple regression with backward variable elimination showed that log Kow was not statistically significant and, therefore, could be removed from the regression (not shown). This is not surprising, because both VX (used in our model) and log Kow can be thought to characterize the ability of a toxicant to move from the aqueous phase to the cell membrane.
As mentioned, the present study was motivated by the difficulty of using a simple log Kow-based model to properly describe the toxicity of toxicants acting by mechanisms of polar and nonpolar narcosis. To demonstrate the superiority of the solvation parameter model developed in this study, we also attempted to model the toxicity of the compounds shown in Table 1 using log Kow as the sole model descriptor. A linear regression resulted in an r value of 0.78, much lower than the radj value (0.91) associated with Equation 2, which takes into account having more than one model predictor in Equation 2. In addition to a lower r value, regressing log (1/EC50) on log Kow also yielded an MSE value of 0.32, more than twice that associated with Equation 2. Consequently, compared to a log Kow-based model, the solvation parameter model yields better modeling capacity when polar and nonpolar narcosis toxicity to Shk1 are modeled together and offers greater prediction accuracy.
Values of solute descriptors used in the model developed in the present study are available for a number of compounds. Regarding compounds for which values of the descriptors are not available, convenient methods to calculate them have been published [28, 31]. Therefore, the nonspecific toxicity of organic compounds to Shk1 can be predicted using the model we developed, which provides a useful tool in predictive toxicology. The capacity to predict toxicity to Shk1 is valuable because of the similarity between the response of Shk1 to toxicants and that of the activated sludge. The QSAR model based on solvation parameters that we developed in the present study provides a convenient way for wastewater treatment plant operators and engineers to estimate the nonspecific toxicity of organic compounds without having to distinguish between polar and nonpolar narcosis.
CONCLUSIONS
We developed a solvation parameter model (Equation 2) to describe and predict the nonspecific toxicity (polar and nonpolar narcosis) of organic compounds to the luminescent bacterium Shk1. The statistically significant model descriptors were the McGowan's characteristic volume (Vx) and the hydrogen-bond basicity (∑βH). The predictive capacity of the model was indicated by a small MSE value of 0.14 associated with the multiple regression that was performed to obtain the model. The model (Equation 2) is similar to the solvation parameter models developed for V. fischeri, but it does not include a term containing excess molar refraction (R). Because the values of the model descriptors are either reported in the literature or can be calculated, this model can be used as a tool to predict the nonspecific toxicity of organic compounds to Shk1.




