A life-history approach to predicting the recovery of aquatic invertebrate populations after exposure to xenobiotic chemicals
Abstract
A combined empirical and theoretical study was conducted to evaluate the degree to which an understanding of the life histories of different freshwater invertebrate taxa could improve our ability to predict their relative rates of recovery after a toxic perturbation. Two chemicals, cypermethrin and 3,4-dichloroaniline, were introduced separately into large freshwater tanks (mesocosms, 1.25 m diameter, 1.25 m depth) containing established freshwater invertebrate communities. Immigration was simulated in selected mesocosms by introducing particular taxa at predetermined intervals. For both chemical treatments, laboratory rank toxicity data successfully predicted the observed relative short-term mortalities of species, whereas the relative times taken for taxa to recover from cypermethrin exposure also correlated with their relative susceptibilities to this compound. Crucially, a significant component of residual variance in rank recovery to cypermethrin was explained by variation in overall rates of reproduction among taxa. A simulation model was therefore developed to allow us to integrate the disparate information on invertebrate life histories into a predictive model. This model was broadly supported, particularly for the cypermethrin exposure data, where observed and predicted rank recovery times were highly correlated. Overall, this study broadly confirms the importance of life-history characters in governing recovery and the validity of simple modeling approaches for predicting recovery.
INTRODUCTION
The environmental risks posed by xenobiotic chemicals in aquatic ecosystems are generally assessed through a combination of laboratory toxicity tests and small-scale field trials using artificial ponds (mesocosms) [1, 2]. Typically, the concentrations that affect individual organisms are measured under controlled conditions and compared with those to which the organisms may be exposed in the environment. Although practical and easy to interpret, the limitations of these standard tests have long been recognized. In particular, it has been widely observed that the recovery of a population after a toxic perturbation may not be predictable from toxicity data alone [3]. Relatively small declines in population size can sometimes have serious implications for the longer-term viability of a population, but, conversely, a marked reduction in population size may have little impact on the longer-term average density [4].
The factors that influence the recovery of a population after a significant perturbation are complex, and it is not surprising that recovery patterns often confound expectations (S.J. Maund, personal communication). Clearly, one important factor governing the recovery of a freshwater invertebrate species after a toxic perturbation is its life history. Aquatic invertebrates are derived from a variety of taxonomic phyla and therefore vary widely in their reproductive and dispersal characteristics. For instance, some species may reproduce continuously, and others reproduce at discrete times of the year. Generation times can range from days for species such as the cladoceran Daphnia magna L. [5] to years for many species of odonate, such as the dragonfly Anax imperator Leach [6]. The ability to colonize ponds may also vary considerably; for instance, most aquatic insects have winged adults, whereas less mobile taxa (e.g., mollusks and crustacea) will necessarily rely on more passive forms of dispersal, such as wind, flooding, or transportation by birds.
In this study, we determined the degree to which a knowledge of the life histories of different freshwater invertebrate species can improve our ability to predict differences in their recovery. First, replicated and long-term aquatic toxicological field trials were used to elucidate the relationship between the recovery of species and their reproductive and dispersive characteristics. We then used some of this information to develop and parameterize appropriate simulation models of the recovery process. Quantitative models are regularly used to facilitate the evaluation of toxicological risk in freshwater systems [7], but the models presented here emphasize recovery rather than initial mortality and are among the first to formally attempt to predict the recovery of macroinvertebrate populations on the basis of their life-history characteristics (see Calow et al. [8] and Kammenga et al. [9] for complementary approaches). To evaluate the validity and usefulness of our modeling approach, we formally tested whether our simulations were better at predicting relative rates of recovery than toxicity data alone.
MATERIALS AND METHODS
Study ponds
The experimental small water bodies (mesocosms) were located at Zeneca Agrochemicals Jealotts Hill Research Station, Bracknell, Berkshire, United Kingdom. They comprised cylindrical fiberglass tanks with a diameter of 1.25 m and a depth of 1.25 m, each with an integral base and filled with water to a height of approx. 1 m. To regulate mesocosm temperature, the tanks were maintained in two 5- × 5- × 1-m outdoor concrete ponds filled with water to a depth of 1 m.
| Offspring per individual | |||||||
|---|---|---|---|---|---|---|---|
| Taxon | Summer | Winter | No. generations per year | γ0a | Kb | Life spanc | References |
| Polycelis tenuis | 0–100 | 0 | 3 | 0.14 | 32 | 2–3 y (max) | [25, 26] |
| Lymnaea peregra | 100–103 | 0 | 2 | 0.71 | 7 | 1–2 y | [27-29] |
| Lymnaea stagnalis | 100–103 | 0 | 2 | 0.71 | 86 | 1-2 y | [27-29] |
| Asellus aquaticus | 100–103 | 0 | 4 | 0.18 | 130 | 3 mo-2 y | [30] |
| Crangonyx pseudogracilis | 100–103 | 0 | 4 | 0.11 | 93 | 2 y (max) | [30] |
| Coenagrion | 4,200 (max) | 0 | 1 | 0 | 3 | 2 y | [31] |
| Notonecta | 1–30 | 0 | 1 | 0.28 | 7 | 12 mo (max) | [31] |
| Helophorus brevipalpis | 1–30 | 0 | 1 | 0 | 9 | 1 y | [27] |
| Oligochaeta | 31–150 | 1–30 | 2 | 0.14 | 25 | 3 y (max) | [27] |
| Chaoboridae | 31–150 | 0 | 2 | 0.36 | 26 | < 12 mo | [27] |
| Planorbis carinatus | 31–150 | 0 | 1 | 0.71 | 54 | 17 ± 2.3 mo | [32, 33] |
- a Estimated initial daily reproductive rate (estimated net per capita daily reproduction on June 25).
- b Estimated sample carrying capacity (densities in samples from no-addition treatments).
- c max = maximum.
The mesocosms were originally established in Spring 1994. At this time, they were filled to a depth of 1 m, using water from a pond on the Jealotts Hill site. To aid mesocosm establishment and increase environmental realism, sediment derived from an established pond on the site was added to a depth of 10 cm. The mesocosms were left uncovered and open to natural colonization between Autumn 1994 and June 1996. All mesocosms were, therefore, relatively mature when the current experiment was undertaken. At the start of the experiment, all mesocosms were covered with individual removable net hoods (0.45- × 0.78-mm mesh), which allowed water and 90% light penetration but prevented entry of macroinvertebrates.
The Zeneca site held 18 mesocosms, all of which were sampled before the experiment began (December 3, 1995, and May 16, 1996). The water was generally clear, and although the mesocosms plant and macroinvertebrate assemblage have no obvious analogues among Britain's seminatural ponds, their biota more closely resembled those of circum-neutral ponds than acid ponds (P. Williams et al., unpublished data). Of these 18 containers, 10 mesocosms were selected on the basis of the range of aquatic invertebrate species they supported. The multivariate classification analysis DECORANA [10] separated the mesocosms into two main groups (essentially a cluster of species-rich and species-poor tanks), and this classification was consistent for the two sampling dates. On the basis of this classification, treatments were divided equally between mesocosms. Within this stratified sample design, treatment and control mesocosms were selected at random.
| Taxon | Cypermethrin 48-h LC50 (μg/L) | DCA 96-h EC50 (mg/L) |
|---|---|---|
| Polycelis tenuis | >100b | 4.6b |
| Planorbis carinatus | > 100b | 4.6b |
| Oligochaeta | > 100 | 0.44 |
| Lymnaea peregra | > 100b | 24b |
| Lymnaea stagnalis | >100 | 24 |
| Asellus aquaticus | 0.0039 | 1.9 |
| Crangonyx pseudogracilis | 0.0026 | 2.9c |
| Coenagrionidae | > 5 | 54 |
| Notonecta spp. | 0.1 | — |
| Helophorus spp. | 0.1b | — |
| Chaoboridae | 0.003 | 9.4 |
- a Data from S.J. Maund et al. (unpublished). EC50 = median effect concentration; LC50 = median lethal concentration.
- b Estimates based on measurements for the closest available species.
- c Value is the 48-h EC50.
Taxa studied
Although initially a wider range of taxa were identified, the taxa considered here are limited to those that had, on average, more than three individuals present in each mesocosm at the start of the experimental period (11 taxa). This constraint was necessary for calculations of mortality and recovery. The taxa were Polycelis tenuis, Planorbis carinatus, Oligochaeta, Lymnaea peregra, L. stagnalis, Asellus aquaticus, Crangonyx pseudogracilis, Coenagrionidae, Notonecta spp., Helophorus spp., and Chaoboridae. Although there were also Chironomidae present in sufficient numbers, these were excluded because of the difficulty of summarizing a family whose subfamilies exhibit a wide range of reproductive outputs.
Both our correlative analysis and modeling depended on qualitative estimates of the relative reproductive output of each of these species. These estimates were made before the experiments began from unpublished databases, compiled through personal observations and reference to the available published literature by Pond Action, Oxford, United Kingdom (see Table 1).
Chemical application
Two chemicals, cypermethrin (a pyrethroid insecticide) and 3,4-dichloroaniline (DCA) (a common intermediate breakdown product of herbicides and detergents), were applied to the mesocosms. These chemicals were chosen because they have well-documented toxic effects on freshwater invertebrate species (cypermethrin [11]; DCA [12-15] see Table 2) and because they differ widely in their dissipation half-lives (cypermethrin: half-life in water, ≈1 d; DCA, half-life in water of ≈30 d).
The chemicals were applied on June 25, 1996, henceforth referred to as day 0 of the experiment, at a rate sufficient to cause substantial mortality (cypermethrin: 70 ng/L [ppt]; DCA, 10 mg/L [ppm]). Cypermethrin was applied to four mesocosms, and DCA was applied to another four mesocosms. Both DCA and cypermethrin were dissolved in solvent (100 ml of methanol) before addition and stirred gently into the water, taking care to avoid disturbing the sediment. Solvent alone was added to an additional two mesocosms, which were used as controls.
| Taxon | Cypermethrin | DCA |
|---|---|---|
| Polycelis tenuis | 0 | 10 |
| Asellus aquaticus | 36 | 32 |
| Crangonyx pseudogracilis | 33 | 20 |
| Notonecta spp. | 1 | 2 |
| Chaoboridae | 5 | 7 |
- a Note that from day 112, additions were performed only in the 3,4-dichloroaniline (DCA) mesocosms and that these were of twice the stated numbers at twice the interval.
Sampling protocols
Macroinvertebrate samples were taken from each mesocosm on the day before and the day after addition of the chemicals (day −1 and day 1, respectively). Sampling continued on days 3, 7, and 14 and then fortnightly until day 112. Invertebrate sampling of the cypermethrin mesocosms ceased after 112 d (October 15, 1996), when recovery was well established. As expected, the effects of DCA persisted for longer, so sampling of these treatments and their controls continued monthly for a total of 280 d (ending April 1, 1997).
Six samples were taken from each mesocosm (two from the top, middle, and bottom each) on every inspection. Each sample took approx. 15 s to collect and was taken by sweeping a D-frame net (15 × 17 cm, 1-mm mesh) through the mesocosm and scraping along the mesocosm sides. The bottom samples skimmed the top of the sediment. Samples were sorted live and identified to the lowest taxonomic level possible in the field (predominantly species level, with the exception of Diptera and Oligochaetes) before being returned to their mesocosm of origin.
Simulation of immigration
The chemically treated mesocosms were further divided into ponds to which selected invertebrate species would be added to simulate immigration and into ponds that would receive no additions and that could, therefore, recover only through internal processes. Thus, from July 10 (day 15), and subsequently whenever sampling was conducted, selected invertebrates (on the basis of their abundance and range of life histories), from untreated mesocosms that were not part of the study, were added to two DCA and two cypermethrin mesocosms (see Table 3).
Because there are few quantitative estimates of immigration of aquatic invertebrates to small water bodies, and because immigration will vary according to the size and number of local source populations, our choice of immigration schedule was necessarily somewhat arbitrary. The purpose of this additional treatment was simply to test whether differences in immigration rate within a given species influenced population recovery. Nevertheless, it would clearly be inappropriate to add more than the original population size of a given species at any one time. To account for variation between species in original population sizes and arrive at sensible immigration schedules, we therefore added quantities of individuals of each species sufficient to achieve their mean pretreatment population sizes after a period of 8 weeks, assuming no further mortality (see Table 3). Invertebrate additions to the mesocosms were made immediately after sampling (fortnightly until day 112). On October 15, 1996, additions to cypermethrin treatments ceased. From this time, additions to DCA treatments continued monthly, but the quantities were doubled to compensate for the greater period between additions.
Empirical measures of recovery
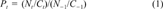 (1)
(1)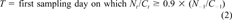 (2)
(2)Modeling methods
Although it is intuitive that certain life-history characteristics, such as reproduction and immigration, facilitate recovery, an evaluation of the relative importance of one characteristic (e.g., reproduction) over another (e.g., immigration) demands more formal quantification. In designing our model, we considered simplicity an important prerequisite for its practical application. It was not our aim to produce detailed models capable of making accurate forecasts for any particular species but rather to test the validity of a general and robust approach based on limited information. Because of the difficulties of parameterization, our representation took no account of age structure. Furthermore, the lack of a spatial component renders our current model appropriate only for relatively small, homogeneous systems.
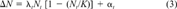 (3)
(3)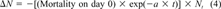 (4)
(4)| Taxon | Cypermethrin | DCA |
|---|---|---|
| Polycelis tenuis | −1.86 | 0.82 |
| Planorbis carinatus | −0.01 | 0.52 |
| Oligochaeta | −0.22 | 0.89 |
| Lymnaea peregra | 0.06 | 0.49 |
| Lymnaea stagnalis | 0.10 | −0.71 |
| Asellus aquaticus | 0.77 | 1.00 |
| Crangonyx pseudogracilis | 0.84 | 1.00 |
| Coenagrionidae | −3.13 | −2.07 |
| Notonecta spp. | 0.53 | 0.41 |
| Helophorus spp. | 0.54 | −0.90 |
- a See text for calculation; negative values represent an increase in numbers. DCA = 3,4-dichloroaniline.
The model output was designed to simultaneously compare the recoveries of populations of a range of different aquatic invertebrate species and to generate their relative recovery ratings. This recovery was measured both as a proportion (Nt/K) and as a time (the period taken for N0 to rise to K or a fraction thereof). In developing the model, it was clear that estimates of parameter values (γt, K, αt, and half-life) would be approximate, so our modeling structure enabled each parameter to be varied at discrete intervals between upper and lower limits to allow us to generate mean recovery ranks. The quantitative properties of this basic model and its spatial derivatives are reviewed elsewhere. Here, we evaluate the success and limitations of our approach in predicting the relative recovery rates of invertebrate species in the field.
RESULTS
Observed mortalities on day 1
In the cypermethrin mesocosms, changes in abundance were highly variable, with some taxa declining markedly and others increasing markedly (Table 4). The highest mortality was found for C. pseudogracilis and A. aquaticus (see Figure 1a to 1c for the dynamics of the latter species). For relatively rare taxa, such as the Coenagrionidae, this may reflect sample variance, but it is likely that flatworms and oligochaetes genuinely increased their rate of body division over this short period, either as a direct or indirect effect of toxin. In the DCA mesocosms, mortalities were highest for A. aquaticus and C. pseudogracilis. No measurable mortality occurred in Coenagrionidae, Chaoboridae, or L. stagnalis (Table 4). When some mortality occurred in both treatment types, mortality was generally higher in the DCA mesocosms (mean = 0.74) than in the cypermethrin mesocosms (mean = 0.54; paired t test, t = −2.19, df = 4, p = 0.05).
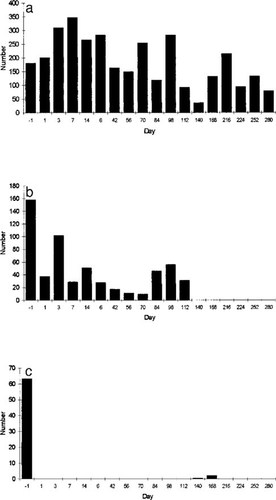
Example of changes through the experimental period for Asellus aquaticus, giving the mean numbers of individuals per mesocosm for the different treatments: (A) controls; (B) cypermethrin, no addition; and (C) 3,4-dichloroaniline, no-addition.
Observed mortalities in relation to median lethal concentration
As we would predict, those taxa with the lowest median lethal concentration (LC50) values (highest susceptibility) had the highest mortality between days 21 and 1 in both the cypermethrin and DCA mesocosms (cypermethrin: r = −0.79, n = 11, p < 0.01; DCA: r = −0.88, n = 9, p < 0.01; see Fig. 2a and 2b).
Observed recovery in relation to median lethal concentration
Observed recovery time from cypermethrin (ranked in increasing order) in nonaddition treatments for those taxa in which mortality occurred was significantly negatively correlated with the cypermethrin LC50 (ranked in increasing order; see Fig. 3; r = −0.84, n = 7, p < 0.05). Recovery times from DCA exposure were not significantly correlated with the DCA median effect concentration (r = −0.49, n = 6, p > 0.05), but only six species for which the median effect concentration was known exhibited mortality, and only three of these species exhibited full recovery before the end of the 280-d experimental period. Even when recovery was measured as a proportion, no correlation between toxicity and recovery was evident (r = −0.217, n = 6, p > 0.05).
Multiple effects
The cypermethrin mesocosm recovery time data (ranked in increasing order) were subjected to a multiple linear regression analysis using backward elimination to test for the relative importance of toxicity, initial reproductive output and immigration (additions or no additions). The process of backward elimination removes variables if they do not contribute significantly to the regression until no more variables are eligible for removal [16]. A regression relationship was obtained with a multiple r squared of 0.79 (p = 0.0001). Toxicity, in the form of LC50 values ranked in increasing order, had the strongest relationship (β = −0.66, T = −4.76, p = 0.0005). Estimated initial reproductive output (ranked in increasing order) was also significantly related (β = −0.42, T = 2.99, p = 0.0112), but in this test, the additions factor did not appear as a significant explanatory variable in the equation. A similar backward multiple regression applied to the DCA treatments failed to detect any significant effect of toxicity, reproduction, or immigration on recovery, either expressed in time (multiple r squared of 0.54, p > 0.05) or proportion (multiple r squared of 0.30, p > 0.05).
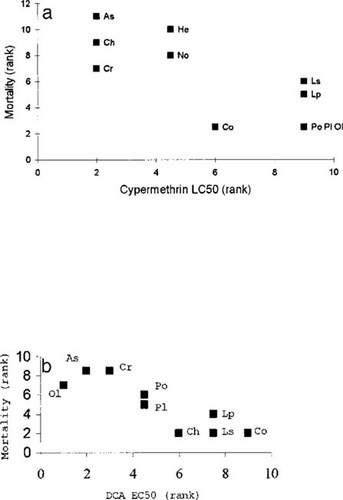
Observed initial mortalities (see text for calculation) in the no-addition mesocosms (ranked in increasing order) in relation to (A) cypermethrin median lethal concentration (LC50) data (ranked in increasing order, which corresponds to decreasing susceptibility) and to (B) 3,4-dichloroaniline (DCA) median effect concentration (EC50) data. Po = Polycelis tenuis; Pl = Planorbis carinatus; Ol = Oligochaeta; Lp = Lymnaea peregra; Ls = Lymnaea stagnalis; As = Asellus aquaticus; Cr = Crangonyx pseudogracilis; Co = Coenagrionidae; No = Notonecta spp.; He = Helophorus spp.; and Ch = Chaoboridae.
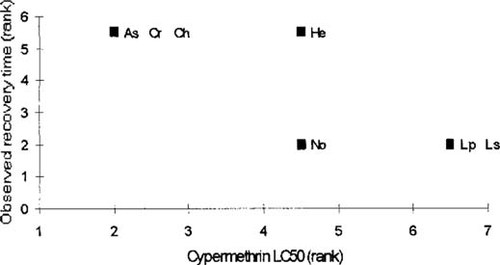
Observed recovery times for those taxa in which mortality occurred in the cypermethrin, no addition, mesocosms (ranked in increasing order) in relation to cypermethrin median lethal concentration (LC50) data (ranked in increasing order).
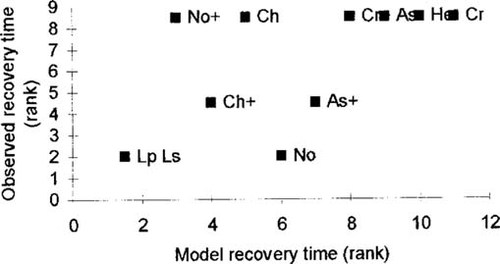
Observed recovery times for those taxa in which mortality occurred (ranked in increasing order) in relation to recovery times from cypermethrin exposure predicted by the model. + = addition (immigration) treatments.
Observed recovery times in relation to model predictions
Our simulation model of recovery was run using the mean observed mortalities in treatment mesocosms, the actual immigration schedules, estimates of the numbers of offspring produced per individual per day (γt), and estimates of K based on the average number of each taxon present in all mesocosms on the day before treatment. Because the estimates of numbers of offspring produced are approximate, we calculated 50% of the best estimate of γt and added or subtracted this amount to get lower and upper estimates. This process was repeated for carrying-capacity estimates. Nine simulations were run in which each combination of γt and K values were used in turn. The results of these simulations were then listed, and the recovery measures were ranked across all simulations, giving, for each taxon, nine ranks, which were then averaged to get mean ranked recovery times and rank recovery proportions. Because the model incorporates both reproduction and immigration, addition and nonaddition cases could be considered as independent data. The observed ranked recovery time from cypermethrin correlated reasonably well with the model predicted mean rank recovery time (Fig. 4; r = 0.63, n = 11, p < 0.05). Indeed, our model was a better predictor of recovery than LC50 alone in this expanded data set (r = −0.57, n = 11, p > 0.05). Observed recovery time from DCA did not correlate with model-simulated recovery however (r = 0.25, n = 12, p > 0.05), but the exclusion of one outlier (Notonecta spp. with additions) would have resulted in a significant positive relationship.
DISCUSSION
A number of authors have argued that the application of more ecology to the science of toxicology would facilitate a more comprehensive evaluation of risk [17]. Some authors have pointed out that the results of toxicity tests in freshwater systems are likely to have been affected by ecological factors [18, 19]. However, it is only recently that authors have proposed using ecological factors as predictors of recovery rather than simply as variables that may confound the effects of toxicity [3, 8, 9, 20, 21].
Our study confirmed that laboratory toxicity data are a good predictor of the relative short-term mortalities of aquatic taxa. The LC50 also predicted the longer-term recovery in our cypermethrin nonaddition treatments, presumably because those species that have the least mortality tend to recover more quickly. An additional contributing factor to the toxicity-recovery relation may be that the effects of chemical exposure continue for some time after the chemical has dissipated, for instance, through delayed mortality or through effects on reproductive rate.
Although our toxicity data predicted the relative short-term mortalities to DCA, they were not a good predictor of recovery. Unfortunately, the power of this test must be considered relatively low, because full recovery was observed in only three species, even with additions. Hence, it was not possible to conduct a comprehensive analysis of the factors that contribute to the recovery of populations after exposure to this particular chemical, even after an experimental period of close to 1 year.
Our results strongly indicate that a significant part of the observed variation in recovery of invertebrate populations after exposure to cypermethrin could be explained by differences in reproductive rates. Although differences in reproductive rates could not explain differences in recovery rates on their own (because they also depended on the degree of population knockdown), our analysis shows that the estimated reproductive output could explain significant additional variance in rank recovery beyond simple LC50. Thus, even a crude consideration of invertebrate life history can improve our ability to predict the longer-term response of a population to a toxic chemical.
A recent review of the role of mesocosm studies in ecological risk analysis [22] made a strong case for toxicologists to develop closer working relationships with mathematical modelers. Our study shows how a simple modeling framework can be used to integrate disparate information on invertebrate reproduction and immigration. It also demonstrates the relative success of such a modeling approach in predicting recovery, compared with LC50 data alone. Clearly, we did not explain all the variation in our data, and this may in part be explained by sampling variation in our initial estimates of population sizes. Like all modeling approaches, our simplistic analysis also has inherent limitations. Perhaps most significantly, our model ignores secondary and communitylevel effects that may occur in freshwater systems [2]. For instance, it is possible that if predators or competitors of a given species are strongly affected by a toxic perturbation, then this species may rapidly undergo a resurgence in population size, freed from predatory or competitive pressure. Although such biotic interactions can and have been modeled [23, 24], it is likely that the complexity of such models will restrict their general practical applicability.
Overall, our study has broadly confirmed the value of laboratory toxicity data for predicting mortality in the field, the dependence of recovery on taxon-specific reproduction rates, and the validity of a simple ecological modeling approach for predicting recovery. Clearly, a major goal of risk assessment will be to continue to develop and test appropriate modeling frameworks that will allow us to integrate more ecology into the science of ecotoxicology.
Acknowledgements
We thank Paul Jepson, Phil Heneghan, and Tim Kedwards for comments. This work is supported by the Zeneca Strategic Research Fund.




