A Review and Perspective on Path Dependency in Batteries
Abstract
Reliability of battery state estimation and lifetime prediction is essential to develop operation strategies that improve lifetime, safety, and sustainability. However, this is difficult, because of complex phenomena such as path dependency of battery aging, path dependency of power capability, voltage hysteresis, or memory effects. Herein, these phenomena as well as test protocols, models, and analysis methods being frequently applied in this context are reviewed. The discussion indicates that insights into path dependency are of great importance to understand battery operation under realistic conditions. Challenges and possible future research directions are outlined.
1 Introduction
Batteries are a key enabler for the transition from a fossil fuel-driven to a sustainable society with mainly renewable energy sources.[1] In particular, for electric vehicles (EV) and stationary battery energy storage systems (BESS), batteries are needed. As the production of batteries is an energy-intensive process and often relies on rare raw materials, it is important to expand the use-phase of the battery system.[2, 3] This can be achieved by anticipating potentially harmful operating conditions to mitigate degradation and failure and by enabling a appropriate second use-phase, for example, reusing an automotive battery system as an electrical storage system for renewable energy.[2] Here, the battery management system (BMS) plays a major role. The BMS should enable an accurate estimation of battery state of charge (SOC) and state of health (SOH) and utilize models, which predict the remaining useful life (RUL) and power capability.[4, 5]Advancements in battery management are of particular importance, considering the manifold challenging operating conditions such as highly dynamic and irregular load in EVs,[6] vehicle-to-grid applications,[7, 8] fast charging,[9] or variation of patterns in environmental conditions due to seasonal and regional differences[10] that a battery faces in the field. Under such conditions, an estimation of RUL and power capability is associated with significant uncertainty, which needs to be addressed.
One cause for uncertainty is that the behavior of batteries under real operating conditions is often significantly different compared with idealized laboratory experiments.[6] Batteries are complex systems, where single processes cannot usually be superimposed to describe the overall system behavior. Instead, understanding interplay and interaction across scales and physical domains is needed.[11] The system complexity can manifest in various phenomena, for example, path dependency of battery aging,[12] path dependency of power capability,[13] voltage hysteresis,[14] or memory effects.[15] In these examples, the future trajectory of the systems seems to depend on the history of operation. Despite the relevance of these phenomena for BMS advancement, they are currently often neglected. The main problem is that appropriate test procedures, modeling approaches, and analysis methods are not established and rarely combined systematically. Moreover, many of the observed phenomena have similar challenges; thus, many concepts, modeling approaches, and characterization methods could be transferred. This is currently impeded because these similarities are often not recognized.
The goal of this article is to review the research that has been done in the field of path dependency of batteries within the past decades. The review discusses path dependency of battery aging, which recently has attracted lot of attention, as well as short- and mid-term path-dependency phenomena, which were studied earlier, but will be also highly important for next-generation battery materials. The article aims to set a basis for a common methodology for both areas. The article discusses applied methods, identifies similarities between various phenomena, points out, and discusses promising modeling approaches.
The article does not aim to summarize battery management methods that focus on other concerns besides path dependency. Therefore, a comprehensive and comparative analysis of the different algorithms for battery management, for example, state estimation, is not within the scope of this review, but can be found elsewhere. Barillas et al.[16] performed a comparative study of different state prediction algorithms for lithium-ion batteries. Wang et al.[17] provided a comprehensive review of different battery modeling and state estimation approaches. Recently, Wang et al.[18] also provided a review on digital twins and cloud-based BMSs that could prove to be a useful tool in using more complex and resource-heavy algorithms for battery state prediction. In contrast to these reviews, this article specifically focuses on the implications of path dependency for battery operation and model based predictions, which is to our best knowledge currently not available. Moreover, the article aims to provide an overview and a first intuitive understanding of the underlying causes for path dependency by depicting the explanation models discussed in literature. However, we note that the overview is neither conclusive nor comprehensive with respect to a mechanistic understanding, because mechanisms are in many cases still under scientific debate.
In Section 2, the path dependency of lithium-ion battery aging is addressed. Afterward, in Section 3, phenomena of short- and mid-term path dependency are reviewed and discussed. The major difference is that path dependency of aging is permanent, while path dependency discussed in Section 3 usually vanish or can be recovered. Finally, in Section 4, challenges and possible future research directions are outlined and discussed.
2 Path Dependency of Lithium-Ion Battery Aging
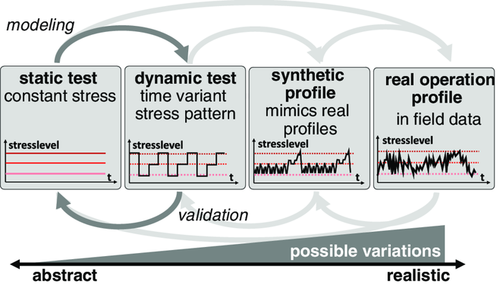
Capacity and power capability of a battery changes over its lifetime. These changes need to be anticipated for optimal operation of the system. Thus, SOH estimation and RUL prediction are essential functions of the BMS. Therefore, a considerable effort is made to characterize battery aging in laboratory experiments. Unfortunately, real-world applications have irregular cycling patterns that yield path-dependent behavior, which make predictions based on laboratory experiments difficult.[6] Figure 1 illustrates different levels of abstraction for characterization of battery operation, which go from static tests with a high level of abstraction up to collection of real field data. The behavior under real conditions is often far from that in laboratory environments.[19]
In this section, the current status of research in the field of path dependency of lithium-ion battery aging is reviewed. First, basic definitions are provided. Second, various test strategies and in particular dynamic battery aging tests are reviewed. Third, characterization methods for degradation pathways are depicted. After that, the current status of understanding path-dependent aging behavior is given. Finally, attempts to cover path dependency in aging models are summarized.
2.1 Definitions
In general, a degradation path could be defined as the trajectory of the battery SOH, for example, the relative resistance, through time.[20] Thus, different degradation paths could be distinguished, for example, by different slopes of the relative resistance. A degradation path could be also differentiated the usage schedule, that is, the sequence of operation conditions, or by the observed degradation processes, that is, degradation modes.[21] As shown, there are various possibilities to define a degradation path. Two approaches to differentiate the path are depicted. 1) The observed processes, for example, degradation processes and 2) the slope of the observed state, for example, SOH.
The usage schedule itself is rather the cause for different paths and is therefore not a sufficient condition to differentiate paths.
Definitions and wording used to define path dependence are not always fully consistent. For instance, Su et al.[22] stated that path dependence means the effect of the past on current performance, while memory effect means impact of path on future evolution of the performance. Karger et al.[23] related the definition of path dependence to whether the future degradation can be explained by the current state. For the following discussion, we define three levels of path dependencies (PD I-III): [leftmargin = 4em]. 1) PD I: The path depends on the usage schedule. 2) PD II: State change depends on the sequence of conditions within a usage schedule and not just on the cumulative conditions. 3) PD III: The future path depends on the history of the path and cannot be explained by the present state alone.
In the following sections, these definitions are elaborated in more detail in the context of battery degradation. PD I depicts that the usage schedule of the battery does have an impact on the observed degradation processes or the slope of the SOH. For instance, if battery cells show different degradation processes or a different slope of the SOH for different temperatures, this fulfills PD I. The definition PD II further depicts that not only the cumulative conditions that appeared in the past impacts the state change, for example, the final SOH, but also their chronological sequence. For instance, the PD II is fulfilled, if the final SOH of a cell aged first at hot temperatures and afterward at cold temperatures is different as compared with being aged first at cold temperatures and afterward at hot temperatures. The definition PD III depicts that for two cells with the same state, for example, same SOH, the future trajectory will depend on how this state was reached. In this case, the SOH is not sufficient to predict the future trajectory, but instead the history of the degradation path needs to be taken into account. In general, definitions at lower levels are included within higher-level definitions, for example, PD III includes PD I and PD II. As can be depicted from this discussion, whether the degradation is path dependent or not depends on the definition of a degradation path and path dependency.
2.2 Dynamic Battery Aging Tests
The overwhelming majority of laboratory experiments are static aging tests.[24-26] In a static test, the stress condition is kept constant during the aging experiment. An example is a cyclic aging test with fixed c-rate and temperature. By varying a single influencing stress condition, for example, the temperature, its isolated impact can be revealed. As an example for a very broad test matrix that studies the impact of several stress conditions using static tests, the study of de Hoog et al.[26] can be highlighted. The advantage of a static test is that the impact of particular stress condition on the battery aging can be observed directly. Further, on the basis of such studies, degradation models can be derived.[27] However, it is uncertain if models being identified at these idealized aging conditions provide good estimates under realistic aging conditions. Therefore, Schmalstieg et al.[27] validated the derived aging models based on synthetic driving profiles, which showed a good agreement for cell capacity. However, deviations with respect to cell resistance were observed. This approach is depicted in Figure 1. It is shown that tests with high level of abstraction are used to derive models being validated at tests under more realistic conditions.
In the review of Sulzer et al.,[6] the need to combine laboratory tests and field data to achieve better predictions is emphasized. They suggest to supplement static laboratory tests by real-world data to take path dependency in case of irregular cycling patterns into account. Baure et al.[28] raised the question of whether experimental data can replace real world data. They investigated if synthetic driving profiles are representative for real driving cycles. They found that the average current and charge capacity during discharge are important parameters and should be used to determine adequate synthetic profiles. This shows that there is a need to identify important features of real profiles to derive adequate synthetic profiles being testable in laboratory environments.
As discussed earlier, it is well known that static tests often do not cover the complexity of battery aging sufficiently. An attempt to make laboratory tests more realistic is to include variation of the stress factors over time in dynamic tests.[29-31] For this type of test, various names are used, for example, “dynamic test,”[29] “time-dependent conditions,”[30] or “transient conditions.”[31] A selection of dynamic tests is shown in Figure 2. The typical goal of a dynamic test is to investigate whether the sequence of stress factors does have an impact on the degradation and sometimes this is directly related to the question of whether there is path dependency. If the sequence of stress conditions impacts the defined metric for battery aging (e.g., capacity, internal resistance), it is usually seen as proof for path dependency. In the following sections, an overview of research using dynamic tests is given.
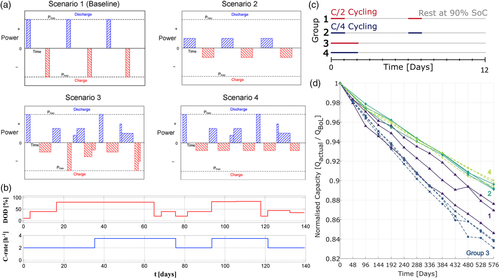
In Figure 2a, different scenarios for pulse sequences are shown. This sequence variations were used by Gering et al.[32] to investigate path dependency. The applied scenarios were designed to include a variation of the magnitude of the applied constant power pulses, while also ensuring equal cumulative discharge energies for all scenarios. They also presented initial results of a second study, which includes temperature cycles with isothermal conditions and transient temperature changes. This study was perused later and published by Dubarry et al.[34] Werner et al.[31] also performed aging experiments with temperature variation over time and space. For the latter the aging could be characterized using the average temperature. In contrast, for the variation over time, significantly different aging behavior's were observed for equal average temperatures. Su et al.[22] used static and dynamic aging tests for temperature and SOC variations. They applied a statistical method, that is, analysis of variance (ANOVA), to investigate the path dependency in consideration of aging uncertainty. ANOVA is a statistical method that can be used to compare the means of two different groups. For testing path dependency, one group can be cells that undergo the same sequences during aging and the other can be the cells that undergo different sequences. The method reveals whether the impact of sequence variation is statistically significant compared with differences caused by cell-to-cell variations. Here, no significant impact of temperature variation was observed. For SOC variations, no impact on capacity but a significant impact on resistance was shown and assigned to a change of the diffusion resistance. Based on their results, they concluded that in this example, capacity fade is a memoryless effect. This confirmed the results of Sarasketa-Zabala et al.,[29] who also investigated the effect of aging sequences of temperature and SOC in calendar aging tests. Here, aging models were parameterized using static aging conditions and validated with dynamic aging tests. Since they observed low prediction errors in the validation, they concluded that the aging sequence plays a minor role. The same authors also investigated the impact of sequence variations in dynamic cycling aging tests.[33] An example aging sequence is shown in Figure 2b. Here, variation of depth of discharge (DOD) and c-rate are superimposed. Again, models were first parameterized using static tests and afterward validated with dynamic tests. They observed that cell aging was lower under dynamic aging conditions than it was expected to be based on the static aging tests. Therefore, they suggested stepwise validation using various combinations of dynamic tests. They emphasized that there is a need to check if sequences matter. Recently, Raj et al.[12] investigated calendar and cycling aging in dynamic tests. They investigated aging for four different groups. Applied sequences are shown in Figure 2c. Capacity fade for the investigated cells is shown in Figure 2d. The results show that in case of higher c-rates, that is, C/2, the aging sequences significantly influences capacity fade, which indicates path-dependent battery aging. Dynamic tests using six different aging conditions were applied by Karger et al.[23] Their study included variations of temperature, mean SOC, DOD, and c-rate. They compared two different methods, that is, cumulative charge throughput and current capacity, for aging modeling. For cycling tests they observed noncumulative capacity fade and labeled that as path dependence through sequence dependence, which is in accordance to other studies and uses definition PD II. However, as this noncumulative behavior can be explained using the current capacity method, they concluded that the capacity fade is not path dependent (PD III). This indicates that definitions of path dependence used in literature are not always consistent. Compared with previous examples, rather complicated duty cycles were investigated by Dubarry et al.[21] They investigated the sequence of two duty cycles of a electrical vehicle battery under grid operation. In total, they studied 12 duty cycle combinations. They concluded that path dependency only occurs with higher c-rates.
To sum up, it is well known that static tests often oversimplify battery aging, which yields errors in battery lifetime prediction. A systematic way to introduce more realistic conditions is a dynamic test. They allow to assess path dependency of the aging process. Studies mostly focused on two or three different aging conditions and investigated the impact of the sequence of these conditions. The sequence variations were sometimes designed to fulfill equal cumulative stress[31, 32] or equal cumulative duration of stress conditions.[12] Evidence for path dependency was not always found and also depended on how path-dependence was defined.[23] Most studies that use dynamic tests focus on testing for PD II. It seems that higher c-rates triggered path-dependent behavior.[12, 21] The relevance of taking aging uncertainty into account was often highlighted,[22, 32] and application of statistical methods like ANOVA was suggested.[22] As an alternative, the error of model predictions can be used to reveal the impact of the sequence variation.[29] A systematic comparative study on various approaches to depict path dependency is currently not available. Further, apart from these generally observed procedures, a common guideline on how to design and utilize dynamic tests to investigate path dependency of battery aging is currently missing.
2.3 Characterization of Degradation Pathways
In the following sections, various approaches to assess and describe degradation paths are reviewed and discussed.
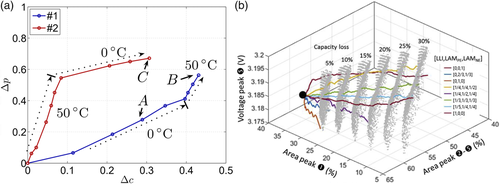
There are many possible degradation processes in lithium-ion batteries. These processes are usually intensified by particular aging stress conditions. For instance, lithium plating will be triggered by low temperatures and high charging rates,[35] while solid–electrolyte interface (SEI) layer growth rate increases at high temperatures and high SOCs.[36] Therefore, it is evident that degradation processes can differ for different stress conditions, for example, different usage schedules. This was addressed by Bauer et al.[37] They investigated battery aging in a sequence of high and low temperatures. Both aging stress conditions cause capacity loss and loss of pulse power capability. In Figure 3a, results of this aging study are shown. The graph shows the loss of pulse power capability against capacity loss. It can be clearly seen that the trajectory of aging depends on the aging stress conditions. Thus, PD I is fulfilled. Further, it can be seen that the sequence variation causes different final states on this plane. This suggests that here PD II is fulfilled as well. However, no conclusions with respect to PD III are possible based on this study. The authors concluded that cell state is better characterized by the position on this plane in contrast to use-only capacity loss or pulse power capability.
As different degradation paths often manifest in different degradation processes, detection and separation of degradation processes is highly important. To separate degradation processes, often differential voltage analysis (DVA) or incremental capacity analysis (ICA) are applied. For both methods, the change of the open-circuit voltage (OCV) during aging is measured. Using OCV, incremental capacity versus voltage or the derivative of voltage versus capacity can be depicted. To differentiate aging processes with ICA, it is assumed that different aging phenomena will influence features of the incremental capacity differently. In Figure 3b, this is illustrated for different aging trajectories that are plotted in a 3D space of selected features of interest of the ICA as given by Dubarry et al.[38] Further, positions with equal capacity loss are indicated. This demonstrates that the same capacity loss can be reached by different degradation pathways and is then also differentiable by its incremental capacity spectra. ICA can be also used to assess degradation modes, for example, loss of active material (LAM) or loss of lithium inventory (LLI). Dubarry et al.[39] utilized ICA in their study of path dependency, which revealed that first LLI and later LAM occurred. Baure et al.[40] used ICA to differentiate degradation paths. They found that the degradation of cells is more complex than just capacity loss and the resistance increase. Besides ICA, DVA can also be used to differentiate different degradation modes.[33] By analysis of the shift of particular features of the differential voltage spectra, degradation modes can be identified. Further, degradation of negative and positive electrode can be differentiated. Ma et al.[41] used both methods, that is, DVA and ICA, to improve SOH estimation in electric buses and could identify different degradation paths. The main advantage of ICA and DVA is that they enable a detailed insight into degradation mechanisms. As discussed above, capacity loss could be caused by a combination of different degradation modes, which can be depicted by these methods. However, time-consuming OCV measurements at both, the full-cell and half-cell level, are needed to achieve this insight.
Apart from OCV-based methods, dynamic methods can be used to differentiate degradation processes.[42] For example, electrochemical impedance spectroscopy (EIS) was used to differentiate different degradation processes for the variation of particle size distribution.[43] Moreover, nonlinear frequency response analysis (NFRA) was used to differentiate between high- and low-temperature aging and identify particular aging mechanisms such as lithium plating.[44-46] Model-supported analysis of EIS spectra was used to differentiate between degradation processes.[47] This approach further enables detailed characterization of single degradation processes such as the degradation of the SEI.[48] Beyond that, also data-driven estimation of SOH is a possible alternative, which was reviewed by Li et al.[49] As described earlier, EIS and NFRA are useful methods to depict lithium-ion battery degradation. In contrast to DVA and ICA, these measurements are less time-consuming. However, analysis of measurement results often requires the use of appropriate battery models. Pastor-Fernandez et al.[50] compared EIS-based identification of degradation modes with equilibrium voltage-based methods. They concluded that both approaches have their advantages and drawbacks for implementation within the BMS. Therefore, they suggest to investigate both approaches for on-board diagnosis.
Another important factor for the characterization of degradation pathways is the identification of a suitable metric of the battery SOH. Thomas et al.[20] stated that observed path dependency of relative resistance might also indicate that this measure does not sufficiently characterize the SOH. Su et al.[22] characterized SOH using a combination of capacity and resistance, which mitigated this issue. The battery state could also be defined as a combination of various features in a higher dimensional space.[38] Dubarry et al.[51] pointed out that SOH should not be defined with a simple equation, but requires a more in-depth understanding of the battery degradation mechanisms. The discussion demonstrates that observation of path-dependent behavior is also related to the definition of the SOH. A poorly defined SOH most certainly is path dependent by PD II, while a better assessment of the actual battery state might resolve this path dependency. However, if the SOH is defined by a rather complex multidimensional state, it is very unlikely that aging with variation of the usage schedule will ever reach the same SOH. In this case the SOH would lose its purpose to provide meaningful information about the state of the system. Ideally, the SOH is a good indicator for the current battery performance and RUL of the battery.
An important issue with respect to degradation paths is that it may not only be influenced by the usage schedule, but also by cell internal properties, which are associated with significant manufacturing uncertainties.[52] This can be also often seen in experimental data, for example, the oxford battery degradation dataset I, which was used for instance by Richardson et al.[53] The dataset has eight cells cycled at the same operating conditions and yet they show a different trajectory of degradation. The impact of manufacturing uncertainty on cell performance was also investigated with a model-based approach by Schmidt et al.[54] The results indicate that uncertainty is significantly influenced by the particular limiting process and optimum of the electrode design. Further, Beck et al.[55] showed that heterogeneity in battery packs will yield different degrees of losses. Baumhofer et al.[52] stated that a low variation in production is helpful to investigate large experimental matrices. This is especially important to study path dependency, because it allows to attribute the observed differences to the variation of usage schedules.[56] In the experimental study conducted by Raj et al.,[12] attempts were made to account for manufacturing variability by considering cells with similar capacities at the beginning of life. Nevertheless, uncertainty cannot be fully mitigated and usually increases with aging. Therefore, adequate statistical methods need to be applied to differentiate difference of degradation paths caused by uncertainty from differences caused by the usage schedule.
2.4 Interaction of Degradation Processes
Most of the literature that has been reviewed here addressed identification and characterization of degradation paths or aimed to test path dependency. Usually, the underlying causes for the observed difference in degradation path or path dependency is not examined in detail.
Analysis of the degradation modes enabled to characterize different aging trajectories in more detail. Dubarry et al.[39] for example differentiated between LLI in the beginning and LAM at the end of degradation paths. Su et al.[22] revealed that the applied sequence variation had little effect on capacity, but significant effect on resistance, which was assigned to change in diffusion processes. Dubarry et al.[21] assigned the observed difference in degradation paths to a LAM at the anode. Raj et al.[12] identified path dependency to be more relevant using high c-rates. They also confirmed that this impacts more the cell resistance than the cell capacity. By analyzing the degradation modes, they revealed that the path dependency mainly leads to a difference in loss of lithiated active material and speculated that this is due to difference in electrode cracking and loss of electrical contact. They concluded that assuming that calendar and cycling tests can be superimposed might not be valid for higher c-rates.
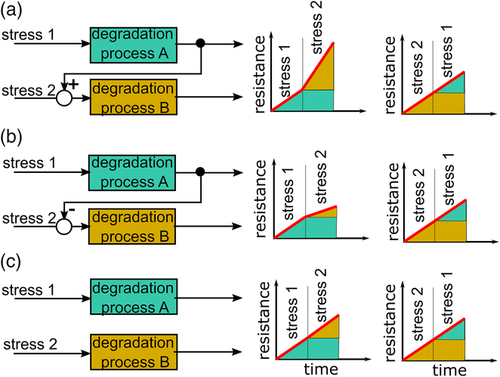
For some studies that investigated sequence variations in dynamic aging tests, path dependency was shown, while for others no path dependency could not be seen. Raj et al.[12] stated that path dependency appears if triggered degradation processes interact and do not appear if degradation processes are independent. This was also suggested by Edge et al.[57] They further specified such interactions as positive and negative feedback between degradation processes. This is illustrated in Figure 4 for degradation with two different degradation processes, A and B. In Figure 4a,b, aging is shown for positive and negative interaction between process A and process B, respectively. In Figure 4c, the aging is shown without interaction. Aging is always shown as rise of resistance for two simple sequences for which the order of stress conditions is switched. If the processes A and B interact, it means that a positive interaction yields larger resistance, if process A is triggered first. It yields lower resistance in case of a negative interaction between process A and process B and process A is triggered first. If there is no interaction, the order of the stress factors does not impact the resistance. Therefore, interaction of degradation processes should result in path-dependent (PD II) behavior. To enable the consideration of path dependency (PD II), feedback and interaction of degradation processes needs to be considered. However, this is usually not considered.[57] Interaction between degradation processes was studied by Reniers et al.[58] using various degradation models. Their results show that degradation mechanisms can interact and influence each other.
Yang et al.[59] investigated the interaction of lithium plating and SEI growth in a model-based approach. Further, Carelli et al.[60] introduced an electrochemical model that couples lithium plating with SEI layer growth, which includes a positive feedback of plating on SEI growth. This interaction is a possible explanation for accelerated aging of battery degradation.[60-62] Schuster et al.[62] showed that extreme conditions can trigger the shift to accelerated aging early. Further, Anseán et al.[63] suggested that interaction of mechanisms can cause accelerated aging, that is, LAM can yield lithium plating. As the phenomenon of accelerated aging is highly important for battery lifetime prediction and for second-use application, interaction of degradation processes should be studied in more detail. Path-dependency studies that utilize dynamic tests seem to be a promising approach to trigger and expose interactions of degradation processes.
2.5 Aging Modeling
There are several modeling approaches for battery aging that range from purely data-driven models to models derived from first principles. An important application of these models is the prediction of battery lifetime. This is challenging, because of the different interdependent degradation processes that lead to path-dependent behavior. Available aging models that consider path-dependent behavior of battery degradation are described in this section. Remaining challenges of these modeling approaches are outlined.
Aging models derived from accelerated aging tests, for example, models used by Schmalstieg et al.,[27] often consider that the different degradation processes can be superimposed and that consideration of cumulative exposure is sufficient to evaluate the SOH.[64] However, if the aging is path dependent by PD II, that is, the current state is affected by sequence of the aging conditions in the usage schedule and not just by the cumulative stress, the assumption is not valid. A possible improvement is to use rate-based aging models, which consider the rate of degradation instead of a cumulative value.[64] However, this will not solve the issue, if the state variable considered to measure degradation is path dependent by PD III, that is, the future degradation path depends on the history of operation and not just on the current state.
Aging models should also consider another important factor, which is the representation of the state, as has been pointed out in Section 2.3. An improved representation of SOH, which enables to describe battery degradation more accurately, can be achieved by consideration of a combination of capacity and internal resistance as suggested by Dubarry et al.[65] They used an equivalent circuit model, which is separated for anode and cathode and considered different degradation modes. Thus, a multidimensional representation of the SOH seems to be important. However, it is currently not clear how many and which specific properties should be considered.
Si[66] built a prognostic model that utilizes the history of the observed data by constructing a state-space model and updating key parameters, which can improve RUL prediction. Li et al.[67] used a time series-based model to make predictions based on the historical path. Li et al.[49] stated that it is difficult to predict aging, if the model has been trained at very different training datasets. A recent work of Lu et al.[68] addresses this challenge by developing machine learning models that predict battery aging by considering varying operating conditions in training and possible future cycling protocols. The main drawback of data-driven methods is that a large amount of training and validation data is required to ensure that path dependency in batteries is learnt accurately.
In physicochemical models, interaction of degradation processes should be considered to account for path dependency. This can be achieved by combining various degradation models as suggested by Reniers et al.[58] and Kupper et al.[69] With this also the effect of accelerated aging can be depicted.[69] However, to accurately identify interactions, larger and more realistic datasets are needed.[58]
The discussed examples indicate that it might not be possible to develop predictive models with very high accuracy based on static laboratory experiments, because it is very different from real operating conditions. Therefore, utilization of dynamic aging tests for model parameterization seems a promising approach to improve lifetime predictions. In case of physicochemical models, interaction of degradation processes should be considered. For data-driven models, operation history should be taken into account.
3 Short- and Mid-Term Path Dependency
In the previous section, path dependency was discussed in the context of long-term battery aging and the SOH. However, path dependency also exists on short- and mid-term time scales. In contrast to the path dependency of battery aging, the phenomena discussed in this section vanish or can be recovered. Nevertheless, from a methodological perspective, there are many similarities with path dependency of battery aging. Therefore, the definitions given in Section 2.1 are also applied in this section.
Short- and mid-term path dependency can have severe implications on the control of the battery.[13] For instance, prediction of the power capability is a basic function of the BMS, while path-dependency effects could cause under- or overestimation.[70] Thus, path dependency of power capability might require to take load history into account. Moreover, to determine the remaining useful energy, it is important to determine the SOC. The SOC is commonly determined using the OCV–SOC relationship.[71] Unfortunately, the OCV often depends on the operation history, which is called voltage hysteresis and needs to be taken into account for battery management.[72] Another prominent example is the memory-effect in nickel–metal hydride (NiMH) batteries, which can be mitigated by ensuring complete charge/discharge cycles.[73, 74]
In this section, research on these short- and mid-term path-dependency effects is reviewed. First, various typically observed phenomena are summarized and differentiated from each other, while examples for several battery materials are given. Second, the current status on understanding these phenomena is reviewed. It is shown that there are manifold explanations and the mechanisms can also depend on the material, while not all phenomena are fully understood, yet. Therefore, the overview rather summarizes the frequently discussed theories and test methods than being comprehensive and conclusive. Finally, various models that are used to consider these effects are discussed.
3.1 Differentiation of Observed Phenomena
Short- and mid-term path-dependency is categorized as follows: 1) the path dependency of the OCV, which is usually called voltage hysteresis, 2) path dependency of the power capability, and 3) memory effects that appear or manifest across several charge/discharge cycles. The latter includes the aforementioned memory effect in NiMH batteries, but also memory effects being observed in current lithium-ion technologies.
In many battery materials, the voltage at a given SOC depends on how the SOC was reached, for example, by charging or discharging. This phenomena is called voltage hysteresis and does not even disappear for very long waiting time under open-circuit conditions.[75] Voltage hysteresis was observed earlier in NiMH batteries,[73] but also appears in many lithium-ion-based batteries. In Figure 5a, an example of the voltage hysteresis for a lithium iron phosphate (LFP) cell from Marongiu et al.[14] is shown. Here, the red line is the OCV for a full charge/discharge cycle. This is often referred to as hysteresis boundary, because cycles within smaller SOC ranges, that is, minor loops, usually lie in between these boundaries. This is shown in Figure 5a for the minor loop between 40% and 60% of the SOC. Not only does the voltage depend on the charge direction, but is also influenced by other factors, such as temperature, current rate, and aging. The impact of the latter is most distinct in the material investigated by Marongiu et al.[14] Barai et al.[72] showed that the OCV is less dependent on current than temperature. Marongiu et al.[14] also studied the impact of the path that was applied before a minor loop, but found a rather limited influence for the investigated cell. Roscher et al.[76] conducted a broad study on the impact of the cycling sequence on the OCV. They observed that the OCV depends on the load history, while the impact of history vanishes. Moreover, Gerschler et al.[77] investigated the impact of charging prehistory on OCV for various materials. Here, SOC was adjusted by various sequences, where the number of steps and rest time between steps are varied. Their results showed that the prehistory indeed has an impact on the OCV at SOC 50%, while voltage decreases with increasing Ah throughput. In general, the observed voltage hysteresis fulfills PD II, because the voltage depends on the sequence of charging/discharging and not just the cumulative charge, that is, the SOC. In this context, PD III denotes that the future trajectory of the voltage depends on previous trajectory and cannot be explained by the current state, that is, voltage, alone. If state is defined by the voltage, PD III is most certainly also fulfilled. However, the state could be also defined by a combination of voltage and SOC, which might resolve the observed path dependency. This is similar to a better definition of the SOH, as discussed in the previous section. Hysteresis behavior was observed in NiMH and many lithium-ion battery materials such as LFP, NMC, lithium titanate oxide (LTO), carbon,[78] and graphite.[79, 80] Various overviews of materials that possess voltage hysteresis can be found in literature.[77, 81, 82]
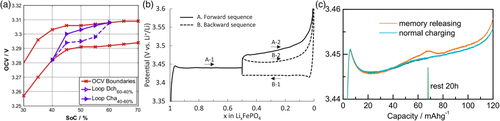
Path dependency of power capability was investigated by Srinivasan et al.[13] Their study shows that the discharge with higher rates, that is, 3C, from SOC 50% depends on whether the cell has been charged or discharged before. The results indicate that the discharge capacity and voltage during discharge is higher, if SOC is adjusted by charging from 0% SOC in comparison with discharging from 100% SOC. This is the first time that path dependency of the high rate capability of an LFP cell is shown, which is a different phenomenon compared with the path dependency of OCV. This observation indicates that PD III is fulfilled. The effect of the sequence, that is, forward (0–50–100% SOC) or backward (100–50–100% SOC), on the electrode polarization was also investigated by Kondo et al.[83] using a simulation-based approach. Example results are shown in Figure 5b. It can be seen that the potential during charge from 50% SOC to 100% SOC, that is, A-2 and B-2, depends on the sequence. It is higher if the cell has been charged to 50% SOC (A-1) and is lower if the cell has been discharged to 50% SOC (B-1). Roscher et al.[70] performed a similar test routine, but instead of charge/discharge they characterized power capability with a pulse test. They observed that the load history has a significant impact on short- and long-term resistance. A similar effect was observed by Christophersen et al.[85] in two different lithium-ion battery cells. They distinguished between charge and discharge pulses and found that in case of charging pulse, the resistance depends on the rate of change of SOC, but for discharge pulse this was not observed. Xie et al.[86] observed similar path-dependent behavior for lithium nickel manganese oxide (LNMO) material. They showed that a very long relaxation can release the path dependency. Even though the path dependency of power capability is important for battery management, it is often neglected.
According to Gerscher et al.,[77] one of the first reports on a memory effect in batteries was provided by Sleight et al.[87] in 1991. They studied lithium manganese oxide (LMO) material and observed that the slope of the voltage during discharge is influenced by the DOD of the previous cycle. Here, the voltage path is followed until new terrain is reached. Another memory effect has been observed in nickel-based batteries for partial discharge of the batteries.[74] Here, the system seems to memorize repeated partial discharges in a way that the cell capacity is limited to this partial discharge capacity in the upcoming cycles. The effect is caused by the formation of an additional phase upon overcharge and can be cured by performing depth discharge and subsequent charge cycle.[74, 88] This phase may also yield different mechanical behavior of the cell.[89] Memory effects were also reported for lithium-ion battery technologies; however, the phenomena are different from the memory effect in nickel electrodes. Sasaki et al.[15] reported memory effects for LFP and LTO. The effect can be seen in Figure 5c as given by Guo et al.[84] Here, the cell was charged and discharged between 0% and 50% SOC within the memory-writing cycle. Afterward, a full cycle, that is, a memory-releasing cycle, was performed and compared with a normal cycle. A distinct kink in the potential, exactly at the end of the partial cycle, can be observed. The study of Sasaki et al.[15] showed that this effect increases with repetition of partial cycles and is more pronounced for charge compared with discharge. Roscher et al.[76] observed a similar effect for complex charge/discharge sequences. Guo et al.[84] showed that the particle size has a significant impact on the memory-effects in LFP. Memory effects in batteries are manifold. The commonality is that prior cycling has an impact on future cycling behavior, which fulfills the definition PD III. Further, in all cases this memory of the cycling history can be released in subsequent cycles, which distinguishes memory effects from path dependency of cell aging.
Similar to dynamic aging tests, sequence variations are also frequently used to asses short and mid-term path-dependency.[13, 70, 77] This indicates that application of sequence variations is a methodological overlap between path dependency of aging and short- and mid-term path-dependency phenomena. The most common sequence variation is to adjust SOC either starting from a fully discharged or a fully charged cell. This can be used to test path dependency of power capability or path dependency of the OCV. However, also much more complicated sequences were tested, for example, by Roscher et al.[76] and by Marongiu et al.[14] Since the path-dependency effect vanishes, only the short-term history needs to be considered. Nevertheless, possible variations are extensive, because there are many possible influencing factors such as temperature, current rates, or resting steps. In case of the voltage hysteresis, an accurate assessment of the OCV is highly important. The effect of the test protocol for assessment of open-circuit potential was studied for example by Barai et al.[90] and by Petzl et al.[75] It was shown that an incremental measurement is beneficial compared with continuous measurement.[75] Weddle et al. showed that the path dependency also impacts the cell impedance.[91] Gaberscek et al.[92] investigated higher harmonics for dynamic characterization of LFP, which revealed that cell impedance is nonlinear for lower frequencies. This phenomena might be caused by path dependency. If resistance depends on the charge direction, dynamic signals will be distorted. Therefore, NFRA[44] seems a promising method to investigate path dependency.
3.2 Theoretical Background
As outlined earlier, path dependency on short- and mid-term time scales was observed in very different manifestations. In this section, theoretical background and various explanation models are reported. It is further discussed, if observed phenomena, such as voltage hysteresis, path dependency of power capability, and memory effects, have different causes or if there is possibly a single mechanistic explanation.
One model for explaining path dependency, which was frequently used in literature, is the shrinking core model.[13] It was applied to explain the behavior of two-phase materials, such as LFP. The shrinking core model is illustrated in Figure 6a for a lithium insertion and extraction process. The upper part illustrates insertion processes of a particle. Here, a lithium-rich phase is formed at the shell of the particle, while the core possesses a lithium-poor phase. During charging the size of the lithium-poor core continuously shrinks. The lower part of the figure shows the lithium extraction process. Comparing middle stage for insertion and extraction, it can be seen that the lithium-rich and lithium-poor phase are flipped. If lithium is extracted from a particle after insertion to 50%, another lithium-poor phase would be formed at the shell of the particle. Based on this model, it can be explained how the battery can possess memory. Here, the path history manifests in the order of separated phases in the particle. This could theoretically influence the power capability, if the diffusion coefficients are different for the two phases.[70] Even so, this model is very intuitive; there is evidence that this model is not valid for LFP. For example, Laffrot et al.[93] used high-resolution electron energy loss spectroscopy to investigate the deinsertion/insertion process in LFP particles and found that phase transition rather occurs by emptying and filling of channels. Other studies also concluded that the core–shell model cannot explain experimentally observed path dependency.[15, 94] Nevertheless, the model is a valuable first assessment of how path dependency could manifest and it is agreed upon that phase separation in two-phase materials plays a major role in explaining path-dependent phenomena like voltage hysteresis.[77, 95]
Phase separation was modeled and investigated using non equilibrium thermodynamics established by Bazant.[98] This approach can explain the voltage hysteresis, which occurs also for very low rates, that is, C/50. The modeling approach can also be used to describe the phase separation in particles,[99, 100] which includes the nucleation and growth of new phases.[101] Moreover, the modeling method can be used to investigate the impact of conversion rates and showed that phase separation can be suppressed by higher rates.[102] This is also supported experimentally by Zhang et al.[103] They showed that for low and medium rates, a phase separation is visible, while for high rates phase separation is suppressed.
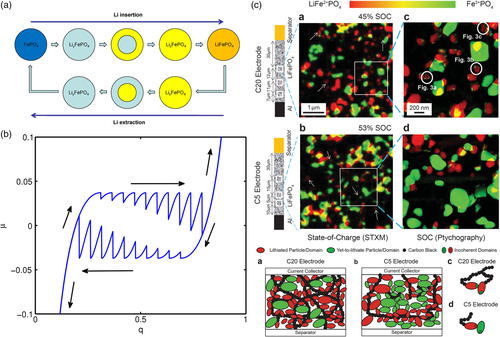
Dreyer et al.[104] suggested a particle-by-particle mechanism to explain the voltage hysteresis. The model considers many particles being electrically and ionically connected, which allow them to interact. Thereby, the charge and discharge processes are described by the same reaction, where only the direction changes. Simulation results for a system with ten particles are shown in Figure 6b. It can be seen that the model can indeed explain the voltage hysteresis. Their model can be used to explain the path dependence of voltage in LFP.[96] The particle-by-particle conversion is also supported by experiments that found that most of particles in LFP electrode have either a single lithium-rich or a lithium-poor phase, while only very few particles have both phases.[97, 105, 106]
The idea of a multiparticle system was further extended by including heterogeneity of the electrode.[83, 107, 108] Heterogeneity can be considered by introducing a resistance distribution[107] or a particle size distribution.[83] The model can explain the voltage hysteresis, the path dependency of the power capability, and the memory effect of the cell voltage. It was shown that the charge/discharge behavior of electrodes is significantly influenced by the particle size distribution and can also change due to degradation of the particles due to cracking or agglomeration.[43, 109] A narrow particle size distribution should be beneficial to avoid heterogeneous particle charging and path dependency.[83, 109] The effect of heterogeneous electrical connection was investigated experimentally by Li et al.[97] In Figure 6c, example results are shown for different carbon black contents. It can be seen that for high carbon content, that is, C20, the order of phase change is rather influenced by the particle size. In case of poor electrical connection, that is, C5, it is mainly influenced by the electrical network.[97]
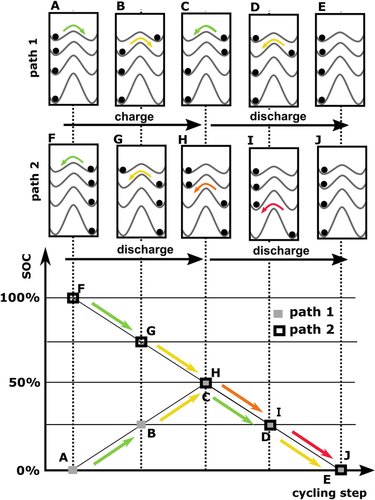
A general explanation model for path dependency was provided by Sleight et al.[87] in 1991. Even though this concept is very old, it still can be used to gain a very intuitive understanding on path dependency of power capability. The concept is adapted and illustrated in Figure 7. The charge and discharge processes are illustrated by transferring entities, for example, particles, between a charged and a discharged state. To transfer them, an energy barrier needs to be overcome. The energy barrier is assumed to be heterogeneous. There are entities with high-energy barriers, for example, being large particles or poorly connected particles, and others with low-energy barriers. During charge and discharge always the entity with the lowest-energy barrier is transferred first. Based on this concept, path dependency can be depicted for the classical tests that compares path 0–50–0% (path 1) with 100–50–0% (path 2). It can be seen that the states at 50%, that is, H and C, are different. For path 1, entities with low-energy barriers are in a charged state. For path 2, entities with high-energy barriers are charged. As a consequence, the energy barriers for further discharge is lower for path 1. This simple and generic energy barrier explanation model can be used to gain an intuitive understanding for path-dependent behavior of power capability.
The detailed mechanisms that yield the complex behavior of two-phase materials are not finally revealed. Thus, further research is needed. A comprehensive review of two-phase separation of LTO and LFP was done by Li et al.[105]. Here, also phase diagrams and mechanistic details for these materials are provided. Malik et al.[110] provided a critical review, which assesses that LFP is the subject of controversial debate, while the various views are discussed in detail. It is very likely that phase change is the main cause for many path-dependent phenomena observed in lithium-ion batteries. Nevertheless, there are also other possible causes for path-dependency such as different reaction pathways for charge and discharge[82, 111] or path-dependent lithium site occupation.[112]
3.3 Modeling
Modeling of short- and mid-term path dependency is important for various reasons. First, models could be used to improve the electrode and material design to mitigate path dependency first hand. Second, models can also help to get a better understanding of these phenomena. This could be used to overcome the associated challenges for battery operation by improving battery management.[113] Finally, models could be directly integrated into the BMS to improve functions like SOC estimation and power capability prediction. In the following, the most relevant physics-based, equivalent circuit-based, and data-driven models are discussed.
Some effort was made to model the aforementioned shrinking core theory.[114] For instance, integration of phase separation in classical particle models was used to simulate graphite hysteresis.[115] Theory of nonequilibrium thermodynamics was used to simulate phase separation as well as the dependency of applied rate.[98, 101] Multiparticle approaches were frequently used to simulate path-dependent effects. They can describe various phenomena,[94] such as voltage hysteresis, path dependency of power capability, and the memory effect of the voltage. The basic ingredients, which are essential for these kinds of models, are 1) the representation of the electrode by multiple particles with 2) heterogeneous properties that are described by distribution functions and 3) a nonmonotonous open-circuit potential.[83] These models can in principle describe path dependency. Nevertheless, there are some differences in their implementation. These kinds of models either consider particle size distribution[83] or heterogeneous distribution of resistance.[94, 107, 108, 116] In addition, the models differ in terms of their level of detail due to consideration of the intercalation channels,[107, 108] being spatially homogeneous[83, 116] or spatially resolved along the thickness of the electrode.[91] As can be depicted, there are several physics-based models that accurately describe various path-dependency phenomena. However, these kinds of models are usually computationally expensive and are not suitable to be integrated into the BMS. Thus, a remaining challenge is to simplify these models to be suitable for BMS application.
According to Yiyang et al.[97] the local electronic connectivity between a particle and the carbon network controls the lithiation pathway. The carbon network is shown to have a significant impact on the electrode performance.[117] Therefore, it is important to have a better representation of the complex electrical networks as suggested by Schmidt et al.[118] An example for various typologies of an electrical network and the according degree distribution functions are shown in Figure 8a. This model approach allows to investigate the impact of the network structure and its degradation on the path dependency and should be elaborated in more detail for systems that possess significant path-dependent behavior.
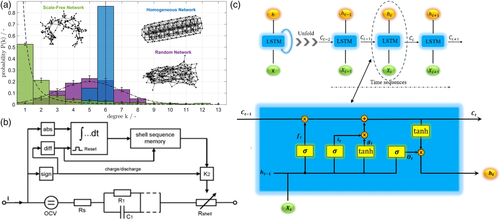
Equivalent circuit models (ECM) are the most common model types for BMS applications and are frequently adapted to consider path dependency effects such as voltage hysteresis. Verbugge et al.[120] used an ECM to estimate the SOC and showed that hysteresis plays a critical role for an accurate estimation in NiMH batteries. Thele et al.[121] adapted an ECM model with an additional element that represents the hysteresis voltage. He et al.[122] used an ECM model combined with Prandtl–Ishlinskii (PI) to model cell voltage hysteresis. They verified their model based on dynamic driving cycles. Roscher et al.[76] included additional resistance within the ECM model, which is adapted based on the operating history to account for the path dependency of the power capability. The model approach is illustrated in Figure 8b. The information of the past operation is stored as shell sequence memory. The model approach is motivated by the shrinking core concept. As the shrinking core theory is most likely not valid to explain voltage hysteresis, future work on ECM-based models should be based on a more profound understanding of these phenomena. This might also facilitate consideration of various phenomena with a single model as it was achieved for physics-based models, that is, multiparticle models,[94] already. It can be seen that classical ECMs need to be refined to accurately consider path dependency.
Path dependency can also be modeled using data-driven approaches. Xu et al.[119] used machine learning in combination with sigma-point kalman filter and ECM to improve SOC estimation. The data-driven part of the model uses long short-term memory (LSTM) to eliminate the effect of voltage hysteresis. LSTM is a type of recurrent neural network that has the ability to make predictions based on sequential input data. In the case of modeling hysteresis, this could be the previous operating history of the cell. The modeling approach is illustrated in Figure 8c. With this approach the OCV voltage is corrected based on the short-term operation history. Remaining challenges are the training of such models as well as choosing appropriate features of the operation history. Further, transferring this modeling approach to other short and mid-term path dependency phenomena should be addressed.
Future work should address the development of novel models that accurately consider path dependency and are applicable within a BMS. This could be achieved by refining ECMs or reducing complexity of physics-based models. Promising alternatives are data-driven models that explicitly take the operation history into account. The development and training of such models is a common challenge for degradation modeling and modeling of short- and mid-term path-dependency phenomena. In all cases it is also important to develop adequate methods to parameterize these models with standardized electrochemical tests. Similar to aging modeling, utilization of test protocols based on sequence variations is needed.
4 Challenges and Future Work
This section describes some challenges and future work that arise in context of path dependency in batteries.
4.1 Next-Generation Battery Materials
To increase the energy density, to replace rare raw materials, or to improve system sustainability, new materials need to be used in future battery technologies.[1] Charge/discharge processes and degradation mechanisms in many promising new materials are even more complex than in current battery technologies. There are indications for several materials that they possess significant path-dependent behavior. Some examples are given.
In lithium–sulfur batteries, the cathode continuously changes its morphology. These changes are significantly influenced by the operating conditions like temperature, voltage, and current.[4] It was shown that Li2S decomposition during charge depends on the previous discharge step as it impacts the structure of the Li2S precipitates.[123] Here, amorphous structure is preferred at fast discharge rates, which is easier to decompose during the subsequent charge. This indicates path-dependent behavior and needs to be taken into account for operation and characterization of these cells.[124] Fotouhi et al.[125] investigated SOC estimation in lithium–sulfur batteries, which was shown to be challenging due to its unique features.
It was shown that the behavior of all solid-state batteries depends on the operating conditions, while it is currently not well understood how various processes might interplay and how that affects the overall cell performance.[126] Therefore, it is highly important to understand the impact of operating conditions and the interplay between various stress conditions such as temperature, pressure, and current density on battery degradation and failure.[126-128]
The plating and stripping process in lithium metal electrodes significantly depends on the operation conditions. Lu et al.[129] studied failure mechanisms in lithium metal batteries for fast charging with sequential c-rate variations and showed a significant effect on capacity fade.
The voltage hysteresis of silicon is more pronounced compared with current anode materials like graphite.[130, 131] The reason for this hysteresis might be lithiation anisotropy.[132] In the first cycle, there is a distinct structural reorganization from crystalline to amorphous structure.[132] The considerable voltage hysteresis of silicon electrodes cannot be neglected for SOC estimation and battery management. The relevance of silicon for next-generation batteries might bring significant attention to short- and mid-term path-dependency phenomena in future.
As shown, path-dependent phenomena play major role in many materials being considered as next-generation materials. Therefore, path-dependent behaviors of batteries need to be anticipated to accelerate the development of new materials and future BMS that facilitate optimal operation.
4.2 Battery Management System
There is a demand for advanced BMS that enables a more reliable estimation of SOH and SOC as well as prediction of RUL and power capability. As discussed in this article, path-dependent behavior significantly disturbs classical BMS approaches, such as SOC estimation based on SOC–OCV relationship, the prediction of power capability based on the SOC, or RUL estimation based on static laboratory experiments. A BMS that considers path dependency can improve battery lifetime, diagnosis for second-use applications, and reliability of the system. This is of particular importance for large BESS as well as EV applications.
Path-dependent behaviors such as voltage hysteresis, path dependency of power capability, and path-dependent aging have to be taken into account for the development of competitive battery systems. Relevant issues that arise from path-dependent behavior of batteries are given as follows: 1) development of BMS models that include short- and mid-term path dependency, 2) including operation history for state estimation, 3) definition of a more informative SOH that considers and anticipates different degradation paths, 4) utilization of dynamic aging tests or in-field data to parameterize aging models, and 5) logging of degradation pathways.
4.3 Battery Characterization
Investigation of path dependency requires special testing sequences. Classical tests to assess battery performance do not anticipate that the battery operation could be path dependent. However, path dependency is relevant for characterization of OCV, rate capability, and aging. Many examples for testing path dependency of aging and short- and mid-term path dependency were depicted in this review. With respect to aging, the importance of dynamic aging tests was highlighted. In a strong relationship, sequence variations are also highly important to investigate path dependency of the OCV and power capability and memory effects. Various approaches to characterize and to investigate path dependency can be depicted. However, currently there is no established standard to test path dependency. Future work should address this issue and develop standardized tests that can be used to assess various phenomena of path dependency.
For battery aging, this should include a systematic approach to test a broad spectra of aging sequences in dynamic tests. This is challenging, because testing of large matrices in static aging tests is already time-consuming and degrees of freedom dramatically increase with dynamic tests. Further, a rigorous interpretation of these aging tests is needed. This requires the application of adequate statistical methods to account for aging uncertainty as well as differentiation of degradation modes.
In the context of short- and mid-term path-dependency, characterization of voltage hysteresis is highly important. This is difficult because voltage hysteresis is influenced by manifold factors. In particular, the impact of battery aging has been shown to be significant. In order to test path dependency of power capability and possible memory effects similar to dynamic aging tests, sequence variations need to be taken into account. Short- and mid-term path dependency vanishes over time. Thus, cycling memory horizon and dependency horizon are critical for the assessment.
4.4 Common Methodology
Currently, there is only a small overlap between research of path dependency of aging and the short- and mid-term path-dependent phenomena. In consideration of the similarity of the problem and the methodological overlaps depicted in this article, this is surprising. Therefore, from our perspective, it is highly important to establish a common methodology for path dependency in batteries. Moreover, path dependency is also relevant in other areas, such as political science.[133] Thus, interdisciplinary efforts could help to develop a sophisticated methodology. A common methodology will advance the research in this field. In particular, this methodology should include common definitions and wording, test protocols, statistical tools, and models. In this article, the current status was summarized, which is a basis for the establishment of such a common methodology. Some specific examples for required common efforts with respect to method development in both fields are given as follows: 1) common definitions for path dependency, for example, PD I-III, as given in this article; 2) common definitions for operation history; 3) common modeling approaches such as data-driven models that consider operation history; 4) common methods to define test protocols that are based on sequence variations; 5) common statistical methods such as ANOVA to elaborate path dependency in the context of uncertainty of internal states; 6) utilization of multidimensional states for SOH and SOC; and 7) state estimation based on dynamic data such as EIS and NFRA
5 Conclusion
Optimal operation is important for the advancement of battery systems. Better operation strategies, monitoring, and control of batteries improve the sustainability, reliability, and customer acceptance of current and future battery technologies. It was shown that path dependency has a significant impact on various aspects of battery operation. Meanwhile, the current understanding is limited, available methods are not broadly established and often insufficient to take these phenomena adequately into account. As a consequence, current battery management usually neglects these phenomena. Therefore, opportunities to improve the reliability of prediction and state estimation methods are currently left out.
The main objective of this article is to summarize the effort that has been made to investigate and understand path dependency in batteries. This is needed to tie loose ends of various research efforts in this field. Research of path dependency of battery aging seems mostly separated from research of short- and mid-term path-dependency effects.
The article provides basic definitions for pathways and path dependency. Here, path-dependency is defined by different levels (PD I-III) being frequently used in literature. On this basis the observed phenomena are categorized and discussed. This discussion shows similarities between path dependency of battery aging and short- and mid-term phenomena. Further, the article reports the methods used to test and model path dependency. There are not many methods available that specifically target path dependency, even though in general there is a broad spectra of methods for battery management. Nevertheless, it is shown that some specific methods are suitable. For instance, it was shown that to characterize path-dependency, sequence variations should be utilized, because this significantly improves testing to be more realistic. Further, it can be seen that sophisticated physics-based models are available, but are not broadly established and validated, which hinders systematic integration into BMS. Operation history should be considered for state estimation and predictions. Data-driven models that use operation history as an input are a highly promising approach in this regard.
To sum up, this article provides a common basis for future research, which eventually will yield a common methodology to study path dependency. In our opinion, the core elements of this methodology are common definitions, tests for path dependency that rely on sequence variations, as well as models for path dependency based on a profound understanding of these phenomena or explicit consideration of the operating history in data-driven models. Special emphasis needs to be set on next-generation materials that may possess path-dependent behavior that is even more pronounced than the current generation. Finally, the methods and models need to be integrated into modern BMS, which will have significant implications for design of the BMS.
Acknowledgements
Open Access funding enabled and organized by Projekt DEAL.
Conflict of Interest
The authors declare no conflict of interest.
Biographies

Fridolin Röder is an assistant professor for methods for battery management at the University of Bayreuth. After a Ph.D. in 2019 at TU Braunschweig (Germany) and a visiting scholar at MIT in 2015, he had a junior research group on multiscale development of batteries at TU Braunschweig until 2020. For 10 years he has been active in the field of modeling and characterization of energy systems with a special focus on batteries.

Srivatsan Ramasubramanian received his bachelor's degree in materials engineering from Nanyang Technological University (Singapore) and master's degree in Energy Science and Technology from Ulm University (Germany). He is currently a Ph.D. at the University of Bayreuth, working with Professor Fridolin Röder. His research interests include path dependency in lithium-ion battery aging and modeling methods based on mechanistic and data-driven approaches for studying battery degradation.




