1 Introduction

With the progressive development of disciplines such as aerospace medicine, the development of materials with exceptional strength and toughness has become a central focus of materials science research. Achieving a combination of high strength as well as ductility remains an arduous task because these properties are often mutually exclusive. Even when one of these properties is maintained, any improvement in the other property is considered a notable accomplishment [1, 2].

In recent years, there has been a surge in multidisciplinary research efforts toward developing materials with exceptional strength and toughness. In metal manufacturing, high-entropy alloys (HEAs)—composed of multiple principal alloying elements—have emerged as a promising class of materials, remarkably demonstrating both enhanced strength and toughness [3, 4]. The complex atomic arrangements present in HEAs disrupt traditional slip mechanisms, providing a strengthening effect while preserving a certain level of ductility, which contributes to toughness. This unique combination of properties has expanded the potential applications of high-performance metallic materials. In addition, several natural biomaterials are also known to have exceptional mechanical properties. One prime example is nacre, a biomaterial composed of alternating layers of minerals and proteins that form a characteristic “brick-and-mortar” structure [5-7]. The soft organic proteins in nacre serve as lubricants, allowing significant relative motion between adjacent tablets. During deformation, this motion leads to substantial energy dissipation, endowing nacre with remarkable toughness [8-11]. The high defect tolerance of the nacreous layer structure has been studied extensively and is widely believed to contribute to its high toughness [12]. Gao et al. [13] were the first to report that nacre platelets with a length below the critical threshold of 30 nm are insensitive to defects [14]. Although Anup investigated the influence of initial defects in the nacreous layer, no defect tolerance was observed [15]. Meanwhile, Mirzaeifar et al. [16] reported that the defect tolerance in nacreous materials increases with their microstructural complexity. Furthermore, Yao et al. [17] proposed that the “brick-and-mortar” structure of nacre effectively reduces stress intensity at crack tips and promotes crack deflection, thereby enhancing defect tolerance. This natural “brick-and-mortar” model has thus inspired the development of novel biomimetic materials. However, the design and manufacturing of such composite materials often involves a high degree of complexity [18]. Therefore, enhancing the performance of existing materials through structural design, without the addition of extra materials, is believed to be a more practical and cost-effective solution. Moreover, this approach has the potential to streamline manufacturing and reduce costs while still meeting the stringent requirements for high-strength and tough materials in advanced applications.

Macroscopic defects in materials often lead to premature or avalanche-like failures under loading conditions, significantly compromising material performance in practical scenarios. However, the strategic and deliberate introduction of artificial defects has been shown to effectively enhance material performance [19, 20]. For instance, Chen et al. [21] recently demonstrated that hierarchical nano-void networks can improve the ductility of metallic composites by 40% through coordinated plastic deformation. Meanwhile, Guo et al. [22] utilized three-dimensional (3D) printing to fabricate biomimetic nacre composites with gradient defect distributions, achieving a 35% increase in tensile elongation. Furthermore, Chen et al. [21] also successfully fabricated nanovoids in metallic (gold) materials, which not only reduced the material's mass but also improved its strength and ductility. In addition to improved stress and strain resistance, these structures showed a higher surface area and greater surface-dislocation interactions, which contributed to strengthening, additional strain hardening, and material toughening. These studies show that by transforming voids from crack-like, detrimental defects into beneficial structural components, a new generation of lightweight, high-performance materials can be produced in an affordable and environmentally friendly manner. Employing a similar approach, Qu et al. [23, 24] incorporated structures with artificial defects into bulk metallic glass, achieving notable macroscopic tensile ductility. Building on this, recent studies have shown that defect-induced stress redistribution in two-dimensional (2D) layered structures can further optimize the balance between strength and ductility; hence, defect density control has emerged as a critical design parameter [22, 25]. Under natural conditions, material damage occurs randomly, and fractures are induced at the most severely weakened points, resulting in poor ductility. Recent evidence has revealed that in conventional materials, the random distribution of defects leads to localized stress concentrations that far exceed the average stress. In contrast, engineered defect patterns can significantly alleviate these stress concentrations [26-29]. The introduction of artificial defects enables multiple regions of the structure to undergo plastic deformation, thereby improving the material's ductility. However, comprehensive theoretical models that fully describe and predict the improvement of material ductility through defect engineering are still lacking.

In this study, we propose a segmented defective structure design inspired by the structure of nacre and conduct an in-depth investigation into its tensile fracture behavior. We first establish representative volume element models of the segmented defective structure, defining geometric parameters and material properties to accurately represent the physical characteristics of the actual structure. Moreover, we introduce relevant numerical calculation methods, which are crucial for precisely simulating and analyzing the mechanical response of the structure under tensile loading. To quantitatively describe the randomness in damage across the structure, we propose a damage factor that serves as a key metric for evaluating the extent of damage in different regions. Using this factor, we systematically examine the impact of defect distribution on structural elongation. This analysis provides valuable novel insights into the relationship between defect distribution and mechanical properties, which are essential for optimizing the design of the segmented defective structures.

While recent studies have explored defect engineering in hierarchical materials [12, 30], the role of geometric segmentation remains underexplored. Although multi-material 3D printing technologies can introduce design complexity, our approach mitigates this by leveraging hierarchical defect segmentation, which aligns well with the layer-by-layer fabrication capabilities of additive manufacturing processes. By programming defect geometry (e.g., size, spacing, and distribution) into digital models, we precisely control the printing process, reducing reliance on trial-and-error iterations. This approach minimizes complexity through parametric design optimization, where defect configurations are pre-simulated using discrete element modeling (DEM) to ensure both manufacturability and mechanical performance, thereby streamlining the transition from digital design to physical prototype development.

2 Model and Problem

2.1 Model Design and Experimental Setup

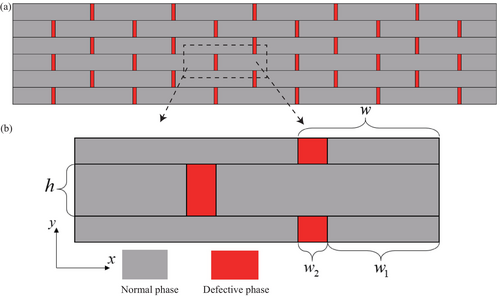
Figure 1 contains a schematic illustration of the tensile fracture behavior of natural and defect-engineered materials. It highlights the contrast between random damage and distributed plastic deformation. The principles illustrated in this diagram guide the development of our segmented defect design strategy.

The representative volume element (RVE) of the model (volume $$$ \Omega $$$) is depicted in Figure 2. It comprises the normal phase $$$ {\Phi}_n $$$ and the defect phase $$$ {\Phi}_d $$$. The interface is denoted by $$$ \Psi $$$.

$$$$ \Omega ={\Phi}_n+{\Phi}_d+\Psi $$$$ (1)

The total strain energy of the system $$$ {\phi}_{\Omega} $$$ is expressed as follows:

$$$$ {\phi}_{\Omega}={\phi}_{\Phi_n}+{\phi}_{\Phi_d}+{\phi}_{\Psi} $$$$ (2)

Strain hardening effects have been observed in various materials. Building on previous research, we employ the bilinear kinematic hardening elastoplastic model to describe material behavior [31, 32]. For a one-dimensional (1D) model, the constitutive model is characterized by the relationship between stress and elongation. The stress–elongation relationship is expressed as follows:

$$$$ \sigma =\left\{\begin{array}{l} E\lambda \kern6.75em 0\le \lambda \le {\lambda}_c\\ {}E{\lambda}_c+\hat{E}\left(\lambda -{\lambda}_c\right)\kern0.75em {\lambda}_c\le \lambda \le {\lambda}_m\end{array}\right. $$$$ (3)

Here, $$$ E $$$ represents the elastic modulus, $$$ \lambda $$$ is the elongation, $$$ \hat{E} $$$ is the plastic modulus, $$$ {\lambda}_c $$$ is the yield elongation, and $$$ {\lambda}_m $$$ is the fracture elongation. The constitutive relationship herein is presented in a 1D form. Assuming that the deformation is small, the strain $$$ {\varepsilon}_{ij} $$$ can be defined by the symmetric part of the spatial gradient of the displacement field $$$ {u}_i $$$, $$$ \partial {u}_i/\partial {x}_j $$$:

$$$$ {\varepsilon}_{ij}=\frac{1}{2}\left(\frac{\partial {u}_i}{\partial {x}_j}+\frac{\partial {u}_j}{\partial {x}_i}\right) $$$$ (4)

The strain energy values of the normal phase and defect phase are as follows:

$$$$ {\displaystyle \begin{array}{l}{\phi}_{\Phi_n}={\int}_{\Phi_n}\frac{1}{2}{\sigma}_{ij}{\varepsilon}_{ij}\mathrm{d}V\\ {}{\phi}_{\Phi_d}={\int}_{\Phi_d}\frac{1}{2}{\sigma}_{ij}{\varepsilon}_{ij}\mathrm{d}V\end{array}} $$$$ (5)

When expressing strain energy, the interlayer shear region $$$ \Psi $$$ involves the relative sliding displacement between layers. Here, we use $$$ \mathbf{u} $$$, which represents the difference between the displacement of the upper and lower elements. A discontinuous displacement jumps on the interface $$$ \mathbf{u} $$$ is described as:

$$$$ \mathbf{u}={\mathbf{u}}^{+}-{\mathbf{u}}^{-} $$$$ (6)

The normal component $$$ {\delta}_n $$$ and the tangential component $$$ {\delta}_t $$$ are derived by

$$$$ {\delta}_n=\mathbf{u}\cdot \mathbf{n},{\delta}_t=\mathbf{u}\cdot \mathbf{t} $$$$ (7)

Here, $$$ \mathbf{n} $$$ and $$$ \mathbf{t} $$$ are the normal and tangential unit vectors, respectively. Given that we primarily focus on tensile deformation behavior, we can assume the normal component to be zero. Under these conditions, the shear strain energy $$$ {\phi}_{\Psi} $$$ can be expressed as follows:

$$$$ {\phi}_{\Psi}={\int}_0^w{\phi}_t\left({\delta}_t,x\right) dx $$$$ (8)

Here, $$$ {\phi}_t $$$ is the shear strain energy density within the interface. Furthermore, the shear stress–sliding displacement relationship can be represented as follows:

$$$$ \tau =\left\{\begin{array}{l}k{\delta}_t\kern1em \left|{\delta}_t\right|<{\delta}_t^c\\ {}0\kern1.75em \left|{\delta}_t\right|\ge {\delta}_t^c\end{array}\right. $$$$ (9)

Here, $$$ k $$$ is the shear stiffness, and $$$ {\delta}_t^c $$$ is the maximum slip limit.

2.2 Discrete Element Model

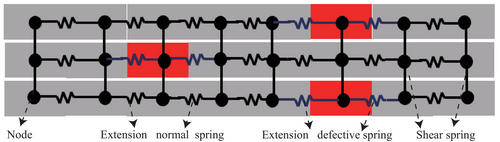
In the present work, a discrete element approach was employed in order to reduce the computational expenses associated with modeling staggered composites. The DEM approach adopted herein is based on the following assumptions [31, 33]: (i) Each element is symbolized by a “node” possessing a single degree of freedom, specifically the displacement along the direction of the applied pulling force; and (ii) the elements (nodes) are interconnected with adjacent elements through nonlinear springs (Figure 3). Each element in the DEM represents a cylindrical or prismatic unit with a diameter/length ratio of 1:5, mimicking the dimensions of a nacreous tablet. The nodes are connected via nonlinear springs with defined friction (coefficient μ = 0.3) and movement constraints (max slip = 10% of element length), calibrated to experimental interlayer shear data derived from nacre [10, 11].

The strain energy function for the principal region can be expressed as follows:

$$$$ {\displaystyle \begin{array}{ll}{\phi}_{\Phi_n}& ={\int}_{\Phi_1}\frac{1}{2}{\sigma}_{ij}{\varepsilon}_{ij}\mathrm{d}V\\ {}& =h{\int}_0^{w_1}\frac{1}{2}{\sigma}_{11}{\varepsilon}_{11}\mathrm{d}x\\ {}& =h\sum \limits_{i=1}^{m_1}{\int}_0^{w_1}\frac{1}{2}{\sigma}_{11}^i(x){\varepsilon}_{11}^i(x)\mathrm{d}x\end{array}} $$$$ (10)

$$$$ {\displaystyle \begin{array}{ll}{\phi}_{\Phi_d}& ={\int}_{\Phi_d}\frac{1}{2}{\sigma}_{ij}{\varepsilon}_{ij}\mathrm{d}V\\ {}& =h{\int}_0^{w_2}\frac{1}{2}{\sigma}_{11}{\varepsilon}_{11}\mathrm{d}x\\ {}& =h\sum \limits_{i=1}^{m_2}{\int}_0^{w_2}\frac{1}{2}{\sigma}_{11}^i(x){\varepsilon}_{11}^i(x)\mathrm{d}x\end{array}} $$$$ (11)

Here, $$$ {m}_1 $$$ and $$$ {m}_2 $$$ represent the number of elements in the normal region and the defective region, respectively. Moreover, $$$ {\sigma}^i $$$ and $$$ {\varepsilon}^i $$$ are the stress and strain corresponding to the $$$ i $$$-th element, respectively.

Meanwhile, the strain energy function for the interlayer region can be expressed as follows:

$$$$ {\phi}_{\Psi}={\int}_0^w{\phi}_t\left({\delta}_t,x\right)\mathrm{d}x=\sum \limits_{i=1}^m{\int}_0^w{\phi}_t^i\mathrm{d}x $$$$ (12)

Here, $$$ {\phi}_t^i $$$ represents the interlayer strain energy density of the $$$ i $$$-th element, and $$$ m $$$ represents the total number of elements. Model validation was performed using experimental data from Qu et al. [24], who generated the tensile stress–strain curves of defect-engineered bulk metallic glass. A 95% correlation in peak stress and fracture elongation was observed, with root-mean-square error values < 5% for both metrics. Experimental data from Qu et al. [24] and DEM simulations revealed strong qualitative agreement in stress–strain trends, with elongation errors within 8% and strength errors within 5%. Minor discrepancies arose from the (i) idealized defect shapes in DEM vs. the rough interfaces in experiments; (ii) material anisotropy not captured in 2D isotropic models; and (iii) fabrication tolerance-induced defect variations (Section 2.3).

3 Result and Discussion

To quantify damage evolution in regions of defects, we defined a dimensionless damage parameter $$$ \rho \in \left[0,1\right] $$$, where ρ = 0 for the pristine material and ρ = 1 indicates complete material degradation. Recognizing the inherent variability in artificial defect creation, we implemented stochastic damage distribution. The ρ value in each region of defect was assigned based on a Weibull distribution [25], consistent with the previously reported statistical characteristics of heterogeneity in plastic deformation. While the Weibull distribution approximates defect randomness, future work may incorporate multi-parameter distributions or machine-learning-driven defect models to more reliably represent experimental variability, particularly for hierarchical materials. Consistent with the strength degradation principle, defective regions were modeled with reduced elastic modulus values, E_d = (1 − ρ)E_n, Ê_d = (1 − ρ) Ê_n. In combination with relevant experimental data, normalization procedures were applied to the relevant parameters [33, 34]. With respect to the relevant calculation parameters, for the damage factor ρ, the mean value and variance were set as 0.1 and 0.1, respectively, with E = 12.5, Ê = 0.01, and λ_c = 0.08. Focusing on defect effects, we first established a 1D analytical framework to explore fundamental deformation mechanisms.

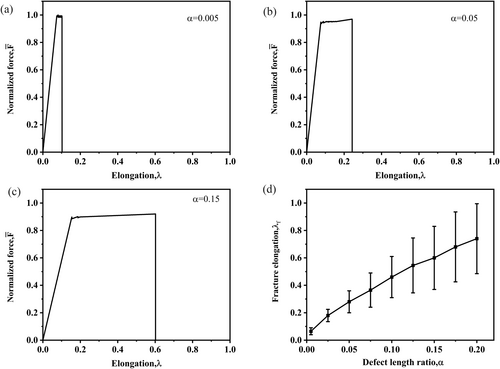
In the 1D structural model, we define three geometric parameters: total length L, individual defect length L_s, and defect count n, with the defects uniformly distributed across the structure. To quantify the cumulative damage effect, we introduce a dimensionless damage index—the defect length ratio α = nL_s/L. The mechanical performance is characterized by two key parameters: ultimate tensile strength F_f and fracture elongation λ_f. To ensure statistical validity, each experimental condition is replicated across a minimum of 50 specimens in our model. Figure 4 illustrates the correlation between the damage index α and the mechanical properties of the material. Figure 4a,b demonstrate the inverse relationship between α and structural strength, where an increase in α leads to the progressive deterioration of F_f. Notably, a critical threshold emerges at α = 0.15, beyond which the strength degradation accelerates significantly. Structural fracture elongation exhibits distinct deformation characteristics across different states of damage. Elastic deformation maintains near-constant values regardless of damage progression, whereas plastic elongation demonstrates a progressive enhancement that is proportional to the severity of structural damage. This behavior shows notable variations in defective structures, wherein both the mean fracture elongation and its statistical dispersion increase systematically with the defect length ratio. The observed mechanical response reveals a critical trade-off in 1D defective structures. While increased defect length ratios promote the distribution of plastic deformation across multiple structural regions, thereby improving overall ductility, this benefit comes at the expense of two significant engineering components: (i) the substantial degradation of structural load-bearing capacity and (ii) increased stochasticity in fracture elongation behavior. These dual effects create an optimal defect length ratio range that balances ductility enhancement against structural reliability requirements.

Inspired by the hierarchical architecture of nacre, we developed a 2D segmented defective structure. The staggered arrangement of segmented components significantly enhances structural ductility through controlled deformation mechanisms. The defect length ratio α, defined as the length of the defect segment relative to the length of the pristine first layer, is a critical design parameter. Figure 5 systematically demonstrates the α-dependent mechanical response of the engineered structure. The fracture elongation exhibits a characteristic convex profile, with ductility peaking at intermediate α values (0.13–0.16) before declining thereafter. This non-monotonic behavior correlates with the activation of distributed plastic zones owing to the staggered defect configuration. Compared to conventional 1D structures, those with the 2D defect arrangement exhibit more efficient strain redistribution. Remarkably, this structure maintains an ultimate tensile strength (F_f) that is > 90% of that of the pristine structure across α values less than 0.16 (Figure 5c), demonstrating exceptional damage tolerance. However, excessive defect density (α > 0.18) induces premature failure via defect coalescence, reducing both strength and ductility. Figure 5 depicts the behavior of two distinct fracture morphologies with different defect densities. Structures with lower α values (α < 0.075) exhibit linear fracture propagation, where plastic deformation is confined to localized regions proximal to the crack tip. In contrast, structures with higher α values (α > 0.075) demonstrate a characteristic Z-shaped fracture path, which may lead to premature shear failure due to enhanced stress concentration around the geometric discontinuity.

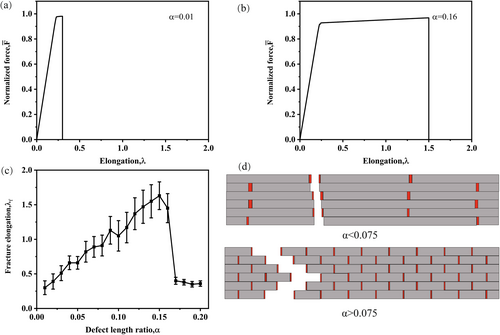
The optimal defect length ratio (α) is material-specific. It is influenced by (i) modulus contrast (En/Ed), where stiffer materials (e.g., ceramics) require lower α values to avoid brittle failure; (ii) the yield strength ratio (σyn/σyd), as larger ratios promote localized deformation in defect phases; and (iii) fracture toughness (KIC), necessitating smaller defect sizes in low-KIC materials such as glass [25]. The optimal defect length ratio (α ≈0.075) represents a balance where ductility gains (30%–50%) outweigh strength losses (< 10%). Beyond this threshold (α > 0.16), the trade-off shifts, with strength degradation accelerating (20%–30% loss) and ductility improvement plateauing. This critical point coincides with the transition from distributed plastic zones to localized shear bands, as shown in Figure 5d.

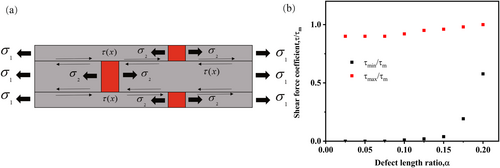
In the 2D layered structure, structural junctions at defect sites consistently serve as critical stress concentration zones, exhibiting peak shear stress values that predispose these regions to preferential failure induction. In symmetrical configurations, numerical simulations indicate that the shear stress is the lowest at the midpoints between adjacent defects in vertically aligned layers. Notably, the stress gradient between the maximum and minimum shear zones demonstrates progressive instability as the defect length ratio increases (α > 0.1). As illustrated in Figure 6, the shear stress distribution exhibits two characteristic transitions. At α = 0.15, the maximum shear stress approaches the critical failure threshold; meanwhile, at α = 0.175, the minimum shear stress displays anomalous amplification. This nonlinear response reflects the emergence of stress redistribution mechanisms when the defect interactions exceed geometric tolerance limits.

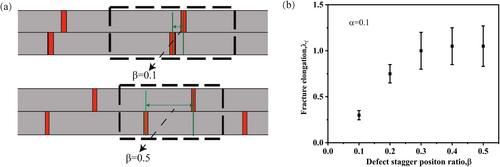
Subsequently, we systematically investigated the sensitivity of defect spatial distribution in 2D defective structures. While conventional studies typically position interlayer defects at the mid-span of adjacent upper-layer defects, here, we quantitatively examined the correlation between defect staggering and structural ductility through the newly proposed defect stagger ratio β (Figure 7). The dimensionless parameter β mathematically characterizes the interlayer defect offset, such that β = 0 represents perfect vertical alignment and β = 0.5 corresponds to maximum mid-span staggering. Notably, the β = 0 configuration was excluded from our analysis due to the detrimental stress concentration effects caused by defect superposition, which induces premature structural failure through uncontrolled damage accumulation. In the remaining analyses, our results revealed a nonlinear relationship between β values and fracture elongation (Figure 7b). We found that the ductility enhancement follows a characteristic saturation curve, initially increasing monotonically under β values of 0.1–0.4 before reaching an asymptotic plateau beyond β = 0.4. This mechanical response confirms our earlier observations that reduced inter-defect spacing between layers facilitates rapid crack propagation through weak interfacial regions. The findings demonstrate that the optimized segmentation of 2D defective structures, coupled with precise control of the degree of damage, enables the simultaneous achievement of three critical mechanical properties: preserved structural strength, enhanced ductility, and maintained stability. This parametric approach provides a systematic framework for designing graded defect structures with tunable failure characteristics.

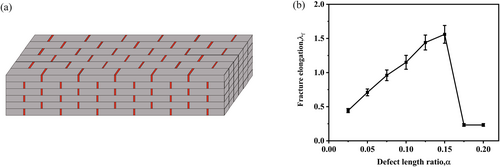
To systematically investigate the influence of defect configuration on the ductility of 3D structures, we comprehensively examined materials with programmable defects. Figure 8a illustrates the proposed design framework for tuning the defect length ratio α in 3D structures. To ensure computational accuracy while maintaining structural stability, the numerical models incorporated sufficient periodic layers along the thickness of the structure. Notably, the fracture elongation characteristics (Figure 8b) demonstrated striking similarities between 3D structures and their 2D counterparts. In particular, we observed that both configurations share a characteristic non-monotonic relationship, where fracture elongation initially increases with increasing α values before reaching an optimal point. This is followed by progressive deterioration at higher defect ratios. This observed trend corroborates the results of our mechanistic analysis. Accordingly, we infer that insufficient defect density leads to the failed activation of distributed plastic deformation zones, whereas excessive defect density predisposes the structure to premature shear localization and catastrophic failure.

4 Summary and Conclusions

In this study, we propose a nacre-inspired segmented defect architecture to enhance material ductility while also maintaining structural integrity. Through the systematic investigation of tensile fracture mechanisms, we establish RVEs for the defect-engineered structure and develop corresponding numerical computation methodologies. A novel damage quantification parameter is introduced to characterize the stochastic nature of defect-induced failure.

Our 1D modeling reveals a ductility–strength trade-off. In particular, progressive defect accumulation enhances elongation, but excessive damage precipitates strength reduction and structural instability. Meanwhile, our 2D bionic analysis demonstrates how optimal defect engineering can be achieved. Notably, moderate defect density (10%–16%) leads to a 50% ductility improvement with < 10% strength loss. Moreover, defect-deficient structures (< 10%) restrict the initiation of plastic deformation, whereas oversaturated defects (> 16%) induce premature shear failure. In our model system, moderate defect density (α = 0.10–0.16) corresponds to ≥ 30% ductility improvement with < 10% strength loss. While material-specific properties (e.g., modulus, yield, and strength) ultimately determine optimal α values, the parametric design framework is scalable. Specifically, defect geometry and damage parameters can be recalibrated for diverse materials (metals, polymers, and composites) to balance performance requirements, as shown in our sensitivity analysis of defect stagger position (Figure 7).

The extension of this model to 3D structures requires the integration of through-thickness defect gradients and layer interlocking, analogous to the hierarchical architecture of nacre [22, 25]. Our initial 3D simulations (Figure 8) demonstrate scalability, although out-of-plane shear effects warrant further investigation. The current framework predominantly focuses on 1D configurations, even though real-world applications typically require 3D defect architectures. Therefore, our future work will focus on 3D validation through two specific approaches: (i) the fabrication of 3D-printed polymer/nanocomposite samples with controlled defect layers (Figure 8a) to experimentally characterize tensile behavior, and (ii) the application of X-ray computed tomography to track 3D crack propagation and validate DEM predictions. These studies will address the out-of-plane shear effects and volumetric strain localization seen in hierarchical defect architectures.

Author Contributions

Chuang Dong: conceptualization, investigation, writing – original draft, writing – review and editing, validation, methodology, formal analysis, data curation.

Conflicts of Interest

The author declares no conflicts of interest.