Engineering Reports
Volume 7, Issue 7 e70288
RESEARCH ARTICLE
Open Access

The Impact of Memory Effects on Lymphatic Filariasis Transmission Using Incidence Data From Ghana

Fredrick A. Wireko, 

Corresponding Author

Fredrick A. Wireko

Department of Mathematics, Kwame Nkrumah University of Science and Technology, Kumasi, Ghana

Correspondence: Fredrick A. Wireko ([email protected])

Joshua Kiddy K. Asamoah ([email protected])

Contribution: Conceptualization, ​Investigation, Writing - original draft, Validation, Methodology, Writing - review & editing, Software, Formal analysis, Supervision

Search for more papers by this author
Rebecca Awerigiya, 

Rebecca Awerigiya

Department of Mathematics, Kwame Nkrumah University of Science and Technology, Kumasi, Ghana

Contribution: Conceptualization, ​Investigation, Writing - original draft, Methodology, Writing - review & editing, Software, Formal analysis, Data curation

Search for more papers by this author
Isaac K. Adu, 

Isaac K. Adu

Department of Mathematical Sciences, Kumasi Technical University, Kumasi, Ghana

Contribution: Writing - original draft, Methodology, Writing - review & editing, Formal analysis

Search for more papers by this author
Joshua N. Martey, 

Joshua N. Martey

Department of Mathematics, African Institute for Mathematical Sciences, Accra, Ghana

Contribution: Writing - original draft, Methodology, Writing - review & editing, Formal analysis

Search for more papers by this author
Bernard O. Bainson, 

Bernard O. Bainson

Department of Mathematics, Kwame Nkrumah University of Science and Technology, Kumasi, Ghana

Contribution: ​Investigation, Writing - original draft, Writing - review & editing, Formal analysis, Supervision

Search for more papers by this author
Joshua Kiddy K. Asamoah, 

Corresponding Author

Joshua Kiddy K. Asamoah

Department of Mathematics, African Institute for Mathematical Sciences, Accra, Ghana

Department of Mathematics, Saveetha School of Engineering SIMATS, Chennai, India

Correspondence: Fredrick A. Wireko ([email protected])

Joshua Kiddy K. Asamoah ([email protected])

Contribution: Writing - original draft, Methodology, Writing - review & editing, Software, Formal analysis, Validation

Search for more papers by this author
First published: 16 July 2025
https://doi.org/10.1002/eng2.70288

ABSTRACT

Lymphatic filariasis is a neglected tropical disease caused by a parasitic worm transmitted to humans by a mosquito bite. In this study, a mathematical model is developed using the Caputo fractional operator. The model also examined the influence of the rate of awareness of the disease and the mass administration of drugs on their contribution to mitigating the spread of the disease during an outbreak. We compared the model with lymphatic filariasis-infected cases in Ghana from 2010 to 2021. Using the Hyers-Ulam and Hyers-Ulam-Rassias stability criterion, we theoretically showed that the proposed model is stable. The basic reproduction number calculated based on the parameters obtained is ℛ 0 = 1 . 5746 $$ {\mathcal{R}}_0=1.5746 $$ with a normalized mean square error of 0.0198. Through sensitivity index analysis and numerical simulations, we noticed that the mosquito bite rate β $$ \beta $$ directly contributes to the spread of the disease. In contrast, the rate of awareness of the disease will help mitigate the spread of the disease during an outbreak.

1 Introduction

Lymphatic filariasis (LF), also known as elephantiasis, is a disease recorded predominantly in poor and unhealthy communities, especially in tropical regions. Although there are known efforts by the World Health Organization (WHO) to address LF, the disease still lacks adequate global attention [1]. In particular, LF is a tropical disease that exerts severe disability, stigma, and economic instability on infected individuals and their families and has been classified as a neglected tropical disease (NTD) [2]. LF is a parasitic disease caused by a thread-like nematode from the Filarioidea family. Wuchereria bancrofti is one of the filarial worms known to have caused about 90% of LF-infected cases. Human beings develop the disease from the long-term growth of this filarial worm in the lymphatic system. This tends to deplete the lymphatic system, causing swelling in various parts of the body. The third stage of the microorganism (microfilariae) is introduced into the skin of humans by an infected mosquito through bites while feeding on human blood. The microfilariae transition to the lymphatic system, where they grow into adult worms to complete their development. Several LF-infected individuals have been reported to experience damage to their lymphatic system without visible symptoms and microfilariae damage in the blood, but may not show symptoms (asymptomatic) [3]. In the case where the LF infection becomes acute, the individual experiences severe fever and lymphadenitis (inflammation of the lymphatic system), painful swelling of the limbs, breasts, and genitalia as a result of lymphatic vessel damage. Those in chronic stages experience swelling of the scrotum (hydroceles), continuous swelling of the limbs (lymphedema), and thickening of the skin, especially the arms, legs, and genitals (popularly called elephantiasis). Infected individuals are given antifilariae drugs that kill microfilariae and minimally affect adult worms to reduce parasite transmission.

In Ghana, LF is classified as an endemic disease. Studies have shown that people in the northern part of Ghana are at increased risk than those in the southern belt, whereas the middle belt is free of LF. The report in Reference [4] indicates that in some communities in the Northern part of Ghana, 33% of the infected cases are men. In 2000, Ghana implemented mass drug administration (MDA) using ivermectin and albendazole, resulting in a median treatment value of 77%–80% over the years and a drop from 81 to 98 districts as of 2016. However, about 17 districts still battle LF infections despite treatment efforts. LF has been reported to be still prevalent in the north due to factors such as cultural beliefs and practices [5]. Recent assessments indicate that Ghana continues to make strides in eliminating LF. The persistent application of research-informed efforts is required, especially in communities where LF persists. Strategies such as enhanced surveillance, community engagement, and education to address cultural beliefs will help eliminate LF. Figure 1 shows the effort of the Ghanaian government to eliminate LF disease and also the life cycle of the disease.

Details are in the caption following the image
FIGURE 1
Open in figure viewerPowerPoint
LF dynamics and cases in Ghana. (a) Ghana's path towards eliminating LF, (b) Life cycle of LF in humans and mosquitoes.

Mathematical modeling has been an essential tool for examining the spread, control strategies, and other epidemiological dynamics of LF in the population. Several integer-order models have been suggested in the literature to study LF transmission by considering dynamics such as vector control, human-vector interactions, and others [6-14]. The model developed in Reference [15] incorporated quarantine for chronically infected individuals and medical treatment for acute cases. It derives the basic reproduction number and performs a sensitivity analysis to identify key parameters that affect disease transmission. The findings suggest that treatment reduces the prevalence of the disease more effectively than quarantine, although combining both strategies yields the best results. However, the study does not account for factors such as drug resistance, climate change, or species-specific parasite prevalence, highlighting gaps for future research.

Michael et al. [16] conducted a thorough review of the application of mathematical models to understand the epidemiological dynamics of LF. The review demonstrated how mathematical models have been applied to implement global control strategies and targets. It was observed that maintaining a high standard of community treatment and vector control mechanisms is pertinent in LF elimination. Furthermore, in Reference [17], a compartmental model for LF was designed and analyzed, incorporating the dynamics of the human age structure, describing the in-depth dynamics of LF, and further investigating how some control strategies could minimize the case of LF in the population. The work in Reference [7] presented some existing mathematical models that sought to suggest efficient control of LF transmission in the population. Recently, [18] developed a mathematical model to suggest effective control measures for LF. They incorporated vaccination and vector control as an efficient way of reducing LF. However, this model did not consider some essential dynamics of LF, such as asymptomatic, untreated, and memory dynamics. Therefore, the current study seeks to extend the ideas in Reference [18] by considering memory loss and the hereditary dynamics of LF in a population and analyzing the impact of information dissemination or awareness of LF disease. In addition, there is little literature on assessing the memory dynamics of LF disease. In the literature, such as [19-21], fractional operators were used to model LF. In particular, in Reference [19], the fractional ABC operator was used to model LF. The model herein did not consider other essential dynamics of LF, including asymptomatic and treatment dynamics, and insufficient information on vector dynamics. To address some other essential dynamics of LF, we focus on the following:
  • a.

    Develop a Caputo fractional derivative model of the LF model and assess its memory dynamics.

  • b.

    Conduct some analysis of the asymptomatic and treatment dynamics of the LF.

  • c.

    Examine various mortality rates in mature and immature mosquitoes.

The remainder of the study is presented in this manner: Section 2 presents some preliminary definitions and theorems related to the study. Section 3 deals with formulating the LF model with its related assumptions. In Section 4, we provide a theoretical analysis of the existence, uniqueness, and stability of the memory dynamics of LF disease. Section 5 presents an analysis of the proposed model using Ghana's LF-infected data. The sensitivity analysis of the LF model is shown in Section 6. Finally, Sections 7 and 8 deal with numerical analysis and conclusions.

2 Preliminary Definitions

This section presents essential concepts and notations in fractional calculus, explicitly emphasizing the commonly used Riemann-Liouville and Caputo definitions.

Remark 2.1.A real function g $$ g $$ is considered to be of class C $$ C $$ if it exhibits continuity over the interval [ m , n ] $$ \left[m,n\right] $$ piecewise and is integrable in any finite subinterval within this range.

Definition 2.1.The left and right Riemann-Liouville fractional (R-LF) integrals I m + α g $$ {I}_{m+}^{\alpha }g $$ and I n − α g $$ {I}_{n-}^{\alpha }g $$ of order α ∈ ℂ ( R e ( α ) ) > 0 $$ \alpha \in \mathbb{C}\left(\mathit{\operatorname{Re}}\left(\alpha \right)\right)>0 $$ are defined by [22]:

I m + α g ( u ) = 1 Γ ( α ) ∫ m u ( u − v ) α − 1 g ( v ) d v $$ {I}_{m+}^{\alpha }g(u)=\frac{1}{\Gamma \left(\alpha \right)}{\int}_m^u{\left(u-v\right)}^{\alpha -1}g(v) dv $$ ()
and
I n − α g ( u ) = 1 Γ ( α ) ∫ u n ( v − u ) α − 1 g ( v ) d v $$ {I}_{n-}^{\alpha }g(u)=\frac{1}{\Gamma \left(\alpha \right)}{\int}_u^n{\left(v-u\right)}^{\alpha -1}g(v) dv $$ ()
where Γ ( . ) $$ \Gamma (.) $$ is the Euler gamma function.

Definition 2.2.The left and right Riemann-Liouville fractional integrals I m + α g $$ {I}_{m+}^{\alpha }g $$ and I n − α g $$ {I}_{n-}^{\alpha }g $$ of order α ∈ ℂ ( R e ( α ) ) > 0 $$ \alpha \in \mathbb{C}\left(\mathit{\operatorname{Re}}\left(\alpha \right)\right)>0 $$ are defined as:

I m + α g ( u ) = 1 Γ ( α ) ∫ m u ( u − v ) α − 1 g ( v ) d v $$ {I}_{m+}^{\alpha }g(u)=\frac{1}{\Gamma \left(\alpha \right)}{\int}_m^u{\left(u-v\right)}^{\alpha -1}g(v)\kern0.3em dv $$ ()
and
I n − α g ( u ) = 1 Γ ( α ) ∫ u n ( v − u ) α − 1 g ( v ) d v $$ {I}_{n-}^{\alpha }g(u)=\frac{1}{\Gamma \left(\alpha \right)}{\int}_u^n{\left(v-u\right)}^{\alpha -1}g(v)\kern0.3em dv $$ ()
where Γ ( . ) $$ \Gamma (.) $$ denotes the Euler gamma function.

Definition 2.3. ([[22]])The left and right Riemann-Liouville fractional derivatives D m + α g $$ {D}_{m+}^{\alpha }g $$ and D n − α g $$ {D}_{n-}^{\alpha }g $$ of order α ∈ ℂ ( R e ( α ) ) > 0 $$ \alpha \in \mathbb{C}\left(\mathit{\operatorname{Re}}\left(\alpha \right)\right)>0 $$ are defined by:

( D m + α g ) ( u ) = d d u p ( I m + p − α g ) ( u ) $$ \left({D}_{m+}^{\alpha }g\right)(u)={\left(\frac{d}{du}\right)}^p\left({I}_{m+}^{p-\alpha }g\right)(u) $$ ()
and
( D n − α g ) ( u ) = − d d u p ( I n − p − α g ) ( u ) $$ \left({D}_{n-}^{\alpha }g\right)(u)={\left(-\frac{d}{du}\right)}^p\left({I}_{n-}^{p-\alpha }g\right)(u) $$ ()
where p = [ R e ( α ) ] + 1 $$ p=\left[\mathit{\operatorname{Re}}\left(\alpha \right)\right]+1 $$ and R e ( α ) $$ \mathit{\operatorname{Re}}\left(\alpha \right) $$ is the largest integer less than or equal to R e ( α ) $$ \mathit{\operatorname{Re}}\left(\alpha \right) $$ .

Definition 2.4. ([[22]])The left and right Caputo fractional derivatives   C D m + α g $$ {}^C{D}_{m+}^{\alpha }g $$ and   C D n − α g $$ {}^C{D}_{n-}^{\alpha }g $$ of order α ∈ ℂ ( R e ( α ) ) > 0 $$ \alpha \in \mathbb{C}\left(\mathit{\operatorname{Re}}\left(\alpha \right)\right)>0 $$ are defined by:

( C D m + α g ) ( u ) = ( I m + p − α g ( p ) ) ( u ) = 1 Γ ( p − α ) ∫ m u g ( p ) ( v ) ( u − v ) α − p + 1 d v $$ \left({}^C{D}_{m+}^{\alpha }g\right)(u)=\left({I}_{m+}^{p-\alpha }{g}^{(p)}\right)(u)=\frac{1}{\Gamma \left(p-\alpha \right)}{\int}_m^u\frac{g^{(p)}(v)}{{\left(u-v\right)}^{\alpha -p+1}} dv $$ ()
and
( C D n − α g ) ( u ) = ( − 1 ) p ( I n − p − α g ( p ) ) ( u ) = ( − 1 ) p Γ ( p − α ) ∫ u n g ( p ) ( v ) ( v − u ) α − p + 1 d v $$ \left({}^C{D}_{n-}^{\alpha }g\right)(u)={\left(-1\right)}^p\left({I}_{n-}^{p-\alpha }{g}^{(p)}\right)(u)=\frac{{\left(-1\right)}^p}{\Gamma \left(p-\alpha \right)}{\int}_u^n\frac{g^{(p)}(v)}{{\left(v-u\right)}^{\alpha -p+1}} dv $$ ()

3 Model Formulation

This section describes the fractional mathematical model formulated to study the dynamics of LF in a population. Consider a population in which heterogeneous interactions occur between humans and a vector. The total human population over some time, N ( Υ ) $$ N\left(\mathrm{Y}\right) $$ , is divided into eight (8) subclasses. Individuals who lack resistance to LF but have not yet interacted with the parasite that causes LF are referred to as the susceptible class, S h ( Υ ) $$ {S}_h\left(\mathrm{Y}\right) $$ . In addition, E h ( Υ ) $$ {E}_h\left(\mathrm{Y}\right) $$ refers to individuals who have come into contact with the LF parasite and may become infected. After having contact with the LF parasite, some individuals will become infected but may not show symptoms and are referred to as asymptomatic, denoted by A h ( Υ ) $$ {A}_h\left(\mathrm{Y}\right) $$ . On the other hand, some individuals may show symptoms after interacting with the LF parasite but at different stages, that is, I h a ( Υ ) $$ {I}_{ha}\left(\mathrm{Y}\right) $$ or chronic I h c ( Υ ) $$ {I}_{hc}\left(\mathrm{Y}\right) $$ . Some infected individuals can visit the health centers available to receive treatment, that is, treated T h ( Υ ) $$ {T}_h\left(\mathrm{Y}\right) $$ . In contrast, others may choose not to receive treatment and therefore are untreated U h ( Υ ) $$ {U}_h\left(\mathrm{Y}\right) $$ . Individuals who recover from LF after treatment are also indicated by R h ( Υ ) $$ {R}_h\left(\mathrm{Y}\right) $$ . Now, we consider both immature and mature mosquitoes for the vector population. A crucial component in mosquitoes' life, that is, eggs, larvae, and pupae, referred to as immature, is denoted as L ( Υ ) $$ L\left(\mathrm{Y}\right) $$ . In addition, mature mosquitoes M ( Υ ) $$ M\left(\mathrm{Y}\right) $$ are divided into three subclasses, that is, susceptible S m ( Υ ) $$ {S}_m\left(\mathrm{Y}\right) $$ , exposed E m ( Υ ) $$ {E}_m\left(\mathrm{Y}\right) $$ , and infected I m ( Υ ) $$ {I}_m\left(\mathrm{Y}\right) $$ mosquitoes. The immature population L ( Υ ) $$ L\left(\mathrm{Y}\right) $$ occurs at the rate c 1 − L ( Υ ) K M ( Υ ) $$ c\left(1-\frac{L\left(\mathrm{Y}\right)}{K}\right)M\left(\mathrm{Y}\right) $$ . The recruitment rate for the susceptible class is indicated by Λ h $$ {\Lambda}_h $$ , while the mosquito bite rate is given as β $$ \beta $$ . The susceptible human becomes exposed at the rate β 1 $$ {\beta}_1 $$ which is defined as
β 1 = δ 1 β ( I m ( Υ ) ) N h ( Υ ) $$ {\beta}_1=\frac{\delta_1\beta \left({I}_m\left(\mathrm{Y}\right)\right)}{N_h\left(\mathrm{Y}\right)} $$ ()
Herein, β 1 $$ {\beta}_1 $$ signifies the probability that an individual bitten by a mosquito contracts the LF disease. In addition, a susceptible mosquito that bites an asymptomatic human, an acutely infected, or a chronically infected human may become infected at a rate π $$ \pi $$ and is thus defined as
π = δ 2 ( A h ( Υ ) + U h ( Υ ) + I h a ( Υ ) + I h c ( Υ ) ) N h ( Υ ) $$ \pi =\frac{\delta_2\left({A}_h\left(\mathrm{Y}\right)+{U}_h\left(\mathrm{Y}\right)+{I}_{ha}\left(\mathrm{Y}\right)+{I}_{hc}\left(\mathrm{Y}\right)\right)}{N_h\left(\mathrm{Y}\right)} $$ ()
Herein, δ 2 $$ {\delta}_2 $$ signifies the rate at which the mosquito can become infected. The other parameters of the model descriptions can be found in Table 1.
TABLE 1. Description of model parameters.
Parameter Description
Λ h $$ {\Lambda}_h $$ Recruitment rate of humans
η $$ \eta $$ Transmission rate from untreated to infected chronic humans
τ $$ \tau $$ Rate from exposed to asymptomatic individuals
κ $$ \kappa $$ Rate of disease awareness
β 2 $$ {\beta}_2 $$ Progression rate from infected-acute individuals to treated
θ $$ \theta $$ Disease-induced death rate of humans
ϵ $$ \epsilon $$ Progression rate from asymptomatic to treated individuals
ϕ $$ \phi $$ Progression rate from asymptomatic to untreated individuals
β 4 $$ {\beta}_4 $$ Transmission rate from exposed to infected acute humans
c $$ c $$ Recruitment rate of immature mosquitoes
K $$ K $$ Carrying capacity of immature mosquitoes
δ 2 $$ {\delta}_2 $$ Probability that contact with an infected human leads to mosquito infection
Λ m $$ {\Lambda}_m $$ Maturity rate of immature mosquitoes
ω $$ \omega $$ Natural death rate of humans
ρ 2 $$ {\rho}_2 $$ Loss of immunity rate from recovered class
ρ 1 $$ {\rho}_1 $$ Recovery rate
β 3 $$ {\beta}_3 $$ Progression rate from infected-chronic to treated
μ $$ \mu $$ Progression rate from infected-acute to chronic infection
γ $$ \gamma $$ Progression rate from untreated to infected-acute individuals
σ $$ \sigma $$ Transmission rate from exposed to infected mosquitoes
α 1 $$ {\alpha}_1 $$ Natural death rate of mature mosquitoes
α 2 $$ {\alpha}_2 $$ Natural death rate of immature mosquitoes
δ 1 $$ {\delta}_1 $$ Probability of humans contracting a disease from a mosquito bite
β $$ \beta $$ Rate at which mosquitoes bite humans

The study model is developed using fractional derivative operators. Interestingly, fractional operators are capable of capturing the memory dynamics of infectious diseases [23, 24]. Therefore, fractional dynamics offers a framework for modeling diseases such as LF. It can incorporate the memory dynamics and hereditary properties of biological systems, which are significant in the transmission and progression of LF [25]. Lymphatic filariasis is known to have a prolonged incubation and progression period, often spanning years, and integer-order models cannot accurately capture these dynamics as they fail to deal with measuring nonlocal behaviors in infectious diseases. In addition, the immune response of the host to LF and the pharmacodynamics of mass drug administration (MDA) are both processes with memory and can be modeled with fractional dynamics [26, 27]. The study therefore adopts the Caputo fractional derivative operator, since it is one of the widely used operators in applied sciencesdue to its enormous strengths over the other fractional operators. Caputo's derivatives permit initial conditions regarding integer-order derivatives to be written. It also preserves the structure of traditional differential equations, since it assumes an integer order when the fractional order becomes unity. Additionally, the Caputo operator is compatible with singular kernels and the Laplace operator under standard initial conditions, thus facilitating the investigation of analytical and semi-analytical solutions of fractional differential equations [27, 28]. Figure 2 shows the flowchart of the proposed LF model.

Details are in the caption following the image
FIGURE 2
Open in figure viewerPowerPoint
Flow diagram of LF model.
We consider the following assumptions to model the epidemiological dynamics of LF:
  1. No mother-to-child (vertical) transmission of LF occurs in human or mosquito populations [29].
  2. Ingestion of microfilariae by mosquitoes is assumed to be the same as that in asymptomatic, acutely, and chronically infected humans [30].
  3. Unequal mortality rates of immature and mature mosquitoes [31].
  4. Individuals recovering from LF have temporal immunity [32].
  5. Infected mosquitoes do not suffer from LF-induced mortality [33].
  6. Public awareness reduces human susceptibility to LF [34, 35].
Following the assumptions and dynamics of LF, we obtain the following Caputo fractional-order LF model.
  C D Υ ϱ S h = Λ h ϱ + ρ 2 ϱ R h − ( ω ϱ + κ ϱ ) S h − β 1 ϱ S h   C D Υ ϱ E h = β 1 ϱ S h − ( β 4 ϱ + ω ϱ + τ ϱ ) E h   C D Υ ϱ A h = τ ϱ E h − ( ω ϱ + ϕ ϱ + ϵ ϱ ) A h   C D Υ ϱ U h = ϕ ϱ A h − ( ω ϱ + η ϱ + μ ϱ ) U h   C D Υ ϱ I h a = β 4 ϱ E h + γ ϱ U h − ( μ ϱ + β 2 ϱ + ω ϱ ) I h a   C D Υ ϱ I h c = η ϱ U h + μ ϱ I h a − ( β 3 ϱ + ω ϱ + θ ϱ ) I h c   C D Υ ϱ T h = ϵ ϱ A h + β 3 ϱ I h c + β 2 ϱ I h a − ( ρ 1 ϱ + ω ϱ ) T h   C D Υ ϱ R h = ρ 1 ϱ T h + κ ϱ S h − ( ρ 2 ϱ + ω ϱ ) R h   C D Υ ϱ L = c ϱ 1 − L K ϱ ( S m + E m + I m ) − ( α 2 ϱ + Λ m ϱ ) L   C D Υ ϱ S m = Λ m ϱ L − ( α 1 ϱ + π ϱ ) S m   C D Υ ϱ E m = π ϱ S m − ( α 1 ϱ + σ ϱ ) E m   C D Υ ϱ I m = σ ϱ E m − α 1 ϱ I m $$ \left\{\begin{array}{ll}\hfill {}^C{D}_{\mathrm{Y}}^{\varrho }{S}_h& ={\Lambda}_h^{\varrho }+{\rho}_2^{\varrho }{R}_h-\left({\omega}^{\varrho }+{\kappa}^{\varrho}\right){S}_h-{\beta}_1^{\varrho }{S}_h\\ {}\hfill {}^C{D}_{\mathrm{Y}}^{\varrho }{E}_h& ={\beta}_1^{\varrho }{S}_h-\left({\beta}_4^{\varrho }+{\omega}^{\varrho }+{\tau}^{\varrho}\right){E}_h\\ {}\hfill {}^C{D}_{\mathrm{Y}}^{\varrho }{A}_h& ={\tau}^{\varrho }{E}_h-\left({\omega}^{\varrho }+{\phi}^{\varrho }+{\epsilon}^{\varrho}\right){A}_h\\ {}\hfill {}^C{D}_{\mathrm{Y}}^{\varrho }{U}_h& ={\phi}^{\varrho }{A}_h-\left({\omega}^{\varrho }+{\eta}^{\varrho }+{\mu}^{\varrho}\right){U}_h\\ {}\hfill {}^C{D}_{\mathrm{Y}}^{\varrho }{I}_{ha}& ={\beta}_4^{\varrho }{E}_h+{\gamma}^{\varrho }{U}_h-\left({\mu}^{\varrho }+{\beta}_2^{\varrho }+{\omega}^{\varrho}\right){I}_{ha}\\ {}\hfill {}^C{D}_{\mathrm{Y}}^{\varrho }{I}_{hc}& ={\eta}^{\varrho }{U}_h+{\mu}^{\varrho }{I}_{ha}-\left({\beta}_3^{\varrho }+{\omega}^{\varrho }+{\theta}^{\varrho}\right){I}_{hc}\\ {}\hfill {}^C{D}_{\mathrm{Y}}^{\varrho }{T}_h& ={\epsilon}^{\varrho }{A}_h+{\beta}_3^{\varrho }{I}_{hc}+{\beta}_2^{\varrho }{I}_{ha}-\left({\rho}_1^{\varrho }+{\omega}^{\varrho}\right){T}_h\\ {}\hfill {}^C{D}_{\mathrm{Y}}^{\varrho }{R}_h& ={\rho}_1^{\varrho }{T}_h+{\kappa}^{\varrho }{S}_h-\left({\rho}_2^{\varrho }+{\omega}^{\varrho}\right){R}_h\\ {}\hfill {}^C{D}_{\mathrm{Y}}^{\varrho }L& ={c}^{\varrho}\left(1-\frac{L}{K^{\varrho }}\right)\left({S}_m+{E}_m+{I}_m\right)-\left({\alpha}_2^{\varrho }+{\Lambda}_m^{\varrho}\right)L\\ {}\hfill {}^C{D}_{\mathrm{Y}}^{\varrho }{S}_m& ={\Lambda}_m^{\varrho }L-\left({\alpha}_1^{\varrho }+{\pi}^{\varrho}\right){S}_m\\ {}\hfill {}^C{D}_{\mathrm{Y}}^{\varrho }{E}_m& ={\pi}^{\varrho }{S}_m-\left({\alpha}_1^{\varrho }+{\sigma}^{\varrho}\right){E}_m\\ {}\hfill {}^C{D}_{\mathrm{Y}}^{\varrho }{I}_m& ={\sigma}^{\varrho }{E}_m-{\alpha}_1^{\varrho }{I}_m\end{array}\right. $$ ()
with associated initial conditions as:
S h 0 ≥ 0 , E h 0 ≥ 0 , A h 0 ≥ 0 , U h 0 ≥ 0 , I h a 0 ≥ 0 , I h c 0 ≥ 0 , T h 0 ≥ 0 , R h 0 ≥ 0 , L 0 ≥ 0 , S m 0 ≥ 0 , E m 0 ≥ 0 , I m 0 ≥ 0 $$ {\displaystyle \begin{array}{ll}\hfill {S}_h^0& \ge 0,{E}_h^0\ge 0,{A}_h^0\ge 0,{U}_h^0\ge 0,{I}_{ha}^0\ge 0,{I}_{hc}^0\ge 0,{T}_h^0\kern0em \\ {}& \ge 0,{R}_h^0\ge 0,{L}^0\ge 0,{S}_m^0\ge 0,{E}_m^0\ge 0,{I}_m^0\ge 0\kern0em \end{array}} $$
where
β 1 ϱ = δ 1 ϱ β ϱ I m N h , π ϱ = δ 2 ϱ β ϱ ( A h + U h + I h a + I h c ) N h $$ {\beta}_1^{\varrho }=\frac{\delta_1^{\varrho }{\beta}^{\varrho }{I}_m}{N_h},\kern1em {\pi}^{\varrho }=\frac{\delta_2^{\varrho }{\beta}^{\varrho}\left({A}_h+{U}_h+{I}_{ha}+{I}_{hc}\right)}{N_h} $$
Here,   C D Υ ϱ $$ {}^C{D}_{\mathrm{Y}}^{\varrho } $$ denotes the Caputo fractional derivative of order ϱ $$ \varrho $$ .

4 Positivity and Boundedness of Solution

4.1 Positivity of Solution

Theorem 4.1.For any set of initial solutions associated with the model, there is a set of positive solutions S h ( Υ ) , E h ( Υ ) , A h ( Υ ) , U h ( Υ ) , I h a ( Υ ) , I h c ( Υ ) , T h ( Υ ) , R h ( Υ ) , L ( Υ ) $$ {S}_h\left(\mathrm{Y}\right),{E}_h\left(\mathrm{Y}\right),{A}_h\left(\mathrm{Y}\right),{U}_h\left(\mathrm{Y}\right),{I}_{ha}\left(\mathrm{Y}\right),{I}_{hc}\left(\mathrm{Y}\right),{T}_h\left(\mathrm{Y}\right),{R}_h\left(\mathrm{Y}\right),L\left(\mathrm{Y}\right) $$ , S m ( Υ ) , E m ( Υ ) , I m ( Υ ) $$ {S}_m\left(\mathrm{Y}\right),{E}_m\left(\mathrm{Y}\right),{I}_m\left(\mathrm{Y}\right) $$ for all Υ ≥ 0 $$ \mathrm{Y}\ge 0 $$ .

Proof.We will show that Theorem 4.1 holds when every solution to the differential equation of model (11) is nonnegative for all Υ ≥ $$ \mathrm{Y}\ge $$ 0.

Considering the first equation. We have,

  C D Υ ϱ S h = Λ h ϱ + ρ 2 ϱ R h − ( ω ϱ + κ ϱ ) S h − β 1 ϱ S h   C D Υ ϱ S h ≥ − ( ( ω ϱ + κ ϱ ) + β 1 ϱ ) S h $$ {\displaystyle \begin{array}{cc}\hfill {}^C{D}_{\mathrm{Y}}^{\varrho }{S}_h& ={\Lambda}_h^{\varrho }+{\rho}_2^{\varrho }{R}_h-\left({\omega}^{\varrho }+{\kappa}^{\varrho}\right){S}_h-{\beta}_1^{\varrho }{S}_h\hfill \\ {}\hfill {}^C{D}_{\mathrm{Y}}^{\varrho }{S}_h& \ge -\left(\left({\omega}^{\varrho }+{\kappa}^{\varrho}\right)+{\beta}_1^{\varrho}\right){S}_h\hfill \end{array}} $$ ()

Applying the Laplace transform to (12), yields

ℒ {   C D Υ ϱ S h } ≥ − ( ( ω ϱ + κ ϱ ) + β 1 ϱ ) ℒ { S h } s ϱ 𝒮 h ( s ) − s ϱ − 1 𝒮 h 0 ≥ − ( ( ω ϱ + κ ϱ ) + β 1 ϱ ) 𝒮 h ( s ) ( s ϱ + ( ( ω ϱ + κ ϱ ) + β 1 ϱ ) ) 𝒮 h ( s ) ≥ s ϱ − 1 𝒮 h 0 𝒮 h ( s ) ≥ s ϱ − 1 s ϱ + ( ( ω ϱ + κ ϱ ) + β 1 ϱ ) 𝒮 h 0 ()

Taking the inverse Laplace of the (12), yields

S h ( Υ ) ≥ S h 0 E ϱ − ( ( ω ϱ + κ ϱ ) + β 1 ϱ ) Υ ϱ > 0 $$ {S}_h\left(\mathrm{Y}\right)\ge {S}_h^0{E}_{\varrho}\left(-\left(\left({\omega}^{\varrho }+{\kappa}^{\varrho}\right)+{\beta}_1^{\varrho}\right){\mathrm{Y}}^{\varrho}\right)>0 $$ ()

Thus, the solution S h ( Υ ) $$ {S}_h\left(\mathrm{Y}\right) $$ of (12) is positive for all, t ≥ 0 $$ t\ge 0 $$ . Using a similar approach (via application of Laplace transform) to evaluate the equations relating to other state variables, we obtain the following results;

E h ( Υ ) ≥ E h 0 E ϱ − ( β 4 ϱ + ω ϱ + τ ϱ ) Υ ϱ > 0 A h ( Υ ) ≥ A h 0 E ϱ − ( ω ϱ + ϕ ϱ + ϵ ϱ ) Υ ϱ > 0 U h ( Υ ) ≥ U h 0 E ϱ − ( ω ϱ + η ϱ + μ ϱ ) Υ ϱ > 0 I h a ( Υ ) ≥ I h a 0 E ϱ − ( μ ϱ + β 2 ϱ + ω ϱ ) Υ ϱ > 0 I h c ( Υ ) ≥ I h c 0 E ϱ − ( β 3 ϱ + ω ϱ + θ ϱ ) Υ ϱ > 0 T h ( Υ ) ≥ T h 0 E ϱ − ( ρ 1 ϱ + ω ϱ ) Υ ϱ > 0 R h ( Υ ) ≥ R h 0 E ϱ − ( ρ 2 ϱ + ω ϱ ) Υ ϱ > 0 L ( Υ ) ≥ L 0 E ϱ − ( α 2 ϱ + Λ m ϱ ) Υ ϱ > 0 S m ( Υ ) ≥ S m 0 E ϱ − ( α 1 ϱ + π ϱ ) Υ ϱ > 0 E m ( Υ ) ≥ E m 0 E ϱ − ( α 1 ϱ + σ ϱ ) Υ ϱ > 0 I m ( Υ ) ≥ I m 0 E ϱ − α 1 ϱ Υ ϱ > 0 $$ {\displaystyle \begin{array}{cc}\hfill {E}_h\left(\mathrm{Y}\right)& \ge {E}_h^0{E}_{\varrho}\left(-\left({\beta}_4^{\varrho }+{\omega}^{\varrho }+{\tau}^{\varrho}\right){\mathrm{Y}}^{\varrho}\right)>0\hfill \\ {}\hfill {A}_h\left(\mathrm{Y}\right)& \ge {A}_h^0{E}_{\varrho}\left(-\left({\omega}^{\varrho }+{\phi}^{\varrho }+{\epsilon}^{\varrho}\right){\mathrm{Y}}^{\varrho}\right)>0\hfill \\ {}\hfill {U}_h\left(\mathrm{Y}\right)& \ge {U}_h^0{E}_{\varrho}\left(-\left({\omega}^{\varrho }+{\eta}^{\varrho }+{\mu}^{\varrho}\right){\mathrm{Y}}^{\varrho}\right)>0\hfill \\ {}\hfill {I}_{ha}\left(\mathrm{Y}\right)& \ge {I}_{ha}^0{E}_{\varrho}\left(-\left({\mu}^{\varrho }+{\beta}_2^{\varrho }+{\omega}^{\varrho}\right){\mathrm{Y}}^{\varrho}\right)>0\hfill \\ {}\hfill {I}_{hc}\left(\mathrm{Y}\right)& \ge {I}_{hc}^0{E}_{\varrho}\left(-\left({\beta}_3^{\varrho }+{\omega}^{\varrho }+{\theta}^{\varrho}\right){\mathrm{Y}}^{\varrho}\right)>0\hfill \\ {}\hfill {T}_h\left(\mathrm{Y}\right)& \ge {T}_h^0{E}_{\varrho}\left(-\left({\rho}_1^{\varrho }+{\omega}^{\varrho}\right){\mathrm{Y}}^{\varrho}\right)>0\hfill \\ {}\hfill {R}_h\left(\mathrm{Y}\right)& \ge {R}_h^0{E}_{\varrho}\left(-\left({\rho}_2^{\varrho }+{\omega}^{\varrho}\right){\mathrm{Y}}^{\varrho}\right)>0\hfill \\ {}\hfill L\left(\mathrm{Y}\right)& \ge {L}^0{E}_{\varrho}\left(-\left({\alpha}_2^{\varrho }+{\Lambda}_m^{\varrho}\right){\mathrm{Y}}^{\varrho}\right)>0\hfill \\ {}\hfill {S}_m\left(\mathrm{Y}\right)& \ge {S}_m^0{E}_{\varrho}\left(-\left({\alpha}_1^{\varrho }+{\pi}^{\varrho}\right){\mathrm{Y}}^{\varrho}\right)>0\hfill \\ {}\hfill {E}_m\left(\mathrm{Y}\right)& \ge {E}_m^0{E}_{\varrho}\left(-\left({\alpha}_1^{\varrho }+{\sigma}^{\varrho}\right){\mathrm{Y}}^{\varrho}\right)>0\hfill \\ {}\hfill {I}_m\left(\mathrm{Y}\right)& \ge {I}_m^0{E}_{\varrho}\left(-{\alpha}_1^{\varrho }{\mathrm{Y}}^{\varrho}\right)>0\hfill \end{array}} $$ ()
It is seen that the solutions of the various equations of the model are nonnegative, which implies that the positivity of the solutions to the model has been established.

4.2 Boundedness of Solution

Theorem 4.2.If the model has solutions S h , E h , A h , U h , I h a , I h c , T h $$ {S}_h,{E}_h,{A}_h,{U}_h,{I}_{ha},{I}_{hc},{T}_h $$ , R h , L , S m , E m , I m $$ {R}_h,L,{S}_m,{E}_m,{I}_m $$ with associated initial conditions, then the solutions are bounded.

Proof.The theorem is proven by showing that the populations of humans, immature and mature mosquitoes, are bounded above by some constants

Considering the total human population for any given time, Υ $$ \mathrm{Y} $$

N h ( Υ ) = S h ( Υ ) + E h ( Υ ) + A h ( Υ ) ( Υ ) + U h ( Υ ) + I h a ( Υ ) + I h c ( Υ ) + T h ( Υ ) + R h ( Υ ) $$ {\displaystyle \begin{array}{ll}\hfill {N}_h\left(\mathrm{Y}\right)& ={S}_h\left(\mathrm{Y}\right)+{E}_h\left(\mathrm{Y}\right)+{A}_h\left(\mathrm{Y}\right)\left(\mathrm{Y}\right)+{U}_h\left(\mathrm{Y}\right)+{I}_{ha}\left(\mathrm{Y}\right)\\ {}\hfill & \kern1em +{I}_{hc}\left(\mathrm{Y}\right)+{T}_h\left(\mathrm{Y}\right)+{R}_h\left(\mathrm{Y}\right)\end{array}} $$ ()
It implies that,
  C D Υ ϱ N h =   C D Υ ϱ S h +   C D Υ ϱ E h +   C D Υ ϱ A h +   C D Υ ϱ U h +   C D Υ ϱ I h a +   C D Υ ϱ I h c +   C D Υ ϱ R h = λ h − ( S h + E h + A h + U h + I h a + I h c + T h + R h ) ω − ( μ + γ ) U h − θ I h c $$ {\displaystyle \begin{array}{cc}\hfill {}^C{D}_{\mathrm{Y}}^{\varrho }{N}_h& ={}^C{D}_{\mathrm{Y}}^{\varrho }{S}_h+{}^C{D}_{\mathrm{Y}}^{\varrho }{E}_h+{}^C{D}_{\mathrm{Y}}^{\varrho }{A}_h+{}^C{D}_{\mathrm{Y}}^{\varrho }{U}_h+{}^C{D}_{\mathrm{Y}}^{\varrho }{I}_{ha}\hfill \\ {}& \kern1em +{}^C{D}_{\mathrm{Y}}^{\varrho }{I}_{hc}+{}^C{D}_{\mathrm{Y}}^{\varrho }{R}_h\\ {}\hfill & ={\lambda}_h-\Big({S}_h+{E}_h+{A}_h+{U}_h+{I}_{ha}+{I}_{hc}+{T}_h\hfill \\ {}\hfill & \kern1em +{R}_h\Big)\omega -\left(\mu +\gamma \right){U}_h-\theta {I}_{hc}\hfill \end{array}} $$ ()
In the absence of disease related death, θ = 0 $$ \theta =0 $$ , and so we obtain
  C D Υ ϱ N h ≤ λ h ϱ − N h ω ϱ $$ {}^C{D}_{\mathrm{Y}}^{\varrho }{N}_h\le {\lambda}_h^{\varrho }-{N}_h{\omega}^{\varrho } $$ ()
Applying the Laplace transform to (18) yields
N h ( Υ ) ≤ N h 0 E ϱ ( − ω ϱ Υ ϱ ) + λ h ϱ ω ϱ ( 1 − E ϱ ( − ω ϱ Υ ϱ ) $$ {N}_h\left(\mathrm{Y}\right)\le {N}_h^0{E}_{\varrho}\left(-{\omega}^{\varrho }{\mathrm{Y}}^{\varrho}\right)+\frac{\lambda_h^{\varrho }}{\omega^{\varrho }}\Big(1-{E}_{\varrho}\left(-{\omega}^{\varrho }{\mathrm{Y}}^{\varrho}\right) $$ ()

Taking the limit as time Υ $$ \mathrm{Y} $$ approaches ∞ $$ \infty $$ , (19) becomes

N h ( Υ ) ≤ λ h ϱ ω ϱ $$ {N}_h\left(\mathrm{Y}\right)\le \frac{\lambda_h^{\varrho }}{\omega^{\varrho }} $$ ()

Likewise, as time Υ $$ \mathrm{Y} $$ approaches ∞ $$ \infty $$ , the population of immature mosquitoes reaches carrying capacity

L ( Υ ) ≤ K $$ L\left(\mathrm{Y}\right)\le K $$ ()

Similarly, as time Υ $$ \mathrm{Y} $$ approaches ∞ $$ \infty $$ , the population of matured mosquitoes N m $$ {N}_m $$ ;

N m ( Υ ) ≤ λ h ϱ K α 1 ϱ $$ {N}_m\left(\mathrm{Y}\right)\le \frac{\lambda_h^{\varrho }K}{\alpha_1^{\varrho }} $$ ()

The solutions of the model are bounded and are feasible in the region

ℱ = ( S h , E h , A h , U h , I h a , I h c , T h , R h , L , S m , E m , I m ) ∈ ℝ 12 + | N h ( Υ ) ≤ λ h ϱ ω ϱ , L ( Υ ) ≤ K , N m ( Υ ) ≤ K λ h ϱ α 1 ϱ $$ \mathcal{F}=\left\{\begin{array}{l}\left({S}_h,{E}_h,{A}_h,{U}_h,{I}_{ha},{I}_{hc},{T}_h,{R}_h,L,{S}_m,{E}_m,{I}_m\right)\\ {}\in {\mathbb{R}}_{12}^{+}\mid {N}_h\left(\mathrm{Y}\right)\le \frac{\lambda_h^{\varrho }}{\omega^{\varrho }},L\left(\mathrm{Y}\right)\le K,{N}_m\left(\mathrm{Y}\right)\le \frac{K{\lambda}_h^{\varrho }}{\alpha_1^{\varrho }}\end{array}\right\} $$ ()

4.3 Basic Reproduction Number

In disease modeling, it is necessary to suggest a mathematical formula that would aid in the determination of the number of secondary infections that may occur in the population when an infected individual enters a fully susceptible population. This formula is referred to as the basic reproduction number. This is very important because it helps the public health workers and policymakers understand how to control the disease and identify the factors contributing to its epidemic status. Therefore, in this section, we will determine the basic reproductive number of the proposed LF model. We employ the next-generation matrix method as proposed in Reference [36]. To compute the basic reproduction number using the next generation matrix, we must first compute an equilibrium point, where there is no disease.

4.4 Disease-Free Equilibrium

To obtain disease-free equilibrium, we equate the derivatives of the model to zero and also put the state variables E h , A h , U h , I h a , I h c , T h , E m , I m $$ {E}_h,{A}_h,{U}_h,{I}_{ha},{I}_{hc},{T}_h,{E}_m,{I}_m $$ to zero.

Considering the susceptible class, at the DFE, we obtain the following.
  C D Υ ϱ S h = 0 0 = Λ h ϱ + ρ 2 ϱ R h − ( ω ϱ + κ ϱ ) S h − β 1 ϱ S h S h ⊕ = Λ h ϱ + ρ 2 ϱ R h ω ϱ + κ ϱ + β 1 ϱ $$ {\displaystyle \begin{array}{cc}\hfill {}^C{D}_{\mathrm{Y}}^{\varrho }{S}_h& =0\hfill \\ {}\hfill 0& ={\Lambda}_h^{\varrho }+{\rho}_2^{\varrho }{R}_h-\left({\omega}^{\varrho }+{\kappa}^{\varrho}\right){S}_h-{\beta}_1^{\varrho }{S}_h\hfill \\ {}\hfill {S}_h^{\oplus }& =\frac{\Lambda_h^{\varrho }+{\rho}_2^{\varrho }{R}_h}{\omega^{\varrho }+{\kappa}^{\varrho }+{\beta}_1^{\varrho }}\hfill \end{array}} $$
For R h $$ {R}_h $$ ;
  C D Υ ϱ R h = 0 0 = ρ 1 ϱ T h + κ ϱ S h − ( ρ 2 ϱ + ω ϱ ) R h R h ⊕ = κ ϱ S h ⊕ ρ 2 ϱ + ω ϱ $$ {\displaystyle \begin{array}{cc}\hfill {}^C{D}_{\mathrm{Y}}^{\varrho }{R}_h& =0\hfill \\ {}\hfill 0& ={\rho}_1^{\varrho }{T}_h+{\kappa}^{\varrho }{S}_h-\left({\rho}_2^{\varrho }+{\omega}^{\varrho}\right){R}_h\hfill \\ {}\hfill {R}_h^{\oplus }& =\frac{\kappa^{\varrho }{S}_h^{\oplus }}{\rho_2^{\varrho }+{\omega}^{\varrho }}\hfill \end{array}} $$
For L $$ L $$ ;
  C D Υ ϱ L = 0 0 = c ϱ 1 − L K ϱ ( S m + E m + I m ) − ( α 2 ϱ + Λ m ϱ ) L L ⊕ = c ϱ S m ⊕ c ϱ S m ⊕ K ϱ + α 2 ϱ + Λ m ϱ $$ {\displaystyle \begin{array}{cc}\hfill {}^C{D}_{\mathrm{Y}}^{\varrho }L& =0\hfill \\ {}\hfill 0& ={c}^{\varrho}\left(1-\frac{L}{K^{\varrho }}\right)\left({S}_m+{E}_m+{I}_m\right)-\left({\alpha}_2^{\varrho }+{\Lambda}_m^{\varrho}\right)L\hfill \\ {}\hfill {L}^{\oplus }& =\frac{c^{\varrho }{S}_m^{\oplus }}{\frac{c^{\varrho }{S}_m^{\oplus }}{K^{\varrho }}+{\alpha}_2^{\varrho }+{\Lambda}_m^{\varrho }}\hfill \end{array}} $$
For S m $$ {S}_m $$ ;
  C D Υ ϱ S m = 0 0 = Λ m ϱ L − ( α 1 ϱ + π ϱ ) S m S m ⊕ = Λ m ϱ L ⊕ α 1 ϱ + π ϱ $$ {\displaystyle \begin{array}{cc}\hfill {}^C{D}_{\mathrm{Y}}^{\varrho }{S}_m& =0\hfill \\ {}\hfill 0& ={\Lambda}_m^{\varrho }L-\left({\alpha}_1^{\varrho }+{\pi}^{\varrho}\right){S}_m\hfill \\ {}\hfill {S}_m^{\oplus }& =\frac{\Lambda_m^{\varrho }{L}^{\oplus }}{\alpha_1^{\varrho }+{\pi}^{\varrho }}\hfill \end{array}} $$
We write the disease-free equilibrium as
𝒟 0 = Λ h ϱ + ρ 2 ϱ R h ω ϱ + κ ϱ + β 1 ϱ , 0 , 0 , 0 , 0 , 0 , 0 , κ ϱ S h ⊕ ρ 2 ϱ + ω ϱ , c ϱ S m ⊕ c ϱ S m ⊕ K ϱ + α 2 ϱ + Λ m ϱ Λ m ϱ L ⊕ α 1 ϱ + π ϱ , 0 , 0 ()
Using the disease-free equilibrium and the next-generation matrix, the basic reproduction number is computed as
ℛ 0 N G = ( β 4 ϱ + τ ω ) ω 3 ϱ + k 0 + k 1 + k 2 + k 3 ( k 3 β ϱ ( β 3 ϱ + ω ϱ + θ ϱ ) δ 2 ϱ σ ϱ δ 1 ϱ K ϱ Λ h ϱ ω ϱ ) c ϱ α 1 2 ϱ Λ h ϱ k 4 $$ {\mathcal{R}}_0^{NG}=\frac{\sqrt{\begin{array}{l}\left(\left({\beta}_4^{\varrho }+{\tau}^{\omega}\right){\omega}^{3\varrho }+{k}_0+{k}_1+{k}_2+{k}_3\right)\\ {}\left({k}_3{\beta}^{\varrho}\left({\beta}_3^{\varrho }+{\omega}^{\varrho }+{\theta}^{\varrho}\right){\delta}_2^{\varrho }{\sigma}^{\varrho }{\delta}_1^{\varrho }{K}^{\varrho }{\Lambda}_h^{\varrho }{\omega}^{\varrho}\right)\end{array}}}{c^{\varrho }{\alpha}_1^{2\varrho }{\Lambda}_h^{\varrho }{k}_4} $$ ()
where,
k 0 = ( β 2 ϱ + β 3 ϱ + 2 μ ϱ + η ϱ + ϕ ϱ + θ ϱ ) τ ϱ + β 4 ϱ ( θ ϱ + ϵ ϱ + β 3 ϱ + 2 μ ϱ + η ϱ + ϕ ϱ ) ω 2 ϱ k 1 = ( μ 2 ϱ + ( β 2 ϱ + 2 β 3 ϱ + η ϱ + ϕ ϱ + 2 θ ϱ ) μ ϱ + ( β 2 ϱ + β 3 ϱ + η ϱ + γ ϱ + θ ϱ ) ϕ ϱ + ( θ ϱ + β 2 ϱ + β 3 ϱ ) η ϱ + β 2 ϱ ( β 3 ϱ + θ ϱ ) τ ϱ + μ 2 ϱ + ( θ ϱ + 2 ϵ ϱ + β 3 ϱ + η ϱ + 2 ϕ ϱ ) μ ϱ + ( θ ϱ + β 3 ϱ + η ϱ ) ϕ ϱ + ( θ ϱ + ϵ ϱ + β 3 ϱ ) η ϱ + ϵ ϱ ( β 3 ϱ + θ ϱ ) β 4 ϱ ) ω ϱ k 2 = ( β 3 ϱ + θ ϱ ) μ 2 ϱ + ( ( β 3 ϱ + η ϱ + γ ϱ + θ ϱ ) ϕ ϱ + ( β 3 ϱ + θ ϱ ) ( β 2 ϱ + η ϱ ) ) μ ϱ + ( η ϱ β 2 ϱ + ( β 2 ϱ + γ ϱ ) ( β 3 ϱ + θ ϱ ) ) ϕ ϱ + β 2 ϱ η ϱ ( β 3 ϱ + θ ϱ ) k 3 = β 4 ϱ ( μ ϱ + η ϱ ) ( ϵ ϱ + ϕ ϱ ) ( θ ϱ + β 3 ϱ + μ ϱ ) ) k 4 = ( α 1 ϱ + α 2 ϱ ) ( ω ϱ + η ϱ + μ ϱ ) ( ω ϱ + β 4 ϱ + τ ϱ ) ( μ ϱ + β 2 ϱ + ω ϱ ) × ( ω ϱ + ϕ ϱ + ϵ ϱ ) ( β 3 ϱ + ω ϱ + ϵ ϱ ) ( ω ϱ + ρ 2 ϱ + κ ϱ ) k 5 = ( μ ϱ + β 2 ϱ + ω ϱ ) ( α 1 ϱ + τ ϱ ) ( ω ϱ + η ϱ + μ ϱ ) ( ω ϱ + ρ 2 ϱ + κ ϱ ) ( ω ϱ + β 4 ϱ + τ ϱ ) ( ω ϱ + ρ 2 ϱ ) ( ω ϱ + θ ϱ + ϵ ϱ ) × ( ( c ϱ − α 1 ϱ ) Λ m ϱ − α 2 ϱ α 1 ϱ ) $$ {\displaystyle \begin{array}{ll}\hfill {k}_0& =\left(\left({\beta}_2^{\varrho }+{\beta}_3^{\varrho }+2{\mu}^{\varrho }+{\eta}^{\varrho }+{\phi}^{\varrho }+{\theta}^{\varrho}\right){\tau}^{\varrho }+{\beta}_4^{\varrho}\Big({\theta}^{\varrho }+{\epsilon}^{\varrho }+{\beta}_3^{\varrho }+2{\mu}^{\varrho}\right.\\ {}\hfill & \kern1em \left.+{\eta}^{\varrho }+{\phi}^{\varrho}\Big)\right){\omega}^{2\varrho}\\ {}\hfill {k}_1& =\left(\Big({\mu}^{2\varrho }+\left({\beta}_2^{\varrho }+2{\beta}_3^{\varrho }+{\eta}^{\varrho }+{\phi}^{\varrho }+2{\theta}^{\varrho}\right){\mu}^{\varrho}\right.\\ {}\hfill & \kern1em +\left({\beta}_2^{\varrho }+{\beta}_3^{\varrho }+{\eta}^{\varrho }+{\gamma}^{\varrho }+{\theta}^{\varrho}\right){\phi}^{\varrho}\\ {}\hfill & \kern1em +\left({\theta}^{\varrho }+{\beta}_2^{\varrho }+{\beta}_3^{\varrho}\right){\eta}^{\varrho }+{\beta}_2^{\varrho}\left({\beta}_3^{\varrho }+{\theta}^{\varrho}\right){\tau}^{\varrho}\\ {}\hfill & \kern1em +\left({\mu}^{2\varrho }+\left({\theta}^{\varrho }+2{\epsilon}^{\varrho }+{\beta}_3^{\varrho }+{\eta}^{\varrho }+2{\phi}^{\varrho}\right){\mu}^{\varrho}\right.\\ {}\hfill & \kern1em +\left({\theta}^{\varrho }+{\beta}_3^{\varrho }+{\eta}^{\varrho}\right){\phi}^{\varrho}\\ {}\hfill & \kern1em \left.+\left({\theta}^{\varrho }+{\epsilon}^{\varrho }+{\beta}_3^{\varrho}\right){\eta}^{\varrho }+{\epsilon}^{\varrho}\left({\beta}_3^{\varrho }+{\theta}^{\varrho}\right)\right){\beta}_4^{\varrho}\Big){\omega}^{\varrho}\\ {}\hfill {k}_2& =\left(\left({\beta}_3^{\varrho }+{\theta}^{\varrho}\right){\mu}^{2\varrho }+\Big(\left({\beta}_3^{\varrho }+{\eta}^{\varrho }+{\gamma}^{\varrho }+{\theta}^{\varrho}\right){\phi}^{\varrho}\right.\\ {}\hfill & \kern1em +\left({\beta}_3^{\varrho }+{\theta}^{\varrho}\right)\left({\beta}_2^{\varrho }+{\eta}^{\varrho}\right)\Big){\mu}^{\varrho}\\ {}\hfill & \kern1em \left.+\left({\eta}^{\varrho }{\beta}_2^{\varrho }+\left({\beta}_2^{\varrho }+{\gamma}^{\varrho}\right)\left({\beta}_3^{\varrho }+{\theta}^{\varrho}\right)\right){\phi}^{\varrho }+{\beta}_2^{\varrho }{\eta}^{\varrho}\left({\beta}_3^{\varrho }+{\theta}^{\varrho}\right)\right)\\ {}\hfill {k}_3& ={\beta}_4^{\varrho}\left({\mu}^{\varrho }+{\eta}^{\varrho}\right)\left({\epsilon}^{\varrho }+{\phi}^{\varrho}\right)\left({\theta}^{\varrho }+{\beta}_3^{\varrho }+{\mu}^{\varrho}\right)\Big)\\ {}\hfill {k}_4& =\left({\alpha}_1^{\varrho }+{\alpha}_2^{\varrho}\right)\left({\omega}^{\varrho }+{\eta}^{\varrho }+{\mu}^{\varrho}\right)\left({\omega}^{\varrho }+{\beta}_4^{\varrho }+{\tau}^{\varrho}\right)\left({\mu}^{\varrho }+{\beta}_2^{\varrho }+{\omega}^{\varrho}\right)\\ {}\hfill & \kern1em \times \left({\omega}^{\varrho }+{\phi}^{\varrho }+{\epsilon}^{\varrho}\right)\left({\beta}_3^{\varrho }+{\omega}^{\varrho }+{\epsilon}^{\varrho}\right)\left({\omega}^{\varrho }+{\rho}_2^{\varrho }+{\kappa}^{\varrho}\right)\\ {}\hfill {k}_5& =\left({\mu}^{\varrho }+{\beta}_2^{\varrho }+{\omega}^{\varrho}\right)\left({\alpha}_1^{\varrho }+{\tau}^{\varrho}\right)\left({\omega}^{\varrho }+{\eta}^{\varrho }+{\mu}^{\varrho}\right)\left({\omega}^{\varrho }+{\rho}_2^{\varrho }+{\kappa}^{\varrho}\right)\\ {}\hfill & \kern1em \left({\omega}^{\varrho }+{\beta}_4^{\varrho }+{\tau}^{\varrho}\right)\left({\omega}^{\varrho }+{\rho}_2^{\varrho}\right)\left({\omega}^{\varrho }+{\theta}^{\varrho }+{\epsilon}^{\varrho}\right)\\ {}\hfill & \kern1em \times \left(\left({c}^{\varrho }-{\alpha}_1^{\varrho}\right){\Lambda}_m^{\varrho }-{\alpha}_2^{\varrho }{\alpha}_1^{\varrho}\right)\end{array}} $$

4.5 Existence and Uniqueness of Model's Solution

Assume a complete metric space induced by the norm such that every sequence converges to a unique point within the space. Let ℳ ( ξ ) $$ \mathcal{M}\left(\xi \right) $$ define the space such that ξ ∈ [ 0 , ℋ ] $$ \xi \in \left[0,\mathscr{H}\right] $$ . Then ℳ 12 ( ξ ) $$ {\mathcal{M}}^{12}\left(\xi \right) $$ is another complete metric space induced by the infinity norm, which is defined as
| | S h | | ∞ = sup Υ ∈ ξ | S h ( Υ ) | , | | E h | | ∞ = sup Υ ∈ ξ | E h ( Υ ) | | | A h | | ∞ = sup Υ ∈ ξ | A h ( Υ ) | , | | U h | | ∞ = sup Υ ∈ ξ | U h ( Υ ) | | | I h a | | ∞ = sup Υ ∈ ξ | I h a ( Υ ) | , | | I h c | | ∞ = sup Υ ∈ ξ | I h c ( Υ ) | | | T h | | ∞ = sup Υ ∈ ξ | T h ( Υ ) | , | | R h | | ∞ = sup Υ ∈ ξ | R h ( Υ ) | | | L | | ∞ = sup Υ ∈ ξ | L ( Υ ) | , | | S m | | ∞ = sup Υ ∈ ξ | S m ( Υ ) | | | E m | | ∞ = sup Υ ∈ ξ | E m ( Υ ) | , | | I m | | ∞ = sup Υ ∈ ξ | I m ( Υ ) | $$ {\displaystyle \begin{array}{cc}\hfill {\left\Vert {S}_h\right\Vert}_{\infty }& =\underset{\mathrm{Y}\in \xi }{\sup}\mid {S}_h\left(\mathrm{Y}\right)\mid, {\left\Vert {E}_h\right\Vert}_{\infty }=\underset{\mathrm{Y}\in \xi }{\sup}\mid {E}_h\left(\mathrm{Y}\right)\mid \hfill \\ {}\hfill {\left\Vert {A}_h\right\Vert}_{\infty }& =\underset{\mathrm{Y}\in \xi }{\sup}\mid {A}_h\left(\mathrm{Y}\right)\mid, {\left\Vert {U}_h\right\Vert}_{\infty }=\underset{\mathrm{Y}\in \xi }{\sup}\mid {U}_h\left(\mathrm{Y}\right)\mid \hfill \\ {}\hfill {\left\Vert {I}_{ha}\right\Vert}_{\infty }& =\underset{\mathrm{Y}\in \xi }{\sup}\mid {I}_{ha}\left(\mathrm{Y}\right)\mid, {\left\Vert {I}_{hc}\right\Vert}_{\infty }=\underset{\mathrm{Y}\in \xi }{\sup}\mid {I}_{hc}\left(\mathrm{Y}\right)\mid \hfill \\ {}\hfill {\left\Vert {T}_h\right\Vert}_{\infty }& =\underset{\mathrm{Y}\in \xi }{\sup}\mid {T}_h\left(\mathrm{Y}\right)\mid, {\left\Vert {R}_h\right\Vert}_{\infty }=\underset{\mathrm{Y}\in \xi }{\sup}\mid {R}_h\left(\mathrm{Y}\right)\mid \hfill \\ {}\hfill {\left\Vert L\right\Vert}_{\infty }& =\underset{\mathrm{Y}\in \xi }{\sup}\mid L\left(\mathrm{Y}\right)\mid, {\left\Vert {S}_m\right\Vert}_{\infty }=\underset{\mathrm{Y}\in \xi }{\sup}\mid {S}_m\left(\mathrm{Y}\right)\mid \hfill \\ {}\hfill {\left\Vert {E}_m\right\Vert}_{\infty }& =\underset{\mathrm{Y}\in \xi }{\sup}\mid {E}_m\left(\mathrm{Y}\right)\mid, {\left\Vert {I}_m\right\Vert}_{\infty }=\underset{\mathrm{Y}\in \xi }{\sup}\mid {I}_m\left(\mathrm{Y}\right)\mid \hfill \end{array}} $$ ()
In an attempt to solve for the differentials in Equation (11), using the idea of the Caputo integral operator and the fundamental theorem of calculus;
S h ( Υ ) = S h 0 + c 𝒟 Υ ϱ S h 𝒴 1 E h ( Υ ) = E h 0 + c 𝒟 Υ ϱ E h 𝒴 2 A h ( Υ ) = A h 0 + c 𝒟 Υ ϱ S h 𝒴 3 U h ( Υ ) = U h 0 + c 𝒟 Υ ϱ U h 𝒴 4 I h a ( Υ ) = I h a 0 + c 𝒟 Υ ϱ I h a 𝒴 5 I h c ( Υ ) = I h c 0 + c 𝒟 Υ ϱ I h c 𝒴 6 T h ( Υ ) = T h 0 + c 𝒟 Υ ϱ T h 𝒴 7 R h ( Υ ) = R h 0 + c 𝒟 Υ ϱ R h 𝒴 8 L ( Υ ) = L 0 + c 𝒟 Υ ϱ L 𝒴 9 S m ( Υ ) = S m 0 + c 𝒟 Υ ϱ S m 𝒴 10 E m ( Υ ) = E m 0 + c 𝒟 Υ ϱ E m 𝒴 11 I m ( Υ ) = I m 0 + c 𝒟 Υ ϱ I m 𝒴 12 ()
where
𝒴 1 = Λ h ϱ + ρ 2 ϱ R h − ( ω ϱ + κ ϱ ) S h − β 1 ϱ S h 𝒴 2 = β 1 ϱ S h − ( β 4 ϱ + ω ϱ + τ ϱ ) E h 𝒴 3 = τ ϱ E h − ( ω ϱ + ϕ ϱ + ϵ ϱ ) A h 𝒴 4 = ϕ ϱ A h − ( ω ϱ + η ϱ + μ ϱ ) U h 𝒴 5 = β 4 ϱ E h + γ ϱ U h − ( μ ϱ + β 2 ϱ + ω ϱ ) I h a 𝒴 6 = η ϱ U h + μ ϱ I h a − ( β 3 ϱ + ω ϱ + θ ϱ ) I h c 𝒴 7 = ϵ ϱ A h + β 3 ϱ I h c + β 2 ϱ I h a − ( ρ 1 ϱ + ω ϱ ) T h 𝒴 8 = ρ 1 ϱ T h + κ ϱ S h − ( ρ 2 ϱ + ω ϱ ) R h 𝒴 9 = c ϱ 1 − L K ϱ ( S m + E m + I m ) − ( α 2 ϱ + Λ m ϱ ) L 𝒴 10 = Λ m ϱ L − ( α 1 ϱ + π ϱ ) S m 𝒴 11 = π ϱ S m − ( α 1 ϱ + σ ϱ ) E m 𝒴 12 = σ ϱ E m − α 1 ϱ I m ()
With the aid of the fractional Caputo integral operator, we transform the equations into (27);
S h ( Υ ) = S h 0 + ( Γ ( ϱ ) ) − 1 ∫ 0 Υ 𝒴 1 ( ϱ , υ , S h ( ϱ ) ) ( Υ − υ ) 1 − ϱ d υ E h ( Υ ) = E h 0 + ( Γ ( ϱ ) ) − 1 ∫ 0 Υ 𝒴 2 ( ϱ , υ , E h ( ϱ ) ) ( Υ − υ ) 1 − ϱ d υ A h ( Υ ) = A h 0 + ( Γ ( ϱ ) ) − 1 ∫ 0 Υ 𝒴 3 ( ϱ , υ , A h ( ϱ ) ) ( Υ − υ ) 1 − ϱ d υ U h ( Υ ) = U h 0 + ( Γ ( ϱ ) ) − 1 ∫ 0 Υ 𝒴 4 ( ϱ , υ , U h ( ϱ ) ) ( Υ − υ ) 1 − ϱ d υ I h a ( Υ ) = I h a 0 + ( Γ ( ϱ ) ) − 1 ∫ 0 Υ 𝒴 5 ( ϱ , υ , I h a ( ϱ ) ) ( Υ − υ ) 1 − ϱ d υ I h c ( Υ ) = I h c 0 + ( Γ ( ϱ ) ) − 1 ∫ 0 Υ 𝒴 6 ( ϱ , υ , I h c ( ϱ ) ) ( Υ − υ ) 1 − ϱ d υ T h ( Υ ) = T h 0 + ( Γ ( ϱ ) ) − 1 ∫ 0 Υ 𝒴 7 ( ϱ , υ , T h ( ϱ ) ) ( Υ − υ ) 1 − ϱ d υ R h ( Υ ) = R h 0 + ( Γ ( ϱ ) ) − 1 ∫ 0 Υ 𝒴 8 ( ϱ , υ , R h ( ϱ ) ) ( Υ − υ ) 1 − ϱ d υ L h ( Υ ) = L h 0 + ( Γ ( ϱ ) ) − 1 ∫ 0 Υ 𝒴 9 ( ϱ , υ , L h ( ϱ ) ) ( Υ − υ ) 1 − ϱ d υ S m ( Υ ) = S m 0 + ( Γ ( ϱ ) ) − 1 ∫ 0 Υ 𝒴 10 ( ϱ , υ , S m ( ϱ ) ) ( Υ − υ ) 1 − ϱ d υ E m ( Υ ) = E m 0 + ( Γ ( ϱ ) ) − 1 ∫ 0 Υ 𝒴 11 ( ϱ , υ , E m ( ϱ ) ) ( Υ − υ ) 1 − ϱ d υ I m ( Υ ) = I m 0 + ( Γ ( ϱ ) ) − 1 ∫ 0 Υ 𝒴 12 ( ϱ , υ , I m ( ϱ ) ) ( Υ − υ ) 1 − ϱ d υ ()

Suppose the rate of change of the various state variables with respect to Υ $$ \mathrm{Y} $$ has limit points that are bounded, then their respective functions { 𝒴 ι } ι = 1 12 are Lipschitz continuous.

Given a pair of functions S h ( Υ ) $$ {S}_h\left(\mathrm{Y}\right) $$ and S h ⋆ ( Υ ) $$ {S}_h^{\star}\left(\mathrm{Y}\right) $$ ;
| | 𝒴 1 ( ϱ , Υ , S h ( Υ ) ) − 𝒴 1 ( ϱ , Υ , S h ⋆ ( Υ ) ) | | ≤ | | ( ( ω ϱ + κ ϱ ) + β 1 ϱ ) ( S h ( Υ ) ) − S h ⋆ ( Υ ) ) | | ()
If we let ϖ 1 = ( ( ω ϱ + κ ϱ ) + β 1 ϱ ) $$ {\varpi}_1=\left(\left({\omega}^{\varrho }+{\kappa}^{\varrho}\right)+{\beta}_1^{\varrho}\right) $$ , then (30) becomes
| | 𝒴 1 ( ϱ , Υ , S h ( Υ ) − 𝒴 1 ( ϱ , Υ , S h ⋆ ( Υ ) | | ≤ | | ϖ 1 ( S h ( Υ ) ) − S h ⋆ ( Υ ) ) | | = ϖ 1 | | ( S h ( Υ ) ) − S h ⋆ ( Υ ) ) | | ()
where ϖ 1 $$ {\varpi}_1 $$ is a Lipschitz constant with associated Lipschitz function, 𝒴 1
Using the same approach, we obtain the following results for the other state variables.
| | 𝒴 2 ( ϱ , Υ , E h ( Υ ) − 𝒴 2 ( ϱ , Υ , E h ⋆ ( Υ ) | | ≤ ϖ 2 | | ( E h ( Υ ) ) − E h ⋆ ( Υ ) ) | | | | 𝒴 3 ( ϱ , Υ , A h ( Υ ) − 𝒴 3 ( ϱ , Υ , A h ⋆ ( Υ ) | | ≤ ϖ 3 | | ( A h ( Υ ) ) − A h ⋆ ( Υ ) ) | | | | 𝒴 4 ( ϱ , Υ , U h ( Υ ) − 𝒴 4 ( ϱ , Υ , U h ⋆ ( Υ ) | | ≤ ϖ 4 | | ( U h ( Υ ) ) − U h ⋆ ( Υ ) ) | | | | 𝒴 5 ( ϱ , Υ , I h a ( Υ ) − 𝒴 5 ( ϱ , Υ , I h a ⋆ ( Υ ) | | ≤ ϖ 5 | | ( I h a ( Υ ) ) − I h a ⋆ ( Υ ) ) | | | | 𝒴 6 ( ϱ , Υ , I h c ( Υ ) − 𝒴 6 ( ϱ , Υ , I h c ⋆ ( Υ ) | | ≤ ϖ 6 | | ( I h c ( Υ ) ) − I h c ⋆ ( Υ ) ) | | | | 𝒴 7 ( ϱ , Υ , T h ( Υ ) − 𝒴 7 ( ϱ , Υ , T h ⋆ ( Υ ) | | ≤ ϖ 7 | | ( T h ( Υ ) ) − T h ⋆ ( Υ ) ) | | | | 𝒴 8 ( ϱ , Υ , R h ( Υ ) − 𝒴 8 ( ϱ , Υ , R h ⋆ ( Υ ) | | ≤ ϖ 8 | | ( R h ( Υ ) ) − R h ⋆ ( Υ ) ) | | | | 𝒴 9 ( ϱ , Υ , L ( Υ ) − 𝒴 9 ( ϱ , Υ , L ⋆ ( Υ ) | | ≤ ϖ 9 | | ( L ( Υ ) ) − L ⋆ ( Υ ) ) | | | | 𝒴 10 ( ϱ , Υ , S m ( Υ ) − 𝒴 10 ( ϱ , Υ , S m ⋆ ( Υ ) | | ≤ ϖ 10 | | ( S m ( Υ ) ) − S m ⋆ ( Υ ) ) | | | | 𝒴 11 ( ϱ , Υ , E m ( Υ ) − 𝒴 11 ( ϱ , Υ , E m ⋆ ( Υ ) | | ≤ ϖ 11 | | ( E m ( Υ ) ) − E m ⋆ ( Υ ) ) | | | | 𝒴 12 ( ϱ , Υ , I m ( Υ ) − 𝒴 12 ( ϱ , Υ , I m ⋆ ( Υ ) | | ≤ ϖ 12 | | ( I m ( Υ ) ) − I m ⋆ ( Υ ) ) | | ()
where
φ 2 = ( β 4 ϱ + ω ϱ + τ ϱ ) φ 3 = ( ω ϱ + ϕ ϱ + ϵ ϱ ) 0 φ 4 = ( ω ϱ + η ϱ + μ ϱ ) φ 5 = ( μ ϱ + β 2 ϱ + ω ϱ ) , φ 6 = ( β 3 ϱ + ω ϱ + θ ϱ ) φ 7 = ( ρ 1 ϱ + ω ϱ ) φ 8 = ( ρ 2 ϱ + ω ϱ ) , φ 9 = ( α 2 ϱ + Λ m ϱ ) , φ 10 = ( α 1 ϱ + π ϱ ) φ 11 = ( α 1 ϱ + σ ϱ ) , φ 12 = α 1 ϱ $$ {\displaystyle \begin{array}{cc}\hfill {\varphi}_2& =\left({\beta}_4^{\varrho }+{\omega}^{\varrho }+{\tau}^{\varrho}\right){\varphi}_3=\left({\omega}^{\varrho }+{\phi}^{\varrho }+{\epsilon}^{\varrho}\right)\hfill \\ {}\hfill 0{\varphi}_4& =\left({\omega}^{\varrho }+{\eta}^{\varrho }+{\mu}^{\varrho}\right)\hfill \\ {}\hfill {\varphi}_5& =\left({\mu}^{\varrho }+{\beta}_2^{\varrho }+{\omega}^{\varrho}\right),{\varphi}_6=\left({\beta}_3^{\varrho }+{\omega}^{\varrho }+{\theta}^{\varrho}\right)\hfill \\ {}\hfill {\varphi}_7& =\left({\rho}_1^{\varrho }+{\omega}^{\varrho}\right)\hfill \\ {}\hfill {\varphi}_8& =\left({\rho}_2^{\varrho }+{\omega}^{\varrho}\right),{\varphi}_9=\left({\alpha}_2^{\varrho }+{\Lambda}_m^{\varrho}\right),{\varphi}_{10}=\left({\alpha}_1^{\varrho }+{\pi}^{\varrho}\right)\hfill \\ {}\hfill {\varphi}_{11}& =\left({\alpha}_1^{\varrho }+{\sigma}^{\varrho}\right),{\varphi}_{12}={\alpha}_1^{\varrho}\hfill \end{array}} $$ ()

It is observed that all functions satisfy the Lipschitz continuity with the Lipschitz constant { φ ι } ι = 1 12 $$ {\left\{{\varphi}_{\iota}\right\}}_{\iota =1}^{12} $$

(44) is written sequentially as
S h t ( Υ ) = ( Γ ( ϱ ) ) − 1 ∫ 0 Υ 𝒴 1 ( ϱ , υ , S h ( t − 1 ) ( υ ) ) ( Υ − υ ) 1 − ϱ d ϱ E h t ( Υ ) = ( Γ ( ϱ ) ) − 1 ∫ 0 Υ 𝒴 2 ( ϱ , υ , E h ( t − 1 ) ( υ ) ) ( Υ − υ ) 1 − ϱ d ϱ A h t ( Υ ) = ( Γ ( ϱ ) ) − 1 ∫ 0 Υ 𝒴 3 ( ϱ , υ , A h ( t − 1 ) ( υ ) ) ( Υ − υ ) 1 − ϱ d ϱ U h t ( Υ ) = ( Γ ( ϱ ) ) − 1 ∫ 0 Υ 𝒴 4 ( ϱ , υ , U h ( t − 1 ) ( υ ) ) ( Υ − υ ) 1 − ϱ d ϱ I h a t ( Υ ) = ( Γ ( ϱ ) ) − 1 ∫ 0 Υ 𝒴 5 ( ϱ , υ , I h a ( t − 1 ) ( υ ) ) ( Υ − υ ) 1 − ϱ d ϱ I h c t ( Υ ) = ( Γ ( ϱ ) ) − 1 ∫ 0 Υ 𝒴 6 ( ϱ , υ , I h c ( t − 1 ) ( υ ) ) ( Υ − υ ) 1 − ϱ d ϱ T h t ( Υ ) = ( Γ ( ϱ ) ) − 1 ∫ 0 Υ 𝒴 7 ( ϱ , υ , T h ( t − 1 ) ( υ ) ) ( Υ − υ ) 1 − ϱ d ϱ R h t ( Υ ) = ( Γ ( ϱ ) ) − 1 ∫ 0 Υ 𝒴 8 ( ϱ , υ , R h ( t − 1 ) ( υ ) ) ( Υ − υ ) 1 − ϱ d ϱ L t ( Υ ) = ( Γ ( ϱ ) ) − 1 ∫ 0 Υ 𝒴 9 ( ϱ , υ , L ( t − 1 ) ( υ ) ) ( Υ − υ ) 1 − ϱ d ϱ S m t ( Υ ) = ( Γ ( ϱ ) ) − 1 ∫ 0 Υ 𝒴 10 ( ϱ , υ , S m ( t − 1 ) ( υ ) ) ( Υ − υ ) 1 − ϱ E m t ( Υ ) = ( Γ ( ϱ ) ) − 1 ∫ 0 Υ 𝒴 11 ( ϱ , υ , E m ( t − 1 ) ( υ ) ) ( Υ − υ ) 1 − ϱ I m t ( Υ ) = ( Γ ( ϱ ) ) − 1 ∫ 0 Υ 𝒴 12 ( ϱ , υ , I m ( t − 1 ) ( υ ) ) ( Υ − υ ) 1 − ϱ ()
The associated seed points of the sequence are
S h 0 ≥ 0 , E h 0 ≥ 0 , A h 0 ≥ 0 , U h 0 ≥ 0 , I h a 0 ≥ 0 , I h c 0 ≥ 0 , T h 0 ≥ 0 R h 0 ≥ 0 , L 0 ≥ 0 , S m 0 ≥ 0 , E m 0 ≥ 0 , I m 0 ≥ 0 $$ {\displaystyle \begin{array}{ll}\hfill {S}_h^0& \ge 0,{E}_h^0\ge 0,{A}_h^0\ge 0,{U}_h^0\ge 0,{I}_{ha}^0\ge 0,{I}_{hc}^0\ge 0,{T}_h^0\ge 0\\ {}\hfill {R}_h^0& \ge 0,{L}^0\ge 0,{S}_m^0\ge 0,{E}_m^0\ge 0,{I}_m^0\ge 0\end{array}} $$
The difference between successive terms and preceding terms becomes;
ℬ S h , t = S h t ( Υ ) − S h ( t − 1 ) ( Υ ) = ( Γ ( ϱ ) ) − 1 × ∫ 0 Υ ( Υ − υ ) ϱ − 1 𝒴 1 ( ϱ , υ , S h ( t − 1 ) ( υ ) ) − 𝒴 1 ( ϱ , υ , S h ( t − 2 ) ( υ ) ) d υ ℬ E h , t = E h t ( Υ ) − E h ( t − 1 ) ( Υ ) = ( Γ ( ϱ ) ) − 1 × ∫ 0 Υ ( Υ − υ ) ϱ − 1 𝒴 2 ( ϱ , υ , E h ( t − 1 ) ( υ ) ) − 𝒴 2 ( ϱ , υ , E h ( t − 2 ) ( υ ) ) d υ ℬ A h , t = A h t ( Υ ) − A h ( t − 1 ) ( Υ ) = ( Γ ( ϱ ) ) − 1 × ∫ 0 Υ ( Υ − υ ) ϱ − 1 𝒴 3 ( ϱ , υ , A h ( t − 1 ) ( υ ) ) − 𝒴 3 ( ϱ , υ , A h ( t − 2 ) ( υ ) ) d υ ℬ U h , t = U h t ( Υ ) − U h ( t − 1 ) ( Υ ) = ( Γ ( ϱ ) ) − 1 × ∫ 0 Υ ( Υ − υ ) ϱ − 1 𝒴 4 ( ϱ , υ , U h ( t − 1 ) ( υ ) ) − 𝒴 4 ( ϱ , υ , U h ( t − 2 ) ( υ ) ) d υ ℬ I h a , t = I h a t ( Υ ) − I h a ( t − 1 ) ( Υ ) = ( Γ ( ϱ ) ) − 1 × ∫ 0 Υ ( Υ − υ ) ϱ − 1 𝒴 5 ( ϱ , υ , I h a ( t − 1 ) ( υ ) ) − 𝒴 5 ( ϱ , υ , I h a ( t − 2 ) ( υ ) ) d υ ℬ I h c , l = I h c t ( Υ ) − I h c ( t − 1 ) ( Υ ) = ( Γ ( ϱ ) ) − 1 × ∫ 0 Υ ( Υ − υ ) ϱ − 1 𝒴 6 ( ϱ , υ , I h c ( t − 1 ) ( υ ) ) − 𝒴 6 ( ϱ , υ , I h c ( t − 2 ) ( υ ) ) d υ ℬ T h , t = T h t ( Υ ) − T h ( t − 1 ) ( Υ ) = ( Γ ( ϱ ) ) − 1 × ∫ 0 Υ ( Υ − υ ) ϱ − 1 𝒴 7 ( ϱ , υ , T h ( t − 1 ) ( υ ) ) − 𝒴 7 ( ϱ , υ , T h ( t − 2 ) ( υ ) ) d υ ℬ R h , t = R h t ( Υ ) − R h ( t − 1 ) ( Υ ) = ( Γ ( ϱ ) ) − 1 × ∫ 0 Υ ( Υ − υ ) ϱ − 1 𝒴 8 ( ϱ , υ , R h ( t − 1 ) ( υ ) ) − 𝒴 8 ( ϱ , υ , R h ( t − 2 ) ( υ ) ) d υ ℬ L t = L t ( Υ ) − L ( t − 1 ) ( Υ ) = ( Γ ( ϱ ) ) − 1 × ∫ 0 Υ ( Υ − υ ) ϱ − 1 𝒴 9 ( ϱ , υ , L ( t − 1 ) ( υ ) ) − 𝒴 9 ( ϱ , υ , L ( t − 2 ) ( υ ) ) d υ ℬ S m , t = S m t ( Υ ) − S m ( t − 1 ) ( Υ ) = ( Γ ( ϱ ) ) − 1 × ∫ 0 Υ ( Υ − υ ) ϱ − 1 𝒴 10 ( ϱ , υ , S m ( t − 1 ) ( υ ) ) − 𝒴 10 ( ϱ , υ , S m ( t − 2 ) ( υ ) ) d υ ℬ E m , t = E m t ( Υ ) − E m ( t − 1 ) ( Υ ) = ( Γ ( ϱ ) ) − 1 × ∫ 0 Υ ( Υ − υ ) ϱ − 1 𝒴 11 ( ϱ , υ , E m ( t − 1 ) ( υ ) ) − 𝒴 11 ( ϱ , υ , E m ( t − 2 ) ( υ ) ) d υ ℬ I m , t = I m t ( Υ ) − I m ( t − 1 ) ( Υ ) = ( Γ ( ϱ ) ) − 1 × ∫ 0 Υ ( Υ − υ ) ϱ − 1 𝒴 12 ( ϱ , υ , I m ( t − 1 ) ( υ ) ) − 𝒴 12 ( ϱ , υ , I m ( t − 2 ) ( υ ) ) d υ ()
In a compact form, the sequences can be expressed as;
S h t ( Υ ) = ∑ r = 0 t ℬ S h , t ( Υ ) , E h t ( Υ ) = ∑ r = 0 t ℬ E h , t ( Υ ) A h t ( Υ ) = ∑ r = 0 t ℬ A h , t ( Υ ) U h t ( Υ ) = ∑ r = 0 t ℬ U h , t ( Υ ) , I h a t ( Υ ) = ∑ r = 0 t ℬ I h a , t ( Υ ) I h c t ( Υ ) = ∑ r = 0 t ℬ I h c , t ( Υ ) T h t ( Υ ) = ∑ r = 0 t ϝ T h , t ( Υ ) , T h t ( Υ ) = ∑ r = 0 t ℬ T h , t ( Υ ) R h t ( t ) = ∑ r = 0 t ℬ R h , t ( Υ ) S m t ( Υ ) = ∑ r = 0 t ℬ S m , t ( Υ ) , E m l ( t ) = ∑ r = 0 t ℬ E m , t ( Υ ) I m t ( Υ ) = ∑ r = 0 t ℬ I m , t ( Υ ) $$ {\displaystyle \begin{array}{cc}\hfill {S}_{ht}\left(\mathrm{Y}\right)& =\sum \limits_{r=0}^t{\mathcal{B}}_{S_{h,t}}\left(\mathrm{Y}\right),\kern.5em {E}_{ht}\left(\mathrm{Y}\right)=\sum \limits_{r=0}^t{\mathcal{B}}_{E_{h,t}}\left(\mathrm{Y}\right)\hfill \\ {}\hfill {A}_{ht}\left(\mathrm{Y}\right)& =\sum \limits_{r=0}^t{\mathcal{B}}_{A_{h,t}}\left(\mathrm{Y}\right)\hfill \\ {}\hfill {U}_{ht}\left(\mathrm{Y}\right)& =\sum \limits_{r=0}^t{\mathcal{B}}_{U_{h,t}}\left(\mathrm{Y}\right),\kern.5em {I}_{ha t}\left(\mathrm{Y}\right)=\sum \limits_{r=0}^t{\mathcal{B}}_{I_{ha,t}}\left(\mathrm{Y}\right)\hfill \\ {}\hfill {I}_{hc t}\left(\mathrm{Y}\right)& =\sum \limits_{r=0}^t{\mathcal{B}}_{I_{hc,t}}\left(\mathrm{Y}\right)\hfill \\ {}\hfill {T}_{ht}\left(\mathrm{Y}\right)& =\sum \limits_{r=0}^t{\mathbbm{\digamma}}_{T_{h,t}}\left(\mathrm{Y}\right),\kern.5em {T}_{ht}\left(\mathrm{Y}\right)=\sum \limits_{r=0}^t{\mathcal{B}}_{T_{h,t}}\left(\mathrm{Y}\right)\hfill \\ {}\hfill {R}_{ht}(t)& =\sum \limits_{r=0}^t{\mathcal{B}}_{R_{h,t}}\left(\mathrm{Y}\right)\hfill \\ {}\hfill {S}_{mt}\left(\mathrm{Y}\right)& =\sum \limits_{r=0}^t{\mathcal{B}}_{S_{m,t}}\left(\mathrm{Y}\right),\kern.5em {E}_{ml}(t)=\sum \limits_{r=0}^t{\mathcal{B}}_{E_{m,t}}\left(\mathrm{Y}\right)\hfill \\ {}\hfill {I}_{mt}\left(\mathrm{Y}\right)& =\sum \limits_{r=0}^t{\mathcal{B}}_{I_{m,t}}\left(\mathrm{Y}\right)\hfill \end{array}} $$
With the concept of continuity in Equation (30) coupled with notions in (), we have that
| | ℬ S h , t ( Υ ) | | = ( Γ ( ϱ ) ) − 1 𝒴 1 ∫ 0 t | | ℬ S h ( t − 1 ) ( υ ) | | ( Υ − υ ) ϱ − 1 d υ | | ℬ E h , t ( Υ ) | | = ( Γ ( ϱ ) ) − 1 𝒴 2 ∫ 0 t | | ℬ E h ( t − 1 ) ( υ ) | | ( Υ − υ ) ϱ − 1 d υ | | ℬ A h , t ( Υ ) | | = ( Γ ( ϱ ) ) − 1 𝒴 3 ∫ 0 t | | ℬ A h ( t − 1 ) ( υ ) | | ( Υ − υ ) ϱ − 1 d υ | | ℬ U h , t ( Υ ) | | = ( Γ ( ϱ ) ) − 1 𝒴 4 ∫ 0 t | | ℬ U h ( t − 1 ) ( υ ) | | ( Υ − υ ) ϱ − 1 d υ | | ℬ I h a , t ( Υ ) | | = ( Γ ( ϱ ) ) − 1 𝒴 5 ∫ 0 t | | ℬ I h a ( t − 1 ) ( υ ) | | ( Υ − υ ) ϱ − 1 d υ | | ℬ I h c , t ( Υ ) | | = ( Γ ( ϱ ) ) − 1 𝒴 6 ∫ 0 t | | ℬ I h c ( t − 1 ) ( υ ) | | ( Υ − υ ) ϱ − 1 d υ | | ℬ T h , t ( Υ ) | | = ( Γ ( ϱ ) ) − 1 𝒴 7 ∫ 0 t | | ℬ T h ( t − 1 ) ( υ ) | | ( Υ − υ ) ϱ − 1 d υ | | ℬ R h , t ( Υ ) | | = ( Γ ( ϱ ) ) − 1 𝒴 8 ∫ 0 t | | ℬ R h ( t − 1 ) ( υ ) | | ( Υ − υ ) ϱ − 1 d υ | | ℬ L , t ( Υ ) | | = ( Γ ( ϱ ) ) − 1 𝒴 9 ∫ 0 t | | ℬ L ( t − 1 ) ( υ ) | | ( Υ − υ ) ϱ − 1 d υ | | ℬ S m , t ( Υ ) | | = ( Γ ( ϱ ) ) − 1 𝒴 10 ∫ 0 t | | ℬ S m ( t − 1 ) ( υ ) | | ( Υ − υ ) ϱ − 1 d υ | | ℬ E m , t ( Υ ) | | = ( Γ ( ϱ ) ) − 1 𝒴 11 ∫ 0 t | | ℬ E m ( t − 1 ) ( υ ) | | ( Υ − υ ) ϱ − 1 d υ | | ℬ I m , t ( Υ ) | | = ( Γ ( ϱ ) ) − 1 𝒴 12 ∫ 0 t | | ℬ I m ( t − 1 ) ( υ ) | | ( Υ − υ ) ϱ − 1 d υ ()

Now, we proceed to establish that the fractional disease model has just a single solution. We use the theorem below;

Theorem 4.3.A unique solution to the disease model exist for Υ ∈ [ 0 , ℋ ] $$ \mathrm{Y}\in \left[0,\mathscr{H}\right] $$ provided that

Ψ ϱ 𝒴 ι Γ ( ϱ ) + 1 < 1 , ι = 1 , 23 , … , 12 ()

Proof.Because the Lipschitz continuity holds for the functions 𝒴 ι , when their respective state variables have limit points, then we can repeatedly express (35) as

| | ℬ S h , t ( Υ ) | | ≤ | | S h 0 ( Υ ) | | ( Ψ ϱ ( Γ ( ϱ ) ) − 1 𝒴 1 ) t | | ℬ E h , t ( Υ ) | | ≤ | | E h 0 ( Υ ) | | ( Ψ ϱ ( Γ ( ϱ ) ) − 1 𝒴 2 ) t | | ℬ A h , t ( Υ ) | | ≤ | | A h 0 ( Υ ) | | ( Ψ ϱ ( Γ ( ϱ ) ) − 1 𝒴 3 ) t | | ℬ U h , t ( Υ ) | | ≤ | | U h 0 ( Υ ) | | ( Ψ ϱ ( Γ ( ϱ ) ) − 1 𝒴 4 ) t | | ℬ I h a , t ( Υ ) | | ≤ | | I h a 0 ( Υ ) | | ( Ψ ϱ ( Γ ( ϱ ) ) − 1 𝒴 5 ) t | | ℬ I h c , t ( Υ ) | | ≤ | | I h c 0 ( Υ ) | | ( Ψ ϱ ( Γ ( ϱ ) ) − 1 𝒴 6 ) t | | ℬ T h , t ( Υ ) | | ≤ | | T h 0 ( Υ ) | | ( Ψ ϱ ( Γ ( ϱ ) ) − 1 𝒴 7 ) t | | ℬ R h , t ( Υ ) | | ≤ | | R h 0 ( Υ ) | | ( Ψ ϱ ( Γ ( ϱ ) ) − 1 𝒴 8 ) t | | ℬ L , t ( Υ ) | | ≤ | | L 0 ( Υ ) | | ( Ψ ϱ ( Γ ( ϱ ) ) − 1 𝒴 9 ) t | | ℬ S m , t ( Υ ) | | ≤ | | S m 0 ( Υ ) | | ( Ψ ϱ ( Γ ( ϱ ) ) − 1 𝒴 10 ) t | | ℬ E m , t ( Υ ) | | ≤ | | E m 0 ( Υ ) | | ( Ψ ϱ ( Γ ( ϱ ) ) − 1 𝒴 11 ) t | | ℬ I m , t ( Υ ) | | ≤ | | I m 0 ( Υ ) | | ( Ψ ϱ ( Γ ( ϱ ) ) − 1 𝒴 12 ) t ()
The norm of the state variables forming the sequences approaches zero as t $$ t $$ gets larger
| | ℬ S h , t ( Υ ) | | → 0 , | | ℬ E h , t ( Υ ) | | → 0 , | | ℬ A h , ( Υ ) | | → 0 | | ℬ U h , t ( Υ ) | | → 0 , | | ℬ I h a , t ( Υ ) | | → 0 , | | ℬ I h c , t ( Υ ) | | → 0 | | ℬ T h , t ( Υ ) | | → 0 , | | ℬ R h , t ( Υ ) | | → 0 , | | ℬ L , t ( Υ ) | | → 0 | | ℬ S m , t ( Υ ) | | → 0 , | | ℬ E m , t ( Υ ) | | → 0 , | | ℬ I m , t ( Υ ) | | → 0 $$ {\displaystyle \begin{array}{cc}\hfill & \left\Vert {\mathcal{B}}_{S_h,t}\left(\mathrm{Y}\right)\right\Vert \to 0,\left\Vert {\mathcal{B}}_{E_h,t}\left(\mathrm{Y}\right)\right\Vert \to 0,\left\Vert {\mathcal{B}}_{A_h,}\left(\mathrm{Y}\right)\right\Vert \to 0\hfill \\ {}\hfill & \left\Vert {\mathcal{B}}_{U_h,t}\left(\mathrm{Y}\right)\right\Vert \to 0,\left\Vert {\mathcal{B}}_{I_{ha},t}\left(\mathrm{Y}\right)\right\Vert \to 0,\left\Vert {\mathcal{B}}_{I_{hc},t}\left(\mathrm{Y}\right)\right\Vert \to 0\hfill \\ {}\hfill & \left\Vert {\mathcal{B}}_{T_h,t}\left(\mathrm{Y}\right)\right\Vert \to 0,\left\Vert {\mathcal{B}}_{R_h,t}\left(\mathrm{Y}\right)\right\Vert \to 0,\left\Vert {\mathcal{B}}_{L,t}\left(\mathrm{Y}\right)\right\Vert \to 0\hfill \\ {}\hfill & \left\Vert {\mathcal{B}}_{S_m,t}\left(\mathrm{Y}\right)\right\Vert \to 0,\left\Vert {\mathcal{B}}_{E_m,t}\left(\mathrm{Y}\right)\right\Vert \to 0,\left\Vert {\mathcal{B}}_{I_m,t}\left(\mathrm{Y}\right)\right\Vert \to 0\hfill \end{array}} $$ ()
By the use of the triangle inequality analogous to (37), we obtain
| | S h ( t + k ) ( Υ ) − S h t ( Υ ) | | ≤ ∑ ι = t + 1 l + k 𝒢 1 = ( 𝒢 1 1 + t − 𝒢 1 t + k + 1 ) ( 1 − 𝒢 1 ) | | E h ( t + k ) ( Υ ) − E h t ( Υ ) | | ≤ ∑ ι = t + 1 l + k 𝒢 2 = ( 𝒢 2 1 + t − 𝒢 2 t + k + 1 ) ( 1 − 𝒢 2 ) | | A h ( t + k ) ( Υ ) − A h t ( Υ ) | | ≤ ∑ ι = t + 1 l + k 𝒢 3 = ( 𝒢 3 1 + t − 𝒢 3 t + k + 1 ) ( 1 − 𝒢 3 ) | | U h ( t + k ) ( Υ ) − U h t ( Υ ) | | ≤ ∑ ι = t + 1 l + k 𝒢 1 = ( 𝒢 4 1 + t − 𝒢 4 t + k + 1 ) ( 1 − 𝒢 4 ) | | I h c ( t + k ) ( Υ ) − I h c t ( Υ ) | | ≤ ∑ ι = t + 1 l + k 𝒢 5 = ( 𝒢 5 1 + t − 𝒢 5 t + k + 1 ) ( 1 − 𝒢 5 ) | | I h a ( t + k ) ( Υ ) − I h a t ( Υ ) | | ≤ ∑ ι = t + 1 l + k 𝒢 6 = ( 𝒢 6 1 + t − 𝒢 6 t + k + 1 ) ( 1 − 𝒢 6 ) | | T h ( t + k ) ( Υ ) − T h t ( Υ ) | | ≤ ∑ ι = t + 1 l + k 𝒢 7 = ( 𝒢 7 1 + t − 𝒢 7 t + k + 1 ) ( 1 − 𝒢 7 ) | | R h ( t + k ) ( Υ ) − R h t ( Υ ) | | ≤ ∑ ι = t + 1 l + k 𝒢 8 = ( 𝒢 8 1 + t − 𝒢 8 t + k + 1 ) ( 1 − 𝒢 8 ) | | L ( t + k ) ( Υ ) − L t ( Υ ) | | ≤ ∑ ι = t + 1 l + k 𝒢 9 = ( 𝒢 9 1 + t − 𝒢 1 t + k + 1 ) ( 1 − 𝒢 9 ) | | S m ( t + k ) ( Υ ) − S m t ( Υ ) | | ≤ ∑ ι = t + 1 l + k 𝒢 10 = ( 𝒢 10 1 + t − 𝒢 10 t + k + 1 ) ( 1 − 𝒢 10 ) | | E m ( t + k ) ( Υ ) − E m t ( Υ ) | | ≤ ∑ ι = t + 1 l + k 𝒢 11 = ( 𝒢 11 1 + t − 𝒢 11 t + k + 1 ) ( 1 − 𝒢 11 ) | | I m ( t + k ) ( Υ ) − I m t ( Υ ) | | ≤ ∑ ι = t + 1 l + k 𝒢 12 = ( 𝒢 12 1 + t − 𝒢 12 t + k + 1 ) ( 1 − 𝒢 12 ) ()
where
𝒢 ι = Ψ ϱ 𝒴 ι Γ ( ϱ ) + 1 < 1
It is evident that the sequence of the state variables is convergent and converges to a unique point within the complete metric space ℳ ( ξ ) $$ \mathcal{M}\left(\xi \right) $$ induced by the norm. This means that the solution of the model (11) will uniformly converge and is unique.

4.6 Stability of the Fractional Model

In this section, we discuss the stability of the proposed model.

Definition 4.1.A fractional-order model exhibits Ulam-Hyers stability if there exists a constant ϑ ι > 0 $$ {\vartheta}_{\iota }>0 $$ , such that, for every positive ψ $$ \psi $$ and each solution p → ( Υ ) ∈ 𝒯 ⋆ of the inequality

|   C D Υ ϱ p → ( Υ ) − Â ( Υ , p → ( Υ ) ) | ≤ ψ ι , Υ ∈ [ 0 , ℋ ] $$ \mid {}^C{D}_{\mathrm{Y}}^{\varrho}\overrightarrow{\mathbf{p}}\left(\mathrm{Y}\right)-\hat{A}\left(\mathrm{Y},\overrightarrow{\mathbf{p}}\left(\mathrm{Y}\right)\right)\mid \le {\psi}_{\iota },\mathrm{Y}\in \left[0,\mathscr{H}\right] $$ ()
There exists yet another solution q → ( Υ ) ∈ 𝒯 ⋆ of the fractional model with the inequality
| p → ( Υ ) − q → ( Υ ) | ≤ ϑ ι ψ ι , Υ ∈ [ 0 , ℋ ] $$ \mid \overrightarrow{\mathbf{p}}\left(\mathrm{Y}\right)-\overrightarrow{\mathbf{q}}\left(\mathrm{Y}\right)\mid \le {\vartheta}_{\iota }{\psi}_{\iota },\mathrm{Y}\in \left[0,\mathscr{H}\right] $$ ()
where
p → ( Υ ) = S h ⋆ ( Υ ) , E h ⋆ ( Υ ) , A h ⋆ ( Υ ) , U h ⋆ ( Υ ) , I h a ⋆ ( Υ ) , I h c ⋆ ( Υ ) , T h ⋆ ( Υ ) , R h ⋆ ( Υ ) , L ⋆ ( Υ ) , S m ⋆ ( Υ ) , E m ⋆ ( Υ ) , I m ⋆ ( Υ ) $$ {\displaystyle \begin{array}{ll}\hfill \overrightarrow{\mathbf{p}}\left(\mathrm{Y}\right)& =\left({S}_h^{\star}\left(\mathrm{Y}\right),{E}_h^{\star}\left(\mathrm{Y}\right),{A}_h^{\star}\left(\mathrm{Y}\right),{U}_h^{\star}\left(\mathrm{Y}\right),{I}_{ha}^{\star}\left(\mathrm{Y}\right),{I}_{hc}^{\star}\left(\mathrm{Y}\right),\right.\\ {}\hfill & \kern1em \left.{T}_h^{\star}\left(\mathrm{Y}\right),{R}_h^{\star}\left(\mathrm{Y}\right),{L}^{\star}\left(\mathrm{Y}\right),{S}_m^{\star}\left(\mathrm{Y}\right),{E}_m^{\star}\left(\mathrm{Y}\right),{I}_m^{\star}\left(\mathrm{Y}\right)\right)\end{array}} $$
and
q → ( Υ ) = S h ( Υ ) , E h ( Υ ) ) , A h ( Υ ) , U h ( Υ ) , I h a ( Υ ) , I h c ( Υ ) , T h ( Υ ) , R h ( Υ ) , L ( Υ ) , S m ( Υ ) , E m ( Υ ) , I m ( Υ ) $$ {\displaystyle \begin{array}{ll}\hfill \overrightarrow{\mathbf{q}}\left(\mathrm{Y}\right)& =\left({S}_h\left(\mathrm{Y}\right),{E}_h\left(\mathrm{Y}\right)\Big),{A}_h\left(\mathrm{Y}\right),{U}_h\left(\mathrm{Y}\right),{I}_{ha}\left(\mathrm{Y}\right),{I}_{hc}\left(\mathrm{Y}\right),{T}_h\left(\mathrm{Y}\right),\right.\\ {}\hfill & \kern1em \left.{R}_h\left(\mathrm{Y}\right),L\left(\mathrm{Y}\right),{S}_m\left(\mathrm{Y}\right),{E}_m\left(\mathrm{Y}\right),{I}_m\left(\mathrm{Y}\right)\right)\end{array}} $$

Remark 4.1.The solution p → ( Υ ) ∈ 𝒯 ⋆ satisfies the property (52) whenever there is a positive function φ ι ( Υ ) $$ {\varphi}_{\iota}\left(\mathrm{Y}\right) $$ that satisfies the conditions

  • | φ ι ( Υ ) | < ψ ι $$ \mid {\varphi}_{\iota}\left(\mathrm{Y}\right)\mid <{\psi}_{\iota } $$ ,
  • |   C D Υ ϱ p → ( Υ ) = Â ( Υ , p → ( Υ ) ) | + φ ι ( Υ ) $$ \mid {}^C{D}_{\mathrm{Y}}^{\varrho}\overrightarrow{\mathbf{p}}\left(\mathrm{Y}\right)=\hat{A}\left(\mathrm{Y},\overrightarrow{\mathbf{p}}\left(\mathrm{Y}\right)\right)\mid +{\varphi}_{\iota}\left(\mathrm{Y}\right) $$ .

Definition 4.2.The Caputo fractional model exhibits Ulam-Hyers-Rassias stability subject to the function ζ ι ( Υ ) ∈ ℝ + $$ {\zeta}_{\iota}\left(\mathrm{Y}\right)\in {\mathbb{R}}_{+} $$ whenever there is a constant ϑ ζ ι > 0 $$ {\vartheta}_{\zeta_{\iota }}>0 $$ such that, for every positive ψ $$ \psi $$ and for each solution p → ( Υ ) ∈ 𝒯 ⋆ of the inequality

|   C D Υ ϱ p → ( Υ ) − Â ( Υ , p → ( Υ ) ) | ≤ ψ ι ζ ι ( Υ ) , Υ ∈ [ 0 , ℋ ] $$ \mid {}^C{D}_{\mathrm{Y}}^{\varrho}\overrightarrow{\mathbf{p}}\left(\mathrm{Y}\right)-\hat{A}\left(\mathrm{Y},\overrightarrow{\mathbf{p}}\left(\mathrm{Y}\right)\right)\mid \le {\psi}_{\iota }{\zeta}_{\iota}\left(\mathrm{Y}\right),\mathrm{Y}\in \left[0,\mathscr{H}\right] $$ ()
there exist yet another solution q → ( Υ ) ∈ 𝒯 ⋆ of the model with the inequality
| p → ( Υ ) − q → ( Υ ) | ≤ ϑ ζ ι ψ ι ζ ι ( Υ ) , Υ ∈ [ 0 , ℋ ] $$ \mid \overrightarrow{\mathbf{p}}\left(\mathrm{Y}\right)-\overrightarrow{\mathbf{q}}\left(\mathrm{Y}\right)\mid \le {\vartheta}_{\zeta_{\iota }}{\psi}_{\iota }{\zeta}_{\iota}\left(\mathrm{Y}\right),\mathrm{Y}\in \left[0,\mathscr{H}\right] $$ ()

Remark 4.2.The solution p → ( Υ ) ∈ 𝒯 ⋆ satisfies the property (52) whenever there is a positive function φ ι ( Υ ) $$ {\varphi}_{\iota}\left(\mathrm{Y}\right) $$ that satisfies the conditions

  • | φ ι ( Υ ) | < ψ ι ζ ι ( Υ ) $$ \mid {\varphi}_{\iota}\left(\mathrm{Y}\right)\mid <{\psi}_{\iota }{\zeta}_{\iota}\left(\mathrm{Y}\right) $$ ,
  • |   C D Υ ϱ p → ( Υ ) = Â ( Υ , p → ( Υ ) ) | + φ ι ( Υ ) $$ \mid {}^C{D}_{\mathrm{Y}}^{\varrho}\overrightarrow{\mathbf{p}}\left(\mathrm{Y}\right)=\hat{A}\left(\mathrm{Y},\overrightarrow{\mathbf{p}}\left(\mathrm{Y}\right)\right)\mid +{\varphi}_{\iota}\left(\mathrm{Y}\right) $$ .

Theorem 4.4.The Caputo fractional model shows the Ulam-Hyers stability defined in [ 0 , ℋ ] $$ \left[0,\mathscr{H}\right] $$ if and only if the function  : [ 0 , ℋ ] × 𝒯 ⋆ → ℝ is continuous and satisfies the property

| Â ( Υ , q → ( Υ ) ) − Â ( Υ , q → ′ ( Υ ) ) | ≤ 𝒞 | q → − q → ′ | ,
where 𝒞 > 0 , for all Υ ∈ [ 0 , ℋ ] $$ \mathrm{Y}\in \left[0,\mathscr{H}\right] $$ and q → ( Υ ) , q → ′ ( Υ ) ∈ 𝒯 ⋆ with 𝒞 ℒ ϱ Γ ( ϱ ) + 1 < 1 .

Proof.Consider the solution p → ( Υ ) ∈ 𝒯 ⋆ and the constant ψ ι > 0 $$ {\psi}_{\iota }>0 $$ satisfying the inequality

|   C D Υ ϱ p → ( Υ ) − Â ( Υ , p → ( Υ ) ) | ≤ ψ ι , Υ ∈ [ 0 , ℋ ] $$ \mid {}^C{D}_{\mathrm{Y}}^{\varrho}\overrightarrow{\mathbf{p}}\left(\mathrm{Y}\right)-\hat{A}\left(\mathrm{Y},\overrightarrow{\mathbf{p}}\left(\mathrm{Y}\right)\right)\mid \le {\psi}_{\iota },\mathrm{Y}\in \left[0,\mathscr{H}\right] $$ ()

From the Remark 4.1, it is evident that p → ( Υ ) ∈ 𝒯 ⋆ is a solution that satisfies the above inequality if there is a positive map φ ι ( Υ ) $$ {\varphi}_{\iota}\left(\mathrm{Y}\right) $$ for which | φ ι ( Υ ) | < ψ ι $$ \mid {\varphi}_{\iota}\left(\mathrm{Y}\right)\mid <{\psi}_{\iota } $$ and |   C D Υ ϱ p → ( Υ ) = Â ( Υ , p → ( Υ ) ) | + φ ι ( Υ ) $$ \mid {}^C{D}_{\mathrm{Y}}^{\varrho}\overrightarrow{\mathbf{p}}\left(\mathrm{Y}\right)=\hat{A}\left(\mathrm{Y},\overrightarrow{\mathbf{p}}\left(\mathrm{Y}\right)\right)\mid +{\varphi}_{\iota}\left(\mathrm{Y}\right) $$ .

Using the Caputo integration, we transform the differential into

p → ( Υ ) − p → 0 ( Υ ) = ( Γ ( ϱ ) ) − 1 ∫ 0 Υ ψ ι ( υ ) ( Υ − υ ) 1 − ϱ d υ + ∫ 0 Υ Â ( Υ , p → ( Υ ) ) ( Υ − υ ) 1 − ϱ d υ $$ {\displaystyle \begin{array}{cc}\hfill & \kern1em \overrightarrow{\mathbf{p}}\left(\mathrm{Y}\right)-{\overrightarrow{\mathbf{p}}}_0\left(\mathrm{Y}\right)\hfill \\ {}\hfill & \kern1em ={\left(\Gamma \left(\varrho \right)\right)}^{-1}\left({\int}_0^{\mathrm{Y}}\frac{\psi_{\iota}\left(\upsilon \right)}{{\left(\mathrm{Y}-\upsilon \right)}^{1-\varrho }} d\upsilon +{\int}_0^{\mathrm{Y}}\frac{\hat{A}\left(\mathrm{Y},\overrightarrow{\mathbf{p}}\left(\mathrm{Y}\right)\right)}{{\left(\mathrm{Y}-\upsilon \right)}^{1-\varrho }} d\upsilon \right)\hfill \end{array}} $$ ()
Since there exist a distinct solution q → ( Υ ) ∈ 𝒯 ⋆ of the model, it implies that
q → ( Υ ) − q → 0 ( Υ ) = ( Γ ( ϱ ) ) − 1 ∫ 0 Υ Â ( Υ , p → ( Υ ) ) ( Υ − υ ) 1 − ϱ d υ $$ \overrightarrow{\mathbf{q}}\left(\mathrm{Y}\right)-{\overrightarrow{\mathbf{q}}}_0\left(\mathrm{Y}\right)={\left(\Gamma \left(\varrho \right)\right)}^{-1}{\int}_0^{\mathrm{Y}}\frac{\hat{A}\left(\mathrm{Y},\overrightarrow{\mathbf{p}}\left(\mathrm{Y}\right)\right)}{{\left(\mathrm{Y}-\upsilon \right)}^{1-\varrho }} d\upsilon $$ ()
and
| q → ( Υ ) − p → ( Υ ) | ≤ ( Γ ( ϱ ) ) − 1 ∫ 0 Υ | Â ( Υ , p → ( Υ ) ) − Â ( Υ , q → ( Υ ) ) | ( Υ − υ ) 1 − ϱ d υ + ∫ 0 Υ | φ ι ( υ ) | ( Υ − υ ) 1 − ϱ d υ ≤ 𝒞 | q → ( Υ ) − p → ( Υ ) | ℒ ϱ Γ ( ϱ ) + 1 + ℒ ϱ Γ ( ϱ ) + 1 φ ι ()
The norm of (48) becomes
| | | q → ( Υ ) − p → ( Υ ) | | ≤ ψ ι ℒ ϱ Γ ( ϱ ) + 1 1 − 𝒞 ℒ ϱ Γ ( ϱ ) + 1 ()
We note that
ℒ ϱ Γ ( ϱ ) + 1 1 − 𝒞 ℒ ϱ Γ ( ϱ ) + 1
is a constant, which is equal to φ ι $$ {\varphi}_{\iota } $$ , and (49) becomes
| | q → ( Υ ) − p → ( Υ ) | | ≤ φ ι ϑ ι , φ ι , ϑ ι > 0 $$ \left\Vert \overrightarrow{\mathbf{q}}\left(\mathrm{Y}\right)-\overrightarrow{\mathbf{p}}\left(\mathrm{Y}\right)\right\Vert \le {\varphi}_{\iota }{\vartheta}_{\iota },{\varphi}_{\iota },{\vartheta}_{\iota }>0 $$ ()
which is equivalent to the inequality in Equation (52), and the fractional disease model is Ulam-Hyers stable under any condition.

Theorem 4.5.The model exhibits Ulam-Hyers-Rassias stability defined on [ 0 , ℋ ] $$ \left[0,\mathscr{H}\right] $$ whenever there is a continuous map  : [ 0 , ℋ ] × 𝒯 ⋆ → ℝ and an increasing function ζ ι ( Υ ) ∈ ℝ + $$ {\zeta}_{\iota}\left(\mathrm{Y}\right)\in {\mathbb{R}}_{+} $$ and a distinct positive function Θ ζ ι ( Υ ) $$ {\Theta}_{\zeta_{\iota }}\left(\mathrm{Y}\right) $$ which satisfies the condition

| Â ( Υ , q → ( Υ ) ) | < Θ ζ ι ζ ι | | q → ( Υ ) | | , q → ( Υ ) ∈ 𝒯 ⋆
and
  C D Υ ϱ ζ ι ( Υ ) ≤ Θ ζ ι ζ ι ( Υ ) $$ {}^C{D}_{\mathrm{Y}}^{\varrho }{\zeta}_{\iota}\left(\mathrm{Y}\right)\le {\Theta}_{\zeta_{\iota }}{\zeta}_{\iota}\left(\mathrm{Y}\right) $$ ()

Proof.Consider the solution p → ( Υ ) ∈ 𝒯 ⋆ and the constant ψ ι > 0 $$ {\psi}_{\iota }>0 $$ satisfying the inequality

|   C D Υ ϱ p → ( Υ ) − Â ( Υ , p → ( Υ ) ) | ≤ ψ ι ζ ι ( Υ ) , Υ ∈ [ 0 , ℋ ] $$ \mid {}^C{D}_{\mathrm{Y}}^{\varrho}\overrightarrow{\mathbf{p}}\left(\mathrm{Y}\right)-\hat{A}\left(\mathrm{Y},\overrightarrow{\mathbf{p}}\left(\mathrm{Y}\right)\right)\mid \le {\psi}_{\iota }{\zeta}_{\iota}\left(\mathrm{Y}\right),\mathrm{Y}\in \left[0,\mathscr{H}\right] $$ ()
From the Remark 4.2, it is noticed that p → ( Υ ) ∈ 𝒯 ⋆ is a solution that satisfies the above inequality if there is a positive map φ ι ( Υ ) $$ {\varphi}_{\iota}\left(\mathrm{Y}\right) $$ for which | φ ι ( Υ ) | < ψ ι ζ ι ( Υ ) $$ \mid {\varphi}_{\iota}\left(\mathrm{Y}\right)\mid <{\psi}_{\iota }{\zeta}_{\iota}\left(\mathrm{Y}\right) $$ and |   C D Υ ϱ p → ( Υ ) = Â ( Υ , p → ( Υ ) ) | + φ ι ( Υ ) $$ \mid {}^C{D}_{\mathrm{Y}}^{\varrho}\overrightarrow{\mathbf{p}}\left(\mathrm{Y}\right)=\hat{A}\left(\mathrm{Y},\overrightarrow{\mathbf{p}}\left(\mathrm{Y}\right)\right)\mid +{\varphi}_{\iota}\left(\mathrm{Y}\right) $$ . With the aid of the Caputo integral, we transform the differential into
p → ( Υ ) − p → 0 ( Υ ) = ( Γ ( ϱ ) ) − 1 ∫ 0 Υ ψ ι ( υ ) ( Υ − υ ) 1 − ϱ d υ + ∫ 0 Υ Â ( Υ , p → ( Υ ) ) ( Υ − υ ) 1 − ϱ d υ $$ {\displaystyle \begin{array}{cc}\hfill & \kern1em \overrightarrow{\mathbf{p}}\left(\mathrm{Y}\right)-{\overrightarrow{\mathbf{p}}}_0\left(\mathrm{Y}\right)\hfill \\ {}\hfill & \kern1em ={\left(\Gamma \left(\varrho \right)\right)}^{-1}\left({\int}_0^{\mathrm{Y}}\frac{\psi_{\iota}\left(\upsilon \right)}{{\left(\mathrm{Y}-\upsilon \right)}^{1-\varrho }} d\upsilon +{\int}_0^{\mathrm{Y}}\frac{\hat{A}\left(\mathrm{Y},\overrightarrow{\mathbf{p}}\left(\mathrm{Y}\right)\right)}{{\left(\mathrm{Y}-\upsilon \right)}^{1-\varrho }} d\upsilon \right)\hfill \end{array}} $$ ()
Since there exist a distinct solution q → ( Υ ) ∈ 𝒯 ⋆ of the model, it implies that
q → ( Υ ) − q → 0 ( Υ ) = ( Γ ( ϱ ) ) − 1 ∫ 0 Υ Â ( Υ , p → ( Υ ) ) ( Υ − υ ) 1 − ϱ d υ $$ \overrightarrow{\mathbf{q}}\left(\mathrm{Y}\right)-{\overrightarrow{\mathbf{q}}}_0\left(\mathrm{Y}\right)={\left(\Gamma \left(\varrho \right)\right)}^{-1}{\int}_0^{\mathrm{Y}}\frac{\hat{A}\left(\mathrm{Y},\overrightarrow{\mathbf{p}}\left(\mathrm{Y}\right)\right)}{{\left(\mathrm{Y}-\upsilon \right)}^{1-\varrho }} d\upsilon $$ ()
and
| q → ( Υ ) − p → ( Υ ) | ≤ ( Γ ( ϱ ) ) − 1 ∫ 0 Υ | Â ( Υ , p → ( Υ ) ) − Â ( Υ , q → ( Υ ) ) | ( Υ − υ ) 1 − ϱ d υ + ∫ 0 Υ | φ ι ( υ ) | ( Υ − υ ) 1 − ϱ d υ ≤ 𝒞 | q → ( Υ ) − p → ( Υ ) | ℒ ϱ Γ ( ϱ ) + 1 + ℒ ϱ Γ ( ϱ ) + 1 φ ι Θ ζ ι ζ ι ()
Taking the norm of (55) gives
| | | q → ( Υ ) − p → ( Υ ) | | ≤ Θ ζ ι ζ ι ψ ι ℒ ϱ Γ ( ϱ ) + 1 1 − 𝒞 ℒ ϱ Γ ( ϱ ) + 1 ()
We note that
Θ ζ ι ℒ ϱ Γ ( ϱ ) + 1 1 − 𝒞 ℒ ϱ Γ ( ϱ ) + 1
is a constant, which is equal to ϑ ζ ι $$ {\vartheta}_{\zeta_{\iota }} $$ , and (56) becomes
| | q → ( Υ ) − p → ( Υ ) | | ≤ φ ι ϑ ζ ι ζ ι ( Υ ) , φ ι , ϑ ζ ι , ζ ι ( Υ ) > 0 $$ \left\Vert \overrightarrow{\mathbf{q}}\left(\mathrm{Y}\right)-\overrightarrow{\mathbf{p}}\left(\mathrm{Y}\right)\right\Vert \le {\varphi}_{\iota }{\vartheta}_{\zeta_{\iota }}{\zeta}_{\iota}\left(\mathrm{Y}\right),{\varphi}_{\iota },{\vartheta}_{\zeta_{\iota }},{\zeta}_{\iota}\left(\mathrm{Y}\right)>0 $$ ()
which is equivalent to the inequality in Equation (44), and the fractional disease model is Ulam-Hyers-Rassias stable under any given condition.

5 LF Model Parameter Estimation

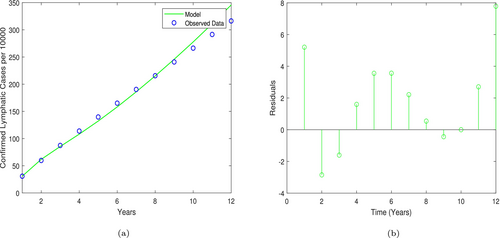
In this section, the parameter values of the LF model are subjected to data to obtain actual parameter values from LF-infected cases. We further describe the sensitivity analysis that identifies how the model's parameters affect the epidemic dynamics of LF. These are crucial aspects of modeling diseases to help give policymakers parameters to control and prevent the disease's persistence in a population.

5.1 Parameter Estimation

Parameter estimation is a critical criterion in modeling infectious diseases, as it makes the mathematical model realistic and applicable to real-world cases [27]. Practically, the parameter estimation technique enhances the understanding of the transmission dynamics of a particular disease and suggests the best fit that shows how close the observed data of a parameter is to its actual value [37]. The parameter estimation process involves the selection of the values of the essential model parameters that best estimate the observed data, such as the number of infections over time. In this section, we perform parameter estimation to realistically assess the actual values of the model's parameters subject to LF-related cases [38]. This study employs the least squares fitting technique, which has been widely reported to be versatile (applicable to both linear and nonlinear models) and exhibits low computational time. It also minimizes the sum of squared differences between the observed data and the model's predictions. So to obtain the parameter values for model (11) using the least squares technique, we use the model to initial guesses and pre-estimated parameter values, such as α $$ \alpha $$ , whose solution passes through all the data points and subsequently minimizes the sum of squared differences between the observed data α i $$ {\alpha}_i $$ and the model solution 𝒢 ( i , α ) , as given by [39].
𝒢 ( α ) = ∑ i = 1 n ( α i − 𝒢 ( i , α ) ) 2
The study adopted LF-infected data to fit the model parameters covering LF-infected cases in Ghana from 2010 to 2021, which were sourced from the Our World in Data website [40]. The initial conditions for the fitting are given as S h ( 0 ) = 1047 , E h ( 0 ) = 45 , A h ( 0 ) = 94 , U h ( 0 ) = 36 , I h a ( 0 ) = 1191 , T h ( 0 ) = 0 , R h ( 0 ) = 63 , L ( 0 ) = 5000 , S m ( 0 ) = 13 , 590 , E m ( 0 ) = 8200 $$ {S}_h(0)=1047,{E}_h(0)=45,{A}_h(0)=94,{U}_h(0)=36,{I}_{ha}(0)=1191,{T}_h(0)=0,{R}_h(0)=63,L(0)=5000,{S}_m(0)=13,590,{E}_m(0)=8200 $$ and I m ( 0 ) = 59 $$ {I}_m(0)=59 $$ where the total human population is defined as N h = S h ( 0 ) + E h ( 0 ) + A h ( 0 ) + U h ( 0 ) + I h a ( 0 ) + T h ( 0 ) + R h ( 0 ) $$ {N}_h={S}_h(0)+{E}_h(0)+{A}_h(0)+{U}_h(0)+{I}_{ha}(0)+{T}_h(0)+{R}_h(0) $$ and the total mosquito population is N m = S m ( 0 ) + E m ( 0 ) + I m ( 0 ) $$ {N}_m={S}_m(0)+{E}_m(0)+{I}_m(0) $$ with the immature mosquito given as L ( 0 ) $$ L(0) $$ . From the parameter fitting graph in Figure 3a, the basic reproduction number for the LF model is obtained as ℛ 0 ϱ = 1 . 5746 $$ {\mathcal{R}}_0^{\varrho }=1.5746 $$ with the fractional order value ϱ = 0 . 99 $$ \varrho =0.99 $$ . In Figure 3b, we observe that there is a randomly distributed normalized mean square error of 𝒢 ( α ) = 0 . 0198 . The fitted parameter values are given in Table 2, along with other assumed parameter values.
Details are in the caption following the image
FIGURE 3
Open in figure viewerPowerPoint
LF dynamics and cases in Ghana. (a) LF human reported cases fit, (b) LF model residual plot.
TABLE 2. Estimated model parameters and their values for ϱ = 0 . 99 $$ \varrho =0.99 $$ .
Parameter Value Source Parameter Value Source
δ 1 $$ {\delta}_1 $$ 0.862 Fitted β 3 $$ {\beta}_3 $$ 0.9588 Fitted
β $$ \beta $$ 0.749 Fitted Λ m $$ {\Lambda}_m $$ 0.00399 Fitted
β 4 $$ {\beta}_4 $$ 0.077 Fitted c $$ c $$ 0.8957 Fitted
τ $$ \tau $$ 0.2926 Fitted K $$ K $$ 5000 Fitted
ϕ $$ \phi $$ 0.1966 Fitted σ $$ \sigma $$ 0.0088 Fitted
η $$ \eta $$ 0.14858 Fitted δ 2 $$ {\delta}_2 $$ 0.99997 Fitted
μ $$ \mu $$ 0.00337 Fitted κ $$ \kappa $$ 0.459 Fitted
Λ h $$ {\Lambda}_h $$ 0.12945 Assumed γ $$ \gamma $$ 0.385 Fitted
α 1 $$ {\alpha}_1 $$ 0.04 Assumed ρ 1 $$ {\rho}_1 $$ 0.85 Fitted
α 2 $$ {\alpha}_2 $$ 0.01 Assumed ρ 2 $$ {\rho}_2 $$ 0.51 Fitted
ω $$ \omega $$ 0.000042529 Assumed β 2 $$ {\beta}_2 $$ 0.35 Fitted
ϵ $$ \epsilon $$ 0.02 Fitted θ $$ \theta $$ 0.003437 Fitted

6 Sensitivity Analysis

In this section, we conduct a thorough sensitivity index analysis to ascertain which model parameters are the most influential in driving the transmission and prevalence of LF disease. This is required as it helps researchers make necessary recommendations to police makers on the specific parameters of the model that, when controlled, can reduce the prevalence of the disease [41]. Therefore, in this study, the normalized forward sensitivity index is employed. To measure the influence of the parameter ⊛ $$ \circledast $$ on the basic reproductive number, the normalized forward sensitivity index is given as:
X ℛ 0 ⊛ = ∂ ℛ 0 ∂ ⊛ × ⊛ ℛ 0 $$ {X}_{{\mathcal{R}}_0}^{\circledast }=\frac{\partial {\mathcal{R}}_0}{\partial \circledast}\times \frac{\circledast }{{\mathcal{R}}_0} $$

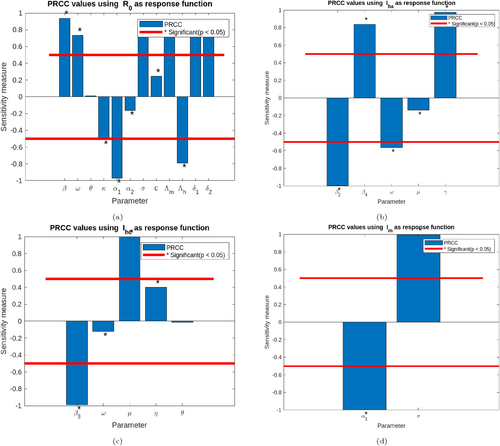
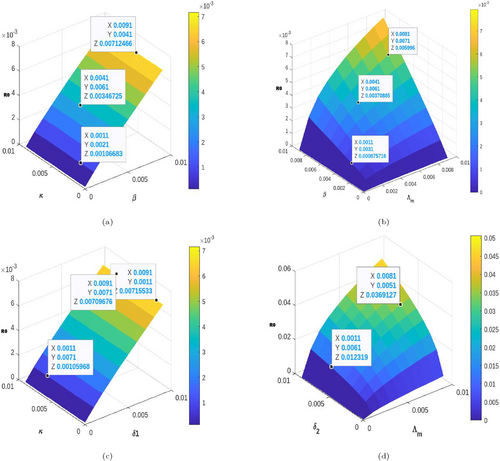
Table 3 below presents the normalized forward sensitivity indices. Parameters with a negative real value are classified as having an inverse relationship with the reproductive number; that is, a decline in the parameter's real value leads to a growth in the disease prevalence. In contrast, those with positive index values directly correlate with the reproduction number. Thus, decreasing the real value of that parameter mitigates the prevalence of the disease in the population. In addition, the study performed a further local sensitivity analysis using 3D graphs as shown in Figures 5 and 6. The study further employs a global stability analysis utilizing PRCC plots with 10,000 sampling strategies to measure the global dynamics of the model parameters in a given neighborhood.

TABLE 3. Sensitivity indices of the parameters.
Parameter Sign Value Parameter Sign Value
δ 1 $$ {\delta}_1 $$ + 0.5 β 3 $$ {\beta}_3 $$ — 0.025126
β $$ \beta $$ + 1 Λ m $$ {\Lambda}_m $$ + 0.566352
β 4 $$ {\beta}_4 $$ — 0.084263 c $$ c $$ + 0.092826
τ $$ \tau $$ + 0.084321 K $$ K $$ + 0.5
ϕ $$ \phi $$ — 0.07846 σ $$ \sigma $$ + 0.409836
η $$ \eta $$ — 0.324670 δ 2 $$ {\delta}_2 $$ + 0.5
μ $$ \mu $$ — 0.009091 κ $$ \kappa $$ — 0.236832
Λ h $$ {\Lambda}_h $$ — 0.5 γ $$ \gamma $$ + 0.173751
α 1 $$ {\alpha}_1 $$ — 1 ρ 1 $$ {\rho}_1 $$ 0.0
α 2 $$ {\alpha}_2 $$ — 0.066352 ρ 2 $$ {\rho}_2 $$ + 0.236812
ω $$ \omega $$ + 0.499744 β 2 $$ {\beta}_2 $$ — 0.191773
ϵ $$ \epsilon $$ — 0.044323 θ $$ \theta $$ — 0.00009

From Figure 4, we perform a global trend analysis of the impact of some parameters on the spread of LF in the population with 10,000 samples with different response functions. Taking the basic reproductive number ℛ 0 $$ {\mathcal{R}}_0 $$ as the response function given in Figure 4a, it was observed that the parameters, thus the rate of awareness of the disease κ $$ \kappa $$ , the natural mortality rate of mature mosquitoes α 1 $$ {\alpha}_1 $$ , the natural mortality rate of immature mosquitoes α 2 $$ {\alpha}_2 $$ and the human recruitment rate Λ h $$ {\Lambda}_h $$ are inversely related to the spread of LF disease in the population. Public health workers are encouraged to improve these parameters as their respective increase causes a decline in the prevalence of LF disease. Despite this, parameters, such as mosquito bite rate β $$ \beta $$ , transmission rate from exposed mosquitoes to infected mosquitoes σ $$ \sigma $$ , and others, directly correlate with the spread of the disease in the population. This implies that such parameters cause the disease to persist as their occurrence increases. Furthermore, in Figure 4b, where the acute infected human is the response function, it was observed that as more acute infected individuals receive treatment β 2 $$ {\beta}_2 $$ , the acute infection decreases, while as many exposed individuals transition to the acute infected class β 4 $$ {\beta}_4 $$ , infection persists in the population. Again, in Figure 4c, we observed that chronic infection persists as the untreated infection progresses to that compartment, but declines as they are given treatment. This implies that interaction in the human population needs to be controlled, especially among exposed and infected humans. In addition, effective treatment and mass drug administration effectively mitigate the spread of LF disease in the population. Furthermore, in Figure 4d, the interaction between exposed and infected mosquitoes contributes significantly to the prevalence of LF in the community. At the same time, the spread declines when more mature mosquitoes die naturally. In addition, the 3D graphs in Figure 5a,c exhibit the effect of individuals becoming aware of the disease on its prevalence in the population. We see that infection declines as their awareness has made them cautious in their interactions and in keeping the environment clean, so LF infection declines. On the other hand, when they do not adhere to the education on the LF disease and are bitten by mosquitoes or interact with the infected mosquitoes, the disease grows. In addition, it was observed that as more immature mosquitoes become mature mosquitoes, the biting rate increases, and the probability that interaction with an infected human can cause infection, in mosquitoes, the LF disease persists significantly, see Figure 5b,d. Similar observations were made in Figure 6.

Details are in the caption following the image
FIGURE 4
Open in figure viewerPowerPoint
The PRCC plot of some parameters and the ℛ 0 $$ {\mathcal{R}}_0 $$ .
Details are in the caption following the image
FIGURE 5
Open in figure viewerPowerPoint
A 3D trend analysis of ℛ 0 $$ {\mathcal{R}}_0 $$ against δ 1 , β , Λ m , κ , δ 2 $$ {\delta}_1,\beta, {\Lambda}_m,\kappa, {\delta}_2 $$ .
Details are in the caption following the image
FIGURE 6
Open in figure viewerPowerPoint
A 3D trend analysis of ℛ 0 $$ {\mathcal{R}}_0 $$ against δ 2 , β , Λ m , ρ 2 $$ {\delta}_2,\beta, {\Lambda}_m,{\rho}_2 $$ .

7 Numerical Simulations and Discussions

In modeling diseases, numerical simulations are always performed to help analyze, understand, and make future predictions concerning the behavior of complex disease systems that may sometimes not possess analytical solutions. Again, numerical simulations help the public health policymaker to comprehend and identify the most influential parameters that, when effectively controlled, may mitigate the persistence of a disease in the population. In this section, the study employs an explicit Runge-Kutta method, which uses the 5th-order method to obtain the model's solutions and further estimates the errors accumulated by a 4th-order method. This numerical approach is very adaptive to the step size, and it can adjust the step size based on the local error estimate to validate accuracy. It also works best for non-stiff ordinary differential equations, ensuring accuracy and efficiency [27, 42, 43]. To simulate the numerical plots for the LF Caputo fractional model, we used the parameter values in Table 2 in addition to the initial conditions as stated under the parameter estimation section. In Figures 7-9, the study seeks to elaborate explicitly the memory patterns on the dynamics of LF disease in the population. A striking pattern observed is the constant reduction in the basic reproduction number's value as the fractional order declines, and this could only be measured accurately by non-integer operators. From Figure 7a, it was observed that the number of individuals susceptible to LF declines drastically for some time but increases after a year. This pattern is observed throughout the plot for 20 years. This observation is a result of the fact that, as the population is given education on the dynamics of the LF disease, they become cautious for a period, and probably become less careful when the education on the disease is minimized, as they may think that the LF disease is no longer a concern. In Figure 7c, as similar dynamics is observed as the rate at which individuals become exposed to LF sharply declines, but after a shorter period, increases for a longer time. Consequently, we observe that a number of the individuals become infected but show no symptoms over a longer time, as seen in Figure 7b, and this results in many of the individuals staying with the disease, not attending the health facilities to receive treatment, see Figure 7d. These dynamics clearly highlight the role played by effectively educating individuals concerning how the disease spreads. It was further observed in Figure 8a,b that there occurs a smooth increase in the number of individuals showing acute symptoms of the LF disease, whereas individuals with chronic symptoms decline for some time and rise slowly, then stabilize throughout the simulation time. Consequently, as seen in Figure 8c, as the infected individuals in the population start showing symptoms for some time, many seek medical assistance, leading to a sharp increase in the treatment class for some time and then declines and subsequently rises again. This observation leads to an increase in the recovery class of the model as observed in Figure 8d, where recovery from the LF disease experiences a sporadic increase throughout the simulation time. In Figure 9a,b, we observe a sharp decrease in immature and mature susceptible mosquitoes simultaneously, and this may be due to several vector dynamics and environmental control-related factors. This result may also come from increased LF-induced mortality rates in the mosquito classes. Indeed, Figure 9c partially responds to the reason behind the decline as we observe that exposure to LF-infection in the mosquito compartments increases sporadically and subsequently leads to more mosquitoes becoming infected with LF disease, see Figure 9d. This also indicates a high prevalence of human infection, vector-human contact, and a weak vector control strategy. These results guide public health policymakers in identifying the exact patterns of a lymphatic filariasis outbreak and putting in place the necessary control mechanisms, such as effective use of insecticide, larviciding, and environmental management. Also, whenever there is a low use of mass drug administration and increased extrinsic incubation success, there could be some unavoidable factors leading to these observations.

Details are in the caption following the image
FIGURE 7
Open in figure viewerPowerPoint
Dynamics of S h ( t ) $$ {S}_h(t) $$ , A h ( t ) , E h ( t ) $$ {A}_h(t),{E}_h(t) $$ , and U h ( t ) $$ {U}_h(t) $$ compartments, using different values of fractional order ϱ $$ \varrho $$ compared to integer order ϱ = 1 $$ \varrho =1 $$ . (a) S h $$ {S}_h $$ dynamics, (b) A L $$ {A}_L $$ dynamics, (c) E h $$ {E}_h $$ dynamics, and (d) I h a $$ {I}_{ha} $$ dynamics.
Details are in the caption following the image
FIGURE 8
Open in figure viewerPowerPoint
Dynamics of I h a ( t ) $$ {I}_{ha}(t) $$ , I h c ( t ) , T h ( t ) $$ {I}_{hc}(t),{T}_h(t) $$ , and R h ( t ) $$ {R}_h(t) $$ compartments, using different values of fractional order ϱ $$ \varrho $$ compared to integer order ϱ = 1 $$ \varrho =1 $$ . (a) I h a $$ {I}_{ha} $$ dynamics, (b) I h c $$ {I}_{hc} $$ dynamics, (c) T h $$ {T}_h $$ dynamics, and (d) R h $$ {R}_h $$ dynamics.
Details are in the caption following the image
FIGURE 9
Open in figure viewerPowerPoint
Dynamics of L ( t ) $$ L(t) $$ , S m ( t ) , E m ( t ) $$ {S}_m(t),{E}_m(t) $$ , and I m ( t ) $$ {I}_m(t) $$ compartments, using different values of fractional order ϱ $$ \varrho $$ compared to integer order ϱ = 1 $$ \varrho =1 $$ . (a) I h a $$ {I}_{ha} $$ dynamics, (b) S m $$ {S}_m $$ dynamics, (c) E m $$ {E}_m $$ dynamics, and (d) I m $$ {I}_m $$ dynamics.

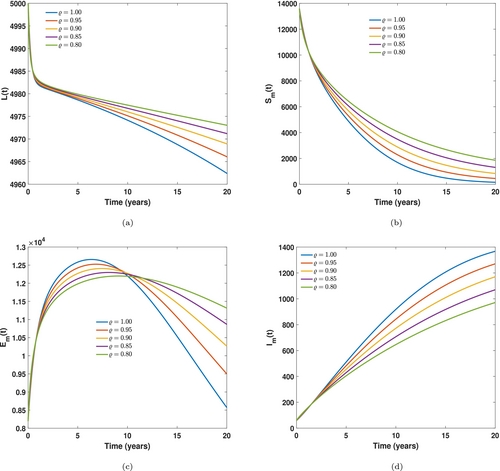
The study further interrogated the influence of some of the model's parameters on the spread of LF in the population. With a memory order of ϱ = 0 . 95 $$ \varrho =0.95 $$ , we performed some simulated sensitivity analysis graphs as seen in Figures 10 through 13. Specifically, in Figure 10, the impact of the natural mortality rate in mature mosquitoes α 1 $$ {\alpha}_1 $$ was significantly observed. We realized that increasing the natural mortality rate of mature mosquitoes α 1 $$ {\alpha}_1 $$ results in a decrease in the number of susceptible mosquitoes, leading to some being exposed to LF disease as seen in Figure 10a,b, respectively. This observation in the mosquito population leads to a decline in the human exposed and recovered compartment because a few human infections are recorded whenever a high vector mortality is recorded. This implies that public health officials are encouraged to promote or enhance environmentally friendly approaches like biological control, genetic and microbial strategies to increase the natural mortality rate of mosquitoes, which helps mitigate the spread of LF in the population.

Details are in the caption following the image
FIGURE 10
Open in figure viewerPowerPoint
Dynamics of S m ( t ) $$ {S}_m(t) $$ , I m ( t ) , E h ( t ) $$ {I}_m(t),{E}_h(t) $$ , and R h ( t ) $$ {R}_h(t) $$ compartments, varying the values of α 1 $$ {\alpha}_1 $$ . (a) S m $$ {S}_m $$ dynamics, (b) I m $$ {I}_m $$ dynamics, (c) E h $$ {E}_h $$ dynamics, and (d) R h $$ {R}_h $$ dynamics.

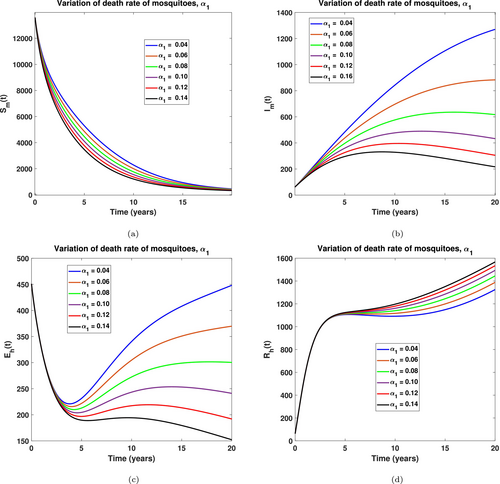
Also, in Figure 11 we examined the effect of the rate at which mosquitoes bite humans β $$ \beta $$ . It was keenly observed in Figure 11a that after a few simulation times, an increase in β $$ \beta $$ leads to a sporadic movement of susceptible human into the exposed class as seen in Figure 11b, and this subsequently leads to a rise in demand for treatment and hence an increased recovered humans, see Figure 11c,d, respectively. This observation is quite expensive as the government must invest more in treatment strategies. Public health officials are therefore encouraged to promote the use of insecticides and enforce clean surroundings by desilting gutters to help mitigate the spread of LF in the population.

Details are in the caption following the image
FIGURE 11
Open in figure viewerPowerPoint
Dynamics of S h ( t ) $$ {S}_h(t) $$ , E h ( t ) , T h ( t ) $$ {E}_h(t),{T}_h(t) $$ , and R h ( t ) $$ {R}_h(t) $$ compartments, varying the values of β $$ \beta $$ . (a) S h $$ {S}_h $$ dynamics, (b) E h $$ {E}_h $$ dynamics, (c) T h $$ {T}_h $$ dynamics, and (d) R h $$ {R}_h $$ dynamics.

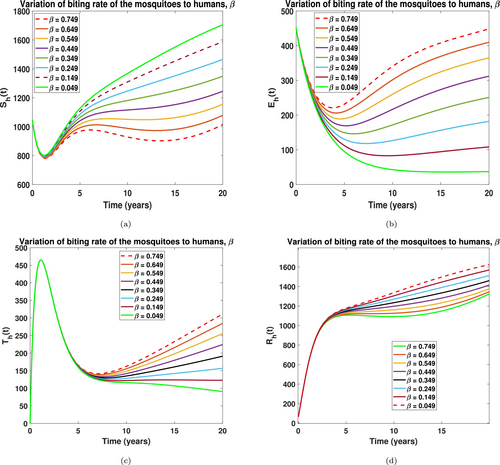
Figure 12 shows that an increase in the maturity rate of immature mosquitoes Λ m $$ {\Lambda}_m $$ causes LF disease to persist in the population. From Figure 12a, we observed that an increase in Λ m $$ {\Lambda}_m $$ causes a rise in the susceptible mosquito compartment and subsequently more LF-infections occur in the mosquito population, see Figure 12b. The effect of this observation is realized as many humans become exposed. Subsequently, it makes LF disease epidemic in the human population, see Figure 12c,d, respectively. Once again, this insists on practicing a clean environment to help impede immature mosquitoes from becoming mature.

Details are in the caption following the image
FIGURE 12
Open in figure viewerPowerPoint
Dynamics of S m ( t ) $$ {S}_m(t) $$ , I m ( t ) , E h ( t ) $$ {I}_m(t),{E}_h(t) $$ , and A h ( t ) $$ {A}_h(t) $$ compartments, varying the values of α 1 $$ {\alpha}_1 $$ . (a) S m $$ {S}_m $$ dynamics, (b) I m $$ {I}_m $$ dynamics, (c) E h $$ {E}_h $$ dynamics, and (d) A h $$ {A}_h $$ dynamics.

Finally, we observed in Figure 13 that the LF disease will persist whenever exposed mosquitoes become infected. This is because they will interact with humans and subsequently infect them. This observation is confirmed by observing the transitions in Figure 13a–d. Generally, the study confirms the WHO recommendations for combating LF disease in the population. Thus, environmental cleanliness, use of insecticides, and mass drug administration effectively mitigate the spread of LF in the population.

Details are in the caption following the image
FIGURE 13
Open in figure viewerPowerPoint
Dynamics of E m ( t ) $$ {E}_m(t) $$ , I m ( t ) , E h ( t ) $$ {I}_m(t),{E}_h(t) $$ , and I h a ( t ) $$ {I}_{ha}(t) $$ compartments, varying the values of σ $$ \sigma $$ . (a) E m $$ {E}_m $$ dynamics, (b) I m $$ {I}_m $$ dynamics, (c) E h $$ {E}_h $$ dynamics, and (d) I m $$ {I}_m $$ dynamics.

8 Conclusion

In this paper, we investigated lymphatic filariasis disease transmission patterns between humans and mosquitoes. The study further examined the memory dynamics observed during and after the outbreak of lymphatic filariasis in a population over a simulated time by using the Caputo fractional operator. We have shown in the studies that the fractional LF disease model has a unique solution given any real time. Also, the fractional LF disease model has positive-valued and bounded solutions for any given real space. By the stability analysis, the model satisfies the Hyers-Ulam and Hyers-Ulam-Rassias stability criteria. The model was examined using real data of LF-infected cases from Ghana between 2010 and 2021. The study observed that the developed model fitted accurately with the available data on the disease. From the parameter estimation, the basic reproduction number was observed to be ℛ 0 = 1 . 5746 $$ {\mathcal{R}}_0=1.5746 $$ and had a fractional order of ϱ = 0 . 99 $$ \varrho =0.99 $$ . For any given model parameter, α $$ \alpha $$ , the distributed normalized mean square error was estimated to be α = 0 . 0198 $$ \alpha =0.0198 $$ . A thorough numerical simulation was performed over time, and it was observed that a change in the memory order had a significant impact on the transmission dynamics of the LF disease. This is justified as the integer order ϱ = 1 $$ \varrho =1 $$ overestimated the number of acute infected humans to be significantly high, but the actual dynamics were measured at varied fractional orders like ϱ = 0 . 80 $$ \varrho =0.80 $$ . The study further showed that an increase in parameters like the biting rate of mosquitoes β $$ \beta $$ , the rate of transmission from exposed to infected mosquitoes σ $$ \sigma $$ , and the natural mortality rate of mature mosquitoes α 1 $$ {\alpha}_1 $$ significantly contribute to the prevalence of the LF disease. These observations indicate that environmental control measures like sterile insect technique (SIT), Wolbachia (procedure applied to reduce the lifespan of infected males and replication), removing stagnant water, and other biological controls are essential to mitigating lymphatic filariasis from the human population. Though the study has elaborated on the memory order dynamics of LF disease and is suitable for future predictions, it did not conduct an optimal control strategy and cost-effectiveness analysis. Future work will focus on an optimal control model for the lymphatic filariasis disease.

Author Contributions

Fredrick A. Wireko: conceptualization; investigation; writing – original draft; validation; methodology; writing – review and editing; software; formal analysis; supervision. Rebecca Awerigiya: conceptualization; investigation; writing – original draft; methodology; writing – review and editing; software; formal analysis; data curation. Isaac K. Adu: writing – original draft; methodology; writing – review and editing; formal analysis. Joshua N. Martey: writing – original draft; methodology; writing – review and editing; formal analysis. Bernard O. Bainson: investigation; writing – original draft; writing – review and editing; formal analysis; supervision. Joshua Kiddy K. Asamoah: writing – original draft; methodology; writing – review and editing; software; formal analysis; validation.

Data Availability Statement

Data sharing is not applicable to this article as no datasets were generated during the current study.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.