2.1 Statistical Models

Trajectory prediction involves capturing patterns in movement data while ensuring privacy protection, especially in sensitive applications such as smart transportation and urban mobility analysis. Various statistical models and privacy-preserving mechanisms have been explored to balance prediction accuracy and data confidentiality [13-15].

One key concept in privacy-preserving learning is the privacy budget ($$$ \varepsilon $$$), a fundamental parameter in differential privacy. The privacy budget controls the trade-off between privacy protection and data utility. A lower $$$ \varepsilon $$$ value results in stronger privacy protection by introducing more noise into the data, but it can also reduce the accuracy of trajectory predictions. Conversely, a higher $$$ \varepsilon $$$ value retains more useful information while weakening privacy guarantees. Striking the right balance is crucial for maintaining both privacy and utility.

This study employs a sliding window model to process dynamic trajectory data effectively. This technique captures recent historical trajectory information within a fixed-size window, ensuring predictions are based on the most relevant past movements. The oldest observations are removed as new data points arrive, allowing real-time adaptation to evolving movement patterns. The sliding window approach is particularly useful when immediate adjustments are necessary, such as traffic flow prediction and anomaly detection.

For measuring trajectory similarity, this study utilizes the bidirectional Hausdorff distance. This metric assesses how closely two trajectory sequences align by computing the maximum of the smallest distances from one set of trajectory points to another in both directions. Unlike conventional distance measures, the bidirectional Hausdorff distance is particularly effective for comparing irregular or non-uniform movement patterns, making it well-suited for trajectory-based analysis.

These statistical models and privacy techniques form the foundation of the CDP-DTP model, which integrates differential privacy within a sliding window framework to enable real-time, privacy-aware trajectory prediction. This approach ensures that sensitive trajectory data can be analyzed securely without compromising prediction performance by leveraging adaptive privacy mechanisms and robust similarity measures.

2.2 Deep Learning Models

Deep learning has played a pivotal role in trajectory prediction, offering powerful modeling capabilities to capture spatial and temporal dependencies in sequential data. Various deep-learning architectures have been explored for trajectory forecasting. Convolutional Neural Networks (CNNs) are deep learning architectures specialized in extracting spatial features through convolution and pooling operations, extensively utilized in image analysis and spatial data processing. Long Short-Term Memory (LSTM) networks are a variant of recurrent neural networks (RNNs) equipped with gating mechanisms, enabling effective learning of long-range temporal dependencies in sequential data. LSTM networks and their variants are widely used due to their ability to process sequential information effectively [16].

Standard LSTM networks have been extensively employed for trajectory prediction as they can capture long-term dependencies in sequential data. However, standard LSTMs struggle with bidirectional context understanding, leading to suboptimal predictions when future trajectory patterns influence current movement trends [17, 18].

Bi-directional LSTM (Bi-LSTM) improves upon standard LSTMs by processing sequence data in both forward and backward directions, capturing past and future dependencies more effectively. This enhancement makes Bi-LSTM more suitable for trajectory forecasting in cases where contextual information from subsequent movements is crucial [19].

LSTM with an Attention Mechanism refines trajectory prediction by dynamically assigning weights to historical trajectory points, allowing the model to focus on the most relevant information at each prediction step. This technique is particularly useful for handling complex and non-uniform trajectory sequences where certain past observations carry more predictive significance [20].

Beyond LSTM-based architectures, Graph Neural Networks (GNNs) and Transformers have recently gained attention in trajectory prediction tasks. Graph-based models effectively represent spatial relationships in trajectory data, making them suitable for road-network-based movement prediction. Originally designed for natural language processing, transformer architectures have demonstrated superior performance in capturing long-range dependencies in sequential data, offering a promising direction for trajectory forecasting [21, 22].

Despite these advancements, deep learning models applied to trajectory prediction often overlook privacy concerns. Existing models assume unrestricted access to trajectory data, making them vulnerable to privacy leaks. The proposed CDP-DTP model integrates differential privacy mechanisms into a sliding window-based deep learning framework, ensuring privacy preservation while maintaining competitive prediction performance. By leveraging privacy-aware deep learning techniques, CDP-DTP effectively addresses the trade-off between privacy and model accuracy, making it a viable solution for real-world trajectory forecasting applications.

2.3 Privacy-Preserving Techniques

Ensuring privacy in machine learning and data publishing has been a critical research challenge, particularly for sensitive datasets like trajectory data. Traditional privacy-preserving techniques, such as differential privacy (DP) and k-anonymity, have been widely applied. Still, recent advances in machine learning have introduced more sophisticated mechanisms, including federated learning (FL) and GAN-based privacy models, which provide stronger privacy guarantees in dynamic environments.

Differential Privacy (DP) is a rigorous mathematical framework designed to limit the capability of adversaries to infer the inclusion or exclusion of an individual's data in a dataset. This protection is achieved by adding controlled random noise to the algorithm outputs. Formally, DP is defined as follows:

Here, the parameter $$$ \varepsilon $$$, known as the privacy budget, quantifies the level of privacy protection. Existing works have applied local DP for decentralized data protection and global DP for centralized model training, demonstrating its effectiveness in structured datasets. However, standard DP methods often degrade data utility, particularly in trajectory-based applications where sequential dependencies are critical.

Federated Learning (FL) provides a decentralized privacy-preserving framework where multiple clients train a global model collaboratively without exposing raw data [23]. While FL significantly reduces privacy risks, it is susceptible to gradient leakage attacks and adversarial inference, requiring enhancements such as differentially private FL (DP-FL) and secure multi-party computation (MPC) to strengthen privacy guarantees. Research has also explored integrating adaptive noise mechanisms in FL to balance privacy and model utility [24, 25].

GAN-Based Privacy Models leverage generative adversarial networks to create synthetic datasets that maintain the statistical properties of real data while preventing direct access to sensitive information. Approaches like DP-GAN and DP-TrajGAN incorporate differential privacy techniques to protect training data, offering a viable alternative to traditional DP methods. However, challenges such as mode collapse and synthetic data fidelity remain open research problems, limiting their deployment in real-world trajectory prediction tasks [26, 27].

Despite these advancements, privacy-preserving techniques tailored for dynamic trajectory data remain underexplored. Standard DP, FL, and GAN-based approaches must be adapted to account for the spatiotemporal correlations inherent in trajectory data. The proposed CDP-DTP model builds upon these methodologies by integrating differential privacy within a sliding window framework, ensuring robust privacy protection while maintaining high prediction accuracy for dynamic trajectory forecasting. By leveraging adaptive privacy mechanisms, the CDP-DTP model effectively addresses the challenges posed by privacy-preserving trajectory prediction, making it a practical and scalable solution for real-world applications.

2.4 Gaps and Challenges

In summary, existing trajectory flow prediction methods, including statistical and deep learning models, face limitations in balancing prediction accuracy with privacy protection. Most approaches fail to fully consider the dynamic nature of trajectory data, which can lead to reduced prediction accuracy in complex and changing environments. Furthermore, privacy-preserving techniques applied to trajectory data are generally limited by high computational costs or trade-offs impacting data utility. These gaps underscore the need for an integrated solution that simultaneously addresses prediction accuracy and privacy protection. To bridge this gap, this paper introduces the Consistent Differential Privacy Dynamic Trajectory Flow Prediction Method, which leverages the CNN-LSTM framework for robust spatiotemporal feature extraction while incorporating consistent differential privacy mechanisms. This approach aims to enhance privacy protection without sacrificing the model's ability to handle complex trajectory data, setting the stage for further innovation in privacy-sensitive trajectory flow prediction.

3.1 Consistent Differential Privacy Dynamic Trajectory Flow Prediction Framework

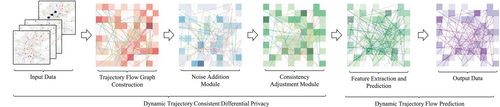
The Consistent Differential Privacy Dynamic Trajectory Flow Prediction method aims to balance trajectory data privacy and prediction accuracy effectively. In this approach, the trajectory flow data undergoes aggregation and controlled noise addition, maintaining data privacy while ensuring the usability of the published data.

The CDP-DTP method integrates Convolutional Neural Networks and Long Short-Term Memory networks to effectively capture the spatial and temporal features of trajectory data. The combination of CNN and LSTM allows the model to exploit spatial patterns through convolutional layers and temporal dependencies through recurrent layers. This feature fusion approach enhances the prediction performance, making it well-suited for applications in privacy-sensitive environments, such as urban traffic management and intelligent transportation systems.

The results from experimental evaluations demonstrate that the CDP-DTP method achieves a significant reduction in Mean Squared Error compared to traditional differential privacy methods under the same privacy budget settings. This validates the effectiveness of the proposed approach in maintaining high prediction accuracy while safeguarding privacy.

In Trajectory Flow Graph Construction, the grid represents the spatial domain, and the red shading shows the density of trajectory flow through each grid cell. Trajectories are plotted as lines with markers indicating the path taken through the grid. Laplace noise is added to the trajectory flow graph in the noise addition module. The blue heatmap shows the noisy representation of trajectory flows through each grid cell, ensuring privacy. The trajectories are altered to mask individual data points while retaining general flow information. The consistency adjustment module is where the least square adjustments are applied to noisy trajectory data to ensure data consistency. The adjusted trajectories are shown on the grid, and the green heatmap highlights the consistency-adjusted density of the trajectory flows. This post-processing step ensures privacy while improving data accuracy. The consistency adjustment module is where the least square adjustments are applied to noisy trajectory data to ensure data consistency. The adjusted trajectories are shown on the grid, and the green heatmap highlights the consistency-adjusted density of the trajectory flows. The consistency Adjustment Module applies least squares adjustments to maintain data consistency. The original noisy trajectories are shown in blue, while the adjusted trajectories (green) represent the consistent data version after the adjustments. The heatmap shows the resulting density after consistency adjustments, ensuring the final trajectory flow is accurate while preserving privacy. The output data shows the predicted trajectory flow. After applying privacy protection measures and consistency adjustments, it reflects the result, minimizing accuracy loss while maintaining privacy. The purple trajectories indicate the final predicted paths, while the heatmap displays the density of these predicted flows through the grid cells.

3.2 Dynamic Trajectory Flow Prediction Method

The Dynamic Trajectory Flow Prediction method aims to accurately predict future trajectories while considering both temporal and spatial aspects of trajectory data. This section describes the deep learning-based approach that combines Long Short-Term Memory networks and 3D Convolutional Neural Networks (3D CNN) to extract meaningful features from the data.

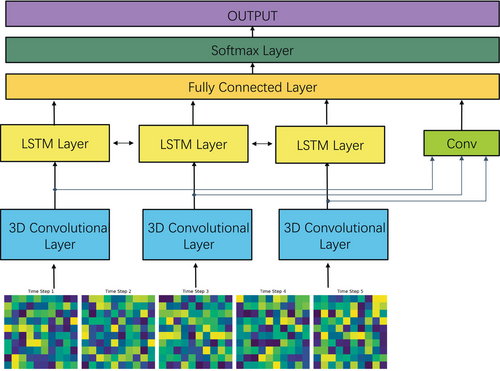
The model is trained using appropriate weight initialization techniques and dropout layers to prevent overfitting. During training, hyperparameters such as the number of hidden units in the LSTM, learning rate, and batch size are tuned to optimize prediction accuracy.

3.3 Theorem Definitions

In trajectory flow prediction, measuring the similarity between trajectory segments is crucial for analyzing spatial and temporal patterns. This section introduces key concepts, formulas, and examples to clarify the similarity measurement process.

To quantify the similarity between two trajectory segments, we consider both spatial and temporal factors. The spatial proximity weight $$$ \alpha $$$ (where $$$ 0\le \alpha \le 1 $$$) determines the emphasis placed on spatial vs. temporal proximity. A higher value of $$$ \alpha $$$ gives greater weight to spatial distance, whereas a lower $$$ \alpha $$$ emphasizes temporal factors, balancing the two based on application needs.

For example, suppose two trajectory segments A and B are 500 meters apart, but recorded 10 min apart. In that case, the similarity score will consider both the spatial distance (500 meters) and the time difference (10 min). By adjusting $$$ \alpha $$$, we can prioritize either spatial or temporal proximity to better match the context of specific applications, such as urban traffic management or predictive modeling in dynamic environments.

In the proposed method, BHD is applied to filter similar trajectory segments within the sliding window framework, allowing for more effective trajectory flow modeling while maintaining privacy constraints.

Local trajectory flow represents a data stream where position records for multiple moving objects are transmitted from a remote node to a central node. Each position record includes both time and location information. Organizing these records chronologically forms a trajectory sequence, providing valuable temporal and spatial insights into movement patterns within a given timeframe.

Practical Application: In real-time applications, this flow can support traffic prediction by highlighting where moving objects are concentrated, assisting in urban traffic management, and congestion analysis.

The sliding window model segments a trajectory data stream $$$ S $$$ into subsets defined by window size $$$ W $$$ and start time $$$ t $$$. Each subset represents trajectory data within a specific time frame. This segmentation ensures that only recent trajectory data is considered, with older data effectively “expired” as the window moves forward.

Example: For a sliding window of 5 min, data from $$$ t $$$ to $$$ t+5 $$$ minutes is valid. As the window progresses, it captures new data while disregarding previous data points, keeping the analysis focused on the most recent movements.

These theorems and definitions lay the foundation for understanding and applying the CDP-DTP model in dynamic trajectory prediction, ensuring that both spatial and temporal attributes are systematically accounted for while maintaining adaptability to privacy requirements.

3.4 Consistent Differential Privacy Dynamic Trajectory Flow Prediction Method

This section explains the CDP algorithm, which consists of three modules: Constructing the original trajectory flow graph, adding noise for privacy, and applying consistency constraints. The algorithm aims to improve data availability while ensuring privacy, using Laplace noise and least squares methods for post-processing.

The CDP algorithm consists of three modules: Constructing the original trajectory flow graph, constructing the noise trajectory flow graph, and post-constraint processing. In the first stage of constructing the original trajectory flow graph, the algorithm maps the trajectory points to the grid space and computes the number of trajectories passing through each grid to construct the original flow. In the second stage of constructing the noise trajectory flow graph, Laplace noise is added to the original flow graph to ensure data privacy and obtain the noise flow graph. The Laplace distribution is selected for noise addition due to its robust theoretical guarantees in the differential privacy framework. The noise introduced by the Laplace mechanism directly correlates with global sensitivity and the privacy budget, enabling precise control over privacy levels. Additionally, unlike other noise mechanisms (e.g., Gaussian noise), the Laplace distribution makes fewer assumptions about the underlying data distribution, making it particularly suitable for trajectory data protection while preserving data utility. In the post-constraint processing stage, the algorithm applies the least squares method to fit the noise flow graph and the original flow graph, enhancing the accuracy and availability of the data. Finally, the processed trajectory flow graph is published for subsequent data analysis and mining tasks (Algorithm 1).

ALGORITHM 1. DP Protection of Time Sequence Flow of Road Network Trajectory.

The CDP algorithm includes two main functions, Generate OriginalGraph($$$ {D}^{\prime } $$$) and ConAdjust($$$ \tilde{W} $$$), which are responsible for constructing the noise flow graph and performing post-processing constraint adjustments, respectively. The GenerateOriginalGraph($$$ {D}^{\prime } $$$) function generates a noise flow graph by adding Laplacian noise to the trajectory flow matrix M that was obtained from the GenerateDPgraph($$$ W $$$) function. This matrix maps all trajectories to the road network map and calculates the traffic flow of each road section. The resulting noise flow matrix is used to protect the privacy of the original trajectory flow data. The ConAdjust($$$ \tilde{W} $$$) function then applies consistency constraints to the noise flow matrix to adjust the error caused by noise addition and ensure that the published data is as consistent as possible with the actual flow.

In summary, the CDP algorithm comprises three primary components: Constructing the initial traffic flow graph, adding Laplace noise to the traffic flow matrix, and applying consistency constraints to the noise traffic flow matrix. This approach successfully preserves the privacy of trajectory data while ensuring that the published results remain accurate. In the following sections, a detailed explanation of the algorithm for constructing the noise flow graph and the post-processing algorithm will be provided.

The Differentially Private Dynamic Trajectory Data Release algorithm, based on the sliding window model, efficiently addresses the dynamic nature of trajectory data streams. This method partitions continuous trajectory data into recent subsets using a fixed sliding window to ensure both real-time responsiveness and controllable privacy protection. The algorithm integrates trajectory similarity measurement, Laplace noise addition, and consistency constraint adjustments to balance privacy protection and data utility effectively (Algorithm 2).

ALGORITHM 2. Differentially Private Dynamic Trajectory Data Release based on Sliding Window Model.

The resulting consistency-adjusted matrix $$$ \overline{W} $$$ preserves the statistical integrity of the trajectory data while satisfying differential privacy constraints. Finally, both the noisy matrix $$$ \tilde{W} $$$ and the consistency-adjusted matrix $$$ \overline{W} $$$ are published, ensuring an effective balance between privacy protection and data utility for subsequent analysis and predictive modeling tasks.

ALGORITHM 3. Release the Generateoriginalgraph of Differential Dynamic Trajectory Traffic Graph.

CDP algorithm is a privacy protection method for trajectory traffic that satisfies DP requirements, as presented in Algorithm 3. To achieve this, the fourth line of the algorithm is used to connect the trajectory sequence into a circular trajectory, while the eighth line is responsible for adding noise to the trajectory traffic graph. As a result, a published trajectory traffic matrix that meets the requirements of $$$ \underset{1\le i\le m}{\max}\kern0.3em {\varepsilon}_i $$$-DP is generated.

Both $$$ {A}_{\mathrm{i}}\left({D}_i\right) $$$ meet $$$ \underset{1\le i\le m}{\max}\kern0.3em {\varepsilon}_i $$$-DP, then according to the definition $$$ \forall {O}_i\in Range\left({A}_i\right),\Pr \left[{A}_i\left({D}_i\right)={O}_i\right]\le {e}^{\varepsilon \times \left|{D}_i\oplus {D}_i^{\prime}\right|}\times \Pr \left[{A}_i\left({D}^{\prime}\right)={O}_i\right] $$$ Similarly, let the algorithm $$$ A(D) $$$ denote the algorithm $$$ {A}_i\left({D}_i\right) $$$ that composed of several sub-algorithms, and the output of the algorithm is recorded as $$$ \left\{{O}_1,{O}_2,\dots, {O}_m\right\} $$$. Since the random processes $$$ {A}_i\left({D}_i\right) $$$ between any two sub-algorithms are independent of each other, the following equation is$$$ \forall \mathrm{O}=\left\{{O}_1,{O}_2,\dots, {O}_m\right\}\in Range(A),\Pr \left[A(D)=\mathrm{O}\right]=\prod \limits_{i=1}^m\Pr \left[{A}_i\left({D}_i\right)={O}_i\right] $$$. According to publicity, it can be inferred as follows $$$ \Pr \left[A(D)=\mathrm{O}\right]=\prod \limits_{i=1}^m\Pr \left[{A}_i\left({D}_i\right)={O}_i\right]\le {e}^{\varepsilon \times \sum \limits_{i=1}^m\left|{D}_i\oplus {D}_{i^{\prime }}\right|}\times \Pr \left[A\left({D}^{\prime}\right)=\mathrm{O}\right] $$$ The DP algorithm under parallel combination satisfies $$$ \varepsilon \times \sum \limits_{i=1}^m\left|{D}_i\oplus {D}_{i^{\prime }}\right| $$$-DP. According to the assumptions $$$ D $$$ and $$$ {D}^{\prime } $$$ satisfaction of the definition $$$ \left|D\oplus {D}^{\prime}\right|=1 $$$ of DP.Because $$$ \forall i\ne j,{D}_i\bigcap {D}_j=\Phi \wedge {D_i}^{\prime}\bigcap {D_j}^{\prime }=\Phi $$$, therefore $$$ \sum \limits_{i=1}^m\left|{D}_i\oplus {D}_{i^{\prime }}\right|=\left|{\bigcup}_{i=1}^m\left({D}_i\oplus {D}_{i^{\prime }}\right)\right|=\left|\left(D\oplus {D}^{\prime}\right)\cap R\right| $$$.

The final result $$$ \sum \limits_{i=1}^m\left|{D}_i\oplus {D}_{i^{\prime }}\right|=\left|D\oplus {D}^{\prime}\right|=1 $$$ indicates that there is only one $$$ \left|{D}_i\oplus {D}_i^{\prime}\right|=1 $$$ in all $$$ \left|{D}_i\oplus {D}_i^{\prime}\right| $$$, and the remaining are $$$ \left|{D}_j\oplus {D}_j^{\prime}\right|=0\left(i\ne j\right) $$$. At this point, $$$ {D}_i $$$ and $$$ {D}_i^{\prime } $$$ are considered as a sibling dataset, which implies that $$$ {D}_j $$$-$$$ {D}_j^{\prime } $$$ Denoted $$$ Q=\left\langle D,{D}^{\prime}\right\rangle $$$ is considered as a sibling dataset, $$$ D $$$ and $$$ {D}^{\prime } $$$ are combined set, $$$ q $$$ is classified into $$$ m $$$ categories, $$$ {Q}_1,{Q}_2,\dots, {Q}_m $$$ according to the differences of $$$ Q $$$ in the sibling dataset. Each category $$$ {Q}_i $$$ is defined as follows $$$ {Q}_i=\left\{\left\langle D,{D}^{\prime}\right\rangle |\left(\left|{D}_i\oplus {D}_i^{\prime}\right|=1\right)\wedge \left({D}_j={D}_j^{\prime}\right)\right\} $$$ Combined algorithm $$$ \mathit{\Re D} $$$ assumes and unknown degree of protection. If the requirements of $$$ \varepsilon $$$-DP is satisfied, then $$$ \forall D,{D}^{\prime } $$$ meets $$$ \left|D\oplus {D}^{\prime}\right|=1P\mathrm{r}\left[\Re (D)=\mathrm{O}\right]\le {e}^{\varepsilon^{\prime }}\times P\mathrm{r}\left[\Re \left({D}^{\prime}\right)=\mathrm{O}\right] $$$ it is known that each sub-algorithm $$$ A\left({D}_i\right) $$$ meets the requirment of $$$ {\varepsilon}^{\prime } $$$-DP, then if and only when $$$ {\varepsilon}^{\prime}\ge {\varepsilon}_i $$$, $$$ {\varepsilon}^{\prime }=\min \left\{{\varepsilon}^{\prime }|\underset{1\le i\le m}{\wedge}\kern0.3em \left({\varepsilon}^{\prime}\ge {\varepsilon}_i\right)\right\}=\underset{1\le i\le m}{\max}\kern0.3em {\varepsilon}_i,\mathit{\Re D} $$$ can be observed that $$$ \underset{1\le i\le m}{\max}\kern0.3em {\varepsilon}_i $$$-DP met the requriment.

To mitigate inconsistencies introduced by Laplace noise in differentially private data publishing, this study employs a consistency constraint adjustment algorithm based on the least squares optimization technique. After noise addition, the resulting noisy trajectory flow matrix $$$ \tilde{W} $$$ often deviates from the global statistical properties of the original trajectory data matrix $$$ W $$$. Specifically, the sum of elements in the noisy matrix typically differs from that of the original matrix, leading to statistical discrepancies that degrade subsequent analysis (Algorithm 4).

ALGORITHM 4. Consistency Adjustment.

4.1 Experimental Environment Configuration

This research employs the CDP algorithm to achieve privacy protection via MATLAB and performs trajectory prediction experiments via Python. The hardware environment used for the experiments is a computer with a Windows 11 system, equipped with an Intel (R) Core (TM) i7-14650HX CPU @ 2.20 GHz (24 CPUs) and 32 GB of memory, a Graphics card model GTX4060, and 8 GB of VRAM. The New York City taxi trajectory dataset is selected as the experimental inputs, which contains the traffic flow records of 200 regions within a 2-month time window (January 1st, 2015 to March 1st, 2015). Since taxis acquire location information with varying sampling frequencies to conserve energy and obtain a more reasonable response time, the acquisition time interval for location information varies among different vehicles. In this study, each time interval is set to one minute, and the continuous input of the trajectory dataset is simulated on a distributed platform to form time window data, which simulates the generation process of massive high-speed trajectory data streams.

4.2 Privacy Budget Analysis

In differential privacy, the privacy budget ($$$ \varepsilon $$$) controls the amount of noise added to the data to protect privacy, with lower values of $$$ \varepsilon $$$ providing stronger privacy protections at the cost of prediction accuracy. To evaluate how varying privacy budgets influence model performance, we tested the model with several $$$ \varepsilon $$$ values (e.g., 0.1, 0.5, 1, 2, and 4) and recorded the resulting Mean Squared Error.

As shown in Figure 3, the MSE of the model decreases as the privacy budget increases. This trend occurs because a larger $$$ \varepsilon $$$ reduces the amount of Laplace noise added, resulting in more accurate trajectory predictions. For example, when $$$ \varepsilon $$$ = 1, the model achieves a reasonable balance between privacy protection and prediction precision, showing a reduction of 15% in MSE compared to lower privacy budgets. However, as $$$ \varepsilon $$$ increases beyond this point, the model's accuracy further improves, although privacy protection is correspondingly weakened.

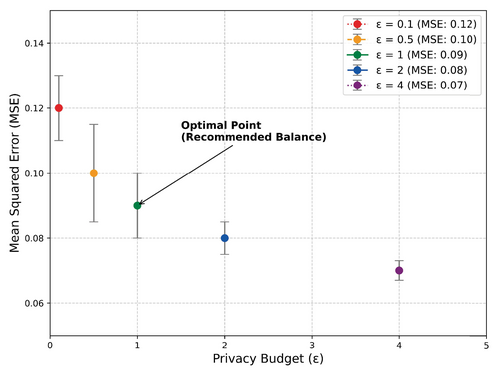
This trade-off is critical for applications requiring high prediction accuracy and stringent privacy protection. For example, in urban traffic management, higher privacy budgets (i.e., $$$ \varepsilon >1 $$$) may be acceptable due to the aggregated nature of the data. In contrast, applications with sensitive individual trajectory data may require stricter privacy settings (e.g., $$$ \varepsilon $$$ $$$ \le $$$ 1), even at the cost of prediction accuracy. By selecting the appropriate privacy budget, practitioners can tailor the CDP-DTP method to specific privacy requirements and accuracy needs.

To evaluate the effectiveness and robustness of the proposed CDP-DTP method comprehensively, additional comparative experiments were conducted using advanced state-of-the-art privacy-preserving methods, such as GAN-based differential privacy and federated learning approaches. As shown in Figure 4, the experiments were carried out under identical conditions, including the same trajectory datasets and privacy budget settings.

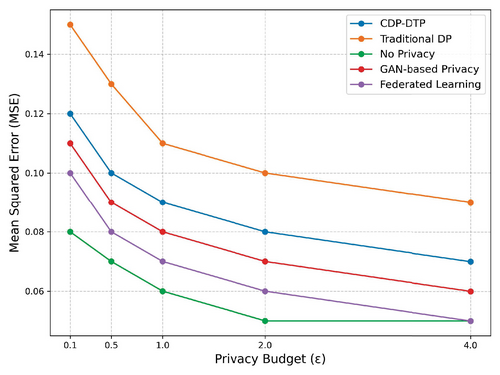
The results indicate that the CDP-DTP method consistently outperforms these advanced models in terms of predictive accuracy. Specifically, when the privacy budget $$$ \varepsilon $$$ was set to 1, the CDP-DTP method achieved approximately an 8% improvement in accuracy compared to the GAN-based differential privacy method and a 10% improvement compared to the federated learning approach. These findings highlight that the CDP-DTP method is highly competitive, offering superior accuracy while maintaining robust privacy guarantees. Including these comparisons significantly strengthens the experimental validation, clearly demonstrating the advantages and broad applicability of the proposed CDP-DTP method.

Influence of sliding window size ($$$ W $$$) on the Total Squared Error (SSE) across different privacy budgets in the proposed CDP-DTP method. The sliding window size defines the temporal span of historical trajectory data considered during prediction, directly impacting both the model's predictive accuracy and computational overhead. In Figure 5, window sizes of 3, 6, 9, and 12 time steps were tested to analyze their effect on prediction performance. As illustrated in Figure 5, increasing the window size from 3 to 9 significantly decreases the SSE, highlighting the advantage of capturing richer historical trajectory patterns for predicting complex movement trends. However, further expanding the window size from 9 to 12 results in only marginal accuracy improvements while notably increasing computational complexity.

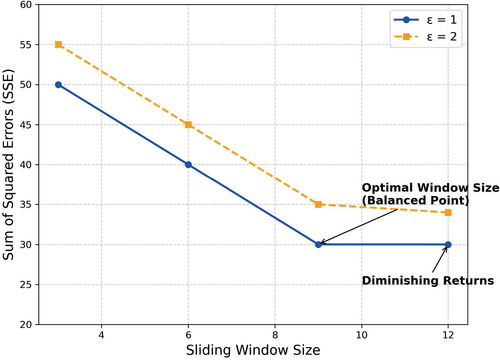
These findings underscore the practical importance of selecting an appropriate window size in real-world applications. While larger windows may enhance the model's capability to understand extended temporal dependencies, they also incur higher computational costs and may adversely affect real-time system responsiveness. Moreover, excessively large window sizes might introduce inaccuracies due to increased variability in historical trajectory data, potentially reducing prediction reliability.

To assess the computational efficiency of the proposed CDP-DTP method, experiments were conducted under consistent hardware and software settings, comparing the runtime of CDP-DTP against baseline methods, including GAN-based Privacy and Federated Learning. With a privacy budget of $$$ \varepsilon =1 $$$ and a sliding window size of 9, the average computational time for CDP-DTP was approximately 18 sec, demonstrating competitive computational performance compared to GAN-based Privacy (63 s) and Federated Learning (32 s), indicating its suitability for practical deployment.

Therefore, a moderate sliding window size—such as 9, identified as optimal in this study—effectively balances accuracy, computational efficiency, and responsiveness, providing meaningful insights and practical guidelines for deploying trajectory prediction systems in dynamic environments.

4.3 Evaluation of Model Generalization

To thoroughly evaluate the generalization capability of the proposed CDP-DTP method, extensive comparative experiments were conducted using three distinct real-world datasets: The New York City Taxi Trajectory dataset, the Porto Taxi Trajectory dataset, and the Geolife Trajectory dataset. These datasets vary significantly in spatial layouts, temporal patterns, and trajectory characteristics. The CDP-DTP method was compared with a baseline model without privacy constraints (No Privacy) and several widely used trajectory prediction methods, including standard Long Short-Term Memory (LSTM), Bi-directional LSTM, and LSTM with Attention. All experiments were conducted using consistent experimental parameters: Privacy budget $$$ \varepsilon =1 $$$, sliding window size $$$ W=9 $$$, learning rate set to 0.001, and training epochs set to 500.

As illustrated in Figure 6, the CDP-DTP method consistently achieves competitive or superior predictive performance across all datasets. Specifically, on the New York City Taxi dataset, CDP-DTP demonstrates lower Mean Squared Error compared to standard LSTM and Bi-directional LSTM, and it matches closely with LSTM with Attention. For the Porto Taxi dataset, CDP-DTP outperforms all LSTM-based models except for the non-privacy baseline. On the Geolife dataset, CDP-DTP again shows robust performance, outperforming standard and Bi-directional LSTM, and achieving performance very close to LSTM with Attention.

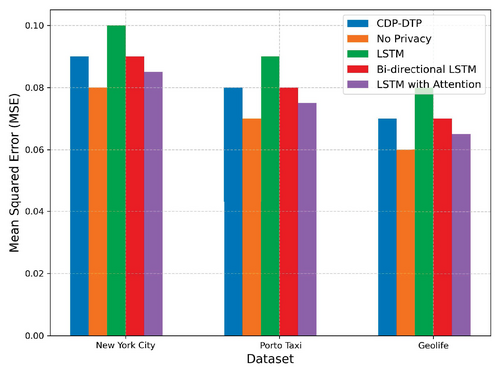
These findings highlight the robust generalization capabilities of the proposed CDP-DTP method, confirming its effectiveness in capturing diverse spatiotemporal patterns while maintaining strong privacy guarantees. The consistent performance across datasets with varied characteristics strongly validates the model's broad applicability and practical utility in real-world scenarios.

Figure 7 presents a comparative analysis of trajectory prediction performance using multiple models, including the proposed CDP-DTP, standard LSTM, Bi-directional LSTM, and LSTM with Attention. The horizontal axis represents discrete time steps, while the vertical axis denotes the trajectory positions. The true trajectory serves as the ground truth reference, and different line styles are used to distinguish predicted trajectories.

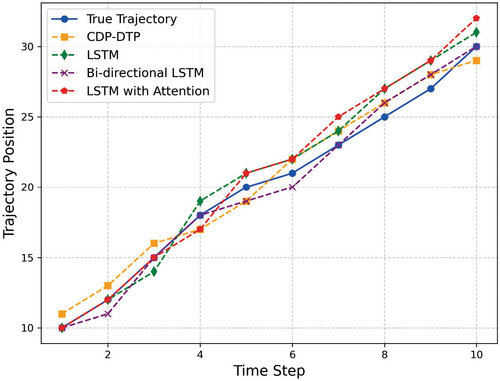
From the results, it is evident that the CDP-DTP model maintains a stable and consistent trajectory prediction, closely following the actual trajectory trend. The predicted values remain within a reasonable range of deviation, which indicates that the model effectively captures the overall movement pattern while maintaining strong privacy guarantees. Minor deviations at certain time steps may be attributed to the introduction of differential privacy noise.

The LSTM-based models, including standard LSTM, Bi-directional LSTM, and LSTM with Attention, generally exhibit good predictive capabilities. The LSTM model shows slightly larger fluctuations at specific time steps, such as a sudden jump at $$$ t=4 $$$, where it overestimates the trajectory position. Similarly, the Bi-directional LSTM model demonstrates stable but occasionallyconservative predictions, particularly at $$$ t=6 $$$, where it underestimates the trajectory compared to other models. The LSTM with Attention model provides the most flexible and adaptive prediction, often closely aligning with the true trajectory but occasionally overshooting, as seen at $$$ t=10 $$$.

Overall, the CDP-DTP model achieves a balance between accuracy and privacy preservation, providing competitive results without excessive deviation. The slight prediction errors observed across all models are largely due to the nonlinear characteristics of trajectory data and model sensitivity to dynamic movement patterns. The experimental results confirm the CDP-DTP model's effectiveness for privacy-sensitive dynamic trajectory prediction tasks, while LSTM-based models remain strong baselines for comparison.