1 INTRODUCTION

Three-phase transformerless (TPT) PV inverters are widely used because of lower cost, higher power density, and higher efficiency compared with the isolated solar three-phase inverters.^1-4 However, there is large common mode leakage current (CMLC) in TPT PV inverters, which leads to personnel security issues and electromagnetic interference, increases losses of inverters, and reduces output voltage quality.^{5, 6} Therefore, the standard of VDE 0126-1-1 requires that the solar inverter should be shut down when the CMLC is larger than 300 mA.⁷

Two methods are often used to limit the CMLC. One method is to add power devices into conventional TPT PV inverters. The H7, H8, H9, H10, and H12 TPT PV inverters were proposed by adding switches into the traditional TPT PV inverters.^8-13 A three-level TPT PV inverter was presented to limit the CMLC by adding a decoupling circuit.¹⁴ In addition, three switches can be added into the three-phase cascaded H4 inverter to reduce the CMLC.¹⁵ The CMLC in the three-level neutral point clamped (NPC) three-phase inverter can be reduced by selecting the damping resistor in a modified LCL filter.¹⁶ A cascaded three-phase grid-connected inverter was also presented to reduce the CMLC.¹⁷ Nevertheless, there are 18 switches in the inverter in Reference 17, which increases complexity and cost of the inverter.

The other method to reduce the CMLC is to change the control method. A modified discontinuous pulse-width modulation (MDPWM) was adopted in the H7 TPT PV inverter by using only one zero vector to limit the CMLC.¹⁸ A new modulation method was adopted in the three-phase four-leg PV inverter by using the Boolean logic function to realize CMLC limitation.¹⁹ In addition, the active damping techniques in αβ-axis and αβ0-axis used in the three-level NPC three-phase inverter with modified LCL filter were investigated to have the ability to reduce the CMLC.²⁰ Moreover, the CMLC closed-loop control in the three-level T-type inverter was also proposed to limit the CMLC.²¹ In Reference 22, a phase-disposition with phase-shift modulation strategy in the three-phase three-level T-type NPC inverter was proposed to reduce the CMLC.

However, all the aforementioned methods to limit the CMLC are affected by variations of the environment and parameters of power devices, which cannot completely eliminate the CMLC. Single-phase common-ground-type PV inverters have become a research hotspot in recent years. Grounds of the grid and PV array are connected directly, so the common-ground-type inverters can completely eliminate the CMLC of PV system.^23-25 However, there are no TPT common-ground-type PV inverters.

Therefore, a TPT PV inverter without CMLC is proposed to solve the abovementioned problem. The main contribution of this article is to completely eliminate the CMLC for the TPT PV inverter. As grounds of three-phase loads and the PV array are directly connected, there is no CMLC in the proposed inverter. Operating principle of the TPT PV inverter without CMLC is elaborated in Section 2. Stability analysis and loss calculation and example of the proposed inverter are given in Sections 3 and 4, respectively. Simulation and experimental results of the TPT PV inverter without CMLC verify the theoretical analysis in Section 5. Last of all, Section 6 concludes the paper.

2 OPERATING PRINCIPLE

Figure 1 shows the TPT PV inverter without CMLC, where u_a–u_c are phase voltages, i_a–i_c are phase currents, R_a–R_c are phase loads, u_aref–u_cref are reference phase voltages, u_af–u_cf are feedback phase voltages, U_in is the input voltage, U_C1 is the voltage across C₁, U_C1ref is the reference signal of U_C1, U_C1f is the feedback signal of U_C1, i_L4 is current through L₄, and i_cm is current through C_PV, that is, CMLC, respectively. As the parasitic capacitor of the PV array C_PV is shorted by the ground, there is no CMLC in the proposed three-phase inverter. The proposed three-phase inverter is derived from three single-phase half-bridge inverters and a boost converter. The voltage closed loop control is used in the boost converter and three half-bridge inverters from Figure 1, which is realized on a digital signal processor (DSP) target board (SEED-DEC2812). The pulse-width modulation (PWM) and sinusoidal PWM control methods are used in the boost converter and three-phase inverter, respectively. The voltage U_C1 is controlled to be constant being equal to 2U_in, so the gain of the boost converter is 2. The voltage U_C1 provides the negative voltage for each of the half-bridge inverter. The three-phase inverter is composed of three half-bridge inverters. Each phase voltage is controlled separately, which is 120° out of phase. The PV source provides the power to each of the half-bridge inverter when the corresponding filter inductor current increases. The capacitor C₁ provides the power to each of the half-bridge inverter when the corresponding filter inductor current decreases. Therefore, the voltage gain of the inverter is unity (ratio between ac peak voltage to PV source voltage). Compared with the conventional three-phase voltage source inverter, the proposed topology provides gain enhancement by double. Assuming that the proposed inverter operates in continuous conduction mode, the detailed operational principle of the TPT PV inverter is elaborated as follows.

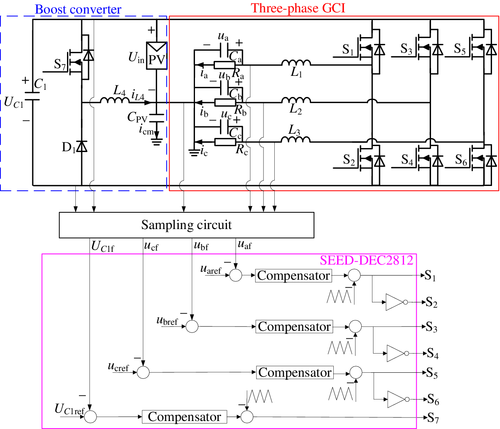
2.1 Boost converter

Voltage U_C1 is equal to 2U_in by regulating duty cycle of S₇, which provides the negative voltage for each of the half-bridge inverter. Figure 2 shows the corresponding circuits of the boost converter without considering the operating modes of the three half-bridge inverters.

2.1.1 Mode 1

From Figure 2A, S₇ is turned on, so D₁ is off. The voltage across D₁ (u_d1) equals to U_C1. The current i_L4 can be expressed as.

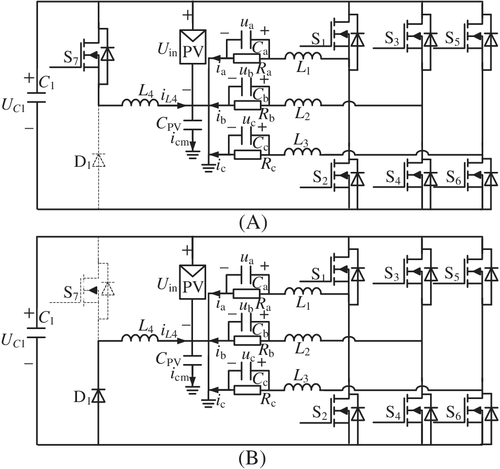
$${\mathit{di}}_{L4}/\mathit{dt}=U_{\text{in}}/L_4.$$ (1)

2.1.2 Mode 2

The switch S₇ is off from Figure 2B, so D₁ conducts. The drain-source voltage of S₇ (u_ds7) equals to U_C1. The current i_L4 can be obtained as.

$${\mathit{di}}_{L4}/\mathit{dt}=\left(U_{\text{in}}-U_{C1}\right)/L_4.$$ (2)

Thus, the voltage U_C1 can be derived from (1) and (2).

$$U_{C1}=U_{\text{in}}/\left(1-{\mathrm{d}}_7\right),$$ (3)

where d₇ is the duty ratio of S₇.

As U_C1 is equal to 2U_in, d₇ can be calculated as 0.5 from (3). Assuming that the output power (P_o) is equal to the input power (P_in), the inductance L₄ can be deduced from (1).

$$L_4=\frac{U_{\text{in}}{\mathrm{d}}_7}{\mathrm{\Delta }{i}_{L4}{f}_s}=\frac{0.5U_{\text{in}}}{0.12\frac{P_o}{U_{\text{in}}}{f}_s}=\frac{5{U_{\text{in}}}^2}{1.2P_o{f}_s},$$ (4)

where f_s is the switching frequency and Δi_L4 is the current ripple of i_L4. The current Δi_L4 is chosen as 12% of the rated input current, so L₄ is calculated as 6.25 mH from (4). Therefore, the inductance L₄ can be selected as 7 mH.

As U_C1 is equal to 2U_in, d₇ can be calculated as 0.5 from (3). Assuming that P_o is equal to P_in, the capacitance C₁ can be obtained as

$$C_1=\frac{I_{\text{in}}{\mathrm{d}}_7}{f_s\mathrm{\Delta }{u}_{C1}}=\frac{\frac{0.5P_o}{U_{\text{in}}}}{0.06U_{\text{in}}{f}_s}=\frac{P_o}{0.12{U_{\text{in}}}^2{f}_s},$$ (5)

where I_in is the average input current and Δu_C1 is the voltage ripple of U_C1. The voltage Δu_C1 is chosen as 3% of U_C1, so C₁ is calculated as 9.6 μF from (5). Therefore, the capacitance C₁ can be selected as 10 μF.

2.2 TPT inverter

The TPT inverter is composed of three half-bridge inverters. Each phase voltage is controlled separately, which is 120 degrees out of phase. Therefore, the half-bridge inverter in phase a is taken as an example to illustrate operating principle of the TPT inverter. Figure 3 gives the corresponding circuits of the half-bridge inverter in phase a without considering the operating modes of the boost converter.

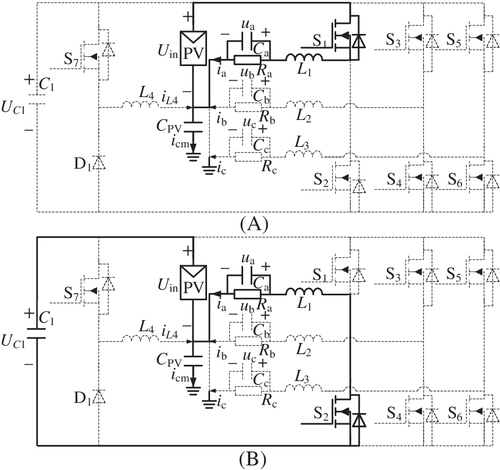
2.2.1 Mode 1

The switch S₁ is on from Figure 3A, so S₂ is switched off. The PV source provides power and positive voltage to the load. The drain-source voltage of S₂ (u_ds2) is equal to U_C1. The current through L₁ (i_L1) can be expressed as.

$${\mathit{di}}_{L1}/\mathit{dt}=\left(U_{\text{in}}-u_{\mathrm{a}}\right)/L_1.$$ (6)

2.2.2 Mode 2

The switch S₁ is switched off from Figure 3B, so S₂ is turned on. The capacitor C₁ provides power and negative voltage to the load. The drain-source voltage of S₁ (u_ds1) is equivalent to U_C1. The current i_L1 can be obtained as.

$${\mathit{di}}_{L1}/\mathit{dt}=\left(U_{\text{in}}-U_{C1}-u_{\mathrm{a}}\right)/L_1.$$ (7)

As U_C1 is equal to 2U_in, the voltage u_a can be derived from (6) and (7).

$$u_{\mathrm{a}}=\left(2{\mathrm{d}}_1-1\right)U_{\text{in}}.$$ (8)

where d₁ is duty cycle of S₁.

3 STABILITY ANALYSIS

Stability of the boost converter and the three-phase inverter are analyzed as follows.

3.1 Boost converter

Transfer function of the boost converter G_{ud_boost}(s) can be obtained as.²⁶

$$G_{\mathrm{ud}\text{\_}\text{boost}}(s)=\frac{-U_{C1}}{\left(1-{\mathrm{d}}_7\right){\mathit{RC}}_1}\frac{s-\frac{{\left(1-{\mathrm{d}}_7\right)}^{2}R}{L_4}}{s^2+\frac{1}{{\mathit{RC}}_1}s+\frac{{\left(1-{\mathrm{d}}_7\right)}^2}{L_4{C}_1}},$$ (9)

where R is the equivalent load of the boost converter, that is, U_C1²/P_o = 4U_in²/P_o, which can be calculated as 144 Ω from Table 1.

TABLE 1. Experimental parameters

Uin	180 V
Output power (Po)	900 W
ua–uc	110 V/60 Hz
Switching frequency (fs)	24 kHz
L1–L3	2.5 mH, winding resistance 0.21 Ω
L4	7 mH, winding resistance 0.264 Ω
C1 and Ca–Cc	10 μF
S1–S7	IPW65R041CFD
D1	C4D20120A
CPV	180 nF

The transfer function of the compensator G_compensator(s) is chosen as

$$G_{\text{compensator}}(s)=K_c{\left(\frac{s}{{\omega }_z}+1\right)}^2/s\left(\frac{s}{{\omega }_p}+1\right).$$ (10)

Therefore, the open-loop transfer function of the boost converter G_boost(s) can be deduced from (9) and (10).

$$G_{\text{boost}}(s)=\frac{-U_{C1}}{\left(1-d_7\right){\mathit{RC}}_1}\frac{K_c\frac{{\left(\frac{s}{{\omega }_z}+1\right)}^2}{s\left(\frac{s}{{\omega }_p}+1\right)}\left(s-\frac{{\left(1-d_7\right)}^{2}R}{L_4}\right)}{s^2+\frac{1}{{\mathit{RC}}_1}s+\frac{{\left(1-d_7\right)}^2}{L_4{C}_1}}.$$ (11)

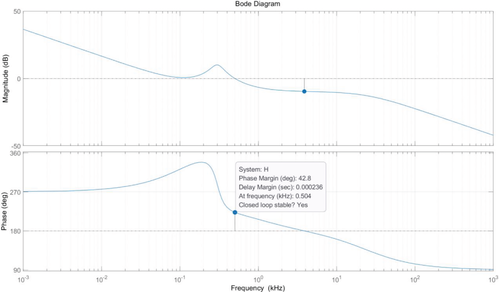
The crossover frequency is selected as 500 Hz, so parameters of K_c, ω_z, and ω_p are designated as 0.584, 945, and 150,796, respectively. The bode diagram of the boost converter is given in Figure 4. From Figure 4, the crossover frequency is 504 Hz, the phase margin is 42.8°. Therefore, the boost converter is stable.

3.2 TPT inverter

The TPT inverter is composed of three half-bridge inverters. Each phase voltage is controlled separately, which is 120 degrees out of phase. Therefore, the half-bridge inverter in phase a is taken as an example to analyze the stability of the TPT inverter.

The average state-space equation of the half-bridge inverter in phase a can be deduced as from (6) and (7).

$$L_1\frac{{\mathit{di}}_{L1}}{\mathit{dt}}={\mathrm{d}}_1\left[U_{\text{in}}-u_{\mathrm{a}}\right]+\left[1-{\mathrm{d}}_1\right]\left[U_{\text{in}}-U_{C1}-u_{\mathrm{a}}\right].$$ (12)

$$C_{\mathrm{a}}\frac{{\mathit{du}}_{\mathrm{a}}}{\mathit{dt}}=i_{\mathrm{a}}-\frac{u_{\mathrm{a}}}{R_{\mathrm{a}}}.$$ (13)

Therefore, the transfer function of the half-bridge inverter in phase a G_{ud_inverter}(s) can be obtained from (12) and (13).

$$G_{\mathrm{ud}\text{\_}\text{inverter}}(s)=\frac{2U_{\text{in}}}{L_1{C}_{\mathrm{a}}{s}^2+\frac{L_1}{R_{\mathrm{a}}}s+1}.$$ (14)

The transfer function of the compensator in the inverter is the same as that in the boost converter, so the open-loop transfer function of the half-bridge inverter in phase a can be deduced from (10) and (14).

$$G_{\mathit{\text{inverter}}}(s)=\frac{2U_{\mathit{\text{in}}}}{L_1{C}_a{s}^2+\frac{L_1}{R}s+1}{K}_c\frac{{\left(\frac{s}{{\omega }_z}+1\right)}^2}{s\left(\frac{s}{{\omega }_p}+1\right)}.$$ (15)

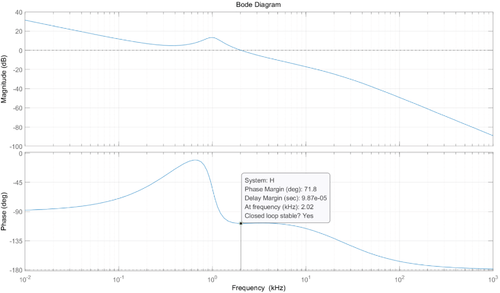
The crossover frequency is selected as 2 kHz, so parameters of K_c, ω_z, and ω_p are selected as 6.467, 3163, and 150,796, respectively. The bode diagram of the half-bridge inverter in phase a is given in Figure 5. From Figure 5, the crossover frequency is 2.02 kHz, the phase margin is 71.8°. Therefore, the three-phase inverter is stable.

4 LOSS CALCULATION AND EXAMPLE

5 EXPERIMENTAL RESULTS

The proposed TPT PV inverter has been constructed to confirm the theoretical analysis. A picture of the experimental setup is shown in Figure 6. Table 1 shows the parameters of the inverter. As C_PV could be estimated as 200 nF/kWp,¹¹ a 180 nF capacitor is used to evaluate i_cm.

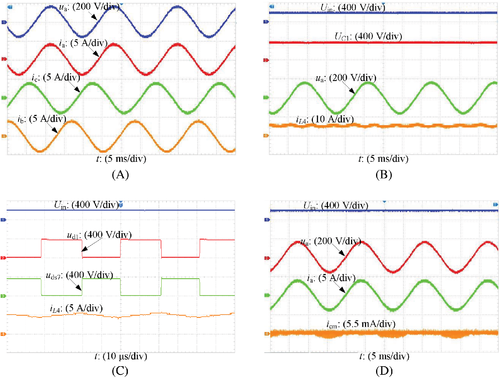
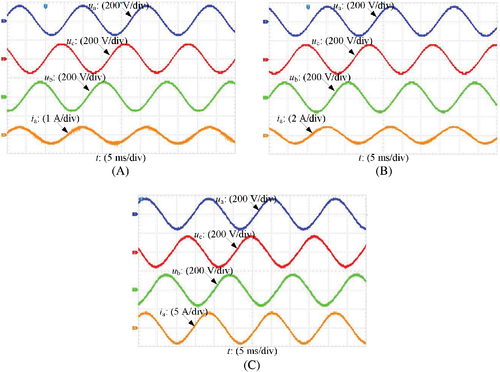
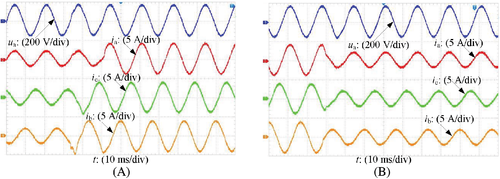
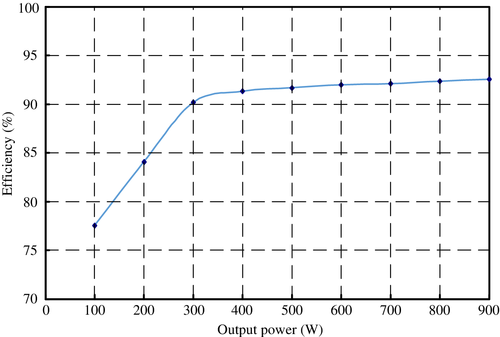
Figure 7 gives the experimental results. From Figure 7A, the load current quality is high. From Figures 7B,C, voltage U_C1 is twice of U_in and voltage stress of D₁ and S₇ is equal to U_C1. In addition, current ripple of i_L4 is small. From Figure 7D, the current i_cm is very small and RMS value of i_cm is about 0.8 mA, which satisfies the standard German DIN VDE 0126-1-1.⁷ The main reason for i_cm in Figure 7D not being zero is mostly caused by the ground line inductor and oscilloscope probe noise. Figure 8 shows the experimental results under different output power. From Figure 8, the output voltage quality is high under different output power. Figure 9 gives the experimental results under load step response. From Figure 9, transient response under step changes is fast. Figure 10 shows the efficiency curve under different output power. The measured efficiency at full power is 92.55%. From Section 4, the calculated losses of switches, the diode, and inductors at full power are 20.426, 3.75, and 36.8 W, respectively, so the theoretical efficiency at full power is 93.23%, which approximates to the measured efficiency.

To verify the effect of different voltage gains on the CMLC, simulation results are shown in Figure 11. The voltage gain changes from 2 to 2.1 at 0.025 s in Figure 11A and from 2.1 to 2 at 0.025 s in Figure 11B. From Figure 11, it can be seen that the CMLC is always equal to 0 under different voltage gains, so the CMLC is not affected by the voltage gain.

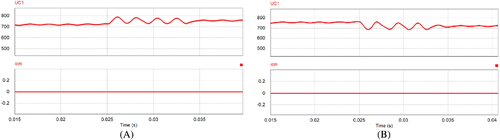
Table 2 shows comparisons among other three-phase inverters and the proposed inverter. Number of switches in the inverter in Reference 29 is the least among the inverters in Table 2. Number of diodes in the proposed inverter and the inverter in Reference 29 is one, but it is six in the inverters in References 16, 20, which is the most among the inverters in Table 2. Number of inductors in the proposed inverter and the inverter in Reference 19 is four, while it is six in the inverters in References 15, 16, 20-22, which is the most among the inverters in Table 2. Number of inductors in the inverters in References 8, 10, 12, 14, 17, 18, 28 is three, while it is two in the inverter in Reference 29, which is the least among the inverters in Table 2. There is no capacitor in the inverters in References 8, 15, 17, 18 because of no output capacitors in the grid-connected inverters. Note that the input capacitor is excluded in the number of capacitors. Number of capacitors in the proposed inverter, inverters in References 10, 12, 14, 19, 29 is less than that in the inverters in References 16, 20-22, 28. The inverter in Reference 16 has damping resistors, but there are no damping resistors in the other inverters in Table 2. Since switching frequency in the proposed inverter is the highest among all the inverters in Table 2, efficiency of the proposed inverter is lower than that in the inverters in References 16, 17, 20, 22. Since grounds of three-phase loads and the PV array are connected directly in the proposed inverter, the CMLC is the smallest among the inverters in Table 2 and is not affected by the parameters of the three-phase inverters. However, the CMLC in the other inverters is affected by variations of the environment and parameters of power devices, which cannot be eliminated thoroughly. The PV inverter can operate at off-grid and grid-tied modes. The proposed inverter and inverters in References 14, 28, 29 operate at off-grid mode, while the other inverters operate at grid-tied mode.

6 CONCLUSION

A TPT PV inverter without CMLC has been presented, which is made up of three half-bridge inverters and a boost converter. The boost converter is adopted to supply the negative voltage for the three-phase inverter. The PWM and sinusoidal PWM control methods are used in the boost converter and three-phase inverter, respectively. Since grounds of the PV array and three-phase loads are shorted in the proposed inverter, there is no CMLC in the proposed inverter, which is not affected by variations of the environment and parameters of power devices. Therefore, problem of the CMLC in the traditional TPT PV inverter is addressed thoroughly. Efficiency of the proposed inverter can be improved by using the silicon carbide MOSFETs.

CONFLICT OF INTEREST

The author declares no potential conflict of interest.

AUTHOR CONTRIBUTIONS

Xiangyu He: Writing – review and editing (equal). Jiwei Gan: Investigation (equal). Saijun Mao: Formal analysis (equal); validation (equal).