Regulatory genetic toxicology testing is essential for identifying potentially mutagenic hazards. Duplex Sequencing (DS) is an error-corrected next-generation sequencing technology that provides substantial advantages for mutation analysis over conventional mutagenicity assays including: improved accuracy of mutation detection, ability to measure changes in mutation spectrum, and applicability across diverse biological models. To apply DS for regulatory toxicology testing, power analyses are required to determine suitable sample sizes and study designs. In this study, we explored study designs to achieve sufficient power for various effect sizes in chemical mutagenicity assessment. We collected data from MutaMouse bone marrow and liver samples that were analyzed by DS using TwinStrand's Mouse Mutagenesis Panel. Average duplex reads achieved in two separates studies on liver and bone marrow were 8.4 × 10⁸ (± 7.4 × 10⁷) and 9.5 × 10⁸ (± 1.0 × 10⁸), respectively. Baseline mean mutation frequencies (MF) were 4.6 × 10⁻⁸ (± 6.7 × 10⁻⁹) and 4.6 × 10⁻⁸ (± 1.1 × 10⁻⁸), with estimated standard deviations for the animal-to-animal random effect of 0.15 and 0.20, for liver and bone marrow, respectively. We conducted simulation analyses based on these empirically derived parameters. We found that a sample size of four animals per group is sufficient to obtain over 80% power to detect a two-fold change in MF relative to baseline. In addition, we estimated the minimal total number of informative duplex bases sequenced with different sample sizes required to retain power for various effect sizes. Our work provides foundational data for establishing suitable study designs for mutagenicity testing using DS.

1 INTRODUCTION

Conventional in vivo mutagenicity tests rely on individual reporter genes for mutation quantification. The most widely used mutagenicity test is the transgenic rodent (TGR) assay (OECD, 2022). This assay relies on bacterial reporter genes for mutation quantification by using viral phages to encapsulate these genes and infect bacteria; mutations are identified by plaque formation in bacterial lawns grown under selective conditions (Lambert et al., 2005). These reporter-based assays have several important limitations: (a) they quantify mutations in single bacterial genes that do not accurately represent the entirety of the mammalian genome; (b) they are impractical for the analysis of mutation spectra and thus cannot effectively inform on mutagenic mechanism (Beal et al., 2020); and (c) they rely on specific rodent strains and cannot be integrated with test methods using other model organisms. Development of methods to circumvent these limitations would allow for better quantification and understanding of mutagenesis to protect human health.

Duplex Sequencing (DS), an error-corrected next-generation DNA sequencing technology, provides an alternative method to quantify mutations that addresses the limitations of reporter-based assays (Valentine et al., 2020). DS quantifies mutation frequency (MF; mutations per bp) with an extremely low error rate of <1 in 10⁷ sequenced nucleotides (Kennedy et al., 2014) in any tissue type and model organism, while simultaneously informing mutagenic mechanisms (Marchetti, Cardoso, Chen, Douglas, Elloway, Escobar, Harper, et al., 2023; Salk & Kennedy, 2020). DS evaluates mutagenicity across custom panels that capture different endogenous genomic loci to reflect genome-wide changes. These panels are composed of twenty 2.4 kb genic and intergenic loci spread across the autosomes, spanning both coding and non-coding regions, and reflecting the GC content of endogenous mammalian genomes. The loci were chosen for being selectively neutral, optimal performance in hybrid capture, and absence of pseudogenes or repetitive elements that could confound alignment or variant calling (Dodge et al., 2023). These panels are commercially available for mutagenesis studies in mouse (LeBlanc et al., 2022), rat (Smith-Roe et al., 2023), and human (Cho et al., 2023) tissues. While not without limitations (e.g., coverage of <1% of the genome, requirement for a reference genome and model-specific panels), DS has gained traction as a powerful tool for regulatory mutagenicity testing (Marchetti, Cardoso, Chen, Douglas, Elloway, Escobar, Harper Jr, et al., 2023).

DS accurately detects and characterizes mutations by creating consensus sequences from both strands of DNA (Kennedy et al., 2014). Briefly, DS labels fragmented DNA molecules with unique molecular identifiers so that, following PCR amplification and sequencing, reads from both strands may be assembled and grouped into tag families. Each read within a tag family is compared to create single strand consensus sequences (SSCS), which are then grouped for a second round of error correction to produce duplex consensus sequences (DCS). True mutations are scored if they are present at the same position in all reads of a tag family and on both strands of the DNA, as it is unlikely that a sequencing or PCR error would occur at the exact same location on the sister strand. Thus, DS eliminates almost all sequencing errors, increasing sensitivity for de novo mutation detection.

DS has been effective at measuring dose-dependent increases in MF following exposure to well-established mutagens. Prior research has analyzed benzo[a]pyrene (LeBlanc et al., 2022), procarbazine hydrochloride (Dodge et al., 2023), N-nitrosodiethylamine (Bercu et al., 2023), and N-ethyl-N-nitrosourea (Smith-Roe et al., 2023) exposures in rodent models. These studies demonstrate the potential for DS in mutagenicity testing. However, every new assay must be evaluated to determine the minimum detectable “signal” and the optimal approach to detect it, given such a signal exists. Power analyses are necessary to establish acceptable study design parameters to advance the use of DS in mutagenicity assessment.

Power is the probability that the null hypothesis can be correctly rejected given the sample size and effect size of the study. An underpowered study is more likely to miss true effects resulting in misleading conclusions, whereas an overpowered study may use more animals than necessary raising ethical concerns. Typically, 80% power is considered standard and what researchers aim for in their studies (Festing, 2018); it indicates an 80% chance of detecting a true effect if it exists and a 20% chance of missing it, balancing ethical and practical considerations with the risk of overlooking true effects.

We conducted simulation studies to evaluate the sample size and required number of informative duplex bases sequenced per sample for different effect sizes relevant to analyses of mouse bone marrow (BM) and liver. These tissues are widely used in regulatory mutagenicity testing and have very different characteristics. BM is highly proliferative, allowing DNA damage to be quickly converted into mutations and fixed in the genome. In contrast, liver is only moderately proliferative, but is the most metabolically active tissue and the first pass organ for detoxication. We simulated different study designs to evaluate how power changes with different parameters and draw conclusions on feasible sample size and depth of sequencing.

2 METHODS

2.1 Baseline data

The DS data used in this study are from two studies on the livers and BM of MutaMouse males exposed daily for 28 days by oral gavage to olive oil (vehicle control: VC) or toxicants of interest (Schuster et al., 2024; LeBlanc et al., in preparation). These studies will henceforth be referred to as “Study A” and “Study B.” The methodology for DNA extraction, DS library preparation, and DS data analysis was as described previously (Dodge et al., 2023), except that DNA was enzymatically fragmented, not ultrasonically sheared, during library preparation. The computational analysis of raw DS data was handled by TwinStrand via their DNAnexus® pipeline. The protocol for this pipeline is detailed by Kennedy et al. (2014) and the underlying code published (Kennedy-Lab-UW/Duplex-Seq-Pipeline, 2023).

The data from Study A and Study B were used to identify a reasonable estimate of baseline MF and the number of informative duplex bases retrieved for mouse BM and liver DNA analyzed with a 500 ng DNA input by DS. The standard deviations used for the power analysis cover a range of values observed in the literature and in our own studies. In BM, these values were 0.06 (Dodge et al., 2023; LeBlanc et al., 2022), 0.10 (Study A), and 0.27 (Study B). In liver, standard deviations were 0.14 (Study A and Study B). There are three other papers that have used DS for mutagenicity assessment in chemically treated rodents (Bercu et al., 2023; Smith-Roe et al., 2023; Valentine et al., 2020). Unfortunately, none of these papers report the standard deviation on their MF. Thus, we use the values from Dodge, LeBlanc and those presented herein as reasonable estimates of possible standard variations to be used for the calculations. To calculate standard deviation, a generalized linear mixed model (GLMM) with a binomial error distribution was used to fit the data, incorporating fixed effects (treatment groups, targets, and their interaction) and random effects (experiment and animal ID) to account for overdispersion and estimate animal-to-animal variation using variance component analysis (Dertinger et al., 2023). These variance component estimates served as the basis for the range of standard deviations used in the simulation experiments for power analyses.

2.2 DS data interpretation

Mutation scoring in the studies used was done under the assumption that all identical mutations within a sample are the result of clonal expansion from a single mutational event and so are counted once (Dodge et al., 2023). Germline mutations (with variant allele frequency (VAF) >0.01) were filtered out and only true de novo mutations were retained. Additionally, the DNAnexus® pipeline removes missing values based on whether a base can be confidently identified for each position.

Sequencing results also give a measurement for the total number of informative duplex bases sequenced for each sample. These values can be converted into a target number of required raw reads. The number of unprocessed reads roughly making up one duplex read was empirically derived by Kennedy et al. (2014). These authors determined that six raw reads are sufficient to make an SSCS and that an average of six SSCSs is needed to make one DCS. Therefore, ideally, we need 36 raw reads to make one DCS. Four more raw reads were added to account for error and low-quality reads that fail to form duplex sequences, making a total of 40 raw reads to make a DCS. Thus, the following formula can be used to convert duplex bases into the number of raw reads needed to achieve a certain power:

N = \frac{40 DG}{R}

(1)

where N is the number of raw paired-end reads per sample, D is the average depth of coverage, G is the genome target size in base pairs, and R is the post-analysis read length in bases (300 bp for all of the datasets). The multiplication of DG is the number of informative duplex bases sequenced. Thus, this formula can be simplified to:

N = \frac{40 S}{R}

(2)

where S is the total number of informative duplex bases sequenced per sample.

2.3 Power analysis

Overdispersion occurs when the observed variance is greater than the variance expected under a standard binomial distribution, often due to heterogeneity among the subjects (animals). GLMM provides a suitable model to estimate this variability, as an input to the simulation for the power analysis. Gelman and Hill (2007) described an approach similar to the one we took for our power analyses, albeit in a more complex multivariate context. We applied a simplified version to simulate univariate overdispersed binomial data using a random intercept model. The first step of simulation-based power analysis was to simulate a large number of data sets. When simulating responses from an overdispersed binomial distribution, we only needed to provide an estimate of the MF and an estimate of the animal-to-animal variability; these were derived from the results of the GLMM from studies A and B or from previously published studies (Dodge et al., 2023; LeBlanc et al., 2022). Estimates for these parameters, or a range of plausible values, are often available from previous studies or from a pilot study. If no data are available, a plausible range of parameter values is justified based on prior knowledge of the study system.

To generate random samples from an overdispersed binomial distribution in R (R: The R Project for Statistical Computing, n.d..; version 4.3.1) using the rbinom() function, three arguments were needed: the individual MF for each simulated observation adjusted for tissue variability (p_i), the number of informative duplex bases (or trials), and the number of random samples (n). Since we were generating only one observation for each sample, i would run from i = 1, 2, … n. The individual p_i's were obtained using the following model:

logit (p_{i}) = \log (\frac{p_{i}}{1 - p_{i}}) = μ + Z_{i}

(3)

where

μ = \ln (MF)

and

Z_{i}

was the overdispersion mechanism with the following distribution

Z_{i} ~ N (0, σ^{2})

. Thus,

Z_{i}

modified the MF based on the sample standard deviation for a particular tissue. Equation (3) could be re-written to closely approximate

p_{i}

p_{i} = \frac{\exp (μ + Z_{i})}{1 + \exp (μ + Z_{i})}

(4)

1 + \exp (μ + Z_{i}) \approx 1

for small MFs, the equation could be further simplified to:

p_{i} \approx \exp (μ + Z_{i}) = MF \times \exp (Z_{i})

(5)

To simulate mutation data for the treatment group, these p_i's were multiplied by a specified fold change:

p_{i} \approx FC \times MF \times \exp (Z_{i})

(6)

with FC representing the desired fold change or effect size.

The rnorm() function was used to randomly generate realizations for the $Z_{i}$ random variable. The rnorm() function required three parameters: the required sample size n which was set to 1, the mean which was set to zero, and the standard deviation which was set to be the animal-to-animal variation parameter determined by the simulation scenario.

We performed a power analysis at varying sample sizes and total number of informative duplex bases and degree of animal-to-animal variation. Simulated data for hypothetical treatment groups were randomly generated to produce defined increases in MF (e.g., 1.2-fold, 1.5-fold, and 2-fold). A generalized linear model (GLM) was used to calculate significance using the Wald statistic estimated using the doBy R library (Halekoh & Højsgaard, 2024; version 4.6.19). Experiments were simulated at least 1000 times for each scenario and the power was estimated as the frequency of experiments resulting in a significant difference between simulated treated and control groups at a significance level of 0.05.

3 RESULTS AND DISCUSSION

The experimental DS data used for the power analysis are summarized in Table 1. The four datasets are described by the following parameters:

The number of test animals used (sample size) per dose group. Study A and Study B used 4 animals per dose group. The data from these experiments were combined and simulated to produce different sample sizes for the power analysis (described below).
Background MF. The VC MF was 5.33 × 10⁻⁸ (± 7.35 × 10⁻⁹) and 3.79 × 10⁻⁸ (± 3.35 × 10⁻⁹) mutations per bp for liver in Study A and Study B, respectively, and 4.13 × 10⁻⁸ (± 1.35 × 10⁻⁹) and 5.02 × 10⁻⁸ (± 1.69 × 10⁻⁸) mutations per bp for BM in Study A and Study B, respectively. The average pooled VC MF (i.e., combining both studies; n = 8 per tissue) for liver and BM was 4.56 × 10⁻⁸ (± 6.75 × 10⁻⁹) and 4.58 × 10⁻⁸ (± 1.14 × 10⁻⁸) mutations per bp, respectively. As the averages for both tissues are very similar, an overall average of 4.57 × 10⁻⁸ mutations per bp was used in the subsequent power analyses.
Informative duplex bases sequenced per sample. The number of raw reads for each dataset was 3.57 × 10⁸, 2.47 × 10⁸, 3.48 × 10⁸, and 3.36 × 10⁸ for liver and BM in Study A and B, respectively. The average total number of informative duplex bases achieved for each sample was 8.34 × 10⁸ (± 9.21 × 10⁷) and 8.51 × 10⁸ (± 6.05 × 10⁷) duplex bases in the liver studies, and 8.32 × 10⁸ (± 7.51 × 10⁷) and 1.12 × 10⁹ (± 7.39 × 10⁷) duplex bases in the BM studies. Note that these numbers are lower that what is expected based on the conversion formula Equation (2) because the studies achieved peak tag family sizes that were larger than the optimal study described therein; peak tag family sizes in these experiments was a minimum of 9.

TABLE 1. Overview of the four DS datasets that served as the foundation for the simulation studies.

Tissue	Study	Sample size per dose group^a	Average background MF^b mutations per bp (± SE)	Average informative duplex bases per sample^c (± SE)
Liver	A	4	5.33 × 10⁻⁸ (±7.35 × 10⁻⁹)	8.51 × 10⁸ (±6.05 × 10⁷)
Liver	B	4	3.79 × 10⁻⁸ (±3.53 × 10⁻⁹)	8.34 × 10⁸ (±9.21 × 10⁷)
Bone marrow	A	4	4.13 × 10⁻⁸ (±1.35 × 10⁻⁹)	8.32 × 10⁸ (±7.51 × 10⁷)
Bone marrow	B	4	5.02 × 10⁻⁸ (±1.69 × 10⁻⁸)	1.12 × 10⁹ (±7.39 × 10⁷)

^a Male mice were exposed for 28 days by oral gavage to olive oil (vehicle control) or toxicants of interest (Study A and Study B).
^b MF of the vehicle controls in each study.
^c Number of informative duplex bases is averaged across all samples used in the experiments (i.e., both exposed and vehicle controls).

These empirical parameters were used to generate a range of hypothetical characteristics for potentially feasible DS experiments: sample sizes of 3–8 per dose group; a background MF of 4.57 × 10⁻⁸ mutations per bp consistent across liver and BM; an average total informative duplex bases sequenced per animal of up to 2 × 10⁹ duplex bases; a fold change of 1.5 from the VC group; and sample standard deviations of 0.1, 0.15, 0.2, and 0.3. The standard deviation in this context represents the sample variability of MF on the ln (natural logarithm) scale as the logit link function was used in the GLMM to model the probability of observing a mutation. For instance, an MF of 4.57 × 10⁻⁸ is −16.90 on the ln scale; with a standard deviation of 0.3, the generated adjusted MF for each observation ( $p_{i}$ ) would then randomly fall anywhere within the range of (−16.90 × 0.97 = −16.39) to (−16.90 × 1.03 = −17.41) based on the density distribution provided in Figure 1. This interval translates back to an MF range of 2.75 × 10⁻⁸ to 7.59 × 10⁻⁸. Figure 1 also shows the distribution of the animal-to-animal random effect for the other standard deviation values as well. As the chosen test parameters are based on empirical data, they enhance the biological relevance of the analysis.

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

The distribution of the animal-to-animal variability for standard deviations 0.1 (black), 0.2 (blue) and 0.3 (red), or $N (0, {0.1}^{2})$ , $N (0, {0.2}^{2})$ , and $N (0, {0.3}^{2})$ (a), adjusted to the individual MFs (i.e., $MF \times \exp (Z_{i})$ (b). Kernel density estimation was conducted using default Gaussian kernel and bandwidth for univariate observations. $Z_{i}$ is the overdispersion mechanism with the following distribution $Z_{i} ~ N (0, σ^{2})$ .

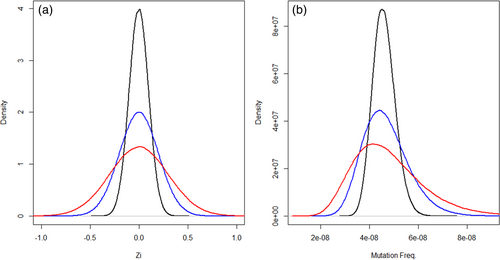
Our study investigated MFs and sequencing depths produced in the analyses of BM and liver in MutaMouse males. These values may vary for other models, tissues, and laboratories. For example, Dodge et al. (2023) and LeBlanc et al. (2022) used sonication for DNA fragmentation and reported higher control MFs (e.g., 1.31 × 10⁻⁷ mutations per bp reported by Dodge et al. (2023) versus our 4.57 × 10⁻⁸ mutations per bp). Dodge et al. (2023) and LeBlanc et al. (2022) sequenced averages of 7.98 × 10⁸ and 8.50 × 10⁸ duplex bases, respectively, which are within our typical range. However, Smith-Roe et al. (2023) sequenced 5.36 × 10⁸ duplex bases and 4.89 × 10⁸ duplex bases in their study, which is below our typical range. Laboratories that achieve lower sequencing depths may need more samples to achieve sufficient power, whereas those with higher depths could require fewer samples. The general power analysis approach presented herein is extendable to other parameters, and other researchers can readily apply the code we have provided (see Supplementary Materials in Data S1) to determine sample sizes to maintain 80% power for their systems.

Our study focused solely on biological variability measured in-house. Comprehensive studies on analytical and technical variability are forthcoming; preliminary data suggest that this variability is negligible with DS. For instance, results showed remarkable reproducibility across two laboratories that sequenced samples from two identically-designed in vitro studies at the same facility (Cho et al., 2023) and in the same samples prepared and sequenced at two different locations (LeBlanc et al., 2022). In both cases, DS produced highly similar results, indicating very low technical variability.

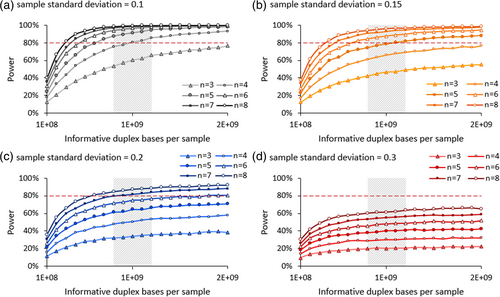
In our study, we first simulated data to determine power to detect a 1.5-fold change in MF between control and exposed groups as the test parameters vary (Figure 2). We found that when the sample standard deviation is 0.1, 3 animals per dose group is insufficient to achieve 80% power with 2 × 10⁹ informative duplex bases sequenced per animal—the maximum investigated in this study. However, increasing sample size to four achieves over 95% power with this number of informative duplex bases and 80% power with 1 × 10⁹ informative duplex bases. Increasing the sample size further decreases the required number of duplex bases for any given power value. When the sample standard deviation is 0.15, 80% power is achieved with a minimum sample size of five animals per dose group and 1 × 10⁹ informative duplex bases. With a standard deviation of 0.2, 80% power is achieved with a minimum sample size of 6 animals per dose group and 1.5 × 10⁹ informative duplex bases; lower samples sizes yield <71% power. When the sample standard deviation is 0.3, 80% power is not achieved with any combination of sample size and numbers of duplex bases investigated here. Overall, increasing either the sample size or the number of informative duplex bases sequenced per animal increases the power of the study design. However, although larger sample sizes notably enhance power, increasing the number of informative duplex bases beyond about 1.2 × 10⁹ duplex bases yields minimal additional power. This convergence occurs when you have sequenced deeply enough to have an accurate measure of changes in MF. Thus, increasing the number of samples has more impact on power than duplex depth by this point. Our analysis sheds light on the dynamics of statistical power as sample size and sequencing depth vary.

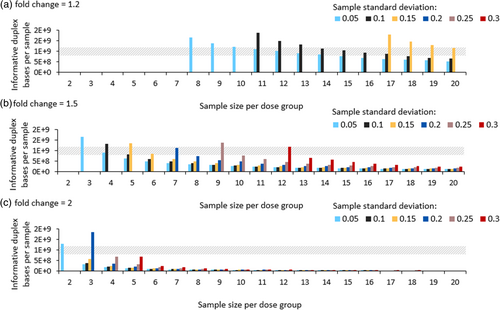
We ran additional modeling experiments to determine the minimum sequencing depth and sample size needed to observe a significant increase in MF with a power of 80% and a p-value of <0.05 for different effect sizes and variances. For this analysis, the investigated parameter range was expanded: sample sizes were varied from 2 to 20 animals per dose group; background MF was kept constant at 4.57 × 10⁻⁸ mutations per bp; the average total number of informative duplex bases sequenced per animal was modeled up to 2 × 10⁹ duplex bases; sample standard deviations ranged from 0.05 to 0.3, with increments of 0.05; and expected fold changes of 1.2, 1.5, and 2 were considered from the VC group to cover a wide range of responses. For each combination of sample size, variance, and expected fold change, we varied the number of informative duplex bases sequenced per animal until we found the minimum value needed to observe a significant increase in MF with a power of 80% (± 0.01%). This analysis provides a foundation to establish study designs required to achieve statistically significant results in diverse mutagenicity studies.

Our results demonstrate that several feasible study designs are suitable across the above range of parameters (Figure 3). A 1.2-fold change is only detectible with a minimum of 8 animals per dose group and an average of 1.6 × 10⁹ informative duplex bases sequenced per sample if the sample standard deviation is extremely low—0.05. Further sample size increases lower this required number of informative duplex bases; however, even with as many as 20 animals per dose group, study designs with sample standard deviation >0.15 cannot detect 1.2-fold changes, given that the required number of duplex bases modeled did not exceed 2 × 10⁹ informative duplex bases. Detecting a 1.5-fold change is more feasible. Studies with a sample standard deviation of 0.05 are sufficiently powered with at least 3 animals per dose group, requiring a corresponding 1.2 × 10⁹ informative duplex bases per sample. Studies where the sample standard deviation is 0.3—the highest investigated variance—are only sufficiently powered with 12 animals per dose group and 8.9 × 10⁸ informative duplex bases. Finally, detecting a 2-fold change requires a sample size of 2 and 1.2 × 10⁹ informative duplex bases when the sample standard deviation is 0.05, and a sample size of 5 and 7.0 × 10⁸ informative duplex bases when the sample standard deviation is 0.3. Overall, our analysis reveals study designs that are amenable to detecting different fold changes using different sample sizes and sequencing depths.

The feasibility of various parameters in rodent DS studies needs to be considered when conducting power analyses. Some designs require more samples per dose group than ethically permissible to achieve sufficient power. One way to reduce sample size requirements is to increase the number of informative duplex bases sequenced per sample. However, with a fixed sample size, power tends to plateau with an increasing number of informative duplex bases (Figure 2). Where this happens depends on the characteristics of the dataset. Therefore, increasing the number of informative duplex bases to use smaller sample sizes might not always be possible. Thus, the trade-off between increasing sample size or the number of informative duplex bases must be carefully considered when designing studies to accommodate high sample deviations and small effect sizes.

Another consideration when increasing the number of informative duplex bases is the biological limit of how deeply we can sequence our samples. There is a limited availability of unique DNA molecules in a given amount of input DNA—known as DNA library complexity. Complexity must be balanced against the number of informative duplex bases achieved. Starting with a more complex sample (i.e., with a larger amount of input DNA) would allow us to increase the number of informative duplex bases. This area presents an opportunity for future research exploration to determine optimal DNA inputs and the number of informative duplex bases for specific DS applications.

Our analysis enabled us to consider acceptable study designs based on two main factors: the minimum sample size per dose group and the most feasible number of informative duplex bases sequenced per sample. In our laboratory, we typically sequence to a depth of 1.2 × 10⁹ informative duplex bases per sample, which is economically feasible at present. Since the required number of informative duplex bases per sample and sample size are inversely correlated, several study designs that minimize sample size are outside the scope of what we can realistically sequence. Given this restriction, we considered study designs for DS that require ≤2.0 × 10⁹ informative duplex bases (Figure 3). Using this restriction, detecting a 1.2-fold change in MF is challenging; large sample sizes are required to compensate for power loss due the lower number of informative duplex bases per sample and the low expected fold change in MF. In contrast, the detection of a 2-fold change is well within our scope. With a sample size of 4, we achieve sufficient power to analyze samples across most variances and at an easily attainable number of informative duplex bases. Increasing the sample size to 5 extends this capability to include samples with a standard deviation of 0.3. Overall, our results suggest that samples sizes of 4–5 are sufficient to detect at least a 1.5-fold change with a feasible number of informative duplex bases even with high sample deviation using the present enzymatic fragmentation protocol in MutaMouse liver and BM samples. The TGR test guideline indicates that a minimum of five mice per dose group should be used to ensure sufficient statistical power to detect at least a 2-fold change in MF (OECD, 2022). Although most OECD mutagenicity tests are designed to be able to detect this level of change, DS can feasibly detect changes as small as 1.5-fold, making it the more sensitive technology. Thus, DS has a higher power to detect the required effect sizes recommended in mutation analyses than the TGR assay.

The parameter range investigated in this study did not encompass all possible values. Study parameters in other experiments may differ, potentially altering the recommended study designs. Sample standard deviation, background MF, and effect size are not under the control of the researcher; they are determined by the study compound characteristics and the biology of the organism. However, researchers can adjust sample size and sequencing depth to optimize the power of the study design. In addition, we calculated power for experiments with two experimental groups: control and treatment. However, the strategy we used is also applicable to studies with multiple treatment groups. The main difference in the analysis would be the application of a Bonferroni correction to adjust the significance level for multiple testing. Our results provide a foundation for strategic optimization of study designs for mutation analysis.

4 CONCLUSIONS

Study designs should be based on the biological characteristics of the test system and the objective of the mutagenicity assessment. With DS, ethical considerations about animal use must be balanced against sequencing (cost) feasibility, anticipated effect size, and group variances. Our power analysis provides a basis for study design selection for liver and BM tissues in MutaMouse animals. We show that a variety of study designs can work to detect fold changes of 1.5 and 2. However, the routine detection of a 1.2-fold change is likely beyond our present capabilities. Curation of historical controls will be critical for DS analyses across different tissues. This will enable us to achieve greater accuracy in our estimates of background MF and sample deviation. Once enough data are collected, a similar power analysis could be done for mutation spectra. Overall, our study informs sample size and the required number of informative duplex bases needed per sample for DS study designs in MutaMouse BM and liver tissue to promote regulatory testing using this powerful new technology.

ACKNOWLEDGMENTS

CLY is grateful for funding from the Natural Sciences and Engineering Research Council of Canada (RGPIN-2021-02806), with infrastructure support through the Canadian Foundation of Innovation John Evan's Leadership Fund (#233109), the Ontario Research Fund (#40569), and uOttawa. CLY acknowledges that this project was conducted thanks, in part, to funding provided through the Canada Research Chairs Program (CRC-2020-00060). CLY and FM are thankful for funding through the Burroughs Wellcome Innovations in Regulatory Sciences Award (#1021737). FM acknowledges support from Health Canada's Genomics Research and Development Initiative and the Chemicals Management Plan.

CONFLICT OF INTEREST STATEMENT

The authors declare that there is no conflict of interest.

Open Research

DATA AVAILABILITY STATEMENT

Data sharing is not applicable to this article as no new data were created or analyzed in this study.

Supporting Information

REFERENCES

Beal, M.A., Meier, M.J., LeBlanc, D.P., Maurice, C., O'Brien, J.M., Yauk, C.L. et al. (2020) Chemically induced mutations in a MutaMouse reporter gene inform mechanisms underlying human cancer mutational signatures. Communications Biology, 3(1), 1–11. Available from: https://doi.org/10.1038/s42003-020-01174-y
10.1038/s42003-020-01174-y
PubMed Google Scholar
Bercu, J.P., Zhang, S., Sobol, Z., Escobar, P.A., Van, P. & Schuler, M. (2023) Comparison of the transgenic rodent mutation assay, error corrected next generation duplex sequencing, and the alkaline comet assay to detect dose-related mutations following exposure to N-nitrosodiethylamine. Mutation Research, Genetic Toxicology and Environmental Mutagenesis, 891, 503685. Available from: https://doi.org/10.1016/j.mrgentox.2023.503685
10.1016/j.mrgentox.2023.503685
CAS PubMed Web of Science® Google Scholar
Cho, E., Swartz, C.D., Williams, A., Rivas, M., Recio, L., Witt, K.L. et al. (2023) Error-corrected duplex sequencing enables direct detection and quantification of mutations in human TK6 cells with remarkable inter-laboratory consistency. bioRxiv, p. 529418. Available from: https://doi.org/10.1101/2023.02.22.529418
Google Scholar
Dertinger, S.D., Li, D., Beevers, C., Douglas, G.R., Heflich, R.H., Lovell, D.P. et al. (2023) Assessing the quality and making appropriate use of historical negative control data: a report of the international workshop on Genotoxicity testing (IWGT). Environmental and Molecular Mutagenesis. Available from: https://doi.org/10.1002/em.22541
10.1002/em.22541
Google Scholar
Dodge, A.E., LeBlanc, D.P.M., Zhou, G., Williams, A., Meier, M.J., Van, P. et al. (2023) Duplex sequencing provides detailed characterization of mutation frequencies and spectra in the bone marrow of MutaMouse males exposed to procarbazine hydrochloride. Archives of Toxicology, 97(8), 2245–2259. Available from: https://doi.org/10.1007/s00204-023-03527-y
10.1007/s00204-023-03527-y
CAS PubMed Google Scholar
Festing, M.F. (2018) On determining sample size in experiments involving laboratory animals. Laboratory Animals, 52(4), 341–350. Available from: https://doi.org/10.1177/0023677217738268
10.1177/0023677217738268
CAS PubMed Web of Science® Google Scholar
Gelman, A. & Hill, J. (2007) Sample size and power calculations. In: Data analysis using regression and multilevel/hierarchical models. Cambridge: Cambridge University Press.
Google Scholar
Halekoh, U. & Højsgaard, S. (2024) doBy: Groupwise Statistics, LSmeans, Linear Estimates, Utilities. (4.6.21) [Computer software] https://cran.r-project.org/web/packages/doBy/index.html
Google Scholar
Kennedy, S.R., Schmitt, M.W., Fox, E.J., Kohrn, B.F., Salk, J.J., Ahn, E.H. et al. (2014) Detecting ultralow-frequency mutations by duplex sequencing. Nature Protocols, 9(11), 2586–2606. Available from: https://doi.org/10.1038/nprot.2014.170
10.1038/nprot.2014.170
CAS PubMed Web of Science® Google Scholar
Kennedy-Lab-UW/Duplex-Seq-Pipeline. (2023) [HTML]. Kennedy-Lab-UW. https://github.com/Kennedy-Lab-UW/Duplex-Seq-Pipeline (Original work published 2020).
Google Scholar
Lambert, I.B., Singer, T.M., Boucher, S.E. & Douglas, G.R. (2005) Detailed review of transgenic rodent mutation assays. Mutation Research, Reviews in Mutation Research, 590(1), 1–280. Available from: https://doi.org/10.1016/j.mrrev.2005.04.002
10.1016/j.mrrev.2005.04.002
CAS Google Scholar
LeBlanc, D.P.M., Meier, M., Lo, F.Y., Schmidt, E., Valentine, C., Williams, A. et al. (2022) Duplex sequencing identifies genomic features that determine susceptibility to benzo(a)pyrene-induced in vivo mutations. BMC Genomics, 23(1), 542. Available from: https://doi.org/10.1186/s12864-022-08752-w
10.1186/s12864-022-08752-w
CAS PubMed Web of Science® Google Scholar
Marchetti, F., Cardoso, R., Chen, C.L., Douglas, G.R., Elloway, J., Escobar, P.A. et al. (2023) Error-corrected next-generation sequencing to advance nonclinical genotoxicity and carcinogenicity testing. Nature Reviews Drug Discovery, 22(3), 165–166. Available from: https://doi.org/10.1038/d41573-023-00014-y
10.1038/d41573-023-00014-y
CAS PubMed Google Scholar
Marchetti, F., Cardoso, R., Chen, C.L., Douglas, G.R., Elloway, J., Escobar, P.A. et al. (2023) Error-corrected next generation sequencing – promises and challenges for genotoxicity and cancer risk assessment. Mutation Research, Reviews in Mutation Research, 792, 108466. Available from: https://doi.org/10.1016/j.mrrev.2023.108466
10.1016/j.mrrev.2023.108466
CAS PubMed Web of Science® Google Scholar
OECD. (2022) Test No. 488: transgenic rodent somatic and germ cell gene mutation assays. Organisation for Economic Co-operation and Development. Paris: OECD Publishing. Available from: https://www.oecd-ilibrary.org/environment/test-no-488-transgenic-rodent-somatic-and-germ-cell-gene-mutation-assays_9789264203907-en
10.1787/9789264203907-en
Google Scholar
R: The R Project for Statistical Computing. (n.d.). Retrieved May 7, 2024, from https://www.r-project.org/
Google Scholar
Salk, J.J. & Kennedy, S.R. (2020) Next-generation Genotoxicology: using modern sequencing technologies to assess somatic mutagenesis and cancer risk. Environmental and Molecular Mutagenesis, 61(1), 135–151. Available from: https://doi.org/10.1002/em.22342
10.1002/em.22342
CAS PubMed Web of Science® Google Scholar
Schuster, D.M., LeBlanc, D.P.M., Zhou, G., Meier, M.J., Dodge, A.E., White, P.A. et al. (2024) Dose-related mutagenic and Clastogenic effects of benzo[b]fluoranthene in mouse somatic tissues detected by duplex sequencing and the micronucleus assay. bioRxiv, 605228. Available from: https://doi.org/10.1101/2024.07.26.605228
Google Scholar
Smith-Roe, S.L., Hobbs, C.A., Hull, V., Todd Auman, J., Recio, L., Streicker, M.A. et al. (2023) Adopting duplex sequencing technology for genetic toxicity testing: a proof-of-concept mutagenesis experiment with N-ethyl-N-nitrosourea (ENU)-exposed rats. Mutation Research, Genetic Toxicology and Environmental Mutagenesis, 891, 503669. Available from: https://doi.org/10.1016/j.mrgentox.2023.503669
10.1016/j.mrgentox.2023.503669
CAS PubMed Google Scholar
Valentine, C.C., Young, R.R., Fielden, M.R., Kulkarni, R., Williams, L.N., Li, T. et al. (2020) Direct quantification of in vivo mutagenesis and carcinogenesis using duplex sequencing. Proceedings of the National Academy of Sciences, 117(52), 33414–33425. Available from: https://doi.org/10.1073/pnas.2013724117
10.1073/pnas.2013724117
CAS PubMed Web of Science® Google Scholar

Citing Literature

Volume65, Issue8

October 2024

Pages 234-242

This article also appears in:

Environmental and Molecular Mutagenesis Editor's Choice

Power analyses to inform Duplex Sequencing study designs for MutaMouse liver and bone marrow

Abstract

1 INTRODUCTION