The spatial and traveling wave effects on a structure with an energy dissipation system can be conveniently considered using the random vibration method. In this study, the pseudo-excitation method is introduced to perform random spatial seismic response analysis of such a structure considering different damper arrangements. The analysis results show the effects of nonproportional damping characteristics due to these arrangements, and the nonproportional damping characteristic index can estimate the strength of these characteristics. Moreover, the virtual excitation method can be used to determine the weak parts of the structure. The effect of the traveling wave on the energy dissipation system and damping structure is relatively low. The response results of the structure in the case of multipoint consistent excitation obtained by the complex vibration decomposition reaction spectrum method are compared. The method accounts for the effects of nonproportional damping and vibration velocity. Accurate time history results can be obtained by complex vibration decomposition time history analysis.

1 INTRODUCTION

The traditional antivibration method applied to buildings and bridges can typically resist the damage caused by natural disasters, such as those caused by earthquakes, wind, snow, and tsunami. This resistance is developed by enhancing the antivibration performance of the structure in terms of strength, stiffness, and ductility. However, due to factors, such as frequency of natural disasters and uncertainty of their intensities, buildings and bridge structures designed according to the traditional earthquake resistance (vibration) methods cannot adjust and restore their original states after a disaster. This results in significant economic loss and severe harm. The energy dissipation and vibration damping technology has been successfully developed and is widely used in engineering. It uses damping characteristics to decelerate vibration and the principle of kinetic energy consumption to install “airbags” on engineering structures, considerably improving the structure's safety. When earthquakes or other external forces act, the installed viscous energy dissipation dampers can absorb and consume the impact energy on the engineering structure to a certain extent, thus reducing damage.

The principle of energy dissipation and vibration damping technology involves arranging specific additional energy dissipation damping elements in the structure. The energy input from ground vibration to the structure is directed to the energy dissipating damping element to absorb part of the energy and thus reduce the degree of damage. Energy dissipation devices have various forms; among these, energy dissipation support combined with dampers is an effective method for damping structural vibrations in high-rise buildings. Viscous dampers may have different structural arrangements depending on their response to earthquake action. In general, the principle involved in damper arrangement is to allow floors to sustain relatively large displacements. For structures that sustain torsional effects, anti-torsion dampers must be installed asymmetrically according to the torsional action on the structure.

Viscous dampers are considerably effective devices for passively controlling earthquake resistance. Under the action of wind and small earthquakes, these devices can increase structural damping and reduce the lateral displacement of the structure. Under a large earthquake, the dampers can increase damping and reduce the horizontal seismic action on the structure. A considerable amount of seismic energy inputted into the structure is also consumed. This greatly attenuates the seismic response of the engineering structure, thus ensuring its safety.

Many local and international scholars have performed numerous related theoretical analyses and studies on the damped characteristics of nonproportionally damped structural systems. In previous research, many scholars suggested using the decoupling transformation of free and forced motions for nonproportionally damped systems.^{1, 2} Within a certain range, this transformation can satisfy the requirements of engineering structure design. Subsequently, a pseudo-force method suitable for the dynamic time history analysis of nonproportionally damped structural systems was proposed.³ However, this method is only effective for structural systems with a few energy dissipating and damping devices. Moreover, the damping of the structural system depends on the interaction between the damper and damped structure.⁴ When the damper fully interacts with the entire structure, the total damping ratio of the first-order model (intrinsic plus supplementary) is approximately 20%, and the system response is optimal.⁵ Numerous studies have been implemented on nonproportionally damped structural systems. Based on the improved matrix perturbation method for solving the complex modal eigenvalues and eigenvectors of nonproportional damping structural systems,^6-8 meaningful complex structures have been derived.⁹ The mode shapes and phases and the eigenvalues and eigenvectors of the nonproportionally damped linear elastic structure^{10, 11} have been studied and compared with the approximate error range of the forced decoupling method.¹² The nonproportionally damped system is divided into energy dissipation and conversion parts, and the pseudo-force method is used for structural analysis. Two indices, coupling and convergence, are given.^{13, 14} This special nonproportionally damped structural system is investigated,^{15, 16} and the real mode decomposition method and Laplace transformation are combined. Furthermore, some simplifications are introduced to establish a system suitable for any structure with multiple degrees of freedom (DOF). In the study of the time-domain dynamic response of nonproportionally damped structural systems, a numerical analysis algorithm is developed to calculate the time-domain dynamic response of these structural systems with any DOF. By establishing the relationship between damped and undamped frequencies in modal analysis,¹⁷ the calculation of damped frequency is transformed into solving the problem of damping ratio and undamped frequency. It is combined with the random vibration theory and response spectrum complete square junction. The complete quadratic combination (CQC) method proposes the complex CQC (CCQC)^18-24 and complex partial quadratic combination formulas²⁵ in real form. The combination is also extended to complex multidimensional seismic inputs. The CCQC formula,²⁶ which avoids using complex expressions, is suitable for engineering practice. Different energy dissipation and vibration damping devices are set up in the hybrid and X-shaped structures.^{27, 28} Further, the required nonlinear damping characteristics are designed through an optimal control of the damper²⁹ to reduce the seismic response and improve the damping characteristics of the structure³⁰ on shock effect. When excited by ground motions dominated by high frequencies, the rate-independent model produces lower damping forces than the linear viscous damped model.³¹ Moreover, the nonlinear function of equivalent damping is high in the resonance region but extremely low in other frequency ranges.

The foregoing studies have investigated the theory of nonproportionally damped systems and the use of energy dissipation and vibration damping devices. Applying the traditional mode decomposition response spectrum method (i.e., CQC) to damped structures ignores the forced decoupling of nondiagonal elements of the modal damping matrix in the dynamic analysis. Consequently, considerable errors affecting the safety of the structure are generated. Furthermore, the method is inconvenient for engineering applications. The three-dimensional structural system was simplified to a two-dimensional multi-DOF structural system. Then, the CCQC theory was applied to the analysis of the seismic action of the two-dimensional structure; however, the influence of the torsional coupling of the structure was not considered. The comprehensive examination of the three-dimensional spatial effect on the structure and the influence of the traveling seismic wave on the time history analysis were not considered. In this study, the nonproportional damping of a three-dimensional multi-DOF structure with energy dissipation systems is investigated, and the CCQC response spectrum method is applied to a nonproportionally damped structural system. The spatial effect on the three-dimensional structure and the influence of traveling seismic wave on the time history analysis are considered. Subsequently, direct integration is implemented. By comparing the methods, the error generated by force decoupling using the CQC response spectrum method is resolved.

2 COMPLEX MODE ANALYSIS METHOD FOR DAMPED STRUCTURES

2.1 Compound mode superposition method

The equation of motion for the elastic vibration of energy dissipation and structure damping under earthquake action is

()

The damping matrix of the energy dissipating damping system can be expressed as . In the foregoing, is the damping matrix of the main structure, and is the equivalent damping matrix of the additional energy dissipating devices.

The damping matrix,

, of the original structure generally uses Rayleigh damping, which typically satisfies the following orthogonality condition:

()

where

is the

vibration damping of the structure.

The damping matrix,

, is attached to the structure by the dissipator. Typically, it does not satisfy the following orthogonality condition:

()

Equation (1) is expressed in the form of equation of state, as follows³²:

()

In the foregoing,

()

where the corresponding eigenvalues of

are obtained from

(

and

are the eigenvalue and eigenvector, respectively);

and

are the coefficient matrices of symmetric nonpositive definite matrices of order 2n × 2n. The eigenvalue and eigenvector are both complex numbers. The eigenvalues form a conjugate relationship in a weakly damped system:

()

where

and

represent the damping ratio and circular frequency of the structure in the ith mode, respectively, and

is a pure imaginary unit. The complex vectors,

and

, represent the ith order complex mode, and the superscript (“—”) of

denotes the conjugate relationship. If the characteristic of the structural system indicates that the eigenvectors are complete, the linear combination of the eigenvectors can be expressed by the state vector as

()

In the foregoing, and represent the eigenvector matrix and generalized coordinate vector, respectively.

According to the orthogonality of the eigenvector,

(with respect to matrices

and

) and eigenvector transformation matrix, the motion equations of n groups of conjugate modes can be derived as follows:

()

In the foregoing expression, and represent the mode shape mass participation coefficients. The orthogonality of matrix determines the eigenvectors, and (specifically, and ).

The displacement and velocity response vectors of structures involved in all mode shapes are obtained using the following:

()

where

and

represent the complex mode and eigenvalue matrices, respectively.

The structural arbitrary response is expressed as

()

where p = [0 ν^T] is the transformation vector of the structural response, and the superposition method for the complex and real modes is applied to the foregoing. Different from the real vibration mode superposition method formula,

, the response of each mode shape in Equation (11) is a complex number. Because of the conjugate form, the final total response remains a real number.

For multi-DOF structural systems, the first d-order mode shapes whose mode mass participation coefficient exceeds 90% are typically combined. The approximate expressions of the displacement and velocity of the structure are as follows:

()

where

, and

represent the first d-order mode shape matrix, spectral matrix, and generalized coordinate vector of the structure, respectively.

2.2 Mass participation coefficient of complex mode in modal analysis

The static reaction method can be applied to structural systems to express the proportion of each mode shape in the total reaction. Let the load time change function be 1. The static representation of any mode shape of the structure considering

(i.e., Equation 1 and Equation 5) is given by

()

The expansion formula of vector

. The static response of the seismic action components,

and

, of the load,

, on each mode shape is

()

Using the mode shape motion equation,

, the static response of the ith mode shape of the structure is solved as

()

Therefore, the two other expressions of the mass participation coefficient of the structural mode shape are as follows:

()

These equations reflect the contribution of the mode shape to the total response of the structure derived directly from state and mode shape spaces, which are fundamentally the same.

If all the mode shapes of the structure are involved in the calculation, then

. When the seismic load acts, then

. If the physical quantity expressed is the shear force at the bottom of the structure, that is,

, Equations (16) and (17) are further simplified into the following:

()

and

()

In the foregoing, the denominator and numerator represent the total mass of the structure. The effective mode mass corresponding to the ith conjugate complex vibration mode is

()

However, the effective mass of the complex vibration type, which relates to the complex vibration type, , can be positive or negative. This indicates that the cumulative effective mass of the complex vibration type eventually tends to the total mass of the structure.

Based on Equations (18) and (19), an expression of the mass participation coefficient of the complex mode suitable for nonclassically damped system for determining the number of required modes can be derived:

()

Generally, the mass participation coefficient, , of the structural mode shape can be considered as 90% or more. Because the cumulative sum of the mass participation coefficient, , of the structure is not monotonic, the recommended m value satisfies Equation (21). The cumulative sum must be stable according to the required number of mode shapes.

During an earthquake, the sum of the mass participation coefficients of the complex vibration modes of the structure in all directions must satisfy certain requirements. Specifically,

()

where

represents the total mass of the structure in the j direction. It also denotes the influence vector corresponding to the jth direction component during the earthquake action. The effective mass of the complex vibration mode of the participating structure (jth direction) in the ith direction is represented by

()

2.3 Fundamental equation of motion of CCQC mode superposition method

Under earthquake action, the motion equation of a linear viscously damped system with N DOF in the system is

()

where

, and

represent the N × N order structural mass, nonclassically damped matrix, and stiffness matrix, respectively, and

is the earthquake influence vector. To decouple the foregoing equation of motion, it must be transformed into a 2N first-order differential equation of motion, as follows:

()

In the foregoing equation,

()

Matrices

and

are both symmetric nonpositive definite matrices. Typically, the eigenvalue,

, corresponding to Equation (25) appears as conjugate pairs. The eigenvector,

, has the form

(where

is the ith vibration deformation mode (i.e., shape mode)). The eigenvalue,

, of the nonclassically damped system can be expressed as

(

); and

and

are the ith order natural frequency and mode damping ratio of the structure, respectively. The damped natural frequency corresponding to

can be obtained by the following:

()

where

and

represent the real and imaginary parts of a complex number, respectively. Using the mode shape,

()

where the superscript (“

”) indicates conjugation.

In solving the total response of the structure according to the principle of complex vibration type superposition, the displacement vector,

, can be expanded as follows:

()

where

is the complex vibration type coordinate matrix. This matrix is obtained from the following decoupled complex vibration type equation of motion:

()

where

is the participation coefficient of the ith mode shape. To facilitate the solution, it is converted into the standard single-degree-of-freedom expression:

()

By considering the derivative form of the Duhamel integral,

can be represented by

and

as follows:

()

By substituting Equation (32) into Equation (29), the following is derived:

()

where

and

. The modal responses,

and

, can be solved by typical numerical approaches,^{33, 34} such as the Newmark-β method. Compared with Equation (29), the coefficient vector (

) and unknown quantity (

) in the foregoing equation are all in the form of real numbers, which are convenient to use in actual calculations. Moreover, the form of the foregoing expression is easy to combine with the response spectrum theory such that the maximum seismic action effect on the structure can be obtained.

3 CCQC MODE SHAPE COMBINATIONS

If the ground motion is assumed to be a stationary Gaussian random vibration process whose mean is zero, the structure's response is also a stationary Gaussian random vibration process with a nonzero mean. In

, the power spectral density function of any response,

, can be expressed as

()

In the foregoing,

, and

;

is the cross-power spectral density function of

and

. Moreover,

()

where

is the bilateral power spectral density function of the ground motion acceleration process,

; and

is the ith-order complex frequency response function. Considering the symmetry of individual components,

is a real-valued function. In engineering practice, attention is focused on the mean square value of the structural response. Integrating Equation (34) considering

, the mean square reaction,

, can be expressed as

()

where

and

are the standard deviations of

and

, respectively. The cross-correlation coefficients of

and

, and

and

are

, and

, respectively. These coefficients can be expressed as

()

where

, and

denote the structural vibration response (

). This response corresponds to the maximum value of the response

and

of the single-degree-of-freedom structural system when the natural vibration frequency is

and the damping ratio

. According to the definition of the response spectrum,

and

represent the displacement and velocity response spectrum values, respectively. According to the literature,^{35, 36} under the assumption of a zero-mean stationary Gaussian random process, the maximum response of the process is the product of the peak coefficient and standard deviation. Accordingly, the maximum response of the structure is

()

where

and

correspond to

and

, respectively, and

, and

are the crest factor ratios (

denotes the crest factor of response g, and

and

represent the shape responses,

and

, of the

mode, respectively).

When the structure only considers the contribution of the first n-order mode shapes, the CCQC mode combination method in which the nonclassically damped system includes the influence of high-order mode shapes degenerates into the traditional seismic analysis response CCQC method. Compared with the classical mode shape decomposition response spectrum CQC method, damping is nonproportional using the CCQC mode combination method. Moreover, the method contains displacement and velocity terms. These two mode-shape combination methods are based on the assumption that the ground motion is a stationary Gaussian random process.

4 MECHANICAL PROPERTIES OF FLUID DAMPERS

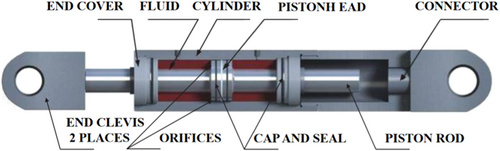
Fluid viscous dampers operate according to the principle of flow of viscous fluid through an orifice. Originally, these devices were developed for military use. Subsequently, they were employed for various applications, such as energy-absorbing buffers in steel mills, canal lock buffers, offshore oil suspension, and in-shock and vibration isolation. For some of these applications, inputs are severe, with peak velocity and acceleration reaching 5 m/s and 200 g (with an extremely short rise time in the order of a few milliseconds), respectively. Some notable examples of military applications are launch gantry dampers for the U.S. Navy with a force output of up to 8900 kN and a travel distance of 5 m; seismic dampers in nuclear power plants with a force output of 1335–4450 kN; payload dampers for space shuttle; wind dampers for the Atlas and Saturn-V rockets; and dampers for most tactical and strategic missiles of the U.S. Armed Forces.

Recently, these devices have been utilized in numerous buildings as elements of a seismic isolation system or as wind or seismic energy-absorbing elements throughout the height of the building.

The damping force is generated by the pressure differential across the piston head. The assumption is that the piston moves toward the right; this causes fluid to flow from chamber 2 to chamber 1, creating a pressure differential between the two chambers. However, another phenomenon also occurs: a volume equal to the product of the piston rod area and piston movement is forced into the cylinder. Because the fluid is compressible, the decrease in volume is the same as the foregoing; consequently, a restoring (stiffness) force develops. This phenomenon can be prevented by using an accumulator or implementing a run-through rod design strategy for the dampers. In the tested dampers, an accumulator was used to prevent the occurrence of fluid compression. For low-frequency motions (i.e., below a certain cut-off frequency specified in the accumulator design), the accumulator valve can effectively operate and prevent fluid compression. However, for high-frequency motions (above the cut-off frequency), the accumulator valve cannot function properly, and the dampers develop a restoring force.

The existence of this restoring force for frequencies higher than the cut-off frequency seems desirable. The dampers can provide further viscous damping to the fundamental mode of the structure (typically with a frequency lower than the cut-off frequency). Furthermore, they can provide additional damping and stiffness to the higher modes. This typically results in the suppression of the contribution of higher modes to the structural response.

Viscous dampers are mainly used to simulate velocity-dependent dissipators. The Maxwell model is used for the program, and the dampers consist of linear springs and viscous dampers in series. The fluidic device uses specially shaped orifices to achieve the following force output:

()

Specifically, when

, the foregoing equation is equivalent to that of a linear damper as expressed by

()

where

is the force;

is the damping constant;

is the piston velocity; and

is a coefficient in the range 0.3–2.0. The value

, achieved using cylindrical orifices, is typically unacceptable in structural applications. Small values of

, approximately 0.5, are effective in attenuating high-velocity shocks, whereas a design in which

(linear damper) is typically preferred for wind and seismic applications (Figure 1).

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Structure of viscous damper.

5 ARRANGEMENT AND PARAMETER OPTIMIZATION OF DAMPERS FOR NONPROPORTIONALLY DAMPED SYSTEMS

5.1 Nonproportional damping characteristic index

For nonproportionally damped linear structural systems, the real vibration superposition method is commonly used for approximation in practical projects because of its advantages, such as its ease of use in calculations. However, the generalized damping matrix in nonproportionally damped linear systems does not satisfy the diagonal matrix condition. The real vibration superposition method ignores all nonzero nondiagonal elements () in its generalized damping matrix. Consequently, is replaced by the diagonal matrix, inevitably introducing computational errors. For a system with strong nonproportional damping characteristics, considerable errors are caused by calculations using the real vibration superposition method.

The equation of motion for a linear multi-DOF structural system under seismic action is

()

where

, and

are the displacement, velocity, and acceleration of the structure, respectively;

, and

are the N × N-dimensional mass, stiffness, and damping matrices, respectively;

is the unit matrix; and

is the ground seismic motion acceleration. Let

be the sheik matrix such that

(here,

is the diagonal matrix). Let

. Multiply

to both sides of Equation (40). This yields

()

where

denotes the N × N-dimensional unit matrix;

; and

If the damping matrix in Equation (40) is nonproportionally damped, matrix

is not a diagonal array and contains modal coupling coefficients. Let

be of the form

()

To study the damping nonproportionality of the structure, let matrix

be a diagonal matrix consisting of diagonal elements of matrix

, that is,

. Denote the minimum and maximum eigenvalues of matrix

and

, respectively. Moreover, define the nonproportional eigen index as

()

where

is a monotonically increasing function whose value range is 0–l. When

, the structure is classified as a proportional damping structure. When the value of

is larger, the farther away from the proportional damping characteristic, the stronger the nonproportional damping characteristic.

5.2 Traveling wave effect

When earthquakes occur, seismic energy is dissipated in the form of waves, which propagate through different paths, topographies, and geological conditions to reach the bottom of the structure; hence, variations in surface vibrations at different locations are inevitable. Accordingly, the traveling wave effect is as follows: the arrival time of a seismic wave with a certain propagation velocity at different support locations varies. The effect of traveling waves on the structure is related to the propagation velocity of seismic waves, column spacing, and other factors. This is expressed by the following:

()

where

, and

are the mass, damping, and stiffness matrices, respectively; subscripts

and

denote the structural support and nonsupporting nodes, respectively;

is the nodal mass;

is the time-varying nodal load applied to each nodal mass; and

is the ground acceleration time range at each support node.

5.3 Complex modal analysis of nonproportionally damped structural systems

By referring to ABAQUS finite element data,^37-39 a three-dimensional shear frame vibration-damping finite element model (Figure 2) is established. The base period for structural design is 50 years; the structural seismic fortification category is key fortification (B); the degree of seismic fortification intensity in this area is 8 (0.20 g); and the site classification is Category II. The seismic design is grouped into the first group; the structural key (i.e., the safety level of components including vertical components) is Class II; the characteristic period is 0.35 s; the damping ratio is 0.18; the ground roughness is Class C; and the basic wind pressure is 0.5 kN/m². The structure has 13 floors with a total height of 39.6 m, dead load of 5.0 kN/m², and live load of 2.5 kN/m². The dimensions of frame and secondary beams are 400 × 800 mm and 250 × 600 mm, respectively. The frame columns are 1350 × 1450 mm, 1250 × 1300 mm, and 800 × 1000 mm; the floor thickness is 120 mm. The damper parameters are summarized in Table 1.

Table 1. Velocity damper parameters.

Damper design damping force (kN)		Design displacement (mm)		Damping factor (kN)(s/mm)^α	Damping index
Lower limit	Upper limit	Lower limit	Upper limit	400	0.30
1200	1500	30	60	400	0.30

α The speed index, which is designed and selected according to engineering requirements, and generally takes a value between 0.01 and 1. When = 1, it is linear damping.

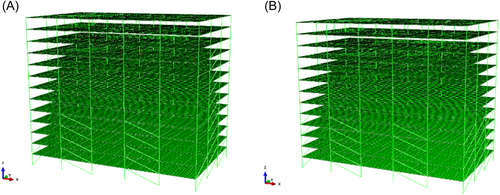
In the V program, the dampers are arranged symmetrically in 2–4 spans in 1–4 floors in the X direction of the structure, the dampers are arranged symmetrically in 1–2 floors in the Y direction, and the dampers are arranged symmetrically in 2 spans in the 3–11 floors. In the P program, the dampers are arranged symmetrically in 2–4 spans in the 1-4 floors in the X direction of the structure, and the dampers are arranged symmetrically in the 1–4 floors in the Y direction (Table 2).

Table 2. Damper arrangement.

Damper arrangement method	Number of dampers		Layout floor
Damper arrangement method	X	Y	X	Y
Planar symmetrical arrangement, P-X	20		1–5 floors; 2-span and 4-span arrangements	–
Planar symmetrical arrangement, P-Y	–	20	–	Full-span arrangement; 1–5 floors
Vertical symmetrical arrangement, V-X	20	–	1–5 floors; 2-span and 4-span arrangements	–
Vertical symmetrical arrangement, V-Y	–	20	–	1–2 full-span arrangement; 3–9 floors with mid-span arrangement

Through calculation and analysis, the vibration modes of the structure are found to be X-direction translation, Y-direction translation, and Z torsion (Figures 3-8).

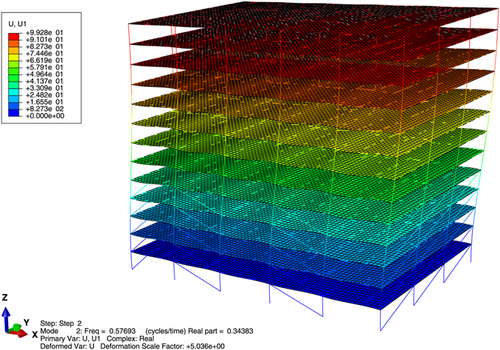
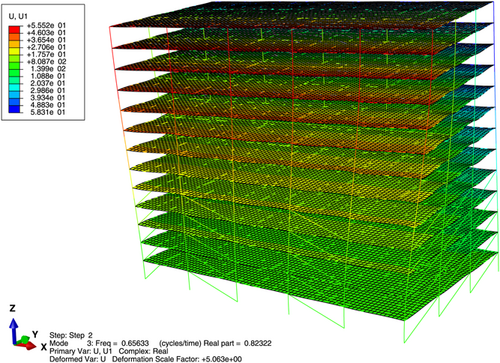
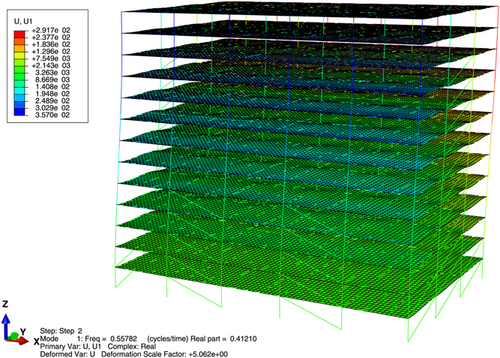
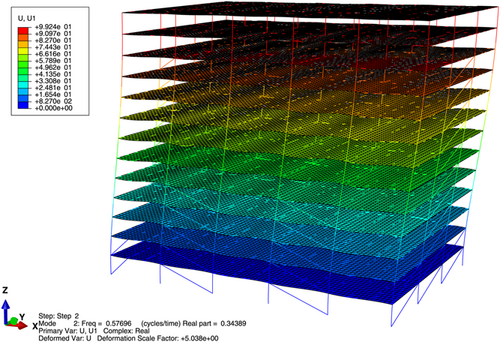
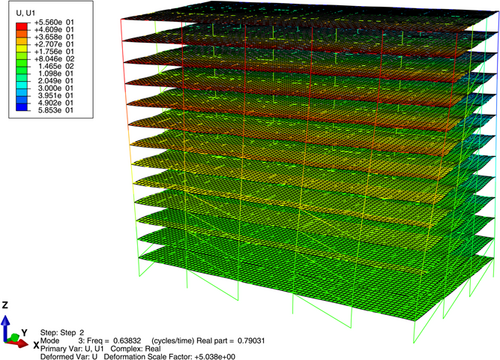
The complex mode shapes of the nonclassically damped elastoplastic shear frame are plotted in Figures 3-5. The shapes indicate the effect of structural nonlinearity considering design earthquakes and when strength reduction is insufficient to force the structure into the nonlinear range of the earthquake. The real part of the nonproportionally damped system represents the effect of energy dissipation, and the imaginary component represents the influence of energy conversion. In the case of a yielding system, softly and heavily damped equivalent modal oscillations are identified. High values of the real part of the eigenvalue lead to high frequencies due to nonlinear and hysteretic behavior, reflecting the improvement in the energy dissipation mechanism. The comparison shows that the damped trend of modal vibration has been amplified, and the value is higher than the corresponding pre-yield value (Table 3).

Table 3. Complex modal analysis results.

Mode shape	Eigenvalues	Circular frequency (rad/s)	Frequency (Hz)	Damping ratio
Undamped linear elastic structure
1st mode	3.16i	3.16	0.50	0
2nd mode	3.29i	3.29	0.52	0
3rd mode	3.77i	3.77	0.60	0
Nonclassically damped pre-yield structure (linear range)
1st mode	−0.25 + 3.52i	3.53	0.56	0.14
2nd mode	−0.18 + 3.64i	3.64	0.58	0.10
3rd mode	−0.62 + 4.04i	4.09	0.65	0.31
Nonclassically damped yield structure (nonlinear range)
1st mode	−0.41 + 3.50i	3.50	0.56	0.23
2nd mode	−0.34 + 3.63i	3.63	0.58	0.19
3rd mode	−0.79 + 4.01i	4.01	0.64	0.39

In the special case of an undamped linear system, all eigenvalues appear in complete imaginary complex pairs (Table 3), whereas the associated eigenvectors are real values, that is, = 0 and . In this study, the eigenvectors are normalized such that the real part of the displacement of a layer is uniform, and the corresponding imaginary number is zero. The study further proves that regardless of whether the damping method is classical or nonclassical, the natural frequency of the highest-order mode shape of the damped system is consistently less than or equal to the corresponding undamped frequency. For linear elastic multi-DOF structural systems, the pseudo-undamped natural frequency of the lowest mode may be equal to or even higher than the corresponding undamped natural frequency.

Note that the quasi-undamped natural frequency has an increasing order. Accordingly, forced vibration modal properties can be used with properly defined linear response spectrum () ordinate readings.

5.4 Comparison of response spectra and time history analysis

Seven seismic waves were calculated using the Chinese seismic design code for time course analysis. Two artificial waves and five natural waves (Figure 9) are used to analyze the elastic time history of a multi-DOF vibration damping structure. Subsequently, the analysis results are compared with those of the CCQC and CQC.

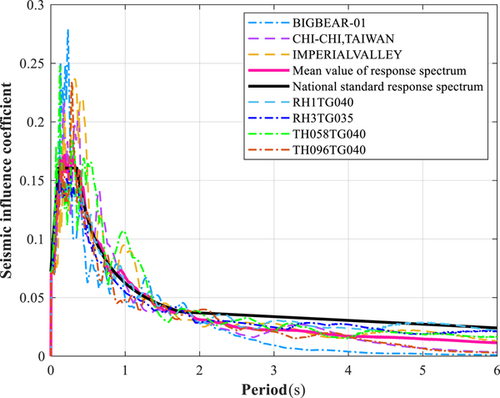
The dynamic elastic time history analysis of the structure is implemented. The ground acceleration time history curve of ground motion is selected from the actual recorded time history curve of the seismic wave database (Tg = 0.35–0.45 s according to the seismic code of China for Class II sites). At the time history point, the difference does not exceed 20%. Note that the calculated shear force at the bottom of the structure, as indicated by the time history curve, must not be less than 65% and not more than 135% of the result calculated by the CQC method. The average value of the shear force at the bottom of the structure given by multiple time history curves must not be less than 80% and not more than 120% of the calculation results of the CQC method.^{40, 41} The calculation results show that two artificial and five natural waves have been selected. Moreover, dynamic elastic–plastic analyses of the three-way seismic wave input and three-way input peak value are implemented. To analyze the structure, the ratios must be X:Y:Z = 1:0.85:0.65 and Y:X:Z = 0.85:1:0.65. The main direction wave peak value is 220 Gal, and the wave duration is 40 s.

In the following tables, GM1, GM2, GM3, GM4, GM5, GM6, and GM7 denote CHI-CHI (TAIWAN), BIGBEAR-01, RH1TG040, RH3TG035, TH096TG040, TH058TG040, and IMPERIAL VALLEY seismic waves, respectively.

When the dampers (P-X, Y) are arranged in a plane, the spectral analysis of the structure shows the following (Figures 10, 11). The ratios of the base shear force in the X direction obtained by the uncontrolled structure CQC, controlled structure time history, and controlled structure CQC methods to the base shear force obtained by the controlled structure CCQC method are 1.27, 1.12, and 0.99, respectively; the ratios in the Y direction are 1.34, 1.30, and 1.00, respectively. When the dampers are arranged vertically, the ratios of the base shear force in the X direction obtained by the uncontrolled structure CQC, controlled structure time history, and controlled structure CQC methods to the base shear force obtained by the controlled structure CCQC method are 1.27, 1.12, and 0.99, respectively; the ratios in the Y direction are 1.30, 1.19, and 0.99, respectively (Table 4).

Table 4. Base shear force results of elastic time history analysis.

Direction	Analysis of working conditions	Base shear
Direction	Analysis of working conditions	No. of control structure CQC	GM1	GM2	GM3	GM4	GM5	GM6	GM7	AVE	CCQC	CQC
P-X	Ratio of spectral analysis results to CCQC	9825	9056	7440	8578	8791	8128	11 420	7151	8652	7720	7675
P-X	Ratio of spectral analysis results to CCQC	1.27	1.17	0.96	1.11	1.14	1.05	1.48	0.93	1.12	1.00	0.99
V-X	Ratio of spectral analysis results to CCQC	9825	9058	7440	8576	8794	8130	11 419	7151	8653	7720	7675
V-X	Ratio of spectral analysis results to CCQC	1.27	1.17	0.96	1.11	1.14	1.05	1.48	0.93	1.12	1.00	0.99
P-Y	Ratio of spectral analysis results to CCQC	10 838	9263	9060	9505	10 770	12 663	11 106	11 381	10 536	8117	8076
P-Y	Ratio of spectral analysis results to CCQC	1.34	1.14	1.12	1.17	1.33	1.56	1.37	1.40	1.30	1.00	1.00
V-Y	Ratio of spectral analysis results to CCQC	10 838	8939	8787	9568	9638	11 713	10 002	10 629	9896	8307	8241
V-Y	Ratio of spectral analysis results to CCQC	1.30	1.08	1.06	1.15	1.16	1.41	1.20	1.28	1.19	1.00	0.99

Note: The values in bold are the mechanical indexes calculated by the average value of time history analysis method (GM1-GM7) of uncontrolled structure and controlled structure, CCQC method and CQC method, in order to highlight the numerical comparison.
Abbreviations: AVE, average value of mechanical indexes of GM1-GM7; CQC, complete quadratic combination; CCQC, complex CQC.

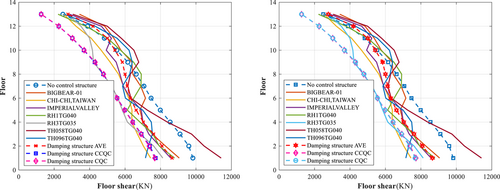
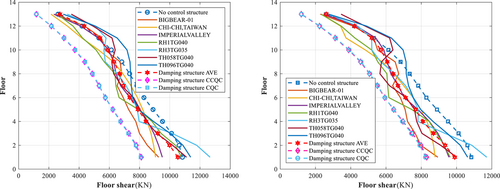
The spectral analysis of the structure shows that when the dampers (P-X, Y) are arranged in a plane, the ratios of the basement overturning moment in the X direction obtained by the uncontrolled structure CQC, controlled structure time history, and controlled structure CQC methods to the basement overturning (Figures 12 and 13) bending moment obtained by the controlled structure CCQC method are 1.33, 1.08, and 1.00, respectively; the ratios in the Y direction are 1.21, 1.00, and 1.00, respectively. When the damper is arranged vertically, the ratios of the basement overturning moment in the X direction obtained by the uncontrolled structure CQC, controlled structure time history, and controlled structure CQC methods to the basement overturning bending moment of the controlled structure CCQC method are 1.33, 1.08, and 1.00, respectively; the ratios in the Y direction are 1.14, 1.00, and 1.00, respectively (Table 5).

Table 5. Base bending moment obtained by elastic time history analysis.

Direction	Analysis of working conditions	Base bending moment
Direction	Analysis of working conditions	No of control structure CQC	GM1	GM2	GM3	GM4	GM5	GM6	GM7	AVE	CCQC	CQC
P-X	Ratio of spectral analysis results to CCQC	258 081	215 249	214 219	2r13 478	218 885	185 075	204 922	209 571	208 771	193 654	193 578
P-X	Ratio of spectral analysis results to CCQC	1.33	1.11	1.11	1.10	1.13	0.96	1.06	1.08	1.08	1.00	1.00
V-X	Ratio of spectral analysis results to CCQC	258 081	215 261	214 235	213 528	218 864	185 129	204 917	209 572	208 787	193 658	193 582
V-X	Ratio of spectral analysis results to CCQC	1.33	1.11	1.11	1.10	1.13	0.96	1.06	1.08	1.08	1.00	1.00
P-Y	Ratio of spectral analysis results to CCQC	288 166	229 996	274 728	256 972	224 294	249 285	208 551	254 795	242 660	201 321	201 253
P-Y	Ratio of spectral analysis results to CCQC	1.43	1.14	1.36	1.28	1.11	1.24	1.04	1.27	1.21	1.00	1.00
V-Y	Ratio of spectral analysis results to CCQC	288 166	222 103	260 364	253 184	212 866	248 331	205 091	263 779	237 960	208 800	208 630
V-Y	Ratio of spectral analysis results to CCQC	1.43	1.06	1.25	1.21	1.02	1.19	0.98	1.26	1.14	1.00	1.00

Note: The values in bold are the mechanical indexes calculated by the average value of time history analysis method (GM1-GM7) of uncontrolled structure and controlled structure, CCQC method and CQC method, in order to highlight the numerical comparison.
Abbreviations: AVE, average value of mechanical indexes of GM1-GM7; CQC, complete quadratic combination; CCQC, complex CQC.

Comparing the seismic responses of the controlled and uncontrolled structures indicates that the arrangement of dampers can effectively reduce the seismic response. The base shear force and overturning bending moment of a regular multilayer energy-dissipating and shock-absorbing frame structure calculated by the CCQC and CQC methods are highly consistent. The results show that the forced decoupling method has an insignificant influence on the mechanical performance index obtained by the CQC response spectrum method to analyze the seismic performance of weakly damped structures. The time history analysis and response spectrum methods yield considerable errors. When the response spectrum method is applied to actual engineering design, time history analysis must be implemented. Moreover, by modifying the position of the damper in the Y direction, the energy dissipation and vibration damping of the vertically arranged dampers (V-X, Y) are better than those of the dampers arranged in a plane (P-X, Y).

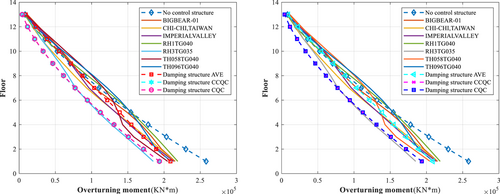
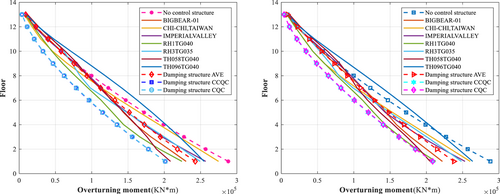
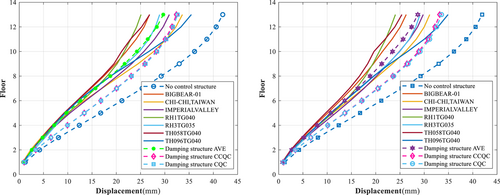
The analysis results show that when the dampers are arranged in a plane, the maximum displacements (Figures 14 and 15) in the X direction of the structure obtained by the uncontrolled structure CQC, controlled structure time history, controlled structure CCQC, and controlled structure CQC methods are 45.960, 34.153, 41.650, and 41.980 mm, respectively; in the Y direction, the maximum displacements are 41.930, 29.677, 32.380, and 32.640 mm, respectively. When the dampers are arranged vertically, the maximum displacements in the X direction of the structure obtained by the uncontrolled structure CQC, controlled structure time history, controlled structure CCQC, and controlled structure CQC methods are 45.960, 29.677, 32.380, and 32.640 mm, respectively; in the Y direction, the maximum displacements are 41.930, 28.667, 33.180, and 33.560 mm, respectively (Table 6).

Table 6. Structural floor displacement.

Direction	Structural floor displacement
Direction	No of control structure CQC	GM1	GM2	GM3	GM4	GM5	GM6	GM7	AVE	CCQC	CQC
P-X	45.960	35.800	33.860	34.830	37.710	28.860	31.580	36.430	34.153	41.650	41.980
V-X	45.960	35.830	33.970	34.460	37.730	28.810	31.590	36.330	34.103	41.650	41.980
P-Y	41.930	26.840	33.620	30.920	25.090	28.930	26.880	35.460	29.677	32.380	32.640
V-Y	41.930	26.280	31.130	29.790	24.060	29.120	25.390	34.900	28.667	33.180	33.560

Note: The values in bold are the mechanical indexes calculated by the average value of time history analysis method (GM1-GM7) of uncontrolled structure and controlled structure, CCQC method and CQC method, in order to highlight the numerical comparison.
Abbreviations: AVE, average value of mechanical indexes of GM1-GM7; CQC, complete quadratic combination; CCQC, complex CQC.

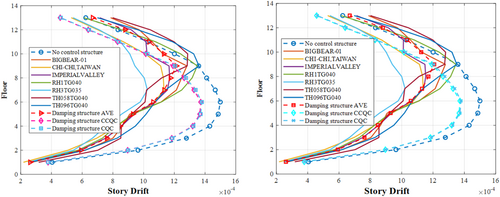
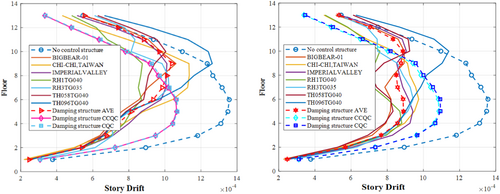
The analysis results show that when the dampers are arranged in a plane, the maximum drifts (Figures 16 and 17) of the structure in the X direction obtained by the uncontrolled structure CQ, controlled structure time history, controlled structure CCQC, and controlled structure CQC methods are 1/667, 1/824, 1/729, and 1/725, respectively; in the Y direction, the maximum drifts are 1/737, 1/963, 1/939, and 1/935, respectively. When the dampers are arranged vertically, the maximum drifts in the X direction of the structure obtained by the uncontrolled structure CQC, controlled structure time history, controlled structure CCQC, and controlled structure CQC methods are 1/667, 1/828, 1/729, and 1/725, respectively; in the Y direction, the maximum drifts are 1/737, 1/1124, 1/921, and 1/914, respectively (Table 7). The dampers absorb seismic energy, constrain the displacement and deformation of the structure, and reduce the structure's seismic response.

Table 7. Structural floor drift.

Direction	Structural floor drift
Direction	No of control structure CQC	GM1	GM2	GM3	GM4	GM5	GM6	GM7	AVE	CCQC	CQC
P-X	1/667	1/780	1/883	1/855	1/741	1/976	1/777	1/735	1/824	1/729	1/725
V-X	667	1/782	1/880	1/867	1/743	1/979	1/781	1/740	1/828	1/729	1/725
P-Y	1/737	1/942	1/881	1/989	1/1143	1/978	1/995	1/792	1/963	1/939	1/935
V-Y	1/737	1/1119	1/1027	1/1062	1/1136	1/1060	1/1082	1/877	1/1124	1/921	1/914

Note: The values in bold are the mechanical indexes calculated by the average value of time history analysis method (GM1-GM7) of uncontrolled structure and controlled structure, CCQC method and CQC method, in order to highlight the numerical comparison.
Abbreviations: AVE, average value of mechanical indexes of GM1-GM7; CQC, complete quadratic combination; CCQC, complex CQC.

The nonproportional damping characteristics of the structure are described by the nonproportional damping characteristic index. For the P and V programs, the nonproportional damping characteristic index () values are 0.3915 and 0.3316, respectively. This indicates that the energy dissipation and damping of the structure are nonproportional with respect to the arrangement of dampers in the P and V programs.

For the energy dissipation and vibration damping structure system, the base shear force and displacement of the structure calculated by the CCQC and CQC response spectrum methods are the same. The errors caused by ignoring the nondiagonal elements in the damped matrix using the traditional CQC response spectrum forced decoupling method are found to have an inconsequential effect on the structure. The results of the elastic time history supplementary analysis method exceed those of the CCQC and CQC response spectrum methods. The response spectrum method does not ignore the irregularity of the structure (irregular load distribution and structure layout) and traveling wave effect. The time history analysis method compensates for the deficiency of the static response spectrum method, further verifying that the elastic time history supplementary calculation is required for the structure. As an approximation technique, the forced decoupling method is valuable because it only involves a small amount of decoupling calculation. Moreover, a sufficiently accurate solution can be obtained when the degree of nonproportional damping is low.

The list in Table 8 indicates that the vibration response and additional damping ratio of the structure improve; the range of improvement is 4.17%–26.83% with an average of 12.83%.

Table 8. Time history analysis and comparison of damping ratio among different arrangement forms.

iWave	iDir	P-ΣWcj	P-WS	V-ΣWcj	V-WS	V-ζa (%)	P-ζa (%)	Δζ/P-ζa (%)
1	1	63,598	127,385	68,425	127,408	4.3	4	7.50
1	2	43,161	101,481	51,550	94,752	4.3	3.4	26.47
2	1	104,517	95,098	115,542	95,572	9.6	8.7	10.34
2	2	110,791	109,738	118,140	101,630	9.3	8	16.25
3	1	63,836	110,138	66,985	110,471	4.8	4.6	4.35
3	2	73,417	109,715	79,879	109,861	5.8	5.3	9.43
4	1	74,078	121,478	81,484	121,460	5.3	4.9	8.16
4	2	63,517	95,652	66,730	88,835	6	5.3	13.21
5	1	123,217	80,227	134,245	80,386	13.3	12.2	9.02
5	2	134,013	116,083	144,594	108,846	10.6	9.2	15.22
6	1	42,018	138,252	43,216	138,170	2.5	2.4	4.17
6	2	34,659	110,522	38,438	98,352	3.1	2.5	24.00
7	1	66,512	123,950	70,364	123,956	4.5	4.3	4.65
7	2	68,760	134,641	84,425	129,022	5.2	4.1	26.83

When dampers are arranged in the structure, the velocity-type energy dissipator can play an improved role in energy dissipation and vibration damping in the location with a fast velocity response.

When the same number of velocity energy dissipators are arranged in the same structure, the hysteresis curve corresponding to the vertical arrangement of dampers is full (Figures 18 and 19); the output force and stroke of the dampers are considerable, and the hysteretic energy consumption is sufficient.

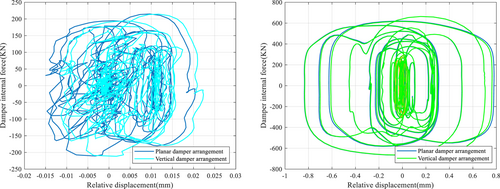
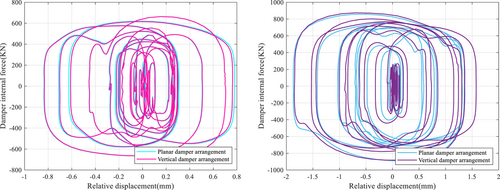
To achieve improved energy dissipation and vibration damping, uniform, symmetrical, and vertical arrangements of velocity energy dissipators in the structure are preferred.

6 CONCLUSIONS

Using structural multidimensional seismic and flat-torsion coupled seismic response analyses with virtual excitation method determines the weak positions of the middle and upper parts of the structure. Moreover, energy dissipation and seismic reduction are affected by the traveling wave effect to a relatively low degree.

The nonproportional damping characteristics of the system can be determined by the nonproportional damping characteristic index based on the different arrangement of dampers. The nonproportional damping characteristic index () values are 0.3915 and 0.3316 for the P and V programs, respectively; both are weakly nonproportionally damped systems. Through analysis and comparison, the calculation accuracy of the complex vibration type superposition method (CCQC) for nonproportionally damped structures is higher than that of the actual vibration type decomposition response spectrum method (CQC). When the energy-dissipating components are evenly distributed in the structure, and the damping ratio does not exceed 0.20, the effective damping ratio introduced by these components to the structure can also be determined by the forced decoupling method. The forced decoupling method ignores the damping term of the off-diagonal matrix. Most errors between the forced decoupling and exact solution can be limited within 5%, which can satisfy engineering design requirements.

Through the spectrum and time history analysis of the uncontrolled structure and the controlled structure, the bottom shear force, bottom bending moment, displacement and drift indexes of the uncontrolled structure and the controlled structure are compared. After the damper is installed, the deformation and force of the uncontrolled structure are effectively controlled. The arrangement of the dampers in the X direction of the V Program and the P Program is the same, and the analysis results of the structural system are consistent. However, compared with the P Program, the bottom shear force of the structure in the Y direction is reduced by 8.46%, the bottom bending moment is reduced by 5.79%, the displacement is reduced by 3.4%, and the drift is reduced by 16.72%.

Depending on the arrangements of dampers in the structure, velocity-type energy dissipators can play an improved role in energy dissipation and vibration damping when the velocity response is considerable. The vibration response of the structure and additional damping ratio of the structure improve. The improvement range is 4.17%–26.83%, with a mean of 12.83%.

ACKNOWLEDGMENTS

This research is funded by the National Key Research and Development Program of China (Grant No. 2021YFC3100701), the National Natural Science Foundation of China (Grant No. 51978185).

CONFLICTS OF INTEREST STATEMENT

The authors declare no conflicts of interest.

REFERENCES

1Ou J, Wu B, Long X. Seismic design method of energy-dissipating and shock-absorbing structures. Earthq Eng Eng Vib. 1998;(2): 98-107.
Google Scholar
2Liu Q, Yuan X, Gao H, Fu X. Mode superposition methods based on hysteretic damped assumption used in seismic calculation of hybrid structures. Future Gener Comput Syst. 2021; 9: 361-368.
10.1016/j.future.2021.06.006
Google Scholar
3Ibrahimbegovic A, Wilson EL. Simple numerical algorithms for the mode superposition analysis of discrete linear systems with nonproportional damped. Comput Struct. 1989; 33(2): 523-531.
10.1016/0045-7949(89)90026-6
Web of Science® Google Scholar
4Pavic G. Analysis of vibration reduction by damped using simple analytical modelling. Shock Vib. 2018; 1-13.
Web of Science® Google Scholar
5Occhiuzzi A. Additional viscous dampers for civil structures: analysis of design methods based on effective evaluation of modal damping ratios. Eng Struct. 2009; 31(5): 1093-1101.
10.1016/j.engstruct.2009.01.006
Web of Science® Google Scholar
6Aydin E, Ozturk B, Bogdanovic A, Farsangi EN. Influence of soil-structure interaction (SSI) on optimal design of passive damping devices. Structures. 2020; 28: 847-862.
10.1016/j.istruc.2020.09.028
PubMed Web of Science® Google Scholar
7Tang D, Sun X, Yue Q, Shi Z, Feng J. Research of complex modal parameters extraction of a multi-degree-of-freedom structure based on similarity search. Ocean Eng. 2015; 108: 307-314.
10.1016/j.oceaneng.2015.07.060
Web of Science® Google Scholar
8Gui G, He Y. Matrix perturbation method for solving complex modal problems of non-proportional damped structures. J. Tongji Univ. (Natural Science Edition). 1996;(6): 613-618.
Google Scholar
9Gui G, He Y. Error research in approximate decoupling analysis of non-proportional damped structural systems. Eng Mech. 1994;(4): 40-45.
Google Scholar
10Gui G, He Y. Pseudo-force real modal superposition method for dynamic analysis of non-proportional damped linear structural systems. Eng Mech. 1992;( 2): 23-35.
Google Scholar
11Wang M. Mode shape decomposition response spectrum method for seismic response calculation of non-proportional damped linear system. Earthq Eng Eng Vib. 2007;( 1): 31-37.
Google Scholar
12Du Y, Xu T, Bao C, Chen K, Hong N. Non-linear response spectrum study of foundation isolation structures considering non-proportional damped. Vib Shock. 2016;( 17): 207-212.
Google Scholar
13Du Y, Zhang S. Matrix perturbation method for dynamic response analysis of non-proportional damped-isolated structures. In: Proceedings of the National Symposium on Structural Vibration and Dynamics; 2011: 146-148.
Google Scholar
14Guo W, Li HN, Guo Z. Perturbation spectrum method for seismic analysis of non-classically damped systems. J Zhejiang Univ Sci (Volume A English Edition). 2010; 11(5): 325-334.
10.1631/jzus.A0900155
Web of Science® Google Scholar
15Wang M. Using virtual excitation method to solve non-stationary random earthquake response of non-proportional damped linear system. Mech Q. 2006;( 4): 598-605.
Google Scholar
16Wang M. A virtual excitation method for the calculation of stationary random seismic response of non-proportional damped linear systems. Chin J Comput Mech. 2008;(1): 94-99.
Google Scholar
17Zhou X, Ma D, Yu R. The perfect square combination of damped and complex seismic response in engineering structures. Chin J Civil Eng. 2005;( 1): 31-39.
Google Scholar
18Zhou X, Yu R. CCQC method based on gauge response spectrum for non-proportional damped linear systems. Eng Mech. 2006;(2):10-17+9.
Google Scholar
19Du Y, Li H, Su P, Zhao G. Actual vibration type decomposition method for seismic response of non-proportional damped-isolated structures. Eng Mech. 2003;( 4): 24-32.
Google Scholar
20Chen H, Bi K, Liu Y, Tan P. Performance evaluation of multiple tuned inerter-based dampers for seismic induced structural vibration control. Struct Control Health Monit. 2022; 29:e2860.
10.1002/stc.2860
Web of Science® Google Scholar
21Chen H, Tan P. Optimal design of TVMD with linear and nonlinear viscous damping subjected to white-noise excitation. Struct Control Health Monitor. 2021; 28:e2694.
10.1002/stc.2694
Web of Science® Google Scholar
22Chen H, Peng L. Dynamic analysis of heavily damped structures with supplemental energy dissipation devices. J Earthq Eng. 2020.
Web of Science® Google Scholar
23Chen H, Tan P, Zhou F. An improved response spectrum method for non-classically damped systems. Bull Earthq Eng. 2017; 15(10): 4375-4397.
10.1007/s10518-017-0144-4
Web of Science® Google Scholar
24Chen H, Hao H, Bi K, Tan P, Peng L, Zhou F. Dynamic analysis of nonclassically damped systems with linear behavior using load-dependent ritz vectors. Int J Struct Stab Dyn. 2019; 19(3):1950022.
10.1142/S0219455419500226
Web of Science® Google Scholar
25Yu R, Zhou X. Partial quadratic combination (CPQC) method for seismic response of non-proportional damped linear systems. Chin J Civil Eng. 2006; 11: 43-49+126.
Google Scholar
26Hao H, Oliveira CS, Penzien J. Multiple-station ground motion processing and simulation based on smart-1 array data. Nucl Eng Des. 1989; 111(3): 293-310.
10.1016/0029-5493(89)90241-0
Web of Science® Google Scholar
27Jing B, Xingjian J. Nonlinear passive damped of the x-shaped structure. Proc Eng. 2017; 199: 1701-1706.
10.1016/j.proeng.2017.09.372
Google Scholar
28Podworna M, Sniady P, Grosel J. Random vibrations of a structure modified by damped absorbers. Probabilistic Eng Mech. 2021; 66(7):103151.
10.1016/j.probengmech.2021.103151
Google Scholar
29Spiteri S. Shock absorber applications. Eur J Eng Technol Res. 2019; 4(1): 37-41.
Google Scholar
30Zhou F. Damped Control of Engineering Structures. Seismological press; 1997.
Google Scholar
31Luo H, Ikago K, Chong C, Keivan A, Phillips BM. Performance of low-frequency structures incorporated with rate-independent linear damped. Eng Struct. 2018; 181(FEB.15): 324-335.
Google Scholar
32Augusti G. Dynamics of Structures: Theory and Applications to Earthquake Engineering. Tsinghua University Press; 2005.
Google Scholar
33Clough RW, Penzien J. Dynamics of Structures. 3rd ed. Computers and Structures, Inc; 1991.
Google Scholar
34Chopra AK. Dynamics of Structures: Theory and Applications to Earthquake Engineering. 4th ed. Pearson Education, Inc; 2012.
Google Scholar
35Vanmarcke EH. Properties of spectral moments with applications to random vibration. J Eng Mech. 1972; 98: 425-446.
10.1061/JMCEA3.0001593
Google Scholar
36Zhou XY, Yu RF, Dong D. Complex mode superposition algorithm for seismic responses of non-classically damped linear MD of system. J Earthq Eng. 2004; 8(4): 597-641.
10.1080/13632460409350503
Web of Science® Google Scholar
37ABAQUS Inc. ABAQUS 6.14 HTML Documentation, Abaqus Theory Guide [TD]; 2014.
Google Scholar
38ABAQUS Inc. ABAQUS 6.14 HTML Documentation, Abaqus Analysis User's Guide [TD]; 2014.
Google Scholar
39ABAQUS Inc. ABAQUS 6.14 HTML Documentation, Abaqus User Subroutines Reference Guide [TD]; 2014.
Google Scholar
40JGJ3-2010 Technical Specifications for Concrete Structures of High-rise Buildings. China Construction Industry Press; 2011.
Google Scholar
41JGJ3-2010 Code for seismic design of buildings. China Construction Industry Press; 2010.
Google Scholar

Volume2, Issue1

March 2023

Pages 5-28

This article also appears in:

Seismic performance analysis of structures with energy dissipation systems

Investigation of nonproportional damping characteristics of structure with energy dissipation system

Abstract

1 INTRODUCTION

2 COMPLEX MODE ANALYSIS METHOD FOR DAMPED STRUCTURES

2.1 Compound mode superposition method

2.2 Mass participation coefficient of complex mode in modal analysis

2.3 Fundamental equation of motion of CCQC mode superposition method

3 CCQC MODE SHAPE COMBINATIONS

4 MECHANICAL PROPERTIES OF FLUID DAMPERS

5 ARRANGEMENT AND PARAMETER OPTIMIZATION OF DAMPERS FOR NONPROPORTIONALLY DAMPED SYSTEMS

5.1 Nonproportional damping characteristic index

5.2 Traveling wave effect

5.3 Complex modal analysis of nonproportionally damped structural systems

5.4 Comparison of response spectra and time history analysis

6 CONCLUSIONS

ACKNOWLEDGMENTS

CONFLICTS OF INTEREST STATEMENT

REFERENCES

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Investigation of nonproportional damping characteristics of structure with energy dissipation system

Abstract

1 INTRODUCTION

2 COMPLEX MODE ANALYSIS METHOD FOR DAMPED STRUCTURES

2.1 Compound mode superposition method

2.2 Mass participation coefficient of complex mode in modal analysis

2.3 Fundamental equation of motion of CCQC mode superposition method

3 CCQC MODE SHAPE COMBINATIONS

4 MECHANICAL PROPERTIES OF FLUID DAMPERS

5 ARRANGEMENT AND PARAMETER OPTIMIZATION OF DAMPERS FOR NONPROPORTIONALLY DAMPED SYSTEMS

5.1 Nonproportional damping characteristic index

5.2 Traveling wave effect

5.3 Complex modal analysis of nonproportionally damped structural systems

5.4 Comparison of response spectra and time history analysis

6 CONCLUSIONS

ACKNOWLEDGMENTS

CONFLICTS OF INTEREST STATEMENT

REFERENCES

Figures

References

Related

Information