Mechanistic Insights into Electrocatalytic Nitrogen Reduction Reaction on the Pd-W Heteronuclear Diatom Supported on C2N Monolayer: Role of H Pre-Adsorption
Abstract
The electrocatalytic N2 reduction reaction (eNRR) is a potential alternative to the Haber–Bosch process for ammonia (NH3) production. Tremendous efforts have been made in eNRR catalyst research to promote the practical application of eNRR. In this work, by means of density functional theory calculations and the computational hydrogen electrode model, we evaluated the eNRR performance of 30 single metal atoms supported on a C2N monolayer (M@C2N), and we designed a new thermodynamically stable Pd-W hetero-metal diatomic catalyst supported on the C2N monolayer (PdW@C2N). We found that PdW@C2N prefers to adsorb H over N2, and then, the pre-generated hydrogen-terminated PdW@C2N selectively adsorbing N2 behaves as the actual functioning “catalyst” to catalyze the eNRR process, exhibiting excellent performance with a low overpotential (0.31 V), an ultra-low NH3 desorption free energy (0.05 eV), and a high selectivity toward eNRR over hydrogen evolution reaction (HER). Moreover, PdW@C2N shows a superior eNRR performance to its monomer (W@C2N) and homonuclear diatom (W2@C2N) counterparts. The revealed mechanism indicates that the preferential H adsorption over N2 on the active site may not always hamper the eNRR process, especially for heteronuclear diatom catalysts. This work encourages deeper exploration on the competition of eNRR and HER on catalyst surfaces.
1 Introduction
Ammonia (NH3) is a vitally important feedstock in nitrogen fertilizer agriculture and chemical industry,[1-3] and it has promising applications in carbon-free energy storage due to its high energy density, safety, and being eco-friendly.[4] Conventionally, the industrial-scale NH3 production is realized by the well-known Haber–Bosch process under harsh reaction conditions (high temperature of 400–600°C and high pressure of 20–40 MPa).[5] Owing to the high bond energy of the covalent triple bond of N2 (940.95 kJ·mol−1) and the large hydrogen demand, the NH3 production by the Haber–Bosch method requires a high energy input (over 1% of the global annual energy supply) and results in excessive CO2 emission.[6] It is desired to develop economical and clean alternatives for NH3 production with minimal energy consumption and CO2 release.
The electrocatalytic N2 reduction reaction (eNRR) [N2(g) + 6H+/e− → 2NH3(g)] with water as proton source has attracted considerable interests over the past several years as a clean, carbon-free, and sustainable NH3 synthesis method under ambient conditions.[7] It is expected to be an ideal alternative to the Haber–Bosch process.[8, 9] Up to now, a wide spectrum of catalysts have been developed for eNRR, including traditional noble metal catalysts (e.g., Ru,[10, 11] Rh,[10, 12] Pd,[13] Pt,[14] and Au[15]) with efficient eNRR activity but high cost and a series of recently reported non-noble-metal-based catalysts (e.g., transition metal oxides,[16-20] carbides,[21-24] nitrides,[25-27] and sulfides[28-33]), metal-free catalysts (e.g., B4C,[34] B-doped black phosphorus,[35] B-doped graphene,[36] N-doped porous carbon,[37] and polymeric carbon nitride[38]), and single-atom catalysts (SACs) with superior catalytic activity, high selectivity, and advantages of high atom utilization.[39-43] Among them, the SACs supported on two-dimensional (2D) materials[44-49] and their derivates, for example, double-atom catalysts (DACs),[50, 51] get widespread concern in recent years.
The porous C2N monolayer reported firstly in 2015,[52] a highly stable[53] 2D material with evenly distributed nitrogenated cavities, is an excellent candidate of substrates for SACs or DACs, because the N atoms of cavities can strongly anchor metal atoms by lone-pair electrons, and the natural large-size cavity makes it also able to support one or two atoms in one cavity. Moreover, the C2N monolayer has an outstanding electrical conductivity needed for electrocatalysts.[52] Recently, C2N-based SAC and DAC catalysts have been designed toward efficient eNRR.[54-58]
Wang et al.[54] predicted theoretically that Mo single atom supported on C2N monolayer (Mo@C2N) has the most excellent eNRR performance with an amazingly low limiting potential (Ulimiting) of −0.17 V among a series of C2N-based SACs (M@C2N, M = Sc, Ti, V, Cr, Mn, Fe, Co, Ni, Cu, Zn, Mo, Ru, Rh, Pd, and Ag). Zhang et al.[55] found the binding strength of the second anchored atom in the same cavity to be comparable to or even stronger than that of the first one for the most metal atoms (M = Fe, Co, Cu, Mo, Ru, Rh, Pd, Ir, and Pt), which indicates the more favorable formation of homonuclear double-atom catalysts (M2@C2N), and so they investigated the catalytic performance of M2@C2N for eNRR and eventually recommended Mo2@C2N with Ulimiting = −0.41 V. More recently, Lv et al.[56] suggested Fe2@C2N being a better eNRR catalyst with an even lower limiting potential (−0.13 V) by the first-principle high-throughput screening over 23 C2N-based homonuclear transition metal DACs. Nevertheless, the NH3 desorption free energies on these homonuclear double-atom catalysts are relatively high (e.g., 0.49 eV for Mo2@C2N and 0.85 eV for Fe2@C2N) because of the negative linear correlation between the strength of N2 activation and the ability of NH3 desorption on the same metal, and it means that the active centers of these catalysts could not recycle rapidly. This undesirable linear scaling relationship has been observed in many studies for eNRR.[59-62]
Besides the C2N-supported transition metal SACs and DACs, there exist some studies about C2N-based metal-free catalysts toward eNRR. For example, in 2019, Ji et al.[57] demonstrated computationally the potential of B-doped C2N monolayer (B@C2N) as a metal-free eNRR catalyst which has a low limiting potential (Ulimiting = −0.15 V) via an enzymatic pathway. In the same year, Cao et al.[58] reported a more negative limiting potential for B@C2N (Ulimiting = −0.45 V) and suggested B2@C2N with a less negative Ulimiting ( −0.35 V) to be more efficient as eNRR catalyst compared to B@C2N. The NH3 desorption free energies on B@C2N and B2@C2N were estimated to be 1.94 eV and 0.81 eV,[58] respectively, again too high to easily remove NH3 from the catalyst surface.
Although some reported numbers are inconsistent, these studies all show that the C2N-based SAC or homonuclear DAC catalyst can sufficiently activate the N2 molecule and then easily hydrogenate it into *NH3, but with a difficult NH3 desorption. In a previous study, we have demonstrated that heteronuclear diatom active centers can break the unfavorable linear constraint between the N2 activation and the NH3 desorption by integrating the advantages of two different metal elements.[63] Therefore, in this work, following the idea of heteronuclear diatom catalysts and considering the excellent performance of C2N-based catalysts on N2 activation, we designed theoretically a hetero-metal Pd-W atom pair supported on the C2N monolayer (PdW@C2N) for eNRR and expected it to exhibit a superior catalytic activity (with a low limiting potential and a small ammonia desorption energy simultaneously) and a high selectivity over the competitive hydrogen evolution reaction (HER). By exploring the catalytic mechanism in detail, we found the important role of hydrogen pre-adsorption on metal active centers in promoting the eNRR by effectively reducing the energy need of the ammonia desorption while keeping a high eNRR activity.
2 Computational Details
All the spin-polarized density functional theory (DFT) calculations were based on Perdew–Burke–Ernzerhof (PBE) exchange-correlation functional[64] as implemented in Vienna ab initio simulations package (VASP).[65-68] The core-valence electron interactions were described by the projector augmented wave (PAW) method[69, 70] The standard PAW potentials were employed for simulating the nuclei and frozen-core electrons of H, C, N, O, Sr-Zn, Y-Cd, and Lu-Hg, and the self-consistently calculated valence electrons were 1s1 for H, 2s22p2 for C, 2s22p3 for N, 2s22p4 for O, 2s23p63d14s2 for Sc, 2s23p63d24s2 for Ti, 2s23p63d34s2 for V, 3p63d54s1 for Cr, 3p63d54s2 for Mn, 3d64s2 for Fe, 3d74s2 for Co, 3d84s2 for Ni, 3d104s1 for Cu, 3d104s2 for Zn, 4s24p64d15s2 for Y, 4s24p64d25s2 for Zr, 4s24p64d45s1 for Nb, 4s24p64d55s1 for Mo, 4p64d55s2 for Tc, 4p64d75s1 for Ru, 4p64d85s1 for Rh, 4d10 for Pd, 4d105s1 for Ag, 4d105s2 for Cd, 5p65d16s2 for Lu, 5p65d26s2 for Hf, 5p65d36s2 for Ta, 5s25p65d46s2 for W, 5d56s2 for Re, 5d66s2 for Os, 5d76s2 for Ir, 5d96s1 for Pt, 5d106s1 for Au, and 5d106s2 for Hg. The kinetic energy cutoff for the plane-wave basis set was set as 400 eV. The empirical dispersion correction in Grimme’s scheme (D3)[71] was used to consider van der Waals (vdW) interactions. The optimized lattice constants of bulk C2N (a = b = 8.33 Å, c = 3.26 Å, α = β = 90° and γ = 120°) agree well with the experimental lattice constants (a = b = 8.24 ± 0.96 Å, c = 3.28 Å, α = β = 90° and γ = 120°).[52] All catalysts were modeled by supporting a single metal atom (or a hetero-metal atom pair) on a 2 × 2 × 1 supercell C2N monolayer with the x-axis and y-axis lengths for the simulation cell of 16.66 Å. To avoid the interactions between two neighboring images, a vacuum space of 20 Å in the z-direction was imposed. The surface Brillouin zone was sampled with a 3 × 3 × 1 Monkhorst-Pack k-point grid. More details for the choice of the supercell size (Table S1) and k-point grid (Figure S10) are given in the SI. The geometric structures were fully relaxed until the energy and the force on each atom were converged to less than 10−4 eV and 0.02 eV/Å, respectively.
The effect of water solvent on the eNRR process has been examined for the selected pathways with an implicit solvation model (with the dielectric constant of 78.4) implemented in VASPsol,[72, 73] a microsolvation model including explicit water molecules hydrogen bonding with the N-containing intermediates to mimic the solvation environment, and a mixed implicit plus explicit solvation model.
3 Results and Discussion
In the light of the design strategy we previously proposed,[63] we firstly screened a series of C2N-based SACs and identified two metal elements as the active centers of heteronuclear diatom catalyst. The specific screening strategy includes the following steps: 1) stability assessment of C2N-based single-atom catalysts; 2) evaluation of N2 adsorption on C2N-based SACs; 3) singling out M@C2N with the high eNRR activity; and 4) singling out M'@C2N with a low NH3 desorption free energy. Then, combining the advantages of the metal elements M and M', we constructed a C2N-based heteronuclear diatom catalyst (M'M@C2N) and evaluated its eNRR performance by exploring 1) the thermodynamic stability; 2) the competitive adsorption of N2 and H; 3) the eNRR performance and detailed mechanism; and 4) the eNRR selectivity competing with HER. In the end, we compared the performance of M'M@C2N with the C2N-based SAC (M@C2N) and C2N-based homonuclear DACs (M2@C2N) and thoroughly discussed the role of hydrogen pre-adsorption in the catalytic mechanism.
3.1 Screening of M@C2N
3.1.1 Structure and Stability of M@C2N
First, we constructed and optimized 180 geometric structures of single metal atoms supported on the C2N monolayer (denoted as M@C2N), which are 30 single transition metals bonding to six different binding sites of the C2N monolayer as shown in Figure 1a. The planar structure of C2N substrate is well maintained after metal atoms are captured. For all metal atoms, the most favorable binding site is the site 1, the corner of the six-fold cavity of the C2N, and in these optimal structures, the single metal atoms are in the C2N plane and bonded to two adjacent N atoms with almost equal bond lengths (see Table S2). The corresponding single-atom binding energies are calculated with eq (1) to estimate the stability of M@C2N and shown in Figure 1b. Our results for 3d metal atoms anchored on C2N are almost the same as those predicted by Wang et al.[54]
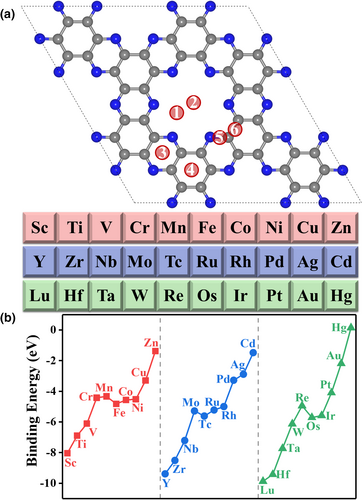
Figure 1b shows that the binding strength of metal atoms in each period generally decreases with the increase of the atomic number (the more negative binding energy means the stronger binding) because the metal atom with more empty d orbitals can better accept the lone-pair electrons of the in-plane sp2 hybrid orbital of N atom of the C2N. The d orbitals of metal atoms in the IB and IIB groups are fully filled, leading to much weaker interactions of these metal atoms with C2N; in particular, the IIB-group metal atoms (Zn, Cd, and Hg) have the weakest binding energy because both of their s and d orbitals are full, and therefore, we expected the poor thermodynamic stability of the associated M@C2N (M = Zn, Cd, and Hg) and would not consider them in the following discussion.
The comparison of the binding energies of metal on the support is not enough to address the relative stability. With the most stable bulk state of the metal as the reference, we can obtain the formation energies. For example, the formation energies of W@C2N and Pd@C2N are 2.87 eV and 1.04 eV, respectively. It indicates that both metals have the risk of clustering on C2N. Thus, to compare the kinetic stabilities of M@C2N, starting from the most stable configuration, we further evaluated the level of difficulty of single metal atom diffusion from the most stable binding site to its neighboring site (site 1 to site 3 in Figure 1a, and the site 3 is also the second most stable anchoring site of metal atoms) as people usually do.[75] The calculated Gibbs free energy changes of the diffusion process for all considered M@C2N SACs are higher than 1.5 eV, indicating that once the M@C2N is synthesized, the single metal atom cannot diffuse easily on the monolayer to form a larger cluster. More encouragingly, a single Co atom embedded in C2N with a positive formation energy (1.07 eV, calculated with the most stable Co bulk state as reference) has been successfully synthesized via an in situ solvothermal method,[76] which suggests that atomic-scale modification of the cavity of C2N is achievable. Therefore, we assume that all the designed M@C2N can be fabricated experimentally via an appropriate method.
3.1.2 N2 Adsorption on M@C2N
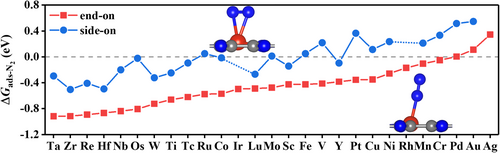
N2 adsorption on the catalyst surface is the first key step of eNRR. We investigated the adsorption of N2 on M@C2N via two possible configurations, namely side-on and end-on configurations, and the calculated adsorption free energies are presented in Figure 2. The optimizations with the initial side-on N2 adsorption structures on Ir@C2N, Rh@C2N, and Ag@C2N lead to the end-on configuration, and so the corresponding side-on adsorption free energies of N2 on the three catalysts are missing in Figure 2. Clearly, N2 molecule prefers to attach to the single metal atom via the end-on configuration for all the considered M@C2N that is consistent with previous theoretical studies for other SACs.[77, 78] This is because there is not only an electronic backdonation from the metal d orbitals into the π* orbital of N2 but also a coordination interaction between the σ orbital of N2 and the metal d orbitals for the end-on adsorbed configuration. It has been reported[79] that the less stable side-on configuration can spontaneously convert to the more stable end-on configuration by overcoming a small dynamic energy barrier, for example, the barrier is only ~0.025 eV for Ni@WS2 system. Therefore, we only consider the end-on configuration in the subsequent eNRR process on M@C2N. The adsorption free energies of N2 in the end-on configuration range from −0.92 eV (on Ta@C2N and Zr@C2N) to 0.34 eV (on Ag@C2N). Ag@C2N and Au@C2N with positive N2 adsorption free energies (0.34 and 0.11 eV, respectively) cannot active N2 sufficiently, and thus, they are not further considered in the following discussion.
3.1.3 eNRR Activity of M@C2N
The eNRR reactions in acid aqueous environment can occur via two possible mechanisms. One is the dissociative mechanism, in which the N2 molecule is dissociated into two isolated N atoms once it interacts with the catalyst surface, and then, the isolated N atoms will be hydrogenated to produce ammonia. The other is the associative mechanism, in which the N2 molecule is firstly activated via the adsorption on the catalyst surface and then hydrogenated. Because of the high kinetic barrier of N2 dissociative mechanism under ambient conditions, we only focus on the associative mechanism in the current study.
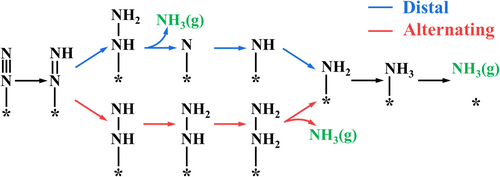
In the associative mechanism, the end-on adsorbed N2 usually goes through the six hydrogenation steps via two different reaction pathways, namely distal and alternating pathways (See Scheme 1). The first hydrogenation step (*NN → *NNH) and the sixth hydrogenation step (*NH2 → *NH3) of these two pathways are the same, and these two steps have been determined as the potential rate-determining step (RDS) for most catalysts.[76, 77, 80] Therefore, to save computational cost, we calculated the free energy changes of the first and sixth hydrogenation steps to single out potential candidates toward efficient eNRR. The obtained free energy changes of the two steps (ΔG*NN→*NNH and ) are marked in Figure 3. The free energy change for the formation of *NNH on Cu@C2N (1.85 eV) is much higher than other M@C2N, and so this value is not shown in Figure 3.
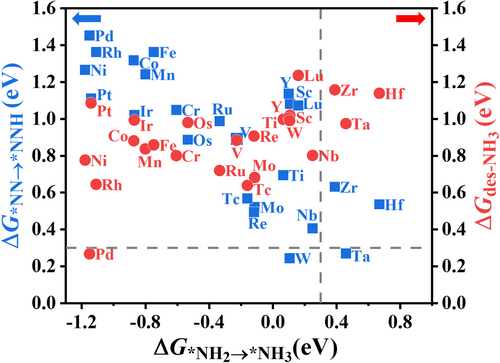
Our computational results show a roughly linear scaling relationship with a negative slope between the ΔG*NN→*NNH and the All considered M@C2N SACs, except for Hf@C2N and Ta@C2N, have a lower value than its corresponding ΔG*NN→*NNH value. So the formation of *NNH is more possible to be the RDS step for these M@C2N with the free energy change (ΔGRDS) ranging from 0.24 eV on W@C2N to 1.85 eV on Cu@C2N, while the sixth hydrogenation steps of N2 on Hf@C2N and Ta@C2N are the potential RDS with the ΔGRDS of 0.67 eV and 0.46 eV, respectively. Figure 3 also indicates that the metals of IVB, VB, and VIB groups have lower ΔGRDS values than the other metal atoms in the same period. If we only consider the two hydrogenation steps, W@C2N is the most promising candidate for catalyzing eNRR (ΔGRDS = 0.24 eV).
3.1.4 NH3 Desorption on M@C2N
Desorption of the produced NH3 from the catalyst surface is another important factor determining the performance of catalysts, because it affects the yield of NH3. The NH3 desorption free energies on M@C2N are also presented in Figure 3. We notice that except for M = Pd, the NH3 desorption free energies from M@C2N surfaces are relatively high ( ≥ 0.64 eV) because of the strong interaction of NH3 with the metal active site of these catalysts. It is difficult to release NH3 from the surface of W@C2N, the most promising candidate for N2 activation and reduction (ΔGRDS = 0.24 eV), due to a high desorption free energy of 0.99 eV. The high energy need for ammonia desorption hinders the next catalytic cycle and thus decreases the yield of NH3. Not surprisingly, although Pd single atoms supported on C2N cannot catalyze well the hydrogenation steps (ΔGRDS = 1.45 eV), they can efficiently promote the release of the produced NH3 from the catalyst surface, similar to the previous observation[63] for Pd single atoms supported on black phosphorus (BP). In particular, Pd@C2N has a quite low NH3 desorption free energy, = 0.27 eV, indicating the rapid NH3 release from the Pd@C2N surface.
Therefore, W and Pd are singled out to construct a hetero-metal diatom catalyst (PdW@C2N) toward high-efficient eNRR by combining the advantages of W@C2N and Pd@C2N. The constructed PdW@C2N with Pd and W as joint metal active centers is expected to exhibit excellent eNRR performance, by the W atom promoting the hydrogenations of N2 into NH3 and the Pd atom functioning for the desorption of NH3. Next, we will evaluate the eNRR performance of PdW@C2N from the perspectives of its stability, N2 activation, mechanism, and selectivity.
3.2 Structure and Stability of PdW@C2N
Considering that the W atom has a stronger binding energy with the C2N ( eV vs. eV on C2N) and a higher diffusion free energy on C2N (4.02 eV for W vs. 1.72 eV for Pd) than the Pd atom does, the more stable W@C2N is used as the substrate to construct the structure of PdW@C2N. As shown in Figure 4a, there are five possible anchoring sites (i.e., a, b, c, d, and e) on W@C2N for the deposition of Pd atom. It is energetically more favorable to anchor the Pd atom to the site a of W@C2N than other sites, and the corresponding binding energy is −3.06 eV (), comparable to the single Pd atom binding energy with the C2N ( = −3.28 eV). In the most stable PdW@C2N structure (Figure 4b), we can see the bonding between the Pd and W atoms, and the W and Pd atoms respectively bond to two N atoms of the six-fold cavity, but the W atom is in the plane of C2N, while the Pd atom is above the plane.
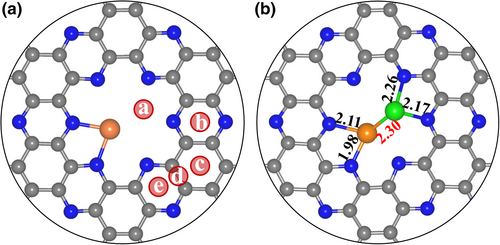
We further examined the thermodynamic stability of PdW@C2N by an ab initio molecular dynamics (AIMD) simulation at 600 K for 10 ps with a time step of 1 fs. As shown in Figure S1, the mean square displacements (MSDs) of all atoms in PdW@C2N keep around 0.25 Å2 during the whole simulation process, with reference to the equilibrium structure. The maximum MSD of the anchored Pd and W atoms is observed at 8703 fs, at which these two metal atoms just rotate a certain angle and do not escape from the original cavity. At the last picosecond, the Pd and W atoms slowly return to their equilibrium positions. Overall, the structure of PdW@C2N is well remained during the simulation, indicating the good long-term stability of the hetero-metal Pd-W pair supported on C2N monolayer. Therefore, we expect that PdW@C2N should be stable enough once synthesized with an appropriate experimental method.
The calculated reaction free energies (at U = 0 V) for the formations of (OH)−PdW−(OH)@C2N, (OH)−PdW=O@C2N, O=PdW=O@ C2N, and (O2)−PdW@C2N are −1.64 eV, −1.94 eV, −2.66 eV, and −1.82 eV, respectively. It means that in the presence of oxygen, these species can be formed spontaneously. Therefore, we suggest to prepare the PdW@C2N in an oxygen-free environment to avoid oxidation.
Under the reducing potential where O2 is unstable, water is the primary oxidant, which may be reduced to produce hydrogen.[45] So we also considered the water adsorption on the surface of PdW@C2N with the implicit solvation model to simulate the real water environment. As shown in Figure S2, H2O molecule is mainly adsorbed on Pd atom of PdW@C2N with an adsorption free energy of −0.30 eV, which is much weaker than the adsorption energy of N2 (−0.76 eV, calculated with the implicit solvation model), and thus, we do not need to worry about the water molecule adsorption blocking the active site of N2.
3.3 N2 Adsorption on PdW@C2N
We considered various possible structures of N2 adsorbed on PdW@C2N as initial guesses and finally located three relatively stable adsorption configurations (namely A, B, and C), which are shown in Figure 5.
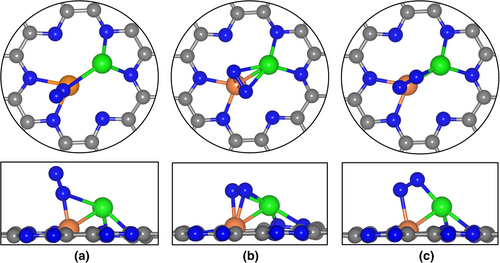
The most stable A is an end-on configuration, in which the proximal N atom is bonded to both Pd and W atoms with the W-N and Pd-N bond lengths being 1.93 Å and 2.65 Å, respectively. The B is a side-on configuration, where the adsorbed N2 molecule lies above the C2N plane, with both two N atoms bonded to both the Pd and W atoms and the N-N bond approximately perpendicular to Pd-W bond. While in the C configuration, the N-N bond of adsorbed N2 molecule is parallel to the Pd-W bond with the two N atoms bonded to the Pd and W atoms, respectively. The N2 adsorption strengths in the three configurations ( = −0.41 eV, −0.27 eV, and −0.12 eV for A, B, and C, respectively) are all between those of Pd@C2N ( = 0 eV) and W@C2N ( = −0.89 eV), indicating that the additional Pd atom weakens the interaction between N2 and the catalyst and leads to moderate N2 activation on PdW@C2N as compared to their monomer counterpart W@C2N. Our Bader charge analyses reveal that the adsorbed N2 molecule gains 0.41 e, 0.79 e, and 0.46 e from PdW@C2N in configurations A, B, and C, respectively. These values are much larger than or comparable to W@C2N (0.39 e for end-on N2; 0.56 e for side-on N2), Pd@C2N (0.16 e), and the ever recommended eNRR catalysts in the literatures, such as Mo@h-BN (0.29 e)[60] and Mo-N1C2 (0.49 e or 0.32 e for the side-on or end-on adsorption).[62] This suggests that PdW@C2N is a good electron donor and can sufficiently activate the inert N≡N triple bond.
To understand better the origin of N2 activation on PdW@C2N, taking the optimal N2 adsorption configuration A as an example, we performed the electronic structure analysis by calculating the projected density of states (PDOSs) shown in Figure 6 and Figures S3-S5.
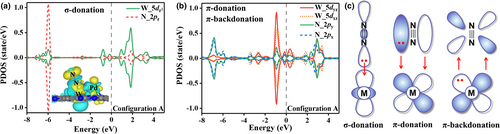
Figure S3 shows that the W 5d orbitals of PdW@C2N are closer to the Fermi energy level than the Pd 4d orbitals, and all the Pd 4d orbitals are basically full-filled. Thus, we expect that the W atom of Pd-W pair will dominantly function for the N2 activation on PdW@C2N. Generally, the N2 molecule can be activated by σ-donation, π-donation, or/and π-backdonation interactions with the active metal atom of catalysts. Figure 6a shows that after the N2 adsorption via the configuration A, the PDOS of N 2pz orbitals overlaps well with the PDOS of W orbital at ~−6 eV. The peak of PDOS of N 2pz orbitals below the Fermi level corresponds to the orbital of adsorbed N2; thus, the overlap of PDOSs near −6 eV indicates that the σ electrons of N2 molecule can be donated to the empty orbital of W atom as illustrated in Figure 6c, which is usually denoted as σ-donation. Similarly, the PDOSs of N 2px/2py orbitals below and above the Fermi level in Figure 6b represent the π bonding and π* antibonding orbitals of adsorbed N2, respectively, and the matching of PDOSs of N 2px/2py orbitals and W 5dxz/5dyz orbitals shown in Figure 6b implies that the 5dxz/5dyz orbitals of W have a strong interaction with both π bonding and π* antibonding orbitals of N2, that is, the π electrons of N2 can be donated to the partially filled W 5dxz/5dyz orbitals, which is denoted as the π-donation, and the π* antibonding orbital of N2 can accept the electrons of W 5dxz/5dyz orbitals, which is denoted as π-backdonation. The π-donation and π-backdonation interactions in the configuration A are also illustrated in Figure 6c. In addition, the two 5dxy/ orbitals of W have a relatively weak interaction with the π orbitals of N2 (Figure S4) by π-donation. We expected that there is only a very weak orbital interaction between Pd and N2, which belongs to the π-backdonation (Figure S4). The strong σ-donation, π-donation, and π-backdonation interactions between the adsorbed N2 molecule and the PdW@C2N in the configuration A account for the strong adsorption free energy of N2 (−0.41 eV) and activation.
In the configurations B and C, N2 is mainly activated by the π-donation and π-backdonation interaction with the catalyst as shown in Figure S5. Due to the absence of σ-donation interaction as compared to the configuration A, the configurations B and C exhibit weaker N2 adsorption energies (−0.27 eV and −0.12 eV).
3.4 eNRR Mechanism on PdW@C2N
3.4.1 Competitive Adsorption of N2 and H on PdW@C2N
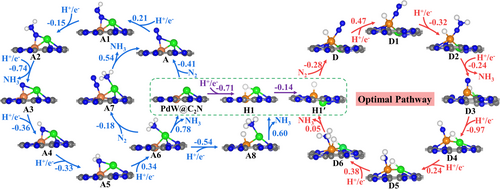
Before exploring in detail the eNRR mechanism, we compared the adsorption free energies of N2 and H on PdW@C2N. As shown in Figure 7, the H atom bonds to both W and Pd atoms to generate H-terminated PdW@C2N (H1), with an adsorption free energy of −0.71 eV, much more negative than that of N2 (−0.41/−0.27/−0.12 eV for configurations A/B/C). It indicates that the active sites will preferentially be occupied by the H atom. Will it hamper the eNRR process by blocking the active sites as we usually recognize? Our further investigation found that the hydrogen-terminated PdW@C2N (H1) can transform spontaneously into a more stable structure H1′ with the free energy decrease by 0.14 eV, in which the W and Pd atoms are slightly above and below the C2N plane, respectively. Such transformation is very easy even from the dynamics perspective, with a barrier of only 0.15 eV (Figure S6a). Then, the H1′ can adsorb one N2 molecule via the end-on configuration to form a H-N2 co-adsorption structure D (Figure 7) with a free energy change (ΔG) of −0.28 eV or adsorb an additional H atom to get a two-H-atoms co-adsorption structure H2 (Figure S6b) with a less negative free energy change of −0.23 eV, indicating that the adsorption selectivity toward N2 is enhanced by the H pre-adsorption. Thereby, next we will comprehensively explore the eNRR mechanism starting from both the N2 adsorption structures (A, B, and C) and H-N2 co-adsorption structure (D), respectively.
3.4.2 Mechanism Starting from the N2 Adsorption Structures on PdW@C2N
Once the N2 molecule is adsorbed on the electrocatalyst surface, it can be fully reduced to ammonia via six hydrogenation steps under a certain electrode potential. To understand the eNRR mechanism on PdW@C2N in detail, we firstly considered all possible pathways of hydrogenation starting from the three relatively stable N2 adsorption configurations, A, B, and C. The calculated free energy changes at zero electrode potential of all the elementary steps along these pathways are shown in Figure 7 and Figure S7, together with the optimized geometries of the involved intermediates.
The first hydrogenation of adsorbed N2 in the configuration A (A→A1) can be easily realized with a small uphill ΔG value of 0.21 eV, which is slightly smaller than that on W@C2N (0.24 eV). Then, it is energetically more favorable to attach the second proton–electron pair to the distal N atom of A1 [ΔG (A1→A2) = −0.15 eV] than to the proximal N atom [ΔG (A1→A2′) = 1.20 eV, see Figure S7a]. We will not consider the further hydrogenations of A2′ because of the high ΔG value of A1→A2′. The subsequent three hydrogenation steps of A2 can be easily achieved with downhill ΔG values of −0.74 eV (A2→A3), −0.36 eV (A3→A4), and −0.33 eV (A4→A5), respectively. Note that the proximal N atom always binds to both the Pd and W atoms during the first five hydrogenation steps. The last hydrogenation step (A5→A6) has a maximum ΔG of 0.34 eV, and the N-species is transferred to the Pd atom in this step. This free energy change of the last hydrogenation step to produce the adsorbed ammonia on PdW@C2N is larger than that on W@C2N ( = 0.10 eV) because the binding of produced NH3 with the Pd atom is weaker than that with the W atom. Overall, the rate-determining step of the pathway starting from A (we will call it A-pathway) is the sixth hydrogenation step with a ΔGRDS value of 0.34 eV, and the corresponding overpotential is 0.18 V.
Similarly, as shown in Figure S7b, the eNRR overpotentials needed for the optimal pathways starting from B and C are 0.33 V and 0.29 V, respectively (more details about these reaction pathways refer to the Supporting Information). Therefore, the A-pathway (A→A1→A2→A3→A4→A5→A6), following the distal mechanism, is energetically the most favorable hydrogenation pathway of N2 adsorbed solely on PdW@C2N.
Next, we considered the NH3 desorption from PdW@C2N. The direct NH3 desorption free energy () from A6 is 0.78 eV, lower than that on W@C2N (0.99 eV) because of the assistance of Pd atom. However, this value is still high. In our previous study[63] for PdNb@BP toward eNRR, we found that the additional N2 adsorption can help to remove the secondly produced NH3. Therefore, we also considered its role in eNRR on PdW@C2N. As shown in Figure 7, the NH3 species mainly interacts with Pd atom in A6, so that the W active center is available for the spontaneous adsorption of an additional N2 via an end-on configuration [ΔG (A6→A7) = −0.18 eV]. Subsequently, A7 releases NH3 with a lower desorption free energy (0.54 eV) and goes back to the configuration A for the next cycle. In this work, we also checked the H adsorption on A6. Actually, the W site of A6 has a stronger adsorption to hydrogen [ΔG (A6→A8) = −0.54 eV]. The H adsorption on W site of A6 also can promote the NH3 desorption from PdW@C2N by decreasing the desorption free energy to 0.60 eV.
Thus, we conclude that if the active sites of PdW@C2N only adsorb one N2 molecule without the pre-adsorption of hydrogen (although it is less possible from the thermodynamic aspect because of the lower adsorption free energy of H atoms on PdW@C2N), the adsorbed N2 molecule can be efficiently reduced with an ultra-low overpotential of 0.18 V through the A-pathway, and then, the formed *NH3 can be desorbed under the assistance of one additional N2 (or H) adsorption with a desorption free energy of 0.54 (or 0.60) eV to ensure a not too bad NH3 yield and catalyst recovery.
3.4.3 Mechanism Starting from the H-N2 Co-adsorption Structure on PdW@C2N
As we presented in Section 3.4.1, from the thermodynamics perspective, the H atom is preferentially adsorbed at the metal active sites of PdW@C2N (H1). After the spontaneous transform of H1 to H1′, the N2 molecule can be co-adsorbed at the W site to generate D in Figure 7. The eNRR process staring from the H-N2 co-adsorption structure (D) (we will call it D-pathway) and the calculated free energy changes (ΔG) at zero electrode potential of involved elementary steps are shown in Figure 7.
The first hydrogenation of adsorbed N2 in D structure to form D1 requires a maximum uphill free energy change of 0.47 eV in all hydrogenation steps of the D-pathway. The subsequent three hydrogenation steps of D1 are exergonic processes with the ΔG values of −0.32 eV (D1→D2), −0.24 eV (D2→D3), and −0.97 eV (D3→D4), respectively. The last two hydrogenation steps (D4→D5 and D5→D6) are endergonic with ΔG values of 0.24 eV and 0.38 eV, respectively. So, the first hydrogenation step is the rate-determining step of the D-pathway, and the corresponding overpotential is 0.31 V.
Note that the co-adsorbed H atom on W atom in the D-pathway would gradually bind to both the W and Pd atoms during the hydrogenation process; meanwhile, the Pd atom is pulled out of the plane of C2N. The co-adsorbed H atom weakens the interaction of the secondly formed NH3 with the W atom, and so the formed NH3 can be easily desorbed with a very small value of 0.05 eV and return to the thermodynamically more stable H1′. It suggests that the H-terminated PdW@C2N functions as an actual working catalyst in the eNRR process.
Although the D-pathway starting from the H-N2 co-adsorption structure on PdW@C2N requires a 0.13 V higher overpotential than the optimal A-pathway starting from the N2 solely adsorbed structure, considering the preferential adsorption of H over N2 on PdW@C2N and the much lower ammonia desorption energy following the D-pathway, we suggest that the eNRR mechanism on PdW@C2N will follow the D-pathway, that is [H1′→D→D1→D2→D3→D4→D5→D6→H1′] with an overpotential of 0.31 V and an NH3 desorption free energy of 0.05 eV.
A very recent study by Liu et al.[81] proposed a hydrogen passivation strategy to protect the active sites of carbon-supported nitrogen coordinated transition metal atoms (M-N-C) catalysts for oxygen reduction reaction, and similar to our discovery, they also observed the enhancement of catalytic activity by the hydrogen-termination of catalysts. It indicates that the PdW@C2N could be pretreated by a similar hydrogen passivation strategy to maintain the performance before use.
3.4.4 Solvent Effect and Ammonia Source
The aqueous solvent environment could influence the eNRR performance of catalysts under the real experimental condition. Therefore, the effect of water solvent on eNRR process on PdW@C2N along the A- and D-pathways was further studied by using an implicit solvation model, a microsolvation model including several explicit water molecules, and a mixed implicit plus explicit model. The way to evaluate the solvent effect on eNRR performance has been utilized previously by Li et al.[45] More calculation details can be found in SI. As shown in Table S3, the calculations in vacuum, with the implicit solvation model, with the microsolvation model, and with the mixed implicit + explicit model, agree with each other in determining the rate-determining step and the optimal mechanism, although they predict different values. They all predict the D-pathway to be the optimal pathway and the first hydrogenation step to be the RDS in the optimal D-pathway, with the calculated eNRR overpotentials of 0.31 V (in vacuum), 0.19 V (with the implicit solvation model), 0.27 V (with the microsolvation model), and 0.24 V (with the mixed implicit + explicit model), respectively. Besides, the NH3 desorption free energies () through the D-pathway obtained with these different treatments also remain consistent, and they are 0.05 eV (in vacuum), 0.19 eV (with the implicit solvation model), 0.10 eV (with the microsolvation model), and 0.08 eV (with the mixed implicit + explicit model), respectively. These results reveal that although the consideration of the solvent effect changes the predicted free energies and the overpotential of the eNRR, it does not alter the potential RDS and mechanism and will not change our conclusion about the eNRR performance obtained in vacuum. Thus, unless otherwise noted, the results shown in this work were obtained using the vacuum model.
Because the C2N support of our catalyst has N atoms, we further examined the possible NH3 formation via the H adsorption onto the lattice N atoms of the electrocatalyst itself. We explored the free energy profiles of the hydrogenation of the lattice N atoms (Nlatt. + 3H+ + 3e− → 3Nlatt.H3) of PdW@C2N and show them in Figure S8) as Li et al.[45] had done. We considered two types of lattice N atom on PdW@C2N (labeled with *Nlatt.1 and *Nlatt.2 in Figure S8). The lattice N atom with the lone-pair electrons can adsorb the first H atom with a free energy change of 0.26 eV to form *Nlatt.1H and of −0.64 eV to form *Nlatt.2H, respectively. Then, the hydrogenation of Nlatt.H to Nlatt.H2 requires a large free energy (0.94 eV for *Nlatt.1H → *Nlatt.1H2 or 1.02 eV for *Nlatt.2H → *Nlatt.2H2). The structure of *Nlatt.H3 is unstable and cannot be located. Therefore, we considered the direct formation of Nlatt.H3(g) via the third hydrogenation step. The third hydrogenation step of *Nlatt.H2 has a negative free energy change of −0.29 eV for *Nlatt.1H2 → Nlatt.1H3(g) or a positive free energy change of 0.22 eV for *Nlatt.2H2 → Nlatt.2H3(g) to directly produce Nlatt.H3(g). Therefore, the hydrogenation of the lattice N atoms to produce NH3 is thermodynamically unfavorable, suggesting that the generated ammonia on the surface of PdW@C2N is mainly from nitrogen gas.
3.5 eNRR Selectivity of PdW@C2N Over HER
Inevitably, the hydrogen evolution reaction (HER) competes fiercely with the eNRR by either the competition of adsorption sites or the consumption of proton–electron pairs. As we mentioned earlier, the PdW@C2N strongly adsorbs the hydrogen atom to generate the H-terminated PdW@C2N (H1) first. Based on the calculated H adsorption free energy (−0.71 eV), we know that it is difficult to occur the HER reaction by hydrogenating the adsorbed H in the H1 configuration into H2 through the Heyrovsky step (*H + H+/e− → H2) because of the large HER overpotential of 0.71 V. The H1 configuration can be spontaneously converted into the more stable H1′ configuration. It is even harder to produce H2 via the H1′, and the N2 molecule can be captured selectively (over H) on the W site of H1′ to form D to initiate the eNRR process. Thus, the H pre-adsorption on PdW@C2N cannot block the active sites of N2, and the overpotential (0.31 V) of eNRR process is much lower than that (0.71 V) of HER on PdW@C2N, indicating the high selectivity of PdW@C2N toward eNRR over HER.
Therefore, we can conclude that the designed heteronuclear diatom catalyst, PdW@C2N, is thermodynamically stable and can achieve both high eNRR activity and good selectivity.
3.6 Comparison of PdW@C2N with W@C2N and W2@C2N
In the end, for comparison, we investigated the entire free energy diagrams of eNRR on the monomer counterpart (W@C2N) and homonuclear counterpart (W2@C2N) of PdW@C2N and show them in Figure S9. Table 1 summarizes the key energetics for the eNRR process on the three catalysts.
| H-PdW@C2Na | PdW@C2N | W@C2N | W2@C2N | |
|---|---|---|---|---|
| ΔGads (H) (eV) | −0.23 | −0.71 | −0.57 | −0.34 |
| ΔGads (N2) (eV) | −0.28 | −0.41 | −0.73 | −0.57 |
| ΔGRDS (eV) | 0.47 | 0.34 | 0.24 | 0.51 |
| (eV) | 0.05 | 0.78 | 0.99 | 0.85 |
| (eV) with aid of H | – | 0.60 | 0.71 | 0.73 |
| (eV) with aid of N2 | – | 0.54 | 0.44 | 0.56 |
| ηeNRR (V) | 0.31 | 0.18 | 0.08 | 0.35 |
- a The eNRR process on the H-terminated PdW@C2N.
The adsorption of N2 is stronger than H atom on W@C2N [ = −0.73 eV vs = −0.57 eV], and so we only considered the eNRR pathways without the pre-adsorption of H atoms. The rate-determining steps in the distal and alternating pathways are the first and the second hydrogenation steps, respectively, with the corresponding free energy changes of 0.24 eV and 0.80 eV. That is, the lowest overpotential of eNRR on W@C2N is only 0.08 V, much smaller than that on PdW@C2N. However, as we presented earlier, it demands a much higher energy ( = 0.99 eV) to desorb directly the formed NH3 from the W@C2N surface. However, with the aid of one H atom or one N2 molecule adsorbed on W site of *NH3 intermediate, the NH3 desorption free energy can be decreased to 0.71 eV or 0.44 eV. These values are still higher than that on PdW@C2N along the optimal D-pathway (0.05 eV). The HER overpotential on W@C2N is 0.57 eV, much higher than the eNRR overpotential, and so the W@C2N has also a good eNRR selectivity. If we comprehensively evaluate the eNRR performance based on the overpotential, the ammonia desorption energy, and the selectivity, the PdW@C2N is slightly superior to the W@C2N.
For some metals M, M2@C2N is easier to be synthesized based on Zhang et al.’ study[55] than M@C2N. We therefore examined the stability of W2@C2N by(−6.12 eV), and similarly, we predicted the higher (or comparable) stability of W2@C2N. The W2@C2N also prefers to adsorb N2 over H [ = −0.57 eV vs = −0.34 eV), and it reduces the adsorbed N2 into NH3 with the maximum uphill free energy change of 0.51 eV. Thus, the overpotential of eNRR on W2@C2N is 0.35 V, higher than those on PdW@C2N and W@C2N. The NH3 desorption from W2@C2N surface is also hard and needs a direct desorption free energy of 0.85 eV, although the desorption free energy can be further reduced to 0.73 eV or 0.56 eV with the assistance of one additional N2 adsorption or a H atom adsorption. In addition, the HER overpotential (0.34 V) on W2@C2N is slightly lower than the eNRR overpotential (0.35 V). Therefore, W2@C2N is inferior to PdW@C2N and W@C2N toward eNRR.
4 Conclusions
In this work, we designed a novel heteronuclear diatom catalyst on C2N monolayer, PdW@C2N, based on the design strategy we proposed previously, and then assessed its potential catalytic performance toward electrocatalytic N2 reduction reaction (eNRR) and explored the eNRR mechanism in depth. In particular, we firstly evaluated the potential catalytic performance of 30 C2N-based transition metal SACs toward eNRR and then singled out the W atom with the best N2 activation ability and the Pd atom beneficial to ammonia desorption to use them as the active centers of heteronuclear diatom catalyst. The AIMD calculation demonstrates the excellent thermodynamic stability of PdW@C2N. We found that PdW@C2N preferentially adsorbs H atom over N2 molecule to form the H-terminated PdW@C2N first, and then, the H-terminated PdW@C2N acts as the actual functioning “catalyst” to selectively adsorb the N2 molecule and promote the subsequent hydrogenations and the desorption of produced ammonia. In the mechanism, the PdW@C2N demonstrates a great eNRR performance with a low overpotential (0.31 V), an ultra-low NH3 desorption free energy (0.05 eV), and a superior selectivity of eNRR over the hydrogen evolution reaction (the HER overpotential is 0.71 eV). We also compared the eNRR performance of PdW@C2N with those of its monomer (W@C2N) and homonuclear diatom (W2@C2N) counterparts and showed its superiority over W@C2N and W2@C2N, which mainly benefits from the pre-adsorption of H atom on the former. We emphasize that the preferential adsorption of H over N2 on the active site may not always hamper the eNRR process, and it also could facilitate the eNRR cycle by accelerating the ammonia desorption without hurting the N2 activation.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (21973053) and the Creative Seed Fund of Shanxi Research Institute for Clean Energy, Tsinghua University.
Conflict of Interest
The authors declare no conflict of interest.




