Shrub encroachment alters the spatial patterns of infiltration
Abstract
Encroachment of open woodlands by shrubs is a global phenomenon associated with marked changes in ecosystem structure and function. We measured sorptivity and steady-state infiltration at two supply potentials under shrubs and grasses and in their interspaces where shrubs were encroaching into grassland. Steady-state infiltration (ponded) and sorptivity were greater at the grassland than the shrubland site, and there was substantially greater infiltration under shrubs (48.2 mm h−1) and grasses (50.0 mm h−1) than the corresponding interspaces (17.0 and 32.3 mm h−1 for shrubland and grassland, respectively). The difference between grasses and their interspaces was substantially less (1.5 times) than that between shrubs and their interspaces (three times). Shrub encroachment also affected the spatial patterns of infiltration. Although the autocorrelation range for shrublands coincided almost exactly with the average distance between shrub canopies (3.5 m), the range for grasslands was three times greater (1.5 m) than the mean grass canopy, indicating a greater connectivity of infiltration in the grasslands than the shrublands. Our study indicates that encroachment by shrubs does not change infiltration under individual plants. Rather, it reduces the interspace infiltration rates significantly, resulting in lower estimated site-level infiltration rates in shrublands. Our research suggests therefore that it is the shrubland interspaces that are the likely drivers of reduced infiltration rates when grasslands are encroached, rather than increase in the total cover of shrubs per se. Management strategies that result in greater retention of grass cover and minimize the level of interspace disturbances are likely to result in increased infiltration. Copyright © 2014 John Wiley & Sons, Ltd.
Introduction
Run-off and infiltration are two fundamental processes responsible for redistributing the precipitation input in drylands (Wang et al., 2012). Soil hydraulic properties affect soil water holding capacity and plant available moisture (Noy-Meir, 1972) and, therefore, plant productivity and diversity. This soil-water–vegetation interaction is most pronounced in resource-limited environments (Le Houérou et al., 1988). In woodlands and mixed savanna systems, infiltration is generally greatest close to the canopies of woody plants because of greater levels of nutrients and organic matter associated with plant litter cycling beneath the canopy (the ‘fertile island’ effect) (Schlesinger et al., 1990; Wilcox et al., 2003a; Ravi et al., 2008). Soils beneath the canopies of woody plants may also have a more extensive distribution of plant roots and a greater number of macropores, biologically-produced pores (Dunkerley, 2000; Colloff et al., 2010). These macropores create a positive feedback on infiltration (Reid et al., 1999; Bhark and Small, 2003). Increases in the cover and density of woody plants, therefore, are likely to have substantial impacts on macropore-driven water flow in these systems (Turnbull et al., 2008).
Over the past 150 years, large areas of open semi-arid woodlands and savanna worldwide have become encroached by woody plants (Archer, 2010; Eldridge et al., 2011). Although some paleoecological studies from South Africa suggest a progressive recovery in grassland extent (Hoffman et al., 1995), an overwhelming number of studies indicate that encroachment or thickening is a more common phenomenon. This encroachment or thickening is a phenomenon of global significance because of its wide-ranging effects on ecological processes as well as ecosystem goods and services. The impacts include altered spatial distribution of soil nutrients, reduced grass cover and therefore pastoral production, altered habitat for plants and animals and changes in infiltration and soil water redistribution (Schlesinger et al., 1996; Bhark and Small, 2003; Neff et al., 2005). Many of these changes reinforce the persistence of shrublands at the expense of grasslands by altering the flow of resources from source (inter-canopy) to sink (shrub hummocks), in many cases leading to ecosystem degradation, particularly when combined with overgrazing by domestic livestock (Schlesinger et al., 1996).
A number of common themes are thought to account for encroachment. These include interactions among factors such as overgrazing, recovery from anthropogenic disturbance, increases in CO2 and N deposition, reduced fire frequency and long-term climate change (Segoli et al., 2008; Archer, 2010; Eldridge et al., 2011; Daryanto et al., 2013). Although the causes of encroachment are relatively well-known, its effects on ecosystem processes are less clearly defined. Recent studies have questioned the view that encroachment is synonymous with degradation, with reports of positive or neutral effects of encroachment on a range of ecosystem response variables (Eldridge et al., 2011). For example, a reassessment of ten response variables associated with ecohydrology in shrub-encroached drylands soils globally (e.g. volumetric soil moisture, depth to wetting front and steady-state infiltration) indicates significant positive effects of encroachment on infiltration (Fisher's exact test: P = 0.003, n = 99; data from Eldridge et al., 2012). Counteracting this, however, is the perception that, although infiltration might increase at the level of individual woody (shrubs and trees) plants, the composite, ecosystem-level effect of woody encroachment may be a decline in water yield due to a combination of increased interception by plants and greater evapotranspiration in woodlands than in grasslands.
We contend that in order to manage grasslands and open woodlands encroached by woody plants, we need to better understand the apparent conundrum of widely reported positive effects of shrubs at the individual plant scale with the apparent negative view of dense patches of woody plants at site, ecosystem or landscape scales. A number of authors have noted the scale dependency of hydrological processes in drylands (e.g. Reid et al., 1999; Wilcox et al., 2003a, 2003b; Ludwig et al., 2005) and demonstrated substantially greater infiltration at larger spatial scales than would be accounted for by a direct up-scaling from the plant scale. This scale dependency is thought to relate to the connectivity of highly conductive patches such as coarse woody debris mounds, grass tussocks and soil hummocks (Wilcox et al., 2003b). The extent to which site-level infiltration changes with encroachment is thought to depend largely on the characteristics of the interspaces in relation to these conductive patches, their sinuosity (Ludwig and Tongway, 1995) and whether they are dominated by herbaceous material or bare soil.
In this study, we examine differences in the magnitude and spatial distribution of infiltration across a grassland-shrubland encroachment front where the grassland has been subjected to ongoing encroachment by shrubs for more than 50 years. We achieve this by measuring a large number of sampling locations at a grassland site into which shrubs are encroaching, to determine the effects of encroachment on infiltration at both the plant (shrub, grass) and the site scale and to understand the quantitative relationships between the spatial distribution of infiltration and plant size, litter and cryptogam cover. The context of our system is one where rainfall is low and evenly distributed throughout the year, differing from previous studies of more mesic systems where rainfall is predominantly driven by summer monsoons (e.g., Wilcox et al., 2003a; Turnbull et al., 2010). In many parts of eastern Australia, shrub patches are associated with interspaces that are bare or degraded and with high levels of run-off (Muñoz-Robles et al., 2010), particularly where current grazing rates are high. Our system therefore is characterized by inter-canopy areas that are dominated by large patches of bare soil and biological soil crusts, a consequence of recovery from previous degradation events in the first part of the 20th century (Booth et al., 1996; Muñoz-Robles et al., 2010).
We measured infiltration using permeameters, allowing us to tease apart the mechanisms responsible for any differences in relation to shrubs and/or grasses and their interspaces. Disc permeameters also allowed us to vary the supply pressures to the soil to create (1) a negative pressure (under tension), which restricted water flow to matrix or micro-pores, and (2) a positive pressure (ponding), which allowed us to determine infiltration over the full range of pore sizes. In addition, the disc permeameters allow measurements to be made of different stages of infiltration: (i) sorptivity, the early phase of infiltration during which water enters the soil in response to gradients in water potential influenced by soil dryness and capillary (pore) structure (White, 1988), and (ii) steady-state infiltration, when the flow rate, which is governed by capillarity, gravity and the area of the disc permeameter in contact with the soil, stabilizes over time. Infiltration theory suggests that the ratio of sorptivity under ponding (+10 mm pressure) to sorptivity under tension (−40 mm pressure) provides an index of the relative contribution of macropores to total water flow (White, 1988). This is an extremely informative measure, as this enables us to determine whether changes in macroporosity (Bouma, 1992) are responsible for potential differences between our two vegetation types or in relation to distance from individual plants.
We expected that infiltration would be greater under shrub canopies and adjacent to perennial grass tussocks than in their respective interspaces and hypothesized that any canopy effects would wane with increasing distance from the canopy. We also predicted that site levels of infiltration would be unaffected by encroachment, largely because a more sparsely distributed pattern of shrubs, with less connected litter cover in the shrublands, would compensate for the greater number of closely spaced grasses in the grassland.
Methods
Study site
The study was conducted at Yathong Nature Reserve, 140 km south-west of Cobar in western New South Wales, Australia (145°35′E, 32°56′S). Although the Reserve has not been grazed by domestic livestock since 1977, it currently carries large populations of kangaroos (Macropus spp.), European rabbits (Oryctolagus cuniculus) and feral goats (Capra hircus).
The study site focussed on two areas typical of an encroachment gradient: (1) the grassland community ahead of the encroachment front, which is dominated by grasses (9.6% basal cover) and their interspaces (87.4%) and sparse shrubs (1.5%), and (2) a dense shrubland behind the front, which is dominated by a high cover of shrubs (37.5%) and their interspaces (58.8%) and sparse grass cover (2.2%). Tree cover is low (1.5%) and constant across the encroachment gradient. The exact age of the shrubs is unknown, but on the basis of comparison with shrubs of known age from similar environments, we believe that they germinated during the prolonged La Niña rainfall events in 1953 and, more recently, 1973–1974. The exact causal mechanisms underlying widespread shrub recruitment across eastern Australia are unknown but probably relate to a long history of overgrazing by both livestock and rabbits, resulting in reduced grass cover and therefore little competition with grass seedlings, combined with a low frequency of fire and, hence, little large-scale control of episodic recruitment events (Booth et al., 1996; Noble, 1997). Our shrubland was dominated by turpentine (Eremophila sturtii) and emu bush (Eremophila longifolia), with individual shrubs spaced at intervals ranging from 5 to 10 m and separated by interspaces with a sparse cover of vascular plants but an extensive cover of biological soil crusts dominated by lichens and mosses (Eldridge and Greene, 1994). The grassland into which the shrubs were encroaching was dominated by the perennial bunchgrasses Aristida jerichoensis, Austrostipa scabra, Austrodanthonia caespitosa and Monochather subparadoxus. Grass tussocks were about 40 cm high and had an average projected foliage diameter of 48 cm. The grass interspaces were characterized by litter and assorted biological soil crusts. Shrublands at Yathong tended to be occupied by large populations of kangaroos (Macropus spp.) and feral goats (C. hircus). Thus, strong interactions between herbivores and shrubs have probably lead to the persistence of the encroached state by maintaining low levels of plant cover in the shrub interspaces.
The study site was located within the extensive colluvial and alluvial plains of Taringa Landsystem, which is characterized by level to slightly undulating erosional slopes and plains (slopes <2%) with poorly defined drainage lines (Walker, 1991). The soils have been classified as deep calcareous loams (Typic Haplargids; Soil Survey Staff, 2010), with surface textures ranging from loams to clay loams. Soil pH averages 6.7 (standard deviation = 0.53), electrical conductivity 0.32–0.36 dS m−1, organic carbon 0.87% at 10 cm to 0.59% at 40 cm, and surface soil aggregates are moderately stable (37%, >2.0 mm; Eldridge and Greene, 1994). The mean maximum temperature for January is 33.1 °C, and the mean minimum temperature is 18.2 °C. The mean January rainfall is 35.5 mm, and the average annual rainfall is 384 mm (Eldridge and Greene, 1994).
Measurements of soil hydrological properties and vegetation cover
We established a 100-m-long transect in both the grassland and shrubland and randomly generated 100 locations within each vegetation community. Distances between adjacent locations varied from 0.5 to 3.6 m (grassland) and 0.5 to 4.6 m (shrubland). The smallest interval of 0.5 m was considered to be the closest that two CSIRO disc permeameters (20 cm in diameter) could be run side-by-side without violating the independence of the measurements. Because of the 0.5 m resolution in permeameter spacing, any variance appearing at a spatial scale smaller than 50 cm would not be captured by the semivariogram models discussed in the succeeding text. For each location, we assessed the cover of litter, bare soil and biocrusts and measured the distance to the nearest grass butt or shrub trunk. Locations beneath the canopy of shrubs or adjacent to grass tussocks were classified as vegetated, whereas other locations were classified as open.
We measured both sorptivity (mm h−0.5) and steady-state infiltration (mm h−1) at the 200 locations using disc permeameters at two supply potentials: −40 mm tension, which measures flow only through matrix pores, and +10 mm tension, which measures flow through both matrix pores and macropores (Perroux and White, 1988). At each of the 200 locations, we placed the two permeameters about 40 cm apart, perpendicular to the direction of the transect. The permeameter under tension (−40 mm tension) was placed on a thin bed of sand to provide satisfactory surface contact. The ponded permeameter (+10 mm tension) was placed on a steel ring and sealed to support a pond of water. The permeameters were run for approximately 20 min by which time steady-state had been achieved. At each supply potential, sorptivity was calculated according to the method of Cook and Broeren (1994), and steady-state infiltration was calculated according to White (1988). The main aim of our study was to determine intrinsic differences in infiltration capacity between an extant grassland and an area of grassland being encroached by shrubs. The saturated (ponded) permeameter tests we made provide information on saturated hydraulic conductivity, which is independent of antecedent soil moisture condition, thus providing us with a meaningful comparison between different microsites within grassland and shrubland. Any litter or organic material present on the surface was retained prior to measurements. We estimated site-level values of steady-state infiltration by measuring the relative cover of grasses, shrubs and their respective interspaces within six 200-m2 plots (50 m by 4 m belt transects) placed within the grassland and shrubland.
Geostatistical calculations
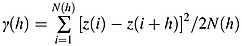 (1)
(1)For patterned data, the semivariogram first rises from a comparison of neighbouring samples that are similar and autocorrelated and then reaches an asymptote, namely, the sill (C0 + C), suggesting the distance beyond which samples are independent. Nugget variance (C0) is the variance that occurs at a scale finer than field sampling. If a large-scale trend in the distribution is found, there is no local pattern within the sampling scale, and therefore, the semivariogram is linear (Schlesinger et al., 1996).
Parameters derived from the model were used to quantify two key aspects of patchiness in a variable distribution: (i) the magnitude of spatial dependence (i.e. the degree to which patches are differentiated from the surrounding area by their distinct, within-patch homogeneity) and (ii) the mean diameter of those patches. The magnitude of spatial structure was obtained using the index of C/(C0 + C). A greater proportion of the total sample is spatially structured if the index approaches 1. The mean diameter of patches and the arrangement of patches across the plot are determined by the distance separating sampling points at which semivariance reaches an asymptote or the autocorrelation range (A0).
Data analysis
For both transects, descriptive statistics (i.e. mean, median, standard deviation and coefficient of variation) were calculated to indicate the overall variability for each observed variable (i.e. litter and biocrust cover). A correlation matrix for those variables was also calculated using the modified t-test (passage software; http://www.passagesoftware.net), which corrects the degrees of freedom based on the amount of autocorrelation in the data (Wang et al., 2007).
In the present study, semivariograms were modelled using gs+ software version 9. There are several commonly used semivariogram models. In most cases, however, semivariograms fitted well with spherical models, which has been proven useful in the interpretation of two-dimensional spatial data (e.g. Wang et al., 2007, 2009). We used the spherical model to compare the observed variables under different treatments. This model was chosen because of its suitable fit with the distribution of those variables based on two criteria: high r2 and fitted model shape (e.g. Wang et al., 2007, 2009).
We compared isotropic and corresponding anisotropic semivariograms at 0°, 45°, 90° and 135° and did not find any significant directional pattern. Therefore, isotropic variograms were used in all analyses. We also ensured that all data had a normal distribution, which is a prerequisite in hypothesis testing using geostatistic theory, by conducting the normal score transformation prior to analysis (Rossi et al., 1993).
We used non-parametric analysis of variance (Kruskal–Wallis test) to test for differences in hydrological responses between open and vegetated locations for shrubland and grassland communities separately and for open areas only, between grassland and shrubland. Relationships between infiltration rates and distance to shrub or grass were examined using exponential decay models in sigmaplot (Systat Software, Inc. CA, USA). We used structural equation modelling (SEM) to test the relationships among litter cover, biocrust cover, sorptivity and steady-state infiltration under both tension and ponding, for grassland and shrubland separately. SEM allowed us to examine the direct and indirect effects of each variable on the response variable and estimate the strength of these effects (Grace, 2006). We used a maximum likelihood-based goodness-of-fit test to assess the degree of fit between observed and predicted covariance structures. Because our models were saturated, i.e. all possible pathways between all variables were accounted for, we could not test the significance of our models. The relative strengths of the pathways are based on the amount of variance explained in our three response variables (Grace, 2006). All SEM models were performed in amos 20 (SPSS Inc. 2009) software.
Results
Canopy effects on infiltration
Relationships between distance from shrub or grass canopy, and sorptivity and steady-state infiltration under ponding were best described by negative exponential curves (Figure 1). There was about a four-fold greater decline in sorptivity and steady-state infiltration in the grassland than in the shrubland, as indicated by the exponent of the negative exponential curves (Figure 1). In the shrubland, distance from the plant explained 18% and 22% of the variance in sorptivity and steady-state infiltration, respectively. However, the relationship was much stronger (sorptivity: R2 = 0.32; steady-state infiltration: R2 = 0.36) for distances up to 2 m from the plant stems. At distances >2 m from the shrubs, sorptivity and steady-state infiltration were largely independent of distance. For grasslands, the relationships between distance from grass tussocks and sorptivity/steady-state infiltration were similar to that of shrubs (R2 = 0.16 and 0.18 for sorptivity and steady-state infiltration, respectively). Grassland sorptivity and steady-state infiltration were independent of distance after 0.5 m, which was the maximum distance we recorded for grass tussocks and is equivalent to the average foliage diameter of grasses (0.48 m).
Infiltration among microsites
In the shrubland, we recorded 2.6 times greater ponded sorptivity (Kruskal–Wallis H = 39.8, df = 1, P < 0.001) and 2.9 times greater ponded steady-state infiltration (H = 40.2, df = 1, P < 0.001) under the shrubs than in the open (Table 1). The trend was the same in the grassland, where both sorptivity (H = 12.0, df = 1, P = 0.001) and steady-state infiltration (H = 12.7, df = 1, P < 0.001) were 1.6 times greater adjacent to the grasses than in the open. Similarly, the macropore ratio was 2.6 times greater under shrubs (H = 37.6, df = 1, P < 0.001) and 1.8 times greater under grasses (H = 11.7, df = 1, P = 0.001) than in the open, in the shrubland and grassland, respectively. Thus, the difference between grass and open was smaller than that between shrubs and open, with values from shrub areas being more than twice the values in open areas. We detected no differences in neither sorptivity nor steady-state infiltration under tension between shrub and open or between grass and open microsites (P > 0.21). When we compared the open sites between grassland and shrubland (Table 2), we detected approximately twice the levels of sorptivity (H = 29.3) and steady-state infiltration (H = 30.1) under ponded conditions (P < 0.001) in the grassland than in the shrubland and a similar trend for the macropore ratio (H = 21.2) but no effects under tension (P > 0.13).
| Parameter | Shrubland | Grassland | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Shrub | Open | P-value | Grass | Open | P-value | |||||
| Mean | SE | Mean | SE | Mean | SE | Mean | SE | |||
| Sorptivity under tension (−40 mm) | 7.08a | 0.57 | 7.52a | 0.34 | 0.21 | 6.02a | 0.51 | 7.94a | 0.94 | 0.15 |
| Infiltration under tension (−40 mm)# | 1.10a | 0.10 | 1.10a | 0.10 | 0.72 | 1.20a | 0.10 | 3.53a | 2.46 | 0.62 |
| Sorptivity under ponding (+10 mm) | 186.61a | 19.60 | 72.91b | 7.93 | <0.001 | 206.44a | 19.73 | 131.48b | 12.39 | 0.001 |
| Infiltration under ponding (+10 mm)# | 48.21a | 4.82 | 16.97b | 2.10 | <0.001 | 50.00a | 5.08 | 32.30b | 2.93 | <0.001 |
| Macropore ratio | 28.7a | 2.63 | 10.9b | 1.21 | <0.001 | 42.2a | 5.89 | 23.4b | 2.73 | 0.001 |
- SE, standard error.
- Different superscript letters indicate a significant difference between the same microsite at a given level of habitat at P < 0.05. The unit of sorptivity is mm h−0.5, and the unit of steady-state infiltration is mm h−1.
- # Infiltration under steady state.
| Response variable | Grassland | Shrubland | P-value | ||
|---|---|---|---|---|---|
| Mean | SE | Mean | SE | ||
| Sorptivity under tension (−40 mm) | 7.9a | 0.86 | 7.5a | 0.34 | 0.65 |
| Infiltration under tension (−40 mm)# | 3.5a | 2.30 | 1.1a | 0.10 | 0.29 |
| Sorptivity under ponding (+10 mm) | 131.0a | 11.00 | 72.9b | 7.93 | <0.001 |
| Infiltration under ponding (+10 mm)# | 32.3a | 2.72 | 17.0b | 2.10 | <0.001 |
| Macropore ratio | 23.4a | 2.50 | 10.9b | 1.21 | <0.001 |
- SE, standard error.
- Different superscript lowercase letters indicate a significant difference between the two habitats at P < 0.05. The unit of sorptivity is mm h−0.5, and the unit of steady-state infiltration is mm h−1.
- # Infiltration under steady state.
Spatial patterns in infiltration
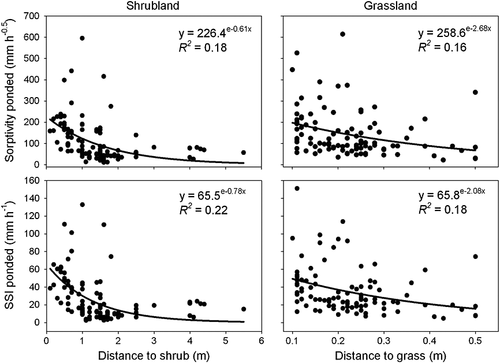
The autocorrelation range for sorptivity, steady-state infiltration under ponding and the macropore index in the shrubland ranged from 3.4 to 4.4 m, which corresponded to the average distance between the centre of individual shrubs (3.78 m; Figure 2b, Table 3). The autocorrelation range under tension, however, was substantially larger (5.9–9.5 m for sorptivity and steady-state infiltration, respectively), which was mainly independent of average inter-shrub distance. For the grassland, however, values of the autocorrelation range for sorptivity, steady-state infiltration and macropore ratio under ponding were substantially smaller (1.4–1.6 m), which was equal to approximately 2.5 times the average distance between individual grass butts. The autocorrelation range for litter cover was substantially greater in the grassland (62.8 m) than in the shrubland (5.1 m; Table 3), which highlights the greater connectivity among plant patches in the grassland than in the shrubland. At the same time, the shrubland was characterized by a substantially greater autocorrelation distance for cryptogram cover (16.5 m) than the grassland (3.4 m).
| Response variables | Shrubland | Grassland | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| C0 | C + C0 | A0 | C/(C + C0) | R2 | C0 | C + C0 | A0 | C/(C + C0) | R2 | |
| Sorptivity under tension | 0.04 | 0.22 | 5.9 | 0.69 | 0.19 | 0.05 | 0.27 | 4.4 | 0.82 | 0.16 |
| Steady-state infiltration under tension | 0.12 | 0.30 | 9.5 | 0.59 | 0.27 | 0.11 | 0.43 | 17.4 | 0.75 | 0.22 |
| Sorptivity under ponding | 0.17 | 0.69 | 3.7 | 0.75 | 0.21 | 0.02 | 0.45 | 1.4 | 0.95 | 0.12 |
| Steady-state infiltration under ponding | 0.10 | 0.91 | 3.5 | 0.89 | 0.21 | 0.01 | 0.47 | 1.5 | 0.97 | 0.11 |
| Macropore ratio | 0.24 | 0.85 | 4.4 | 0.72 | 0.19 | 0.01 | 0.81 | 1.6 | 1.00 | 0.16 |
| Shrub and grass occurrence | 0.02 | 0.24 | 2.8 | 0.90 | 0.25 | 0.01 | 0.17 | 0.9 | 0.91 | 0.02 |
| Biocrust cover (%) | 0.25 | 0.51 | 16.5 | 0.50 | 0.24 | 0.01 | 0.48 | 3.4 | 0.99 | 0.20 |
| Litter cover (%) | 0.08 | 0.32 | 5.1 | 0.81 | 0.27 | 0.11 | 0.55 | 62.8 | 0.80 | 0.81 |
Grasslands and shrublands as a system
Averaged over the open and grass/shrub patches, and based on the corresponding cover, water flow under ponded (sorptivity and steady-state infiltration) conditions was greater in the grasslands than in the shrublands (P < 0.018), but there were no differences for measurements under tension (P > 0.28). The estimated site-level infiltrations were 33.0 and 28.4 mm h−1 in the grasslands and shrublands, respectively. The results indicate a 14% decline in steady-state infiltration with a conversion from grassland to shrubland.
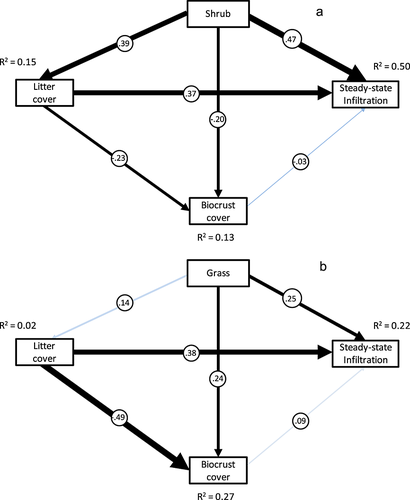
The structural equation models were reasonably successful at predicting infiltration in the shrublands (R2 = 0.50) and the grasslands (R2 = 0.22; Figure 3a and b). For the shrublands, shrub cover had strong positive effects on steady-state infiltration and litter cover but a suppressive effect on biocrust cover (Figure 3a). For the grasslands, however, the effect of grasses was substantially diminished, although litter cover had a stronger suppressive effect on biocrust cover. Surprisingly, there was no effect of biocrust cover on steady-state infiltration at either shrubland or grassland (Table 4).
| Response variable | Plant to infiltration | Biocrust to infiltration | Litter to infiltration | Model R2 |
|---|---|---|---|---|
| Shrubland | ||||
| Sorptivity under ponding | −0.49*** | 0.06 | 0.29*** | 0.46 |
| Infiltration under pondinga | 0.47*** | −0.03 | 0.37*** | 0.50 |
| Sorptivity under tension | −0.22 | −0.29** | 0.03 | 0.10 |
| Infiltration under tensiona | 0.01 | −0.30** | −0.12 | 0.09 |
| Grassland | ||||
| Sorptivity under ponding | 0.26** | 0.12 | 0.36*** | 0.21 |
| Infiltration under pondinga | 0.25** | 0.09 | 0.38 | 0.22 |
| Sorptivity under tension | −0.11 | −0.14 | −0.11 | 0.04 |
| Infiltration under tensiona | −0.02 | −0.09 | −0.06 | 0.01 |
- The model structure is identical to that presented in Figure 3 but with different path coefficient estimates. The three columns list the path coefficients corresponding to three paths in the models. R2 is proportion of variance explained in the response variable listed on the left. All models are saturated, so the χ2 goodness-of-fit test cannot be calculated.
- a Infiltration under steady state.
- *** P < 0.001.
- ** P < 0.01.
Discussion
Consistent with a large number of studies worldwide (e.g. Bhark and Small, 2003; Casmereiro et al., 2003; Wilcox et al., 2003a, 2003b; Eldridge and Freudenberger, 2005; Eldridge et al., 2010; Pierson et al., 2008), we recorded greater depths of ponded infiltration adjacent to both shrubs and grasses than in their interspaces. Our data are also consistent with field observations of the rapid declines in infiltration with increasing distance from the stems of Dodonaea and Eremophila shrubs in shrub-encroached woodland (Daryanto et al., 2013). Overall, our results support the notion that the hydrological impact of encroaching shrubs will depend on the relative proportion of canopy (both grass and shrub) and interspace (Reid et al., 1999; Pierson et al., 2008; Petersen and Stringham, 2008).
Mechanisms accounting for greater water flow under shrubs and grasses
We attribute the greater infiltration adjacent to shrubs and grasses to the greater number of macropores (biopores >0.84 mm in diameter), as indicated by our macropore ratios. Support for a macropore-driven mechanism is the observation that no differences in water flow were recorded when macropores were prevented from conducting water, i.e. when infiltration was measured under a negative tension. The macropore ratio was consistently larger for shrub and grass soils than for interspace soils. The autocorrelation range of the macropore ratio and infiltration rates were similar (Table 3), indicating that the spatial distribution of the macropores and therefore the ratio play an important role in the spatial distribution of infiltration rates.
Macropore ratios exceeding ten have been reported for similar encroached woodland on Haplargid soils in eastern Australia (Eldridge, 1994). Large macropore ratios suggest that the preferential pathways for water movement are voids and channels associated with plant roots and root channels close to shrubs and grasses, as well as nest entrances and burrows constructed by surface-active arthropods such as ants and termites.
Encroachment alters the amount and spatial patterns of infiltration
Infiltration rates in the grassland interspaces were greater than the shrub interspaces, indicating that the effects of encroachment are largely tied to how shrubs influence the spatial distribution of interspaces and therefore their capacity to infiltrate water. Infiltration rates under individual shrubs were comparable with those under individual grasses. Overall, therefore, we found higher rates of infiltration and sorptivity (under ponded conditions) in the grassland than in the shrubland. Our research therefore points to activity associated with shrub interspaces as the likely driver of reduced rates of infiltration when grasslands are encroached, rather than increase in the total cover of shrubs per se.
Litter cover appears to play an important role, given the marked differences in their cover between shrub and grass interspaces. We did not remove litter prior to running our infiltration measurements as greater litter cover could enhance infiltration rates beneath the canopies of both grasses and shrubs as litter has higher porosity than soil. Apart from direct effects, litter could also alter the density and size of macropores by moderating soil moisture, soil surface temperature and therefore maintain soil moisture in the surface layers (Whitford, 2002), as well as increasing water stable aggregation (Pressland and Lehane, 1982). The combination of more stable temperature and greater surface moisture provided by litter cover would also be expected to have positive feedback on the activity of subterranean and surface-active termites (Whitford, 2002), which are the main macropore-producing agents in these soils (Eldridge, 1994). Litter also influences overland flow processes by forming micro-dams and terraces (Eddy et al., 1999), extending the period over which water ponds on the surface, contributing to the discontinuity of run-off, potentially increasing the hydraulic head (Boeken and Orenstein, 2001) and reducing soil particle detachment (Wainwright et al., 1999).
Shrub encroachment changed not only the total amount of infiltration but also the spatial patterns of infiltration and the spatial arrangement of unvegetated interspaces. Our spatial analysis of infiltration rates revealed two interesting effects. Firstly, the range (A0) of steady-state infiltration under ponding was markedly different between grassland (A0 = 1.5 m) and shrubland (A0 = 3.5 m). Secondly, there were marked differences in the area of influence of each plant in relation to their range. For example, the statistical range (A0) for individual grasses and shrubs was very different. The range for grasses indicates that grasses have an effect on infiltration far beyond the edge of their canopy, whereas the shrub effect is limited to the area directly beneath the canopy (Figure 2c and d). Thus, even though infiltration rates for individual grasses were comparable with those of shrubs, estimated site-level rates are likely to be higher because of the greater cover of grasses than shrubs. We attribute the greater estimated site-level infiltration in the grassland to the greater connectivity of grasses. The autocorrelation range for grass occurrence was 0.9 m, indicating that the grasses themselves were unconnected. However, litter was highly connected in the grassland (autocorrelation range is 62.8 m), and such connectivity reduced the area of bare soil and thus enhanced the maintenance of higher infiltration rates at the ecosystem level in the grassland. Litter is known to have a substantial effect on soil and ecological processes (Facelli and Pickett, 1991) and may account for a large proportion of the variance in infiltration (Meeuwig, 1970).
Given that the positive effect of litter on infiltration was similar for shrubs (path coefficient = 0.37) and grasses (0.38), litter alone cannot explain differences in the canopy influence between grasses and shrubs. Part of the difference, which we are unable to account for, may be idiosyncratic soil effects such as subtle changes in texture and structure (Young et al., 2004) or differences in microtopography, which would be expected to alter the connectivity of sites of enhanced infiltration (Turnbull et al., 2010). These idiosyncratic soil effects may also explain the observed variance in steady-state infiltration rates along the distance away from shrub/grass centre. The similar autocorrelation range of litter cover (5 m) and shrub canopy size (3.4 m) is consistent with the notion of a fertile island phenomenon of higher levels of resources under the canopies of woody species (e.g. Bhark and Small, 2003; Casmereiro et al., 2003; Wang et al., 2009, 2012). The current results show that, at least in our system, which has probably been shaped by more than 150 years of grazing, the fertile island effect also applies to infiltration (A0 = 3.5 m), with shrub encroachment localizing infiltration and inhibiting rates in the interspaces. We acknowledge, however, that our effect is probably also due to grazing history and management, with recent research showing that the fertile island effect may be due more to grazing than to the singular effect of woody plants per se (Allington and Valone, 2013).
Water availability is a major driver of vegetation dynamics in arid and semi-arid regions (Wang et al., 2012), and shrub encroachment could potentially alter ecosystem water balances. Although our current study only quantifies the amount and spatial pattern of infiltration rates, our point-scale-based measurements may not easily be translated into landscape-scale phenomena. Our results offer some insights into hydrological processes such us run-off at larger scales. The site has a low slope (1–2%), and substantial run-off is generated on these soils when rainfall intensity exceeds about 30–40 mm h−1 over a period of 5–7 min, the time taken for run-off to commence (Eldridge and Koen, 1993; Eldridge et al., 2013). We have not measured run-off within shrub patches at Yathong, but run-off studies on similar encroached soils about 150 km north of Yathong indicate that run-off coefficients under 35 mm h−1 of simulated rainfall are about 40% for shrub interspaces (Muñoz-Robles et al., 2010), which is similar to our own data. It appears therefore, that although shrubs themselves have levels of infiltration not dissimilar to grasses, their interspaces have substantially reduced infiltration (and thus substantially greater levels of run-off), which potentially leads to reduced soil water storage and negative effects of water movement downslope.
We acknowledge that there are limitations when up-scaling point-scale methods to estimate ecosystem-level infiltration. For example, we did not quantify differences in soil texture nor microtopography between sub-canopy soils. Although we would expect a long transect of 100 m to capture any location variation in soil texture, the lack of such information may affect the estimation of site-level infiltration rates. We note that grazing could also have a strong mediating effect on infiltration. For example, a study of the effects of shrubs and grazing on ecosystem functions in a similar system indicates that grazing can dampen the positive effect of shrubs on infiltrability, a surrogate for infiltration (Eldridge et al., 2013). In fact, the effects of encroachment are very difficult to separate from those of historic grazing because encroachment and the reduced interspace infiltration may both be associated with grazing. There is a need therefore to more adequately address the relative effects of grazing and shrub encroachment on these and other functions within the semi-arid woodlands.
Conclusions
In our study, both grasses and shrubs had substantial positive effects on water flow. Steady-state infiltration was greater under shrubs and grasses than in the interspaces, and the clearly defined gradient of decline in infiltration with increasing distance from the plants was stronger for grasses than shrubs. Furthermore, our data on spatial patterning indicate a greater connectivity among grass patches than shrub patches, suggesting that although the shrub effect on infiltration is largely restricted to the environment of the canopy, grass effects extend to neighbouring grass tussocks. The higher connectivity in grasslands explains why infiltration rates were higher under individual shrubs but lower at the ecosystem level in the shrublands. Overall, our study suggests that encroachment of grasslands by shrubs will result in substantial changes in the volume of water infiltrating into the soil and in the spatial arrangement of infiltration. Management practices should concentrate on retaining patches of water-capturing vegetation in the interspaces, such as perennial tussock grasses, in order to maximize the capture of water and increase infiltration.
Acknowledgements
We thank Gabby Radnan for assistance with field work and the NSW National Parks and Wildlife Service for allowing us to undertake research at Yathong Nature Reserve. We are grateful to Brad Wilcox for providing insightful comments on a draft manuscript and drawing our attention to previously published literature on the connectivity of dryland infiltration.




